Обобщенный метод наименьших квадратов
1. Обобщенный метод наименьших квадратов
Вопрос об эффективности линейной несмещенной
оценки вектора β для
обобщенной регрессионной модели решается с помощью следующей теоремы.
Теорема Айткена. В классе линейных несмещенных
оценок вектора β для
обобщенной регрессионной модели оценка
b* = (X'Ωˉ№X)ˉ№X'Ωˉ№Y
имеет наименьшую ковариационную матрицу.
Доказательство. Убедимся в том, что оценка b*
является несмещенной. Учитывая обобщенную линейную модель множественной
регрессии (Y = X
β
+ ε), представим ее в
виде:
b* = (X'Ωˉ№X)ˉ№X'Ωˉ№(Xβ
+ ε) = (X'Ωˉ№X)ˉ№(X'Ωˉ№X)β
+ (X'Ωˉ№X)ˉ№X'Ωˉ№ε
= β
+ (X'Ωˉ№X)ˉ№X'Ωˉ№ε.
Математическое ожидание оценки b*,
т.е. М(b*) = β,
ибо М(ε) = 0, т.е.
оценка b* есть несмещенная
оценка β.
Для доказательства оптимальных свойств оценки b*
преобразуем исходные данные - матрицу X,
вектор Y и возмущение ε
к виду, при котором выполнены требования классической модели регрессии.
Из матричной алгебры известно, что всякая
невырожденная симметричная (n*n)
матрица А допускает представление в виде А=РР', где Р - некоторая невырожденная
(n*n)
матрица.
Поэтому существует такая невырожденная (n*n)
матрица Р, что
Ω = РР'
(представление матрицы Ω
в виде Ω = РР' не
единственно, но для нас это не имеет значения).
Учитывая свойства обратных квадратных матриц, т.
е.
(AВ)
ˉ№= Вˉ№Аˉ№ и (Р') ˉ№ = (Pˉ№)'
, это означает, что
Ωˉ№=(P
ˉ№)'
P ˉ№
Заметим, что если обе части равенства (умножить
слева на матрицу PЇ№, а справа
- на матрицу (Р') Ї1=(РЇ1)', то в произведении получим
единичную матрицу.
Действительно,
РЇ1 Ω
(Р') ˉ№ = РЇ1 РР')(Р') ˉ№ =(Р ˉ№Р)Р'(Р') ˉ№ =Е
п.т.е.РЇ1 Ω
(P ˉ№)'
= Еп.
Теперь, умножив обе части обобщенной
регрессионной модели
Y=X
β
+ ε на матрицу РЇ1
слева, получим
Y.=Х. β
+ ε.,
Где
У = РЇ1 Y,
Х.=РЇ1 X, ε.=РЇ1
ε.
Убедимся в том, что модель Y=Х
β
+ ε удовлетворяет всем
требованиям классической линейной модели множественной регрессии:
М(ε.)
=М(РЇ1 ε)=РЇ1
М (ε) = 0, ибо М(ε)
= 0;
Σε.
= М(ε. ε
'.) = М [(РЇ1 ε
)( РЇ1 ε')
'] =М [РЇ1 ε
ε'(РЇ1 )
']=
= РЇ1 М(ε
ε ')( РЇ1)'=
РЇ1 Ω(РЇ1
) '= Еп
r(X)=p
+ 1 < n (так как матрица Р
- невырожденная).
Следовательно, на основании теоремы
Гаусса-Маркова наиболее эффективной оценкой в классе всех линейных несмещенных
оценок является оценка
Ь* =(Х. 'Х.) Ї1 X.'Y.
Возвращаясь к исходным наблюдениям X и Y
и учитывая Ωˉ№=( P
ˉ№)'
Pˉ№, получим
b*=[(PЇ1X)
c(PЇ1X)]
Ї1(PЇ1 X)'PЇ1Y
=
=[X
'(PЇ1 )'PЇ1X]
Ї1X '(PЇ1
) ' PЇ1Y=(X
'Ω Ї1X)
Ї1 X 'Ω
Ї1Y,
т. е. выражение b*
= (X'Ωˉ№X)ˉ№X'Ωˉ№Y,
что и требовалось доказать.
Нетрудно проверить, что в случае классической
модели, т. е. при выполнении предпосылки Σε
= Ω = σ2Еп
, оценка обобщенного метода наименьших квадратов b*
(b* = (X'Ωˉ№X)ˉ№X'Ωˉ№Y)
совпадает с оценкой «обычного» метода b.
При выполнении предпосылки 5 о нормальном законе
распределения вектора возмущений ε
можно убедиться в том, что оценка b*
обобщенного метода наименьших квадратов для параметра β
при известной матрице Ω
совпадает с его оценкой, полученной методом максимального правдоподобия.
Оценка b*
= (X 'X)
Ї1 X'Y
является точкой минимума по b
остаточной суммы квадратов
S = 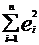 . = e. 'e.
=(Y.-X.b) '(Y.-X.b).
. = e. 'e.
=(Y.-X.b) '(Y.-X.b).
Переходя к исходным наблюдениям,
S = [PЇ1
(Y-Xb]'[PЇ1
(Y-Xb)]
= = (Y- Xb)
' (PЇ1 ) ' PЇ1
(Y - Xb)
= (Y- Xb)
'
ΩЇ1
(Y- Xb)
=е' ΩЇ1е,
т. е. оценка b*
обобщенного метода наименьших квадратов может быть определена как точка
минимума обобщенного критерия е' ΩЇ1е
.
Следует отметить, что для обобщенной
регрессионной модели, в отличие от классической, коэффициент детерминации
вычисленный по формуле
RІ=1- 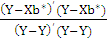
(где b*
- оценка обобщенного метода наименьших квадратов (b*
= (X'Ωˉ№X)ˉ№X'Ωˉ№Y)),
не является удовлетворительной мерой качества модели. В общем случае R2
может выходить даже за пределы интервала [0;1], а добавление (удаление)
объясняющей переменной не обязательно приводит к его увеличению (уменьшению).
Причина состоит в том, что разложение общей
суммы квадратов Q на
составляющие Qr и Qe
выводилось в предположении наличия свободного члена в обобщенной модели. Однако,
если в исходной модели содержится свободный член, то мы не можем гарантировать
его присутствие в преобразованной модели (Y
= Х β
+ ε.). Поэтому
коэффициент детерминации R2
в обобщенной модели может использоваться лишь как весьма приближенная
характеристика качества модели.
В заключение отметим, что для применения
обобщенного метода наименьших квадратов необходимо знание ковариационной
матрицы вектора возмущений Ω,
что встречается крайне редко в практике эконометрического моделирования. Если
же считать все п(п+1)/2 элементов симметричной ковариационной матрицы Ω
неизвестными параметрами обобщенной модели (в дополнении к (p+1)
параметрам βi),
то общее число параметров значительно превысит число наблюдений п, что сделает
оценку этих параметров неразрешимой задачей. Поэтому для практической
реализации обобщенного метода наименьших квадратов необходимо вводить
дополнительные условия на структуру матрицы Ω.
Так мы приходим к практически реализуемому (или доступному) обобщенному методу
наименьших квадратов.
. Разложение временного ряда в ряд Фурье
Преобразование Фурье
<#"560156.files/image003.gif">
Отметим, что разные источники могут
давать определения, отличающиеся от приведенного выбором коэффициента перед
интегралом, а также знака «-» в показателе экспоненты. Все свойства в этом
случае будут аналогичны, хотя вид каких-то формул может измениться.
Кроме этого, существуют
разнообразные обобщения этого понятия, которые будут приведены ниже.
Свойства
Хотя формула, задающая
преобразование Фурье, имеет ясный смысл только для функций 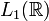 ,
преобразование Фурье может быть определено и для более широкого класса функций,
и даже обобщённых функций
<#"560156.files/image005.gif">
,
преобразование Фурье может быть определено и для более широкого класса функций,
и даже обобщённых функций
<#"560156.files/image005.gif">
· Справедливо равенство Парсеваля
<#"560156.files/image006.gif">, то
преобразование Фурье сохраняет L2-норму:
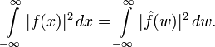
Это свойство позволяет по
непрерывности распространить определение преобразования Фурье на всё
пространство 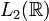 <#"560156.files/image009.gif">.
<#"560156.files/image009.gif">.
· Формула обращения:
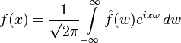
справедлива, если интеграл в правой части имеет
смысл. В частности, это верно, если функция f является достаточно гладкой. Если
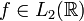 ,
то формула также верна, поскольку равенство Парсеваля позволяет придать
интегралу в правой части смысл с помощью предельного перехода.
,
то формула также верна, поскольку равенство Парсеваля позволяет придать
интегралу в правой части смысл с помощью предельного перехода.
Эта формула объясняет физический смысл
преобразования Фурье: правая часть - (бесконечная) сумма гармонических
колебаний eiωx
с частотами ω, амплитудами 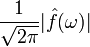 и
фазовыми сдвигами
и
фазовыми сдвигами 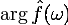 соответственно.
соответственно.
· Теорема о свертке: если 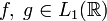 ,
тогда
,
тогда
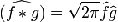 , где
, где
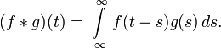
Эта формула может быть распространена и на
случай обобщённых функций.
· Преобразование Фурье и дифференцирование. Если 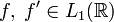 ,
то
,
то
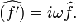
Из этой формулы легко выводится формула для n-й
производной:
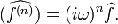
Формулы верны и в случае обобщённых функций.
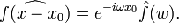
Эта и предыдущая формула являются
частными случаями теоремы о свёртке, так как сдвиг по аргументу - это свёртка
со сдвинутой дельта-функцией
<#"560156.files/image020.gif">
· Преобразование Фурье обобщённых
функций. Преобразование Фурье можно определить для широкого класса обобщённых
функций. Определим вначале пространство гладких быстро убывающих функций
(пространство Шварца <#"560156.files/image021.gif">
Ключевым свойством этого
пространства является то, что это инвариантное подпространство
<#"560156.files/image022.gif">. Это некоторое
подпространство в пространстве всех обобщённых функций
<#"560156.files/image023.gif">её
преобразованием Фурье называется обобщённая функция 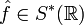 ,
действующая на основные функции по правилу
,
действующая на основные функции по правилу

Например, вычислим преобразование
Фурье дельта-функции
<#"560156.files/image026.gif">
Таким образом, преобразованием Фурье
дельта-функции является константа 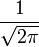 .
.
Применения преобразования Фурье
Преобразование Фурье используется во
многих областях науки - в физике
<#"560156.files/image028.gif">, определяется
формулой
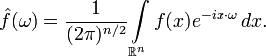
Здесь ω и x -
векторы пространства  ,
, 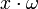 - их
скалярное произведение
<#"560156.files/image031.gif">
- их
скалярное произведение
<#"560156.files/image031.gif">
Эта формула может быть
интерпретирована как разложение функции f в линейную комбинацию (суперпозицию
<#"560156.files/image032.gif">с
амплитудами 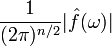 , частотами ω и фазовыми
сдвигами
, частотами ω и фазовыми
сдвигами 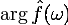 соответственно.
Как и прежде, в разных источниках определения многомерного преобразования Фурье
могут отличаться выбором константы перед интегралом.
соответственно.
Как и прежде, в разных источниках определения многомерного преобразования Фурье
могут отличаться выбором константы перед интегралом.
Замечание относительно области
задания преобразования Фурье и его основные свойства остаются справедливыми и в
многомерном случае, со следующими уточнениями:
· Взятие частных производных под действием
преобразования Фурье превращается в умножение на одноимённую координату:
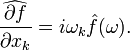
· Изменяется константа в теореме о свёртке:

· Преобразование Фурье и сжатие координат:
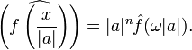
· Более обще, если 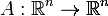 - обратимое
линейное отображение
<#"560156.files/image038.gif">
- обратимое
линейное отображение
<#"560156.files/image038.gif">
Ряды Фурье
Непрерывное преобразование само
фактически является обобщением более ранней идеи рядов Фурье
<#"560156.files/image039.gif">
Разложение в ряд Фурье применимо
также к функциям, заданным на ограниченных промежутках, поскольку такие функции
могут быть периодически продолжены на всю прямую.
Ряд Фурье является частным случаем
преобразования Фурье, если последнее понимать в смысле обобщённых функций
<#"560156.files/image040.gif">
Иными словами, преобразование Фурье
периодической функции представляет собой сумму точечных нагрузок в целых
точках, и равно нулю вне их.
Дискретное преобразование Фурье
Дискретное преобразование Фурье -
преобразование конечных последовательностей (комплексных) чисел, которое, как и
в непрерывном случае, превращает свёртку
<#"560156.files/image041.gif"> - последовательность комплексных
чисел. Рассмотрим многочлен
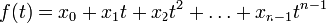
Выберем какие-нибудь n точек на
комплексной плоскости  . Теперь
многочлену f(t) мы можем сопоставить новый набор из n чисел:
. Теперь
многочлену f(t) мы можем сопоставить новый набор из n чисел:
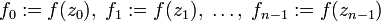
Заметим, что это преобразование
обратимо: для любого набора чисел 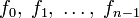 существует единственный многочлен
f(t) степени не выше n − 1 с такими значениями в
существует единственный многочлен
f(t) степени не выше n − 1 с такими значениями в 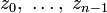 соответственно(см.
Интерполяция <#"560156.files/image047.gif">.
соответственно(см.
Интерполяция <#"560156.files/image047.gif">.
Такой выбор продиктован тем, что в
этом случае обратное преобразование принимает простую форму, а также тем, что
вычисление преобразования Фурье может быть выполнено особенно быстро
<#"560156.files/image048.gif">
где 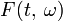 даёт (вообще говоря несколько
искажённое) распределение частот части оригинального сигнала f(t) в окрестности
времени t.
даёт (вообще говоря несколько
искажённое) распределение частот части оригинального сигнала f(t) в окрестности
времени t.
Классическое преобразование Фурье
имеет дело со спектром <#"560156.files/image050.gif">, зависят от соглашения, какая форма
определения для Фурье преобразования использовалась прежде (хотя в общем виде
соотношения, конечно, правильны).
|
Функция
|
Образ
|
Примечания
|
|
1
|
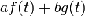
|
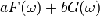
|
Линейность
|
|
2
|
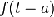
|
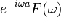
|
Запаздывание
|
|
3
|

|
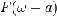
|
Частотный
сдвиг
|
|
4
|
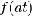
|
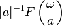
|
Если
a большое, то f(at) сосредоточена около 0 и 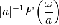 становится
плоским становится
плоским
|
|
5
|
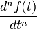
|
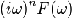
|
Свойство
преобразования Фурье от n-й производной
|
|
6
|
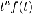
|
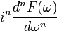
|
Это
обращение правила 5
|
|
7
|
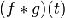
|
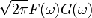
|
Запись
f * g означает свёртку
<#"560156.files/image066.gif">
|
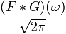
|
Это
обращение 7
|
|
9
|
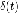
|
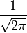
|
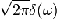
|
Обращение
9.
|
|
11
|
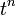
|
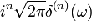
|
Здесь,
n - натуральное число
<#"560156.files/image074.gif">
|

|
Следствие
3 и 10
|
|
13
|
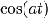
|
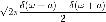
|
Следствие
1 и 12 с использованием формулы Эйлера
<#"560156.files/image078.gif">
|
|
14
|
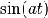
|
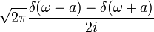
|
Также
из 1 и 12
|
|
15
|
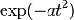
|
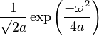
|
Показывает,
что функция Гаусса
<#"560156.files/image083.gif">
|
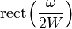
|
Прямоугольная
функция - идеальный фильтр низких частот <#"560156.files/image085.gif">
|
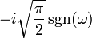
|
Здесь
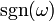 -
sign функция
<#"560156.files/image088.gif"> -
sign функция
<#"560156.files/image088.gif">
|
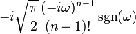
|
Обобщение
17
|
|
19
|
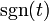
|
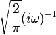
|
Обращение
17
|
|
20
|
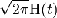
|
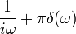
|
Здесь
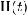 -
функция Хевисайда
<http://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%A5%D0%B5%D0%B2%D0%B8%D1%81%D0%B0%D0%B9%D0%B4%D0%B0>.
Следует из правил 1 и 19 -
функция Хевисайда
<http://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%A5%D0%B5%D0%B2%D0%B8%D1%81%D0%B0%D0%B9%D0%B4%D0%B0>.
Следует из правил 1 и 19
|
Список использованных источников и литературы
1. Афонский
А.А., Дьяконов В.П. Цифровые анализаторы спектра, сигналов и логики. Под ред.
проф. В.П. Дьяконова - М: СОЛОН-Пресс, 2009. - С. 248.
2. Дьяконов
В.П. MATLAB 6.5 SP1/7.0/7.0 SP1 + Simulink 5/6/ Обработка сигналов и
проектирование фильтров - М: СОЛОН-Пресс, 2005. - С. 676.
. Сергиенко
А.Б. Цифровая обработка сигналов - 2-е. - Спб: Питер, 2006. - С. 751.
4. М.А.
Павлейно, В.М. Ромаданов Спектральные преобразования в MatLab
<http://ru.wikipedia.org/wiki/MatLab> - СПб, 2007. - С. 160.