Множественная регрессия и пошаговая регрессия
Министерство образования и науки РФ
Государственное образовательное учреждение высшего профессионального
образования
Ульяновский Государственный Технический Университет
Типовой расчет
по дисциплине «Эконометрика»
Тема:
Множественная регрессия и пошаговая регрессия
Вариант № 16
Выполнил:
студент группы БАз-21
Гафурова Л.Ф.
Ульяновск 2011
Содержание:
1.Задание
.Таблица экспериментальных данных
. Результаты
.1 Множественная регрессия
.1.1 Результаты
.1.2 Оценка качества
.1.3 Диагностика соблюдения условия РА-МНК
.2 Пошаговая регрессия
.2.1 Результаты
.2.2 Оценка качества
.2.3 Диагностика соблюдения условия РА-МНК
Выводы
Графики
Список литературы:
1.Задание
1.
Применить
процедуры MR и ПР с Ро
2.
Оценить качество
постулируемой (MR) и оптимальной
(ПР) моделей по F и R- критериям.
3.
Проверить
соблюдение условий РА-МНК для постулируемой и оптимальной модели.
4.
Сделать общие
выводы по анализу.
2.Таблица
экспериментальных данных
По данным, представленным в таблице, изучается
зависимость общего объема кредитования населения города на покупку жилья у от
переменных:
Х1 - среднедневной душевой доход, руб.
Х2 - доля расходов на покупку продовольственных
товаров в общих расходах
ХЗ - доля общих среднедневных расходов в среднедневных
доходах одного работающего
Х4 - средняя цена одного кв. метра площади, тыс. руб.;
Х5 - среднегодовая процентная ставка по ипотечным
кредитам, %
|
№
|
Y Общий объём кредитования
населения города на покупку жилья, млн. руб.
|
X1Среднедневной душевой
доход, руб.
|
X2 Доля расходов на покупку
продовольственных товаров в общих расходах
|
X3 Доля общих среднедневных
расходов в среднедневных доходах одного работающего
|
X4 Средняя цена одного кв.
метра площади, тыс. руб.
|
X5 Среднегодовая процентная
ставка по ипотечным кредитам, %
|
|
1.
|
88,60
|
217,00
|
0,76
|
0,95
|
47,30
|
17,80
|
|
2.
|
801,30
|
604,00
|
0,84
|
0,53
|
37,50
|
13,80
|
|
3.
|
489,60
|
339,00
|
0,74
|
0,93
|
41,60
|
16,00
|
|
4.
|
660,30
|
429,00
|
0,65
|
0,71
|
41,90
|
12,90
|
|
5.
|
356,70
|
587,00
|
0,54
|
0,61
|
44,60
|
15,00
|
|
6.
|
430,80
|
604,00
|
0,65
|
0,74
|
47,20
|
14,00
|
|
7.
|
78,60
|
166,00
|
0,68
|
0,68
|
36,10
|
18,00
|
|
8.
|
88,60
|
127,00
|
0,85
|
0,78
|
36,50
|
19,00
|
|
9.
|
902,60
|
715,00
|
0,89
|
0,63
|
36,30
|
11,50
|
|
10.
|
150,80
|
219,00
|
0,58
|
0,91
|
36,60
|
14,00
|
|
11.
|
220,70
|
507,00
|
0,41
|
0,88
|
31,10
|
11,00
|
|
12.
|
336,40
|
668,00
|
0,47
|
0,92
|
47,30
|
18,00
|
|
13.
|
208,60
|
319,00
|
0,71
|
0,70
|
37,30
|
18,00
|
|
14.
|
989,60
|
357,00
|
0,83
|
0,58
|
57,80
|
11,00
|
|
15.
|
178,60
|
258,00
|
0,62
|
0,98
|
37,50
|
17,90
|
|
16.
|
502,60
|
339,00
|
0,85
|
0,72
|
40,00
|
14,00
|
|
17.
|
499,50
|
361,00
|
0,81
|
0,69
|
51,60
|
13,00
|
|
18.
|
178,50
|
208,00
|
0,65
|
0,96
|
41,90
|
13,80
|
|
19.
|
477,80
|
329,00
|
0,36
|
0,62
|
43,40
|
11,50
|
|
20.
|
889,60
|
730,00
|
0,38
|
0,62
|
44,60
|
13,90
|
|
21.
|
656,70
|
507,00
|
0,38
|
0,63
|
45,30
|
14,00
|
|
22.
|
660,30
|
587,00
|
0,52
|
0,55
|
47,20
|
13,30
|
|
23.
|
1030,80
|
994,00
|
0,32
|
0,63
|
69,30
|
12,00
|
|
24.
|
800,50
|
604,00
|
0,48
|
0,74
|
51,40
|
13,50
|
|
25.
|
301,60
|
468,00
|
0,51
|
0,87
|
52,80
|
15,90
|
|
26.
|
623,30
|
914,00
|
0,39
|
0,38
|
44,60
|
12,80
|
|
27.
|
526,70
|
585,00
|
0,70
|
0,70
|
48,30
|
11,30
|
|
28.
|
450,80
|
568,00
|
0,65
|
0,79
|
37,80
|
15,80
|
|
29.
|
589,60
|
439,00
|
0,58
|
0,71
|
41,90
|
14,00
|
|
30.
|
778,60
|
628,00
|
0,48
|
0,85
|
44,60
|
13,30
|
|
31.
|
1078,50
|
767,00
|
0,41
|
0,42
|
57,20
|
13,30
|
|
32.
|
689,60
|
994,00
|
0,41
|
0,58
|
52,80
|
14,00
|
|
33.
|
360,30
|
304,00
|
0,54
|
0,71
|
36,10
|
19,30
|
|
34.
|
1130,80
|
987,00
|
0,68
|
0,62
|
67,10
|
12,00
|
|
35.
|
856,50
|
639,00
|
0,36
|
0,83
|
45,30
|
12,50
|
|
36.
|
801,30
|
604,00
|
0,84
|
0,62
|
37,50
|
13,80
|
|
37.
|
356,70
|
587,00
|
0,54
|
0,79
|
44,60
|
15,00
|
|
38.
|
78,60
|
209,00
|
0,68
|
0,78
|
36,10
|
18,00
|
|
39.
|
902,60
|
258,00
|
0,89
|
0,98
|
36,30
|
11,50
|
|
40.
|
150,80
|
208,00
|
0,58
|
0,68
|
36,60
|
14,00
|
|
41.
|
220,70
|
404,00
|
0,41
|
0,88
|
31,10
|
14,00
|
|
42.
|
989,60
|
868,00
|
0,83
|
0,58
|
57,80
|
13,80
|
|
43.
|
499,50
|
528,00
|
0,81
|
0,69
|
51,60
|
11,50
|
|
44.
|
656,70
|
507,00
|
0,38
|
0,63
|
13,50
|
|
45.
|
1030,80
|
1094,00
|
0,22
|
0,53
|
69,30
|
11,30
|
|
46.
|
800,50
|
604,00
|
0,48
|
0,74
|
51,40
|
13,30
|
|
47.
|
450,80
|
568,00
|
0,65
|
0,79
|
37,80
|
12,00
|
|
48.
|
778,60
|
628,00
|
0,36
|
0,62
|
44,60
|
13,80
|
|
49.
|
689,60
|
994,00
|
0,32
|
0,63
|
41,90
|
14,00
|
|
50.
|
360,30
|
304,00
|
0,39
|
0,70
|
36,10
|
19,30
|
|
51.
|
1130,80
|
908,00
|
0,41
|
0,62
|
36,30
|
12,00
|
|
52.
|
856,50
|
639,00
|
0,84
|
0,68
|
37,30
|
13,80
|
|
53.
|
660,30
|
429,00
|
0,74
|
0,71
|
43,40
|
15,00
|
|
54.
|
430,80
|
639,00
|
0,89
|
0,74
|
69,30
|
19,00
|
|
55.
|
88,60
|
266,00
|
0,81
|
0,78
|
41,90
|
18,00
|
|
56.
|
902,60
|
619,00
|
0,69
|
0,93
|
67,10
|
17,90
|
|
57.
|
989,60
|
994,00
|
0,83
|
0,78
|
44,60
|
11,50
|
|
58.
|
178,60
|
294,00
|
0,92
|
0,98
|
31,10
|
17,90
|
|
59.
|
477,80
|
639,00
|
0,36
|
0,62
|
43,40
|
11,50
|
|
60.
|
889,60
|
730,00
|
0,38
|
0,63
|
44,60
|
13,90
|
3. Результаты
Решение данного типового расчета осуществлялось с
использованием пакета программ статистической обработки данных STATISTICA.
.1Множественная
регрессия
.1.1
Результаты
Зададим зависимую переменную Y и независимые X1,
Х2, Х3, Х4, Х5 Итоги анализа с использованием пакета STATISTICA
Результаты множ. регрессии
Зав.перем.:Y Множест. R =
,82291525 F = 22,65616= ,67718950 сс = 5,54
Число набл.: 60 скоррект.R2= ,64729964 p = ,000000
Стандартная ошибка оценки:184,39683277
Своб.член: 608,02662453 Ст.ошибка: 273,7725 t( 54) = 2,2209 p =
,0306бета=,501 X2 бета=,153 X3 бета=-,12бета=,166 X5 бета=-,32
(выделены значимые бета)
Программа выделяет значимые регрессоры. Значимыми оказались X1 и Х5.
Объем выборки, среднее стандартное отклонение:
|
Means
|
Std.Dev.
|
N
|
|
X1
|
543,1667
|
244,6487
|
60
|
|
X2
|
0,5988
|
0,1909
|
60
|
|
X3
|
0,7210
|
0,1375
|
60
|
|
X4
|
44,9467
|
9,5387
|
60
|
|
X5
|
14,3400
|
2,4282
|
60
|
|
Y
|
573,9450
|
310,4921
|
60
|
Стандартное отклонение показывает вариацию признака
относительно среднего значения.
Матрица корреляций:
|
X1
|
X2
|
X3
|
X4
|
X5
|
Y
|
|
X1
|
1,000000
|
-0,382598
|
-0,524580
|
0,529433
|
-0,477591
|
0,742958
|
|
X2
|
-0,382598
|
1,000000
|
0,285537
|
-0,129108
|
0,216740
|
-0,161846
|
|
X3
|
-0,524580
|
0,285537
|
1,000000
|
-0,285167
|
0,372517
|
-0,500947
|
|
X4
|
0,529433
|
-0,129108
|
-0,285167
|
1,000000
|
-0,167995
|
0,497819
|
|
X5
|
-0,477591
|
0,216740
|
0,372517
|
-0,167995
|
1,000000
|
-0,594804
|
|
Y
|
0,742958
|
-0,195242
|
-0,500947
|
0,497819
|
-0,602422
|
1,000000
|
Матрица корреляций показывает значение парных
коэффициентов корреляции между откликом и факторами и межфакторной корреляции.
Парные коэффициенты корреляции rx1x2, rx1x3, rx1x4, rx1x5 значительно отличаются от нуля, значит
присутствует мультиколлинеарность.
Дисперсионный анализ:
|
Sums of
|
df
|
Mean
|
F
|
p-level
|
|
Regress.
|
3851796
|
5
|
770359,1
|
22,65616
|
0,000000
|
|
Residual
|
1836118
|
54
|
34002,2
|
|
|
|
Total
|
5687914
|
|
|
|
|
Дисперсионный анализ - статистический метод,
позволяющий анализировать влияние различных факторов (признаков) на исследуемую
(зависимую) переменную. Так как F =
22,65616- значение статистики, р = 0- вероятность слишком мала, чтобы поверить
в истинность гипотезы Н0 об отсутствии влияния факторов. Вывод: факторы X1, Х2, Х3, Х4, Х5 влияют на
переменную У.
Регрессионная сумма:
|
Beta
|
Std.Err.
|
B
|
Std.Err.
|
t(54)
|
p-level
|
|
Intercept
|
|
|
608,02662
|
273,77249
|
2,22092
|
0,03057
|
|
X1
|
0,50127
|
0,11467
|
0,63617
|
0,14553
|
4,37136
|
0,00006
|
|
X2
|
0,15334
|
0,08457
|
249,35156
|
137,52001
|
1,81320
|
0,07536
|
|
X3
|
-0,11624
|
0,09261
|
-262,50298
|
209,12788
|
-1,25523
|
0,21480
|
|
X4
|
0,16574
|
0,09218
|
5,39506
|
3,00037
|
1,79813
|
0,07775
|
|
X5
|
-0,31749
|
0,08982
|
-40,59804
|
11,48574
|
-3,53465
|
0,00085
|
В столбце Beta показаны стандартизованные коэффициенты регрессии, а в столбце В -
нестандартизованные.
Стандартизированные коэффициенты Beta позволяют провести ранжирование
предикторов по степени их влияния на отклик. Из таблицы следует, что предикторы
можно проранжировать по степени влияния на отклик в следующем порядке:X1, X5, X4, X2, X3 В этой таблице немаловажное значение имеет p-level - показатель, находящийся в убывающей зависимости от
надежности результата. Более высокий p-level соответствует более низкому уровню
доверия к найденной в выборке зависимости между переменными. P-level не должен превышать 0,05. В нашем случае
удовлетворяют условию регрессоры Х1 и Х5. Метод можно улучшить, исключив
незначимые факторы. Искомая модель имеет вид:
=608,02662+0,63617X1+249,35156 X2-262,50298X3+5,39506X4-40,59804X5
Статистика Дарбина - Уотсона:
|
Durbin-
|
Serial
|
|
Estimate
|
1,950929
|
0,007937
|
Статистика Дарбина-Уотсона имеет небольшое значение
(1,950929) при умеренной сериальной корреляции (0,007937). Это свидетельствует
о некоторой зависимости наблюдений, следовательно, можно говорить о
недостаточной устойчивости некоторых значений коэффициентов регрессии, а значит
о невысокой адекватности модели изучаемому процессу.
3.1.2 Оценка
качества
Так как фактическое значение критерия Фишера больше,
чем табличное, то необходимо сделать вывод о значимости модели уравнения
регрессии, исследуемая зависимая переменная хорошо описывается переменными X1 и Х5. Из приведенных результатов
анализа следует, что зависимость между откликом и предикторами высокая (0,7<R=0,82291525<0,9). Свободный член
является статистически значим (p=0,03057<0,05).
.1.3 Диагностика
соблюдения условия РА-МНК
Проверим соблюдение основных предположений РА
<2.1> - <5.2>.
Соблюдение предположений <1.1> - <1.4>
экспериментатор старается обеспечить при организации эксперимента.
<2.1> В случае с множественной регрессией модель
избыточна, т.к. для регрессоров Х2, ХЗ, Х4 р-level превышает уровень значимости = 0,05, не превышает
только для Х1, Х5.
<2.2> Специальных признаков нарушения
<2.2> не существует. Косвенными признаками могут быть признаки нарушения
предположения <3.1>, а именно, значимые коэффициенты парной корреляции.
<3.1> Нарушение этого предположения трактуется
как явление мультиколлинеарности. Наиболее часто мультиколлинеарность
обнаруживается по коэффициентам парной корреляции ХУ матрицы R.
статистический регрессионный выборка
отклонение
|
X1
|
X2
|
X3
|
X4
|
X5
|
Y
|
|
X1
|
1,000000
|
-0,382598
|
-0,524580
|
0,529433
|
-0,477591
|
0,742958
|
|
X2
|
-0,382598
|
1,000000
|
0,285537
|
-0,129108
|
0,216740
|
-0,161846
|
|
X3
|
-0,524580
|
0,285537
|
1,000000
|
-0,285167
|
0,372517
|
-0,500947
|
|
X4
|
0,529433
|
-0,129108
|
-0,285167
|
1,000000
|
-0,167995
|
0,497819
|
|
X5
|
-0,477591
|
0,216740
|
0,372517
|
-0,167995
|
1,000000
|
-0,594804
|
|
Y
|
0,742958
|
-0,195242
|
-0,500947
|
0,497819
|
-0,602422
|
1,000000
|
Парные коэффициенты корреляции rx1x2, rx1x3, rx1x4, rx1x5 значительно отличаются от нуля, значит присутствует
мультиколлинеарность.
<3.2> О нарушении условия неслучайности rij можно судить по косвенному признаку
- резкому различию между внутренней и внешней точности прогноза.
<4.1> Обычно нарушение предположения об
аддитивности е происходит при переходе от нелинейной по b модели (внутренне линейной) к
линейной. В данном примере мы имеем дело с линейной моделью.
<4.2> Ошибки e, распределены нормально, что видно из графиков: за пределами
полосы Зσ точек нет.
<4.3> Условие М[e], = 0, не требует особого внимания при наличии b0 в модели.
<4.4> Как видно из графиков, условие
однородности наблюдений не нарушается.
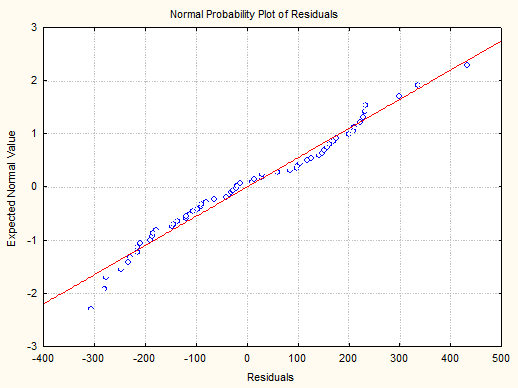
<4.5>
Авторегрессия положительна, т.к. D находится в интервале 0-2:
|
Durbin-
|
Serial
|
|
Estimate
|
1,950929
|
0,007937
|
<5.1> Основным признаком нарушения условия о
точной идентификации является несоблюдение условия <3.1>. Формальным
признаком является применение неполного метода перебора.
<5.2> Для многооткликовой задачи правомерно
применение МНК к каждой из регрессий в отдельности. В данном случае модели
однооткликовые.
3.2 Пошаговая
регрессия
.2.1
Результаты
Зададим зависимую переменную Y и независимые X1,
Х2, Х3, Х4, Х5 Итоги анализа с использованием пакета STATISTICA
Шаг 0
Результаты множ. регрессии(Шаг 0)
Число набл.: 60 скоррект.R2= ,64729964 p = ,000000
Стандартная ошибка оценки:184,39683277
Своб.член: 608,02662453 Ст.ошибка: 273,7725 t( 54) = 2,2209 p =
,0306бета=,501 X2 бета=,153 X3 бета=-,12бета=,166 X5 бета=-,32
(выделены значимые бета)
Шаг 1
Результаты множ. регрессии(Шаг 1)
Зав.перем.:Y Множест. R =
,81717234 F = 27,63707= ,66777064 сс = 4,55
Число набл.: 60 скоррект.R2= ,64360850 p = ,000000
Стандартная ошибка оценки:185,35921149
Своб.член: 425,37895333 Ст.ошибка: 233,1118 t( 55) = 1,8248 p =
,0735бета=,547 X2 бета=,142 X4 бета=,170бета=-,34
(выделены значимые бета)
Уравнение регрессии значимо, так как Ft(4,55)<Ff=27,63707
Шаг 2
Результаты множ. регрессии(Шаг 2)
Зав.перем.:Y Множест. R =
,80665645 F = 34,77272= ,65069463 сс = 3,56
Число набл.: 60 скоррект.R2= ,63198184 p = ,000000
Стандартная ошибка оценки:188,35846060
Своб.член: 575,72466483 Ст.ошибка: 218,7626 t( 56) = 2,6317 p =
,0110бета=,487 X4 бета=,184 X5 бета=-,33
(выделены значимые бета)
Уравнение статистически значимо, так как Ft(3,56)<Ff=34,77272
Шаг 3
Результаты множ. регрессии(шаг 3, оконч. решение)
другие F-исключить не выше указ. значения
Зав.перем.:Y Множест. R =
,79157512 F = 47,82385= ,62659117 сс = 2,57
Число набл.: 60 скоррект.R2= ,61348911 p = ,000000
Стандартная ошибка оценки:193,03291779
Своб.член: 734,19552600 Ст.ошибка: 208,4142 t( 57) = 3,5228 p =
,0008бета=,594 X5 бета=-,31
(выделены значимые бета)
Уравнение статистически значимо, так как Ft(2,57)<Ff=47,82385
Программа выделяет значимые регрессоры. Значимыми
оказались Х1 и Х5. Значения коэффициента детерминации R, близкое к единице, говорит о хорошем приближении линии
регрессии к наблюдаемым данным и о возможности построения качественного прогноза.
Регрессионная сумма:
|
Beta
|
Std.Err.
|
B
|
Std.Err.
|
t(57)
|
p-level
|
|
Intercept
|
|
|
734,19553
|
208,41417
|
3,52277
|
0,00085
|
|
X1
|
0,59448
|
0,09212
|
0,75448
|
0,11692
|
6,45308
|
0,00000
|
|
X5
|
-0,31088
|
0,09212
|
-39,75302
|
11,77997
|
-3,37463
|
0,00134
|
На третьем шаге нами получена оптимальная искомая модель:
Y=734,19553+0,75448 X1-39,75302X5
Дисперсионный анализ:
|
Sums of
|
df
|
Mean
|
F
|
p-level
|
|
Regress.
|
3563997
|
2
|
1781998
|
47,82385
|
0,000000
|
|
Residual
|
2123917
|
57
|
37262
|
|
|
|
Total
|
5687914
|
|
|
|
|
Статистика Дарбина - Уотсона:
|
Durbin-
|
Serial
|
|
Estimate
|
2,005139
|
-0,010950
|
.2.2 Оценка
качества
Так как фактическое значение критерия Фишера больше,
чем табличное, то необходимо сделать вывод о значимости модели уравнения
регрессии, исследуемая зависимая переменная хорошо описывается переменными X1 и Х5. Из приведенных результатов
(0,7<R=0,79157512<0,9). Свободный член
статистически значим (p=0,00085.
.2.3 Диагностика
соблюдения условия РА-МНК
Проверим соблюдение основных предположений РА
<2.1> - <5.2>.
Соблюдение предположений <1.1> - <1.4> экспериментатор
старается обеспечить при организации эксперимента.
<2.1> В случае с пошаговой регрессией модель
неизбыточна, т.к. для регрессоров Х1, Х5, р-level не превышает уровень значимости = 0,05.
<2.2> Специальных признаков нарушения
<2.2> не существует. Косвенными признаками могут быть признаки нарушения
предположения <3.1>, а именно, значимые коэффициенты парной корреляции.
<3.1> Нарушение этого предположения трактуется
как явление мультиколлинеарности. Наиболее часто мультиколлинеарность
обнаруживается по коэффициентам парной корреляции ху матрицы R.
|
X1
|
X5
|
Y
|
|
X1
|
1,00000
|
-0,48528
|
0,74296
|
|
X5
|
-0,48528
|
1,00000
|
-0,60242
|
|
Y
|
0,74296
|
-0,60242
|
1,00000
|
Парный коэффициент корреляции rx1x5,значительно
отличается от нуля, значит присутствует мультиколлинеарность.
<3.2> О нарушении условия неслучайности rij можно судить по косвенному признаку
- резкому различию между внутренней и внешней точности прогноза.
<4.1> Обычно нарушение предположения об
аддитивности е происходит при переходе от нелинейной по b модели (внутренне линейной) к
линейной. В данном примере мы имеем дело с линейной моделью.
<4.2> Ошибки e, распределены нормально, что видно из графиков: за пределами
полосы Зσ
точек нет.
<4.3> Условие М[e], = 0, не требует особого внимания при наличии b0 в модели.
<4.4> Как видно из графиков, условие
однородности наблюдений не нарушается.
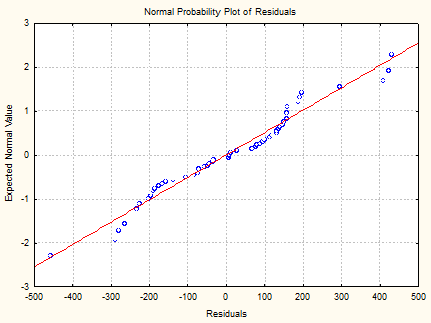
<4.5>
Авторегрессия незначительна, т.к. D близко к 2.
|
Durbin-
|
Serial
|
|
Estimate
|
2,005139
|
-0,010950
|
<5.1> Основным признаком нарушения условия о
точной идентификации является несоблюдение условия <3.1>. Формальным
признаком является применение неполного метода перебора.
<5.2> Для многооткликовой задачи правомерно
применение МНК к каждой из регрессий в отдельности. В данном случае модели однооткликовые.
Выводы
Вывод для множественной регрессии.
В настоящее время множественная регрессия - один из
наиболее распространённых методов в эконометрике. Основная цель множественной
регрессии - построить модель с большим числом факторов, определив при этом
влияние каждого из них в отдельности, в также совокупное их воздействие на
моделируемый показатель. В нашем примере мы получили следующую модель:
=608,02662+0,63617X1+249,35156 X2-262,50298X3+5,39506X4-40,59804X5
Проанализировав эту модель мы можем сделать выводы.
Коэффициенты регрессии при переменной X1 показывает, что с ростом среднедневного душевого дохода на 1 ед. общий
объем кредитования растет в среднем на 0,636 млн. руб., с ростом, при
переменной X5 показывает, что с ростом
среднегодовой процентной ставки по ипотечным кредитам на 1 % общий объем
кредитования снижается в среднем на 40,598 млн. руб.
Проанализируем качество постулируемой модели.
Значимость уравнения множественной регрессии в целом
оценим с помощью F -критерия
Фишера. Задача состоит в проверке нулевой гипотезы Но о статистической не
значимости уравнения регрессии в целом. Анализ выполняется при сравнении
фактического и табличного значения F-критерия Фишера Fтабл
и Fфакт. Сравнивая Fтабл и Fфакт. получим:
Fфакт. = 22,65616; Fтабл (5,54)=2,39, следовательно Fфакт.> Fтабл . С
вероятностью
-α=0,95 приходим к выводу о
необходимости отклонить гипотезу Но и делаем заключение о статистической
значимости уравнения.
Оценим уравнение регрессии о возможности использовать
для прогноза. Для этого воспользуемся следующей формулой: Fфакт.>4Fтабл. В нашем уравнении: Fфакт =22,65616, а 4Fтабл=4·2,39=9,56, следовательно с вероятностью 1-α=0,95 приходим к выводу о значимости
уравнения в целом и уравнение следует использовать для прогноза.
Оценим модель по коэффициенту детерминации. Для оценки
качества подбора функции рассчитывается коэффициент детерминации (R2). Величина коэффициента
детерминации служит одним из критериев оценки качества модели. Он характеризует
долю дисперсии результативного признака Y объясняемую регрессией в общей дисперсии результативного
признака. В нашем случае R2 =
0, 67906710.
Следовательно уравнением регрессии объясняется 68%,
дисперсии результативного признака, а на долю прочих факторов приходится 32% ее
дисперсии.
Результаты диагностики:
По результатам диагностики <2.1> мы можем
сделать следующий вывод, что модель линейна по b; в ней нет лишних слагаемых и все регрессоры
присутствуют.
Результаты диагностики <3.1 >. По значениям
коэффициентов парной корреляции мультиколлениарность обнаружена (коэффициенты rx1x2, rx1x3, rx1x4, rx1x5 значимо отличаются от нуля)
Результаты диагностики <4.2>. Данное нарушение
проверили по графикам остатков. Сделаем вывод о том, что условие не нарушено
Результаты диагностики <4.4>. Данное нарушение проверили
по графикам остатков. Явного нарушения условия нет.
Результаты диагностики <4.5>. Для проверки
данного условия независимости ошибок из-за неучёта фактора времени
воспользуемся графиком остатков (d,T), где Т - время или номер наблюдения, а
также статистику Дарбина - Уотсона. В нашем примере Авторегрессия положительна,
т.к. D находится в интервале 0-2.
Выводы для пошаговой регрессии.
Во втором случае, когда используем пошаговую
регрессию, регрессоры Х2, Х3, Х4 оказались не значимыми. Результат улучшения
модели:
=734,19553+0,75448 X1-39,75302X5
Проанализируем качество постулируемой модели.
Значимость уравнения множественной регрессии в целом
оценим с помощью F -критерия
Фишера. Задача состоит в проверке нулевой гипотезы Но о статистической не
значимости уравнения регрессии в целом. Анализ выполняется при сравнении
фактического и табличного значения F-критерия Фишера Fтабл
и Fфакт. Сравнивая Fтабл и Fфакт. получим:
Fфакт. = 47,82385, a Fтабл (2,57)=3,16,
следовательно Fфакт.> Fтабл С вероятностью 1-α=0,95 приходим к выводу о необходимости
отклонить гипотезу Но и делаем заключение о статистической значимости
уравнения.
Оценим уравнение регрессии о возможности использовать
для прогноза. Для этого воспользуемся следующей формулой: Fфакт.>4Fтабл. В нашем уравнении: Fфакт =47,82385, а 4Fтабл=4·3,16=12,64, следовательно с вероятностью 1-α=0,95
приходим к выводу о
значимости уравнения в целом и уравнение следует использовать для прогноза.
Оценим модель по коэффициенту детерминации. Для оценки
качества подбора функции рассчитывается коэффициент детерминации (R2). Величина коэффициента
детерминации служит одним из критериев оценки качества модели. Он характеризует
долю дисперсии результативного признака Y объясняемую регрессией в общей дисперсии результативного признака.
В нашем случае R2 =0,62659117.
Следовательно уравнением регрессии объясняется 63%,
.дисперсии результативного признака, а на долю прочих факторов приходится 37%
ее дисперсии.
Результаты диагностики:
По результатам диагностики <2.1> мы можем сделать
следующий вывод, что модель линейна по b; в ней нет лишних слагаемых и все регрессоры присутствуют.
Результаты диагностики <3.1 >. По значениям
коэффициентов парной корреляции мультиколлениарность обнаружена (коэффициенты
rx1x5 значимо отличается от нуля)
Результаты диагностики <4.2>. Данное нарушение
проверили по графикам остатков. Сделаем вывод о том, что условие не нарушено
Результаты диагностики <4.4>. Данное нарушение
проверили по графикам остатков. Явного нарушения условия нет.
Результаты диагностики <4.5>. Для проверки
данного условия независимости ошибок из-за неучёта фактора времени
воспользуемся графиком остатков (d,T), где Т - время или номер наблюдения, а
также статистику Дарбина - Уотсона. В нашем примере авторегрессия положительна,
т.к. D находится в интервале 0-2.
Вывод: Модель, полученная в результате пошаговой
регрессии предпочтительнее, т.к. в ней нет лишних слагаемых и все регрессоры
значимы. Авторегрессия для данной модели незначительна.
Графики
Диаграммы рассеяния

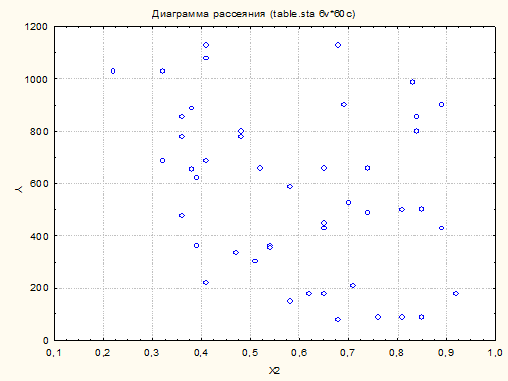
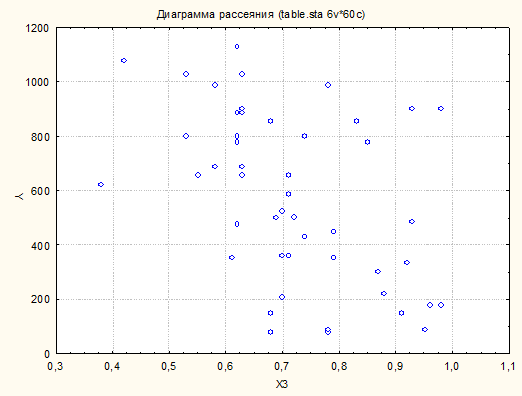

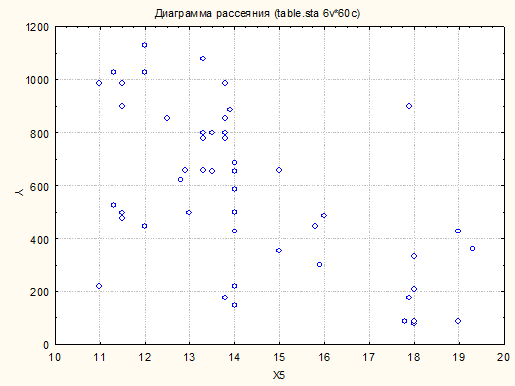
Графики
остатков

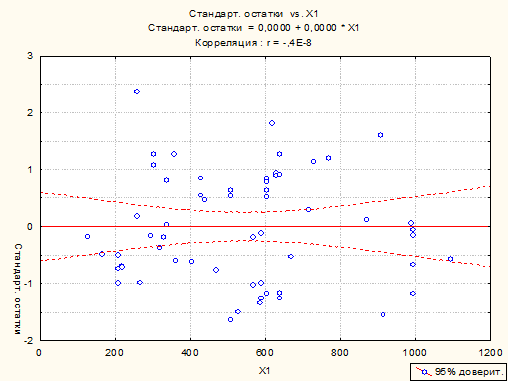


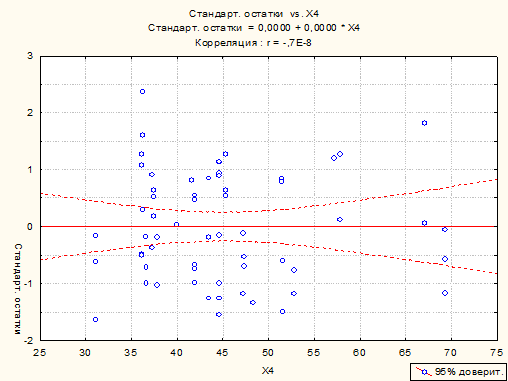

Список
литературы
1. Валеев
С.Г. Регрессионное моделирование при обработке данных. - Казань: ФЭН. 2001.-296
с.
2. Валеев
С.Г., Куркина С.В. Эконометрика - Ульяновск: УлГТУ, 2008-99с.