Изучение взаимодействия заряженных частиц на примере многократного кулоновского рассеяния

Изучение взаимодействия заряженных частиц на примере многократного кулоновского рассеяния

Введение

Физика микромира стала неимоверно сложна. По мере усложнения и углубления теоретических знаний, усложняется и физический эксперимент.

В компьютерные программы моделирования в физике элементарных частиц закладываются только проверенные или ожидаемые свойства взаимодействия элементарных частиц. Численное моделирование составляет неотъемлемую часть современной фундаментальной и прикладной науки, причём по важности оно приближается к традиционным экспериментальным и теоретическим методам. Моделирование занимает промежуточное положение между теоретической подготовкой и непосредственным проведением эксперимента.

Целью данной курсовой работы является изучение взаимодействия заряженных частиц, на примере многократного кулоновского рассеяния, а так же его моделирование с помощью метода Монте-Карло и Mathematica.

1. Взаимодействие заряженных частиц с веществом

.1 Упругое рассеяние

.1.1   Сечение рассеяния

Упругое рассеяние заряженных частиц одной на другой - например, электрона на ядре атома - может быть описано методами классической механики. Для начала введем требуемые для дальнейшего понятия.

Отношение количества частиц dN, рассеянных на некотором центре в единицу времени, к плотности потока частиц J, падающих на центр, имеет размерность площади и называется сечением рассеяния:

d = dN/J.         (1)

Обычно интересует количество частиц, рассеянных на определенный угол 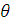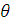, называемый углом рассеяния (рис. 1.1). Считая, что угол рассеяния однозначно связан с прицельным параметром , находим количество частиц, рассеянных на угол, оно равно количеству частиц, попавших в кольцо с радиусами  и + d: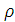

.

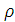(модуль взят потому, что производная обычно отрицательна: угол рассеяния уменьшается с увеличением прицельного параметра). Следовательно, дифференциальное сечение рассеяния на угол 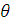 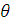равно

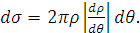
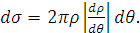 (2)

Если же интересует сечение рассеяния в определенный телесный угол 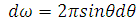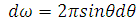, то выражение для соответствующего сечения принимает вид

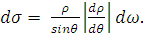
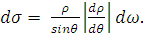 (3)

1.1.2 Центр масс

Суммарная энергия двух частиц - рассеивающей и рассеиваемой - может быть записана в виде

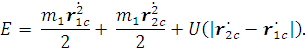
Индексы «С» означают, что начало координат для векторов положения частиц мы взяли в так называемом центре масс, положение которого определяется вектором

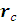
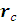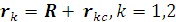
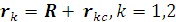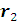
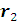Радиус-вектор в произвольной системе отсчета r связан с радиус - вектором в системе центра масс соотношением.Складывая радиус-векторы и, получаем условие

.         (4)

Центр масс всегда движется равномерно и прямолинейно. Действительно, законы движения частиц в произвольной системе отсчета имеют вид:

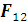
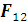- сила, действующая на первую частицу со стороны второй частицы (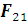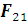, вводится аналогично). По третьему закону Ньютона, поэтому складывая оба приведенных выше выражения, подставляя выражения для радиус-векторов и используя (1.4), находим:

;

.

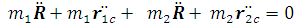
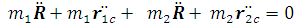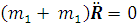
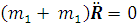Следовательно, все, что может делать центр масс системы - это двигаться с постоянной скоростью.

Вводя вектор расстояния между частицами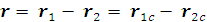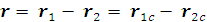, получаем, что в системе центра масс радиус-векторы частиц могут быть выражены через r следующим образом:

Подставляя полученные соотношения в выражение для энергии, находим:

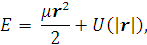
где  - приведенная масса.

Когда масса одной из частиц намного больше другой (например, электрон и атом), приведенная масса приблизительно равна массе легкой частицы; если же массы частиц равны, приведенная масса равна половине массы частицы.

Таким образом, задача о движении двух частиц, энергия взаимодействия которых зависит только от расстояния между ними, может быть сведена к задаче о движении одной частицы с приведенной массой в поле внешних сил. Такое представление удобно, однако описание в системе центра масс, положение которого меняется со временем, может вызвать некоторые трудности в интерпретации результатов. Часто после получения решения в системе центра масс переводят ответ в неподвижную систему отсчета - так называемую лабораторную систему координат.

1.1.3 Кулоновское рассеяние частиц

Перейдем непосредственно к рассмотрению рассеяния частиц. Как было показано выше, такую задачу можно свести к задаче о рассеянии на центре одной частицы массой 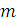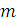; мы так и поступим, так как решение в этом случае будет не только просто, но и наглядно. Итак, рассмотрим рассеяние частицы, налетающей на центр с прицельным расстоянием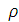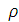, на угол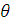 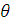 (рисунок 1); частица взаимодействует с центром по закону Кулона. Рассеяние в поле дальнодействующего потенциала отличается от соударения двух шариков: частица начинает «чувствовать» центр задолго до подлета к нему, проходит мимо центра на некотором минимальном расстоянии 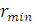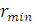, а затем удаляется по траектории, симметричной траектории подлета частицы. Так как частица движется всегда в одной плоскости, можно ввести в этой плоскости координаты r и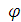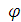, тогда угол , соответствующий минимальному расстоянию между частицей и центром , связан с углом рассеяния: .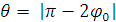

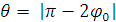В координатах r и выражение для энергии частицы записывается в виде

(5)

Рисунок 1: Рассеяние частицы (1) на неподвижном центре (2): а - между частицей и центром действуют силы отталкивания; б - между частицей и центром действуют силы притяжения

где  - энергия кулоновского взаимодействия;

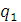
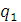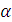
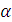и - заряды частиц;  - параметр взаимодействия. Энергия в результате упругого рассеяния не изменяется:

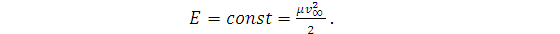
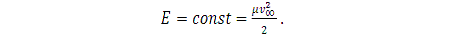(6)

( - скорость налетающей частицы на бесконечности, где частица еще не взаимодействует с центром), сохраняется также момент импульса относительно центра:

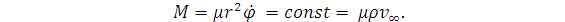
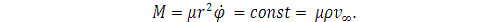(7)

Выразим из (7)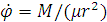 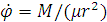и подставим эту величину в (5), откуда выразим уже :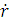

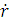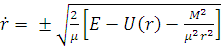
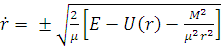. (8)

Знак «-» соответствует движению частицы к центру - «до столкновения», т.е. до прохождения минимального радиуса, знак «+» - движению частицы от центра, т.е. «после столкновения».

Уравнения (7) и (8) позволяют записать уравнение для линии движения частицы в плоскости :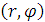

.

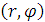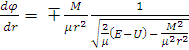
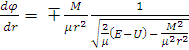Интегрируя, находим выражение для угла 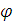 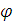при изменении расстояния между частицей и центром от 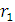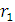до:

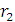
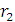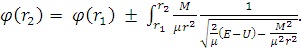
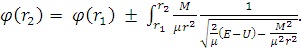 (9)

Найдем угол  (соответствующийминимальному расстоянию между частицей и центром 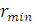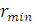). В точке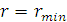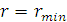частица «поворачивает», изменяя знак производной 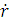 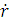с отрицательного на положительный, так что при. Следовательно, при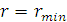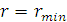полная энергия частицы равна

.   (10)

Из условия (10) можно найти непосредственно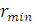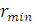, решив квадратное уравнение. Воспользуемся фактом того, что минимальный радиус является решением этого уравнения.

При движении к центру в (8), (9) надо выбирать знак «-».

Тогда выражение для определения  имеет вид:

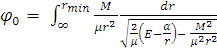
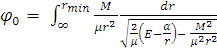 (11)

Решаем интеграл. Потом находим

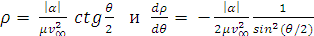
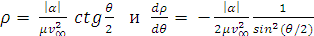. (12)

Подставляя (12) в выражение (2), находим сечение рассеяния в полярный угол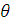

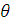
 (13)

а подставляя (12) в (3) - сечение рассеяния в телесный угол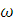

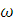
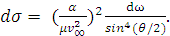
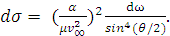 (14)

Как видно из (13), (14), сечение рассеяния не зависит от знака 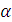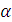, т.е. от знака зарядов частиц.

Сечение рассеяния (13) называется формулой Резерфорда. Интересно, что именно изучение рассеяния - частиц на атомах способствовало возникновению современной, так называемой, планетарной модели атома.

1.2   
Ионизация

Для начала продолжим изучение взаимодействия частиц с точки зрения классической механики. Рассмотрим столкновение двух частиц с одинаковой массой, причем одна из частиц (вторая) до столкновения покоилась. Запишем законы сохранения энергии и импульса в лабораторной системе координат, отметив штрихом величины после столкновения:

Возводя в квадрат второе выражение, получаем соотношение которое может быть совместимо с законом сохранения энергии только в том случае, если косинус угла между векторами скоростей частиц после соударения равен нулю, т.е. сам угол 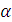 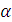= 90° - частицы после столкновения разлетаются под прямым углом.

,

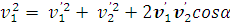
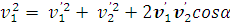Как было показаноранее, центр масс движется с постоянной скоростью. Таким образом, и до и после соударения центр масс имеет одну и ту же скорость; если до удара одна из частиц двигалась со скоро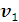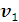стью, а другая покоилась, то центр масс перемещается с постоянной скоростью

.

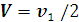
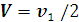Найдем теперь связь между углами рассеяния налетающей частицы в системе центра масс 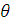 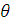и в лабораторной системе координат 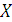 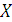(угол рассеяния - это угол отклонения частицы от направления первоначального движения).

В лабораторной системе координат закон сохранения импульса в проекциях на ось х, направленную вдоль первоначального движения первой частицы (рис. 1.2), запишется как

,

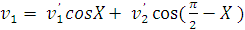
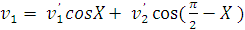Рисунок 2: Диаграмма скоростей при рассеянии частиц одинаковой массы в лабораторной системе координат:

угол между

в проекции на ось у, перпендикулярную направлению движения -

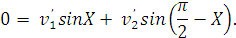
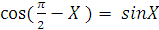
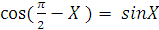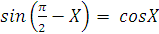
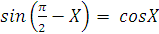Так как и получаем:

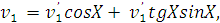
откуда

Таким образом, в лабораторной системе координат проекции скорости первой частицы после соударения на оси равны 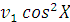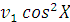и В системе центра масс указанные проекции скорости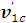 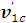равны соответственно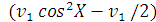 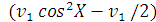и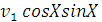 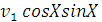(центр масс движется вдоль оси х со скоростью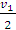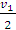). Косинус угла между векторами скорости первой частицы до и после столкновения в системе центра масс равен

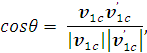
где 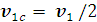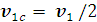- скорость в системе центра масс до удара.

Подставляя выражения для скоростей, находим:

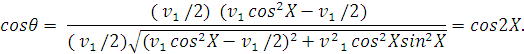
Следовательно, угол рассеяния в системе центра масс в 2 раза больше угла рассеяния в лабораторной системе координат:

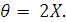
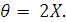 (15)

1.2.2 Ионизация электронами (I)

Задачу об ионизации атома электроном можно свести к задаче о взаимодействии двух электронов: налетающего и электрона оболочки, который мы будем считать свободным. При соударении электроны обмениваются энергией: налетающий электрон теряет энергию

(где E - энергия налетающего электрона на бесконечности); такую же энергию  приобретает электрон оболочки. Если эта энергия превысит энергию ионизации I, т.е. энергию связи электрона с атомом, электрон покинет оболочку атома - произойдет ионизация атома.

Сечение ионизации в данном приближении совпадает с сечением Резерфорда упругого соударения двух электронов (13):

в котором следует записать приведенную массу через массу электронов: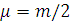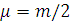, а также выразить угол рассеяния в системе центра масс через угол рассеяния в лабораторной системе координат (15):

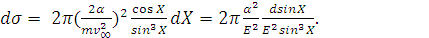
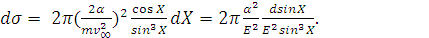(16)

Подставляя связь угла рассеяния с энергией 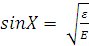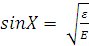, получаем сечение рассеяния в зависимости от передаваемой при столкновении энергии:

 (17)

Вообще передаваемая при столкновении энергия может меняться от 0 до Е, однако интересующий нас диапазон энергий - от I до Е.

Найдем полное сечение ионизации:

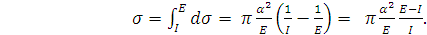
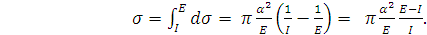 (18)

Обратим еще раз внимание, что задача об ионизации атома была сведена нами к взаимодействию двух электронов. Это означает, что параметр взаимодействия записывается как .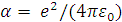

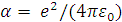1.2.3 Ионизация произвольными частицами

Рассмотрим соударение частиц с произвольным соотношением масс. Пусть в лабораторной системе координат частица массой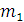

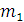
имела до соударения скорость 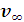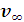, частица массой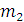 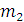 покоилась.

В системе центра масс начальные скорости частиц равны:

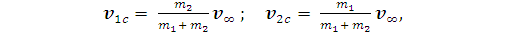
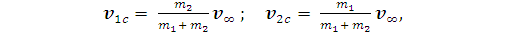(19)

так как начальная скорость их относительного движения равна .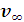

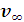В системе центра масс суммарный импульс частиц до столкновения рав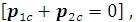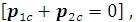ен нулю         следовательно, после столкновения суммарный импульс частиц также будет равен нулю  вследствие закона сохранения импульса. Тогда из закона сохранения энергии

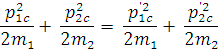
следует, что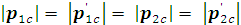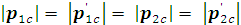, т.е. импульсы частиц и после соударения по абсолютной величине остаются такими же; в результате столкновения меняются только направления скоростей. Пусть после столкновения скорость первой частицы направлена по единичному вектору 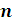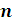, тогда угол между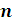 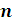и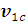 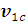есть не что иное как угол рассеяния 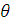 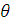в системе центра масс.

Следовательно, скорости частиц после соударения можно записать как

(20)

Чтобы получить выражения для скоростей в лабораторной системе координат, следует к (20) прибавить скорость центра масс

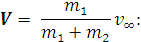
Энергия, приобретаемая второй частицей в результате соударения:

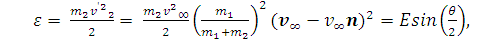
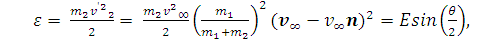       (21)

где- максимальная энергия, которую может приобрести первоначально покоившаяся частица;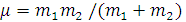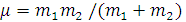- приведенная масса.

Естественно, и для соударения частиц с произвольными массами справедлива формула (13) - сечение Резерфорда в системе центра масс. Подставляя в него, находим:

(22)

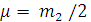
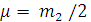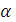
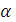При столкновении двух электронов и формула (22) переходит в (17), как и должно быть. Другой интересующий нас случай - столкновение налетающей -частицы и покоившегося электрона. При этом можно смело полагать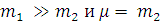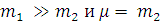, максимальная энергия, которую может получить электрон, равна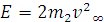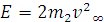.Дифференциальное сечение принимает вид:

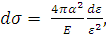
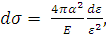 (23)

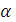
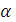где параметр взаимодействия, так как -частица имеет положительный заряд, равный двум зарядам электрона. Интегрируя (23) от энергии ионизации I до Е, находим полное сечение ионизации:

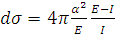
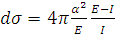. (24)

заряженный ионизация кулоновский частица

1.2.4 Ионизационные потери

Если известно полное сечение ионизации, можно грубо оценить потери энергии частицей на ионизацию в веществе на единицу длины ее пробега. Пусть J - плотность потока частиц, каждая из которых имеет энергию n - количество электронов в единице объема среды, тогда в объеме площадью dS и длиной dx будет содержаться ndSdx электронов. Энергия, которая будет затрачена потоком частиц на ионизацию объема dV за времяdt, определяется с помощью сечения ионизации:

 (25)

Так как JdSdt = N есть общее количество частиц, которые пролетят через объем dV за время dt, то отношение общей энергии, затраченной всеми частицами на ионизацию, к этому числу частиц N даст энергию, которая теряется одной частицей на длине dx:

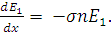
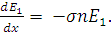 (26)

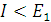
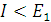Формула (26) имеет оценочный характер, так как содержит параметр n, который означает количество электронов в единице объема, которые могут быть вырваны из атома частицей с энергиейт.е. число электронов, для которых. Для прочих электронов подсчитанное «напрямую» сечение (24) получится бессмысленно отрицательным.

Для оценок формула (26) вполне годится. Например, из (26) с использованием (24) следует, что потери энергии на единицу длины обратно пропорциональны энергии частицы: чем меньше энергия ионизирующей частицы, тем больший от нее будет «ионизирующий эффект». Также из (26) вытекает, что потери энергии на ионизацию частиц с зарядом ze пропорциональны .

.3.1 Дипольное излучение

Тормозное излучение возникает при ускоренном движении заряженных частиц в электрическом поле (создаваемом другими заряженными частицами) и сопровождается потерей энергии излучающих частиц. Именно этот механизм мешал становлению планетарной модели атома в классической постановке: считалось, что электроны, вращающиеся вокруг ядра, растеряют всю свою энергию на излучение и «попадают» на ядро, дискредитировав тем самым планетарную модель. Как известно, ситуацию реанимировал Н. Бор, введя квантовое описание внутриатомного движения, однако нас будет интересовать не оно, а сам механизм тормозного излучения, причем в классической постановке. Прежде чем рассмотреть его непосредственно, изложим общие принципы классической теории электромагнитного излучения.