Числовые характеристики выборки
1.
Таблица значений выборки случайных величин
|
5,6
|
7,2
|
5,2
|
8
|
4,6
|
6
|
5,2
|
6,4
|
8
|
5
|
4,2
|
5,2
|
|
7,6
|
4,2
|
6
|
6,4
|
6,6
|
5
|
5,6
|
6,8
|
5,4
|
4,4
|
6,8
|
5
|
|
6,6
|
6
|
5,6
|
7
|
5,4
|
7,2
|
4
|
5
|
7
|
4,8
|
4,4
|
6
|
|
6,4
|
7,6
|
4,6
|
4
|
5
|
6,8
|
5,4
|
4,2
|
7,8
|
5,8
|
4
|
7,6
|
|
5,2
|
6,6
|
7,4
|
5,8
|
6,2
|
4,8
|
6,4
|
5
|
6,8
|
5,6
|
5,8
|
4,6
|
|
7,4
|
4,8
|
8
|
6,2
|
4,2
|
8
|
6,2
|
7,8
|
4
|
8
|
6,4
|
5,2
|
|
5,8
|
7
|
6,2
|
5,6
|
7,4
|
5,8
|
5
|
6,6
|
5,6
|
5,2
|
7,2
|
5,8
|
|
7,6
|
4,4
|
7,4
|
6,4
|
4
|
6,4
|
7,6
|
5,4
|
6
|
7,8
|
6,6
|
4,2
|
|
6,2
|
6,8
|
5,2
|
7,2
|
5,8
|
5
|
4,4
|
6
|
7
|
4,6
|
8
|
4,6
|
|
8
|
5,4
|
6,8
|
6
|
5,2
|
6,6
|
8
|
4,6
|
6,4
|
7
|
5
|
7,4
|
|
4
|
5,6
|
4,8
|
7,4
|
6,8
|
5,2
|
6,6
|
7,2
|
5
|
8
|
4,4
|
6
|
|
5,8
|
6,8
|
7
|
4,2
|
5,8
|
4
|
4,6
|
5,2
|
7,4
|
5,6
|
6,4
|
6,8
|
Выборка в диапазоне от Xmin = 4 до Xmax = 8; n =
144.
2.
Таблица значений выборки дискретных случайных величин в упорядоченном виде
|
4
|
4
|
4
|
4
|
4
|
4
|
4,2
|
4,2
|
4,2
|
4,2
|
4,2
|
4,2
|
|
4,4
|
4,4
|
4,4
|
4,4
|
4,4
|
4,6
|
4,6
|
4,6
|
4,6
|
4,6
|
4,6
|
4,6
|
|
4,8
|
4,8
|
4,8
|
4,8
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
|
5
|
5
|
5,2
|
5,2
|
5,2
|
5,2
|
5,2
|
5,2
|
5,2
|
5,2
|
5,2
|
5,2
|
|
5,2
|
5,4
|
5,4
|
5,4
|
5,4
|
5,4
|
5,6
|
5,6
|
5,6
|
5,6
|
5,6
|
5,6
|
|
5,6
|
5,6
|
5,8
|
5,8
|
5,8
|
5,8
|
5,8
|
5,8
|
5,8
|
5,8
|
5,8
|
6
|
|
6
|
6
|
6
|
6
|
6
|
6
|
6
|
6,2
|
6,2
|
6,2
|
6,2
|
6,2
|
|
6,4
|
6,4
|
6,4
|
6,4
|
6,4
|
6,4
|
6,4
|
6,4
|
6,4
|
6,6
|
6,6
|
6,6
|
|
6,6
|
6,6
|
6,6
|
6,6
|
6,8
|
6,8
|
6,8
|
6,8
|
6,8
|
6,8
|
6,8
|
6,8
|
|
6,8
|
7
|
7
|
7
|
7
|
7
|
7
|
7,2
|
7,2
|
7,2
|
7,2
|
7,2
|
|
7,4
|
7,4
|
7,4
|
7,4
|
7,4
|
7,4
|
7,4
|
7,6
|
7,6
|
7,6
|
7,6
|
7,6
|
|
7,6
|
7,8
|
7,8
|
7,8
|
8
|
8
|
8
|
8
|
8
|
8
|
8
|
8
|
X
min = 4; X max = 8;= 144; R = 12;
Определяем
шаг: 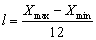 ;
;
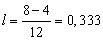 ;
;
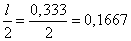 ;
;
Определяем
начальное значение X0: 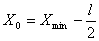 ;
; 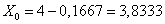 ;
;
Определяем
конечное значение Xk: 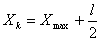 ;
; 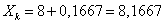 .
.
3.
Таблица интервального статистического ряда относительных частот
|
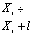
|
3,833÷4,167
|
4,167÷4,5
|
4,5÷4,833
|
4,833÷5,167
|
5,167÷5,5
|
5,5÷ 5,833
|
5,833÷6,167
|
6,167÷6,5
|
6,5÷ 6,833
|
6,833÷7,167
|
7,167÷7,5
|
7,5÷ 7,833
|
7,833÷8,167
|
|
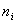
|
6
|
11
|
11
|
10
|
16
|
17
|
8
|
14
|
16
|
6
|
12
|
9
|
8
|
|
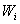
|
0,042
|
0,076
|
0,076
|
0,069
|
0,111
|
0,118
|
0,056
|
0,097
|
0,111
|
0,042
|
0,083
|
0,063
|
0,056
|
Проверка: ∑ni
= 144; 6 + 11 + 11 +10+ 16 + 17 + 8 + 14 + 16 + 6 + 12 + 9 + 8 = 144
∑Wi =
1; 0,042 + 0,076 + 0,076 + 0,069 + 0,111 + 0,118 + 0,056 + 0,097 + 0,111 +
0,042 + 0,083 + 0,063 + 0,056 =1
Математическое ожидание дискретной случайной
величины - это сумма произведений всех возможных значений действительных
случайных величин на их вероятности.
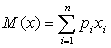
Математическое ожидание случайной дискретной
величины Х есть неслучайная величина, некоторая постоянная, в которой сходится
ряд 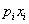 .
.
Математическое ожидание числа появления события
в одном испытании, равно вероятности этого события.
Математическое ожидание случайной величины
приблизительно, тем точнее, чем больше число испытаний, и равно среднему
арифметическому наблюдаемой величины.
Математическое ожидание случайной величины
больше ее наименьшего и меньше наибольшего значений, т.е. на числовой оси
значений случайной величины расположены слева и справа от математического
ожидания. Иначе математическое ожидание называют центром распределения.
Свойства математического ожидания.
Математическое ожидание постоянной равно этой
постоянной.
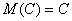
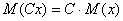
Математическое ожидание произведения случайной
величины равно произведению математических ожиданий этих величин.
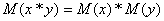
Математическое ожидание суммы равно сумме
математических ожиданий.
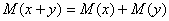

Определяем математическое ожидание:
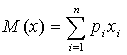

М
(х) = 4*0,042 + 4,333*0,076 + 4,667*0,076 + 5*0,069 + 5,333*0,111 + 5,667*0,118
+ 6*0,056 + 6,333*0,097 + 6,667*0,111 + 7*0,042 + 7,333*0,083 + 7,667*0,063
+8*0,056 = 0,168 + 0,329 + 0,355 + 0,345 + 0,592 + 0,669 + 0,336 + 0,614 + 0,74
+ 0,294 + 0,609 + 0,483 + 0,448 = 5,982
М
(х) =5,982
Дисперсией D(X) случайной величины Х
характеризует степень разброса значений этой величины около ее математического
ожидания.
Дисперсией или рассеянием дискретной случайной
величины называют математическое ожидание квадрата отклонения случайной
величины от ее математического ожидания.
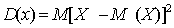
Свойства дисперсии:
Дисперсия постоянной величины равна нулю.
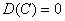
Постоянный множитель можно выносить за знак
дисперсии, возводя его в квадрат.
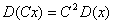
Дисперсия суммы случайной величины равна сумме
дисперсий, но если одна из величин const, то
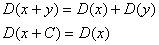
Дисперсия разности случайных величин равна сумме
дисперсий.
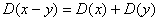
Определяем выборочную дисперсию:
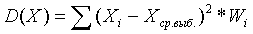 (X)
= (4,0 - 5,982)2*0,042 + (4,333 - 5,982)2*0,076 + (4,667 - 5,982)2*0,076 + (5 -
5,982)2*0,069 + (5,333 - 5,982)2*0,111 + (5,667 - 5,982)2*0,118 + (6 -
5,982)2*0,056 + (6,333 - 5,982)2*0,097 + (6,667 - 5,982)2*0,111 + (7 -
5,982)2*0,042 + (7,333 - 5,982)2*0,083 + (7,667 - 5,982)2*0,063 + (8 -
5,982)2*0,056 = 0,165 + 0,207 + 0,131 + 0,067 + 0,047 + 0,012 + 0 + 0,012 +
0,052 + 0,044 + 0,151 + 0,179 + 0,228 = 1,295(X) = 1,295
(X)
= (4,0 - 5,982)2*0,042 + (4,333 - 5,982)2*0,076 + (4,667 - 5,982)2*0,076 + (5 -
5,982)2*0,069 + (5,333 - 5,982)2*0,111 + (5,667 - 5,982)2*0,118 + (6 -
5,982)2*0,056 + (6,333 - 5,982)2*0,097 + (6,667 - 5,982)2*0,111 + (7 -
5,982)2*0,042 + (7,333 - 5,982)2*0,083 + (7,667 - 5,982)2*0,063 + (8 -
5,982)2*0,056 = 0,165 + 0,207 + 0,131 + 0,067 + 0,047 + 0,012 + 0 + 0,012 +
0,052 + 0,044 + 0,151 + 0,179 + 0,228 = 1,295(X) = 1,295
Определяем дисперсию:
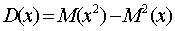
М(Х2
) = 16,00*0,042 + 18,77*0,076 + 21,78*0,076 + 25,00*0,069 + 28,44*0,111 +
32,11*0,118 + 36,00*0,056 + 40,11*0,097 + 44,45*0,111 + 49,00*0,042 +
53,77*0,083 + 58,78*0,063 + 64,00*0,056 = 0,672 + 1,427 + 1,655 + 1,725 + 3,157
+ 3,789 + 2,016 + 3,891 + 4,934 + 2,058 + 4,463 + 3,703 + 3,585 = 37,075
М
(Х2 ) = 37,075(X) = (5,982)2 = 35,78(X) = 37,075 - 35,78 = 1,295(X) = 1,295
Среднее квадратичное отклонение
Средним квадратичным отклонением случайной
величины X называют квадратный корень из дисперсии.
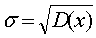
Определяем среднеквадратичное отклонение:
σ = 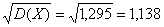
σ = 1,138
4.
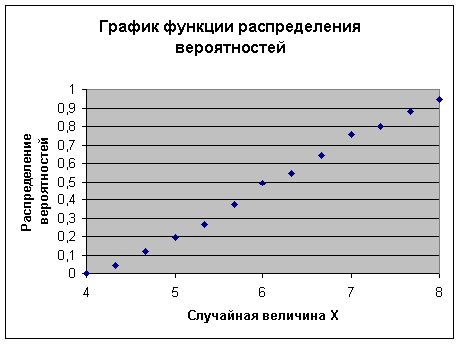
Задание эмпирической функции распределений и построение ее графика
|
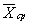
|
4
|
4,333
|
4,667
|
5
|
5,333
|
5,667
|
6
|
6,333
|
6,667
|
7
|
7,333
|
7,667
|
8
|
|
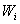
|
0,042
|
0,076
|
0,076
|
0,069
|
0,111
|
0,118
|
0,056
|
0,097
|
0,111
|
0,042
|
0,083
|
0,063
|
0,056
|
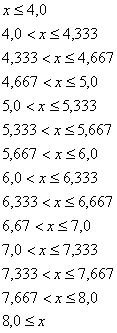
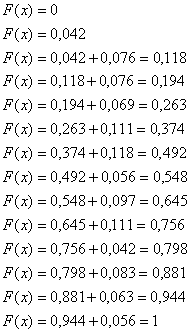
5.
Полигон и распределение случайной величины
выборка случайная величина ряд
Полигоном частот называют ломаную линию, отрезки
которой соединяют точки с координатами (Xi;Wi)
Полигоном относительных частот называют
ломанную, которая соединяет значение случайных величин и соответствующие им
значения относительных частот. (Хi ;Wi )
Для построения полигона на оси абсцисс
откладывают варианты Хi случайной величины, на оси ординат соответствующие им
частоты. Соединяют соответствующие линии и получают полигон.
|
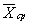
|
4
|
4,333
|
4,667
|
5
|
5,333
|
5,667
|
6
|
6,333
|
6,667
|
7
|
7,333
|
7,667
|
8
|
|
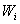
|
0,042
|
0,076
|
0,076
|
0,069
|
0,111
|
0,118
|
0,056
|
0,097
|
0,111
|
0,042
|
0,083
|
0,063
|
0,056
|
6.
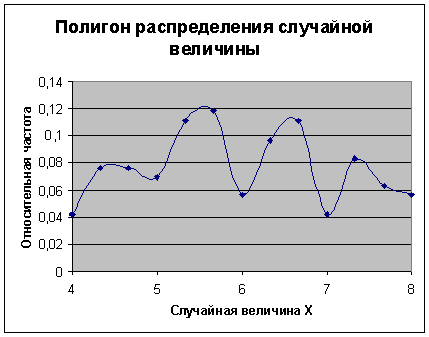
Гистограмма
Гистограммой называют ступенчатую фигуру,
состоящую из прямоугольников, основаниями которых служат частичные интервалы
длиной l, а высота равна отношению частоты Wi к l - плотности частоты. Wi/l.
Площадь i-того частичного интервала S равна
сумме частот i-того интервала S = ∑ni , т.е. площадь всей гистограммы
частот равна объему выборки.
|
№
интервала
|
Частичный
интервал Xi=Xi+1
|
Сумма
частот ni
|
Плотность
частот ni/l
|
|
1
|
3,833÷4,167
|
6
|
18
|
|
2
|
4,167÷4,5
|
11
|
33
|
|
3
|
4,5÷4,833
|
11
|
33
|
|
4
|
4,833÷5,167
|
10
|
30
|
|
5
|
5,167÷5,5
|
16
|
48
|
|
6
|
5,5÷5,833
|
17
|
51
|
|
7
|
5,833÷6,167
|
8
|
24
|
|
8
|
6,167÷6,5
|
14
|
42
|
|
9
|
6,5÷6,833
|
16
|
48
|
|
10
|
6,833÷7,167
|
6
|
18
|
|
11
|
7,167÷7,5
|
12
|
36
|
|
12
|
7,5÷7,833
|
9
|
27
|
|
13
|
7,833÷8,167
|
8
|
24
|
7.
Вычислим плотности распределения вероятности
Плотностью распределения вероятности дискретных
случайных величин называют первую производную от функции распределения f’’(x).
Для описания распределения вероятности дискретных
случайных величин плотность распределения не применима.
Вероятность того, что некоторая случайная
величина Х примет значение из промежутка (а; в) равна определенному интегралу
от плотности распределения в интервале от а до в.
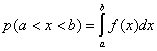
Свойства плотности распределения вероятности:
Плотность распределения неотрицательная функция;
Несобственный интеграл от плотности
распределения = 1 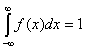
Вероятность того, что некоторая случайная
величина примет значение из промежутка (Х + ΔХ),
приближенна равна произведению плотности вероятности в точке Х на длину
интервала ΔХ.
Плотности распределения непрерывных случайных
величин называют законами распределения.
Наиболее часто встречаются законы равномерного
нормального показательного распределений.
Нормальным распределением - называют
распределение случайной величины, которое описывается плотностью распределения
вероятности:
F(х)
= 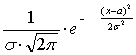
Параметрами нормального распределения являются а
и σ,
где
через а обозначено математическое ожидание случайной величины, а σ
- среднее
квадратичное отклонение нормального распределения.
Общим называют нормальное распределение с
произвольными параметрами а и σ.
Нормированным называют распределение, у которого
а = 0, а σ = 1.
Замечание:
Плотность нормального распределения есть
функция: 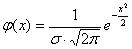 -
табличное значение;
-
табличное значение;
Функция общего нормального распределения:
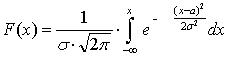 ;
;
Вероятность попадания нормированной нормальной
величины Х в интервале (0; Х) можно найти, пользуясь формулой Лапласа:
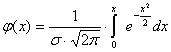 ;
;
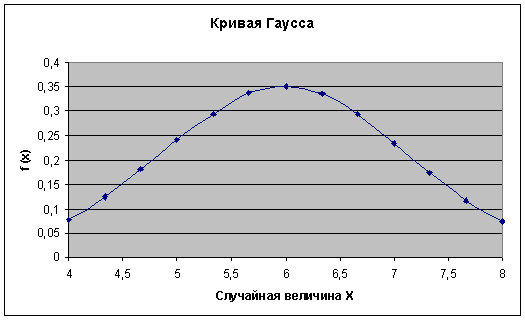
Графиком функции распределения случайной
величины Х - называется кривая Гаусса.
Свойства нормальной кривой Гаусса:
Нормальная кривая Гаусса определена на всей
числовой оси;
При всех значениях Х функция принимает
положительное значение;
Т.к. 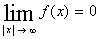 ,
ось ОХ является асимптотой графика;
,
ось ОХ является асимптотой графика;
При некотором значении Х равным а, функция имеет
максимум;
Разность (Х - а) входит в выражение функции в выражение
функции в квадрате, следовательно график функции симметричен относительно
прямой Х = а;
График функции переходя от убывания к
возрастанию и снова к убыванию имеет точки перегиба.
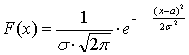 ;
;
 ;
;
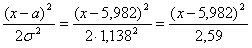 ;
;
|
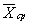
|
4
|
4,333
|
4,667
|
5
|
5,333
|
5,667
|
6
|
6,333
|
6,667
|
7
|
7,333
|
7,667
|
8
|
|
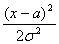
|
1,517
|
1,05
|
0,668
|
0,372
|
0,163
|
0,038
|
0
|
0,048
|
0,181
|
0,4
|
0,705
|
1,096
|
1,572
|
|
f(x)
|
0,077
|
0,123
|
0,18
|
0,242
|
0,293
|
0,338
|
0,351
|
0,335
|
0,293
|
0,235
|
0,173
|
0,117
|
0,073
|

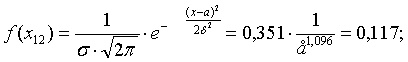
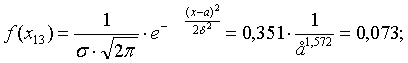
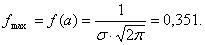
8.
Построение кривой Гаусса
9.
Построение нормальной кривой Гаусса по опытным данным
Для построения нормальной кривой по опытным
данным, зная выборочную среднюю (М; Хiср.выд ; а) и σ,
определяют:
Выравнивающие частоты:
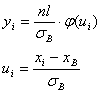
Строят точки Хi; Yi в прямоугольной системе
координат и соединяют их плавной кривой;
Если выравнивающие частоты Yi близки к
наблюдаемым ni, то это подтверждает правильность допущения о том, что
обследуемый признак распределения нормален.
|
хi
|
ni
|
xi
- xв
|
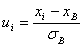
|
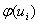
|
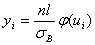
|
|
4
|
6
|
-1,982
|
-1,531
|
0,1236
|
5,213
|
5
|
|
4,333
|
11
|
-1,649
|
-1,273
|
0,1774
|
7,483
|
7
|
|
4,667
|
11
|
-1,315
|
-1,015
|
0,2383
|
10,051
|
10
|
|
5
|
10
|
-0,982
|
-0,758
|
0,2993
|
12,624
|
12
|
|
5,333
|
16
|
-0,649
|
-0,501
|
0,3519
|
14,843
|
15
|
|
5,667
|
17
|
-0,315
|
-0,243
|
0,3873
|
16,336
|
16
|
|
6
|
8
|
0,018
|
0,014
|
0,3989
|
16,825
|
16
|
|
6,322
|
14
|
0,351
|
0,271
|
0,3846
|
16,222
|
16
|
|
6,667
|
16
|
0,685
|
0,529
|
0,3469
|
14,632
|
14
|
|
7
|
6
|
1,018
|
0,786
|
0,2929
|
12,354
|
12
|
|
7,333
|
12
|
1,351
|
1,043
|
0,2316
|
9,769
|
9
|
|
7,667
|
9
|
1,685
|
1,301
|
0,1711
|
7,217
|
7
|
|
8
|
8
|
2,018
|
1,558
|
0,1185
|
4,998
|
5
|
|
∑=144
|
|
|
|
|
∑=144
|
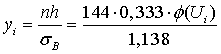 =
42,18
=
42,18
Построение графика:
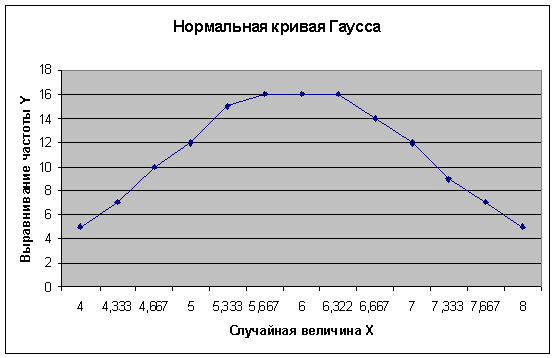
Сравнение графиков нормальной (теоретической)
кривой по выравнивающим частотам (они отмечены кружочками) и полигона
наблюдаемых частот показывает, что построенная теоретическая кривая
удовлетворительно отражает данные наблюдений. Для того, чтобы более уверенно
считать, что данные наблюдений свидетельствуют о нормальном распределении
признака, воспользуемся критериями согласия.