|
n
|
a0
|
a1
|
a2
|
a3
|
a4
|
a5
|
b
|
|
1
|
- 1
|
1
|
0
|
0
|
0
|
0
|
1
|
|
2
|
− 3
|
4
|
- 1
|
0
|
0
|
0
|
2
|
|
3
|
− 11
|
18
|
− 9
|
2
|
0
|
0
|
6
|
|
4
|
− 25
|
48
|
− 36
|
16
|
− 3
|
0
|
12
|
|
5
|
− 137
|
300
|
− 300
|
200
|
− 75
|
12
|
60
|
1.
Погрешность вычислений
Погрешность вычисляется по формуле

где h - шаг сетки, а точка ξ расположена где-то между i-тым и (i +
n)-тым узлами. Примером может служить известная формула (n = 2)
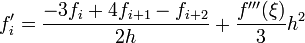 .
.
При n = 1 формула может быть получена и из определения производной. Эта
формула известна под названием формулы дифференцирования вперед.
Формулы "в конце таблицы" могут быть представлены в общем виде
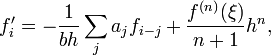
в которых коэффициенты берутся из уже приведенной таблицы. В частности,
при n = 1 получается известная формула дифференцирования назад.
Численное дифференцирование - некорректная задача, так как отсутствует
устойчивость решения. При численном дифференцировании приходится вычитать друг
из друга близкие значения функции. Это приводит к уничтожению первых значащих
цифр, т.е. к потере части достоверных знаков числа. А так как значения функции
обычно известны с определенной погрешностью, то все значащие цифры могут быть
потеряны. На графике кривая (1) соответствует уменьшению погрешности
дифференцирования при уменьшении шага; кривая (2) представляет собой
неограниченно возрастающий вклад неустранимой погрешности исходных данных -
значений функции y(x). Критерий выхода за оптимальный шаг
при его уменьшении - решение: зависимость результатов
вычислений становится нерегулярно зависящей от величины шага.

Пусть ϕ(x,a̅) введена как интерполяционный многочлен Ньютона. В этом случае для
произвольной неравномерной сетки:
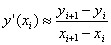 ,
,
для i = 0, 1…n-1, интерполяция полиномом первой степени.
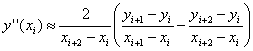 ,
,
интерполяция полиномом второй степени.

Минимальное число узлов, необходимое для вычисления k-й производной, равно k+1.
Оценка погрешности при численном дифференцировании может быть осуществлена
по формуле,
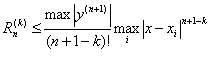 ,
,
где n - число узлов функции, k - порядок производной.
На практике чаще всего используются упрощенные формулы для равномерной
сетки, при этом точность нередко повышается. Часто используются следующие формулы
для трех узлов:
 , где h = x1 - x0 = const.
, где h = x1 - x0 = const.
 .
.
Исходя из общего вида интерполяционного полинома можно вывести формулы
для более высокого порядка точности или для более высоких производных.
2.
Порядок точности
Алгебраический порядок точности численного метода (порядок точности
численного метода, степень точности численного метода, порядок точности,
степень точности) - наибольшая степень полинома, для которой численный метод
даёт точное решение задачи.
Другое определение: говорят, что численный метод имеет порядок точности ,
если его остаток равен нулю для любого полинома степени , но не равен нулю для
полинома степени .
Очевидно, что метод левых (или правых) прямоугольников имеет порядок
точности 0, метод Рунге - Кутты (решения дифференциалных уравнений) четвёртого
порядка - 4. Широко известный метод Гаусса по пяти точкам имеет порядок
точности 9. Менее очевидно, но легко показывается, что порядок точности метода
трапеций - 2, а метода Симпсона - 4.
Наивысшая возможная алгебраическая степень точности для методов
численного интегрирования достигается для метода Гаусса.
Для метода Рунге - Кутты решения ОДУ порядок точности имеет другое
значение - максимальное число первых членов ряда Тейлора полученного решения,
совпадающих с действительным решением ОДУ
3. Суммарная погрешность
Окончательный результат многократного измерения содержит в себе как
случайную, так и приборную погрешности. Случайная погрешность уменьшается с
увеличением количества отдельных измерений, а приборная погрешность не
меняется, оставаясь в пределах ±q. При
выполнении многократного измерения желательно получить столько отдельных
измерений, сколько необходимо для выполнения соотношения
(ᴧ̲x)случ<<0
В таком случае погрешность окончательного результата будет целиком
определена лишь приборной погрешностью. Однако чаще встречается ситуация, когда
случайная и приборная погрешности близки по значению, а поэтому обе влияют на
окончательный результат. Тогда их необходимо учитывать совместно и за суммарную
погрешность принимают
 . (1)
. (1)
Поскольку случайную погрешность обычно оценивают с доверительной
вероятностью 0,68 , а 0 - оценка максимальной погрешности прибора, то можно
считать, что выражение (1) задает доверительный интервал также с вероятность не
меньшей 0,68. При выполнении однократного измерения оценкой погрешности
результата служит ᴧ̲x =
0/3, учитывающая только предельно допустимую приборную погрешность.
Встречаются ситуации, когда случайную и приборную погрешности удается
сравнить без вычислений (ᴧ̲x)случ. Это возможно, если результаты отдельных
измерений не выходят за пределы допустимой приборной погрешности:
(xmax- xmin)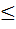 20,
20,
где xmin, xmax - наибольшее и наименьшее значения
измеряемой величины. Повышение точности многократного измерения в таком случае
невозможно, а погрешностью окончательного результата будет 0/3 .
4.
Численное дифференцирование на основе интерполяционной формулы Лагранжа
дифференцирование алгебраический полином интерполяционный
Итак, применяя для численного дифференцирования на отрезке [а; Ь]
интерполяционный полином, естественно строить на этом отрезке систему равноотстоящих
узлов а = х0 < x1 < х2 < ... < xn-1 < хn = b,
которыми отрезок делится на n
равных частей: хi+1 - xi= h = const (i = 0, 1, 2,….,n-1);
шаг интерполирования при этом имеет значение h = (b - а) / n. В этом случае многочлен Лагранжа
строится на равноотстоящих узлах и имеет более удобный вид. Примем подстановку:
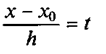

Пn+1(x) и П n+1(xi)
Используя (1), последовательно находим:
- x0 =ht- x1 = x - x0- h =
h(t - 1) - x2 = x - x0
- 2h= h(t-2)
т. е. в общем случае:
- xi =x- x0- ih= h(t- i), i=0, 1, …,n
(3)
Используя (3) получаем:
Пn+1(x)=hn+1t(t-
1)(t- 2)….(t- n).
В целях сокращения записей введем обозначение
t(t- 1)(t- 2)….(t- n)=t[n+1]
тогда выражение Пn+1(x)принимает вид
Пn+1(x)=hn+1,[n+1] (4)
Учитывая, что при постоянном шаге имеет место xi= x0 +ih, i = 0, 1, …n, последовательно находим:
i- x0=hi, xi- x1 =xi-
x0- h =h(i- 1),i- x2 =xi- x0-
h =2h(i- 2),…,xi- xn= xi- xo-nh =
h(i- n). (5)
Заметим, что в (5) равно n
строк (i-я строка отсутствует), причем
значения первых i строк
положительны, а остальных - отрицательны. Используя (5), получаем
П́n+1 (xi) = (xi-x0)….(x1-xi-1)(xi-xi+1)…(xi-xn)=hni(i-1)…
.l (-1)…[-(n-i)],
П́n+1(xi)=hni
l(n-i)(-1)n-i (6)
С учетом представлений (4) и (6) формула Лагранжа (2) для равноотстоящих
узлов принимает вид
 (7)
(7)
Пример 1. Составить интерполяционный многочлен Лагранжа для функции,
заданной своими значениями на равноотстоящих узлах (n = 2, h = 1):
Используя формулу (7),
запишем:
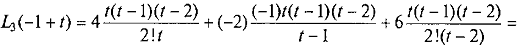
=2(t- 1)(t- 2)+ 2t(t- 2)+ 3t(t- 1)= 7t2- 3+ 4.
Узловые табличные значения функции (4; -2; 6) получаются по этой формуле
соответственно при t = 0; 1; 2.
Будем дифференцировать многочлен Лагранжа (7) по х как функцию от t:

Учитывая, что согласно (1) х = х0 + th, а также dx/dt = h, получим окончательно
 (8)
(8)
Пользуясь формулой (8), можно вычислять приближенные значения производной
функции f(x), если она задана на отрезке [a;b] значениями в
равноотстоящих узлах а = х0 < x1
< х2 < ... < xn-1
<хn = b (при этом параметр t пробегает значения от 1 до n).
Пример 2. Вычислить приближенное значение производной функции, заданной
таблицей
в точке х = 4.
Применяя формулу (8), получим (здесь n= 2, h= 1)

Учитывая, что узел x = 4 соответствует значению t = 1 (т. е. t = x-x0/h), получаем f(4)~2
Если известно аналитическое выражение функции f(х), то формулу для оценки погрешности численного дифференцирования
можно при этом же условии получить на основе формулы погрешности
интерполирования

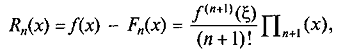 (9)
(9)
где ξ=ξ(x) - значение из отрезка [a;b], отличное от
узлов и х.
Учитывая (9) и допуская, что f(x) дифференцируема n+ 1 раз, запишем
 (10)
(10)
Формула (10) значительно упрощается, если оценка находится для значения
производной f'(x) в узле хi
таблицы. В этом случае, учитывая (6), получаем
 (11)
(11)
где ξ- промежуточное значение между x0, x1, x2,…xn.
Обозначив Мn + 1 = 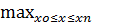 |f (n+1)(x)|, получим верхнюю оценку абсолютной
ошибки численного дифференцирования в узлах:
|f (n+1)(x)|, получим верхнюю оценку абсолютной
ошибки численного дифференцирования в узлах:

5.
Численное интегрирование
дифференциальных уравнений второго порядка
Задача Коши для дифференциального уравнения n-го порядка
(n)=f(x,y,y’,…,y(n-1)) (2.5.1)
при начальных условия у(k) (х0) =y(k)0 (k = 0, 1, 2, …,n- 1) , сводится к задаче Коши для
системы
 (2.5.2)
(2.5.2)
где yk (x0) = у(k)0 (k =0,
1, 2, n - 1; у0 = у).
Поэтому изложенные методы приближенного интегрирования систем
дифференциальных уравнений применимы также к уравнению (2.5.1).
Однако общие схемы для приближенного решения дифференциальных систем, не
учитывающие специфических особенностей системы (2.5.2), оказываются излишне
сложными. Поэтому целесообразно вывести формулы, специально приспособленные для
численного интегрирования дифференциального уравнения вида (2.5.1). Мы
ограничимся рассмотрением дифференциального уравнения второго порядка
"=f(x,y,y’) (2.5.3)
при начальных условиях у(х0)=у0, у'(х0)=у'0.
Выведем формулы для приближенного вычисления интеграла у = у (х) дифференциального
уравнения (2.5.3) с помощью метода Адамса. Для этого выберем шаг 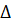 x =h и введем стандартные обозначения:
x =h и введем стандартные обозначения:
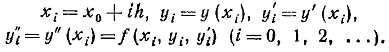
Допустим, чтo известны значения
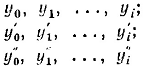
(i ). Тогда можно вычислить разности
∆y"i-1,
). Тогда можно вычислить разности
∆y"i-1, 2yi-2,
2yi-2, 3yi-3
3yi-3
Применяя вторую интерполяционную формулу Ньютона, с точностью до
разностей четвертого порядка будем иметь
 (2.5.4)
(2.5.4)
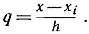 (2.5.5)
(2.5.5)
Так как в силу формулы (2.5.5) dx = h dq то, очевидно, имеем
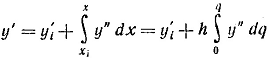 (2.5.6)
(2.5.6)
 (2.5.7)
(2.5.7)
Интегрируя последовательно на отрезке [0, q] два раза по q
формулу (2.5.4), на основании формул (2.5.6) и (2.5.7) получим
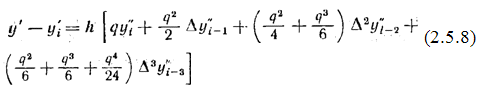
Отсюда, полагая q= 1 в
формулах (2.5.6') и (2.5.7'), находим
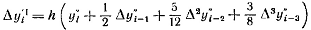 (2.5.8)
(2.5.8)
 (2.5.9)
(2.5.9)
где положено 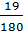
 Mожно принять
Mожно принять
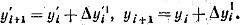 (2.5.10)
(2.5.10)
Более точный вариант счета следующий [14]: найдя y’i+1, по
формулам (2.5.8) и (2.5.10) вычисляют 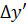 i,
i,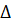 2y’i-1,
2y’i-1, 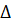 3’yi-2 ,после чего определяют
3’yi-2 ,после чего определяют 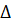 yi.
yi.
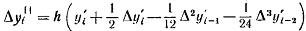
Затем, приняв
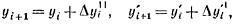 (2.5.11)
(2.5.11)
из дифференциального уравнения можно найти
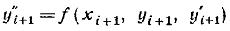
 (2.5.12)
(2.5.12)
В случае необходимости повторяют аналогичный пересчет величин уi+1 и у’i+1 до тех пор, пока не прекратятся
изменения. Рекомендуется шаг h
выбирать столь малым, чтобы формулы (2.5.10) и (2.5.11) давали одинаковые
результаты в пределах заданной точности. Что
касается начального отрезка y0,y1,y2,y3; y’0,y’1,y’2,y’3 то он предварительно
определяется каким-нибудь подходящим методом. В частности, для дифференциального уравнения вида
"=f (x,y)
имеется весьма точный метод Б. В. Нумерова.
Пример 1. На отрезке [0, 1] найти интеграл у = у (х) уравнения
"+ y ch x+0 (2.5.13)
удовлетворяющий начальным условиям
(0)=0, y’(0)=1 (2.5.14)
Решение. Примем шаг h=0,2. Для подсчета начального отрезка применим метод
степенных рядов. Имеем
"= - y ch x
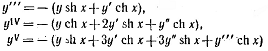
Следовательно, в силу начальных условий (2.5.14) получаем:

Полагая xi=0,2 i ( i= -1,
0, 1, 2), из формул (2.5.15) с точностью до 10-3 находим:

Дальнейшие вычисления производим по формулам (2.5.8), (2.5.9), (2.5.10)
без пересчета. Результаты вычислений приведены в таблицах 1 и 2.
Таблица 1 Основной бланк для решения задачи
Коши
|
i
|
x
|
y
|
∆y
|
y’
|
∆y’
|
ch x
|
y"
|
|
∆2y"
|
∆3y"
|
|
-1 0 1 2 3 4 5
|
-0,2 0 0,2 0,4
0,6 0,8 1,0
|
-0,199 0 0,199
0,389 0,563 0,710 0,819
|
0,174 0,147
0,109
|
0,980 1 0,980
0,918 0,810 0,649
|
-0,108
-0,161
|
1,020 1 1,020
1,081 1,185 1,337
|
0,203 0 -0,203
-0,421 -0,667 -0,949
|
-203 -203 -218
-246 -282
|
0 -15 -28 -36
|
-15 -13 -8
|
Таблица
2 Вспомогательный бланк
для решения задачи Коши
|
i
|
2
|
3
|
4
|
|

|
-0,421 -0,109
-0,006 -0,006
|
-0,667 -0,123
-0,012 -0,005
|
|
|
 1 1  y’i=h∑1 y’i=h∑1
|
-0,542 -0,108
|
-0,807 -,0161
|
|
|
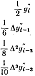
|
-0,210 36 2 2
|
-0,334 -0,041
-0,004 -0,001
|
-0,474 -0,047
-0,004 -0,001
|
|
∑2
|
-0,250
|
-0,380
|
-0,526
|
|
h2∑2
hy’i
|
-0,010 +0,184
|
-0,015 +0,162
|
-0,021 +0,130
|
|
 yi yi
|
0,174
|
0,147
|
0,109
|
Список
литературы
) Численные методы: Учеб. пособие для студ. вузов /
М.П.Лапчик, М.И.Рагулина, Е.К.Хеннер; Под ред. М.П.Лап-чика. - М.: Издательский
центр "Академия", 2004.
) http://solidbase.karelia.ru/edu/meth_calc/files/06.shtm
) http://ru.wikipedia.org/wiki/Численное_диференцирование
) Б.П Демидович, И.А Марон, Э.З. Шувалова; "Численные
методы анализа"