Формула Грина

Формула Грина

Содержание

Введение

1. Формула Грина и её доказательство

2. Формула Грина в векторной форме.

3. Вывод формулы Грина из формулы Стокса

4. Применение формулы Грина

Заключение

Список использованной литературы:

Введение

Джордж Грин (George Green, 1793 - 1841) - английский математик и физик, самостоятельно изучил математику и лишь в 1837 окончил Кембриджский университет. Он ввел понятие и термин “потенциала”, Опираясь на найденное им соотношение между интегралом по объему и интегралом по поверхности, ограничивающей этот объем (формула Грина), развил теорию электричества и магнетизма. Простейшая из них связывает двойной интеграл по области  с криволинейным интегралом по границе области. Эта формула была известна еще Л. Эйлеру (1771 г.).

Актуальность исследования: в ходе выполнения курсовой работы, могу отметить, что формула Грина применяется в решении разных задач, не только в математике, но и физике. К сожалению, в учебном курсе формуле Грина отводится не много времени.

Проблема исследования: применение формулы Грина к решению задач.

Объект исследования: Формула Грина.

Предмет исследования: задачи решаемые с помощью формулы Грина.

Цель курсовой работы: ознакомится с теоретическими сведениями по теме «Формула Грина», рассмотреть её применение в решение задач на примерах.

Основные задачи исследования:

1.   Выполнить анализ литературы по теме исследования.

2.       Выделить основные теоретические понятия, используемые в работе.

.        Привести теоремы и их доказательства по данной теме.

.        Подобрать и решить задачи по данной теме.

Для решения поставленных задач были использованы следующие методы исследования:

.        Анализ учебной литературы по данной теме.

.        Обобщение материала, найденного по теме исследования.

Практическая значимость Практическая значимость данной курсовой работы определяется тем, что подобранный материал может быть использован при изучении и применении формулы Грина.

Курсовая работа состоит из введения, 4 параграфов, списка задач, заключения и списка используемой литературы.

В списке используемой литературы - 6 наименований.

1. Формула Грина и её доказательство

Определение 1. Ориентация контура  называется положительной, если при обходе (соответствующего возрастанию параметра) контура , область  остается слева (такой обход обычно называется обходом контура против часовой стрелки), в противном случае - отрицательным.

Будем обозначать положительно ориентированный контур ⁺, а отрицательно ориентированный - ^-.

Формулу Грина докажем для простых областей .

Определение 2. Плоская область G называется простой относительно оси Оу, если её граница Г состоит из графиков двух непрерывных на  функций ,  и, может быть, двух отрезков прямых  .

Формулировка:

Пусть C - положительно ориентированная кусочно-гладкая замкнутая кривая на плоскости, а D - область, ограниченная кривой C. Если функции <#"556361.files/image009.gif">, , то

На символе интеграла часто рисуют окружность, чтобы подчеркнуть, что кривая С замкнута.

Доказательство:

Формулу Грина докажем для простых областей D.

Пусть область D - криволинейная трапеция (область, цилиндрическая в направлении OY):

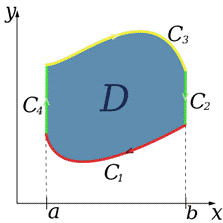
Для кривой C, ограничивающей область D зададим направление обхода по часовой стрелке.

Тогда:

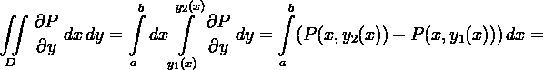
Заметим, что оба полученных интеграла можно заменить криволинейными интегралами:

Интеграл по C₁ берётся со знаком "минус", так как согласно ориентации контура C направление обхода данной части - от b до a.

Криволинейные интегралы по C₂ и C₄ будут равны нулю, так как :

Заменим в (1) интегралы согласно (2) и (3), а также прибавим (4) и (5), равные нулю и поэтому не влияющие на значение выражения:

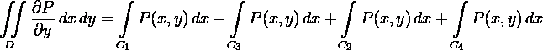
Так как обход по часовой стрелке при правой ориентации плоскости является отрицательным направлением, то сумма интегралов в правой части является криволинейным интегралом по замкнутой кривой C в отрицательном направлении:

Аналогично доказывается формула:

если в качестве области D взять область, правильную в направлении OX.

Складывая (6) и (7), получим:

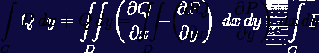
Если , то формула Грина принимает вид

где S − это площадь области R, ограниченной контуром C.

2. Формула Грина в векторной форме

Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля.

Пусть векторное поле описывается функцией

Ротором или вихрем векторного поля  называется вектор, обозначаемый  или  и равный

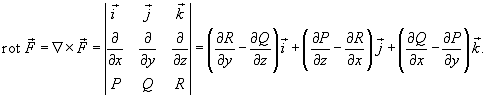
Формула Грина в векторной форме записывается в виде

Заметим, что формула Грина вытекает из "теоремы Стокса <#"556361.files/image033.gif"> - дифференцируемое векторное поле <#"556361.files/image034.gif"> равна потоку <#"556361.files/image035.gif">

или в координатной записи:

Вывод из теоремы Стокса:

Рассмотрим дифференциальную форму <#"556361.files/image038.gif">.

Тогда, используя свойство дифференциала дифференциальной формы :

Отсюда, используя теорему Стокса:

Вывод формулы Грина из формулы Стокса:

Определяя дифференциальную форму <#"556361.files/image043.gif">, найдём её внешний дифференциал <#"556361.files/image044.gif">

Принимая во внимание, что

 и :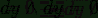

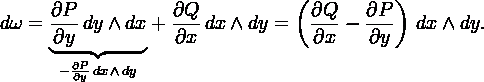
Отсюда используя теорему Стокса:

4. Применение формулы Грина

Задача 1.

Применяя формулу Грина, вычислить следующий криволинейный интеграл:

где С - пробегаемый в положительном направлении контур, ограничивающий область D = {(x,y) 0<x<π, 0<y<sinx.}

Решение:

По формуле Грина, имею:

Задача 2.

На сколько отличаются друг от друга криволинейные интегралы

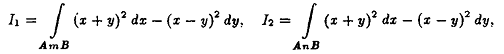
где AmB - отрезок прямой, соединяющий точки А=(1, 1) и В=(2, 6), AnB - дуга параболы с вертикальной осью, проходящей через те же точки А, В и начало координат? формула грин криволинейный интеграл

Решение:

Уравнение параболы, проходящей через начало координат и точки А, В, имеет вид  а разность I₂ ̴ I₁ является криволинейным интегралом по замкнутому контуру AnBmA, ограничивающему область  и пробегаемому в положительном направлении, в силу чего можем применить формулу Грина:

Следовательно, I₁ - I₂=2.

Задача 3.

Вычислить криволинейный интеграл

где AmO - верхняя полуокружность, заданная уравнением x2+y2=ax, пробегаемая от точки А (а, 0) до точки О (0, 0).

Решение:

На сегменте [0, а] подынтегральное выражение равно нулю, поэтому интеграл кривой AmO равен интегралу по замкнутому контуру AmOА, состоящему из кривой AmO и сегмента [0, а], ограничивающему область D =

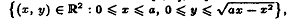в силу чего могу применить формулу Грина:

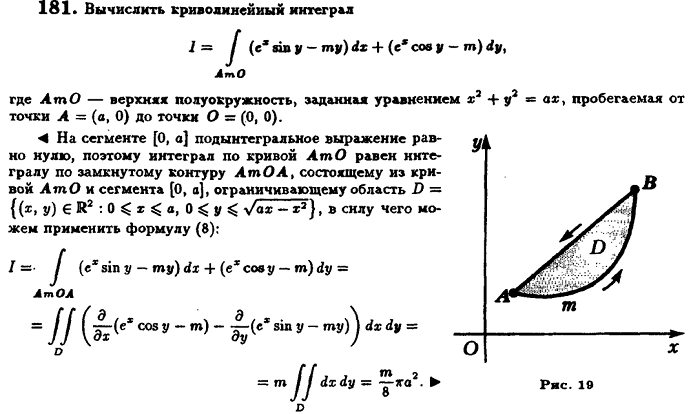
Задача 4.

Вычислить криволинейный интеграл

где φ(у) и φ́(у) - непрерывные функции и AmB - произвольный путь, соединяющий точки А(х₁, у₁) и В(х₂, у₂), но ограничивающий вместе с отрезком АВ площадь AmBA фигуру D, площадь которой равна данной величине Р.

Решение:

Интеграл по кривой AmB представлю в виде суммы интегралов по замкнутому контуру AmBA и по отрезку АВ.

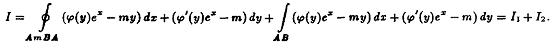
Интеграл I₁ вычислим, применив формулу Грина:

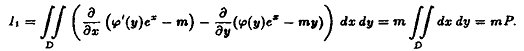
Для вычисления интеграла I₂ преобразуем подынтегральное выражение к виду

где du - полный дифференциал некоторой функции. Следовательно,

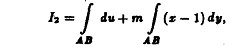
где первый интеграл в правой части этого равенства не зависит от выбора пути интегрирования, соединяющего точки А и В. Таким образом,

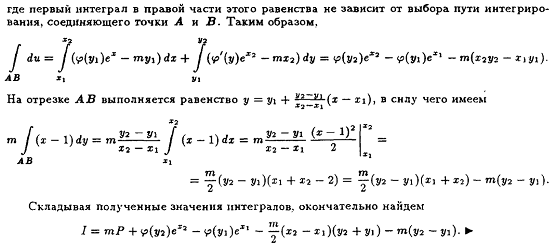
На отрезке АВ выполняется равенство

в силу чего имеем

Складывая полученные значения интегралов, окончательно найдём:

Задача 5.

для любого замкнутого контура γ не зависит от постоянных α и β.

Решение:

Если функции P и Q удовлетворяют поставленному условию, то должно выполнятся равенство

для любого замкнутого контура γ, в силу чего имеем

где

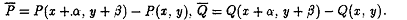
Для того, чтобы криволинейный интеграл I₁ по любому замкнутому контуру γ был равен нулю, необходимо и достаточно, чтобы в односвязной области, ограниченной этим контуром, и на самом контуре выполнялось равенство 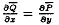 (которое следует из формулы Грина). Обозначив получим написанное условие в виде

откуда имеем равенство

Левая часть этого равенства не зависит от ζ и η, поскольку правая его часть зависит только от х и у, следовательно,

Из условия 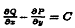 получаем равенство 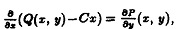 справедливо лишь в том случае, когда

дважды непрерывно дифференцируемые функции. Окончательно находим:

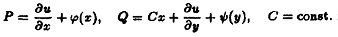
Задача 6.

Вычислить

где γ - простой замкнутый контур, не проходящий через начало координат, пробегаемый в положительном направлении.

Решение:

Если контур γ не окружает начало координат, то применив формулу Грина, получу:

Если контур γ окружает начало координат, то применять формулу Грина нельзя, поскольку область D в этом случае неодносвязна. В этом случае будем вычислять интеграл I непосредственно.

Обозначу через w дифференциальное выражение под знаком интеграла I. Покажем, что интеграл

не зависит от выбора кривой γ, окружающий начало координат.

Пусть γ₁ и γ₂ - произвольные непересекающиеся замкнутые гладкие или кусочно-гладкие контуры, окружающие начало координат и ограничивающие простую область 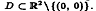При положительной ориентации границы  области D направления обхода кривых γ₁ и γ₂ будут противоположны

Двухсвязная простая область D не содержит особой точки подынтегрального выражения w, поэтому, согласно формуле Грина, имею:

откуда следует равенство

показывающее, что интеграл I не зависит от выбора замкнутой кривой γ, окружающей начало координат. Взяв окружность

 получим:

Задача 7.

Найти с помощью формулы Грина площадь, ограниченную эллипсом

Решение:

Воспользуемся формулой (следствие из формулы Грина)

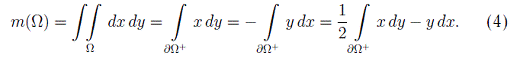
и стандартной параметризацией эллипса

Г =  

Задача 8.

Вычислить криволинейный интеграл

Где Г - верхняя полуокружность

Решение:

Обозначим дополним контур Г до замкнутого контура L отреком оси Ох, соединяющим концы полуокружности О(0, 0) и А(а, 0). Тогда

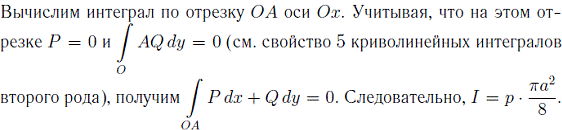
Задача 9.

Используя формулу Грина, вычислить интеграл 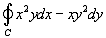. Кривая C представляет собой окружность  , обход которой производится против часовой стрелки.

Решение.

Запишем компоненты векторного поля и их производные:

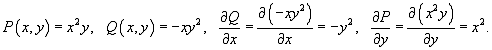 Тогда

где R − круг радиуса a с центром в начале координат. Переходя к полярным координатам, находим искомый интеграл:

Задача 10.

Используя формулу Грина, найти интеграл , где кривая C представляет собой эллипс  

Решение.

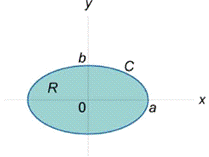
Очевидно, здесь

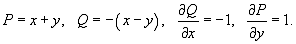
Следовательно,

Поскольку двойной интеграл  численно равен площади эллипса 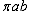, то интеграл равен

Задача 11.

Вычислить интеграл 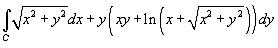 с помощью формулы Грина. Контур интегрирования C представляет собой окружность  .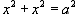

Решение.

Компоненты векторного поля и их частные производные равны

Тогда по формуле Грина получаем

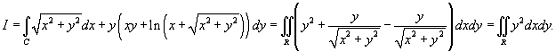
Для вычисления двойного интеграла удобно перейти к полярным координатам.

Здесь

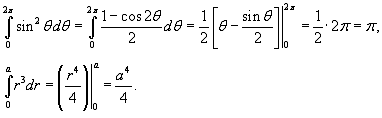
Таким образом, интеграл равен

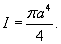
Заключение

В данной курсовой работе я рассмотрела формулу Грина и смежные понятия, мною были подобраны и разобраны упражнения по данной теме. Подводя итог курсовой работы можно сказать, что поставленная цель достигнута.

При выполнении данной курсовой работы были решены, поставлены задачи и выполнено следующее:

.        Выполнен анализ литературы по теме исследования.

.        Выделены основные теоретические понятия, используемые в работе.

.        Изучены основные способы решения задач.

.        Подобраны и решены задачи по данной теме.

Список литературы

1.   Демидович Б.П. сборник задач и упражнений по математическому анализу: Учеб.пособие. - 13-е изд., испр. - М.: Изд-во Моск. Ун-та, ЧеРо, 1997. - 624с.

2.       Запорожец Г. И. Руководство к решению задач по математическому анализу. - М.: Высшая школа, 1966.

.        Зорич В. А. Математический анализ. Часть II. М.: Наука, 1984. 640 с.

.        Камынин Л. И. Курс математического анализа (в двух томах). М.: Издательство Московского Университета, 2001.

5.       Картан А. <http://ru.wikipedia.org/wiki/%D0%9A%D0%B0%D1%80%D1%82%D0%B0%D0%BD,_%D0%90%D0%BD%D1%80%D0%B8> Дифференциальное исчисление. Дифференциальные формы. - М.: Мир, 1971.

.        Кудрявцев Л.Д. Краткий курс математического анализа. Т.1. Дифференциальное и интегральное исчисления функций одной переменной. Ряды. Учебник. - 3-е изд., перераб. - М.: ФИЗМАТЛИТ, 2005. - 400 с.

.        Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, т.III. М., Наука, 1956.- 656 стр. с ил.