Теорема Ляпунова
Министерство
образования и науки Украины
Днепропетровский
национальный университет
им.
О. Гончара
Механико-математический
факультет
Кафедра
дифференциальных уравнений
Курсовая
работа
по
асимптотическим методам в теории
дифференциальных
уравнений
Выполнила: студентка группы ММ-08-3
Харчук А.Н.
г.
Днепропетровск - 2011
Содержание
Теоретическая
часть
Раздел
1.
Система Ляпунова ─ случай одной степени свободы
1. Система
Ляпунова
2. Приведение
к каноническому виду
3. Преобразование
интеграла H
4. Периодичность
решений системы Ляпунова
5.
Теорема Ляпунова
Раздел
2.
Условия существования периодических решений
.
Необходимые и достаточные условия периодичности
Раздел
3.
Метод Ляпунова
1.
Алгоритм
Практическая
часть
Индивидуальное
задание
Решение
задания
Список
литературы
Теоретическая часть
Раздел 1. Система Ляпунова ─
случай одной степени свободы.
. Система Ляпунова
Рассмотрим систему дифференциальных
уравнений
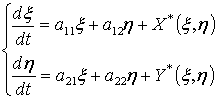 (1.1)
(1.1)
где 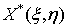 и
и  ─ аналитические функции своих
переменных в окрестности точки
─ аналитические функции своих
переменных в окрестности точки 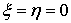 и такие, что их разложение по
степеням
и такие, что их разложение по
степеням 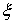 и
и 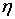 начинается
с членов, порядок которых не ниже второго:
начинается
с членов, порядок которых не ниже второго:
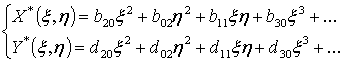 (1.2)
(1.2)
Систему (1.1) будем называть системой
Ляпунова, если выполняются следующие условия:
1) уравнение
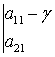
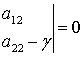 (1.3)
(1.3)
имеет чисто мнимые корни  ;
;
2) система (1.1) допускает аналитический
первый интеграл
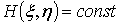 , (1.4)
, (1.4)
разложение которого по степеням
переменных 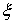 и
и 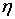 начинается с
членов второго порядка малости, т. е. функция
начинается с
членов второго порядка малости, т. е. функция 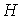 в окрестности точки
в окрестности точки 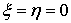 является
аналитической функцией своих переменных и представима в следующем виде:
является
аналитической функцией своих переменных и представима в следующем виде:

. Приведение к каноническому виду
Рассмотрим вспомогательную систему уравнений
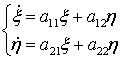 (1.5)
(1.5)
Система (1.5) описывает колебание с постоянной
амплитудой, поскольку её характеристическое имеет пару чисто мнимых корней.
Исключая из уравнения (1.5)
переменную 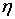 , получим
, получим
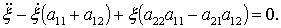 (1.6)
(1.6)
Для того, чтобы удовлетворилось
условие 1), коэффициент при 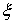 должен быть равен нулю, т. е.
должно быть
должен быть равен нулю, т. е.
должно быть  и, кроме
того, должно иметь место неравенство
и, кроме
того, должно иметь место неравенство
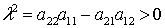 .
.
Сделаем замену
 ,
, 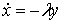 , (1.7)
, (1.7)
где 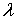 ─ арифметическое значение
корня
─ арифметическое значение
корня 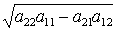 .
.
Таким образом, получим
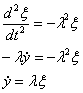
Как мы видим при помощи замены (1.7)
уравнение (1.6) сводится к эквивалентной системе двух уравнений
 .
.
Также
 (1.7’)
(1.7’)
Поэтому, если в исходной системе (1.1) сделать
замену (1.7), то эта система будет приведена к виду (1.8).
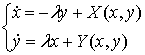 (1.8) -
система Ляпунова в каноническом виде
(1.8) -
система Ляпунова в каноническом виде
где 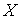 и
и 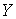 ─ аналитические функции своих
переменных, разложение которых начинается с членов второго порядка малости.
Таким образом, вместо системы (1.1) нам достаточно рассмотреть систему (1.8).
─ аналитические функции своих
переменных, разложение которых начинается с членов второго порядка малости.
Таким образом, вместо системы (1.1) нам достаточно рассмотреть систему (1.8).
3. Преобразование интеграла H
Остановимся ещё на выражении
интеграла 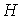 . Согласно
положению 2) его представление имеет вид
. Согласно
положению 2) его представление имеет вид
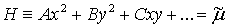 , (*)
, (*)
где 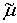 ─ некоторая постоянная.
─ некоторая постоянная.
Но сначала рассмотрим ситуацию,
когда первый интеграл имеет вид:
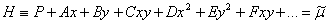 (1.9)
(1.9)
Так как (1.9) ─ первый интеграл,
то вдоль каждой кривой семейства (1.8) он должен обращаться в 0.
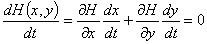 .
.
Подставим и получим
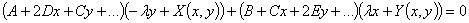
Сравнивая коэффициенты при 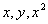 ,
,  и
и 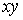 , получим
, получим
При y:
При х:
При ху:
При х2:
При у2: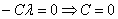
Отсюда 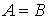 =
=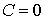 , D=E. Не нарушая
общности можно принять
, D=E. Не нарушая
общности можно принять 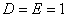 .
.
Итак, интеграл H можно
представить в виде
 , (1.10)
, (1.10)
где  ─ аналитическая функция своих
переменных, разложение которой начинается с членов не ниже третьего порядка
малости,
─ аналитическая функция своих
переменных, разложение которой начинается с членов не ниже третьего порядка
малости,  ─
некоторая постоянная, которую всегда мы можем считать положительной для
достаточно малых
─
некоторая постоянная, которую всегда мы можем считать положительной для
достаточно малых  и
и 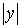 .
.
Таким образом, мы видим, что
представление первого интеграла всегда имеет вид (*) и, кроме того, его можно
представить в виде (1.10)
. Периодичность решений системы
Ляпунова
Докажем теперь, что существует
периодическое решения системы (1.8) для достаточно малых значений 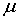 . И что это
решение ─ периодические функции
. И что это
решение ─ периодические функции 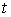 . Для этого достаточно доказать, что
фазовые траектории в плоскости
. Для этого достаточно доказать, что
фазовые траектории в плоскости  замкнутые и
замкнутые и 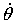 сохраняет
знак. Для этого введём полярные координаты
сохраняет
знак. Для этого введём полярные координаты
 ;
;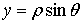
и заметим, что любая замкнутая траектория
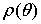 должна быть
периодической функцией аргумента
должна быть
периодической функцией аргумента 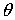 . Составим выражение для
. Составим выражение для 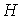 :
:
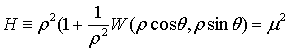 (1.11)
(1.11)
Здесь  ─ аналитическая функция
─ аналитическая функция 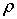 , разложение
которой имеет вид
, разложение
которой имеет вид
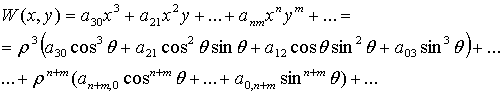
Следовательно, в формуле (1.11)
функция 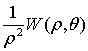 может быть представлена
в виде ряда
может быть представлена
в виде ряда
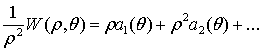 ,
,
причем, все коэффициенты 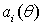 ─
полиномы от
─
полиномы от 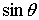 и
и 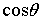 , т. е.
периодические функции
, т. е.
периодические функции  . Таким
образом, выражение (1.11) можно переписать так:
. Таким
образом, выражение (1.11) можно переписать так:
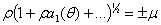
Это равенство мы можем рассматривать
как уравнение для определения 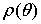 .
.
Используя аналитичность функций,
которые в него входят, будем функцию 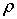 разыскивать в виде ряда
разыскивать в виде ряда
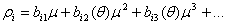 , i=1, 2. (1.12)
, i=1, 2. (1.12)
Прямым вычислением убеждаемся в том,
что коэффициенты в разложении (1.12) являются полиномами от 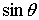 и
и 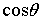 . Так,
например,
. Так,
например,
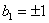 ,
, 
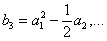
Таким образом, коэффициенты 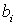 ─
степенные функции коэффициентов
─
степенные функции коэффициентов 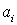 , а последние в свою очередь
являются полиномами от
, а последние в свою очередь
являются полиномами от 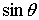 и
и 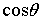 . Вследствие
такой структуры коэффициентов ряд (1.12) определяет периодическую функцию
. Вследствие
такой структуры коэффициентов ряд (1.12) определяет периодическую функцию  периода
периода 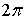 , т. е. при
изменении
, т. е. при
изменении  на
на 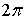 величина
величина 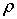 возвращается
к своему исходному значению. Если при этом окажется, что
возвращается
к своему исходному значению. Если при этом окажется, что 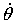 сохраняет
знак, то это и будет означать, что фазовая траектория замкнутая.
сохраняет
знак, то это и будет означать, что фазовая траектория замкнутая.
Таким образом, решения системы (1.8)
─ функции 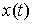 и
и 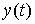 ─
будут периодическими функциями времени.
─
будут периодическими функциями времени.
Функции 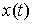 и
и 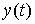 являются
аналитическими по параметру
являются
аналитическими по параметру 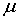 . В самом деле, в силу аналитичности
правых частей системы (1.8) её решения будут аналитическими функциями начальных
значений
. В самом деле, в силу аналитичности
правых частей системы (1.8) её решения будут аналитическими функциями начальных
значений
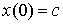 ,
,  .
.
Постоянная 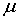 так же
определяется этими значениями
так же
определяется этими значениями
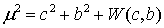 . (1.13)
. (1.13)
Так как правые части системы (1.8) не зависят от
времени, то без ограничений общности начальные условия можно записать в виде
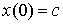 ,
,  . (1.14)
. (1.14)
Отсюда видно, что решения системы
(1.8) представляют собой аналитические функции 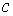 .
.
5. Теорема Ляпунова
Теперь вычислим период, для этого
составим дифференциальные уравнения, которым удовлетворяют переменные ρ и θ. Вычислим
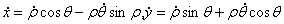 (1.15)
(1.15)
Заменяя в системе (1.15) производные
 и
и 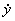 их
выражениями из уравнений (1.8) и разрешая полученную систему относительно
производных
их
выражениями из уравнений (1.8) и разрешая полученную систему относительно
производных  и
и 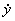 , найдем
искомые уравнения
, найдем
искомые уравнения
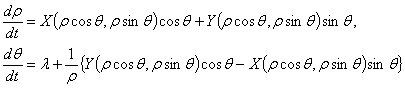 (1.16)
(1.16)
Из второго уравнения определим t:
 (1.17)
(1.17)
Для того чтобы удовлетворить
условиям (1.13), необходимо константу (1.17) принять равной нулю. Используем
тот факт, что ρ
- аналитическая
функция μ.
Это
позволит разложить подынтегральную функцию в выражении (1.17) в ряд по степеням
μ
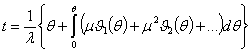 (1.17’)
(1.17’)
где 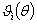 - периодические функции θ периода 2π. Следовательно,
подынтегральная функция в (1.17’) также периодическая функция θ периода 2π.
Следовательно, интеграл
- периодические функции θ периода 2π. Следовательно,
подынтегральная функция в (1.17’) также периодическая функция θ периода 2π.
Следовательно, интеграл

не зависит от θ0 и его можно
записать в виде
 ,
,
где 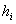 - вполне определенные числа. Таким
образом, при измени θ
на
2π
время
t получает приращение Т
- вполне определенные числа. Таким
образом, при измени θ
на
2π
время
t получает приращение Т
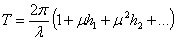 , (1.18)
, (1.18)
не зависящие от θ0.
Пусть теперь Ф(θ) - некоторая
периодическая функция θ
периода
2π,
тогда
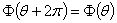 . (1.19)
. (1.19)
Рассматривая ее как функцию t, будем
иметь
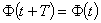 . (1.20)
. (1.20)
Равенство (1.19) справедливо для
любых θ,
следовательно,
и равенство (1.20) справедливо для любых t, т. е. Ф(t) - периодическая функция
t. Значит, величина Т, определенная формулой (1.18) как функция μ, и есть
период решения.
Используя (1.17), мы можем записать
его в следующем виде:

где  период Т стремится к периоду
линейных колебаний 2π/λ,
т.
е. к периоду колебаний в системе (1.8) при
период Т стремится к периоду
линейных колебаний 2π/λ,
т.
е. к периоду колебаний в системе (1.8) при 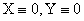 .
.
Покажем теперь, что Т- четная
функция μ.
Вернемся
сова к интегралу (1.11). рассматривая его как уравнение относительно ρ, мы получаем
в окрестности точки ρ=0
два
решения. Одно из них
 (1.21)
(1.21)
другое
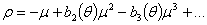 (1.21’)
(1.21’)
Теперь заметим, что левая часть
уравнения (1.11) не изменится, если заменим ρ на -ρ и θ на θ +
2π. Следовательно,
на основании (1.21) будем иметь
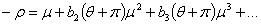 (1.22)
(1.22)
Значение ρ, определенное
рядом (1.22), будет корнем уравнения (1.11), не совпадающее с (1.21) (потому,
что для малых ρ
из
(1.21) следует ρ
= μ+О(μ2), а из
(1.22) ρ
= - μ+О(μ2)).
Следовательно, оно будет определяться рядом (1.21’).
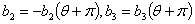
и т.д.
Отсюда следует, что если в выражении
(1.21) заменить μ
на
- μ,
а
θ
на
θ
+ π, то
величина ρ
примет
свое значение с обратным знаком:
 .
.
Выпишем теперь выражение для периода
Т. На основании (1.17) имеем
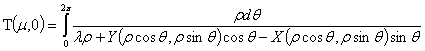 . (1.23)
. (1.23)
Сделаем замену в (1.23) замену μ на -μ, а θ на θ + π.
Тогда
получим величину
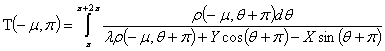 .
.
Согласно доказанному величины  и
и  сохраняют
свои значения. Следовательно, то же самое можно сказать и о функциях Х и Y. В
то же время
сохраняют
свои значения. Следовательно, то же самое можно сказать и о функциях Х и Y. В
то же время  ,
,  и
и 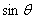 изменяют
свои знаки. Следовательно, знаменатель изменит знак на обратный, но и числитель
изменит знак на обратный. Следовательно,
изменяют
свои знаки. Следовательно, знаменатель изменит знак на обратный, но и числитель
изменит знак на обратный. Следовательно,
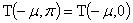 .
.
Итак,
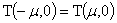 ,
,
т. е. период - четная функция
величины μ.
Таким образом, выше было доказано
теорему Ляпунова, а теперь сформулируем ее.
Теорема Ляпунова.
Если постоянная  достаточно
мала, то все решения системы уравнения (1.8) ─ периодические функции t, причем
период ─ четная функция величин
достаточно
мала, то все решения системы уравнения (1.8) ─ периодические функции t, причем
период ─ четная функция величин  и при
и при 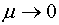 стремится к
стремится к
 . Решения
системы (1.8) являются аналитическими функциями величины c ─
начального отклонения переменной x.
. Решения
системы (1.8) являются аналитическими функциями величины c ─
начального отклонения переменной x.
Имея в виду формулу 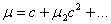
выражение периода можно переписать в
следующем виде:
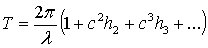 (1.24)
(1.24)
Раздел 2.
Условия существования периодических
решений
. Необходимые и достаточные условия
периодичности
Рассмотрим систему:
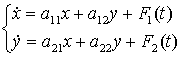 (2.1)
(2.1)
Сначала мы не будем делать никаких
предположений о природе коэффициентов  , кроме предположения об их
периодичности по
, кроме предположения об их
периодичности по 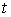 .
.
Пусть 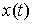 и
и 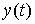 ─ решение системы (2.1),
удовлетворяющее следующим данным Коши:
─ решение системы (2.1),
удовлетворяющее следующим данным Коши:
 ,
,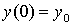 .
.
Для того чтобы это решение было
периодическим с периодом 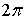 , необходимо
и достаточно, чтобы оно удовлетворяющее следующим условиям:
, необходимо
и достаточно, чтобы оно удовлетворяющее следующим условиям:
 ,
, 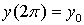 . (2.2)
. (2.2)
Очевидно, что условия (2.2)
необходимы, так как функция называется периодической, если она удовлетворяет
условиям:
 ,
,  (2.3)
(2.3)
каково бы не было  . Условия
(2.2) являются частным случаем (2.3) при
. Условия
(2.2) являются частным случаем (2.3) при 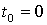 . Эти условия являются так же
достаточными. В самом деле, правые части системы (2.1) ─ периодические
функции времени периода
. Эти условия являются так же
достаточными. В самом деле, правые части системы (2.1) ─ периодические
функции времени периода 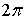 и,
следовательно, они инвариантны относительно замены переменного
и,
следовательно, они инвариантны относительно замены переменного  , тогда в
силу (2.2) по
, тогда в
силу (2.2) по 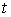 и
и 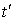 мы будем
иметь одну и ту же задачу Коши и, следовательно,
мы будем
иметь одну и ту же задачу Коши и, следовательно,
 ;
;
Или
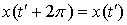 ;
;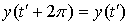 .
.
Так как это равенство справедливо
для любых 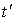 , то оно
совпадает с (2.3) и, следовательно, функции
, то оно
совпадает с (2.3) и, следовательно, функции 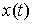 и
и 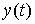 ─ периодические.
─ периодические.
Предположим далее, что система
фундаментальных решений систем
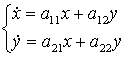 (2.4)
(2.4)
нам известна. Обозначим эти функции
через 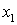 ,
,  ,
, 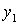 и
и  , и решение
системы (2.1) будем искать методом вариации произвольных постоянных, полагая
, и решение
системы (2.1) будем искать методом вариации произвольных постоянных, полагая
 ,
, 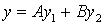 . (2.5)
. (2.5)
где  и
и 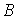 ─ некоторые функции времени,
подлежащие определению.
─ некоторые функции времени,
подлежащие определению.
Подставим выражения (2.5) в (2.1).
Принимая во внимание, что функции 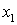 ,
,  ,
, 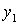 и
и  удовлетворяют системе (2.4), мы
получим следующие уравнения для определения функций
удовлетворяют системе (2.4), мы
получим следующие уравнения для определения функций  и
и 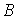 ;
;
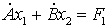 ,
,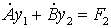 ,
,
откуда
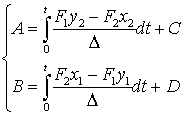 (2.6)
(2.6)
где  и
и 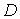 ─ новые произвольные
постоянные, а
─ новые произвольные
постоянные, а  ─
определитель Вронского
─
определитель Вронского
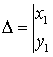
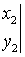 .
.
Постоянные  и
и 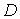 определяются
из начальных условий
определяются
из начальных условий 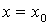 ,
, 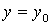 при
при 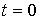 . Так как
интегральные слагаемые в выражениях (2.6) при
. Так как
интегральные слагаемые в выражениях (2.6) при 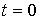 обращается в нуль, то постоянные
обращается в нуль, то постоянные  и
и 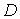 определяются
из уравнений
определяются
из уравнений
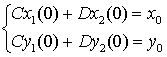 (2.7)
(2.7)
Используя полученные выражения, выпишем теперь
условия периодичности (2.2)
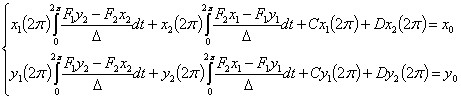 (2.8)
(2.8)
Для того чтобы система (2.1)
допускала периодические решения, необходимо и достаточно, чтобы функции 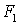 и
и  удовлетворяли
условиям (2.8).
удовлетворяли
условиям (2.8).
Рассмотрим эти условия для некоторых
специальных случаев, так как это будет играть в дальнейшем изложении особую
роль.
Сначала рассмотрим тот частный
случай, когда фундаментальные решения 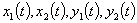 - периодические функции, Заметим,
что уравнения в вариациях, отвечающие изохорным системам, т. е. системам,
период колебаний которых не зависит от начальных условий, всегда имеют
периодические решения.
- периодические функции, Заметим,
что уравнения в вариациях, отвечающие изохорным системам, т. е. системам,
период колебаний которых не зависит от начальных условий, всегда имеют
периодические решения.
Так как C и D -
постоянные числа, то в силу периодичности функции 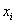 и
и 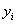 из (2.7),
мы получаем следующие условия:
из (2.7),
мы получаем следующие условия:
 (2.7’)
(2.7’)
Равенства (2.7’) позволяют упростить
систему (2.8), которую можно теперь рассматривать как систему однородных
алгебраических уравнений относительно интегралов
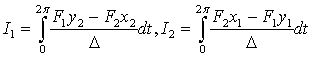 .
.
Перепишем эту систему в следующем
виде:
 (2.9)
(2.9)
Определитель системы (2.9) есть
определитель Вронского для функций 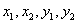 . В силу независимости этих функций
он отличен от нуля. Таким образом, система (2.9) имеет только тривиальное
решение. Поэтому
. В силу независимости этих функций
он отличен от нуля. Таким образом, система (2.9) имеет только тривиальное
решение. Поэтому
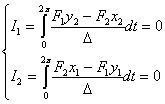 (2.10)
(2.10)
Итак, мы пришли к следующему
результату: если фундаментальное решение системы (2.4) выражается
периодическими функциями, то для того, чтобы любое решение системы (2.1) было
периодическим необходимо и достаточно, чтобы функции 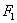 и
и  удовлетворяли
условиям (2.10).
удовлетворяли
условиям (2.10).
Сейчас рассмотрим тот частный случай,
когда система (2.1) имеет вид
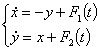 (2.11)
(2.11)
Система (2.11) сводится к уравнению
колебаний математического маятника под действием периодической внешней силы

где

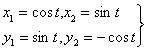 (2.12)
(2.12)
Определитель Вронского этих функций
равен единице, поэтому условия (2.10) будут приведены к такому виду:
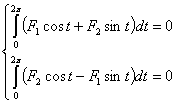 (2.13)
(2.13)
ляпунов периодический решение уравнение
Раздел 3. Метод Ляпунова
. Алгоритм
Ляпунов предложил простой и очень эффективный
метод построения периодических решений для достаточно малых значений постоянной
с решения системы (1.8). Алгоритм Ляпунова использует аналитичность искомых
решений по параметру с и дает правило построения решений в форме рядов
специального вида, разложенных по степеням этого параметра.
Таким образом, на основании теоремы в разделе 1,
решение системы уравнений (1.8) можно искать в виде:
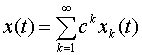 ,
,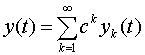 .
.
но это невозможно, так как период
решения Т неизвестен. Тогда Ляпунов предложил видоизменить масштаб времени так,
чтобы решения полученной системы имели фиксированный период, не зависящий от с
(например, равный 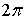 ).
).
Обратим внимание на формулу (1.24).
Она показывает, что если ввести замену
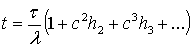 (3.1)
(3.1)
то период колебаний по переменной 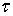 будет равен
будет равен
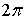 . Сделав в
системе уравнений (1.8) замену (3.1), получим
. Сделав в
системе уравнений (1.8) замену (3.1), получим
 (3.2)
(3.2)
Так как правые части системы (3.2)
мы умножили на аналитические функции параметра 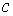 , то решение этой системы, так же
как и системы (1.8), аналитические по
, то решение этой системы, так же
как и системы (1.8), аналитические по 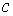 и для любого достаточно малого
и для любого достаточно малого  периодические
по
периодические
по 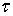 . Но период
по независимой переменной теперь уже фиксирован, он равен
. Но период
по независимой переменной теперь уже фиксирован, он равен 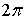 .
.
Периодические решения системы (3.2)
будем искать в виде рядов
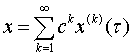 ,
,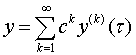 . (3.3)
. (3.3)
Подставим ряды (3.3) в систему
уравнений (3.2) и сравним коэффициенты при одинаковых степенях параметра 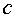 . Функции
. Функции 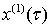 и
и 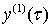 будут
удовлетворять следующей системе уравнений:
будут
удовлетворять следующей системе уравнений:
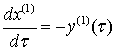 ,
, 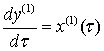 . (3.4)
. (3.4)
В самом деле, функции 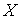 и
и 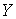 , будучи
аналитическими функциями своих переменных, таковы, что их разложение начинается
с членов второго порядка малости. Следовательно, при подстановке в эти функции
рядов (3.3) функции
, будучи
аналитическими функциями своих переменных, таковы, что их разложение начинается
с членов второго порядка малости. Следовательно, при подстановке в эти функции
рядов (3.3) функции 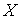 и
и 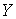 не будут
содержать членов, линейных относительно
не будут
содержать членов, линейных относительно 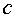 . Начальные значения для системы
(3.2) определены равенствами (1.13)
. Начальные значения для системы
(3.2) определены равенствами (1.13)
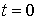 :
: 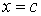 ,
,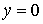 .
.
Следовательно, функции  и
и  будут соответствовать
следующим начальным условиям:
будут соответствовать
следующим начальным условиям:
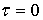 :
: 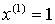 ,
,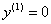 ,
,
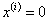 ,
, 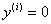 , где i =2,3… (3.5)
, где i =2,3… (3.5)
Функции  и
и 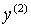 будут
удовлетворять системе уравнений
будут
удовлетворять системе уравнений
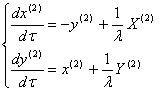 (3.6)
(3.6)
где  и
и 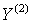 ─ квадратичные члены
разложения функций
─ квадратичные члены
разложения функций 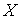 и
и 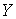 по степеням
параметра
по степеням
параметра 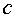 . Так как
. Так как 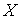 и
и 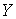 ─
аналитические функции переменных
─
аналитические функции переменных 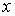 и
и  , причем их разложение начинается с
квадратичных членов, то
, причем их разложение начинается с
квадратичных членов, то  и
и 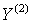 являются
квадратичными формами переменных
являются
квадратичными формами переменных  и
и 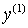 .
.
Точно так же каждая пара функций 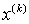 и
и 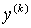 , входящая в
разложение (3.3), определяется системой уравнений
, входящая в
разложение (3.3), определяется системой уравнений
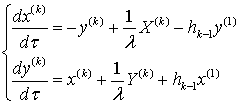 (3.7)
(3.7)
причем функции 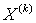 и
и  будут
содержать величины
будут
содержать величины  и
и  только тех
номеров
только тех
номеров 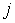 , которые
меньше чем
, которые
меньше чем  .
.
Кроме того, функции 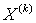 и
и  будут
содержать величины
будут
содержать величины 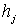 , причем
, причем 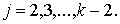 Заметим,
что величины
Заметим,
что величины 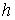 входят в
правые части (3.7) только уравнений относительно
входят в
правые части (3.7) только уравнений относительно 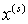 и
и 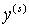 , для которых
, для которых  :
:
 (3.8)
(3.8)
и т. д.
Из уравнений (1.13) следует, что
функции 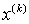 и
и 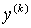 при
при 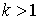 удовлетворяют
начальным условиям
удовлетворяют
начальным условиям
 ,
,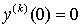 . (3.9)
. (3.9)
Вернемся снова к уравнениям (3.2).
Хотя числа 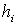 нам неизвестны
заранее, но они на основании теоремы Ляпунова определяются однозначно для
данной системы и не зависят от параметра
нам неизвестны
заранее, но они на основании теоремы Ляпунова определяются однозначно для
данной системы и не зависят от параметра 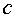 , ни от начальных условий.
, ни от начальных условий.
Далее члены рядов (3.3) также
определяются однозначно, причём 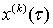 и
и 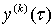 ─ периодические функции
переменного
─ периодические функции
переменного 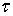 периода
периода 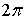 . В самом
деле,
. В самом
деле, 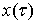 и
и  ─
периодические функции, следовательно,
─
периодические функции, следовательно,
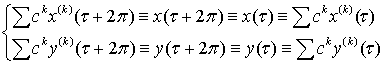 (3.10)
(3.10)
Так как функции 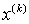 и
и 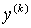 не зависят
от параметра
не зависят
от параметра 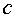 , а
равенства (3.10) справедливы для любого малого
, а
равенства (3.10) справедливы для любого малого 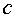 , то
, то
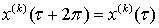 ,
, 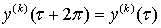 .
.
Таким образом, мы можем утверждать
заранее, что функции 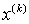 и
и 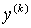 , которые
определяются как решение задачи Коши (3.9) для системы уравнений (3.7), будут
периодическими функциями времени периода
, которые
определяются как решение задачи Коши (3.9) для системы уравнений (3.7), будут
периодическими функциями времени периода 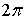 . С другой стороны, уравнения (3.7)
относятся к виду
. С другой стороны, уравнения (3.7)
относятся к виду
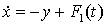 ,
, 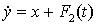 , (2.11)
, (2.11)
где 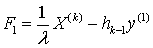 ,
,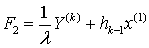
являются периодическими функциями
времени, поскольку они определяются периодическими функциями  …,
…, 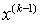 ,
, 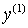 , …,
, …, 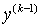 . Система
вида (2.11) имеет периодическое решение тогда и только тогда, когда функции
. Система
вида (2.11) имеет периодическое решение тогда и только тогда, когда функции  удовлетворяют
условиям
удовлетворяют
условиям

На этом основании можно
сформулировать следующее вспомогательное утверждение:
функции 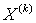 ,
,  и числа
и числа 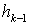 всегда
удовлетворяют условиям (3.11)
всегда
удовлетворяют условиям (3.11)
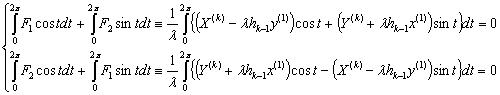
Практическая часть
Индивидуальное задание
Построить приближенное периодическое решение
задачи Коши для системы дифференциальных уравнений:
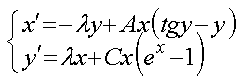
при начальных условиях 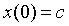 ,
, 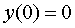 . Здесь A, С=const.
. Здесь A, С=const.
Решение задания

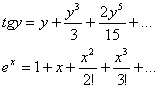
Подставив эти разложения в систему.
Получим

Замена,
 ,
,
тогда

Согласно методу Ляпунова решение
ищем в виде степенного ряда по малому параметру с.
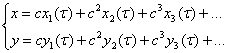
Так как 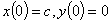 , тогда
, тогда
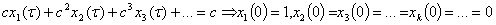
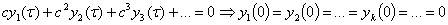
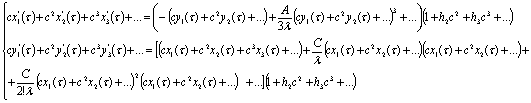
Теперь найдем коефициенты при с, с2,
с3,…, тоесть найдем  .
.
с: 

уравнение окружности, тогда
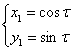
с2 :
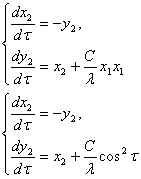


Найдем  :
:
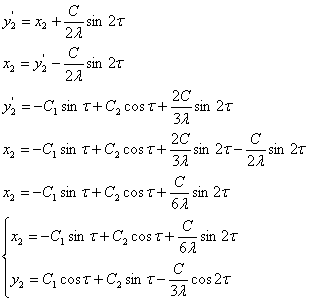
Так как
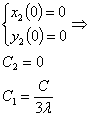
Таким образом, получим
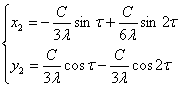
с3:
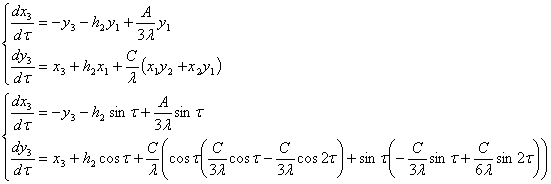
Теперь найдем h2 и проверим
необходимое и достаточное условие существования периодического решения. Тоесть

Необходимое и достаточное условие:
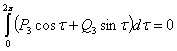 , где
, где
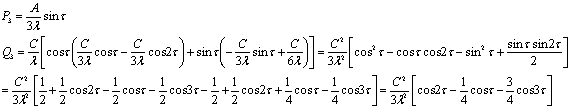
Таким образом
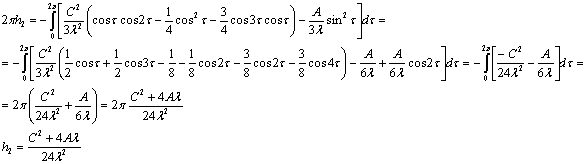
Сейчас проверим условие
существования периодического решения
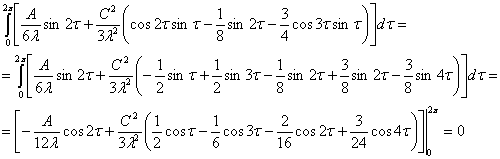
Таким образом, периодическое решение
существует. Далее подставим полученное выражение для h2 в систему
для с3

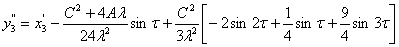
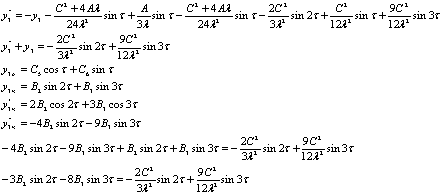
sin2τ:
sin3τ:
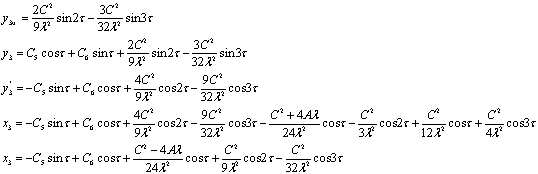


с4:

Теперь для удобства обозначим
некоторые числовые выражения
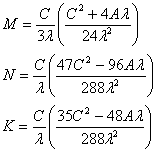 тогда
тогда

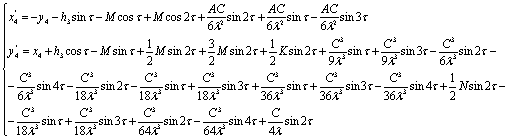
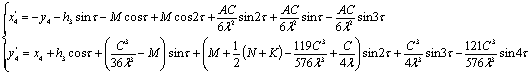
Снова переобозначим
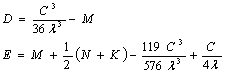
Тогда
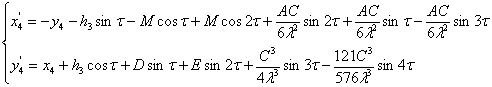
Далее найдем h3
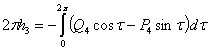 , где
, где

Теперь подставим найденные значения
для 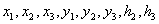 в систему
в систему
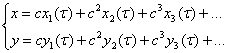
При этом вернувшись к замене
 ,
,
Откуда

Тогда наше решение примет вид

Список литературы
1.
Моисеев Н.Н. Асимптотические методы нелинейной механики, Наука, М.,
г.
.
Малкин И.Г. Некоторые задачи теории нелинейных колебаний, ГИТТЛ, М., 1956.