Интегрирование обыкновенных дифференциальных уравнений

Содержание

1. Постановка задачи

. Исследование методов решения

. Аналитическое решение задачи

. Численное решение

.1 Исходные данные

.2 Описание функций программы

.3 Исходный код

.4 Отладка и тестирование программы

.5 Исследование

. Выводы

1. Постановка задачи

Построить таблицу и график решения линейного дифференциального уравнения, заданным численным методом и аналитически, а также с использованием стандартной процедуры ode45.

Дифференциальное уравнение:

₀ y’’’(t) + a₁ y’’(t) + a₂ y’(t) + y(t) = 10.

Начальные условия:

(0) = y’(0) = y’’(0) = 0.

Интервал:

Є [0, t_m].

Сравнить полученные результаты с аналитическим решением. Исследовать зависимость погрешности решения от выбора шага интегрирования.

Исходные данные:

₀ = 2;₁ = 1.02;₂ = 2.01;_m = 20 (с).

В ходе работы будет использоваться метод Адамса-Башфорта 3-го порядка.

2. Исследование методов решения

Общая формула Адамса-Башфорта:

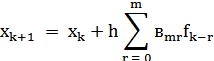
Метод Адамса-Башфорта 3-го порядка является трехшаговым (поскольку использует информацию в трех точках), явным и имеет формулу:

.

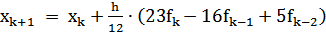Общая форма ЛДУ:

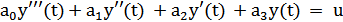
ЛДУ уравнение можно привести к системе, а именно:

.     пусть ,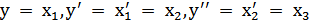

где 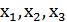 - неизвестные числа;

2.   подставим выше указанную замену в ЛДУ и выразим оттуда  . Получим:

;

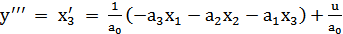3.   в результате получаем систему ЛДУ(СЛДУ):

Полученную СЛДУ можно переписать в матричном виде:

, где ; ;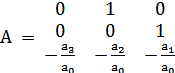

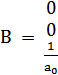= f, следовательно можно записать для конкретного заданного уравнения:

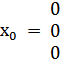; ; ; n = 3

количество узлов.

Для расчёта дополнительных начальных условий требуется стартовый метод, например, одношаговый метод Рунге-Кутты.

_k+1 = x_k+h*(k1+2*k2+2*k3+k4)/6, где= f(t_k, x_k)= f(t_k+h/2, x_k+h*k1/2)= f(t_k+h/2, x_k+h*k2/2)= f(t_k+h, x_k+h*k3)= (t_k -t₀ )/n

3. Аналитическое решение задачи

y’’’(t) + 1.02 y’’(t) + 2.01 y’(t) + y(t) = 10

Из заданного дифференциального уравнения найдем корни характеристического многочлена.

С помощью следующей программы:

= [0 1 0; 0 0 1; -1/2 -2.01/2 -1.02/2];= eig(A)

Результат:

.5000

.0050 + 1.0000i

.0050 - 1.0000i

Так как собственные значения различаются больше, чем на порядок, то из этого следует, что эта система достаточно жесткая. Кроме того, ввиду того, что вещественные части всех собственных значений отрицательны, система асимптотически устойчива.

Соответствующие им частные решения ДУ:

Общее решение нашего ДУ:

Начальные условия:

(0) = y’(0) = y’’(0) = 0.’’’(0) = 10 / a₀ = 5

.m

= vpa(dsolve('2 * D3y + 1.02 * D2y + 2.01 * Dy + y = 10', 'y(0) = 0', 'D2y(0) = 0', 'Dy(0) = 0', 'x'))

Результат:= 10.0 - (1.9678714859437751004016064257028 * cos(0.99998749992187402342224094390368*x)) / exp(0.005*x) - (4.0259539391966028659938403448691 * sin(0.99998749992187402342224094390368*x)) / exp(0.005*x) - 8.0321285140562248995983935742972 / exp(0.5*x)

4. Численное решение

.1 Исходные данные

) Дано:

₀ = 2;₁ = 1.02;₂ = 2.01;_m = 20 (с);= [0;0;0].

) Приведение ДУ к форме Коши

) Расчет общего решения ДУ Y(k) аналитическим методом

) Расчет с помощью ode45

) Расчет первых трёх значений с помощью метода Рунге-Кутты

) Расчет с помощью метода Адамса-Башфорта 3 -го порядка

) Вывод графиков расчета разными методами на экран

4.2 Описание функций программы

дифференциальный уравнение интегрирование программа

[T,Y] = AB(tspan,a)- - функция, осуществляющая стартовый метод; выходными параметрами являются вектор-столбец Y и параметр T; входными параметрами являются начало и конец отрезка интегрирования; исходная матрица а

.3 Исходный код

kursach2(a, y0, t0, tm, h)= [2, 1.02, 2.01]; % коэффициенты ДУ= [ 0, 1, 0; 0, 0, 1; - 1/a(1), - a(3)/a(1), - a(2)/a(1)]; % матрица A= 0;= 20;= [0; 0; 10/a(1)];= 1; % шаг= [0; 0; 0]; % начальные условия= (tm - t0)/h; % количество точекk = 1:n + 1 % цикл по всем точкам для задания аналитического решения(k) = t0 + (k - 1) * h;(k) = 10. -8.03212851405622489959839357430 * exp(-.5 * T(k)) - 4.02595393919660286599384034488 * exp(-.5e-2 * T(k)) * sin(.999987499921874023422240943905 * T(k)) - 1.96787148594377510040160642570 * exp(- .500000000000000000000000000000e-2 * T(k)) * cos(.999987499921874023422240943905 * T(k));= odeset('RelTol', 1e-10, 'AbsTol', 1e-5); % точность ode45

[T1, Y1] = ode45('F', T, y0, options); % решение ode45

%

[T2, Y2] = AB(T, a); % метод Адамса - Башфорта для шага h

[T3, Y3] = AB(T/2, a); % метод Адамса - Башфорта для шага h/2

% построение графиков(1);(2, 1, 1);(T, (Y1(:, 1)));on;('Решение ode45');(2, 1, 2);(T, (Y' - Y2(:, 1)));on;('Погрешность ode45');(2);(2, 1, 1);(T, (Y' - Y1(:, 1)));on;('Метод Адамсa-Башвортa');(2, 1, 2);(T, (Y2(:, 1)));on;('Погрешность Адамса-Башворта');(3);(T, Y);on;('Аналитическое');X1 = R(t, a) % Рунге= [ 0, 1, 0; 0, 0, 1; - 1/a(1), - a(3)/a(1), - a(2)/a(1)];= [0; 0; 10/a(1)];= [0; 0; 0]; % начальные условия= A * y + f;(:, 1) = y;= t; %k = 1:2 % цикл= A * y + f; %= A * (y + h/2 * k1) + f;= A * (y + h/2 * k2) + f;= A * (y + h * k3) + f;= y + h * (k1 + 2 * k2 + 2 * k3 + k4)/6;= A * y + f;(:, k + 1) = y;% конец

% явный метод адамса - башфорта[T, Y] = AB(tspan, a) % диапазон времени= length(tspan); % кол - во шагов и точек разбиения= tspan(n)/(n - 1); % шаг

% X(:, 1) = y0'; % начальные значения_own = (R(h, a)); % рассчитываем с помощью метода Рунге - Кутты первые три значения(:, 1) = f_own(:, 1);(:, 2) = f_own(:, 2);(:, 3) = f_own(:, 3); % записываем их в столбцыk = 3:n - 1(:, k + 1) = X(:, k) + h/12 * (23 * F(tspan(k), X(:, k)) - 16 * F(tspan(k - 1), X(:, k - 1)) + 5 * F(tspan(k - 2), X(:, k - 2)) ); % метод адамса - башфорта= tspan; Y = X';

4.4 Отладка и тестирование программы

Для сравнения погрешностей при разных шагах и анализа устойчивости, будут проводиться вычисления с различным шагом.

Найдём h критическое для метода Адамса-Башфорта 3го порядка:*| л | < 6/11

л = -0.5< 6/(11*| л |)

критическое ~1,1критическое получилось больше единицы, поэтому критическим шагом в данной работе будем считать h = 1.

Ниже представлены графики для различных h и анализ погрешностей.= 0,005

= 0,01

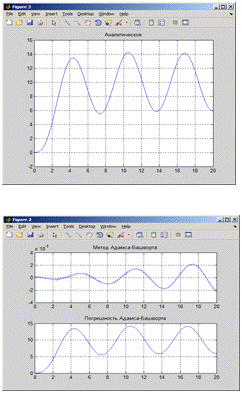
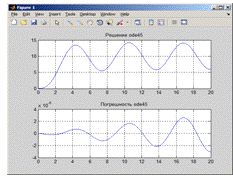
h = 0,05

= 0,1

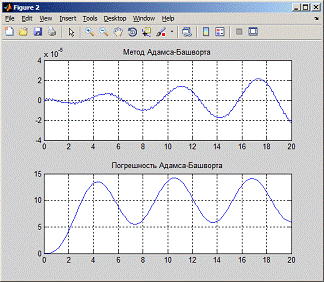
= 0,5

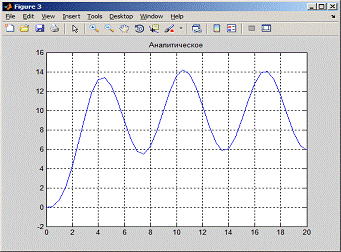
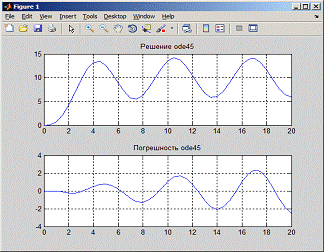
= 1

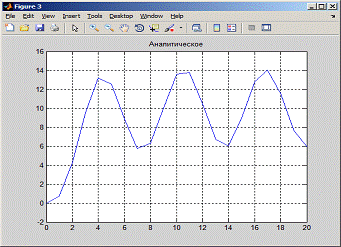
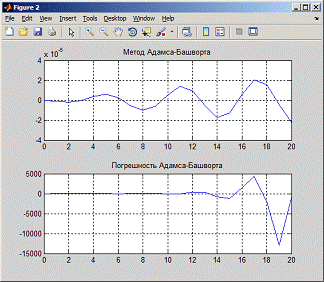
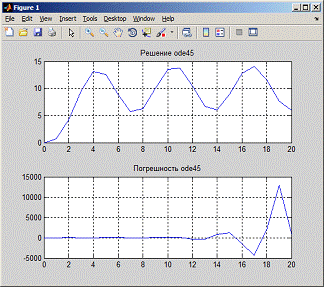
4.5 Исследование

После проведения тестирования видно, что погрешность метода Адамса-Башфорта увеличивается с увеличением ширины шага. На шаге h < 0,01 она становится меньше погрешности стандартного ode45.

Можно сделать вывод, что при равномерном выборе величины шага метод Адамса-Башфорта является недостаточно устойчивым для большой величины шага.

Точности решения можно добиться, если подбирать величину шага с течением времени, обращая внимание на требования устойчивости.

5. Выводы

В ходе работы была реализована программа решения ДУ методом Адамса-Башфорта 3-го порядка, использующая также метод Рунге-Кутты.

Была проведена отладка и тестирование программы, где полученное с помощью данного метода решение было сравнено с решением с помощью встроенного ode45. В результате работы была найдена зависимость погрешности интегрирования от выбранного шага.