Изучение свойств случайных величин, планирование эксперимента и анализ данных

Изучение свойств случайных величин, планирование эксперимента и анализ данных

Изучение свойств случайных величин, планирование эксперимента и анализ данных

Содержание

Введение

. Одномерные случайные величины

.1 Формирование выборки объёмом n=15

1.1.1 Вычисление среднего и дисперсии

1.1.2 Оценка нормальности выборки объёмом 15

.1.3 Определение доверительного интервала для математического ожидания

.1.4 Определение доверительного интервала для дисперсии

.2 Получение второй выборки объёмом 100

.2.1 Оценка нормальности выборки объёмом 100

.2.2 Вычисление среднего и дисперсии

.2.3 Проверка гипотезы о равенстве математических ожиданий этих двух выборок при условии равенства их генеральных дисперсий

.2.4 Оценка доверительного интервала для среднего первой выборки, используя данные второй выборки

. Двумерные случайные величины

.1 Выбор двух функций и построение корреляционного поля

.2 Изучение зависимости выбранного У от одного из факторов Х

.2.1 Вычисление условных средних У для фиксированных значений Х

.2.2 Вычисление условных дисперсий У для фиксированных значений Х

.3 Построение линии регрессии У по Х (эмпирической и приближённой)

. Дисперсионный анализ и планирование эксперимента

.1 Выбор факторов Х и функций отклика показателей качества У₁ и У₂, краткое описание эксперимента

.2 Составление плана эксперимента

.3 Составление матрицы эксперимента

.4 Дисперсионный анализ греко-латинского куба второго порядка

.5 Проверка условий применимости дисперсионного анализа, критерий Дункана для показателей качества Y₁ и Y₂

4. Регрессионный анализ

Заключение

Список литературы

математический ожидание дисперсия регрессия

Введение

Целью курсовой работы является изучение показателей качества (ПК), как случайных величин, и доказательство факта влияния на них нескольких факторов, действующих одновременно. По имитационной модели процесса необходимо получить значения двух функций отклика (ПК), выбрав несколько факторов и задавая им градации. Модель является таблицей EXCEL.

В ходе курсовой работы необходимо выявить, какие факторы и их градации достоверно влияют на выбранные показатели качества.

Одномерные случайные величины

.1 Формирование выборки объемом n=15

Используя модель переменных, выбираем функцию отклика Y3 и формируем выборку объемом 15. Выборка представлена в таблице 1.

Таблица 1 - Выборка объемом n=15

123,2
130,0
131,0
132,8
133,0
135,8
138,6
141,0
143,4
143,4
143,6
148,4
150,0
150,4
157,2

.1.1 Вычисление среднего и дисперсии

Определяем среднее результатов наблюдений:

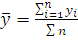, (1)

где n - объем выборки;

y_i - наблюдаемые значения выборки.

Определяем дисперсию:

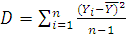, (2)

Для нашей выборки имеем:

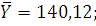
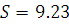
Проверка наличия грубых погрешностей

Под грубой погрешностью измерения понимается погрешность, существенно превышающая ожидаемую при данных условиях. Она может быть сделана вследствие неправильного применения прибора, неверной записи показаний прибора, ошибочно прочитанного отсчета и т.п.

Для выявления грубых погрешностей можно воспользоваться следующими критериями:

критерий "трех сигм" (надежен при числе измерений n>20);

критерий Романовского (применяется, если число измерений n<20);

критерий Шарлье (используется, если число наблюдений в ряду великоn>20);

вариационный критерий Диксона (мощный критерий с малыми вероятностями ошибок).

Для полученной выборки объема n=15 воспользуемся критерием Романовского:

- вычисляем отношение для каждого значения из выборки по формуле:

 

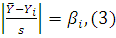
и сравниваем с табличным критерием.

         по таблице 7.1 [3] на уровне значимости 0,05 для n=15 находим табличный критерий 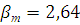. Если  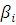окажется больше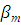, то этот результат следует отбросить.

 

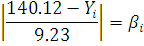
По результатам расчета, используя данные таблицы 1 делаем вывод о том что грубых погрешностей нет.

1.1.2 Оценка нормальности

Одним из способов проверки нормальности распределения является вычисление особых параметров выборочной совокупности результатов анализа, носящих название асимметрии А и эксцесса Е.

Воспользуемся описательной статистикой для нахождения значений асимметрии и эксцесса:

Столбец1
Среднее	140,127
Стандартная ошибка	2,383
Медиана	141,000
Мода	143,500
Стандартное отклонение	9,229
Дисперсия выборки	85,168
Эксцесс	-0,509
Асимметричность	0,023
Интервал	34,000
Минимум	123,200
Максимум	157,200
Сумма	2101,900
Счет	15,000
Уровень надежности(95,0%)	5,111

По величине асимметрии и эксцесса можно косвенно судить о нормальности распределения. Более достоверной является оценка с использованием дисперсий этих величин, которые являются функциями от кратности анализа:

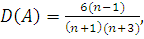 (4)

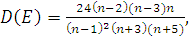 (5)

где n - число результатов в выборке.

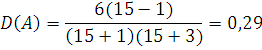
Последующее сопоставление этих асимметрии и эксцесса и их дисперсий с помощью так называемого критерия согласия позволяет решить вопрос о том, наблюдается ли в данном случае нормальное распределение результатов анализа. Критерий согласия формулируется следующим образом: если выборочная асимметрия и эксцесс удовлетворяют неравенствам

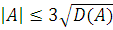 и ,

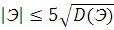то наблюдаемое распределение можно считать нормальным.

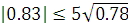В нашем случае:  и ,

 и

Так как значение асимметрии и эксцесса близки к нулю, а их значения не превышают соответствующие значения дисперсий, то мы можем сделать вывод о нормальности распределения.

Для оценки нормальности распределения можем воспользоваться не только критерием асимметрии и эксцесса, но и такими критериями, как:

критерий Пирсона (;

критерий Колмогорова-Смирнова;

критерий Шапиро-Вилка;

критерий Жака-Берра;

критерий Андерсена-Дарлинга;

критерий Дэвида-Хартли-Пирсона;

критерий Саркади;.

критерий Оя и др..

Воспользуемся критерием Дэвида-Хартли-Пирсона.

Критерий нормальности распределения случайной величины основанный на распределении отношения размаха к стандартному отклонению.

Статистика критерия имеет вид:

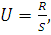 (6)

где R- размах, вычисляемый по формуле : R=Y_max-Y_min;

S - стандартное отклонение.

Гипотеза нормальности принимается, если .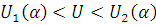

Зададимся уровнем значимости 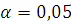, тогда

R=157,2-123,2=34,00

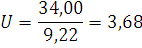
По таблице 75 [4] для n=15 и 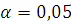 находим ,

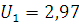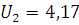
,97<3.68<4.17,

так как условие 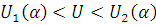 выполняется следовательно гипотезу о нормальности распределения принимаем.

1.1.3 Определение доверительных интервалов для математического ожидания

Доверительные интервалы для математического ожидания находим, используя критерий Стьюдента.

Рассмотрим случайную величину 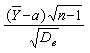, которая согласно следствию из теоремы о распределении выборочных характеристик распределена по закону Стьюдента 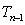. При заданном значении 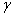, пользуясь таблицей П2 [1], вычислим значение 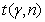 из условия:

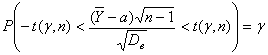, (7)

где 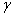 - надежность интервальной оценки.

α - генеральное среднее.

Из условия (7) получаем:

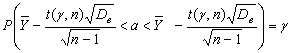       (8)

Таким образом, интервальная оценка надежности 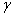 для неизвестной генеральной средней а имеет границы:

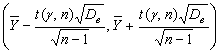    (9)

Выразим границы интервала через исправленную дисперсию . Так как =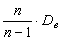, то 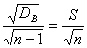. Поэтому

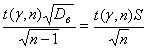.    (10)

Значит, границы доверительного интервала можно записать так:

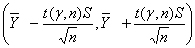,      (11)

По выборке объема 15 нормально распределенной найдено среднее значение 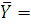140,12. Построим доверительный интервал для математического ожидания с надежностью γ =0,95.

Пользуясь таблицей П2 [1] находим величину t(0,95;15)=2,15.

Тогда доверительные границы для математического ожидания с доверительной вероятностью 0,95:

;

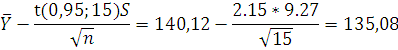
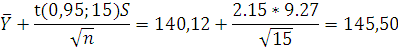
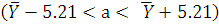Окончательно с надежностью 0,95 получаем, что параметр а заключен в интервале: .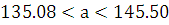

 

1.1.4 Определение доверительных интервалов для дисперсии

По выборке объёма 15, имеющей нормальное распределение, найдено значение S=9.23. Найдем доверительный интервал для σ с надежностью γ=0,95

Доверительный интервал покрывающий  с заданной надежностью находим по формуле:

 

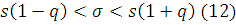
По таблице приложения 4 [2] по данным γ=0,95 и n=15 находим q=0,46, подставляя значения в (12) получаем: 9,23(1-0,46)< 9.23(1+0.46)

Искомый доверительный интервал: 4,98<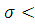13.47

.2 Формирование выборки объемом более 60

.2.1 Вычисление среднего и дисперсии

С помощью модели эксперимента формируем вторую выборку (Y₃) объемом 100

Таблица 2 - Значения функции Y₃

№ опыта	Y3	№ опыта	Y3	№ опыта	Y3	№ опыта	Y3
1	113,80	26	131,80	51	140,20	76	148,20
2	118,20	27	131,80	52	140,60	77	149,00
3	119,80	28	133,00	53	141,2	78	149,20
4	120,80	29	133,20	54	141,30	79	149,20
5	120,80	30	133,30	55	142,20	80	149,2
6	121,20	31	133,60	56	142,40	81	149,40
7	121,80	32	133,80	57	142,60	82	149,40
8	122,80	33	134,20	58	142,80	83	150,00
9	122,80	34	134,20	59	143,20	84	150,20
10	122,80	35	135,00	60	143,80	85	150,40
11	124,60	36	135,00	61	144,40	86	150,60
12	124,60	37	135,60	62	144,40	87	150,80
13	124,80	38	136,00	63	144,80	88	152,90
14	126,60	39	136,00	64	145,00	89	153,00
15	126,80	40	136,40	65	145,40	90	153,20
16	127,20	41	136,60	66	145,50	91	154,20
17	127,60	42	137,80	67	145,60	92	155,20
18	128,20	43	138,40	68	145,70	93	155,20
19	128,80	44	138,60	69	146,10	94	155,30
20	129,00	45	139,00	70	146,30	95	155,50
21	129,20	46	139,00	71	146,30	156,20
22	129,60	47	139,20	72	146,30	97	156,80
23	130,40	48	139,40	73	146,40	98	159,80
24	130,80	49	139,60	74	147,40	99	163,80
25	131,20	50	139,60	75	147,80	100	164,20

Определяем среднее результатов наблюдений по формуле (1)

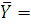139,6

Дисперсию вычисляем по формуле (2):

D=122,15

S=11.05

Проверим на наличие грубых погрешностей по критерию "трех сигм": Критерий "трех сигм" применяется для результатов измерений, распределенных по нормальному закону. По этому критерию считается, что результат, возникающий с вероятностью q £ 0,003, маловероятен и его можно считать промахом, если |x_i - x| < 3σ, где σ - оценка СКО измерений. Данный критерий надежен при числе измерений n ≥ 20…50.

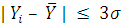 (13)

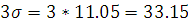
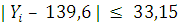
При проверке условия (13) грубых погрешностей не обнаружено.

1.2.2 Проверка "нормальности" полученной выборки

Воспользуемся критерием Дэвида-Хартли-Пирсона.

Критерий нормальности распределения случайной величины основанный на распределении отношения размаха к стандартному отклонению.

Статистика критерия имеет вид:

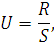
где R- размах, вычисляемый по формуле : R=Y_max-Y_min;

S - стандартное отклонение.

Гипотеза нормальности принимается, если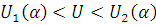

Зададимся уровнем значимости 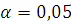, тогда R=164,2-113,8=50,4

S=11,05

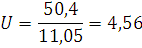
По таблице 75 [4] для n=100 и 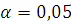 находим ;

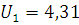,31<4,56<5,90. так как условие 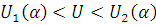 выполняется следовательно гипотезу о нормальности распределения принимаем.

Также для оценки нормальности данного распределения построим гистограмму и проведем описательную статистику.

Таблица 3 - Описательная статистика для выборки n=100

Параметр	Значение	Параметр	Значение
Среднее	139,627	Асимметричность	-0,113
Стандартная ошибка	1,105	Интервал	50,400
Медиана	139,900	Минимум	113,800
Мода	122,800	Максимум	164,200
Стандартное отклонение	11,052	Сумма	13 962,700
Дисперсия выборки	122,154	Счет	100,000
Эксцесс	-0,621	Уровень надежности(95,0%)	2,193

Проверим не превышают ли значения асимметрии и эксцесса соответствующие значения дисперсий, чтобы сделать вывод о нормальности распределения. Дисперсии рассчитываем по формулам (4) и (5)

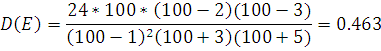
Критерий согласия формулируется следующим образом: если выборочная асимметрия и эксцесс удовлетворяют неравенствам

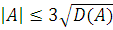 и ,

то наблюдаемое распределение можно считать нормальным.

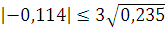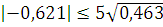В нашем случае:  и ,

 и ,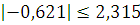

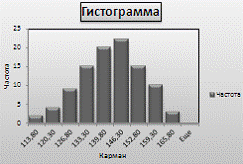
Рисунок 1 - Гистограмма для выборки n=100

Из таблицы 4 видно, что среднее, медиана и мода приблизительно равны, эксцесс и асимметричность не превышают соответствующие значения дисперсий, график близок к графику нормального распределения.

1.2.3 Проверка гипотезы о равенстве двух математических ожиданий двух выборок в предположении равенства их генеральных дисперсий

Проверим нулевую гипотезу H₀: M(Y₁)=M(Y₂) на уровне значимости 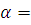0,05 для двух выборок n=15 и m=100

В качестве критерия проверки нулевой гипотезы примем случайную величину:

 

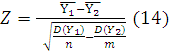
Критерий Z - нормированная нормальная случайная величина, так как М(Z)=0, при справедливости нулевой гипотезы (Z)=1. Критическая область строится в зависимости от вида конкурирующей гипотезы.

Первый случай: нулевая гипотеза H₀: M(Y₁)=M(Y₂). Конкурирующая гипотеза H₁: M(Y₁)≠M(Y₂). В этом случае строим двустороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости 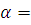0,05

По таблице функции Лапласа (приложение 2 [2]) находим критическую точку по равенству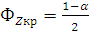

Если 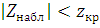 - нет оснований отвергать нулевую гипотезу, если  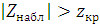- нулевую гипотезу отвергают.

Найдем  для наших выборок:

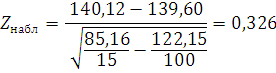
По таблице 2 [2] находим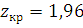

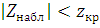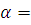Так как  следовательно наблюдаемое значение попало в область допустимых значений. Нулевую гипотезу о равенстве математических ожиданий принимаем на уровне значимости 0,05.

Второй случай: нулевая гипотеза H₀: M(Y₁)=M(Y₂). Конкурирующая гипотеза H₁: M(Y₁)>M(Y₂). В этом случае строим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости 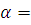0,05

Найдем :

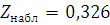
По таблице функции Лапласа (приложение 2 [2]) находим критическую точку по равенству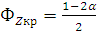

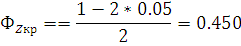
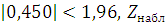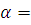Так как  попадает в область принятия гипотезы, нулевую гипотезу о равенстве математических ожиданий принимаем на уровне значимости 0,05.

Третий случай: нулевая гипотеза H₀: M(Y₁)=M(Y₂). Конкурирующая гипотеза H₁: M(Y₁)<M(Y₂). В этом случае строим левостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости 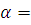0,05

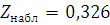
По таблице функции Лапласа (приложение 2 [2]) находим критическую точку по равенству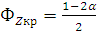

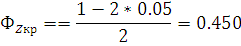
Полагая, что 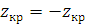 находим: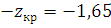

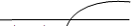
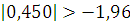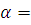Так как  нулевую гипотезу о равенстве математических ожиданий принимаем на уровне значимости 0,05.

1.2.4 Оценивание доверительных интервалов первой выборки, используя данные второй выборки, как оценки параметров генеральной совокупности

Генеральная совокупность (данные второй выборки) распределена по нормальному закону, причем параметр  известен и равен 11,05. По выборке объема n=15 найдено 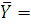140,12 определим интервальную оценку для математического ожидания с надежностью .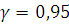

Доверительный интервал имеет вид :

 

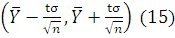
Находим t из соотношения 2Ф(t)=0.95 получаем Ф(t)=0.475. По таблице приложения 2[2] находим t=1,96.

Подставляем полученные значения в (15) получаем искомый интервал:

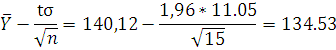
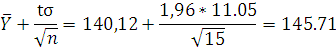
C надежностью 0,95 параметр а находится в интервале: ;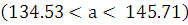

2. Двумерные случайные величины

Методы корреляционного и регрессионного анализов широко применяются для выявления и описания зависимостей между случайными величинами по экспериментальным данным. Для экспериментального изучения зависимости между величинами проведем 100 опытов. Результат каждого опыта дает пару значений (Y_2i , Y_3i).

.1 Построение корреляционного поля для двух функций (Y₂ и Y₃)

О наличии или отсутствии корреляции между величинами можно судить по виду поля корреляции. Корреляция на графике может быть положительной или отрицательной. Отрицательная корреляция(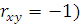 - корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция (- корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.

Рисунок 2 - Примеры корреляционных полей

а - отсутствие корреляции; б - линейная положительная и отрицательная связи; в -корреляционная положительная связь; г - корреляционная отрицательная связь;

Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты.

Таблица 5 - Значения Y₂ и Y₃ при постоянных уровнях всех действующих факторов.

№ п/п	Y2	Y3	№ п/п	Y2	Y3	№ п/п	Y2	Y3	№ п/п	Y2	Y3
1	139,57	153,00	26	112,17	123,60	51	109,37	131,80	76	138,37	151,80
2	134,57	144,00	27	138,77	155,20	52	115,17	140,60	77	105,77	123,20
3	121,37	144,80	28	137,37	147,80	53	127,17	137,60	78	108,77	126,20
4	129,77	142,20	29	121,77	137,20	54	151,77	165,20	79	121,57	137,00
5	120,37	135,80	30	120,17	135,60	55	130,77	138,20	80	121,17	133,60
6	112,37	121,80	31	123,57	133,00	56	133,37	142,80	81	105,37	119,80
7	119,77	132,20	32	148,77	157,20	57	121,77	141,20	82	135,97	148,40
8	115,37	133,80	33	146,37	159,80	58	129,37	138,80	83	127,77	148,20
9	137,77	155,20	34	114,77	131,20	59	123,17	144,60	84	136,37	155,80
10	142,37	156,80	35	120,77	133,20	60	154,77	161,20	85	108,77	126,20
11	127,97	141,40	36	131,97	140,40	61	122,17	137,60	86	132,37	149,80
12	106,37	120,80	37	119,97	138,40	62	128,57	142,00	87	138,77	160,20
13	116,77	134,20	38	125,77	137,20	63	136,57	143,00	88	105,37	125,80
14	137,57	155,00	39	134,37	157,80	64	122,77	134,20	89	138,77	158,20
15	124,57	139,00	40	106,37	119,80	65	144,37	153,80	90	117,77	135,20
16	121,97	137,40	41	115,17	132,60	66	112,37	136,80	91	149,80
17	114,77	132,20	42	131,97	144,40	67	126,17	138,60	92	121,17	143,60
18	132,17	143,60	43	123,57	142,00	68	121,77	137,20	93	113,77	136,20
19	130,57	146,00	44	125,97	131,40	69	120,57	141,00	94	137,97	146,40
20	116,77	136,20	45	130,57	147,00	70	107,17	122,60	95	121,77	134,20
21	127,77	145,20	46	139,77	148,20	71	126,37	142,80	96	135,97	153,40
22	127,57	142,00	47	113,37	135,80	72	110,77	135,20	97	123,37	131,80
23	125,97	143,40	48	107,37	123,80	73	98,37	120,80	98	127,97	139,40
24	134,37	147,80	49	116,97	138,40	74	123,57	141,00	99	136,77	153,20
25	141,37	159,80	50	126,17	146,60	75	109,17	126,60	10	118,77	137,20

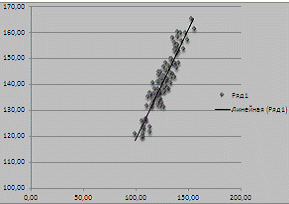
Рисунок 3 - Корреляционное поле

Коэффициент корреляции вычисляется по формуле:

 

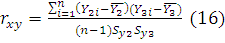
Рассчитаем коэффициент корреляции .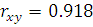

Так как коэффициент близок к +1 можем сделать вывод о существовании положительной линейной корреляционной зависимости между величинами.

2.2 Изучение зависимости Y₂ от одного из факторов -от X₄

Значения Y₂ сводим в таблицу, изменяя значение фактора X₄=0, X₄=1, X₄=2, X₄=3, X₄=4.

Таблица 6 - Зависимость Y₂ от X₄

№ опыта	X4=0	X4=1	X4=2	X4=3	X4=4

Продолжение таблицы 6

№ опыта	X4=0	X4=1	X4=2	X4=3	X4=4
1	50,37	59,47	90,37	101,37	114,57
2	37,37	59,67	83,17	113,87	111,37
3	44,37	74,94	89,97	109,87	124,17
4	49,37	67,87	77,77	90,37	117,37
5	40,37	63,67	94,17	105,87	139,57
6	31,37	52,37	75,77	95,67	123,97
7	49,37	65,87	77,57	104,97	131,97
8	61,37	67,77	87,97	87,67	125,57
9	53,37	63,47	99,57	106,97	141,77
10	37,37	82,97	63,37	134,17	119,17
11	28,37	60,57	68,37	98,97	125,97
12	58,37	56,37	95,17	108,87	140,37
13	46,37	52,47	65,37	91,67	116,17
14	38,37	72,97	90,37	103,87	136,97
15	49,37	68,67	86,77	94,97	123,37
16	55,37	64,67	92,37	92,27	123,17
17	25,37	71,77	91,57	96,97	114,57
18	50,37	56,57	71,57	112,17	129,17
19	38,37	62,57	79,77	92,67	129,37
20	41,37	65,67	91,17	117,87	132,97
21	55,37	75,67	77,77	106,57	125,37
22	34,37	74,97	92,97	114,87	117,57
23	52,37	55,37	100,57	103,37	142,37
24	33,37	74,87	62,37	114,57	106,37
25	50,37	62,77	90,97	98,67	127,97

2.2.1 Вычисление условных средних

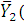X₄=0)=44.49

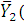X₄=1)=65.36

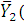X₄=2)=83.83

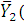X₄=3)=103.96

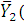X₄=4)=125.65

2.2.2 Вычисление условных дисперсий Y₂ для фиксированных значений X₄

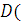X₄=0)=94.19

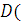X₄=1)=63.23

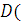X₄=2)=126.56

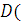X₄=3)=112.77

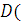X₄=4)=96.10

2.2.3 Построение линий регрессии

Приближенная линия регрессии:

Уравнение регрессии имеет следующий вид:

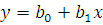
Вычислим коэффициенты 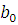 и :

 

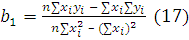
 (18)

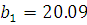
Уравнение регрессии примет вид: 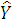 = 44.48 + 20.09x.

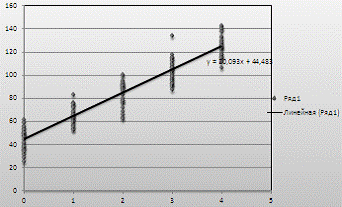
Рисунок 4 - Линия приближенной регрессии

Эмпирическая линия регрессии: Регрессией Y от X называется функциональная зависимость между значениями x и соответствующими условными средними значениями 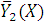. Это ломаная, построенная по серединам интервалов для X и  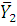для каждого интервала.

Коэффициенты уравнения вычисляются по средним значениям функции 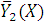 по формулам (17) и(18).

Таблица 7 - Значения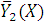

X
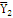
0	44,49
1	65,36
2	83,87
3	103,97
4	125,65

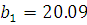
Уравнение регрессии примет вид:

Y = 44.48 + 20.09x.

 

 

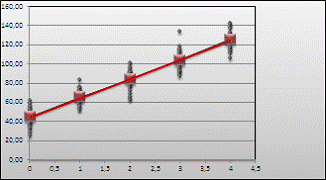
Рисунок 4 - Линия эмпирической регрессии

Приближенная линия регрессии и эмпирическая совпадают.

3. Дисперсионный анализ и планирование эксперимента

Рассмотрим в качестве объекта исследования методы измерения прочности. Выберем ультразвуковой неразрушающий метод измерения прочности бетона.

Ультразвуковой метод основан на связи между скоростью распространения ультразвуковых колебаний в бетоне и его прочностью. Прочность бетона в конструкциях определяют по экспериментально установленным градуировочным зависимостям "скорость распространения ультразвука - прочность бетона" или "время распространения ультразвука - прочность бетона" в зависимости от способа прозвучивания.

Градуировочную зависимость "скорость - прочность" устанавливают при испытании конструкций способом сквозного прозвучивания.

На точность измерения прочности при измерении неразрушающими методами могут оказывать влияние такие факторы как: тип цемента, состав цемента, тип заполнителя, условия твердения, возраст бетона, влажность и температура поверхности, тип поверхности, карбонизация поверхностного слоя бетона и еще ряд других менее значимых факторов.

Чем выше скорость распространения ультразвука, тем выше прочность бетона.

.1 Краткое описание эксперимента

Рассмотрим показатели качества ультразвукового метода измерения прочности и факторы, влияющие на эти показатели.

Исследуемые показатели качества метода измерения прочности:

Y₁ - точность;

Y₂ - скорость ультразвука , 4500-4800 м/с.

Факторы, оказывающие влияние на показатели качества представлены в таблице 8.

Таблица 8 - Факторы и их уровни, изучаемые в эксперименте

Факторы	Уровни факторов
X1- квалификация персонала (A)	- оператор с опытом работы более трех лет (A0); - оператор с опытом работы менее года(A1); - оператор без опыта работы (A2); - студент-практикант (A3); - (A4).
X2- калибровка прибора (B)	-прибор не прошедший поверку (B0); - калибровка произведена на влажных образцах (B1); - калибровка произведена на сухих образцах (B2); - калибровка прибора произведена не в срок (B3); - (B4).
X3-производитель (C)	- производитель 1 (C0); - производитель 2 (C1); - производитель 3 (C2); - производитель 4 (C3); - производитель 5 (C4).
X4- условия проведения испытания (D)	- температура (D0); - влажность (D1); - давление (D2); - загрязнение прибора (D3); - (D4).	- температура, влажность и давление соответствуют указанным в ГОСТ (E0); - температура не соответствует указанной в ГОСТ (E1); - влажность не соответствует ГОСТ (E2), - давление не соответствуют указанному в ГОСТ Е3 - условия не соответствуют (E4).
X6 - вид материала, Х7 - содержание примесей; Х8 - возраст бетона; Х9 - плотность; Х10 - водоцементное отношение.	Исследуются на постоянном уровне

3.2 Планирование эксперимента

Планирование эксперимента - комплекс мероприятий, направленных на эффективную постановку опытов. Основная цель планирования эксперимента - достижение максимальной точности измерений при минимальном количестве проведенных опытов и сохранении статистической достоверности результатов.

Полную систему ортогональных латинских квадратов для n=p можно построить, используя поля Галуа. Построим поле Галуа вычетов по модулю 5. В поле содержится пять различных элементов 0, 1, 2, 3, 4, 5. Составим таблицу сложения и умножения в этом поле:

Сложение	Умножение
0 1 2 3 4  1 2 3 4 0  2 3 4 0 1  3 4 0 1 2  4 0 1 2 3	1 2 3 4  2 4 1 3  3 1 4 2  4 3 2 1

Получим второй квадрат путем умножения (К=2)

2*0=0		0	1	2	3	4
2*1=2		2	3	4	0	1
2*2=4		4	0	1	2	3
2*3=1		1	2	3	4	0
2*4=3		3	4	0	1	2

Получим третий квадрат (К=3)

3*1=0		0	1	2	3	4
3*1=3		3	4	1	1	2
3*2=1		1	2	3	4	0
3*3=4		4	0	1	2	3
3*4=2		2	3	4	0	1

Получим четвертый квадрат (К=4)

4*0=0		0	1	2	3	4
4*1=4		4	0	1	2	3
4*2=3		3	4	0	1	2
4*3=2		2	3	4	0	1
4*4=1		1	2	3	4	0

При 5 уровнях в план можно ввести n+1 фактор. Число степеней свободы остаточной суммы будет равно нулю. Такие планы называют насыщенными. Построим насыщенный квадрат для n=5. Наложим для этого четыре полученных выше ортогональных латинских квадрата 5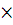5, составляющих полный ряд ортогональных латинских квадратов 5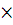5. Полученный план является насыщенным, так как число степеней свободы остаточной суммы, определяемое по формуле  где k-число изучаемых факторов, равно нулю.

По этой модели проводится эксперимент из 25 опытов. Такая модель наиболее оптимальна для данного количества факторов, то есть позволяет учесть максимальное количество сочетаний факторов при минимальном количестве опытов.

Таблица 8 - Гипер-греко-латинский квадрат четвертого порядка

А	В
		0	1	2	3	4
	0	C=0 D=0 E=0 F=0	C=1 D=1 E=1 F=1	C=2 D=2 E=2 F=2	C=3 D=3 E=3 F=3	C=4 D=4 E=4 F=4
	1	C=1 D=2 E=3 F=4	C=2 D=3 E=4 F=0	C=3 D=4 E=0 F=1	C=4 D=0 E=1 F=2	C=0 D=1 E=2 F=3
	2	C=2 D=4 E=1 F=3	C=3 D=0 E=2 F=4	C=4 D=1 E=3 F=0	C=0 D=2 E=4 F=1	C=1 D=3 E=0 F=2
	3	C=3 D=1 E=4 F=2	C=4 D=2 E=0 F=3	C=0 D=3 E=1 F=4	C=1 D=4 E=2 F=0	C=2 D=0 E=3 F=1
	4	C=4 D=3 E=2 F=1	C=0 D=4 E=3 F=2	C=1 D=0 E=4 F=3	C=2 D=1 E=0 F=4	C=3 D=2 E=1 F=0

Таблица 9 - Матрица эксперимента n=5, N=25

Номер опыта	А	В	С	D	E	F	X7	X8	X9	X10
1	0	0	0	0	0	0	1	1	1	1
2	0	1	1	1	1	1	1	1	1	1
3	0	2	2	2	2	2	1	1	1	1
4	0	3	3	3	3	3	1	1	1	1
5	0	4	4	4	4	4	1	1	1	1
6	1	0	1	2	3	4	1	1	1	1
7	1	1	2	3	4	0	1	1	1	1
8	1	2	3	4	0	1	1	1	1	1
9	1	3	4	0	1	2	1	1	1	1
10	1	4	0	1	2	3	1	1	1	1
11	2	0	2	4	1	3	1	1	1	1
12	2	1	3	0	2	4	1	1	1	1
13	2	2	4	1	3	0	1	1	1	1
14	2	3	0	2	4	1	1	1	1	1
15	2	4	1	3	0	2	1	1	1	1
16	3	0	3	1	4	2	1	1	1	1
17	3	1	4	2	0	3	1	1	1	1
18	3	2	0	3	1	4	1	1	1
19	3	3	1	4	2	0	1	1	1	1
20	3	4	2	0	3	1	1	1	1	1
21	4	0	4	3	2	1	1	1	1	1
22	4	1	0	4	3	2	1	1	1	1
23	4	2	1	0	4	3	1	1	1	1
24	4	3	2	1	0	4	1	1	1	1
25	4	4	3	2	1	0	1	1	1	1

3.3 Проведение модельного эксперимента

Проводим модельные эксперименты с выбранными значениями факторов, фиксируя остальные факторы. Заполняем матрицу эксперимента.

Таблица 10 - Матрица эксперимента n=5, N=25

Номер опыта	А	В	С	D	E	F	X7	X8	X9	X10	Y1	Y2
1	0	0	0	0	0	0	1	1	1	1	23,97	26,37
2	0	1	1	1	1	1	1	1	1	1	31,67	30,37
3	0	2	2	2	2	2	1	1	1	1	51,57	48,37
4	0	3	3	3	3	3	1	1	1	1	87,07	95,47
5	0	4	4	4	4	4	1	1	1	1	209,57	147,57
6	1	0	1	2	3	4	1	1	1	1	84,67	63,37
7	1	1	2	3	4	0	1	1	1	1	173,30	143,67
8	1	2	3	4	0	1	1	1	1	1	95,97	82,17
9	1	3	4	0	1	2	1	1	1	1	76,33	62,37
10	1	4	0	1	2	3	1	1	1	1	55,77	63,47
11	2	0	2	4	1	3	1	1	1	1	51,57	44,17
12	2	1	3	0	2	4	1	1	1	1	73,83	50,37
13	2	2	4	1	3	0	1	1	1	1	177,63	109,97
14	2	3	0	2	4	1	1	1	1	1	148,20	126,27
15	2	4	1	3	0	2	1	1	1	1	99,10	117,37
16	3	0	3	1	4	2	1	1	1	1	237,10	133,37
17	3	1	4	2	0	3	1	1	1	1	94,83	35,87
18	3	2	0	3	1	4	1	1	1	1	75,83	78,87
19	3	3	1	4	2	0	1	1	1	1	221,47	199,37
20	3	4	2	0	3	1	1	1	1	105,10	85,37
21	4	0	4	3	2	1	1	1	1	1	240,33	122,87
22	4	1	0	4	3	2	1	1	1	1	206,17	178,37
23	4	2	1	0	4	3	1	1	1	1	242,30	134,17
24	4	3	2	1	0	4	1	1	1	1	96,27	81,47
25	4	4	3	2	1	0	1	1	1	1	261,27	192,47

3.4 Дисперсионный анализ

Дисперсионный анализ является статистическим методом анализа результатов наблюдений, зависящих от различных факторов и оценки их влияния на исследуемый процесс.

С помощью дисперсионного анализа устанавливаются изменения дисперсии результатов эксперимента при изменении уровней изучаемых факторов. Если дисперсии будут отличаться значимо, то следует вывод о значимом влиянии фактора на среднее значение наблюдаемой случайной величины.

Метод дисперсионного анализа основывается на следующих предпосылках: распределение исходных случайных величин нормально; дисперсии экспериментальных данных одинаковы для всех условий эксперимента (т. е. для экспериментов, выполненных на различных уровнях изучаемого фактора).

Поэтому при проведении дисперсионного анализа следует предварительно проверить нормальность распределения и неразличимость дисперсий.

3.4.1 Проверка применимости дисперсионного анализа

- проверим выборки на наличие грубых погрешностей по правилу "трех сигм" по формуле (13):

Для ПК Y₁: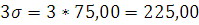

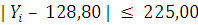
При проверке условия (13) для ПК Y₁ грубых погрешностей не обнаружено.

Для ПК Y₂: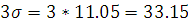

При проверке условия (13) для ПК Y₂ грубых погрешностей не обнаружено.

- проверка нормальности полученной выборки

Воспользуемся критерием Дэвида-Хартли-Пирсона.

По формуле (6) вычисляем значение критерия для ПК Y₁:

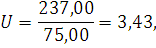
R=Y_max-Y_min=261,26-23,96=237,00

Гипотеза нормальности принимается, если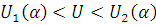

По таблице 75 [4] для n=25 и 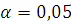 находим ;

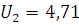
,34<3,43<4,71 следовательно условие 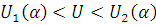 выполняется, гипотезу о нормальности распределения принимаем на уровне значимости 0,05.

По формуле (6) вычисляем значение критерия для ПК Y₂:

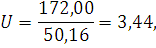
R=Y_max-Y_min=199,37-26,37=172,00

По таблице 75 [4] для n=25 и 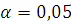 находим ;

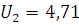
,34<3,44<4,71 следовательно условие 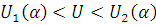 выполняется, гипотезу о нормальности распределения принимаем на уровне значимости 0,05. следовательно гипотезу о нормальности распределения принимаем.

- проверка гипотезы о неразличимости дисперсий

Условие однородности дисперсий - это равенство дисперсий. Его проверим по критерию Кохрена:

 (18)

Оценка дисперсии определяется по формуле

 (19)

Сформируем 5 выборок из ПК Y₁ и Y₂

Таблица 11 - Оценка дисперсии для ПК Y₁

Выборки	1	2	3	4	5
	23,97	31,67	51,57	87,07	209,57
	84,67	173,30	95,97	76,33	55,77
	51,57	73,83	177,63	148,20	99,10
	237,10	94,83	75,83	221,47	105,10
	240,33	206,17	242,30	96,27	261,27
S2у	10765,81	5187,87	6278,83	3618,32	7335,37

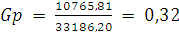< G _кр(5;5;0,05)=0,63

Так как условие G_p<G _кр выполняется, то гипотезу об однородности дисперсий принимаем.

Таблица 12 - Оценка дисперсии для ПК Y₂

Выборки	1	2	3	4	5
	26,37	30,37	48,37	95,47	147,57
	63,37	143,67	82,17	62,37	63,47
	44,17	50,37	109,97	126,27	117,37
	133,37	35,87	78,87	198,37	85,37
	122,87	178,37	134,17	81,47	192,47
S2у	2275,83	4680,07	1066,38	2832,19	2601,50

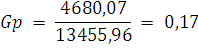
G _кр(5;5;0,05)=0,63

Так как условие G_p<G _кр выполняется, то гипотезу об однородности дисперсий для ПК Y₂ принимаем.

Делаем вывод, что мы можем воспользоваться дисперсионным анализом.

3.4.2 Алгоритм дисперсионного анализа

1) определяем итоги для всех факторов на каждом уровне

Таблица 13 -Итоги по факторам А, B, C, D, E, F

Итоги фактора А
	0	1	2	3	4
Y1	403,8333	486,0333	550,3333	734,3333	1046,333
Y2	637,63	579,80	643,30	629,33	730,80
Итоги фактора В
	0	1	2	3	4
Y1	348,15	415,05	448,15	531,85	709,35
Y2	390,15	438,65	453,55	563,95	606,25
Итоги фактора С
	0	1	2	3	4
Y1	509,93	679,20	477,8	755,2333	798,7
Y2	473,35	543,65	403,05	553,85	478,65
Итоги фактора D
	0	1	2	3	4
Y1	521,53	598,43	640,5333	675,6333	784,7333
Y2	358,65	418,65	466,35	558,25	650,65
Итоги фактора Е
	0	1	2	3	4
Y1	410,13	496,6667	642,9667	660,6333	1010,467
Y2	343,25	408,25	483,45	532,55	685,05
Итоги фактора F
	0	1	2	3	4
Y1	857,63	621,2667	670,2667	531,5333	540,1667
Y2	670,85	447,05	539,85	373,15	421,65

2) Сумма квадратов всех наблюдений:

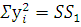, (20)

) Сумма квадратов итогов по каждому из факторов:

, (21)

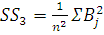, (22)

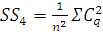, (23)

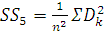, (24)

, (25)

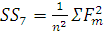, (26)

) Квадрат общего итога, деленный на число всех наблюдений (корректирующий член)

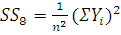, (27)

) Суммы квадратов, обусловленные фактором:

SS_A = SS₂ - SS₈, (28)_B = SS₃ - SS₈, (29)

SS_C = SS₄ - SS₈, (30)

SS_D = SS₅ - SS₈, (31)_E = SS₆ - SS₈, (32)_F = SS₇ - SS₈, (33)

6) Общая сумма квадратов:

SS_общ = SS₁ - SS₈, (34)

) Остаточная сумма квадратов:

SS_ост = SS_общ - ΣSS_факт, (35)

) Дисперсия фактора:

, (36)

) Дисперсия ошибки:

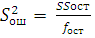, (37)

10) Дисперсионное отношение:

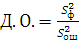, (38)

При расчете SS_ост исключим из расчета фактор В для Y₁ и фактор С для Y_2.

Таблица 14 - Результаты расчетов Y₁и Y₂

	Y1	Y2
SS1	550086,46	301007,27
SS2	467247,09	256071,04
SS3	417341,66	247183,42
SS4	431587,31	243584,10
SS5	422537,85	251273,69
SS6	457154,51	254223,11
SS7	429014,46	251672,22	414959,28	240600,06
SSA	52287,80	15470,98
SSB	2382,37	6583,36
SSC	16628,03	2984,04
SSD	7578,56	10673,63
SSE	42195,23	13623,05
SSF	14055,18	11072,16
SS общ	135127,17	60407,21
SSост	2382,37	2984,04
S²A	13071,95	3867,74
S²B	595,59	1645,84
S²C	4157,01	746,01
S²D	1894,64	2668,41
S²E	10548,80	3405,76
S²F	3513,79	2768,04
S²ош	595,59	746,01

Значимость факторов проверяют по критерию Фишера:

Д.О. = 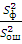 > F _{1- p} (f₁ ,f₂) (39)

где р - уровень значимости;

f₁ - число степеней свободы фактора, (f₁ = 4);

f₂ - число степеней свободы остатка, (f₂ = 4).

Если дисперсионное отношение удовлетворяет неравенству, то принимаются нулевые гипотезы. Если дисперсионное отношение будет больше табличного, то соответствующая нулевая гипотеза отвергается, и влияние фактора считается значимым.

По таблице 7[2] значение критерия Фишера для всех факторов Y₁, Y₂:

F _0,05(4;4)=6.4

Таблица15- Итоговая таблица дисперсионного анализа для Y₁

Источник дисперсии	Число степеней свободы f	Сумма квадратов	Средний квадрат	Д.О.
A	4	52287,80	13071,95	21,95
B	4	2382,37	595,59	1,00
C	4	16628,03	4157,01	6,98
D	4	7578,56	1894,64	3,18
E	4	42195,23	10548,80	17,71
F	4	14055,18	3513,79	5,90
Остаток	4	2382,37	595,59
Общая сумма	24	135127,17

На ПК Y₁ оказывают влияние факторы: А, С, E.

Таблица16- Итоговая таблица дисперсионного анализа для Y₂

Источник дисперсии	Число степеней свободы f	Сумма квадратов	Средний квадрат	Д.О.
A	4	15470,98	3867,74	5,18
B	4	6583,36	1645,84	2,21
C	4	2984,04	746,01	1,00
D	4	10673,63	2668,41	3,58
E	4	13623,05	3405,76	4,57
F	4	11072,16	2768,04	3,71
Остаток	4	2984,04	746,01
Общая сумма	24	60407,21

На ПК Y₂ факторы влияния не оказывают.

3.4.3 Вычисление множественного рангового критерия Дункана

Вычисление критерия Дункана будем производить по тем показателям качества, для которых обнаружено факторное влияние.

В качестве нулевой примем гипотезу Н₀: отсутствие значимой разности.

При вычислении критерия Дункана необходимо:

проранжировать средние значения, расположив их в порядке возрастания

определить ошибку воспроизводимости результатов с соответствующим числом степеней свободы (таблица 15, 16);

определить ошибку для каждого среднего по формуле:

 (40)

где S²_ош - ошибка воспроизводимости результатов.

S_Y1(А) = S_Y1(С) = S_Y1(E)= 10,91

выписать из таблицы критерия Дункана значения рангов числом k-1 (где k - количество градаций фактора) с выбранным уровнем значимости 0,05 и числом степеней свободы f=4 и умножаем эти ранги на соответствующие ошибки средних.

Таблица 17 - Параметры влияющих факторов

Факторы	Параметры	Значения
	Градации	0	1	2	3	4
А	Среднее значение	80,76	97,20	110,06	146,86	209,26
	Ранги		3,98	4,01	4,02	4,02
	РангSy		43,43	43,76	43,87	43,87
С	Градации	2	0	1	3	4
	Среднее значение	95,56	101,98	135,84	151,04	159,74
	Ранги		3,98	4,01	4,02	4,02
	РангSy		43,43	43,76	43,87	43,87
Е	Градации	0	1	2	3	4
	Среднее значение	82,026	99,33	128,59	132,12	202,09
	Ранги		3,98	4,01	4,02	4,02
	РангSy		43,438	43,76	43,87	43,87

вычисляем разности средних по градациям и сравниваем полученные значения с соответствующими рангами для нахождения значимости разностей.

А4-A0	642,50	>43,87	различие значимое
A4-A1	560,30	>43,87	различие значимое
A4-A2	496,00	>43,76	различие значимое
A4-A3	312,00	>43,43	различие значимое
A3-A0	330,50	>43,87	различие значимое
A3-A1	248,30	>43,76	различие значимое
A3-A2	184,00	>43,43	различие значимое
A2-A0	146,50	>43,76	различие значимое
A2-A1	64,30	>43,43	различие значимое
A1-A0	82,20	>43,43	различие значимое
C4-C0	64,18	>43,87	различие значимое
C4-C1	119,50	>43,87	различие значимое
C4-C2	320,90	>43,76	различие значимое
C4-C3	43,47	>43,43	различие незначимое
C3-C0	245,30	>43,87	различие значимое
C3-C1	76,03	>43,76	различие значимое
C3-C2	277,43	>43,43	различие значимое
C2-C0	40,28	>43,76	различие незначимое
C2-C1	33,85	>43,43	различие незначимое
			различие значимое
C1-C0	6,43	>43,43	различие незначимое
E4-E0	600,33	>43,87	различие значимое
E4-E1	513,80	>43,87	различие значимое
E4-E2	367,50	>43,76	различие значимое
E4-E3	349,83	>43,43	различие значимое
E3-E0	250,50	>43,87	различие значимое
E3-E1	163,97	>43,76	различие значимое
E3-E2	17,67	>43,43	различие значимое
E2-E0	232,83	>43,76	различие значимое
E2-E1	146,30	>43,43	различие значимое
			различие значимое
E1-E0	86,53	различие значимое

Анализ по критерию Дункана показал, что следующие градации влияющих факторов:

градации 0, 1, 2, 3, 4 фактора А для показателя качества Y₁ являются значимыми

градации 0, 1, 2, 3, 4 фактора C для показателя качества Y₁ являются значимыми

градации 0, 1, 2, 3, 4 фактора E для показателя качества Y₁ являются значимыми

. Регрессионный анализ

Получим зависимость точности метода измерения прочности от факторов: А, С, E. Вычислим

z⁰_j = (z^max_j + z^min_j)/2 (41)

∆z_j = (z^max_j - z^min_j)/2 (42)

x_j = (z_j - z⁰_j)/ ∆z_j (43)

Составим матрицу планирования.

Таблица 18 - Матрица планирования

№	z1	z2	z3	z4	x1	x2	x3	x4	Y2
1
2
3
4
5
6
7
8

Составим расширенную матрицу планирования

Таблица 19 - Расширенная матрица планирования

№

x0

x1

x2

x3

x4

x12

x13

x14

x23

x24

x34

x1234

Y2

1

2

3

4

5

6

7

8

Уравнение регрессии с коэффициентами взаимодействия:

y = b₀+b₁∙x₁+b₂∙x₂+b₃∙x₃+b₄∙x₄+b₁₂∙x₁₂+b₁₃∙x₁₃+b₁₄∙x₁₄+

+b₂₃∙x₂₃+b₂₄∙x₂₄+b₃₄∙x₃₄+b₁₂₃₄∙x₁₂₃₄ (44)

Список литературы

1. Воскобойников Ю. Е. Математическая статистика: учебное пособие/ Ю. Е. Воскобойников, Е. И. Тимошенко. - Новосибирск: НГАСУ, 2000.

. Гмурман В.Е. Теория вероятности и математическая статистика: Учеб. пособие для вузов /В.Е Гмурман. - М.: Высш. шк., 1997. - 480 с.

. Сергеев А. Г. Метрология: учебное пособие/А. Г. Сергеев, В. В, Крохин. - М.: Логос, 2000. - 408 с.

. Кобзарь А. И. Прикладная математическая статистика. Для инженеров и научных работников / А. И. Кобзарь - М.:ФИЗМАТЛИТ, 2006 - 816 с.

. ГОСТ Р 1.5. Государственная система стандартизации РФ. Стандарты. Общие требования к построению, изложению, оформлению, содержанию и обозначению. - М.: ИПК Изд-во стандартов, 2004