Дифференциальные включения
Дифференциальные
включения
Введение
Курсовая
работа посвящена изучению теории дифференциальных включений. Дифференциальные
включения - разновидность дифференциальных уравнений с многозначной правой
частью, которые являются обобщением обыкновенных дифференциальных уравнений.
Дифференциальные включения моделируют процессы состояний которые в каждый
момент времени описываются некоторым множеством в 
 Совокупность
этих множеств образует многозначную траекторию процесса.
Совокупность
этих множеств образует многозначную траекторию процесса.
Рассмотрим
управляемую систему
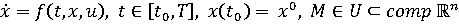
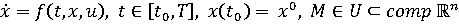 (1)
(1)
Каждое
конкретное управление порождает свою траекторию, тогда совокупность всех
траекторий порождаемых всеми допустимыми управлениями можно объединить.
Подставим
в (1) вместо u всё множество, тогда получим
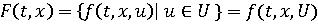
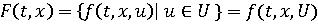 .
.
Таким
образом из (1) получаем включение 
 .
.
Представленное
преобразование уравнения управляемого движения говорит об очевидной
актуальности изучения дифференциальных включений для систем управления. Для
исследования дифференциальных включений необходимо изучать свойства
многозначных отображений.
В
курсовой работе рассматриваются вопросы исторического развития теории
дифференциальных включений, вопросы существования и единственности решений.
1. История развития теории дифференциальных включений
дифференциальное включение математика
Первые работы по уравнениям с многозначной правой частью появились в
середине 30х годов у А. Маршо (A. Marchaud)[] и С.К. Зарембы (S.K. Zaremba)[] где
рассматривались вопросы существования решений и изучались некоторые свойства
множества всех решений. Это были уравнения в контингенциях и паратингенциях.
Авторы расширили понятия производной - ввели соответственно контингентную и
паратингентную производные.
После работ Маршо и Зарембы дифференциальные включения в течении 25 лет
не было публикаций по дифференциальным включениям, кроме двух работ А.Д.
Мышкиса []. Это объясняется тем, что в то время дифференциальные включения не
имели практической реализации в приложениях.
Новые работы по дифференциальным включениям появились в конце 50х, начале
60х годов. В то время активно исследовались задачи теории управления,
рассматривались различные математический модели для описания управляемых
систем, разрабатывались методы решения задач управления и анализа свойств
решений.
Особо следует выделить работы Т. Важевского [] и А.Ф. Филиппова [] в
которых были получены принципиальные результаты по существованию и свойствам
решений дифференциальных уравнений с многозначной правой частью (
дифференциальных включений ).
 (1)
(1)
Важным
является установление связи между дифференциальными включениями и дифференциальными
уравнениями, описывающими поведение управляемых объектов. Эту связь установил
А.Ф. Филиппов в лемме о неявных функциях []. Уравнения движения объекта
управления обычно записывается в виде дифференциального уравнения

 , (2)
, (2)
где
 - вектор управления.
- вектор управления.
Очевидно,
что уравнение управляемого движения (2) можно интерпретировать как выбор
вектора скорости из множества

т.е.
рассматривать дифференциальное включение (3).
Наличие
установленной связи между управляемыми системами и дифференциальными
включениями позволяло сводить задачи отыскания оптимального управления к
задачам отыскания оптимального решения соответствующего дифференциального
включения.
В
работах Т. Важевского (T. Wazevski) и его учеников было проведено фундаментальное
исследование решений дифференциальных включений: вопросы взаимосвязи между
различными понятиями решений дифференциального включения, существования
глобальных решений, компактности и связности сечений интегральной воронки
дифференциального включения.
Следует
заметить, что все эти свойства были установлены для дифференциального включения
с выпуклой правой частью. На первоначальном этапе изучения дифференциальных
включений центральным вопросом была взаимосвязь определений решения,
дифференциального включения в смысле А. Маршо и С.К. Зарембы с естественным
определением решения, а также вопросы существования и свойств всех решений
дифференциального включения.
Обобщения
полученных результатов на случай выпуклых правых частей являлось проблематичным
в силу наличия трудностей принципиального характера, прежде всего связанных с
обоснованием существования решения.
Только
в конце 70х годов А.Ф. Филиппову удалось доказать теорему существования
локальных решений дифференциальных включений с невыпуклой правой частью.
Затем
появились работы Качинского и Олеха (C. Olech),
Антосевича и Челлини касающихся так же теорем существования дифференциальных
включений с невыпуклой правой частью.
2.Элементы многозначного анализа
.1 Операции над множествами
Пусть
 -
- 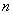 - мерное
евклидово векторное пространство с элементами
- мерное
евклидово векторное пространство с элементами  Пространство
Пространство
 является линейным пространством с обычными операциями
сложения векторов, умножения вектора на число и скалярным произведением
является линейным пространством с обычными операциями
сложения векторов, умножения вектора на число и скалярным произведением  а также нормированным пространством с нормой
а также нормированным пространством с нормой  .
.
Рассмотрим
пространство  , состоящее из всех непустых компактных подмножеств
пространства
, состоящее из всех непустых компактных подмножеств
пространства 
Определение
1. Алгебраической суммой или просто суммой двух множеств  и
и  из пространства
из пространства
 называется множество
называется множество
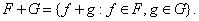
Сумма
 +
+ двух множеств
двух множеств  и
и  из пространства
из пространства  является
также Элементом пространства
является
также Элементом пространства 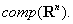 Кроме
того, если множества
Кроме
того, если множества  ,
, выпуклы, то их алгебраическая сумма
выпуклы, то их алгебраическая сумма  +
+ также будет выпуклым множеством.
также будет выпуклым множеством.
Если
множество  состоит из единственной точки, то есть
состоит из единственной точки, то есть  , то множество
, то множество  получается
параллельным сдвигом множества
получается
параллельным сдвигом множества  на
вектор
на
вектор  .
.
Пусть
 шар радиуса
шар радиуса  с
центром в точке
с
центром в точке  то есть
то есть

Тогда

то
есть при сложении двух шаров их радиусы суммируются и векторы, задающее центры
шаров, также суммируется.
Из
этой формулы при  мы получаем, что
мы получаем, что

Операция
алгебраической суммы для любых множеств  удовлетворяет
следующим свойствам:
удовлетворяет
следующим свойствам:
)
коммутативности 
)
ассоциативности 
)
существует нулевой элемент  :
:
Следует
отметить, что если множество  состоит
более чем из одной точки, то у такого множества нет обратного элемента
относительно введенной операции суммы множеств, то есть не существует такое
множество
состоит
более чем из одной точки, то у такого множества нет обратного элемента
относительно введенной операции суммы множеств, то есть не существует такое
множество  что
что 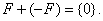 Если же
Если же  то
то 
Определение
2. Произведением множества  на число
на число
 называется множество
называется множество

Произведение
 на произвольное число
на произвольное число  является
элементом пространства
является
элементом пространства 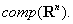 Кроме того, если множество
Кроме того, если множество  выпуклое, то и множество
выпуклое, то и множество  также выпуклое.
также выпуклое.
При
умножении шара радиуса  с центром в a на число
с центром в a на число  радиус шара умножается на
радиус шара умножается на  а центр - на
а центр - на  то есть
то есть

Таким
образом, учитывая формулу , имеем

Непосредственно
проверяется, что для любых чисел  и любых
двух множеств
и любых
двух множеств  выполняются следующие свойства:
выполняются следующие свойства:
)

)

)

Пространство
 не является линейным пространством с введенными
операциями алгебраической суммы двух множеств и умножения множества не число
хотя бы потому, что не у каждого элемента
не является линейным пространством с введенными
операциями алгебраической суммы двух множеств и умножения множества не число
хотя бы потому, что не у каждого элемента  есть
обратный элемент
есть
обратный элемент  Кроме того, не всегда выполняется необходимый для
линейности закон дистрибутивности, то есть не всегда выполняется равенство:
Кроме того, не всегда выполняется необходимый для
линейности закон дистрибутивности, то есть не всегда выполняется равенство:

Вместо
равенства в формуле справедливо лишь одностороннее включение

Оказывается,
что если  и множество
и множество  выпукло,
то формула в этом случае справедлива.
выпукло,
то формула в этом случае справедлива.
Пусть
 и в пространстве
и в пространстве  задано
линейное преобразование с помощью матрицы
задано
линейное преобразование с помощью матрицы  (с
действительными элементами) размером
(с
действительными элементами) размером 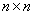 .
.
Определение
3. Образом множества  при линейном преобразовании, задаваемом матрицей
при линейном преобразовании, задаваемом матрицей  , называется множество
, называется множество

Легко
проверить, что образ множества  при
линейном преобразовании также является элементом пространства
при
линейном преобразовании также является элементом пространства 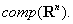 Кроме того, если множество
Кроме того, если множество  выпуклое, то и множество
выпуклое, то и множество  также выпукло.
также выпукло.
.2 Опорная функция и ее основные свойства
Определение
4. Пусть задано некоторое множество  Опорной
функцией множества
Опорной
функцией множества  называется скалярная функция
называется скалярная функция  векторного аргумента
векторного аргумента 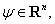 определяемая
условием
определяемая
условием

Множество
 также считается одним из аргументов функции
также считается одним из аргументов функции  . Зафиксируем множество
. Зафиксируем множество  . Функция
. Функция
 как функция аргумента
как функция аргумента  отображает
пространство
отображает
пространство  в числовую ось
в числовую ось 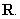 Максимум
в правой части равенства достигается, так как скалярное произведение
Максимум
в правой части равенства достигается, так как скалярное произведение 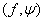 непрерывно по
непрерывно по  а множество
а множество  компактно.
компактно.
Пусть
 некоторый фиксированный вектор, а
некоторый фиксированный вектор, а  один из векторов множества
один из векторов множества  , на котором достигается максимум в определении
опорной функции для вектора
, на котором достигается максимум в определении
опорной функции для вектора  , то есть
выполняется равенство
, то есть
выполняется равенство
В
этом случае вектор  называется опорным вектором к множеству
называется опорным вектором к множеству  в точке
в точке  , а
совокупность
, а
совокупность  всех векторов
всех векторов  ,
удовлетворяющих равенству , называется опорным множеством к множеству
,
удовлетворяющих равенству , называется опорным множеством к множеству  в направлении вектора
в направлении вектора 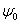 .
Гиперплоскость
.
Гиперплоскость  в пространстве
в пространстве  определяемая
соотношением
определяемая
соотношением
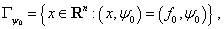
называется
опорной гиперплоскостью к множеству  в
направлении вектора
в
направлении вектора 
Для
опорного множества  справедливо представление
справедливо представление 
Гиперплоскость
 разбивает все пространство
разбивает все пространство  на два полупространства
на два полупространства  и
и 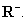 Множество
Множество
 лежит в отрицательном полупространстве
лежит в отрицательном полупространстве  относительно вектора
относительно вектора 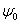 , так как
для всех точек
, так как
для всех точек  выполняется неравенство
выполняется неравенство 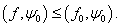
Свойства опорных функций
1.
Опорная функция 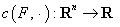 положительно однородна, то есть
положительно однородна, то есть

для
любого вектора  и любого числа
и любого числа  . В
частности,
. В
частности, 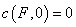 .
.
.
Для любых двух векторов  опорная функция удовлетворяет неравенству
опорная функция удовлетворяет неравенству

Следствие
1. Опорная функция 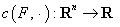 является выпуклой.
является выпуклой.
.
Пусть  Тогда опорная функция
Тогда опорная функция  суммы
суммы  равняется сумме двух опорных функций
равняется сумме двух опорных функций  и
и  , то есть
, то есть

4.
Пусть  - матрица размером
- матрица размером 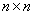 , а
, а  Тогда
Тогда

где
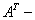 матрица, транспонированная к матрице А.
матрица, транспонированная к матрице А.
.
Пусть  a
a  произвольное
число. Тогда
произвольное
число. Тогда

Следствие
2. Опорная функция  положительно однородна по первому аргументу
положительно однородна по первому аргументу  , то есть
, то есть  для
любого числа
для
любого числа  .
.
.
Пусть  Если выполняется включение
Если выполняется включение  , то для любого вектора
, то для любого вектора  справедливо
неравенство
справедливо
неравенство

Следствие
3. Пусть  Если точка
Если точка  принадлежит
множеству
принадлежит
множеству  , то для любого вектора
, то для любого вектора  выполняется
неравенство
выполняется
неравенство 
.
Пусть  Тогда опорные функции множеств
Тогда опорные функции множеств  и
и  совпадают,
то есть
совпадают,
то есть
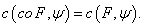
.
Пусть заданы множество  и его опорная функция
и его опорная функция  . Тогда
выпуклая оболочка
. Тогда
выпуклая оболочка  множества
множества  представляется
в виде
представляется
в виде

Здесь
и далее S - единичная сфера с центром в начале координат.
9. Пусть 
 Если для любого вектора
Если для любого вектора  выполняется неравенство
выполняется неравенство

то
точка  принадлежит выпуклой оболочке
принадлежит выпуклой оболочке  множества
множества 
Следствие
4. Пусть множество  В таком случае точка
В таком случае точка  принадлежит
множеству
принадлежит
множеству  тогда и только тогда, когда неравенство выполняется
для любого вектора
тогда и только тогда, когда неравенство выполняется
для любого вектора  .
.
.
Пусть  Если для любого вектора
Если для любого вектора  выполняется неравенство
выполняется неравенство

то справедливо включение GÌ coF.
Следствие
5. Пусть  и множество
и множество  выпукло.
Тогда включение
выпукло.
Тогда включение  справедливо тогда и только тогда, когда для любого
вектора
справедливо тогда и только тогда, когда для любого
вектора  выполняется неравенство (8).
выполняется неравенство (8).
.
Пусть  Если множества
Если множества  и
и  равны, то их опорные функции совпадают. Наоборот,
если их опорные функции совпадают, то
равны, то их опорные функции совпадают. Наоборот,
если их опорные функции совпадают, то 
Следствие
6. Множества 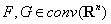 равны тогда и только тогда, когда их опорные функции
совпадают. Таким образом, множество
равны тогда и только тогда, когда их опорные функции
совпадают. Таким образом, множество  можно
однозначно восстановить по его опорной функции
можно
однозначно восстановить по его опорной функции  .
.
.
Пусть  . Если множества
. Если множества  и
и  пересекаются, то есть
пересекаются, то есть  , то для
любого вектора
, то для
любого вектора  выполняется неравенство
выполняется неравенство
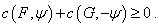
Наоборот,
если выполняется соотношение для любого вектора  , то
, то 
Следствие
7. Два множества  пересекаются тогда и только тогда, когда неравенство
выполняется для любого вектора
пересекаются тогда и только тогда, когда неравенство
выполняется для любого вектора  .
.
.
Опорная функция  для любых двух множеств
для любых двух множеств  и любых двух векторов
и любых двух векторов 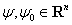 удовлетворяет
неравенству
удовлетворяет
неравенству

Следствие
8. Опорная функция  непрерывна по совокупности переменных
непрерывна по совокупности переменных 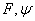 в любой точке
в любой точке 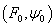 и,
следовательно, непрерывна по каждой из переменных
и,
следовательно, непрерывна по каждой из переменных 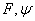 в отдельности.
в отдельности.
.
Пусть Если точка
Если точка  является
внутренней точкой множества
является
внутренней точкой множества  , то для
любого вектора
, то для
любого вектора  выполняется неравенство
выполняется неравенство

Наоборот,
если соотношение выполняется для любого вектора  , то
, то 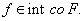
Следствие
9. Точка  принадлежит внутренности множества
принадлежит внутренности множества 
 тогда и
только тогда, когда неравенство справедливо для любого вектора
тогда и
только тогда, когда неравенство справедливо для любого вектора  .
.
.
Пусть заданы два множества  Тогда
справедливо соотношение
Тогда
справедливо соотношение

Следствие
10. Для множеств 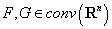 справедливо равенство
справедливо равенство

Заметим,
что если множества  не являются выпуклыми, то в формуле может быть
строгое неравенство.
не являются выпуклыми, то в формуле может быть
строгое неравенство.
Многозначные отображения. Интеграл Ауманна
Определение
5. Многозначным отображением будем называть произвольную функцию  то есть функцию, аргументом которой является время
то есть функцию, аргументом которой является время  а значениями - элементы пространства
а значениями - элементы пространства  то есть непустые компактные множества из
то есть непустые компактные множества из 
Так
как пространства  и
и  метрические,
то можно говорить о непрерывности многозначного отображения.
метрические,
то можно говорить о непрерывности многозначного отображения.
Определение
6. Многозначное отображение  непрерывно
в точке
непрерывно
в точке  если для любого
если для любого  существует
существует
 такое, что при всех
такое, что при всех  удовлетворяющих
условию
удовлетворяющих
условию  справедливо неравенство
справедливо неравенство 
По
определению расстояния по Хаусдорфу это означает, что многозначное отображение  непрерывно в точке
непрерывно в точке  если для
любого
если для
любого  существует
существует  такое,
что при всех
такое,
что при всех  удовлетворяющих условию
удовлетворяющих условию  выполняются одновременно следующие два включения
выполняются одновременно следующие два включения
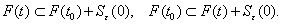
В
случае, когда выполняется лишь первое включение, многозначное отображение  называется полунепрерывным сверху в точке
называется полунепрерывным сверху в точке 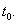 Если же выполняется второе включение, то многозначное
отображение
Если же выполняется второе включение, то многозначное
отображение  называется полунепрерывным снизу в точке
называется полунепрерывным снизу в точке 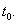 Таким образом, многозначное отображение
Таким образом, многозначное отображение  непрерывно в точке
непрерывно в точке  тогда и только
тогда, когда оно полунепрерывно сверху и снизу в данной точке.
тогда и только
тогда, когда оно полунепрерывно сверху и снизу в данной точке.
Определение
7. Многозначное отображение 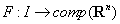 назовем
непрерывным на отрезке
назовем
непрерывным на отрезке  , если оно непрерывно в каждой точке этого отрезка.
, если оно непрерывно в каждой точке этого отрезка.
Теорема
1 [Благодатских]. Пусть  непрерывное многозначное отображение. Тогда опорная
функция
непрерывное многозначное отображение. Тогда опорная
функция  непрерывна по
непрерывна по  при
каждом фиксированном значении
при
каждом фиксированном значении  Наоборот,
если функция
Наоборот,
если функция  непрерывна по
непрерывна по  при
каждом фиксированном значении
при
каждом фиксированном значении  то
многозначное отображение
то
многозначное отображение  непрерывно.
непрерывно.
Следствие
11. Многозначное отображение  непрерывно
тогда и только тогда, когда опорная функция
непрерывно
тогда и только тогда, когда опорная функция  непрерывна
по
непрерывна
по  при каждом фиксированном значении
при каждом фиксированном значении 
Определение
8. Многозначное отображение 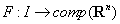 назовем
измеримым на отрезке
назовем
измеримым на отрезке 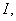 если его опорная функция
если его опорная функция  измерима по
измерима по  на
отрезке
на
отрезке  для каждого фиксированного вектора
для каждого фиксированного вектора 
Такое
определение измеримости является очень общим, и широкий класс отображений  измерим в указанном смысле. Обычно в литературе по
многозначным отображениям измеримость определяют для более узкого класса
отображений
измерим в указанном смысле. Обычно в литературе по
многозначным отображениям измеримость определяют для более узкого класса
отображений 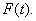 Поскольку по опорной функции
Поскольку по опорной функции  можно восстановить лишь выпуклую оболочку
можно восстановить лишь выпуклую оболочку  данное определение измеримости накладывает
ограничение на поведение лишь многозначного отображения
данное определение измеримости накладывает
ограничение на поведение лишь многозначного отображения  и никак не отражает того, что происходит с той частью
множества
и никак не отражает того, что происходит с той частью
множества  которая лежит внутри
которая лежит внутри  Тем не менее
все приводимые ниже результаты справедливы для многозначных отображений
Тем не менее
все приводимые ниже результаты справедливы для многозначных отображений  измеримых в указанном смысле.
измеримых в указанном смысле.
Любое
непрерывное многозначное отображение 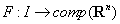 измеримо,
поскольку его опорная функция
измеримо,
поскольку его опорная функция  непрерывна
по
непрерывна
по  при каждом фиксированном
при каждом фиксированном  и, следовательно, измерима.
и, следовательно, измерима.
Определение
9. Функция  называется однозначной ветвью многозначного
отображения
называется однозначной ветвью многозначного
отображения  если при всех
если при всех  выполняется
включение
выполняется
включение 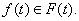
Ясно,
что однозначная ветвь  всегда существует, поскольку множество
всегда существует, поскольку множество  непусто при всех
непусто при всех 
Теорема
2 (теорема А.Ф.Филиппова) [ ]. Если многозначное отображение 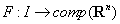 измеримо, то у него существует измеримая однозначная
ветвь
измеримо, то у него существует измеримая однозначная
ветвь 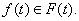
Пусть
заданы отрезок времени  и некоторое отображение
и некоторое отображение 
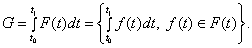
Здесь
в правой части интеграл Лебега берется по всем однозначным ветвям отображения  для которых он существует. Ясно, что
для которых он существует. Ясно, что  является подмножеством пространства
является подмножеством пространства 
Теорема
3 (теорема А.А. Ляпунова) [ ]. Пусть многозначное отображение  измеримо на отрезке
измеримо на отрезке  и
и  где
где  суммируема
на
суммируема
на  Тогда интеграл от этого многозначного отображения
является непустым выпуклым компактным множеством в пространстве
Тогда интеграл от этого многозначного отображения
является непустым выпуклым компактным множеством в пространстве  то есть
то есть 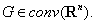
Следствие
12. Пусть многозначное отображение  непрерывно
на отрезке
непрерывно
на отрезке  Тогда
Тогда 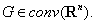
Теорема
4 [Благодатских]. Пусть многозначное отображение  измеримо
на отрезке
измеримо
на отрезке  и
и 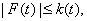 где
где  суммируема на
суммируема на  Тогда
имеет место равенство
Тогда
имеет место равенство

Следствие
4. Пусть многозначное отображение  непрерывно
на отрезке
непрерывно
на отрезке  Тогда имеет место равенство .
Тогда имеет место равенство .
С
помощью данной теоремы можно довольно просто находить интегралы от многозначных
отображений 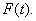 Действительно, для этого достаточно в соответствии с
формулой построить опорную функцию
Действительно, для этого достаточно в соответствии с
формулой построить опорную функцию  проинтегрировать
уже однозначную функцию
проинтегрировать
уже однозначную функцию  по
по  при
каждом значении
при
каждом значении  а затем восстановить по полученной опорной функции
непустое выпуклое компактное множество
а затем восстановить по полученной опорной функции
непустое выпуклое компактное множество  Заметим,
что для восстановления выпуклого множества
Заметим,
что для восстановления выпуклого множества  достаточно
подобрать такое множество
достаточно
подобрать такое множество 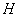 , чтобы его опорная функция
, чтобы его опорная функция  совпадала с
совпадала с 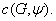 Тогда
согласно следствию 6 из свойства 11 опорных функций
Тогда
согласно следствию 6 из свойства 11 опорных функций 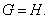
3.Дифференциальные включения
.1 Уравнения в паратингенциях и контингенциях
Паратингенцией функции  в точке
в точке  будем называть множество
будем называть множество

Контингенцией функции  в точке
в точке  будем называть множество
будем называть множество

Пример.
Пусть 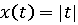
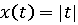 , тогда
, тогда 
 .
.
Рассматривая
уравнения с многозначной правой частью, С.Заремба ввел понятие
дифференциального уравнения в паратингенциях
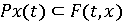
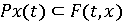 (3.1.1.)
(3.1.1.)
а
А. Маршо - понятие дифференциального уравнения в контингенциях

 (3.1.2.)
(3.1.2.)
где

 -
многозначное отображение.
-
многозначное отображение.
3.2 Понятия решения ДВ: обычные, обощенные и R-решения
Теоремы

 Примеры.
Примеры.
Определение
Непрерывная функция 
 ,
называется решением дифференциального уравнения в паратингенциях
(контингенциях), если включение (3.1.1.) (соответственно (3.1.2.)) справедливо
для всех
,
называется решением дифференциального уравнения в паратингенциях
(контингенциях), если включение (3.1.1.) (соответственно (3.1.2.)) справедливо
для всех 
 .
.
Ниже
Определение
Абсолютно непрерывная функция 
 называется
обычным решением дифференциального включения (3), если
называется
обычным решением дифференциального включения (3), если

 (3.2.1.)
(3.2.1.)
почти
всюду на отрезке 

Теоремы
существования обычных дифференциальных включений
Дифференциальное
включение 
 с
начальным условием
с
начальным условием 
 -
существует, если выполняется одно из следующих условий:
-
существует, если выполняется одно из следующих условий:

 -непрерывно
и
-непрерывно
и 
 -непустое
замкнутое подмножество для всех
-непустое
замкнутое подмножество для всех


)
 -
измеримо
-
измеримо
Для
почти всех t, для каждой точки х, 
 имеет
замкнутый график и
имеет
замкнутый график и 
 -
выпукло или
-
выпукло или 
 в
некоторой окрестности х полунепрерывно снизу
в
некоторой окрестности х полунепрерывно снизу
Функция

 -
локально интегрально ограничена, т.е. для каждого ограниченного подмножества
-
локально интегрально ограничена, т.е. для каждого ограниченного подмножества 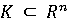
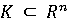 существует
функция
существует
функция 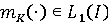
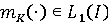 такая,
что
такая,
что 
 для
для 

)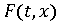
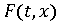 -
измеримо.
-
измеримо.
Для
каждого t, 
 имееет
замкнутый график и в каждой точке х, для которой
имееет
замкнутый график и в каждой точке х, для которой 
 невыпукло,
невыпукло,

 -
полунепрерывно снизу.
-
полунепрерывно снизу.

 - локально
слабо интегрально ограничено, т.е. для каждого
- локально
слабо интегрально ограничено, т.е. для каждого 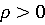
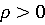 ,
, 
 - слабо
интегрально ограничено для
- слабо
интегрально ограничено для 
 c
функцией
c
функцией 
 .
.
При
выполнении одного из данных предположений, будет существовать хотя бы одно
обычное решение включения 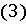
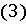 на
некотором сегменте
на
некотором сегменте 
 .
.
Если
же в 3ем предположении заменить последнее условие на более жесткое:

 - слабо
интегрально ограничено, т.е. существуют
- слабо
интегрально ограничено, т.е. существуют 
 такая,
что для почти всех t и x
такая,
что для почти всех t и x 
 , то
обычное решение дифференциального включения (3) будет существовать на всём
, то
обычное решение дифференциального включения (3) будет существовать на всём 
 .
.
Теорема
Пусть 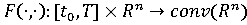
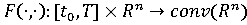 полунепрерывно
сверху по
полунепрерывно
сверху по 
 на
на 
 Тогда
система соотношений
Тогда
система соотношений
) 
 непрерывна на
непрерывна на 
 .
.
) 
 всюду на
всюду на 
 .
.
эквивалентна системе следующих соотношений:
3) 
 абсолютно непрерывна на
абсолютно непрерывна на 
 .
.
) 
 почти
всюду на
почти
всюду на 
 .
.
Определение
Непрерывная функция 
 называется
решением уравнения (2), если для почти всех
называется
решением уравнения (2), если для почти всех 


 .
.
Можно
сделать следующее утверждение: Пусть 
 и
и
)отображение

 измеримо
по x при каждом фиксированном х;
измеримо
по x при каждом фиксированном х;
)отображение

 полунепрерывно
по х при каждом фиксированном t.
полунепрерывно
по х при каждом фиксированном t.
Тогда
множество OB(F) совпадает с множеством решений в смысле последнего
определения.
Но
данное утверждение неверно, а указанная в нём эквивалентность не может быть
получена ни при каких условиях, накладываемых на правые части, если решение
уравнения в контингенциях понимается в смысле последнего уравнения. Покажем это
на примере:
Пусть

 Обычным
решением включения
Обычным
решением включения 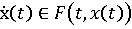
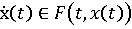 является
единственная функция
является
единственная функция 
 . В
качестве решения уравнения в контингенциях в смысле последнего определения можно
взять, например, функцию
. В
качестве решения уравнения в контингенциях в смысле последнего определения можно
взять, например, функцию 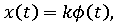
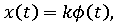 где
где 
 -
произвольная константа, а
-
произвольная константа, а 
 -
непрерывная монотонно возрастающая функция производная которой почти всюду
равна 0 и
-
непрерывная монотонно возрастающая функция производная которой почти всюду
равна 0 и 
 Построим
такую функцию: Выберем
Построим
такую функцию: Выберем 
 ,
зададим по индукции последовательность функций
,
зададим по индукции последовательность функций 
 следующим
образом: положим
следующим
образом: положим 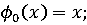
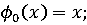 пусть
пусть 
 определена,
непрерывна и линейна на каждом интервале вида
определена,
непрерывна и линейна на каждом интервале вида 
 , где
, где 


 ; тогда
; тогда 
 мы
зададим так, чтобы
мы
зададим так, чтобы 
 равнялось
равнялось

 для
для 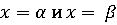
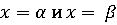 ; в
средних точках указанных интервалов; т.е. при
; в
средних точках указанных интервалов; т.е. при 
 ,
положим
,
положим


а
в интервалах 
 будем
считать
будем
считать 
 линейной.
Определённые таким образом функции
линейной.
Определённые таким образом функции 
 ,
очевидно, возрастают. Далее,
,
очевидно, возрастают. Далее,


поэтому
последовательность 
 сходится
к некоторой неубывающей функции
сходится
к некоторой неубывающей функции 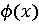
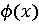 .
Докажем, что
.
Докажем, что 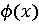
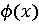 строго
возрастает, непрерывна и
строго
возрастает, непрерывна и
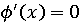
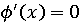
почти
всюду.
Пусть
x - какая-нибудь точка интервала [0,1]. Возьмем
последовательность вложенных интервалов вида 
 где
где


окружающих
точку х. Мы имеем, очевидно,


Так
как 
 , то
, то


откуда
получаем

 .
.
Отсюда
следует, что


и
таким
образом, 
 -
функция непрерывная и строго возрастающая. Далее, производная
-
функция непрерывная и строго возрастающая. Далее, производная 
 там, где
она существует, равна пределу выражения
там, где
она существует, равна пределу выражения


при

 ; но
такой предел либо не определён, либо бесконечен, либо, наконец, равен 0.
Следовательно
; но
такой предел либо не определён, либо бесконечен, либо, наконец, равен 0.
Следовательно 
 во всех
точках, где
во всех
точках, где 
 существует,
т.е. почти всюду.
существует,
т.е. почти всюду.
Тем
самым данная функция не является абсолютно непрерывной, а значит не является
решением 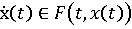
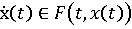 , т.е.
эквивалентности решений нет. Очевидно, что данная функция будет решением любого
уравнения в контингенциях в смысле последнего определения при любой правой
части, которая содержит точку 0 при всех
, т.е.
эквивалентности решений нет. Очевидно, что данная функция будет решением любого
уравнения в контингенциях в смысле последнего определения при любой правой
части, которая содержит точку 0 при всех 

Так
же очевидно, что 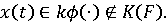
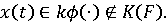
Определение
Функция 
 называется
обобщенным решением включения (3), если
называется
обобщенным решением включения (3), если 
 и
интегральное включение
и
интегральное включение

 (6)
(6)
справедливо
для всех 

Обозначим
через G(F) множество обобщенных решений включения (3).
Теорема
Пусть 
 -
удовлетворяет следующим условиям:
-
удовлетворяет следующим условиям:
) 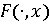
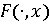 -
измеримо для всех
-
измеримо для всех 
 ;
;
) 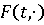
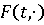 -
непрерывно для всех
-
непрерывно для всех 

) 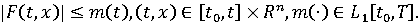
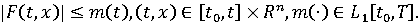
Тогда OB(F) = G(F).
Следствие
Пусть 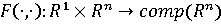
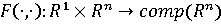 -
многозначное отображение, удовлетворяющее условиям 1)-3) теоремы.
-
многозначное отображение, удовлетворяющее условиям 1)-3) теоремы.
Тогда OB(conv F) = G(F).
Определение
Функция 
 называется
квазирасширением дифференциального включения (3), если существует
последовательность функций
называется
квазирасширением дифференциального включения (3), если существует
последовательность функций 
 такая,
что
такая,
что
1) 

) 

) 
 = x(t),
= x(t), 

) 

Множество квазирешений включения (3) обозначим через Q(F).
Теорема
Пусть 
 -
удовлетворяет следующим условиям:
-
удовлетворяет следующим условиям:
) 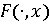
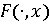 -
измеримо для всех
-
измеримо для всех 
 ;
;
) 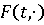
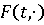 -
непрерывно для всех
-
непрерывно для всех 

) 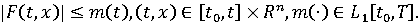
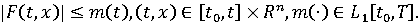
Тогда
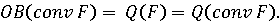
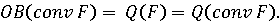
Следствие
При предположениях теоремы имеем:


Определение
Функция 
 называется
римановым решением дифференциального включения (3), если
называется
римановым решением дифференциального включения (3), если 
 -
интегрируема по Риману и
-
интегрируема по Риману и 
 для всех
для всех
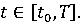
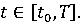
Обозначим
через Ri(F) множество всех римановых решений.
Определение
Функция 
 называется
классическим решением дифференциального включения (3), если
называется
классическим решением дифференциального включения (3), если 
 для всех
для всех 
 .
.
Обозначим
множество всех классических решений через KL(F).
Непосредственно
из определения следует, что 
 .
.
Теорема
Пусть многозначное отображение F(t, x) в каждой точке (t, x)
области 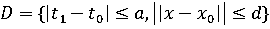
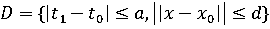 удовлетворяет
следующим условиям: 1)множество F(t, x) - непусто и замкнутое;
удовлетворяет
следующим условиям: 1)множество F(t, x) - непусто и замкнутое;
)
F(∙,x) - измеримо на D;
)множество
F(t, x) - выпукло;
)
для любого r > 0 при |x - y|
 r для
почти всех t имеем
r для
почти всех t имеем

 (7)
(7)
где
функция 
 измерима
по t и непрерывна по х,
измерима
по t и непрерывна по х,



 .
.
Пусть
при 
 функция
функция 
 абсолютно
непрерывна, её график содержится в D,
абсолютно
непрерывна, её график содержится в D, 
 и при
почти всех
и при
почти всех 



где


Тогда
для
 найдётся
такое решение
найдётся
такое решение 
 задачи
задачи

 , (8)
, (8)
что

 (9)
(9)
при
почти всех 


 ,
,

 - любое
такое, что
- любое
такое, что 
 .
.
Замечание
Если в данной теореме вместо условия 5) выполняется условие Липшица, т.е.

то
от требования 3) можно отказаться, а в (9)


Функция

 называется
функцией Камке, если она непрерывна по r, измерима по t,
называется
функцией Камке, если она непрерывна по r, измерима по t, 


 для
любого c и при
для
любого c и при 
 единственным
решением задачи
единственным
решением задачи 
 является
функция
является
функция 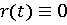
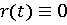 .
Например, если функция
.
Например, если функция 
 суммируема,
то k(t)r - функция Камке
суммируема,
то k(t)r - функция Камке 

Теорема
Пусть многозначное отображение 
 удовлетворяет
следующим условиям:
удовлетворяет
следующим условиям:
)
множество 
 непустое
и замкнутое;
непустое
и замкнутое;
)
 функция
функция 
 суммируема;
суммируема;
)
функция 
 измерима
по t при каждом фиксированном x;
измерима
по t при каждом фиксированном x;
)

 -
функция Камке.
-
функция Камке.
Тогда каждое решение включения

cначальным
условием 
 является
пределом равномерно сходящейся последовательности решений включения (7).
является
пределом равномерно сходящейся последовательности решений включения (7).
Теорема
Пусть в ограниченной замкнутой области D выполнены
следующие условия:
1) множество F(t,x) - невыпуклое и замкнуто
2) 

) 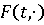
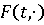 -
полунепрерывна сверху на D;
-
полунепрерывна сверху на D;
) 
 измерим
на D;
измерим
на D;
) множество

 выпукло.
выпукло.
Определение
Многозначная функция 
 называется
R-решением, порожденным дифференциальным включением
(7), если при каждом t множество R(t) замкнуто,
функция R(∙) абсолютно непрерывна и для почти всех t
называется
R-решением, порожденным дифференциальным включением
(7), если при каждом t множество R(t) замкнуто,
функция R(∙) абсолютно непрерывна и для почти всех t

Теорема
Пусть F(x, t) при каждом t, x - выпуклый
компакт и как многозначная функция непрерывна по совокупности переменных. Тогда
существует 
 такое,
что на полуинтервале
такое,
что на полуинтервале 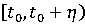
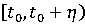 существует
R- решение, попрождённое многозначной функцией F(t,x).
существует
R- решение, попрождённое многозначной функцией F(t,x).
Теорема
Пусть F(t,x) удовлетворяет условию Липшица в некоторой
окрестности 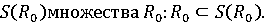
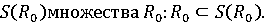 Тогда при
всех
Тогда при
всех 
 , для
которых решение
, для
которых решение 
 определено
и
определено
и 
 , оно
единственно. Более того, имеет место непрерывная зависимость решения от
начального множества
, оно
единственно. Более того, имеет место непрерывная зависимость решения от
начального множества 
 .
.
Теорема
Пусть 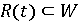
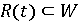 при
при 
 , где
множество
, где
множество 
 открыто
и ограничено и в
открыто
и ограничено и в 
 функция F(t,x)
липшецева. Тогда множество R(t) при
функция F(t,x)
липшецева. Тогда множество R(t) при 
 является
множеством достижимости в момент t из
является
множеством достижимости в момент t из 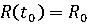
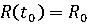 .
.
Теорема
Для любого компакта 
 существует
R-решение с начальным условием
существует
R-решение с начальным условием 
 .
Интегральная воронка является графиком R-решения R(∙).
Если выполнено условие 5) с функцией Камке
.
Интегральная воронка является графиком R-решения R(∙).
Если выполнено условие 5) с функцией Камке 
 , то R-
решение с начальным условием
, то R-
решение с начальным условием 
 единственно,
непрерывно зависит от К и его график
единственно,
непрерывно зависит от К и его график 
 является
интегральной воронкой.
является
интегральной воронкой.
Пример
Пусть
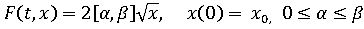
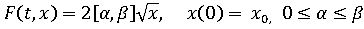 .
.
При

 отображение
отображение

 не
удовлетворяет условию Липшица.
не
удовлетворяет условию Липшица.
Пусть

 Проверим,
что многозначное отображение
Проверим,
что многозначное отображение

является
R - решением дифференциального включения
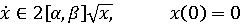
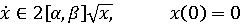 ,
,
т.е. удовлетворяет уравнению
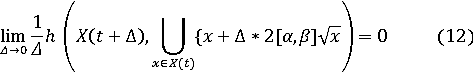
При

 очевидно,
что
очевидно,
что 
 удовлетворяет
(12).
удовлетворяет
(12).
Пусть




Пусть


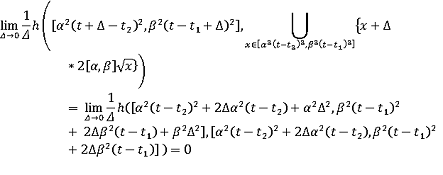
При
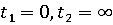
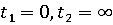

 совпадает
с интегральной воронкой
совпадает
с интегральной воронкой 
 .
.
Все
остальные 
 соответствующие
произвольным значениям
соответствующие
произвольным значениям 
 , таковы,
что
, таковы,
что 

Если


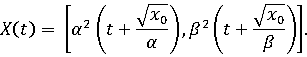
единственно
и совпадает с интегральной воронкой.
Выводы
Таким образом в курсовой работе изучена теория дифференциальных
включений, рассмотрен исторический аспект рассматриваемого объекта, изучены
основы многозначного анализа. Для дифференциальных включений рассмотрены
различные понятия решения: обычные, обобщенные и R-решения, изучены условия существования и единственности этих
решений, рассмотрены примеры.