Высшая математика
Контрольная работа №1
Вариант 5
Задача №1. Даны четыре вектора 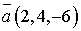 ,
, 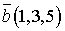 ,
, 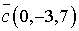 ,
, 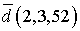 в некотором
базисе. Показать, что векторы
в некотором
базисе. Показать, что векторы 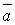 ,
, 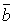 ,
, 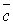 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора 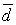 в этом
базисе.
в этом
базисе.
Решение.
Проверим, образуют ли векторы 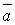 ,
, 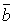 ,
, 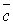 базис.
базис.
Три вектора образуют базис, если они
не лежат в одной плоскости. Найдем смешанное произведение векторов 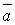 ,
, 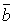 ,
, 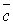 .
.
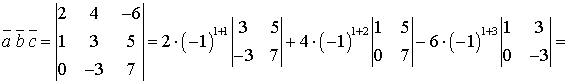
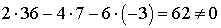
Поскольку смешенное произведение
векторов не равно 0, то векторы 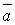 ,
, 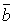 ,
, 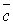 образуют базис.
образуют базис.
Найдем координаты вектора 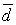 в базисе
в базисе 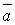
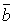
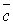 .
.
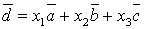 .
.
Подставляя координаты векторов,
получим систему линейных алгебраических уравнений, которую решим по формулам
Крамера.
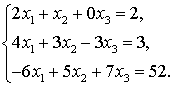
Воспользуемся формулами Крамера:
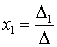 ,
,  ,
, 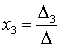 ,
,
где  - определитель, составленный из
коэффициентов при неизвестных.
- определитель, составленный из
коэффициентов при неизвестных.
 =
=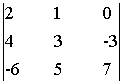 = 42 + 0 +18 +0 +30 - 28 = 62;
= 42 + 0 +18 +0 +30 - 28 = 62;
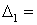
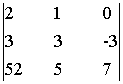 = 42 + 0 - 156 +0 + 30 - 21 = -105;
= 42 + 0 - 156 +0 + 30 - 21 = -105;
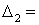
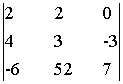 = 42 +0 +36 +0 + 312 - 56 = 334;
= 42 +0 +36 +0 + 312 - 56 = 334;
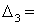
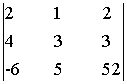 = 312 + 40 -18 +36 - 30 -208 = 132.
= 312 + 40 -18 +36 - 30 -208 = 132.
Найдем 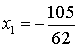 ,
, 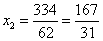 ,
, 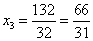 .
.
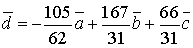 . Ответ:
. Ответ: 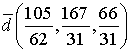
Задача №2 Даны вершин пирамиды 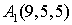 ,
, 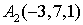 ,
, 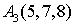 ,
, 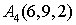 . Найти:
. Найти:
длину ребра 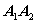 ;
;
угол между ребрами 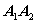 и
и  ;
;
угол между ребром  и гранью
и гранью 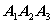 ;
;
площадь грани 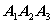 ;
;
1) объем
пирамиды;
уравнения прямой 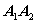 ;
;
уравнение плоскости 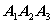 ;
;
уравнение высоты, опущенной из
вершины 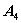 на грань
на грань 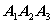 ;
;
Сделать чертеж.
Решение:
1) Длина d отрезка,
проходящего через точки с координатами  ,
,  вычисляется по формуле:
вычисляется по формуле: 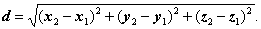
Поставим в формулу координаты точек 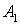 и
и 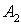 .
.
Получим
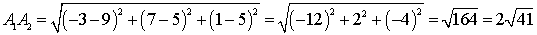 .
.
2) Угол φ между
векторами 
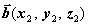 находится
по формуле:
находится
по формуле:
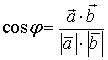 =
= 
Найдем координаты векторов 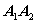 и
и  .
.
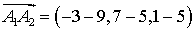 =
= 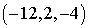 .
.
 =
=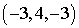 .
.
Тогда 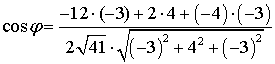 =
= 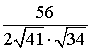 =
=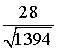 .
.
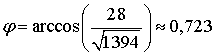 радиан.
радиан.
) Угол 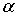 между
прямой
между
прямой  и
плоскостью
и
плоскостью 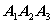 находится
по формуле:
находится
по формуле:
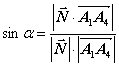 , где
, где 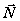 - нормальный вектор плоскости.
- нормальный вектор плоскости.
Так как 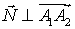 и
и 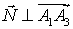 ,
,
то вектор 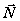 можно найти
как векторное произведение векторов
можно найти
как векторное произведение векторов 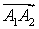 и
и 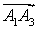 .
.
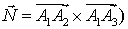 =
=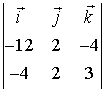 =
= 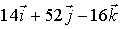 .
.
Нормальный вектор плоскости равен
(7, 26, -8).
Тогда 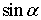 =
=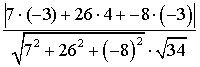 =
= 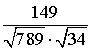 =
= 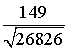 .
.
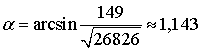 радиан.
радиан.
) Найдем площадь грани 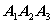 по формуле
по формуле 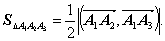
Из пункта 3 имеем 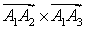 =
=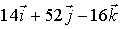 .
.
Тогда 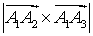 =
= 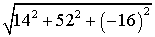 =
=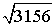 =
= 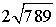 .
.
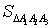 =
= 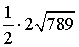 =
= 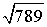 .
.
) Объем пирамиды вычислим по формуле
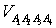 =
= 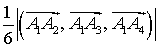 ,
,
где 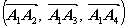 - смешанное произведение векторов
- смешанное произведение векторов 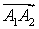 ,
, 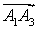 ,
, 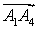 .
.
Вычислим 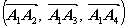 .
.
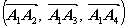 =
=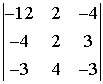 =
= 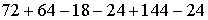 =
=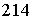 .
.
Значит, 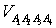 =
=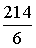 =
=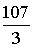 .
.
) Канонические уравнения прямой,
проходящей через точку 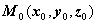 параллельно
вектору
параллельно
вектору 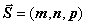 имеет вид:
имеет вид: 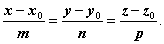
Подставим координаты точки 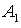 и вектора
и вектора 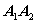 , получим:
, получим:
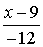 =
= 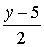 =
= 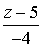 - канонические уравнения прямой
- канонические уравнения прямой 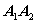 .
.
) Уравнение плоскости, проходящей
через точку 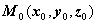 ,
перпендикулярной вектору
,
перпендикулярной вектору 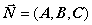 имеет вид:
имеет вид:
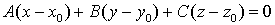 .
.
Нормальный вектор плоскости 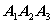 имеет
координаты (7, 26, -8) (вычислено п. 3).
имеет
координаты (7, 26, -8) (вычислено п. 3).
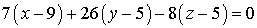 , откуда
, откуда 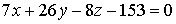 - уравнение
плоскости
- уравнение
плоскости 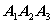 .
.
) Найдем уравнение высоты, опущенной
из вершины 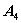 на грань
на грань 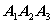 .
Направляющим вектором прямой является нормальный вектор плоскости
.
Направляющим вектором прямой является нормальный вектор плоскости 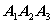 -
-  = (7, 26,
-8).
= (7, 26,
-8).
Сделаем чертеж:
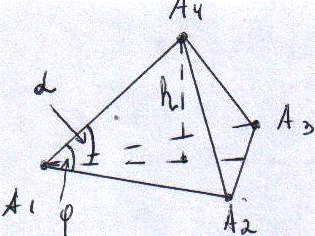

Задача №3 Составить уравнение линии,
каждая точка которой является центром окружности, касающейся оси абсцисс и
проходящей через точку 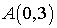
Решение.
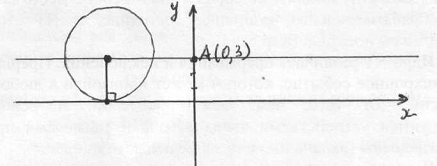
Т.к. каждая точка линии является центром
окружности, касающейся оси абсцисс, то радиус окружности в произвольной точке
линии будет перпендикулярен оси абсцисс. Значит, линия параллельна оси абсцисс.
Тогда уравнение линии имеет вид:
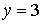
Ответ: 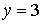 .
.
Задача №4. Доказать совместность
данной системы линейных уравнений и решить ее двумя способами. 1) методом
Гаусса; 2) средствами матричного исчисления.
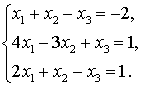
Решение
Докажем совместность системы. По
теореме Кронекера-Капелли если ранг основной матрицы равен рангу расширенной,
то система совместна. Найдем ранг расширенной матрицы. Сведем матрицу к
ступенчатому виду с помощью элементарных преобразований.
Умножим первую строку матрицы на -4
и прибавим ко второй.
Умножим первую строку матрицы на -2
и прибавим к третьей.
Далее вторую строку матрицы прибавим
к третьей, умноженной на -7.

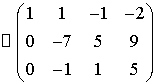
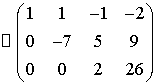 .
.
Получили ступенчатую матрицу. 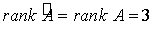 и равен
количеству неизвестных, следовательно, система совместна и определена, т.е.
имеет единственное решение.
и равен
количеству неизвестных, следовательно, система совместна и определена, т.е.
имеет единственное решение.
Решим систему методом Гаусса.
Запишем систему линейных уравнений
полученную после преобразования матрицы 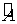 .
.
 .
.
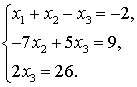
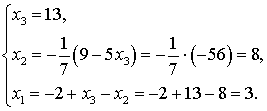
(3, 8, 13) - решение системы.
. Решим систему матричным способом.
Запишем систему в матричной форме 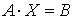 , где
, где
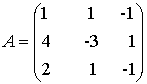 ,
, 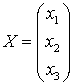 ,
, 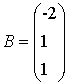
Решение системы в матричной форме
имеет вид 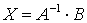 , где
, где 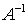 - матрица,
обратная матрице
- матрица,
обратная матрице 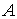 . Найдем
матрицу
. Найдем
матрицу 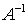 по формуле
по формуле
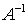 =
=  ,
,
где  - алгебраическое дополнение к
элементу.
- алгебраическое дополнение к
элементу.
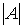 =
= 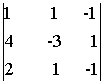 = 3 - 4 + 2 -6 -1 +4 = -2
= 3 - 4 + 2 -6 -1 +4 = -2
Обратная матрица имеет вид:
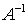 =
=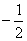
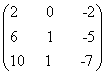 .
.
Найдем решение системы.
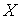 =
=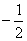
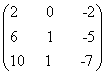
 =
= 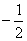
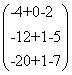 =
= .
.
(3, 8, 13) - решение системы.
Ответ: (3, 8, 13).
Задача №5. Найти размерность и базис
пространства решений однородной системы линейных уравнений.
линейный
алгебраическое уравнение пространство
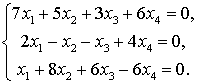
Решение.
Составим матрицу, из коэффициентов
системы.
Поменяем первую и третью строки
местами.
Умножим первую строку матрицы на -2
и прибавим ко второй.
Умножим первую строку матрицы на -7
и прибавим к третьей.
Далее вторую строку матрицы умножим
на -3 и прибавим к третьей.
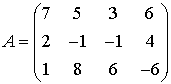
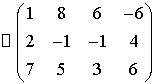
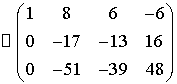
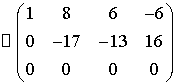
Получили трапециевидную матрицу,
следовательно, система совместна и не определена.
Очевидно, что ранг матрицы 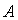 равен 2.
Следовательно, две неизвестные являются главными, и две - свободными. Значит, фундаментальная
система решений системы содержит 4-2=2 линейно независимых решения. Выберем в
качестве главных неизвестных
равен 2.
Следовательно, две неизвестные являются главными, и две - свободными. Значит, фундаментальная
система решений системы содержит 4-2=2 линейно независимых решения. Выберем в
качестве главных неизвестных 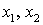 , тогда переменные
, тогда переменные 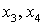 будут
свободными.
будут
свободными.
Система, соответствующая
преобразованной матрице, имеет вид
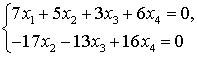
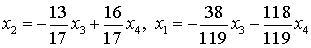 .
.
Или иначе:
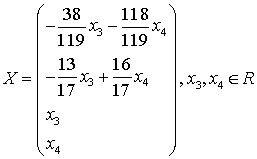 .
.
Фундаментальная совокупность
решений, является базисом линейного пространства решений исходной системы.
Следуя общему правилу, полагаем 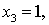
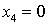 ; затем -
; затем - 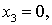
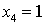 . В
результате приходим к двум частным решениям, которые и составляют
фундаментальный набор.
. В
результате приходим к двум частным решениям, которые и составляют
фундаментальный набор.
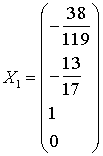 ;
; 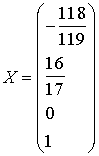 .
.
Размерность искомого пространства равна 2.
Все решения данной системы выражаются через
фундаментальный набор:
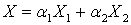 , где
, где 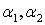 произвольные числа.
произвольные числа.
Ответ: 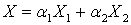 .
.
Задача №6. Найти собственные
значения и собственные векторы линейного преобразования, заданного в некотором
базисе матрицей.
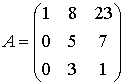
Решение.
Пусть 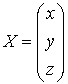 есть столбец координат неизвестного
собственного вектора, принадлежащего собственному значению
есть столбец координат неизвестного
собственного вектора, принадлежащего собственному значению 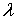 .
. 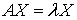 , т.е.
, т.е.
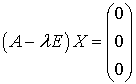 (1).
(1).
Эта система имеет ненулевые решения
только при условии равенства нулю её определителя 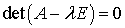 .
.
Составим характеристическое
уравнение.
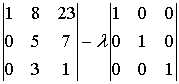 =
= 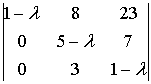 =
= 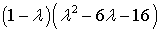 ;
;
 ,
, 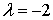 ,
,  . - собственные значение матрицы.
. - собственные значение матрицы.
При  система 1 примет вид.
система 1 примет вид.
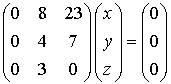 ,
, 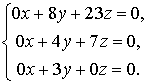
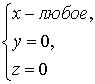
Собственный является любой вектор
вида: 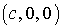 ,
, 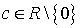 .
.
При 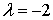 система 1 примет вид.
система 1 примет вид.
 ,
, 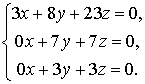
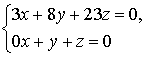
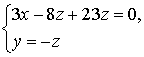
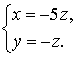
Собственный является любой вектор
вида: 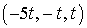 ,
, 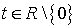 .
.
При  система 1 примет вид.
система 1 примет вид.
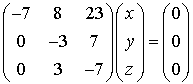 ,
, 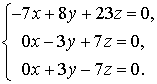
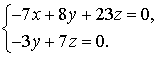

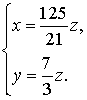
Собственный является любой вектор
вида: 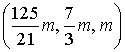 ,
, 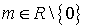 .
.
Задача№7. Привести к каноническому виду
уравнение линии второго порядка, используя теорию квадратичных форм.
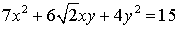 .
.
Решение.
Матрица квадратичной части
многочлена второй степени равна
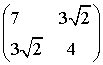 .
.
Собственными числами данной матрицы
будут
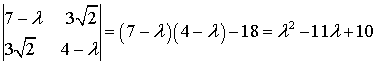 .
.
Решим уравнение 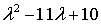 =0 получим:
=0 получим:  ,
, 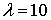 .
.
При  имеем:
имеем:
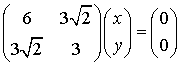 ,
, 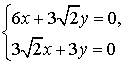
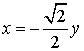
Собственным является любой вектор
вида: 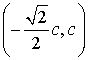 ,
, 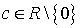 .
.
При 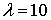 имеем:
имеем:
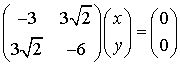 ,
, 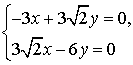
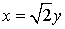
Собственный является любой вектор
вида:  ,
, 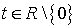 .
.
Получим собственные векторы
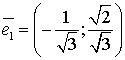 ;
; 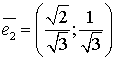
Выполним преобразование:
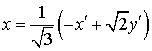 ;
; 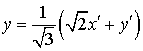
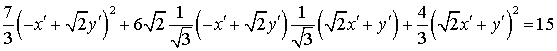 ;
;
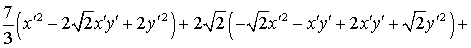
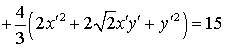 ;
;
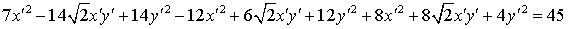 ;
;
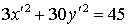 ;
;
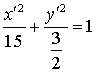 - эллипс с полуосями
- эллипс с полуосями 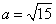 и
и 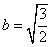 .
.
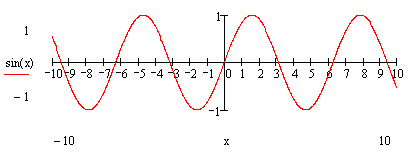
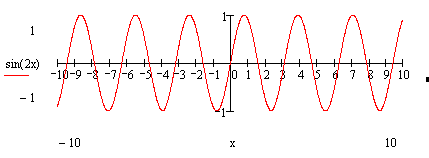
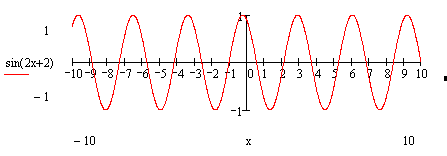
Задача №8 Построить график функции 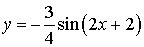 преобразованием
графика функции
преобразованием
графика функции 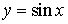 .
.
Решение

Задача №9 Дана функция 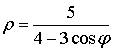 на отрезке
на отрезке 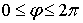 . Требуется:
1) построить график функции в полярной системе координат по точкам, давая
. Требуется:
1) построить график функции в полярной системе координат по точкам, давая 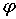 значения
через промежуток
значения
через промежуток 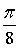 , начиная от
, начиная от
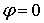 ; 2) найти
уравнение полученной линии в прямоугольной декартовой системе координат, начало
которой совпадает с полюсом, а положительное полуось абсцисс - с полярной осью,
и по уравнению определить, какая это будет линия.
; 2) найти
уравнение полученной линии в прямоугольной декартовой системе координат, начало
которой совпадает с полюсом, а положительное полуось абсцисс - с полярной осью,
и по уравнению определить, какая это будет линия.
Решение.
Построим кривую  . Сведем
данные в таблицу:
. Сведем
данные в таблицу:
|
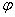 0 0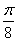 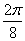 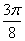 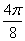 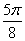 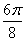 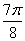 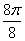 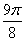 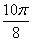
|
|
|
|
|
|
|
|
|
|
|
|
|
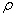 54,072,661,751,250,970,820,740,710,740,82 54,072,661,751,250,970,820,740,710,740,82
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
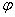 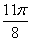 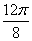 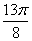 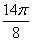 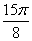 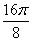
|
|
|
|
|
|
|
|
|
|
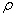 0,971,251,752,664,075 0,971,251,752,664,075
|
|
|
|
|
|
|
|
|
Построим график функции  по данным
таблицы.
по данным
таблицы.
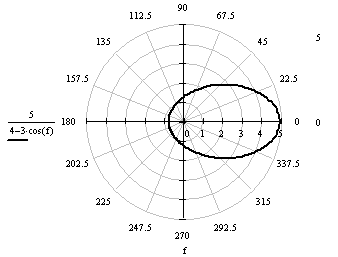
Найдем уравнение кривой в
прямоугольных координатах.
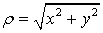 ;
; 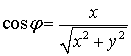 ;
; 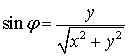 .
.
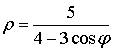 ;
; 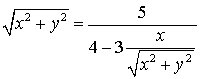 ;
; 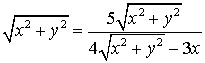 ;
; 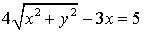 ;
; 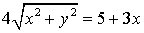 ;
; 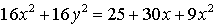 ;
;
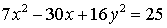 ;
; 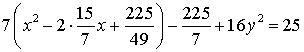 ;
;
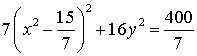 ;
; 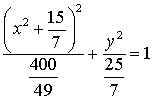 - эллипс с центром в точке
- эллипс с центром в точке 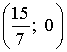 и большей
полуосью
и большей
полуосью 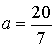 , и меньшей
полуосью
, и меньшей
полуосью 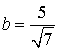
Задача №10 Найти указанные пределы,
не пользуясь правилом Лопиталя.
Решение.
а)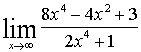 =
= 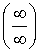 =
=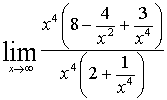 =
= 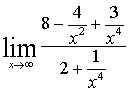 =
=
=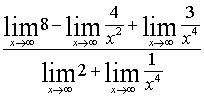 =
=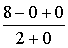 =4.
=4.
Чтобы раскрыть неопределенность 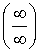 поделили
числитель и знаменатель на старшею степень.
поделили
числитель и знаменатель на старшею степень.
б) 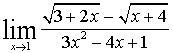 =
=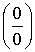 =
=
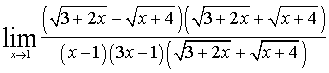 =
=
=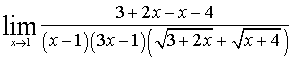 =
=
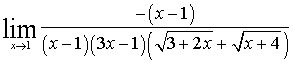 =
=
=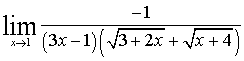 =
=  .
.
Чтобы раскрыть неопределенность 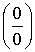 помножили
числитель на сопряженное выражение, знаменатель разложили на множители.
помножили
числитель на сопряженное выражение, знаменатель разложили на множители.
в) 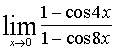 =
= 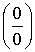 =
= 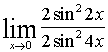 =
= 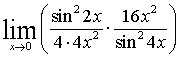 =
=
=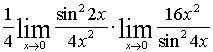 =
=
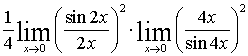 =
=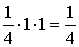 .
.
При решении примера использовали
первый замечательный предел 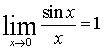 и его следствие
и его следствие 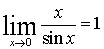 .
.
) 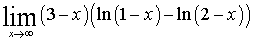 =
=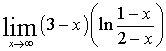 =
=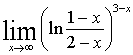 =
=
=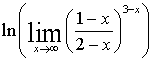 =
=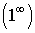 =
=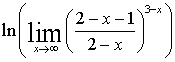 =
= 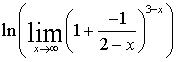 =
=
=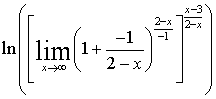 =
= 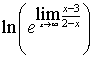 =
= 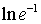 = -1. При решении примера был
использован второй замечательный предел
= -1. При решении примера был
использован второй замечательный предел 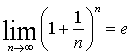 .
.
Задача №11 Заданы функция 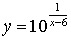 и два
значения аргумента
и два
значения аргумента 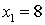 и
и 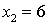 . Требуется:
1) установить является ли заданная функция непрерывной или разрывной для
каждого из заданных значений; 2) в случае разрыва найти пределы при приближении
к точке слева и справа; 3) сделать схематический чертеж.
. Требуется:
1) установить является ли заданная функция непрерывной или разрывной для
каждого из заданных значений; 2) в случае разрыва найти пределы при приближении
к точке слева и справа; 3) сделать схематический чертеж.
Решение.
Найдем область определения функции: 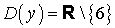 . Функция
неопределенна при
. Функция
неопределенна при 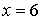 .
.
Чтобы определить является ли функция
непрерывной в заданной точке, воспользуемся критерием непрерывности функции.
Для этого для каждой точки найдем односторонние пределы.
Для точки 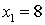
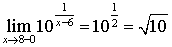 ;
; 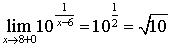 ;
;  .
.
Согласно критерия т.к. 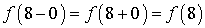 , то функция
непрерывна в точке
, то функция
непрерывна в точке 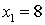 .
.
Для точки 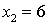
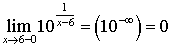 ;
; 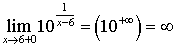 .
.
Согласно критерия т.к. 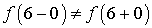 , то функция
имеет в точке
, то функция
имеет в точке 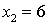 разрыв
второго рода.
разрыв
второго рода.
Сделаем схематический чертеж
функции.
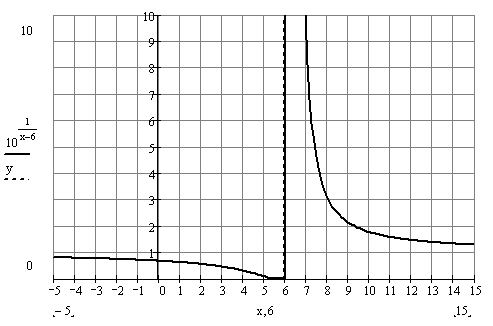
Задача №12 Заданы функция 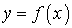 различными
аналитическими выражениями для различных областей изменения независимой
переменой. Найти точки разрыва функции, если они существуют сделать чертеж.
различными
аналитическими выражениями для различных областей изменения независимой
переменой. Найти точки разрыва функции, если они существуют сделать чертеж.
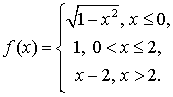
Решение.
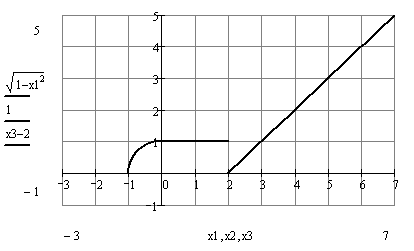
Область определения функции 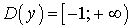 . На
интервалах (-1, 0),
. На
интервалах (-1, 0),
(0, 2), (2, +¥) функция
непрерывна, так как задана на них элементарными функциями. Следовательно,
разрыв возможен только в точках 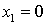 и
и 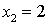 , в которых изменяется аналитическое
задание функции.
, в которых изменяется аналитическое
задание функции.
Рассмотрим точку 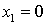 . Найдем
односторонние пределы в точке
. Найдем
односторонние пределы в точке 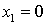 .
.
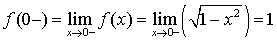 ,
, 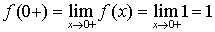 .
.
Так как 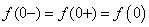 , то в точке
, то в точке
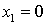 имеет
непрерывна.
имеет
непрерывна.
Рассмотрим точку 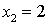 .
.
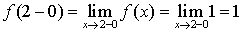 ,
, 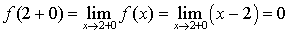 .
.
Так как 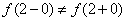 , то в точке
, то в точке
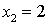 имеет
разрыв первого рода. Скачек равен
имеет
разрыв первого рода. Скачек равен 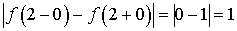 .
.
Строим график функции:
Задача №13 Найти производную 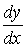 данных
функций.
данных
функций.
а) 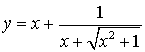 ;
;
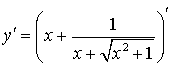 =
=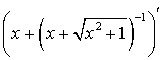 =
=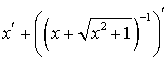 =
=
=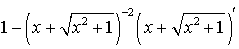 =
=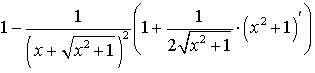 =
=
=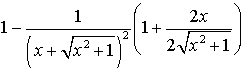 =
=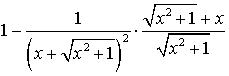 =
=
=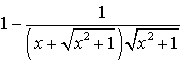 =
= 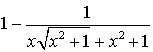 .
.
б) 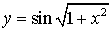 ;
;
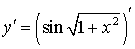 =
=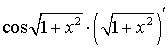 =
= 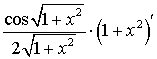 =
=
=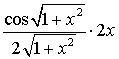 =
=  .
.
в) 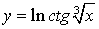 .
.
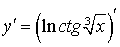 =
= 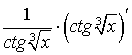 =
=  =
=
= 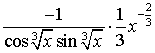 =
= 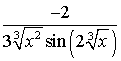 .
.
г) 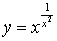 .
.
Данная функция является степенно-показательной.
Применим метод логарифмического дифференцирования. Прологарифмируем функцию: 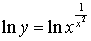 . Применим
свойство логарифмов:
. Применим
свойство логарифмов: 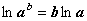 .
.
Тогда 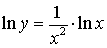 . Дифференцируем обе части равенства
. Дифференцируем обе части равенства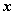 :
:
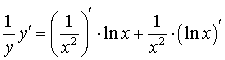 ;
; 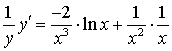 ;
;
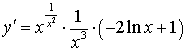 ;
; 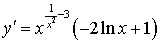 .
.
)  .
.
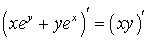 ;
; 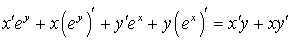 ;
;
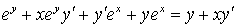 ;
; 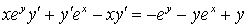 ; .
; .
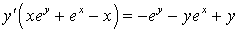
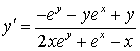 .
.