Аналитическая геометрия
Контрольная
работа по аналитической геометрии
Задача
1. Написать уравнение прямой, проходящей через точку А
(2, 4) и удаленной от начала координат на расстояние 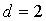
Решение:
1)
Пусть искомое уравнение имеет вид  (ясно,
что точка А (2, 4) удовлетворяет этому уравнению).
(ясно,
что точка А (2, 4) удовлетворяет этому уравнению).
)
Расстояние от начала координат до прямой  равно
равно
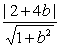
Приравняв
это выражение к 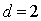 , получим уравнение
, получим уравнение 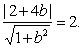
)
Возведя обе части уравнения в квадрат, получим
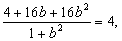

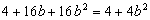 ,
,
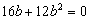 ,
,

Таким
образом, искомое уравнение  .
Преобразуем полученное уравнение
.
Преобразуем полученное уравнение
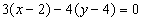 ,
,
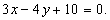

Рисунок
1.
4)
Прямая  проходит через точку
проходит через точку 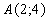 и
расстояние от этой прямой до начала координат равно 2. То есть
и
расстояние от этой прямой до начала координат равно 2. То есть  также является решением задачи (см. рисунок 1).
также является решением задачи (см. рисунок 1).
Ответ.
Искомая прямая  либо
либо 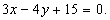
Задача
2. Стороны АВ и ВС параллелограмма заданы уравнениями у = х - 2 и 5у = х + 6,
диагонали его пересекаются в точке М(1, 4). Найти длины его высот
координата плоскость параллелограмм прямая
Решение:
1)
Точка  пересечения прямых
пересечения прямых 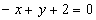 ,
, 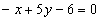 находится как решение системы
находится как решение системы
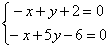 .
.
Вычитая
из первого уравнение второе, получим 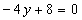 , или
, или 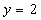 . Из первого уравнения
. Из первого уравнения 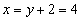 . Таким
образом, координаты точки
. Таким
образом, координаты точки  . Координаты
. Координаты  .
.
)
Координаты  Координаты D совпадают с координатами вектора
Координаты D совпадают с координатами вектора 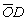 ,
, 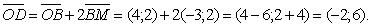 Таким
образом, координаты точки
Таким
образом, координаты точки 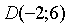 .
.
)
Находим расстояние от D до прямой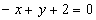 ,
воспользовавшись формулой
,
воспользовавшись формулой
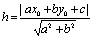 .
.
 .
.
Находим
расстояние от D до прямой 
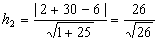 .
.
Ответ.
Длины высот 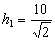 ,
, 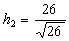 .
.
Задача
3. Даны точки А(-4, 0) и В(0, 6). Через середину отрезка провести прямую, отсекающую на оси
провести прямую, отсекающую на оси 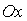 отрезок, вдвое больший, чем на оси
отрезок, вдвое больший, чем на оси 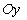
Решение:
1)
Середина отрезка 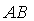 - точка
- точка
 .
.
)
Пусть уравнение искомой прямой в отрезках  . По
условию задачи
. По
условию задачи 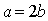 , таким образом уравнение искомой прямой
, таким образом уравнение искомой прямой
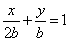

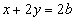 .
.
Подставим
координаты точки  в уравнение. Получим
в уравнение. Получим
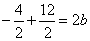
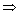
 .
.
Уравнение
искомой прямой  .
.


Рисунок
2.
Ответ.
Уравнение искомой прямой 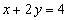 .
.
Задача
4. Построить плоскость х + у - z = 0 и прямую, проходящую через точки А(0, 0,
4) и В(2, 2, 0). Найти точку пересечения прямой и плоскости и угол между ними
1)
Найти три точки, лежащие на плоскости, и через них построить плоскость.
Решение:
1)
Если в уравнение 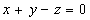 подставить
подставить ,
, 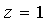 , получим
, получим 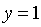 . Таким
образом, точка
. Таким
образом, точка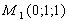 лежит на плоскости. Аналогично, при
лежит на плоскости. Аналогично, при 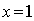 ,
, 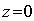 получаем
получаем
 и точка
и точка 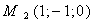 лежит на
плоскости. Третья точка, лежащая на плоскости -
лежит на
плоскости. Третья точка, лежащая на плоскости -  .
Построим плоскость и прямую
.
Построим плоскость и прямую  .
.

Рисунок
3.
)
Запишем уравнение прямой  , подставляя в уравнение
, подставляя в уравнение 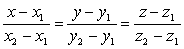 координаты точек А(0, 0, 4) и
координаты точек А(0, 0, 4) и 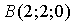 . Получим уравнение прямой
. Получим уравнение прямой 
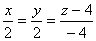 . Приравняем к параметру
. Приравняем к параметру 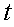 все соотношения
все соотношения  и
перепишем уравнение прямой в параметрическом виде
и
перепишем уравнение прямой в параметрическом виде


 .
.
)
Подставим полученные выражения 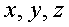 в
уравнение плоскости
в
уравнение плоскости 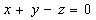 . Получим для
. Получим для 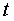 уравнение
уравнение
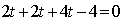

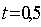 .
.
Таким
образом, точка пересечения прямой и плоскости (при 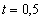 )
)
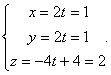
)
Если дано уравнение плоскости в виде 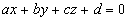 , то
координаты нормального вектора
, то
координаты нормального вектора  К
плоскости
К
плоскости 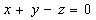 нормальный вектор
нормальный вектор 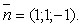 Вектор
Вектор  . Синус угла между прямой и плоскостью равен
. Синус угла между прямой и плоскостью равен
 ,
,
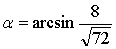 .
.
Ответ.
Точка пересечения прямой и плоскости  , угол
между прямой и плоскостью
, угол
между прямой и плоскостью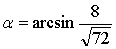 .
.
Задача
5. Написать уравнение плоскости, проходящей через точки Р(3, 0, -1) и Q(-1, -1,
3) и перпендикулярной плоскости 3х + 2у - z + 5 = 0
Решение:
Пусть
уравнение искомой плоскости 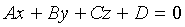 . Так как
точка
. Так как
точка 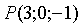 лежит на плоскости, то подставляя в уравнение
плоскости ее координаты, получим уравнение
лежит на плоскости, то подставляя в уравнение
плоскости ее координаты, получим уравнение 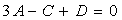 .
.
Подставляя
в уравнение плоскости координаты точки 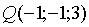 , получим
уравнение
, получим
уравнение 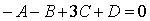 .
.
Так
как искомая плоскость перпендикулярна к плоскости 3х + 2у - z + 5 = =0, их
нормальные вектора перпендикулярны. К плоскости в 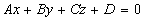 нормальный вектор
нормальный вектор  , к
плоскости 3х + 2у - z + 5 = 0 нормальный вектор
, к
плоскости 3х + 2у - z + 5 = 0 нормальный вектор 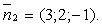 Равенство
нулю скалярного произведения
Равенство
нулю скалярного произведения 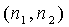 дает
уравнение
дает
уравнение 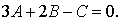
Таким
образом имеем систему

Из
третьего уравнения 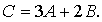 Подставляя в первое и второе уравнения, получим
систему
Подставляя в первое и второе уравнения, получим
систему
 ,
,
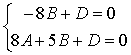
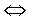


 .
.
Из
уравнения 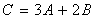 получим
получим 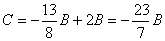 .
Подставив полученные выражения
.
Подставив полученные выражения 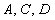 в
уравнение
в
уравнение 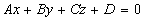 , получаем уравнение искомой плоскости в виде
, получаем уравнение искомой плоскости в виде
Умножим
уравнение на 8:
 .
.
Разделив
уравнение на 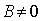 , получим искомое уравнение
, получим искомое уравнение
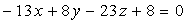 .
.
Ответ.
Уравнение искомой плоскости 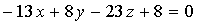 .
.
Задача 6. Найти углы и площадь треугольника, образованного
прямыми у = 2х, у = -2х+1 и у = -х + 2
Решение:
1). Вычисление вершин.
а)
Точка 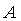 пересечения прямых
пересечения прямых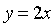 ,
,  находится как решение системы
находится как решение системы 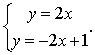
Подставляя
выражение для  из второго уравнения в первое, получим
из второго уравнения в первое, получим  , откуда
, откуда 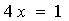 , или
, или . Учитывая, что
. Учитывая, что  , при
, при 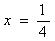 получаем
получаем 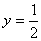 .
.
Координаты
точки 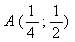 .
.
б)
Точка  пересечения прямых
пересечения прямых  ,
,  находится как решение системы
находится как решение системы 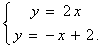
Подставляя
выражение для 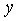 из первого уравнения во второе, получим
из первого уравнения во второе, получим
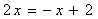 ,
,
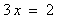 ,
,
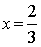 ,
,
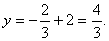
Координаты
точки 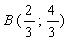 .
.
с)
Точка С пересечения прямых  ,
,  находится как решение системы
находится как решение системы 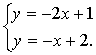
Подставляя
выражение для 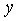 первого уравнения во второе, получаем
первого уравнения во второе, получаем  . Следовательно,
. Следовательно, 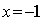 . При
. При  получим
получим 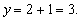
Координаты
точки 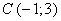 .
.

Рисунок
4.
).
Вычисление основания. Находим координаты вектора  Длина
Длина
 .
.
).
Вычисление высоты. Если дано уравнение прямой в виде  и координаты точки
и координаты точки 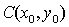 , то
расстояние от точки С до прямой находится по формуле
, то
расстояние от точки С до прямой находится по формуле
 .
.
Уравнение
прямой AB  , или
, или 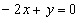 (то есть
(то есть
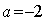 ,
, 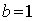 ,
, 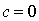 ). Координаты
). Координаты  .
Подставляя в формулу расстояния от точки до прямой, получаем высоту
.
Подставляя в формулу расстояния от точки до прямой, получаем высоту
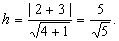 .
.
).
Нахождение площади. Площадь треугольника равна половине произведения основания
и высоты, то есть  .
.
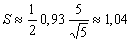 кв.ед.
кв.ед.
).
Нахождение углов треугольника. Чтобы найти углы треугольника, нужно все
уравнения прямых записать как уравнения с угловым коэффициентом, то есть в виде
 ,
, 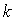 -
угловой коэффициент. Упорядочив коэффициенты по убыванию,
-
угловой коэффициент. Упорядочив коэффициенты по убыванию, 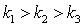 , тангенсы внутренних углов находят по формулам
, тангенсы внутренних углов находят по формулам  (тангенс угла между прямыми с коэффициентами
(тангенс угла между прямыми с коэффициентами 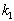 ,
,  );
);  (тангенс угла между прямыми с коэффициентами
(тангенс угла между прямыми с коэффициентами  ,
, 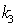 );
); 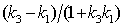 (тангенс угла между прямыми с коэффициентами
(тангенс угла между прямыми с коэффициентами 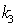 ,
, 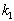 ). Прямая
AB имеет уравнение
). Прямая
AB имеет уравнение  угловой коэффициент равен 2. Прямая AС имеет
уравнение
угловой коэффициент равен 2. Прямая AС имеет
уравнение , угловой коэффициент равен -2. Прямая CB имеет
уравнение
, угловой коэффициент равен -2. Прямая CB имеет
уравнение  , угловой коэффициент равен -1. Упорядочим угловые
коэффициенты по убыванию
, угловой коэффициент равен -1. Упорядочим угловые
коэффициенты по убыванию 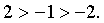 Угловой коэффициент АВ
Угловой коэффициент АВ 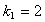 , угловой
коэффициент ВС
, угловой
коэффициент ВС  , угловой коэффициент СB
, угловой коэффициент СB  . Вычисляем тангенсы углов
. Вычисляем тангенсы углов
 (угол
между СВ и АС),
(угол
между СВ и АС),
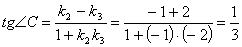 (угол
между АС и АВ),
(угол
между АС и АВ),
 (угол между
АВ и СВ).
(угол между
АВ и СВ).
Ответ:
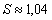 кв.ед.;
кв.ед.; 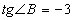 ;
; 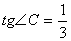 ;
;  .
.
Задача
7. Стороны АВ и ВС параллелограмма заданы уравнениями 2х - у + 5 = 0 и х - 2у +
4 = 0, диагонали его пересекаются в точке М(1, 4). Найти длины его высот
Решение:
)
Точка 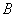 пересечения прямых
пересечения прямых  ,
, 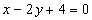 находится как решение системы
находится как решение системы
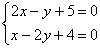 .
.
Умножаем
второе уравнение на 2.

Вычитая
из первого уравнение второе, получим 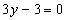 , или
, или 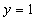 . Из первого уравнения
. Из первого уравнения 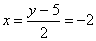 . Таким
образом, координаты точки
. Таким
образом, координаты точки 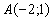 . Координаты
. Координаты 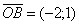 .
.
)
Координаты 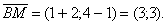 Координаты D совпадают с координатами вектора
Координаты D совпадают с координатами вектора 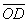 ,
,  Таким
образом, координаты точки
Таким
образом, координаты точки 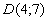 .
.
)
Находим расстояние от D до прямой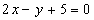 ,
воспользовавшись формулой
,
воспользовавшись формулой
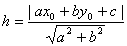 .
.
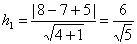 .
.
Находим
расстояние от D до прямой 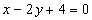
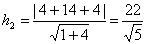 .
.
Ответ.
Длины высот 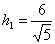 ,
, 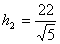 .
.
Задача
8. Через начало координат проведена прямая на одинаковом расстоянии от точек
А(2, 2) и В(1, 0). Найти это расстояние
Схема
решения задачи.
)
Записав уравнение искомой прямой в виде  , найти
параметр
, найти
параметр 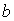 из условия, что точка
из условия, что точка 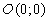 лежит на
прямой.
лежит на
прямой.
)
Записать расстояние от точки  до
искомой прямой, затем расстояние от точки
до
искомой прямой, затем расстояние от точки  до
искомой прямой.
до
искомой прямой.
)
Приравняв полученные в пункте 2 выражения для расстояний, получить уравнение,
содержащее параметр 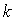 . Решить уравнение
. Решить уравнение
)
Написать уравнения полученной прямой (прямых). Найти расстояние от точек А и В
до прямой (прямых). Сделать чертеж.
Решение:
1.
Подставив (0;0) в уравнение  , получим
, получим
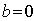 , то есть искомое уравнение имеет вид
, то есть искомое уравнение имеет вид  или
или 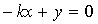 .
.
.
Расстояние от точки 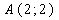 до прямой
до прямой  вычисляется
по формуле
вычисляется
по формуле
 и равно
и равно 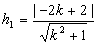 .
.
Аналогично
расстояние от точки  до прямой
до прямой  равно
равно
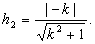
.
Из условия  получаем уравнение
получаем уравнение 
Разделим
уравнение на 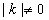 (ясно, что
(ясно, что 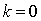 не
является решением). Получаем
не
является решением). Получаем
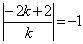 .
.
Следовательно,
возможно два решения 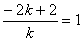 или
или  .
.
Из
первого уравнения получим  , или
, или 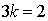 ,
,  .
.
Из
второго уравнения получим 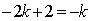 , или
, или 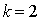 ,
, 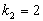 .
.
.
Таким образом, условию задачи удовлетворяют две прямые  и
и  .
Расстояние от точек
.
Расстояние от точек  и
и  до прямой
до прямой
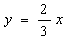 равно
равно
 .
.
Расстояние
от точек 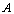 и
и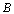 до прямой
до прямой
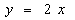 равно
равно
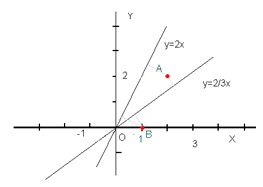
Рисунок
5.
Ответ.
Расстояние от точек 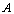 и
и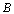 до прямой
до прямой
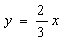 равно,
равно, 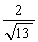 до
прямой
до
прямой  равно
равно 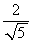 .
.
Задача
9. Написать уравнение биссектрис углов между прямыми 3х + 4у = 12 и у = 0
Решение:
Биссектриса
- это геометрическое место точек, равноудаленных от обеих прямых. Пусть 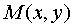 - точка, лежащая на биссектрисе. Запишем расстояния
от
- точка, лежащая на биссектрисе. Запишем расстояния
от  до прямой
до прямой 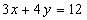 и до
прямой
и до
прямой  Расстояние от
Расстояние от 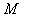 до прямой
до прямой
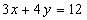 равно
равно 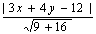 ,
расстояние от
,
расстояние от 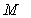 до прямой
до прямой 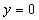 равно
равно 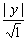 .
.
Так
как эти расстояния равны между собой, то получаем уравнение
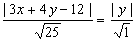 ;
; 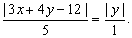
Умножая
это уравнение на 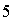 и деля на
и деля на 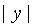 ,
получаем
,
получаем 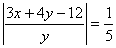 .
.
Если
модуль числа равен  , то это число равно
, то это число равно  или
или 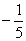 . Следовательно, для точки
. Следовательно, для точки 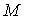 получим два уравнения
получим два уравнения
)
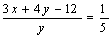 или 2).
или 2). 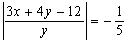
Первое
уравнение равносильно уравнению 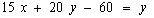 или
или 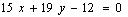 . Аналогично второе уравнение равносильно
. Аналогично второе уравнение равносильно  или
или 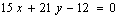 .
.
Ответ.
Уравнения биссектрис 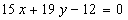 и
и 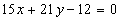 .
.
Задача
10. Найти точку пересечения медиан и точку пересечения высот треугольника: А(-
4, 2), В(2, -5) и С(5, 0)
Решение.
I.
Точка пересечения медиан.
)
Координаты средины 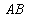 :
: 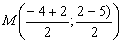 или
или  . Координаты средины
. Координаты средины 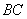 :
:  или
или 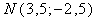 .
.
)
Найдем уравнение медианы 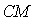 (уравнение прямой, проходящей через точки
(уравнение прямой, проходящей через точки 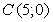 и
и  ).
).
Уравнение
 :
:


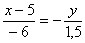

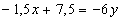


Найдем
уравнение медианы  (уравнение прямой, проходящей через точки
(уравнение прямой, проходящей через точки 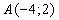 и
и 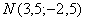 .
Уравнение
.
Уравнение  :
:
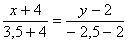

 ,
,
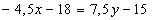

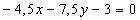
)
Точка пересечения медиан - точка пересечения прямых
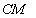 (
( ) и
) и 
 .
.
Решим
систему
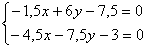 .
.
Умножим
первое уравнение на 3 и вычтем из него второе:
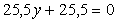

Подставим
значение у во второе уравнение: 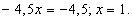
Координаты точки пересечения медиан (1;-1).. Точка пересечения высот.
1)
Координаты 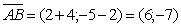 . Вектор
. Вектор 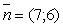 перпендикулярен
вектору
перпендикулярен
вектору 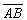 .
.
)
Уравнение высоты  :
:
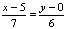

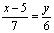


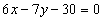
)
Координаты вектора 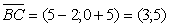 . Вектор
. Вектор  перпендикулярен
вектору
перпендикулярен
вектору 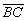 .
.
)
Уравнение высоты 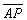 :
:


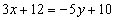

 .
.
)
Точка пересечения высот - точка пересечения прямых  (
(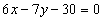 ) и
) и 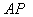 (
( ).
).
Координаты
точки пересечения высот - решение системы
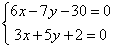 .
.
Умножаем
второе уравнения на 2 и вычитаем его из первого:
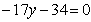
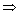
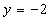
Подставляя
в первое уравнение у=-2, получим 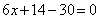
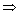
 .
.
Координаты
точки пересечения высот (-2; 2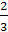
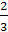 ).
).
Ответ.
Точка пересечения медиан (1;-1), точка пересечения высот (-2; 2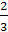
 ).
).
Задача
11. Написать уравнение плоскости, проходящей через точки А(1, -1, 2), В(2, 1,
2), С(1, 1, 1)
Решение:
Уравнение плоскости, проходящей через
три точки
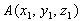 ,
, 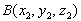 ,
, 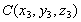 имеет
вид
имеет
вид
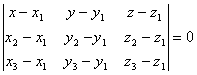 .
.
Подставляя
координаты точек А(1, -1, 2), В(2, 1, 2), С(1, 1, 1), получим уравнение
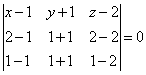

 .
.
Вычисляем
определитель методом треугольника.
 .
.
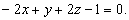
Итак,
искомое уравнение плоскости 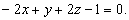 Для
проверки можно подставить в это уравнение координаты точек А(1, -1, 2), В(2, 1,
2), С(1, 1, 1) и убедиться в том, что точки лежат на плоскости.
Для
проверки можно подставить в это уравнение координаты точек А(1, -1, 2), В(2, 1,
2), С(1, 1, 1) и убедиться в том, что точки лежат на плоскости.
Действительно,
для точки 
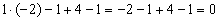 (верно).
(верно).
Для
точки 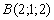
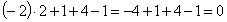 (верно).
(верно).
Для
точки 
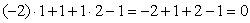 (верно).
(верно).
Ответ.
Искомое уравнение плоскости 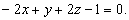
Задача
12. Найти расстояние от точки М(a, b, c) до плоскости, отсекающей на осях
координат отрезки a, b и с
Решение:
Уравнение
плоскости в отрезках 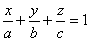 .
.
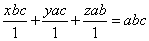


Найдем
расстояние от точки 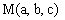 до этой плоскости.
до этой плоскости.
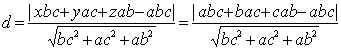 .
.
Ответ.
Искомое расстояние равно  .
.
Задача
13. Найти угол между прямой  и
прямой, проходящей через точку М(1, -1, -1) и начало координат
и
прямой, проходящей через точку М(1, -1, -1) и начало координат
Решение:
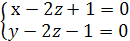
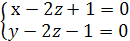 ,
,
получим
систему
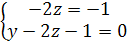
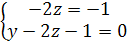 .
.
Из
первого уравнения 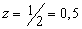 . Подставляем z=0,5 во второе уравнение: y=1+2×0,5=2. Таким образом, координаты точки
. Подставляем z=0,5 во второе уравнение: y=1+2×0,5=2. Таким образом, координаты точки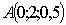 .
.
Подставив
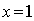 в систему
в систему
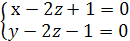
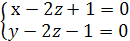 , получим
систему
, получим
систему 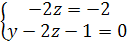
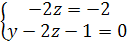 .
.
Из
первого уравнения 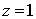 . Из второго уравнения
. Из второго уравнения 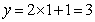 . Таким образом,
координаты точки
. Таким образом,
координаты точки 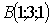 .
.
)
Координаты направляющих векторов прямых
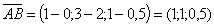 ;
; 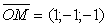 .
.
3)
Косинус угла 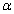 между прямыми равен
между прямыми равен
 .
.

Ответ.
Угол между прямыми равен 
Задача
14. Найти проекцию точки А(3, 1, -1) на прямую x = y = z
Решение:
1)
Если уравнение прямой записано в виде  , то
, то 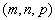 - направляющий вектор данной прямой. Из уравнения
- направляющий вектор данной прямой. Из уравнения  видно, что направляющий вектор
видно, что направляющий вектор  .
.
Подставим
в уравнение 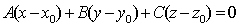 вместо
вместо  координаты
координаты
 , вместо
, вместо  координаты
координаты
 . Получим уравнение
. Получим уравнение
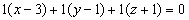

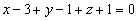

 .
.
)
Запишем уравнение прямой x = y = z в параметрическом виде. Для этого приравняем
к параметру 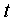 все соотношения x = y = z=t.
все соотношения x = y = z=t.
Получим
систему 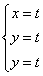 .
.
Подставим
полученные выражения 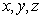 в уравнение плоскости из пункта 1
в уравнение плоскости из пункта 1 .
.
Получим
для  уравнение
уравнение 


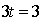

 .
.
Из
системы 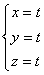 ,
,
при
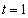 получаем
получаем 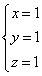 .
.
Координаты
проекции 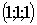 .
.
Ответ.
Координаты проекции 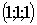 .
.
Задача
15. Написать уравнение плоскости, проходящей через прямую l: (x - 1)/1 = (y +
1)/2 = (z + 2)/2 и перпендикулярно к плоскости р: 2x + 3y - z = 4
Решение:
1)
Если уравнение прямой записано в виде  , то
, то 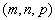 - направляющий вектор данной прямой. Из уравнения
- направляющий вектор данной прямой. Из уравнения  видно, что направляющий вектор прямой
видно, что направляющий вектор прямой  .
.
Если
дано уравнение плоскости в виде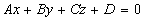 , то
координаты нормального вектора
, то
координаты нормального вектора 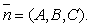 Таким
образом, к плоскости
Таким
образом, к плоскости 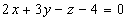 нормальный вектор
нормальный вектор 
)
Обозначим координаты нормального к искомой плоскости вектора 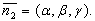 Из условий
Из условий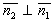 ,
, 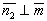 следует, что равны нулю скалярные произведения
следует, что равны нулю скалярные произведения 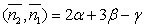 ,
, 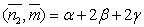 . То есть
координаты
. То есть
координаты 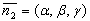 удовлетворяют системе уравнений
удовлетворяют системе уравнений
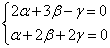 .
.
Умножим
второе уравнение на -2 и сложить оба уравнения:
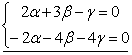
 .
.
Таким
образом, 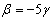 . Из второго уравнения системы
. Из второго уравнения системы  . Если взять
. Если взять  , получим
координаты нормального вектора
, получим
координаты нормального вектора 
)
Чтобы найти точку  , лежащую на искомой плоскости, найдем любую точку,
лежащую на прямой
, лежащую на искомой плоскости, найдем любую точку,
лежащую на прямой 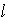 (так как прямая принадлежит искомой плоскости).
Подставляя в уравнение
(так как прямая принадлежит искомой плоскости).
Подставляя в уравнение 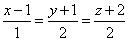 значение
значение 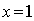 , получим
равенства
, получим
равенства 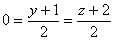 , откуда
, откуда  ,
, 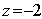 . Таким образом, координаты точки
. Таким образом, координаты точки 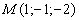 .
.
)
Искомое уравнение плоскости, проходящей через точку 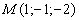 перпендикулярно вектору
перпендикулярно вектору 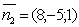 имеет вид
имеет вид
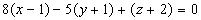



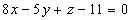 .
.
Ответ.