Системы автоматического управления
Курс лекций
по теории автоматического управления
Системы
автоматического управления
Содержание
Лекция 1. Общие сведения о системах
управления
Лекция 2. Переходные процессы в САУ
Лекция 3. Устойчивость линейных
систем САУ
Лекция 4.Частотные характеристики
систем САУ
Лекция 5. Электрические модели
типовых динамических звеньев
ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ
Лабораторная работа № 1
Лабораторная работа № 2
Лабораторная работа № 3
Билеты
Примерный перечень задач для
итогового контроля знаний студентов III
курса
устойчивость частота система автоматическое управление
Лекция
1. Общие сведения о системах управления
Предмет «Теория автоматического управления»
знакомит вас с основными принципами построения широкого класса систем
автоматического управления, методами формализованного описания и анализа
качества функционирования этих систем.
Рассмотрим с вами основные понятия, с которыми
оперирует теория управления и которые вы должны хорошо себе представлять и
использовать при изучении последующих разделов теории.
Объект управления.
Под объектом управления следует понимать объект, на достижение желаемых
результатов функционирования которого направлены специально организованные
воздействия.
Воздействие.
Воздействие есть внешнее влияние на объект управления, вызывающее в последнем
изменение его свойств и (или) состояния.
Управление.
Управление есть процесс выработки и осуществления управляющих воздействий в
виде заданий для целенаправленного изменения каких-либо свойств или параметров
объекта управления, под которым мы будем также понимать любой физический объект
или процесс, свойства или параметры которых подвергаются изменению посредством
определенного физического воздействия на них.
Возмущение
- есть внешнее воздействие на любой элемент системы управления, включая объект
управления, затрудняющее достижение цели управления. Компенсация действий
возмущений на объект управления есть задача автоматического регулирования.
Регулирование.
Регулирование - есть регулирующее воздействие на объект управления с целью
обеспечения близости фактических значений одного или нескольких параметров
объекта управления к их заданным значениям.
Что же требуется для управления, при том,
следует отметить, качественного управления.
Во-первых, должно быть известно задание, а
именно, какой параметр объекта управления мы хотим изменить, и какое значение
этого параметра нас устроит. Следовательно, необходимо задающее устройство.
Во-вторых, необходим инструментарий для
непосредственного физического воздействия на объект управления. Другими словами
необходимо исполнительное устройство для выполнения задания.
В-третьих, очевидно, необходим контроль над
ходом выполнения задания и проверка соответствия результатов исполнения
заданию, т.е. необходимо иметь контрольно-измерительные устройства.
Рассмотрим примеры возможных схем управления.
Пример 1.
Дачник копает лопатой на своем участке яму определенных известных только ему
размеров. Здесь дачник является задающим устройством, а яма - объектом
управления.
В качестве исполнительного устройства использованы
руки и ноги человека, воздействующие на лопату. Изменяемой (регулируемой)
величиной являются размеры ямы. Для получения требуемого результата
используется мерная линейка, с помощью которой человек измеряет текущие размеры
ямы. Здесь органы зрения и мерная линейка служат контрольно-измерительным
устройством. Человек перестает копать, когда истинные размеры ямы будут
соответствовать заданным, для чего человек мысленно выполняет логическую работу
по анализу результатов измерения фактических размеров ямы, в зависимости от
которых от продолжает копать или прекращает работу, т.е. в данном случае
человек выполняет еще функции сравнивающего устройства.
Представим рассмотренный процесс управления в
виде формализованной функциональной схемы некоторой системы управления.
Задающее устройство - дачник, хранящий в памяти
требуемые размеры ямы.
Сравнивающее устройство - логика мышления
дачника
Регулирующее устройство - логика мышления
человека
Исполнительной устройство - руки и ноги
человека, воздействующие на лопату
Объект управления - яма
Контрольно-измерительное устройство - зрение
человека и мерная линейка.
Так как для обеспечения точных размеров ямы
человек вынужден по ходу дела менять режим работы (уменьшать усилия нажатия на
лопату и темп работы по мере приближения к заданным размерам), то он в этом
случае исполняет еще роль регулирующего устройства.
Как видно из приведенной схемы в процессе
управления практически все функции выполняет один человек, т.е. мы имеем дело
чисто с ручным управлением процессом копания.
Пример 2.
Рабочий по заданию дачника копает на садовом участке яму заданных размеров. Что
же в этом случае меняется в нашей функциональной схеме? Дачник здесь исполняет
роль только внешнего источника первичной информации для рабочего, который выполняет
в дальнейшем все функции системы управления.
Пример 3.
При термической обработке изделия в термокамере необходимо автоматически без
участия человека поддерживать определенную заданную температуру.
Сейчас мы убедимся в том, что формализованная
функциональная схема системы автоматического управления практически идентично
той, которую мы рассматривали для системы ручного управления. Действительно:
Задающее устройство
- задает требуемое значение температуры в виде сигнала определенной физической
природы (например, электрического напряжения, пропорционального значению
температуры). Значение температуры может задаваться человеком-оператором с
помощью ряда кнопок на пульте управления или вырабатываться автоматически
управляющим вычислительным комплексом на основе входной информации об изделии,
его свойствах и назначении.
Сравнивающее устройство
- производит сравнение значений двух сигналов одной физической природы,
соответствующих заданному и фактическому значениям температуры, и вырабатывает
разностный сигнал ошибки. Сравнение может осуществляться, как в аналоговом виде
сигналов, так и в цифровом.
Регулирующее устройство
или просто регулятор - вырабатывает соответствующее регулирующее воздействие на
объект управления в зависимости от величины сигнала ошибки - сигнала
расстройки. Регулятор может содержать усилитель разностного сигнала ошибки,
исполнительное устройство или преобразователь сигнала одной физической природы
в другую, более удобную для воздействия на объект управления (например,
преобразование электрического сигнала в тепловой сигнал).
Объект управления
- термокамера, температура в которой является регулируемым параметром.
Контрольно-измерительное устройство
- преобразует значение фактической температуры в определенный уровень сигнала
другой физической природы, аналогичный заданному сигналу. Как правило,
устройство содержит чувствительный элемент для пропорционального преобразования
значения текущей температуры в сигнал, удобный для последующего измерения, и
измерительное устройство для измерения уровня преобразованного сигнала. В
качестве контрольно-измерительного устройства может, например, использоваться
термопара.
В реальных условиях эксплуатации на регулируемые
параметры объекта управления могут влиять внешние возмущающие воздействия
различного рода, например, температура окружающей среды.
Таким образом, любую систему автоматического
управления (САУ) можно рассматривать как совокупность некоторого ряда составных
частей - звеньев. Деления на звенья может осуществляться как по функциональному
признаку (измерительные, усилительные, преобразовательные, исполнительные и
другие элементы), так и по динамическим свойствам.
Системы автоматического управления по принципу
действия могут быть классифицированы на системы замкнутые, разомкнутые,
комбинированные и адаптивные.
К замкнутым системам относятся системы
управления по отклонению, представляющие собой системы с обратной связью и
представляющие собой основной тип САУ.
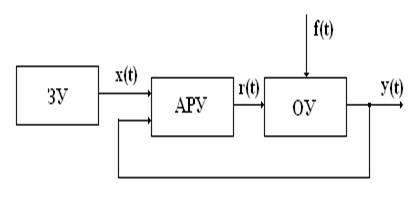
Структурная схема САУ по отклонению
На приведенном рисунке приняты следующие
обозначения:
ЗУ - задающее устройство, вырабатывающее
управляющее воздействие x(t);
АРУ - устройство автоматического регулирования,
вырабатывающее регулирующее воздействие r(t);
ОУ - объект управления:
y(t)
- регулируемый параметр объекта управления:
f(t)
- внешнее возмущающее воздействие на ОУ.
К разомкнутым системам относятся системы
управления по возмущению, в которых регулирующее воздействие вырабатывается в
зависимости от результатов измерения возмущения.
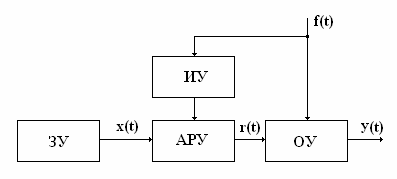
Структурная схема САУ по возмущению
Системы САУ с комбинированным управлением
сочетают в себе принципы управления по отклонению и возмущению.
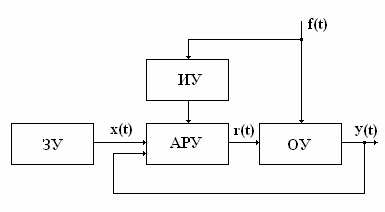
Структурная схема САУ с комбинированным
управлением
Адаптивные системы САУ обладают способностью
приспособляться в процессе функционирования к изменению окружающей среды и
улучшать свои свойства.
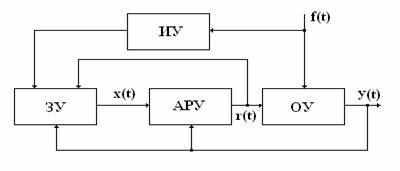
Структурная схема адаптивной системы САУ
В зависимости от назначения системы автоматического
управления делят на системы стабилизации, программного управления и следящие
системы.
Системы стабилизации предназначены для
поддержания постоянного значения регулируемой величины, задаваемого ЗУ.
Системы программного управления предназначены
для изменения значения регулируемой величины по заранее заданной программе,
называемой программой управления.
Следящие системы предназначены для изменения
регулируемой величины по закону изменения задающего воздействия.
По виду используемых сигналов САУ можно
подразделить на непрерывные и дискретные системы. Дискретные системы можно
подразделить на импульсные и релейные.
В зависимости от числа регулируемых параметров
системы САУ подразделяются на одномерные и многомерные системы. При изучении
процессов управления все многообразие САУ можно рассматривать как различные
комбинации из небольшого количества стандартных элементов - динамических
звеньев. Любой элемент характеризуется связью между его входным и выходным
сигналами. Эта связь определяет физические процессы в элементе как в
статическом режиме, когда входной и выходной сигналы - постоянные величины, так
и в динамическом режиме, при котором входной и выходной сигналы являются
некоторой функцией времени. В статическом режиме взаимосвязь между входной и выходной
величинами определяет статические свойства элемента, в динамическом режиме -
динамические свойства элемента. Для формализованного описания динамических
свойств элементов используются следующие способы:
дифференциальные уравнения;
передаточные функции W(p),
которые представляют собой запись дифференциальных уравнений в операторной
форме путем перехода к преобразованиям Лапласа;
временные функции, характеризующие изменение во
времени выходного сигнала определенного вида;
частотные характеристики, устанавливающие
зависимость между амплитудой и фазой входного и выходного гармонических
сигналов при изменении частоты входного сигнала.
Удобство использования формализованного описания
динамических свойств заключается в том, что независимо от физической природы
элементов их поведение во времени (динамика) может быть описана одинаковыми
дифференциальными уравнениями, а, следовательно, одинаковыми передаточными
функциями, временными и частотными характеристиками.
Поэтому динамические элементы, которые описываются
одинаковыми дифференциальными уравнениями, могут быть формально представлены
одним и тем же стандартным типом динамического звена.
При этом следует отметить, что элементарным
динамическим звеном называется звено, динамические свойства которого описываются
линейным дифференциальным уравнением не выше второго порядка.
a2∙y(2)(t)
+ a1∙y(1)(t) + a0∙y(t) = b2∙x(2)(t)
+ b1∙x(1)(t) + b0∙x(t) (1)
Здесь: y(t)
- временная функция выходного сигнала;
x(t)
- временная функция входного сигнала;
y(j)(t)
- j-я производная
функции y(t);
x(j)(t)
- j-я производная
функции y(t);
am,
bm - постоянные
коэффициенты уравнения при соответствующих переменных.
Передаточная функция W(p)
есть отношение выходного сигнала к входному сигналу, представленное в
операторной форме:
W(p)
= y/х
Представим выражение (1) в операторной форме,
для чего заменим знак производной по времени d/dt
на оператор Лапласа - р, а именно:
y(2)(t)
= d2y/dt2 = p2y; y(1)(t)
= dy/dt = py;(2)(t) = d2x/dt2
= p2x; x(1)(t) = dx/dt = px.
Произведя соответствующие замены в
дифференциальном уравнении, получим следующее уравнение в операторной форме:
a2∙p2y
+ a1∙py + a0∙y = b2∙p2x
+ b1∙px + b0∙x . (2)
Здесь выражение (1) является оригиналом
дифференциального уравнения, а выражение (2) называется его изображением по
Лапласу.
Вынесем за скобки в уравнении (2) переменные у и
х:
у∙(a2∙p2
+ a1∙p
+ a0)
= х∙(b2∙
p2
+ b1∙
p + b0).
(3)
Из уравнения (3) легко находим выражение для
передаточной функции:
W(p)
= y/х
= (b2∙ p2 + b1∙ p +
b0)/ (a2∙p2 + a1∙p + a0)
(4)
Если вынести в выражении (4) за скобки
постоянные коэффициенты a0
и b0,
то получим стандартное представление передаточной функции в операторном виде:
W(p)
= (b0/a0)∙[(b2/b0)∙p2
+ (b1/b0)∙p
+ 1]/[(a2/a0)∙p2
+ (a1/
a0)∙p
+ 1], или
W(p)
= К∙(T2x∙p2
+ T1x∙p
+ 1)/(T2y∙p2
+ T1y∙p
+ 1) (5)
Здесь: T2x
и T1x
- постоянные времени выражения в скобках числителя;
T2у
и T1у
- постоянные времени выражения в скобках знаменателя.
В общем виде постоянные времени определяют
характер изменения содержащих их функций от времени. Если с течением времени
значение функции не меняется, то производная от этой функции будет равна нулю,
следовательно, и оператор Лапласа р = 0. И тогда переходная функция, как это
следует из выражения (5), будет равна статическому коэффициенту усиления К: W(p
=
0) = K, что соответствует
уравнению: у = К∙х.
К временным характеристикам динамических звеньев
относят переходную и весовую функции.
Переходная функция
h(t)
определяет характер изменения во времени выходного сигнала звена, если входной
сигнал является единичной ступенчатой функцией x(t)
= 1(t):
y(t)
= h(t)∙1(t).
(6)
Весовая функция g(t)
(импульсная переходная функция) определяет характер изменения во времени
выходного сигнала звена, если входной сигнал является импульсной функцией x(t)
= δ(t) = 1′(t),
которая представляет собой производную от единичной ступенчатой функции, т.е.
ее кривая на плоскости охватывает площадь, равную 1:
y(t)
= g(t)∙δ(t)
= g(t)∙1′(t)
(7)
Для нахождения временных характеристик
динамических звеньев необходимо решить дифференциальные уравнения звена при
нулевых начальных условиях [у(х = 0)] и соответствующих входных сигналах 1(t)
или δ(t).
Весовая функция является производной от
переходной функции. Следовательно весовую функцию g(t)
можно определить путем аналитического и графоаналитического дифференцирования
переходной функции h(t):
g(t)
= dh(t)/dt.
Рассмотрим с вами далее дифференциальные
уравнения основных типов элементарных динамических звеньев и их переходные
функции.
Интегрирующее звено
Характерная особенность интегрирующего звена
заключается в том, что скорость изменения значения выходного сигнала y(t)
звена (производная y′(t))
прямо пропорциональна значению выходного сигнала, т.е.:
y′(t)
= K∙x(t).
(8)
или в операторной форме:
p∙y
= K∙x.
(9)
При подаче на вход единичной ступенчатой функции
x(t)
= 1(t) выражение (8)
примет следующий вид: y′(t)
= K, или dy
= K∙dt.
Интегрируя обе части полученного уравнения, получим аналитическое выражение
переходной функции интегрирующего звена:
y(t)
= h(t)
= K∙t.
(10)
Из уравнения (9) можно получить аналитическое
выражение передаточной функции интегрирующего звена:
W(p)
= y/x
= K/p.
(11)
Из уравнения 10 следует, что весовая функция
интегрирующего звена равна его статическому коэффициенту усиления К:
g(t)
= h′(t)
= K (12)
Апериодическое (инерционное) звено
Динамические свойства апериодического звена
определяются дифференциальным уравнением первой степени:
T∙
y′(t)
+ y(t)
= K∙ x(t).
(13)
Из данного выражения следует, что динамические
свойства звена зависят от аргумента Т, называющегося постоянной времени и
определяющего длительность переходного процесса от начального значения выходной
функции y(t)
к установившемуся постоянному ее значению при подаче на вход единичной
ступенчатой функции 1(t).
Уравнение (13) может быть также представлено в
операторной форме:
T∙p∙y
+ y = y(T∙p
+ 1) = K∙ x.
(14)
Из уравнения (14) легко получаем аналитическое
выражение для передаточной функции апериодического звена:
W(p)
= y/x
= K/(T∙p
+ 1). (15)
Учитывая, что передаточная функция есть ничто
иное, как изображение по Лапласу L[g(t)]
весовой функции, найдем оригинал весовой функции, представив передаточную
функцию в виде произведения изображений простейших функций, оригиналы которых
можно найти из справочных таблиц изображений функций.
L[g(t)] =
W(p) = K/(T∙p + 1) = (K/T)∙1/(p + 1/T). (16)
В нашем случае изображение некоторой неизвестной
функции f(t)
равно L[f(t)]
= 1/(p + 1/T),
которому соответствует оригинал f(t)
= ept, где p
- есть ничто иное, как решение (корень) характеристического уравнения,
получаемого приравниванием выражения в знаменателе изображения L[f(t)]
к нулю: p + 1/T
= 0, откуда р = - 1/T.
Следовательно, выражение для весовой функции будет иметь вид:
g(t) = (K/T)∙f(t)
= (K/T)∙e-t/T (17)
Переходную функцию h(t)
можно найти интегрированием правой части выражения (17), которое производим в
операторной форме путем умножения изображения весовой функции L[g(t)]
на отношение (1/р), представляющее собой передаточную функцию интегрирующего
звена со статическим коэффициентом усиления, равным 1:
L[h(t)] =
L[g(t)]∙ 1/р
= (1/р)∙
(K/T)∙1/(p + 1/T). (18)
Для отыскания оригинала функции h(t)
разложим правую часть выражения (18) на элементарные дроби, используя метод
неопределенных коэффициентов.
(K/T)/[p∙(p
+ 1/T)] = A/p + B/(p + 1/T) = [A∙(p + 1/T) + B∙p]/[p∙(p +
1/T)], откуда
K/T
= A/T
+ A∙p
+ B∙p
= A/T
+ p∙(A
+ B).
Приравнивая коэффициенты в левой и правой частях
полученного выражения при одинаковых степенях оператора р, получим:
K/T
= A/T,
или А = К;
А + В = 0, откуда В = -А = -К;
следовательно:
(K/T)/[p∙(p
+ 1/T)] = K/p - K/(p + 1/T) = K∙[1/p - 1/(p + 1/T)]. (19)
Переходя от изображений (19) к оригиналам
простейших функций, получим выражение для переходной функции апериодического
звена:
h(t)
= K∙(1 - e-t/T).
(20)
Корень характеристического уравнения в
изображении (1/р) элементарной функции f(t)
равен нулю (р = 0), поэтому ее оригинал равен:
f(t)
= ept = e0t
= e0
= 1.
Колебательное звено.
Динамические свойства колебательного звена определяются дифференциальным
уравнением второй степени и зависят не только от постоянной времени Т, но и от
коэффициента кси ξ, называемого
коэффициентом демпфирования, характеризующего степень затухания колебаний:
T2∙y′′(t)
+ 2ξ∙T∙y′(t)
+ y(t) = K∙ x(t). (21)
Представим уравнение (21) в операторной форме и
найдем из него выражение для передаточной функции:
T2∙p2∙y
+ 2ξ∙T∙p∙y
+ y = (T2∙p2
+ 2ξ∙T∙p
+ 1)∙y = K∙
x;
W(p)
= y/x
= K/( T2∙p2
+ 2ξ∙T∙p
+ 1). (22)
С целью экономии времени в виду громоздкости
вывода формулы для переходной характеристики приводим ее без вывода:
h(t) = K∙[1 - (e-ξt/T/r)∙sin(rt/T
+ α)] (23)
Здесь: r
= 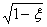 >
0 - условие наличия колебаний в звене;
>
0 - условие наличия колебаний в звене;
α = arctg(r/ξ)
- фазовый начальный угол;
r/(2πT)
= f - частота
затухающих колебаний звена.
Весовую функцию g(t)
колебательного звена можно найти, взяв производную от переходной функции h(t):
g(t) = h′(t)
= (K/T)∙e-ξt/T∙[(ξ/r)∙sin(rt/T
+ α) - cos(rt/T + α)]
(24)
Лекция
2. Переходные процессы в САУ
В результате наличия переходных процессов в
динамических звеньях САУ требуемое заданное значение регулируемой величины
устанавливается не мгновенно, а в течение некоторого промежутка времени,
называемого временем регулирования tp.
Обычно принято временем регулирования называть промежуток времени, за который
значение переходной функции h(t)
достигает 95% от своего установившегося значения при h(t→∞)
= K.
Следовательно, по виду кривой переходной функции
САУ можно определить время регулирования tp.
Рассмотрим переходную функцию апериодического
звена:
h(t)
= K∙(1 - e-t/T).
Из приведенной формулы видно, что время регулирования
для инерционного звена зависит только от значения постоянной времени Т и
связано с ней приближенным соотношением: tp
≈
3Т, так как
h(t) = K∙(1 - e-t/T)
= K∙(1 - e-tp/T) = K∙(1 - e-3T/T) = K∙(1
- e-3) ≈ 0,95K.
Постоянную времени Т инерционного звена можно
определить по графику переходной функции h(t),
если провести касательную к переходной функции из начала координат.
Действительно, производная от любой непрерывной функции в произвольной точке
приближенно равна тангенсу угла наклона касательной к этой точке. Для
переходной функции апериодического звена справедливо: h′(t
= 0) = (K/T)∙
e-t/T
= (K/T)∙
e-0/T
= K/T
= tgψ, где ψ
- угол
наклона касательной к h(t)
в точке t = 0. При t
= T значение функции h(t)
= K∙(1 - e-1)
= 0, 632K.
Для динамических звеньев второго порядка кривые
переходных процессов могут иметь как колебательный, так и апериодический
характер, который зависит от значения коэффициента демпфирования ξ.
При ξ < 0 переходной
процесс носит колебательный характер; при ξ ≥ 0 переходной
процесс носит апериодический характер.
Время регулирования tp
для звена второго порядка также измеряется промежутком времени, в течение
которого значение переходной функции h(t)
достигает 95% от h(t
→
∞), т.е. когда значение h(t)
окажется в пределах от 0,95К ≤ h(t)
≤ 1,05К и в дальнейшем не выходит из них.
Для звеньев второго порядка время регулирования tp
зависит не только от постоянной времени Т, но и от параметра ξ.
Минимальное
значение tp
имеет место при ξ = 0,707, при
котором значения функции h(t)
носят затухающий колебательный характер, но не выходят за пределы 1,05К.
При меньших значениях ξ
характерным
для колебательных переходных процессов является превышение кривой переходного
процесса над своим установившимся значением.
Отношение максимальной величины превышения [Δhmax
= hmax - h(t
→
∞)] к установившемуся значению h(t
→
∞), выраженное в процентах, называется перерегулированием δhmax
.
δhmax
= Δhmax∙100%
/ h(t
→
∞) = [hmax
- h(t
→
∞)]∙100% / h(t
→
∞)
Время регулирования tp
и перерегулирование δhmax
относятся к показателям качества регулирования. Качество регулирования
считается удовлетворительным, если δhmax
≤
(30 - 40)%.
Структура любой САУ определяется составом
входящих в нее звеньев и способом их соединения. С помощью эквивалентных
преобразований любую систему САУ можно привести к стандартному виду, свойства
которой будут полностью определяться характером передаточной функции W(p).

Рис. 1
На рис. 1 представлена структурная схема САУ,
состоящая из одного динамического звена с передаточной функцией W(p),
охваченного жесткой обратной связью с коэффициентом усиления Кос
цепи обратной связи, равным 1.
Передаточную функцию W(p),
которая называется передаточной функцией САУ в разомкнутом состоянии, можно
представить в виде произведения или суммы передаточных функций элементарных
типовых звеньев.
Передаточная функция Wз(p)
замкнутой САУ определяется по следующей формуле:
Wз(p)
= W(p)/[1
+ Кос∙ W(p)].
Для САУ, представленной на рис. 1, Wз(p)
= W(p)/[1
+ W(p)].
По виду W(p)
все системы САУ делятся на статические и астатические.
САУ называется статической, если ее передаточная
функция в разомкнутом состоянии не содержит множителей (1/р), соответствующих
операции интегрирования, т.е.:
W(p)
= Ko∙Wo(p).
(1)
Здесь: Ko
- статический коэффициент усиления системы;
Wo(p)
- рациональная дробь, которая при р → 0 стремится к 1.
Например, к статической системе САУ можно
отнести систему, состоящую из апериодического звена, охваченного жесткой
обратной связью:
W(p)
= K/(T∙p
+ 1) = K∙[1/(T∙p
+
1)] = Ko∙Wo(p)
Здесь: Ко = К; Wo(p)
= 1/(T∙p
+ 1).
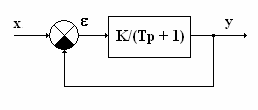
Рис. 2
Основное свойство статических систем наличие
установившейся ошибки εуст
= хо - ууст ≠ 0 при t
→
∞.
В статических системах установившаяся ошибка
системы может быть определена по формуле:
εуст
= хо/(1 + Ко) (2)
Из формулы (2) следует, что с увеличением
коэффициента усиления Ко (при хо = const)
статическая ошибка уменьшается, т.е. точность системы увеличивается. Однако
увеличение коэффициента усиления приводит к увеличению перерегулирования и
колебательности системы. Поэтому в статических системах САУ не всегда возможно
получить требуемые качество переходного процесса и точность регулирования.
САУ называется астатической, если ее
передаточная функция в разомкнутом состоянии содержит множитель (1/ps),
т.е.:
W(p)
= Ko∙Wo(p)/ps,
(3)
где s
- порядок астатизма системы.
Например, к астатической системе САУ первого
порядка можно отнести систему, состоящую из интегрирующего звена, охваченного
жесткой обратной связью:
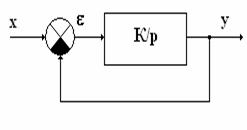
Рис. 3
W(p)
= K/p
= K∙(1/p)
= Ko∙Wo(p)(1/р)
Здесь: Ко = К; Wo(p)
= 1; s = 1.
В астатических системах установившаяся ошибка εуст
равна нулю при любом значении коэффициента Ko.
Поэтому коэффициент Ko
можно выбирать только исходя из требований к качеству переходного процесса.
Как следует из формулы (3), астатизм вводится в
систему САУ путем последовательного включения одного или s
интегрирующих звеньев. Например, астатическую систему САУ можно получить, если
последовательно с инерционным звеном на рис. 2 включить интегрирующее звено:
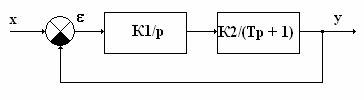
Рис. 4
Принимая во внимание, что передаточная функция
системы, состоящей из последовательно включенных звеньев, равна произведению
передаточных функций отдельных звеньев, составим формулу для передаточной
функции разомкнутой системы САУ, представленной на рис. 4.
W(p)
= (K1/p)∙[K2/(T∙p
+ 1)] = K1∙K2∙(1/p)∙[1/(T∙p
+ 1)].
Здесь: Ко = K1∙K2;
Wo(p)
= 1/(T∙p
+ 1); s = 1.
Передаточная функция для ошибки равна:
S(p)
= ε/x
= (T∙p
+ 1)∙p/[(T∙p
+ 1)∙p + Ко]
(4)
При постоянном сигнале х = хо = const
установившееся значение ошибки находим по формуле εуст
= S(p
= 0)∙ хо. Из формулы (4) следует, что S(p
= 0) = 0, а, следовательно, и ошибка εуст
= 0 при любых постоянных значениях хо ≠ 0 и Ко ≠
0.
Лекция
3. Устойчивость линейных систем САУ
САУ называется устойчивой, если с течением
времени выходная величина стремится к установившемуся значению при постоянном
значении входного сигнала. Линейная САУ называется неустойчивой, если выходная
величина неограниченно возрастает с течением времени. Динамика линейных САУ,
как отмечалось нами ранее, описывается линейным дифференциальным уравнением с
постоянными вещественными коэффициентами:
an∙y(n)
+ a(n-1)∙y(n-1) + ∙∙∙ + a0∙y
= bm∙x(m) + b(m-1)∙x(m-1)
+ ∙∙∙ + b0∙x (1)
Равенство (1) выводится из уравнений отдельных
звеньев, образующих систему САУ. Параметры же переходного процесса в САУ
определяются решением однородного дифференциального уравнения, получаемого
путем приравнивания левой части равенства (1) нулю:
an∙y(n)
+ a(n-1)∙y(n-1) + ∙∙∙ + a0∙y
= 0 (2)
Решение данного уравнения имеет вид: y(t)
= 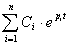 ,
(3)
,
(3)
где Ci
- постоянные интегрирования;
pi
- корни характеристического уравнения, получаемого путем замены в уравнении (2)
знака дифференцирования на оператор Лапласа р:
an∙р(n)
+ a(n-1)∙р(n-1)
+ ∙∙∙ + a0
= 0 (4)
Как видим, выражение (3) представляет собой
сумму экспоненциальных функций. Система будет устойчивой, если выполняется
условие:
y(t)
→ 0, при t
→
∞.
Это условие будет выполнено только в одном
случае, если все экспоненты в правой части равенства (3) будут стремиться к
нулю. А любая экспоненциальная функция от времени будет стремиться к нулю, если
показатель ее степени будет отрицательным числом. Отсюда можно сделать
следующие выводы. Система САУ будет устойчива, если:
1) все корни pi
характеристического уравнения являются действительными отрицательными числами (pi
<
0);
2) если имеется пара комплексных и
сопряженных корней типа pi,i+1
= α +_ jβ, то в
равенство (3) входят слагаемые:
Cie(α
+ jβ)t
+ Ci+1e(α
- jβ)t
= Cieαt∙e
jβt
+ Ci+1eαt∙e
-jβt
=
= Cieαt∙[cos(βt)
+ jsin(βt)]
+ Ci+1eαt∙[cos(βt)
- jsin(βt)].
Поэтому при α < 0 и
Ci = Ci+1
в график функции y(t)
данные слагаемые входят как затухающие по амплитуде косинусоидальные
составляющие.
Следовательно, необходимым и
достаточным условием устойчивости САУ является наличие отрицательного знака
действительной части корней характеристического уравнения.
Впервые это условие для механических систем сформулировал и доказал русский
ученый А.М. Ляпунов.
При наличии, хотя бы одного корня с
положительной действительной частью график функции y(t)
будет представлять собой возрастающую экспоненту или косинусоиду, и процесс
регулирования будет неустойчивым.
Если хотя бы один из корней (pi
=
0), то функция y(t)
будет содержать постоянную составляющую Ciepit
= Ci, что соответствует
нахождению САУ на грани устойчивости.
В аналогичном состоянии будет находиться система
в случае наличия чисто мнимых корней характеристического уравнения.
Рассмотренное условие устойчивости относится к
линейным САУ. Но практически все реальные САУ являются нелинейными и только
приближенно многие из них можно описать линейными уравнениями. Так, например,
Ляпунов доказал, что по устойчивости линеаризованной системы можно судить об
устойчивости исходной нелинейной системы.
Однако, для того, чтобы выяснить, устойчива
система или нет, не обязательно решать дифференциальное уравнение, что весьма
трудоемко при порядке уравнения более 3. Достаточно определить знаки
действительных частей корней характеристического уравнения по другим критериям.
С этой целью разработаны различные
алгебраические критерии устойчивости систем САУ, в основу которых положен следующий
принцип, Поскольку корни pi
характеристического уравнения определяются коэффициентами аi
, то по знакам последних можно приближенно оценить устойчивость систем.
Так алгебраические критерии, предложенные
Раусом, Гурвицем и Неймарком, позволяют оценить устойчивость системы с помощью
алгебраических операций над коэффициентами характеристического уравнения, в
случае, если все они имеют положительные знаки.
Ограничимся с вами рассмотрением критерия
устойчивости Гурвица.
По характеристическому уравнению (4) составляется
главный определитель n-го
порядка Δn,
для чего по его главной диагонали слева на право выписываются коэффициенты в
порядке убывания их индексов, начиная с аn-1.
В строках левее главной диагонали выписываются коэффициенты с последовательно
убывающими индексами, а правее - с возрастающими. Места коэффициентов с
индексами больше n и меньше
нуля заполняются нулями.
Δn
=
 (5)
(5)
Из главного определителя последовательным
отчеркиванием m строк и m
столбцов, начиная с диагонального элемента an
- 1 с индексом (n
- 1), находятся определители (диагональные миноры):
Δ1
= 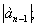 Δ2
=
Δ2
= 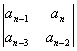 ;
Δ3
=
;
Δ3
= 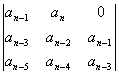 ;
…; Δm
= … (6)
;
…; Δm
= … (6)
Для устойчивости системы необходимо, чтобы все
коэффициенты характеристического уравнения и все определители от Δ1
до Δn
были
положительны: Δ1
> 0; Δ2
> 0; Δ3
> 0; … ; Δm
> 0; …
В частности, для системы третьего порядка
критерий Гурвица принимает более простой вид: a3
> 0; a2
> 0; a1
> 0; a0
> 0;
Δ2
= 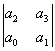 =
a1∙a2
- a0∙a3
> 0. (7)
=
a1∙a2
- a0∙a3
> 0. (7)
Наряду с алгебраическими методами оценки
устойчивости систем САУ часто применяют частотные методы устойчивости. В
практике наиболее широкое применение получил критерий устойчивости Михайлова,
основанный на анализе левой части характеристического уравнения (4) замкнутой
системы САУ после замены в нем оператора Лапласа р на комплексную переменную jω:
V(jω)
= an∙(jω)(n)
+ a(n-1)∙(jω)(n-1)
+ ∙∙∙ + a1∙(jω)
+ a0. (8)
Многочлен V(jω)
представляет собой вектор в комплексной плоскости, значение которого
определяется величинами действительной N(ω)
и
мнимой M(jω)
составляющих: V(jω)
= N(ω) + jM(ω).
При изменении частоты от нуля до бесконечности
вершина вектора V(jω)
вычерчивает на комплексной плоскости кривую, которая называется годографом или
кривой Михайлова. Для построения такого годографа достаточно определить
частоты, при которых происходит его пересечение с вещественной и мнимой осями
координат.
Частоты ωm,
при которых годограф пересекается с вещественной осью, определяются из
уравнения M(ω)
= 0. После чего найденные частоты подставляются в выражение для действительной
части N(ωm).
Частоты ωn,
при которых годограф пересекается с мнимой осью, определяются из уравнения N(ω)
= 0. После чего найденные частоты подставляются в выражение для мнимой части М(ωn).
Например, для характеристического уравнения
третьего порядка (n = 3)
многочлен (8) V(jω)
принимает следующий вид:
V(jω)
= a3∙(jω)3
+ a2∙(jω)2
+ a1∙(jω)
+ a0 = (a0 - a2∙ω2)
+ jω∙(
a1 - a3∙ω2),
(9)
Здесь: N(ω)
= a0 - a2∙ω2;
M(ω) = ω∙(
a1 - a3∙ω2).
Приравнивая к нулю поочередно действительную N(ω)
и
мнимую M(ω)
части уравнения (9), можно найти в аналитической форме значения ω,
N(ω) и
M(ω):
M(ω)
= 0;  ;
;
N(ω)
= 0; 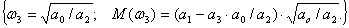 .
(10)
.
(10)
Подставив численные значения коэффициентов a0,
a1, a2
и a3 в выражения (10),
можно построить на комплексной плоскости годограф Михайлова, по внешнему виду
которого определяют устойчивость САУ следующим образом.
САУ будет устойчивой, если годограф Михайлова
при изменении частоты от нуля до бесконечности, начиная с точки M(0)
= a0,
лежащей на вещественной положительной полуоси, охватывает начало координат и
последовательно проходит в направлении против часовой стрелки количество
квадрантов, равное степени n
характеристического уравнения, нигде не обращаясь в нуль и уходя в последнем
квадранте в бесконечность.
Если кривая Михайлова проходит через начало
координат, то САУ находится на границе устойчивости.
Есть еще ряд частотных критериев устойчивости
САУ, к которым мы возможно вернемся после знакомства с частотными
характеристиками САУ.
Лекция
4.Частотные характеристики систем САУ
Частотные характеристики САУ характеризуют
реакцию систем на синусоидальное входное воздействие в установившемся режиме.
К частотным характеристикам относятся:
АФЧХ - амплитудно-фазовая частотная
характеристика;
АЧХ - амплитудно-частотная характеристика;
ФЧХ - фазовая частотная характеристика;
ЛАЧХ - логарифмическая АЧХ;
ЛФЧХ - логарифмическая ФЧХ.
АФЧХ представляет собой частотную передаточную
функцию W(jω),
которая получается путем замены в передаточной функции W(p)
оператора Лапласа p на
комплексную переменную jω.
АФЧХ представляет собой вектор на комплексной плоскости в полярных координатах
Н(ω)
и
φ(ω),
которые являются соответственно АЧХ и ФЧХ:
W(jω)
= Н(ω)∙еjφ(ω)
= N(ω) + jM(ω).
(1)
Здесь: Н(ω) - АЧХ,
которая представляет собой зависимость значения модуля вектора АФЧХ от круговой
частоты;
φ(ω)
- ФЧХ, которая представляет собой зависимость аргумента вектора АФЧХ от
круговой частоты;
N(ω) = Н(ω)∙cosφ(ω)
- проекция вектора АФЧХ на действительную ось комплексной плоскости;
M(ω) = Н(ω)∙sinφ(ω)
- проекция вектора АФЧХ на мнимую ось комплексной плоскости;
При изменении частоты ω
от
нуля до бесконечности АФЧХ представляет собой кривую в комплексной плоскости,
называемую годографом.
Рассмотрим частотные характеристики отдельных
типовых звеньев.
Апериодическое звено.
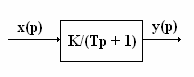
Основные формулы и соотношения
W(jω)
= K/(1 + jωT)
= 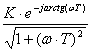 =
=
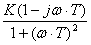 .
.
Н(ω) = 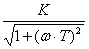 ;
φ(ω)
= - arctg(ωT);
;
φ(ω)
= - arctg(ωT);
N(ω) = K/[1
+ (ω∙T)2];
M(ω) = - K∙
ω∙T/[1
+ (ω∙T)2].
(2)
φ(0)
= 0o; Н(0)
= K; N(0) = K; M(0) = 0;
φ(ω
= 1/T) = - 45o; Н(T)
= K/√2; N(T) = K/2; M(T) = - K/2;
φ(ω
→
∞) = - 90o;
Н(∞) = N(∞) = M(∞)
= 0.
Интегрирующее звено.

Основные формулы и соотношения
W(jω)
= K/jω
= K∙e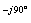 /ω;
/ω;
Н(ω)
= K/ω;
φ(ω)
= - 90o;(ω)
= 0; M(ω)
= - K/ω;
(3)
φ(0)
= - 90o; Н(0)
= ∞; N(0) = 0; M(0) = - ∞;
φ(ω
→ ∞) = - 90o; Н(∞)
= N(∞) = M(∞) = 0.
Колебательное звено.
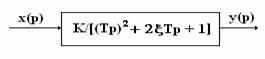
Основные формулы и соотношения
W(jω)
= K/[- (ω∙T)2
+ j2ξ∙T∙ω
+ 1] = 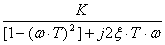 =
=
= 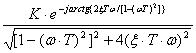 =
=
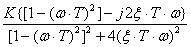 ;
;
Н(ω) = 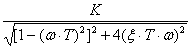 ;
φ(ω)
= - arctg{2ξ∙T∙ω/[1-
(ω∙T)2]};
;
φ(ω)
= - arctg{2ξ∙T∙ω/[1-
(ω∙T)2]};
N(ω) = K∙[1
- (ω∙T)2]/{[1-
(ω∙T)2]2
+ 4(ξ∙T∙ω)2};
M(ω) = - 2K∙ξ∙T∙ω/{[1-
(ω∙T)2]2
+ 4(ξ∙T∙ω)2};
(4)
φ(0)
= 0o; Н(0)
= K; N(0) = K; M(0) = 0;
φ(ω
= 1/T) = - 90o; Н(T)
= K/(2ξ);
N(T) = 0; M(T) = - K/(2ξ);
φ(ω
→
∞) = - 180o;
Н(∞) = N(∞) = M(∞)
= 0.
Идеальное дифференцирующее звено.

Основные формулы и соотношения
W(jω)
= jK∙ω
= K∙ω∙e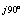 ;
;
Н(ω)
= K∙ω;
φ(ω)
= 90o;(ω)
= 0; M(ω)
= K∙ω;
(5)
φ(0)
= 90o; Н(0)
= 0; N(0) = 0; M(0) = 0;
φ(ω
→ ∞) = 90o; Н(∞)
= M(∞) = ∞; N(∞) = 0.
Кроме перечисленных ранее частотных
характеристик при анализе свойств САУ широко используются логарифмические
частотные характеристики, к которым относятся:
ЛАЧХ - логарифмическая амплитудно-частотная
характеристика;
ЛФЧХ - логарифмическая фазовая частотная
характеристика.
ЛАЧХ представляет собой график зависимости L(ω)
= 20lg[H(ω)]
от
десятичного логарифма частоты lg(ω).
При
построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе,
а по оси ординат L(ω). Единицей
L(ω)
является децибел (дБ), равный одной десятой Бела. L(ω)
= 20 означает, что на данной частоте при прохождении сигнала через звено его
амплитуда увеличивается в 10 раз.
ЛФЧХ - это график зависимости частотной функции φ(ω)
от десятичного логарифма частоты lg(ω).
При
его построении по оси абсцисс откладывают частоту в логарифмическом масштабе,
по оси ординат откладывают φ(ω)
в градусах или радианах.
В обоих случаях за единицу масштаба по оси
абсцисс принимается декада - это частотный интервал, соответствующий изменению
частоты в 10 раз. Ось ординат при построении этих характеристик проводят часто
через точку (ω = 1) которая
соответствует началу координат lg(1)
= 0.
На практике часто кривую линию ЛАЧХ заменяют
приближенным графиком, состоящим из нескольких пересекающихся прямых отрезков
(асимптот), к которым стремится логарифмическая функция при определенных
значениях частот, называемых сопрягающими частотами.
Рассмотрим аналитические выражения для ЛАЧХ и
правила построения асимптотических ЛАЧХ для ряда характерных типовых звеньев.
Апериодическое звено.
Формула ЛАЧХ согласно (2) принимает следующий вид:
L(ω)
= 20lg[H(ω)] = 20lgК
- 20lg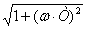 .
(6)
.
(6)
В области низких частот ω
< ωc
= 1/T, меньших по
значению, чем сопрягающая частота ωc,
L(ω) = 20lgК.
В этой области частот кривая ЛАЧХ заменяется прямой линией, параллельной оси
абсцисс и проходящей на уровне 20lgК.
В области высоких частот ω
> ωc
L(ω) = 20lgК
- 20lg(ω∙Т).
В этой области частот кривая ЛАЧХ заменяется прямой линией, имеющей наклон
минус 20 дБ на декаду.
Обе прямые или иначе асимптоты пересекаются в
точке, соответствующей сопрягающей частоте ωc
= 1/T.
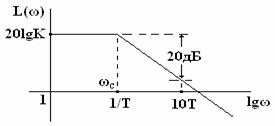
Интегрирующее звено.
Формула ЛАЧХ согласно (3) принимает следующий вид:
L(ω)
= 20lg[H(ω)] = 20lgК
- 20lgω.
(7)
Так как при частоте ω
= 1 согласно
выражению (7) функция L(ω)
= 20lgК, то
естественно асимптота в виде прямой линии с отрицательным наклоном в 20 дБ
должна проходить через эту точку при ω = ωc
= 1.
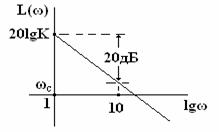
Колебательное звено.
Формула ЛАЧХ согласно (4) принимает следующий вид:
L(ω)
= 20lg[H(ω)] = 20lgK - 20lg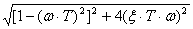 . (8)
. (8)
В области низких частот ω
< ωc
= 1/T, меньших по
значению, чем сопрягающая частота ωc,
L(ω) = 20lgК,
а при значениях частоты ω > ωc
можно под корнем пренебречь единицей и слагаемым 4(ξ∙ω∙T)2.
В результате получаем уравнение асимптотической ЛАЧХ:
L(ω)
= 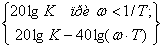 .
(9)
.
(9)
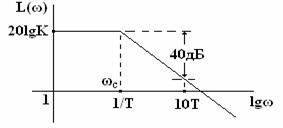
Согласно уравнению (9) асимптотическая ЛАЧХ при ω
< ωc
= 1/T, где ωc
- сопрягающая частота, параллельна оси частот, а при ωc
имеет минус 40 децибел на декаду.
Идеальное дифференцирующее звено.
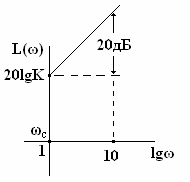
Формула ЛАЧХ согласно (5) принимает следующий вид:
L(ω)
= 20lg[H(ω)] = 20lgК
+ 20lgω.
(10)
По аналогии с интегрирующим звеном
асимптотическая ЛАЧХ представляет собой прямую, проходящую через точку 20lgK
при ωc
= 1 с наклоном плюс 20дб/дек.
После того, как мы познакомились с частотными
характеристиками САУ и правилами их построения, можно вернуться к рассмотрению
других частотных критериев устойчивости систем САУ.
Частотный критерий Найквиста.
Данный критерий предложен в 1932 году американским ученым Г. Найквистом и
позволяет судить об устойчивости замкнутой системы по АФЧХ разомкнутой системы.
Для того, чтобы замкнутая САУ была устойчивой необходимо и достаточно, чтобы ее
АФЧХ W(jω)
при разомкнутой цепи обратной связи не охватывала в комплексной плоскости точку
с координатами (- 1; j0).
Если разомкнутая система статическая (не имеет
интегрирующих звеньев), то при ω = 0 ее
АФЧХ начинается на вещественной оси в точке N(0)
= H(0) = K,
где К - коэффициент усиления разомкнутой системы. Заканчивается АФЧХ при ω
= ∞ вначале координат.

Логарифмический критерий Найквиста.
Для оценки устойчивости САУ по данному критерию используются графики ЛАЧХ и
ЛФЧХ разомкнутой системы САУ. Система САУ считается устойчивой, если при φ(ω)
= - 180о кривая ЛАЧХ находится в отрицательной области: L(ω)
= 20lg[H(ω)]
< 0, т.е. ЛАЧХ должна пересечь ось абсцисс раньше, чем фаза, спадая,
перейдет за значение -180о. Систему САУ можно считать также
устойчивой, если на частоте среза ωср,
на которой L(ωср)
= 20lg[H(ωср)]
= 0, значение аргумента φ(ωср)
> - 180o.
При оценке устойчивости САУ необходимо
определить запас устойчивости, т.е. степень удаленности системы от границы
устойчивости. В качестве меры запаса устойчивости используется запас
устойчивости по амплитуде h(ω)
и запас устойчивости по фазе ψ(ωср).
Запас устойчивости САУ по амплитуде h(ω)
определяется на частоте ωу,
при которой φ(ωу)
= - 180о: h(ωу)
= - L(ωу)
и показывает допустимое увеличение ЛАЧХ , при котором система окажется на грани
устойчивости. Запас по амплитуде представляет собой запас по коэффициенту
усиления К разомкнутой системы по отношению его к критическому по устойчивости
значению.
Запас устойчивости по фазе ψ(ωср)
определяется на частоте среза ωср,
как: ψ(ωср)
= φ(ωср)
+ 180о и показывает, на какую величину должно возрасти запаздывание
по фазе в системе на частоте среза ωср,
чтобы система оказалась на грани устойчивости.
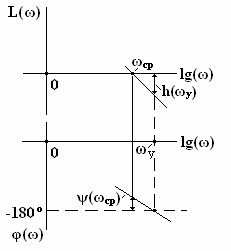
При проектировании САУ рекомендуется выбирать ψ(ωср)
≥ 30о, а h(ωу)
≥ 6 дБ, что соответствует примерно двойному запасу коэффициента усиления
К по устойчивости.
Лекция
5. Электрические модели типовых динамических звеньев
Каждое из рассмотренных нами динамических
звеньев может быть представлено в виде электрического, механического или
электро-механического аналогов, процессы в которых математически описываются
соответствующим одним и тем же дифференциальным уравнением.
Рассмотрим электрические модели наиболее часто
встречающихся типовых звеньев. Апериодическое звено. Апериодическими
звеньями являются RC
и RL цепи, входные и
выходные величины которых связаны соответствующей передаточной функцией.
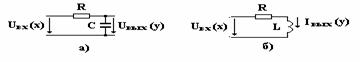
Для схемы а) напряжение на выходе в комплексном
виде равно:
Uвых(jω)
= I(jω)∙xc/j
= I(jω)∙1/(jωC);
I(jω)
= Uвх(jω)/[R
+ 1/(jωC)] = jωC∙
Uвх(jω)/(jωRC
+1);
Uвых(jω)
= Uвх(jω)/(jωRC
+1). (1)
Представим уравнение (1) в операторной форме,
заменив комплексную переменную jω
на оператор Лапласа р:
Uвых(р)
= Uвх(p)/(рRC
+1) = Uвх(p)/(рТ
+1). (2)
Как следует из уравнения (2), передаточная
функция схемы а) соответствует передаточной функции типового апериодического
звена:
W(p)
= y/x
= Uвых(р)/Uвх(p)
= 1/(рТ +1), где (3)
коэффициент усиления К равен 1, а постоянная
времени Т равна произведению RC.
Для схемы б) ток на выходе в комплексном виде
равен:
Iвых(jω)
= Uвх(jω)/(R
+ jxL) = Uвх(jω)/(R
+ jωL);
Iвых(jω)
= Uвх(jω)∙(1/R)/[jω∙(L/R)
+1)]. (4)
Заменяя в уравнении (4) комплексную переменную jω
на оператор Лапласа р, получим уравнение схемы б) в операторной форме:
Iвых(р)
= Uвх(р)∙(1/R)/[р∙(L/R)
+1)] = Uвх(р)∙K/(рТ
+1). (5)
Из выражения (5) следует, что передаточная
функция данной схемы устанавливает связь между выходным током и входным
напряжением:
W(p)
= y/x
= Iвых(р)/Uвх(p)
= K/(рТ +1), где (6)
коэффициент усиления К равен 1/R,
а постоянная времени Т равна отношению L/R.
моделировать апериодические звенья с требуемыми
характеристиками.
Колебательное звено.
Оно представляет собой последовательное соединение RLC
элементов:
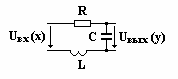
Представим напряжение на выходе колебательного
звена сразу в операторной форме:
Uвых(р)
= I(p)∙1/pC
= Uвх(p)∙(1/pC)/[R
+ pL + (1/pC)]
=
= Uвх(p)/(p2CL
+ pRC + 1) = Uвх(p)/(p2T2
+ p2ξT
+ 1), (7)
где Т2 = CL;
2ξT = CR.
Тогда передаточная функция колебательного звена:
W(p)
= y/x
= Uвых(р)/Uвх(p)
= 1/( p2T2
+ p2ξT
+ 1), (8)
где коэффициент усиления равен К = 1.
Коэффициент демпфирования ξ можно
найти из следующих соотношений:
T
= √CL; 2ξ√CL
= CR,
откуда ξ = CR/(2√CL)
= 0,5∙R∙C/√(C∙L).
(9)
Для случая отсутствия активных потерь в
колебательном контуре (R
= 0) имеем согласно выражению (9): ξ = 0, т.е.
в контуре имеют место незатухающие колебания. Колебательное звено превращается
в апериодическое звено второго порядка, когда ξ = 1, т.е.
при условии, что 0,5∙R∙C
= √(C∙L)
или R2∙C
= 4L.
Интегрирующее звено.
Идеальными интегрирующими звеньями являются цепи
с элементами С и L. В схеме а)
входной величиной х является ток заряда конденсатора, а напряжение на нем -
выходной величиной у. В схеме б) входной величиной х является напряжение на
индуктивности, а ток - выходной величиной у.
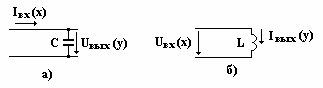
Представим напряжение на выходе схемы а) в
операторной форме:
Uвых(р)
= Iвх(р)∙1/(рС).
(10)
Следовательно, передаточная функция данного
звена равна:
W(p)
= y/x
= Uвых(р)/Iвх(p)
= (1/C)/p
= К/р, (11)
где К = 1/С.
Отличительным свойством интегрирующего звена
является то, что после прекращения действия входного сигнала выходной сигнал
звена остается на том уровне, на котором был в момент исчезновения входного
сигнала. Иначе говоря, интегрирующее звено обладает свойством «запоминать»
последнее значение выходной величины, благодаря чему достигается астатизм
автоматической системы. Другой особенностью интегрирующего звена является то,
что скорость изменения выходной величины у прямопропорциональна значению
входной величины х.
В операторной форме уравнение интегрирующего
звена по схеме б):
Iвых(р)
= Uвх(р)/(рL).
(12)
Соответственно, передаточная функция звена равна:
W(p)
= y/x
= Iвых(р)/Uвх(p)
= (1/L)/p
= К/р, (13)
где К = 1/L.
Дифференцирующее звено.
Идеальными дифференцирующими звеньями являются цепи с конденсатором и элементом
индуктивности. Входной величиной х в схеме а) является напряжение, а ток через
конденсатор - выходной величиной у. В схеме б) входной величиной х является
входной ток, а напряжение на индуктивности - выходной величиной у.
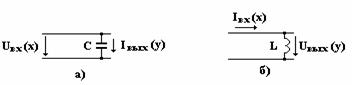
Представим выходной ток схемы а) в операторной
форме:
Iвых(р)
= Uвх(р)∙рС.
(14)
Соответственно, передаточная функция данного
звена равна:
W(p)
= y/x
= Iвых(р)/Uвх(p)
= pC = Кр, (15)
где К = С.
Особенностью дифференцирующего звена является
то, что значение выходной величины у прямопропорциональна скорости изменения
входной величины х.
В операторной форме уравнение дифференцирующего
звена по схеме б):
Uвых(р)
= Iвх(р)∙рL.
(16)
Соответственно, передаточная функция звена
равна:
W(p)
= y/x
= Uвых(р)/Iвх(p)
= pL = К∙р, (17)
где К = L.
Лекция
6. Передаточные функции и характеристики разомкнутых САУ
Системы САУ в большинстве случаев являются
замкнутыми системами.
Однако при их анализе (например, устойчивости) и
проектировании часто предварительно рассматривается разомкнутая цепь звеньев,
которая затем замыкается.
Различают последовательное, параллельное и
параллельное с обратной связью соединение звеньев.
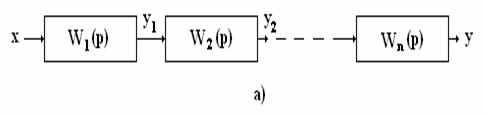
Последовательным соединением звеньев называют
такое соединение, когда выходная величина предыдущего звена является входной
величиной последующего звена (схема а), т.е. ym-1
= хm.
Передаточная функция разомкнутой цепи n
последовательно соединенных звеньев равна произведению передаточных функций
всех звеньев:
W(p)
= y(p)/x(p)
= W1(p)∙W2(p)
∙…∙Wn(p).
(1)
Полагая p
= jω, перейдем от
передаточных функций в операторном виде к частотным характеристикам.
АФЧХ = W(jω)
= W1(jω)∙W2(jω)
∙…∙Wn(jω)
= H(ω)∙exp[φ(ω)]
=
= H1(ω)∙H2(ω)
∙…∙Hn(ω)∙expj[φ1(ω)
+ φ2(ω)
+ … + φn(ω)].
(2)
АЧХ = H(ω)
= H1(ω)∙H2(ω)
∙…∙Hn(ω).
(3)
ФЧХ = φ(ω) = φ1(ω)
+ φ2(ω)
+ … + φn(ω).
(4)
ЛАЧХ = L(ω)
= 20lg H(ω) = 20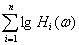 .
(5)
.
(5)
Таким образом, при последовательном соединении
звеньев амплитудно-частотные характеристики перемножаются , а логарифмические
амплитудно-частотные и фазовые частотные характеристики складываются.
Рассмотрим получение асимптотической ЛАЧХ
разомкнутой цепи при последовательном соединении звеньев на следующем примере.
Пусть передаточная функция разомкнутой цепи
описывается следующей формулой:
W(p)
= 
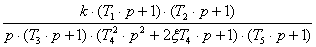 . (6)
. (6)
При этом коэффициент демпфирования ξ
принимаем
0,5 < ξ < 1 (при таких
значениях ξ можно не учитывать
«горб» АЧХ колебательного звена).
Асимптотическую ЛАЧХ можно построить
непосредственно по передаточной функции. При этом каждому сомножителю (Тр + 1)
в знаменателе соответствует точка излома характеристики при ω
= 1/Т
с последующим наклоном минус 20 дБ/декаду, а каждому сомножителю такого же типа
в числителе соответствует точка излома также при ω = 1/Т,
но с последующим наклоном плюс 20дБ/декаду. Сомножителю (Т2р2
+ 2ξТр + 1) в знаменателе соответствует излом
характеристики при ω = 1/Т
с наклоном минус 40 дБ/декаду.
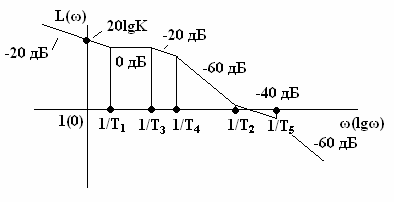
Методика построения асимптотической ЛАЧХ
сводится к следующему:
1) определяем сопрягающие частоты типовых
звеньев в порядке возрастания. Так, например, для случая Т1 > T3
> T4 > T2
> T5:
ω1
= 1/Т1; ω2
= 1/Т3; ω3
= 1/Т4; ω4
= 1/Т2; ω5 = 1/Т5;
2) вычисляем на частоте ω
= 1 ординату
L(1) = 20lgK,
где К - общий коэффициент усиления разомкнутой системы.
) Через полученную точку проводим
низкочастотную асимптоту ЛАЧХ, представляющую собой прямую с наклоном минус 20∙m
дБ/декаду, где m - число
интегрирующих звеньев (в нашем примере согласно формуле (6) m
= 1).
4) изменяем наклон асимптот ЛАЧХ на сопрягающих
частотах по отношению с наклоном, который имела ЛАЧХ до рассматриваемой
частоты.
Фазовая частотная характеристика определяется по
выражению:
φ(ω) = - 90о
+ arctg(ωT1)
+ arctg(ωT2)
- arctg(ωT3)
- arctg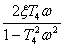 - arctg(ωT5)
- arctg(ωT5)
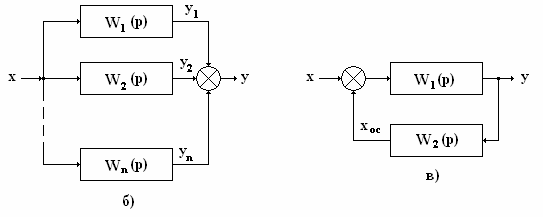
Параллельным соединением звеньев называется
такое соединение, когда на входы всех звеньев подается одна и та же величина, а
выходные сигналы суммируются (схема б). Если соединяются n
звеньев, то входной сигнал равен: х = х1 = х2 = … хi
= … = хn,
а выходной сигнал у = 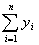 .
.
Переходя к операторной форме представления
выходной функции, получим:
y(p)
= x(p)∙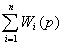 ,
,
откуда: W(p)
= y(p)/x(p)
= 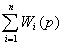 .
(7)
.
(7)
Таким образом, при параллельном соединении
звеньев передаточные функции каждого звена суммируются.
Так как передаточная функция W(p)
есть ничто иное, как изображение весовой функции, то весовая функция g(t),
а, следовательно, и переходная функция h(t)
разомкнутой цепи, состоящей из параллельно соединенных n
звеньев, равны сумме соответственно весовых и передаточных функций отдельных
звеньев:
g(t)
= 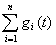 ;
h(t)
=
;
h(t)
= 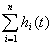 .
(8)
.
(8)
При параллельном соединении звеньев с обратной
связью (схема «в» замкнутой системы САУ) обратная связь может быть
положительной, если сигнал обратной связи хос складывается с входным
сигналом х, или отрицательной, если сигнал обратной связи хос
вычитается из х.
При отрицательной обратной связи схема
описывается следующим уравнением:
y(p)
= W1(p)∙[x(p)
- xoc(p)].
(9)
Вместе с тем сигнал обратной связи хос
определяется в соответствии с выражением:
xoc(p)
= W2(p)∙y(p).
(10)
Подставляя значение хос из формулы (10) в
уравнение (9), получим:
y(p)
= W1(p)∙[x(p)
- W2(p)∙y(p)]
(11)
Решим уравнение (11) относительно y(p):
y(p)∙[1
+ W1(p)∙W2(p)]
= W1(p)∙x(p).
(12)
Отсюда:
у(р) = W1(p)∙x(p)/[1
+ W1(p)∙W2(p)]
= Wз(p)∙x(p).
(13)
Передаточная функция замкнутой системы при
отрицательной обратной связи Wз(p)
определяется в соответствии с выражением (13):
Wз(p)
= у(р)/х(р) = W1(p)/[1
+ W1(p)∙W2(p)]
(14)
При положительной обратной связи:
Wз(p)
= у(р)/х(р) = W1(p)/[1
- W1(p)∙W2(p)]
(14)
Лекция
7. Точность систем САУ
Требования к процессу управления.
Системы САУ выполняют задачу стабилизации или управления. В первом случае
система поддерживает регулируемую величину на заданном уровне, а во втором - с
заданной точностью изменяет регулируемую величину по определенному закону.
Режим работы системы, при котором отклонение
регулируемой величины от заданного значения не превышает допустимого,
называется установившимся режимом. В общем случае, за установившийся режим
принимается такой режим, при котором ошибка системы (разность между заданным и
фактическим значением регулируемой величины) постоянна во времени.
Установившийся режим часто называют невозмущенным движением системы.
Если на систему действуют возмущающие внешние
воздействия, то в системе возникает возмущенное движение, которое называют
переходным процессом. Процесс управления во времени определяется решением
уравнения динамики системы:
y(t)
= yв(t)
+ yсв(t),
(1)
где yв(t)
- вынужденная составляющая, yсв(t)
- свободная (переходная) составляющая.
За невозмущенное движение принимается
вынужденная составляющая yв(t),
представляющая собой установившуюся часть процесса управления. На нее
накладывается переходной процесс yсв(t),
который теоретически длится бесконечно долго, но его влияние практически
становится существенно малым через определенное конечное время. После затухания
переходной составляющей устанавливается yв(t).
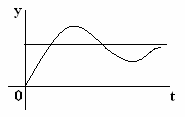
По графику установившегося процесса определяется
точность САУ. При этом установившаяся ошибка системы равна:
εус(t)
= yв(t)
- x(t),
(2)
а полное значение ошибки: ε
(t) = y(t)
- x(t).
(3)
С целью обеспечения нормального протекания
процесса управления к системе САУ предъявляются требования по точности,
устойчивости и качеству переходного процесса.
Точность системы задается и определяется в
установившихся режимах. Устойчивость гарантирует затухание переходного
процесса, после чего обеспечивается желаемое качество затухающего переходного
процесса.
Точность при типовых воздействиях.
Значение установившейся ошибки можно найти по теореме операционного исчисления
о конечном значении функции. Суть теоремы звучит так: если известно изображение
F(p)
функции f(t),
то конечное значение оригинала f(t
→
∞) можно вычислить по формуле:
f(t
→
∞) = lim[p∙F(p)]
при р → 0.
Применяя эту формулу для решения поставленной
задачи, получим:
εус
= lim[р∙Wε(p)∙x(p)]
при р → 0, (4)
где Wε(p)
- передаточная функция, представляющая собой отношение установившейся ошибки εус
к входной величине х.
В общем случае задающее воздействие является
сложной функцией времени, при которой вычисление ошибки значительно
усложняется. Поэтому реальные управляющие воздействия заменяют типовыми, в
качестве которых применяют известную вам ступенчатую функцию m∙1(t),
линейную функцию а∙t
или квадратичную функцию at2/2.
Эти воздействия называются детерминированными
или регулярными, поскольку их значения можно вычислить для любого момента
времени.
Передаточная функция ошибки замкнутой системы
определяется в соответствии с выражением:
Wε(p)
= 1/[1 + W(p)],
(5)
где W(р)
- передаточная функция разомкнутой системы.
Подставляя выражение (5) в уравнение (4),
получим:
εус
= lim{р∙x(p)/[1
+ W(p)]}
при р → 0. (4)
Если W(0)
= К, т.е. структурная схема разомкнутой системы не содержит интегрирующих
звеньев, то САУ называется статической, где К - статический коэффициент
усиления разомкнутой системы.
Астатическими системами первого и второго
порядка называют такие, у которых передаточные функции соответственно равны W(p)
= К·W*(p)/р
и W(p)
= К·W*(p)/р2,
т.е. структурные схемы систем содержат одно или два интегрирующих звена. При
этом W*(p)
- передаточная функция без учета интегрирующих звеньев и их коэффициентов
усиления.
При вычислении ошибок необходимо иметь в виду,
что изображение по Лапласу типовых воздействий для х = хо, х = а∙t
и х = at2/2
равно соответственно:
х(р) = хо/р; х(р) = а/р2;
х(р) = а/р3. (5)
Рассмотрим ошибки некоторых САУ при типовых
воздействиях.
Подставив в выражение (4) значение х(р) для
ступенчатого воздействия найдем установившуюся ошибку статической системы САУ
при р = 0:
εус
= р∙x(p)/[1
+ W(p)]
= p∙ хо/{р∙[1
+ W(p)]}
=
= хо/[1
+ W(p)]
= хо/[1 + W(0)]
= хо/(1 + K).
(6)
Эта ошибка называется статической ошибкой. Она
пропорциональна задающему воздействию и уменьшается с увеличением коэффициента
К разомкнутой системы. При изменяющихся во времени воздействиях типа х(t)
= а∙t или х = at2/2
ошибка непрерывно возрастает и при р → 0 εус
→ ∞.
εус
= а/[p∙(1 + K)];
εус
= а/[p2∙(1
+ K)]. (7)
Наличие статической ошибки является характерным
свойством статических САУ.
Астатические системы первого порядка точно
отрабатывают ступенчатое воздействие.
εус
= р∙x(p)/[1
+ W(p)]
= p∙ хо/{р∙[1
+ К·W*(p)/p]}
=
= хо∙p/[p
+ К·W*(p)]
= 0/[0 + W(0)] = 0/K
= 0. (8)
В то же время при отработке линейно
возрастающего сигнала эти системы имеют постоянную ошибку εус
= а/K:
εус
= р∙x(p)/[1
+ W(p)]
= p∙ а/{р2∙[1
+ К·W*(p)/p]}
=
= а/[p
+ К·W*(p)]
= а/[0 + W(0)] = а/K.
(9)
Эта ошибка пропорциональна скорости изменения
входного сигнала «а», поэтому ее называют скоростной ошибкой, а коэффициент
усиления разомкнутой системы К - добротностью системы по скорости.
При отработке квадратичного сигнала отклонение εус
→ ∞.
εус
= р∙x(p)/[1
+ W(p)]
= p∙ а/{р3∙[1
+ К·W*(p)/p]}
=
= а/{р∙[p
+ К·W*(p)]}.
(10)
Астатические системы второго порядка точно
отрабатывают ступенчатый и линейно возрастающие сигналы. При отработке
квадратичного сигнала имеет место ошибка εус
= а/K, которая
пропорциональна ускорению «а» входного сигнала и обратно пропорциональна
коэффициенту усиления разомкнутой системы К, который называется добротностью
системы по ускорению, а сама ошибка - ошибка системы по ускорению.
С увеличением коэффициента усиления К
разомкнутой системы установившиеся ошибки уменьшаются. Однако с возрастанием К
ухудшается устойчивость автоматических систем, т.е. требование к точности
противоречит требованию к устойчивости. При заданном относительно большом
значении К улучшение устойчивости достигается включением в систему
корректирующих устройств.
Порядок астатизма системы также влияет на
точность системы. Чем выше астатизм, тем точнее система отрабатывает более
сложные воздействия. Однако с увеличением порядка астатизма системы ее
устойчивость ухудшается. Поэтому системы САУ с порядком астатизма более двух
встречаются редко.
Лекция
8. Показатели качества САУ и их коррекция
Качество системы САУ определяется качеством
переходного процесса, которое оценивают по переходной функции h(t),
представляющей собой реакцию системы на внешнее воздействие типа единичной
ступенчатой функции 1(t).
На примере переходной функции колебательного
звена рассмотрим основные показатели качества переходного процесса: время
регулирования, перерегулирование, частоту колебаний, число колебаний,
максимальную скорость и максимальное ускорение регулируемой величины.
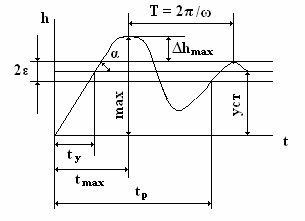
Время регулирования tp
определяет длительность переходного процесса. Теоретически переходной процесс
длится бесконечно долго, однако он заканчивается практически, как только
отклонение регулируемой величины от установившегося значения не будет превышать
допустимых пределов ε = (3-5)%∙hуст.
Временем регулирования характеризуют быстродействие системы. Однако иногда
быстродействие системы характеризуют временем tу
достижения переходной функцией первый раз установившегося значения или временем
tmax достижения
максимального значения hmax.
Перерегулирование Δhmax
или выброс представляет собой максимальное отклонение регулируемой величины от
установившегося значения. Обычно, первый максимум является наибольшим.
Относительное перерегулирование определяется следующей формулой:
ε = Δhmax∙100%
/ hуст.
(1)
Время регулирования и перерегулирование тесно
связаны между собой. Перерегулирование появляется вследствие того, что система
к установившемуся состоянию подходит с определенной скоростью, которая
определяется тангенсом угла наклона α касательной
в точке, соответствующей времени tу:
Δh/Δt
= tgα при t
= ty.
Чем больше эта скорость (круче кривая переходной
функции), тем больше будет перерегулирование Δhmax.
Для уменьшения перерегулирования необходимо снизить скорость, с которой система
подходит к установившемуся состоянию, что приведет к увеличению времени
регулирования tp.
Если система подходит к установившемуся состоянию с нулевой скоростью, то
перерегулирования не происходит, но время регулирования значительно возрастает.
Таким образом, можно сделать вывод, что, как отсутствие, так и очень большое
перерегулирование являются нежелательными. Поэтому перерегулирование допускают
в пределах 20-30% от установившегося значения. При этом число полупериодов
колебаний переходной функции равно двум-трем.
Качество переходного процесса оценивают на
основе анализа кривой переходной функции. Однако на практике при анализе
качества регулирования часто используют косвенные оценки, которыми являются
некоторые числа, характеризующие отдельные моменты переходного процесса и
которые можно найти без построения графика переходного процесса. Рассмотрим
некоторые из косвенных оценок.
Частотные оценки.
Для оценки используется относительная АЧХ в виде зависимости отношения H(ω)/К
от частоты ω: Δ(ω) = H(ω)/К.
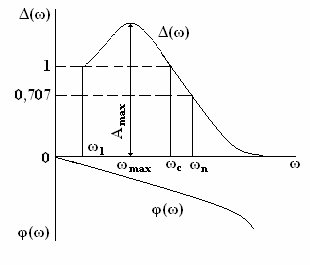
Относительная АЧХ на резонансной частоте ωmax
имеет максимум, соответствующий значению Δ(ωmax)
= Δmax.
При дальнейшем увеличении частоты система в следствие своей инерционности не
успевает реагировать на колебания больших частот и Δ(ω)
резко
«падает».
Установлено, что чем больше Δmax,
тем более колебательным является переходной процесс. Отношение Δmax/Δ(0)
= М
называют показателем колебательности. Для следящих систем Δ(0)
= 1, поэтому
М = Δmax.
Обычно М = 1,2 - 1,5. При малых М система имеет большое время регулирования.
При больших М увеличивается перерегулирование и система приближается к границе
устойчивости. Кроме частоты ωmax
характерными частотами АЧХ являются частота среза ωс
и полоса пропускания ωп.
Частота среза замкнутой системы ωс
определяется на уровне Δ(ω) = 1.Для
следящих систем частота среза определяет диапазон вынужденных колебаний,
которые система пропускает без ослабления.
На этой частоте амплитуды входного и выходного
колебаний равны. Полоса пропускания ωп
замкнутой системы определяется на уровне Δ(0)/√2 =
0,707. Так
как в диапазоне частот (ωс
- ωп) АЧХ резко
«падает», то числовые значения частот ωс
и ωп
близки.
Полоса пропускания влияет на точность и
быстродействие системы. С увеличением полосы пропускания быстродействие системы
растет. Чем больше полоса пропускания, тем больший спектр частот входного
сигнала передается без искажений.
О качестве регулирования можно судить по ЛАЧХ.
Установлено, что для удовлетворительного качества регулирования участок средних
частот, на котором ЛАЧХ пересекает ось абсцисс, должен имеет наклон минус 20
дБ/декаду.
Протяженность этого участка влияет на
перерегулирование. С его увеличением уменьшается колебательность переходного
процесса. Приемлемое качество переходного процесса имеет место, если
протяженность этого участка примерно равна декаде. Время регулирования tp
зависит от частоты среза, при которой ЛАЧХ пересекает ось абсцисс. Чем больше
частота среза, тем меньше tp.
Корневые оценки.
Корневыми называются оценки, которые
основываются на расположении корней характеристического уравнения замкнутой
системы, которые являются полюсами передаточной функции замкнутой системы и
находятся из уравнения Wз(ω)
= ∞.
Корневой оценкой качества является степень
устойчивости - расстояние η от
мнимой оси до ближайшего корня на плоскости корней характеристического
уравнения замкнутой системы.
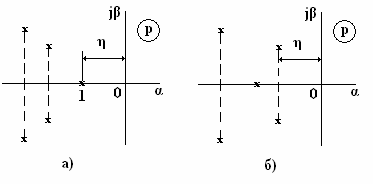
Если ближайшим является вещественный корень
(схема а), то ему соответствует экспоненциальная составляющая решения для
переходного процесса С1 = ехр(-η∙t)
- апериодическая степень устойчивости η. Время
ее затухания tп
= 3/η при погрешности 5% характеризует общую
длительность переходного процесса, так как все остальные члены решения ,
соответствующие основным корням затухают быстрее.
Если же ближайшей к мнимой оси окажется пара
комплексных сопряженных корней (схема б), то доминирующей составляющей решения
для переходного процесса является С1 = ехр(-η∙t)∙sin(β1∙t
+ C2),
которая называется колебательной составляющей - колебательная степень
устойчивости η. При этом оценка
длительности переходного процесса остается прежней tп
= 3/η.
Колебательность переходного процесса
определяется величиной μ = β/η, где
β
и
η
- соответственно
мнимая и вещественная части корней характеристического уравнения. Эта величина
характеризует быстроту затухания колебаний за каждый период. Чем больше
величина μ, называемая
колебательностью, тем слабее затухания колебаний в переходном процессе.
Для уменьшения амплитуд отклонений в переходном
процессе желательно, чтобы нули передаточной функции замкнутой системы Wз(р),
представляющие собой значения р, при котором Wз(р)
= 0, располагались вблизи ее полюсов.
Понятие о коррекции.
Основная задача корректирующих устройств в улучшении точности и качества
переходных процессов систем САУ. Кроме того, корректирующие устройства
предварительно используются для обеспечения устойчивости неустойчивых систем.
Для уменьшения ошибок в установившемся режиме
необходимо повышать коэффициент усиления К системы в разомкнутом состоянии. Но
с увеличением К, как мы с вами уже отмечали ранее, уменьшается запас
устойчивости САУ. С возрастанием К увеличивается и частота среза ωс
(ωс2
> ωс1).
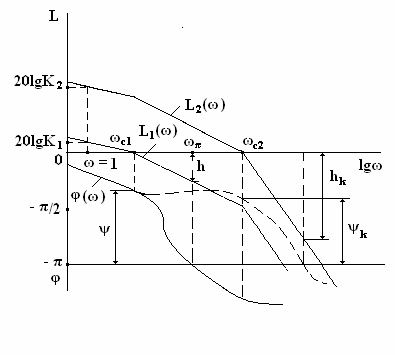
Большим значениям ωс
соответствуют меньшие значения запаса устойчивости по фазе ψ.
При
ωс
= ωс2 система
неустойчива из-за вносимого инерционными звеньями системы запаздывания
колебаний по фазе, которое растет с увеличением частоты.
Для того, чтобы при увеличении К система
оставалась устойчивой и обеспечивала требуемый запас устойчивости по фазе ψ
и
амплитуде h, необходимо
частично компенсировать запаздывание в полосе частот, которая расположена около
частоты среза ωс2,
соответствующей увеличенному коэффициенту К2 системы, и тем самым
деформировать ЛФЧХ системы, приподняв ее вверх (штриховая кривая). Такую
деформацию ЛФЧХ можно осуществить, включив последовательно элементам системы
устройство, которое вносило бы опережение по фазе синусоидальных колебаний.
Коррекция САУ осуществляется с использованием
последовательных и параллельных корректирующих устройств.
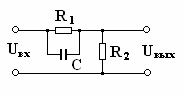
Последовательные корректирующие
устройства. К числу последовательных корректирующих
устройств относится дифференцирующая фазоопережающая цепь, которая называется
форсирующей цепью.
Передаточная функция этой цепи имеет следующий
вид:
W(p)
= Uвых(р)/Uвх(р)
= R2∙(1 + pR1∙C)/(R2 + R1
+ pR1∙R2∙C) (2)
Разделим числитель и знаменатель дроби (2) на
сумму сопротивлений (R1
+ R2),
в результате получим
W(p)
= 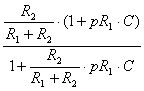 .
(3)
.
(3)
Обозначим отношение R2/(R1
+ R2)
как K
-
статический коэффициент усиления, произведение (R1∙С)
как постоянную времени Т1, а К∙Т1 = Т2.
Здесь постоянные времени характеризуют соответственно опережение Т1
и отставание Т2 (поскольку К < 1, то Т2 < Т1).
Подставив в формулу (3) соответствующие замены, получим стандартное изображение
передаточной функции форсирующего звена:
W(p)
= К∙(1 + р∙Т1)/(1 + р∙Т2). (4)
ЛАЧХ данного звена имеет вид:
L(ω)
= 20lgH(ω)
= 20lgK + 20lg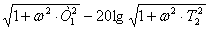 .
(5)
.
(5)
ЛФЧХ форсирующего звена:
φ(ω) = arctg(ωТ1)
- arctg(ωТ2).
(6)
Примечание:
L(ω) = 20lgK
в диапазоне частот (0 - 1/Т1), (20lgK
+ 20дБ/дек) в диапазоне частот (1/Т1 - 1/Т2) и (20lgK
+ 20дБ) = const в диапазоне
частот ω
> 1/Т2.
Фазовый угол φ(ω) с ростом частоты до
ωmax
изменяется от 0о до +45о, а затем вновь падает до 0о.
Опережение создается благодаря тому, что Т1
> Т2. Частоту ωmax,
при которой цепь создает максимальное опережение, находим из условия dφ(ω)/dω
= 0: ωmax
= 1/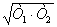 .
.
Подставляя в формулу (6) выражение для ωmax,
определяем значение фазового угла, соответствующее данной частоте:
φ(ω) = arctg(Т1
/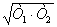 )
- arctg(Т2 /
)
- arctg(Т2 /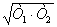 )
= arctg
)
= arctg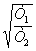 - arctg
- arctg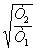 .
(7)
.
(7)
Из формулы (7) следует, что получение больших
углов опережения связано с уменьшением коэффициента усиления цепи К. Для
компенсации ослабления вносимого фазоопережающей цепью, необходимо увеличивать
коэффициент усиления системы другими ее элементами.
Для уменьшения влияния помех САУ целесообразно
корректировать, используя интегрирующее устройство, которое позволяет
увеличивать К, не повышая ее частоты среза.
Передаточная функция наиболее распространенной
пассивной интегрирующей цепи имеет следующий вид:
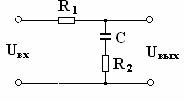
W(p)
= Uвых(р)/Uвх(р)
= (pR2∙C
+ 1)/(pR1∙C
+ pR2∙C
+ 1). (8)
Обозначим произведение R2∙C
как Т2 - постоянная времени опережения контура, С∙(R1
+ R2)
= Т1 - постоянная времени отставания. Подставив замены в выражение
(8), получим:
W(p)
= (1 + р∙Т2)/(1 + р∙Т1). (9)
Наличие отставания, вносимого интегрирующим
устройством, является недостатком корректирующего устройства. Однако при
соответствующем выборе параметров этого устройства область отставания может
быть смещена в диапазон низких частот значительно левее частоты среза системы,
поэтому запас устойчивости системы при включении интегрирующего звена
практически не уменьшается.
ЛАЧХ данного звена имеет вид:
L(ω)
= 20lgH(ω)
= 20lg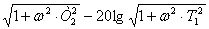 .
(10)
.
(10)
ЛФЧХ интегрирующего звена:
φ(ω) = arctg(ωТ2)
- arctg(ωТ1).
(11)
Примечание:
L(ω) = 0 в
диапазоне частот (0 - 1/Т1), (- 20дБ/дек) в диапазоне частот (1/Т1
- 1/Т2) и (- 20дБ) = const
в диапазоне частот ω > 1/Т2.
Фазовый угол φ(ω) с ростом частоты до
ωmax
изменяется от 0о до некоторого отрицательного максимума (больше - 90о),
а затем вновь падает до 0о.
На практике для коррекции САУ часто применяют
интегро-дифференцирующие цепи.
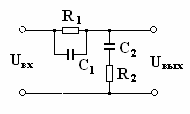
Передаточная функция этой цепи имеет вид:
W(p)
= Uвых(р)/Uвх(р)
= (1 + р∙Т1)∙(1 + р∙Т2)/[ (1 + р∙Т3)·(1
+ р∙Т4)], (12)
где Т1
= R1∙C1; Т2
= R2∙C2; T3 + T4 = R1∙C1
+ (R1 + R2)∙C2; T3 · T4
= T1 · T2.
ЛФЧХ интегро-дифференцирующего звена:
φ(ω)
= arctg(ωТ2)
+ arctg(ωТ1)
- arctg(ωТ3)
- arctg(ωТ4).
(13)
Примечание:
L(ω) = 0 в
диапазоне частот (0 - 1/Т3), (- 20дБ/дек) в диапазоне частот (1/Т3
- 1/Т1), (- 20дБ) = const
в диапазоне частот (1/Т1 - 1/Т2), (+ 20дБ/дек) в
диапазоне частот (1/Т2 - 1/Т4) и 0 в диапазоне частот в
диапазоне частот ω > 1/Т4.
Фазовый угол φ(ω) с ростом частоты
имеет два максимума: отрицательный более - 90о и положительный менее
90о, а также нулевой угол в средней части диапазона частот (1/Т1
- 1/Т2).
Используя последовательную
интегро-дифференцирующую цепь можно значительно повысить коэффициент усиления
системы и увеличить ее частоту среза, а следовательно повысить точность системы
в установившемся и переходном режимах.
Параллельные корректирующие
устройства. Параллельное корректирующее устройство
выполняет функции обратной связи, которая охватывает один из элементов прямой
цепи системы.
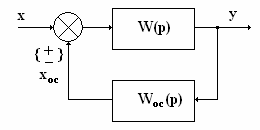
Передаточная функция этой части системы Wохв(р)
= W(p)/[1
+ W(p)∙Woc(p)]
может быть представлена в следующем виде: Wохв(р)
= W(p)∙Wn(p),
где Wn(p)
= 1/[1 + W(p)∙Woc(p)]
- передаточная функция последовательно включенного звена, эквивалентного
параллельному корректирующему устройству с передаточной функцией Woc(p).
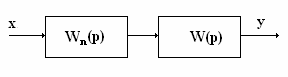
Таким образом, если удается повысить показатели
качества, используя последовательные корректирующие устройства, то такое же
повышение показателей качества можно осуществить и, используя параллельные
корректирующие устройства. Если известно Wn(p),
то можно найти Woc(p):
Woc(p)
= [1 - Wn(p)]/[Wn(p)∙W(p)].
(14)
Если в какой-либо области частот выполняется
условие |W(jω)∙Woc(jω)|
>> 1, то
Wохв(jω)
= W(jω)/[1
+ W(jω)∙Woc(jω)]
≈ 1/Woc(jω),
(15)
т.е. передаточная функция части системы,
охваченной обратной связью, в этой области частот полностью определяется
передаточной функцией параллельного корректирующего устройства. Благодаря этому
применением параллельных корректирующих устройств удается изменить частотные
характеристики систем САУ в желаемом направлении.
Корректирующие обратные связи делятся на жесткие
и гибкие. Жесткая обратная связь действует на систему в переходном и
установившемся режимах, т.е. Wжос(0)
≠ 0, и реализуется она безинерционным (Wжос
= Кос) или инерционным [Wжос(p)
= Кос/(Tocp
+ 1)] звеньями.
Гибкая обратная связь действует лишь в
переходных режимах. Реализуется она дифференцирующим [Wгос(р)
= Коср] или инерционно-дифференцирующим звеном [Wгос(p)
= Коср/(Tocp
+ 1)]. При охвате интегрирующего звена [Wδ(p)
= K/p]
отрицательной жесткой обратной связью (Wжос
= Кос) получим:
W(p)
= K/(p
+ K∙Koc)
= K1/(T1p
+ 1), (16)
где К1 = 1/Кос: Т1
= 1/К∙Кос.
Таким образом, под действием жесткой обратной
связи теряется интегрирующее свойство звена и оно превращается в апериодическое
с коэффициентом усиления, который полностью определяется только обратной
связью. Постоянная времени Т1 мала при большом коэффициенте усиления
звена К.
При охвате инерционного интегрирующего звена
гибкой обратной связью:
W(p)
= K/[p∙(Tp
+ 1); Woc(p)
= Koc∙p;
Wохв(р)
= K/[p∙(Tp
+ 1 + K∙Koc)]
= K1/[p∙(T1p
+ 1), (17)
где K1
= К/(1 + К∙Кос); Т1 = Т/(1 + К∙Кос).
Т.е. в этом случае сохраняется тот же тип
интегрирующего звена, но с уменьшенной инерционностью.
ЗАДАНИЕ
НА КОНТРОЛЬНУЮ РАБОТУ
Задача 1. Расчет динамических
характеристик линейных САУ
Определить весовую функцию g(t)
и переходную функцию h(t)
линейной САУ, состоящей из последовательного соединения апериодического и
идеального интегрирующего звеньев, по заданным в табл. 1 параметрам ее
передаточной функции в соответствии с последними двумя цифрами учебного шифра:
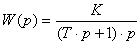 ,
где р - оператор Лапласа.
,
где р - оператор Лапласа.
Составить таблицу расчетных значений искомых
временных характеристик и построить их графики для временного интервала: t
= 0 - 5T с шагом
дискретизации, равным 0,5Т. Масштаб по оси ординат студентом выбирается
самостоятельно, исходя из того, что высота графика должна быть не менее 8-10
см.
Таблица 1
|
Номер
варианта
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
0
|
|
последняя
цифра шифра
|
К
|
5
|
10
|
8
|
6
|
4
|
3
|
2
|
1
|
7
|
9
|
|
предпоследняя
цифра шифра
|
Т
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
Пример.
В качестве примера рассмотрим САУ, передаточная функция которой имеет следующий
вид:
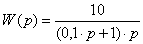 .
.
Известно, что изображение весовой функции L[g(t)]
любой линейной САУ есть ничто иное, как ее передаточная функция:
L[g(t)]
= 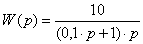 .
.
Для отыскания оригинала весовой функции g(t)
= L-1[W(p)]
разложим W(p)
на элементарные дроби, соответствующие передаточным функциям отдельных звеньев
системы САУ, и воспользуемся методом неопределенных коэффициентов для
определения неизвестных статических коэффициентов усиления этих звеньев
(коэффициенты А и В в знаменателе элементарных дробей):
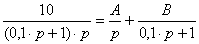 . (1)
. (1)
После приведения правой части выражения (1) к
общему знаменателю можно приравнять числители левой и правой частей полученного
уравнения:
10 = А∙(0,1∙р
+ 1) + В∙р = р∙(0,1∙А + В)
+ А (2)
Приравнивая коэффициенты левой и правой частей
уравнения (2) при одинаковых степенях р, получим систему двух уравнений из двух
неизвестных:
= А;
= 0,1∙А + В, откуда
А= 10; В
= - 0,1∙А = - 1.
Подставляя вычисленные значения коэффициентов А
и В в уравнение (1), получим:
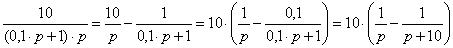 .
(3)
.
(3)
Переход от изображений элементарных функций f(p)
в операторной форме записи к их оригиналам, как функций времени f(t),
осуществляется, как правило, с использованием стандартных таблиц изображений,
приводимых в справочной литературе. Так, например:
оригинал L-1[1/р]
функции 1/р равен: L-1[1/р]
= 1.
оригинал L-1[1/(р
+ 10)] функции 1/(р + 10) равен: L-1[1/(р
+ 10)] = е -10∙t.
Заменив в правой части уравнения (3) изображения
элементарных функций на их оригиналы, получим искомое выражение для весовой
функции:
g(t)
= 10∙(1 - е -10∙t)
(4)
Задаваясь различными значениями t,
заполним таблицу расчетных значений и построим график g(t).
По известной весовой функции g(t)
можно найти переходную функцию h(t),
принимая во внимание, что h(t)
= 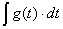 .
.
Изображение L[h(t)]
функции h(t)
можно получить путем умножения передаточной функции W(p)
исходной САУ на передаточную функцию 1/р идеального интегрирующего
звена, что соответствует включению последовательно с САУ интегрирующего звена.
L[h(t)]
= W(p)∙1/р
=  .
5)
.
5)
Разложим правую часть уравнения (5) на
элементарные дроби с тем, чтобы получить более простые изображения функций для
нахождения их оригиналов.
 =
=
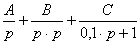 .
(6)
.
(6)
После приведения правой части выражения (6) к
общему знаменателю приравняем числители левой и правой частей полученного
уравнения:
10 = А∙р∙(0,1∙р
+1) + В∙(0,1∙р + 1) + С∙р2.
(7)
Приравнивая коэффициенты левой и правой частей
уравнения (7) при одинаковых степенях р, получим систему трех уравнений из трех
неизвестных:
10 = В;
= 0,1∙В + А;
= 0,1∙А + С, откуда
В= 10; А
= - 0,1∙В = - 1; С = - 0,1∙А = 0,1.
Подставляя вычисленные значения коэффициентов А,
В и С в уравнение (6), получим:
 .
(8)
.
(8)
Воспользовавшись известными таблицами
изображений, найдем оригиналы простейших функций:
L-1[1/р]
= 1;
L-1[1/р2]
= t;
L-1[1/(р
+ 10)] = е -10∙t.
Заменив в правой части уравнения (8) изображения
элементарных функций на их оригиналы, получим искомое выражение для переходной
функции:
h(t)
= 10∙[t
- 0,1∙(1 - е -10∙t)]
(9)
Задаваясь различными значениями t,
заполним таблицу расчетных значений и построим график h(t).
Этот результат можно получить путем
непосредственного интегрирования весовой функции g(t):
h(t)
= 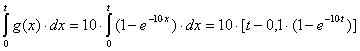
Задача 2. Расчет частотных
характеристик линейных САУ
Определить круговую частоту ω,
с которой устройство САУ, состоящее из последовательно включенных двух
апериодических и одного идеального интегрирующего звеньев, дает заданный сдвиг
по фазе между выходным и входным сигналами. При этом следует определить амплитуду
выходного сигнала Ym
на данной частоте, если известна амплитуда входного сигнала Xm.
Передаточная функция заданной САУ имеет
следующий вид:
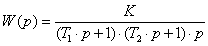 .
(10)
.
(10)
Исходные данные для решения задачи приведены в
табл. 2.
Таблица 2
Последняя
цифра шифра
|
Предпоследняя
цифра шифра
|
|
К
|
Т1,
с
|
Т2,
с
|
Хm
|
φ,
град
|
|
1
|
10
|
0,05
|
0,5
|
2
|
-
150
|
|
2
|
9
|
0,1
|
0,05
|
4
|
-
160
|
|
3
|
8
|
0,02
|
0,2
|
6
|
-
170
|
|
4
|
7
|
0,01
|
0,1
|
8
|
-
150
|
|
5
|
6
|
0,1
|
0,03
|
10
|
-
160
|
|
6
|
5
|
0,2
|
0,02
|
3
|
-
170
|
|
7
|
4
|
0,4
|
0,04
|
5
|
-
140
|
|
8
|
3
|
0,8
|
0,08
|
4
|
-
150
|
|
9
|
2
|
0,5
|
0,05
|
1
|
-
160
|
|
0
|
1
|
0,025
|
0,25
|
7
|
-
170
|
Пример.
По передаточной функции W(p),
представленной в операторной форме, найдем выражение для частотной передаточной
функции W(jω)
путем замены в выражении (10) оператора Лапласа р на комплексную
переменную jω.
W(jω)
= 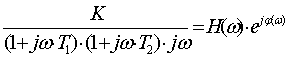 ,
(11)
,
(11)
где: Н(ω) = 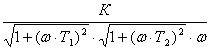 -
модуль частотной передаточной функции, представляющий собой
амплитудно-частотную характеристику (АЧХ) системы САУ;
-
модуль частотной передаточной функции, представляющий собой
амплитудно-частотную характеристику (АЧХ) системы САУ;
φ(ω) = - 90о
- arctg(ω∙T1)
- arctg(ω∙T2)
- аргумент частотной передаточной функции, представляющий собой фазочастотную
характеристику (ФЧХ) системы САУ.
Задаваясь значениями круговой частоты ω
с
шагом 1-2 рад/с определим значения функции φ(ω), занесем
их в таблицу расчетных значений и построим график ФЧХ, на котором проведем
горизонтальную прямую через точку, соответствующую заданному углу сдвига фаз φ,
до
пересечения с кривой ФЧХ. Через найденную точку пересечения проведем
горизонтальную прямую до пересечения с осью частот, на которой отметим искомую
круговую частоту ωи,
которая дает заданный табл. 2 сдвиг фазы φ(ωи)
= φ.
Подставляя найденное значение круговой частоты ωи
в выражение для модуля Н(ω) частотной
передаточной функции вычислим его значение Н(ωи).
Затем определяем искомую амплитуду выходного
сигнала, как
Ym
= Н(ωи)∙Xm.
Задача 3. Построение логарифмических
частотных характеристик и годографа АФЧХ
. Построить асимптотическую логарифмическую
амплитудно-частотную характеристику (ЛАЧХ) и логарифмическую фазочастотную
характеристику ЛФЧХ для линейной системы САУ, состоящей из четырех
последовательно включенных звеньев:
одного реального дифференцирующего звена с
передаточной функцией W1(р)
= К1∙(Т1∙р + 1);
двух апериодических звеньев первого порядка с
передаточными функциями W2(р)
= К2/(Т2∙р + 1) и W3(р)
= К3/(Т3∙р + 1);
одного идеального интегрирующего звена с
передаточной функцией К4/р.
Исходные данные приведены в табл. 3.
Таблица 3
|
Номер
варианта
|
Последняя
цифра шифра
|
Предпоследняя
цифра шифра
|
|
К
|
Т1,
с
|
Т2,
с
|
Т3,
с
|
|
1
|
100
|
0,125
|
0,2
|
0,02
|
|
2
|
50
|
0,1
|
0.2
|
0.01
|
|
3
|
40
|
0.2
|
0,5
|
0,01
|
|
4
|
20
|
0,5
|
1,0
|
0,05
|
|
5
|
10
|
0,8
|
1,5
|
0,05
|
|
6
|
4
|
0,5
|
2,0
|
0,1
|
|
7
|
1
|
0,8
|
5,0
|
0,2
|
|
8
|
0,5
|
0,5
|
5,0
|
0,1
|
|
9
|
0,2
|
0,4
|
4,0
|
0,04
|
|
0
|
10
|
0,1
|
2,0
|
0,5
|
По условиям задачи передаточная функция заданной
линейной САУ имеет следующий вид:
 , (12)
, (12)
где К = К1∙ К2∙
К3∙ К4.
2. Построить годограф АФЧХ W(jω)
заданной САУ.
Пример.
Найдем выражение для логарифмической АЧХ и ФЧХ, для чего сначала определим АФЧХ
системы по ее передаточной функции W(р),
заменяя в ней оператор Лапласа р на комплексную переменную jω.
W(jω)
= 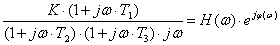 ,
(13)
,
(13)
где: Н(ω) = 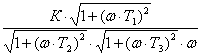 -
амплитудно-частотная характеристику (АЧХ) системы САУ;
-
амплитудно-частотная характеристику (АЧХ) системы САУ;
φ(ω) = [- 90о
+ arctg(ω∙T1)
- arctg(ω∙T2)
- arctg(ω∙T3)]
- аргумент частотной передаточной функции, представляющий собой фазочастотную
характеристику (ФЧХ) системы САУ.
По известной АЧХ определим выражение для ЛАЧХ L(ω):
L(ω)
= 20∙lgH(ω)
=
= 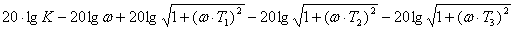 ,
дБ (14)
,
дБ (14)
Асимптотическую ЛАЧХ строим путем замены
непрерывной кривой ЛАЧХ несколькими прямыми отрезками, которые сопрягаются
между собой в точках, соответствующих круговым частотам ωс
(сопрягающим частотам), численно равным обратной величине от постоянных
времени, входящих в выражение (14). В нашем примере имеем три сопрягающие
частоты:
ωс1
= 1/Т1, рад/с; ωс2
= 1/Т2, рад/с; ωс3
= 1/Т3, рад/с.
Расположим сопрягающие частоты в порядке
возрастания при следующих исходных данных нашего примера: К = 10; Т1
= 0,4 с; Т2 = 2 с; Т3 = 0,02 с. Учитывая,
что чем больше значение постоянной времени, тем меньше значение сопрягающей
частоты, можем написать следующее неравенство:
ωс2
= 0,5 < ωс1
= 2,5 < ωс3
= 50 рад/с.
Выбираем масштаб для одной декады частот так,
чтобы в этом масштабе на оси абсцисс (частот) разместить три декады
логарифмической шкалы. Если значения всех сопрягающих частот больше или равно 1
(ωс
≥ 1рад/с), то в качестве границ декад выбираем круговые частоты 1, 10,
100 и 1000 рад/с. В том случае, когда значение хотя бы одной из сопрягающих
частот находится в диапазоне 0,1 ≤ ωс
< 1, то границы декад необходимо сместить влево на одну декаду, т.е. выбрать
0,1, 1, 10 и 100 рад/с.
В пределах каждой декады можно выделить
промежуточные значения частот, используя для этих целей логарифмическую шкалу.
Затем на логарифмической оси частот отмечаем точки, соответствующие сопрягающим
частотам ωс1,
ωс2,
ωс3, и
проводим через них вертикальные пунктирные линии. Ось ординат проводим через
частотную отметку 1 рад/с и выбираем соответствующий масштаб, исходя из
значения величины 20∙lgK,
так, чтобы можно было отложить значения (20∙lgK
+ 20) и (20∙lgK
- 40), дБ.
В нашем случае откладываем на оси ординат
следующие точки:
20∙lg10
= 20; 20∙lg10
+ 20 = 40; 20∙lg10
- 40 = -20 дБ.
С целью удобства построения асимптотической ЛАЧХ
выбираем масштаб 1 см на 10 дБ. Проводим через точку 20∙lgK
вправо от оси ординат прямую линию с наклоном -20 дБ на декаду, для чего
соединяем эту точку с точкой (20∙lgK
- 20), расположенной на частотной отметке 10 рад/с. Так как в нашем примере
первая по порядку следования сопрягающая частота ωс2
< 1, то продолжим эту прямую влево от оси ординат до пересечения с
вертикальной пунктирной линией, исходящей из точки 0,1 рад/с на оси частот.
Очевидно, что ордината точки пересечения равна (20∙lgK
+ 20) = 40 дБ.
На отрезке логарифмической оси частот 0,1 ≤
ω
≤ ωс2
асимптотическая ЛАЧХ описывается выражением: L(ω)
= 20∙lgK
- 20∙lgω и
представляет собой отрезок проведенной ранее прямой с наклоном -20 дБ/дек,
соединяющий точки ее пересечения с вертикальными пунктирными линиями,
проведенными из точек 0,1 и ωс2
и имеющими ординаты, соответственно: L(0,1)
= 20∙lg10 - 20∙lg0,1
= 40 дБ и L(ωс2)
= L(0,5) = 20∙lg10
- 20∙lg0,5 = (40 -
20∙lg5) дБ.
Первая сопрягающая частота ωс2
принадлежит инерционному звену, поэтому после этой частоты асимптотическая ЛАЧХ
на отрезке частотной оси ωс2
≤ ω ≤ ωс1
описывается выражением: L(ω)
= 20∙lgK
- 20∙lgω - 20∙lg(ω∙Т2)
и, следовательно, ее наклон увеличивается на -20 дБ/дек и становится равным -40
дБ/дек. Соединяя ординаты (40 - 20∙lg5)
в точке ωс2
= 0,5 рад/с с ординатой (- 20∙lg5)
в точке ω
= 10∙ωс2
= 5 рад/с пунктирной линией получим отрезок прямой с наклоном -40 дБ/дек,
который пересекает вертикальную пунктирную линию, соответствующую круговой
частоте ωс1
= 2,5 рад/с, в точке с ординатой L(ωс1)
= L(2,5) = 20∙lg10
- 20∙lg2,5 - 20∙lg(2,5∙2)
= (20 - 20∙lg12,5)
= (-20 lg1,25) дБ.
Соединяя ординату L(ωс2)
= (40 - 20∙lg5)
дБ сплошной прямой линией с ординатой L(ωс1)
= (-20∙lg1,25),
соответствующей точке пересечения наклонной пунктирной линии с вертикальной
пунктирной линией), получим на отрезке логарифмической оси частот ωс2
≤ ω ≤ ωс1 очередную
асимптоту ЛАЧХ с наклоном -40 дБ/дек.
Вторая сопрягающая частота ωс1
принадлежит дифференцирующему звену, поэтому после этой частоты асимптотическая
ЛАЧХ на отрезке частотной оси ωс1
≤ ω ≤ ωс3
описывается выражением: L(ω)
= 20∙lgK
- 20∙lgω - 20∙lg(ω∙Т2)
+ 20∙lg(ω∙Т1)
и, следовательно, ее наклон уменьшается на 20 дБ/дек и становится вновь равным
-20 дБ/дек. Соединяя пунктирной линией ординаты (-20∙lg1,25)
в точке ωс1
= 2,5 рад/с с ординатой (-20 - 20∙lg1,25)
в точке ω
= 10∙ωс1
= 25 рад/с получим отрезок прямой с наклоном -20 дБ/дек. Продолжим эту
наклонную прямую до пересечения с вертикальной пунктирной линией,
соответствующей круговой частоте ωс3
= 50 рад/с, в точке с ординатой L(ωс3)
= L(50) = 20∙lg10
- 20∙lg50 - 20∙lg(50∙2)
+ 20∙lg(50∙0,4)
= (-40 + 20∙lg4)
дБ. Соединяя ординату L(ωс1)
= (-20∙lg1,25) дБ
сплошной прямой линией с ординатой L(ωс3)
= (-40 + 20∙lg4),
соответствующей точке пересечения наклонной пунктирной линии с вертикальной
пунктирной линией), получим на отрезке логарифмической оси частот ωс1
≤ ω ≤ ωс3
очередную асимптоту ЛАЧХ с наклоном -20 дБ/дек.
Третья сопрягающая частота ωс3
принадлежит интегрирующему звену, поэтому после этой частоты асимптотическая
ЛАЧХ на отрезке частотной оси ω ≥ ωс3
описывается выражением: L(ω)
= 20∙lgK
- 20∙lgω - 20∙lg(ω∙Т2)
+ 20∙lg(ω∙Т1)
- 20∙lg(ω∙Т3)
и, следовательно, ее наклон вновь увеличивается на -20 дБ/дек и становится
равным -40 дБ/дек. Соединяя сплошной линией ординаты (-40 + 20∙lg4)
в точке ωс3
= 50 рад/с с ординатой (-80 + 20∙lg4)
в точке ω
= 10∙ωс3
= 500 рад/с получим асимптоту ЛАЧХ с наклоном -40 дБ/дек.
На рис. 1 показан график асимптотической ЛАЧХ,
построенный в соответствии с вышеприведенным алгоритмом.
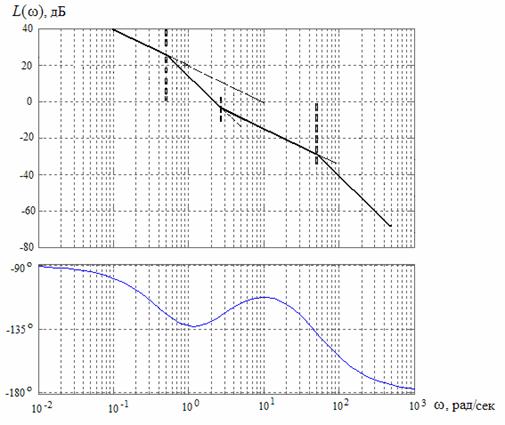
Рис. 1 Логарифмические асимптотическая
амплитудно-частотная и фазочастотная характеристики
Для построения логарифмической ФЧХ воспользуемся
выражением
φ(ω) = [- 90о
+ arctg(ω∙T1)
- arctg(ω∙T2)
- arctg(ω∙T3)].
Задаваясь численными значениями круговой частоты
от 0,1 до 100 рад/с (при ωс2
< 1) или от 1 до 1000 рад/с (при ωс2
≥ 1), заполнить соответствующий столбец табл. 4 значениями частотной
функции φ(ω)
и
выполнить ее построение так, как показано применительно к нашему примеру на
рис. 1. Для построения годографа АФЧХ необходимо также заполнить
соответствующие столбцы табл. 4, для чего необходимо произвести расчет модуля Н(ω)
частотной
передаточной функции W(jω)
и его проекций на мнимую (М(ω) = Н(ω)∙sin[φ(ω)])
и
действительную (N(ω)
= Н(ω)∙cos[φ(ω)]),
Н(ω)
= 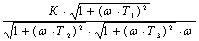
а также использовать данные выполненного ранее
расчета фазочастотной характеристики.
Таблица 4
|
ω,
рад/с
|
Н(ω)
|
N(ω)
|
М(ω)
|
φ(ω),
град
|
|
0,1
|
98,04
|
-16,40
|
-96,66
|
-99,63
|
|
.
. .
|
.
. .
|
.
. .
|
.
. .
|
.
. .
|
|
1
|
4,816
|
-3,270
|
-4,05
|
-132,77
|
|
.
. .
|
.
. .
|
.
. .
|
.
. .
|
.
. .
|
|
10
|
0,285
|
-0,109
|
-0,263
|
-112,48
|
|
.
. .
|
.
. .
|
.
. .
|
.
. .
|
.
. .
|
|
100
|
0.0089
|
-0,008
|
-0,0052
|
-154,57
|
Так как значение модуля Н(ω)
АФЧХ
обратно пропорционально круговой частоте, то для построения годографа следует
брать более высокие частоты с наиболее близкими относительно малыми значениями
модуля. Так, например, в нашем примере это частоты в диапазоне от 1 до 10
рад/с.
Откладываем на отрицательной действительной
полуоси комплексной плоскости значения проекции N(ω)
модуля
Н(ω),
а
на отрицательной полуоси - значения проекции М(ω)
этого
модуля, выбрав предварительно наиболее удобный масштаб. Затем через отложенные
точки проводим вертикальные или горизонтальные линии параллельно
противоположным координатным осям. Соединив точки пересечения этих линий с
началом координат, получим векторы АФЧХ, соответствующие частотам, при которых
вычислялись проекции их модуля на координатные оси. Соединив точки пересечения
этих линий между собой и с началом координат, получим фрагмент годографа АФЧХ,
представляющего собой кривую, которую описывает конец вектора W(jω)
при изменении частоты в выбранном диапазоне частот.
Другой способ построения годографа АФЧХ основан
на использовании полярных координат, для чего на комплексной плоскости через
начало ее координат проводят ряд линий под углами, взятыми из табл. 4 для
соответствующих частот, и на этих линиях откладывают в произвольно выбранном
масштабе значения модуля Н(ω) АФЧХ.
Соединяя затем концы векторов между собой и с началом координат, получим
искомый фрагмент годографа АФЧХ.
Фрагмент годографа АФЧХ, построенного на
основании данных табл. 4, показан на рис. 2.
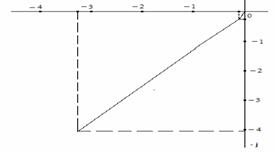
Рис. 2 Фрагмент годографа АФЧХ
Для построения ЛАЧХ, ЛФЧХ и годографа АФЧХ можно
воспользоваться программой МАТЛАБ. Пример фрагмента годографа АФЧХ,
построенного с применением этой программы, показан на рис. 3 для области частот
1 - 15 рад/с.
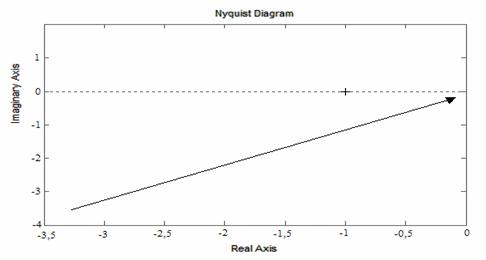
Рис. 3 Фрагмент годографа АФЧХ, построенного с
использованием программы МАТЛАБ
Лабораторная
работа № 1
ИССЛЕДОВАНИЕ ВРЕМЕННЫХ И ЧАСТОТНЫХ
ХАРАКТЕРИСТИК ЛИНЕЙНЫХ САУ
Цель работы:
изучение основных характеристик и параметров линейных систем автоматического
управления (САУ).
Теоретическая часть
Линейной САУ называется динамическая система,
поведение которой во времени описывается линейным дифференциальным уравнением n-степени:
an∙y(n)
+ a(n-1)∙y(n-1) + … + a1∙y(1)
+ a0∙y = bm∙x(m)
+ b(m-1)∙x(m-1) + … +
b1∙x(1)
+ b0∙x,
где a0,
b0,
… , an,
bn
- постоянные коэффициенты уравнения;
y
- регулируемая переменная (выходная функция САУ);
х - входная
переменная (функция) САУ;
y(i)
= diy(t)
/ dti
- i-я производная
функции у, (i = 1, … , n);
xj
= djx(t)
/ dtj
- j-я производная
функции x (j
= 1, … , m).
Так, например, подлежащие исследованию две
линейные САУ описываются следующими дифференциальными уравнениями,
соответственно, второй и третьей степени:
1) а2∙у(2)
+ а1∙у(1) = b0∙x;
) a3∙y(3)
+ а2∙у(2) = b0∙x.
Представленные выше уравнения запишем в
стандартной форме записи этих уравнений:
1) Т22∙у(2)
+ Т1∙у(1) = К∙x;
2) Т33∙y(3)
+ Т22∙у(2) = К∙x,
где К = b0
- статический коэффициент усиления САУ;
Т33
= а3, Т22 = а2,
Т1 = а1 - постоянные времени САУ,
характеризующие ее динамические свойства.
Дифференциальные уравнения можно представить в
операторной форме путем замены в них знака производной d/dt
оператором Лапласа р:
1) Т22∙р2∙у
+ Т1∙р∙у = [(Т2∙р)2
+ Т1∙р]∙ у = К∙x;
2) Т33∙р3∙у
+ Т22∙р2∙у =
[(Т3∙р)3 + (Т2∙р)2]∙у
= К∙x.
Отношение выходной величины у к входной
переменной x в
операторной форме есть передаточная функция W(p)
САУ:
W(p)
= y / x
= К / [(Т2∙р)2 + Т1∙р];
W(p)
= y / x
= К / [(Т3∙р)3 + (Т2∙р)2].
Для формализованного описания динамических
свойств САУ наряду с дифференциальными уравнениями и передаточной функцией W(p)используются
следующие способы:
временные функции, характеризующие изменение во
времени выходного сигнала определенного вида;
частотные характеристики, устанавливающие
зависимость между амплитудой и фазой входного и выходного гармонических
сигналов при изменении частоты входного сигнала.
К временным характеристикам динамических звеньев
относят переходную и весовую функции.
Переходная функция
h(t)
определяет характер изменения во времени выходного сигнала звена, если входной
сигнал является единичной ступенчатой функцией x(t)
= 1(t): y(t)
= h(t)∙1(t)
= h(t).
Весовая функция g(t)
(импульсная переходная функция) определяет характер изменения во времени
выходного сигнала звена, если входной сигнал является импульсной функцией x(t)
= δ(t)
= 1′(t), которая
представляет собой производную от единичной ступенчатой функции, т.е. ее кривая
на плоскости охватывает площадь, равную 1:
y(t)
= g(t)∙δ(t)
= g(t)∙1′(t)
Весовая функция является производной от
переходной функции. Следовательно, переходную функцию h(t)
можно определить путем аналитического и графоаналитического интегрирования
весовой функции g(t):
g(t)
= dh(t)/dt; h(t) = ∫ g(t)
∙ dt.
Изображением весовой функции L[g(t)],
т.е. представлением ее в операторной форме, является передаточная функция W(p):
1) L[g(t)]
= W(p) = K / [(T2∙р)2
+ Т1∙р];
2) L[g(t)]
= W(p) = К
/ [(Т3∙р)3
+ (Т2∙р)2].
С целью упрощения нахождения оригинала L-1[W(p)]
функции g(t),
представленной в операторной форме, относительно сложное изображение W(p)
можно разложить на сумму изображений более простых функций в виде элементарных
дробей, воспользовавшись методом неопределенных коэффициентов:
1)  ;
;
) 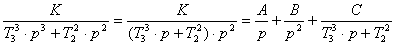 .
.
Приведя правую часть полученных выражений к
общему знаменателю, получим:
1) 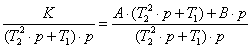 ;
;
) 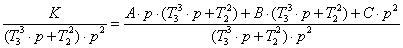 .
.
Так знаменатели левой и правой частей выражений
равны, то, соответственно, равны и их числители, т.е.:
) 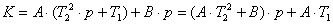 ;
;
)  .
.
Приравняем коэффициенты при одинаковых степенях
оператора Лапласа р левой и правой частей полученных формул:
1) К = А∙Т1;
0 = А∙Т22 + В;
) К = В∙Т22;
0 = А∙Т22 + В∙Т33;
0 = А∙Т33 + С.
Решая систему уравнений (1) и (2), получим:
1) А
= К / Т1; В = - А∙Т22
= - К∙Т22 / Т1;
2) В
= К / Т22; А = - В∙Т33
/ Т22 = - К∙Т33
/ (Т22)2;
С = - А∙Т33
= К∙(Т33 / Т22)2.
Подставляя значения коэффициентов А, В и С в
соответствующие исходные формулы, получим:
1) 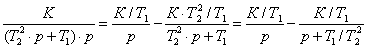 =
=
= 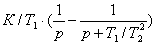 ;
;
) 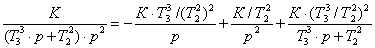 =
=
= 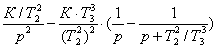 =
=
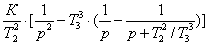 .
.
Оригиналы изображений элементарных функций имеют
следующий вид:
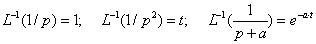 .
.
Заменяя в формулах 1) и 2) соответствующие
изображения элементарных функций на их оригиналы, получим следующие выражения
для весовых функций линейных САУ:
1) g(t)
= 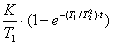 ;
2) g(t) =
;
2) g(t) = 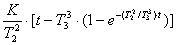 .
.
Так как переходная функция h(t)
есть интеграл от весовой функции g(t),
то найти ее можно либо путем непосредственного интегрирования функции g(t),
либо путем нахождения сначала изображения L[h(t)]
функции h(t),
а затем ее оригинала. Изображение переходной функции можно получить путем
умножения передаточной функции (изображения L[g(t)]
весовой функции) на передаточную функцию идеального интегрирующего звена со
статическим коэффициентом усиления, равным 1. Рассмотрим в качестве примера САУ
с передаточной функцией W(p)
= К / [(Т2∙р)2 + Т1∙р]:
L[h(t)]
= W(p)∙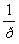 =
= 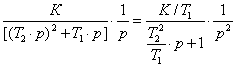 .
.
Разложим полученное изображение передаточной
функции на сумму изображений более простых функций в виде элементарных дробей,
воспользовавшись методом неопределенных коэффициентов по аналогии с ранее рассмотренными
примерами:
L[h(t)]
= 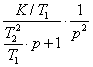 =
=
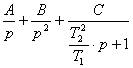 .
.
Найдем значения коэффициентов А, В
и С:
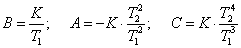 .
.
Находим оригиналы элементарных функций:
L-1(1/p)
= 1; L-1(1/p2) = t; L-1[(T1
/ T22) / (p + T1 / T22)]
= [(T1 / T22)∙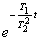 .
.
Используя полученные выражения, находим оригинал
искомой передаточной функции:
h(t)
= 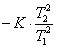 +
+
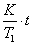 +
+
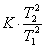 ∙
∙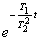 =
=
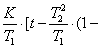
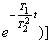 .
.
Частотные характеристики
САУ характеризуют реакцию системы на синусоидальное входное воздействие в
установившемся режиме.
К частотным характеристикам относятся:
АФЧХ - амплитудно-фазовая частотная
характеристика;
АЧХ - амплитудно-частотная характеристика;
ФЧХ - фазовая частотная характеристика;
ЛАЧХ - логарифмическая АЧХ;
ЛФЧХ - логарифмическая ФЧХ.
АФЧХ представляет собой частотную передаточную
функцию W(jω),
которая получается путем замены в передаточной функции W(p)
оператора Лапласа p
на комплексную переменную jω.
АФЧХ W(jω)
можно представить в виде вектора на комплексной плоскости с координатами [M(ω),
N(ω)]
или в полярных координатах Н(ω) и
φ(ω),
которые являются соответственно АЧХ и ФЧХ:
W(jω)
= N(ω)
+ jM(ω)
= Н(ω)∙еjφ(ω).
(1)
Здесь: Н(ω)
- АЧХ, которая представляет собой зависимость значения модуля вектора W(jω)
от круговой частоты ω;
φ(ω)
- ФЧХ, которая представляет собой зависимость аргумента вектора W(jω)
от круговой частоты ω;
N(ω)
= Н(ω)∙cosφ(ω)
- проекция вектора W(jω)
на вещественную ось комплексной плоскости;
M(ω)
= Н(ω)∙sinφ(ω)
- проекция вектора W(jω)
на мнимую ось комплексной плоскости;
При изменении частоты ω
от нуля до бесконечности конец вектора W(jω)
вычерчивает кривую в комплексной плоскости, которая называется годографом АФЧХ.
Определим в качестве примера частотную
передаточную функцию для САУ с передаточной функцией в операторной форме W(p)
= К / [(Т2∙р)2 + Т1∙р],
которую для удобства дальнейших преобразований представим в виде:
W(p)
= К / [(Т2∙р)2 + Т1∙р]
= К1 / [(T∙p
+ 1)∙p],
где К1 = К / Т1;
Т = (Т2)2 / Т1.
Произведя замену оператора Лапласа р на
комплексную переменную jω,
получим:
W(jω)
= К1 / [(jωT
+ 1)∙jω]
=  =
=
= 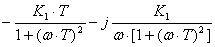 .
(2)
.
(2)
Из выражения (2) получаем формулы для нахождения
модуля Н(ω) и
аргумента φ(ω)
вектора АФЧХ, а также его проекций на вещественную N(ω)
и мнимую М(ω) оси:
Н(ω)
= 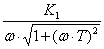 ;
φ(ω)
= - [90o + arctg(ω∙T)];
;
φ(ω)
= - [90o + arctg(ω∙T)];
N(ω)
= 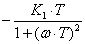 ;
М(ω) =
;
М(ω) =  .
(3)
.
(3)
Фазовую частотную характеристику φ(ω)
можно найти также из следующего соотношения: φ(ω)
= arctg[М(ω)
/ N(ω)]
= -[180o
- arctg(1/ω∙T
)].
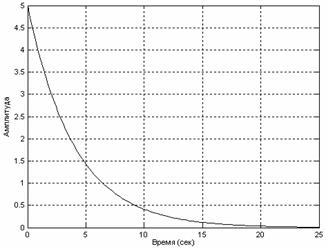
Рис. 1 График весовой функции g(t)
системы САУ, описываемой передаточной функцией 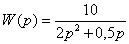
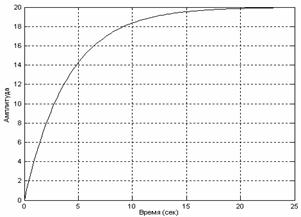
Рис. 2 График переходной функции h(t)
системы САУ, описываемой передаточной функцией 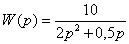
Лабораторная
работа № 2
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ
САУ
Цель работы:
изучение особенностей практического использования алгебраических и частотных
критериев устойчивости для анализа динамики линейных САУ 2-го и 3-го порядков.
Теоретическая часть
САУ называется устойчивой, если с течением
времени выходная величина стремится к установившемуся значению при постоянном
значении входного сигнала. Линейная САУ называется неустойчивой, если выходная
величина неограниченно возрастает с течением времени.
Система САУ будет устойчива, если:
3) все корни pi
характеристического уравнения являются действительными отрицательными числами (pi
<
0);
4) если имеется пара комплексных и
сопряженных корней типа pi,i+1
= α +_ jβ.
Характеристическое уравнение можно получить,
приравняв знаменатель передаточной функции САУ, приведенной к стандартному
виду, к нулю.
Как правило, на устойчивость и показатели качества
исследуются замкнутые системы САУ с коэффициентом обратной связи Кос,
равным 1, рис. 3.
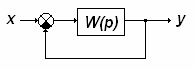
Рис. 3 Структурная схема замкнутой САУ
Передаточная функция замкнутой САУ Wз
имеет следующий вид:
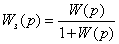 , где W(p)
- передаточная функция разомкнутой САУ.
, где W(p)
- передаточная функция разомкнутой САУ.
Найдем в качестве примера передаточную функцию
замкнутой САУ второго порядка, полученную введением цепи обратной связи в
разомкнутую систему с передаточной функцией
W(p)
= 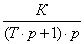 .
Wз
=
.
Wз
= 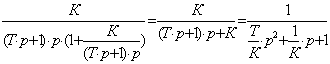 .
(4)
.
(4)
Формулу (4) для передаточной функции Wз
представим в стандартном виде:
Wз
= 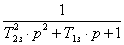 ,
(5)
,
(5)
где 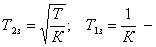 постоянные
времени замкнутой САУ.
постоянные
времени замкнутой САУ.
Преобразуем выражение (5) к более удобному виду
для оценки типа динамического звена, описываемого данным выражением:
Wз
= 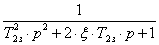 ,
(6)
,
(6)
где ξ
= 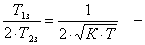 коэффициент
демпфирования, позволяющий определить тип динамического звена второго порядка
(при ξ
< 1 - колебательное звено, при ξ
≥ 1 - апериодическое звено второго порядка).
коэффициент
демпфирования, позволяющий определить тип динамического звена второго порядка
(при ξ
< 1 - колебательное звено, при ξ
≥ 1 - апериодическое звено второго порядка).
Найдем корни характеристического уравнения,
приравняв знаменатель передаточной функции (6) нулю:
Так как действительная часть корней
характеристического уравнения носит отрицательный характер при любых
положительных значениях ξ
и Т2з, то можно утверждать, что все линейные САУ второго
порядка представляют собой устойчивые системы. Из выражения (7) следует, что
при 0 ≤ ξ < 1 характеристическое
уравнение динамического звена второго порядка имеет два сопряженных комплексных
корня и, соответственно, переходная функция h(t)
носит колебательный характер; при ξ ≥ 1 - два
отрицательных вещественных корня, что соответствует передаточной функции САУ,
состоящей из последовательного соединения двух апериодических звеньев первого
порядка с постоянными времени, равными:
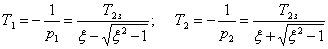 .
(8)
.
(8)
При исследовании замкнутых САУ более высокого
порядка используются алгебраические критерии Рауса, Гурвица или Неймарка,
которые с помощью выполнения ряда алгебраических операций над коэффициентами
характеристического уравнения позволяют косвенно оценить наличие или отсутствие
корней характеристического уравнения, удовлетворяющих условиям устойчивости
САУ.
К частотным критериям устойчивости замкнутых
систем САУ относятся критерии Найквиста и Михайлова. Оценка устойчивости
замкнутых САУ с использованием критериев Найквиста производится на основе
анализа АФЧХ или ЛАЧХ (логарифмический критерий Найквиста).
Согласно частотному критерию Найквиста для того,
чтобы замкнутая САУ была устойчивой необходимо и достаточно, чтобы годограф ее
АФЧХ W(jω)
при разомкнутой цепи обратной связи не охватывала в комплексной плоскости точку
с координатами (- 1; j0).
Рассмотрим применение частотного критерия
Найквиста на примере замкнутой САУ с передаточной функцией Wз(р):
Wз(р)
= W(р) /
[1 + W(р)],
где
W(р)
= 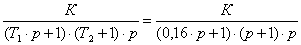 .
.
При замене переменной р на jω
частотная передаточная функция разомкнутой САУ примет вид:
W(jω)
= 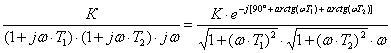 =
=
= 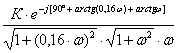 .
.
На рис. 4 представлен фрагмент графика функции W(jω)
при К = 1, иллюстрирующий момент пересечения годографом АФЧХ
действительной отрицательной полуоси. Ввиду того, что точка пересечения
приведенного графика с действительной отрицательной полуосью находится правее
точки с координатами (-1, j0),
то в соответствии с частотным критерием Найквиста при выбранном значении
статического коэффициента усиления разомкнутая САУ, будучи охвачена жесткой
отрицательной обратной связью, сохранит свою устойчивость.
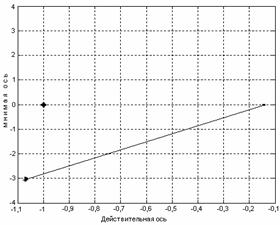
Рис. 4. Фрагмент графика годографа АФЧХ
разомкнутой САУ третьего порядка при К = 1, соответствующий устойчивому
состоянию замкнутой САУ
При увеличении коэффициента К точка
пересечения годографа функции W(jω)
с отрицательной действительной полуосью будет смещаться влево и при превышении
граничного значения Кгр, соответствующего границе
устойчивости САУ, будет находиться левее точки с координатами (-1, j0),
как это показано для рассмотренной ранее САУ на рис. 5., но при К = 15.
Следовательно, при значении статического коэффициента усиления, равном 15, и
охвате разомкнутой САУ жесткой отрицательной обратной связью, полученная
замкнутая САУ будет неустойчивой.
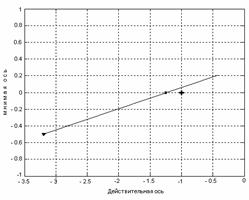
Рис. 5 Фрагмент графика годографа АФЧХ
разомкнутой САУ третьего порядка при К = 15, показывающий на
неустойчивость замкнутой САУ
Полученные выводы, как увидим ниже, полностью
подтвердятся и в случае использования логарифмического критерия устойчивости
Найквиста.
Логарифмическая амплитудная частотная
характеристика (ЛАЧХ) представляет собой зависимость логарифмической функции
вида L(ω)
= 20lg[H(ω)]
от круговой частоты. Однако при построении графика ЛАЧХ по оси абсцисс
откладывают круговую частоту в логарифмическом масштабе lg(ω),
а по оси ординат значение L(ω)
в дБ. Так, например, L(ω)
= 20 означает, что при прохождении сигнала через звено на данной частоте его
амплитуда увеличивается в 10 раз.
ЛФЧХ - это график зависимости частотной функции φ(ω)
от десятичного логарифма частоты lg(ω).
При его построении по оси абсцисс откладывают частоту в логарифмическом
масштабе, по оси ординат откладывают φ(ω)
в градусах или радианах.
В обоих случаях за единицу масштаба по оси
абсцисс принимается декада - это частотный интервал, соответствующий изменению
частоты в 10 раз. Ось ординат при построении этих характеристик проводят часто
через точку (ω = 1)
которая соответствует началу координат lg(1)
= 0.
Для оценки устойчивости САУ по логарифмическому
критерию Найквиста используются графики ЛАЧХ и ЛФЧХ разомкнутой системы САУ.
Система САУ считается устойчивой, если при φ(ω)
= - 180о кривая ЛАЧХ находится в отрицательной области: L(ω)
= 20lg[H(ω)]
< 0. Систему САУ можно считать также устойчивой, если на частоте среза ωср,
при которой справедливо равенство L(ωср)
= 20lg[H(ωср)]
= 0, значение аргумента φ(ωср)
> - 180o.
При оценке устойчивости САУ необходимо
определить запас устойчивости, т.е. степень удаленности системы от границы
устойчивости. В качестве меры запаса устойчивости используется запас
устойчивости по амплитуде h(ω)
и запас устойчивости по фазе ψ(ωср).
Запас устойчивости САУ по амплитуде h(ω)
позволяет оценить критическое значение коэффициента усиления системы, при
котором она окажется на грани устойчивости, и определяется на частоте ωу,
при которой φ(ωу)
= - 180о: h(ωу)
= - L(ωу),
рис. 6.
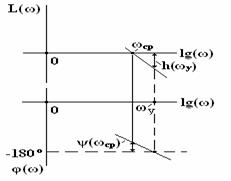
Рис. 6 Определение запаса устойчивости САУ по
амплитуде и фазе на основе использования логарифмического Критерия Найквиста
Запас устойчивости по фазе ψ(ωср)
определяется на частоте среза ωср,
как: ψ(ωср)
= φ(ωср)
+ 180о и показывает, на какую величину должно возрасти запаздывание
по фазе в системе на частоте среза ωср,
чтобы система оказалась на грани устойчивости.
Задание к лабораторной работе № 2
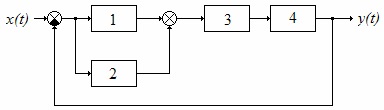
Рис. 7 Структурная схема замкнутой линейной САУ
Лабораторная
работа № 3
ИССЛЕДОВАНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА
ЛИНЕЙНЫХ САУ.
Цель работы:
определение основных показателей качества регулирования САУ с использованием
прямых и косвенных критериев.
Теоретическая часть
Наряду с обеспечением устойчивости САУ, как
одного из основных показателей работоспособности системы, необходимо обеспечить
требуемое качество переходного процесса при ступенчатых воздействиях, которое
оценивают по переходной функции h(t),
представляющей собой реакцию системы (у(t)
= h(t))
на входное единичное воздействие (х(t)
= 1(t)).
Основными показателями качества переходного
процесса являются:
. Время регулирования tp,
которое представляет собой отрезок времени от момента появления единичного
скачка входной величины до момента достижения регулируемой величиной уровня,
равного 0,95 от установившегося значения hу
= h(t
→
∞), т.е. y(tp)
= 0,95∙ hу.
. Максимальное перерегулирование
Δh, которое
представляет собой максимальное отклонение регулируемой величины относительно
установившегося значения hу
(Δh = hmax
- hy),
что характерно для затухающего колебательного процесса. Для оценки
перерегулирования обычно используют относительную величину σ:
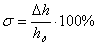 .
.
3. Количество перерегулирований
δ определяется
количеством максимумов регулируемой величины, превышающих значение m,
равное: m = 1,05∙hу.
. Частота колебаний fк
регулируемой величины обратно пропорциональна интервалу времени Тк
между соседними максимумами (периоду частоты): fк
= 1/Тк.
. Число колебаний n
определяется числом целых периодов Тк за время переходного
процесса tп,
окончание которого соответствует моменту времени, когда переходная функция h(t)
входит в диапазон значений регулируемой величины 0,95∙ hу
- 1,05∙ hу
и далее при t
≥
tп
из него не выходит, стремясь к значению hу.
. Колебательность системы ξ
оценивают,
как отношение двух соседних максимумов: ξ = h(t1
+ Тк)/ h(t1),
где t1
соответствует первому максимуму.
. Максимальная скорость vmax
изменения регулируемой величины определяется графически как тангенс угла
наклона переходной характеристики в точке первого пересечения с линией
установившегося значения hу:
vmax
= tgα
= dh/dt.
. Статическая погрешность
εст замкнутой САУ в
установившемся режиме есть разность между установившимися значениями сигналов
на входе (x(t)
= 1) и выходе (y(t)
= hу):
εст = 1- hу).
Наряду с переходной функцией h(t)
для оценки качества переходного процесса широко применяются косвенные критерии,
к которым относится частотная оценка.
Для указанной оценки используется относительная
АЧХ в виде зависимости отношения H(ω)/К
от частоты ω: Δ(ω) = H(ω)/К,
рис. 8.
Относительная АЧХ на резонансной частоте ωmax
имеет максимум, соответствующий значению Δ(ωmax)
= Δmax.
При дальнейшем увеличении частоты система вследствие своей инерционности не
успевает реагировать на колебания больших частот и Δ(ω)
резко
«падает».
Установлено, что чем больше Δmax,
тем более колебательным является переходной процесс. Отношение Δmax/Δ(0)
= М
называют показателем колебательности. Для статических САУ, не содержащих в
своей передаточной функции множителя (1/р), Δ(0) = 1, поэтому
М
= Δmax.
Обычно М = 1,2 - 1,5. При малых М система имеет большое время
регулирования. При больших М увеличивается перерегулирование и система
приближается к границе устойчивости.
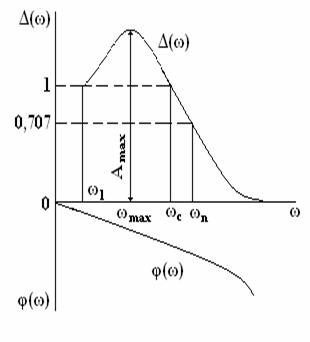
Рис. 8 Относительная амплитудно-частотная
характеристика САУ
Кроме частоты ωmax
характерными частотами АЧХ являются частота среза ωс
и полоса пропускания ωп.
Частота среза замкнутой системы ωс
определяется на уровне Δ(ω) = 1. Для
статических САУ частота среза определяет диапазон вынужденных колебаний,
которые система пропускает без ослабления. На этой частоте амплитуды входного и
выходного колебаний равны. Полоса пропускания ωп
замкнутой системы определяется на уровне Δ(0)/√2 =
0,707. Так
как в диапазоне частот (ωс
- ωп) АЧХ резко
«падает», то числовые значения частот ωс
и ωп
близки.
Полоса пропускания влияет на точность и
быстродействие системы. С увеличением полосы пропускания быстродействие системы
растет. Чем больше полоса пропускания, тем больший спектр частот входного
сигнала передается без искажений.
О качестве регулирования можно судить также по
ЛАЧХ. Установлено, что для удовлетворительного качества регулирования участок
средних частот, на котором ЛАЧХ пересекает ось абсцисс, должен имеет наклон
минус 20 дБ/декаду. Протяженность этого участка влияет на перерегулирование. С
его увеличением уменьшается колебательность переходного процесса. Приемлемое
качество переходного процесса имеет место, если протяженность этого участка
примерно равна декаде. Время регулирования tp
зависит от частоты среза, при которой ЛАЧХ пересекает ось абсцисс. Чем больше
частота среза, тем меньше tp.
Задание к лабораторной работе № 3
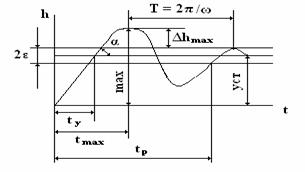
Рис. 9 Пример переходной характеристики
колебательной системы
БИЛЕТ 1
1. Понятие об управлении и объекте управления.
2. Методы коррекции систем автоматического
управления.
. Задача.
БИЛЕТ 2
1. Функциональная схема системы автоматического
управления. Назначение основных элементов схемы.
. Показатели качества систем автоматического
управления.
3. Задача.
БИЛЕТ 3
1. Классификация САУ по принципу действия.
. Апериодическое звено систем автоматического
управления. Основные характеристики.
. Задача.
БИЛЕТ 4
1. Структурная схема САУ по отклонению.
. Интегрирующее звено систем автоматического
управления. Основные характеристики.
. Задача.
БИЛЕТ 5
1. Структурная схема САУ по возмущению.
2. Колебательное звено систем автоматического
управления.
Основные характеристики.
3. Задача.
БИЛЕТ 6
1. Структурная схема САУ с комбинированным
управлением.
. Дифференцирующее звено систем
автоматического управления. Основные характеристики.
. Задача.
БИЛЕТ 7
1. Структурная схема адаптивной системы
автоматического управления.
2. Понятие об устойчивости систем
автоматического регулирования. Алгебраические критерии устойчивости.
3. Задача.
БИЛЕТ 8
1. Классификация САУ по назначению.
. Частотный критерий устойчивости систем
автоматического регулирования Михайлова.
. Задача.
БИЛЕТ 9
1. Основные способы формализованного описания
динамических свойств элементов САУ.
. Последовательное соединение динамических
звеньев САУ.
3. Задача.
БИЛЕТ 10
1. Временные функции динамических звеньев САУ.
2. Параллельное соединение звеньев САР.
. Задача.
БИЛЕТ 11
1. Переходные процессы в САУ и их
характеристики.
2. Частотные оценки показателей качества
САУ.
. Задача.
БИЛЕТ 12
1. Передаточная функция замкнутой САУ.
2. Электрические аналоги апериодического
звена.
. Задача.
БИЛЕТ 13
1. Понятие о статических и астатических САУ.
2. Электрические аналоги интегрирующего
звена.
. Задача.
БИЛЕТ 14
1. Основные понятия и определения систем
автоматического управления. Классификация САУ.
. Электрические аналоги колебательного звена.
3. Задача.
БИЛЕТ 15
1. Частотные характеристики САУ.
2. Электрические аналоги дифференцирующего
звена.
. Задача.
БИЛЕТ 16
1. Частотные характеристики апериодического
звена.
2. Корневые оценки показателей качества САУ.
. Задача.
БИЛЕТ 17
1. Частотные характеристики интегрирующего
звена.
2. Последовательные корректирующие
устройства.
. Задача.
БИЛЕТ 18
1. Частотные характеристики колебательного
звена.
2. Параллельные корректирующие устройства.
. Задача.
БИЛЕТ 19
1. Частотные характеристики дифференцирующего
звена.
2. Ошибки статических САУ при типовых
воздействиях.
. Задача.
БИЛЕТ 20
1. Методика построения асимптотической ЛАЧХ
системы автоматического управления.
. Ошибки астатических САУ при типовых
воздействиях.
3. Задача.
БИЛЕТ 21
1. Передаточная функция замкнутой САУ при
отрицательной жесткой обратной связи.
. Понятие об установившемся процессе и
точности САУ.
3. Задача.
БИЛЕТ 22
1. Передаточная функция замкнутой САУ при
отрицательной гибкой обратной связи.
. Частотный и логарифмический критерии
устойчивости Найквиста.
3. Задача.
3. Примерный перечень вопросов к зачетам для
студентов III курса:
1) Понятие об управлении и объекте управления.
) Функциональная схема системы
автоматического управления. Назначение основных элементов схемы.
) Классификация САУ по принципу действия.
4) Структурная схема САУ по отклонению.
) Структурная схема САУ по возмущению.
) Структурная схема САУ с комбинированным
управлением.
7) Структурная схема адаптивной системы
автоматического управления.
) Классификация САУ по назначению.
) Основные понятия и определения систем
автоматического управления. Классификация САУ.
10) Основные способы формализованного
описания динамических свойств элементов САУ.
11) Временные функции динамических звеньев САУ.
12) Переходные процессы в САУ и их
характеристики.
) Передаточная функция замкнутой САУ.
) Понятие о статических и астатических
САУ.
) Частотные характеристики САУ.
) Частотные характеристики
апериодического звена.
) Частотные характеристики интегрирующего
звена.
) Частотные характеристики колебательного
звена.
) Частотные характеристики
дифференцирующего звена.
20) Методика построения асимптотической ЛАЧХ
системы автоматического управления.
21) Передаточная функция замкнутой САУ при
отрицательной жесткой обратной связи.
) Передаточная функция замкнутой САУ при
отрицательной гибкой обратной связи.
) Апериодическое звено систем
автоматического управления. Основные характеристики.
24) Электрические аналоги апериодического
звена.
) Интегрирующее звено систем автоматического
управления. Основные характеристики.
) Электрические аналоги интегрирующего звена.
27) Колебательное звено систем
автоматического управления.
Основные характеристики.
28) Электрические аналоги колебательного
звена.
) Дифференцирующее звено систем
автоматического управления. Основные характеристики.
) Электрические аналоги дифференцирующего
звена.
) Понятие об устойчивости систем
автоматического регулирования. Алгебраические критерии устойчивости.
32) Частотный критерий устойчивости систем
автоматического регулирования Михайлова.
33) Частотный и логарифмический критерии
устойчивости Найквиста.
34) Последовательное соединение динамических
звеньев САУ.
) Параллельное соединение звеньев САР.
) Показатели качества систем
автоматического управления.
) Частотные оценки показателей качества
САУ.
) Корневые оценки показателей качества
САУ.
) Понятие об установившемся процессе и
точности САУ.
) Ошибки статических САУ при типовых
воздействиях.
) Ошибки астатических САУ при типовых
воздействиях.
) Методы коррекции систем автоматического
управления.
) Последовательные корректирующие
устройства.
44) Параллельные корректирующие устройства.
Примерный
перечень задач для итогового контроля знаний студентов III
курса
ЗАДАЧА 1
Построить график переходной функции h(t)
интегрирующего звена при изменении t
от 0 до 5 сек, если К = 10.
ЗАДАЧА 2
Построить график переходной функции h(t)
апериодического звена, если К = 10, а Т = 0,1.
ЗАДАЧА 3
Определить модуль и аргумент частотной
передаточной функции системы САУ, состоящей из двух последовательно включенных
апериодических звеньев. Параметры первого звена: Т1 и К1, второго звена: Т2 и
К2.
ЗАДАЧА 4
Найти оригинал весовой функции g(t)
системы САУ, передаточная функция которой описывается выражением:
W(p)
=  .
.
ЗАДАЧА 5
Найти изображение и оригинал переходной функции h(t)
системы САУ, передаточная функция которой описывается выражением:
W(p)
=  .
.
ЗАДАЧА 6
Построить асимптотическую ЛАЧХ для системы САУ,
состоящей из двух последовательно соединенных интегрирующих звеньев. Параметры
первого звена: К1 = 10, второго звена: К2 = 5.
ЗАДАЧА 7
Построить асимптотическую ЛАЧХ для системы САУ,
состоящей из двух последовательно соединенных апериодических звеньев. Параметры
первого звена: К1 = 10, Т1 = 0,01; второго звена: К2 = 5, Т2 = 0,05.
ЗАДАЧА 8
Построить асимптотическую ЛАЧХ для системы САУ,
состоящей из двух последовательно соединенных интегрирующего и апериодического
звеньев. Параметры интегрирующего звена: К1 = 10; апериодического звена: К2 =
5, Т2 = 0,05.
ЗАДАЧА 9
Построить АФЧХ и логарифмическую ФЧХ для системы
САУ, состоящей из двух последовательно соединенных интегрирующих звеньев.
Параметры первого звена: К1 = 10, второго звена: К2 = 5.
ЗАДАЧА 10
Построить АФЧХ и логарифмическую ФЧХ для системы
САУ, состоящей из двух последовательно соединенных апериодических звеньев.
Параметры первого звена: К1 = 10, Т1 = 0,01; второго звена: К2 = 5, Т2 = 0,05.
ЗАДАЧА 11
Построить АФЧХ и логарифмическую ФЧХ для системы
САУ, состоящей из двух последовательно соединенных интегрирующего и
апериодического звеньев. Параметры интегрирующего звена: К1 = 10;
апериодического звена: К2 = 5, Т2 = 0,05.
ЗАДАЧА 12
Определить частоту ω1,
на
которой устройство с передаточной функцией
W(p)
= 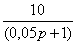 ,
,
дает сдвиг по фазе между входным и выходным
сигналами, равный ψ(ω1) = - 45о.
ЗАДАЧА 13
Определить амплитуду Y(ω1)
выходного
сигнала на частоте ω1, при которой
устройство с передаточной функцией
W(p)
= 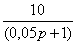 ,
,
дает сдвиг по фазе между входным и выходным
сигналами, равный ψ(ω1) = - 45о.
Амплитуда входного сигнала постоянна и равна Х = 2.
ЗАДАЧА 14
Передаточная функция разомкнутой статической САУ
в операторной форме имеет вид:
W(p)
= 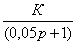 .
.
Определить ошибку регулирования замкнутой
системы с жесткой отрицательной обратной связью (Кос = 1) при подаче
ступенчатого сигнала Хо = 2 при различных значениях К = 1; 10 и 100.
ЗАДАЧА 15
Передаточная функция разомкнутой астатической
САУ в операторной форме имеет вид:
W(p)
= 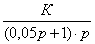 .
.
Определить ошибку регулирования замкнутой
системы с жесткой отрицательной обратной связью (Кос = 1) при подаче
линейно возрастающего сигнала Хо = 2·t
при различных значениях К = 1; 10 и 100.
ЗАДАЧА 16
Система автоматического управления состоит из
апериодического звена, охваченного жесткой обратной связью с коэффициентом
обратной связи Кос = 10. Требуется оценить, как повлияло введение указанной
связи на статический коэффициент усиления Кз и постоянную времени Тз замкнутой
системы, если известны статический коэффициент усиления апериодического звена К
= 10 и его постоянная времени Т = 0,01. Проиллюстрировать рисунком.
ЗАДАЧА 17
Система автоматического управления состоит из
апериодического звена, охваченного гибкой обратной связью с коэффициентом
обратной связи Кос(р) = рК2, где К2 = 10.
Требуется оценить, как повлияло введение указанной связи на статический
коэффициент усиления Кз и постоянную времени Тз замкнутой системы, если
известны статический коэффициент усиления апериодического звена К = 5 и его
постоянная времени Т = 0,05. Проиллюстрировать рисунком.
ЗАДАЧА 18
Оценить с помощью частотного критерия Найквиста
устойчивость САУ, описываемую дифференциальным уравнением в операторной форме:
(0,04p2
+ 2p + 5)·у = 10·х.
ЗАДАЧА 19
Представить динамическое звено с передаточной
функцией
W(р) = 100/(0,01р2
+ 0,5р +1)
в виде последовательного соединения двух
апериодических звеньев и определить постоянные времени каждого звена.
ЗАДАЧА 20
Построить асимптотическую ЛАЧХ дифференцирующего
звена с передаточной функцией: W(р)
= К·р/(1 + рТ).
ЗАДАЧА 21
Построить асимптотическую ЛАЧХ апериодического
звена при К = 10 и Т = 0,01.
ЗАДАЧА 22
Оценить с помощью частотного критерия Михайлова
устойчивость САУ, описываемую дифференциальным уравнением в операторной форме:
(0,04p3
+ p2 +
2p + 5)·у = 10·х.