Оптимизация процессов деревообработки на моделях линейного и нелинейного программирования
БРЯНСКАЯ
ГОСУДАРСТВЕННАЯ
ИНЖЕНЕРНО-ТЕХНОЛОГИЧЕСКАЯ
АКАДЕМИЯ
Кафедра
технологии деревообработки
Пояснительная
записка
к курсовой
работе по дисциплине
«Математическое
моделирование и оптимизация процессов деревообработки»
ОПТИМИЗАЦИЯ
ПРОЦЕССОВ ДЕРЕВООБРАБОТКИ НА МОДЕЛЯХ ЛИНЕЙНОГО И НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Разработал
А.Ю. Видалко
Брянск 2010
Содержание
Введение
.Оптимизация
решения на моделях нелинейного программирования
. Решение
задачи линейного программирования графическим методом
3. Двойственная
задача линейного программирования
4.
Оптимизация раскроя древесностружечных плит на заготовки
5.
Транспортная задача и задачи транспортного типа
6.
Упорядочение последовательности запуска n на m
станках
7.
Обоснование решений на моделях СПУ
Заключение
Список
использованных источников
Введение
В наше время все больше внимания уделяется вопросам организации и
управления на производстве. И это закономерно.
Быстрое развитие и усложнение техники, небывалое расширение масштабов
проводимых мероприятий и спектра их возможных последствий, внедрение
автоматизированных систем управления (АСУ) во все области практики - все это
приводит к необходимости анализа сложных целенаправленных процессов под углом
зрения их структуры и организации. От науки требуются рекомендации по
оптимальному управлению такими процессами.
Прошли времена, когда правильное, эффективное управление находилось
организаторами «наощупь», методом «проб и ошибок» - сегодня слишком велики
потери связанные с ошибками. Потребности практики вызвали в жизни специальные
научные методы, которые объединены под названием «исследование операций». Под
этим термином подразумевают применение математических, количественных методов,
для обоснования решений во всех областях целенаправленной человеческой деятельности.
Для применения количественных методов исследования в любой области всегда
требуется математическая модель (ММ). Математическая модель объекта - это
совокупность математических зависимостей, описывающих его функционирование.
Опыт показывает, что самые удачные модели создаются специалистами в данной
области практики, получивший глубокую математическую подготовку. В курсовой
работе по «моделированию и оптимизации процессов деревообработки» студент
должен получить опыт составления моделей и решение различными методами семи
задач, которые могут встретиться инженерно-техническому работнику на
производстве.
1.Оптимизация решений на моделях нелинейного программирования
модель программирование раскрой древесная стружечная плита
Спроектировать
зубчатую передачу, для которой i= 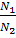
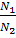 *
*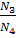
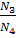 было бы
как можно ближе к
было бы
как можно ближе к 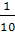
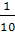 . Схема
передачи изображена на рисунке 1.1. Число зубьев Nj
должно быть заключено в интервале [20…100], j=1, 2, 3, 4.
. Схема
передачи изображена на рисунке 1.1. Число зубьев Nj
должно быть заключено в интервале [20…100], j=1, 2, 3, 4.

Рисунок
1.1 - Схема передачи
Так
как данная зубчатая передача состоит из двух ступеней, то общее передаточное
отношение передачи i равно произведению передаточных отношений этих
ступеней i1 и i2 соответственно, т.е.
i= i1*i2→ 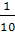
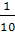 . (1.1)
. (1.1)
Передаточные
отношения i1 и i2 равны отношениям чисел зубев соответствующих колёс,
т. е.
i1=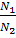
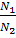 и i2=
и i2=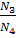
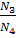 . (1.2)
. (1.2)
Таким
образом, с учётом выражений (1.2) целевая функция имеет вид
W= i= i1*i2=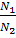
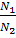 *
*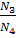
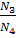 =
=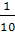
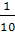 . (1.3)
. (1.3)
Поскольку
величина целевой функции определена заданием, то решение данной задачи можно
получить комбинаторным методом (методом перебора).
Начнём
подбор оптимальных решений с определения предельных значений i1 и i2. Т. к.
число зубьев должно находиться в пределах [20…100], то нижние границы
диапазонов определяются с учётом (1.2) следующим образом
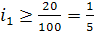
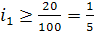 ;
; 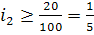
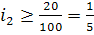 .
.
Подставляем
нижние границы диапазонов значений передаточных отношений i1 и i2 в
целевую функцию и находим соответствующие верхние границы диапазона, т. е.

 ;
; 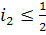
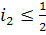 . (1.4)
. (1.4)
Получаем
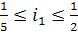
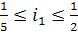 ;
; 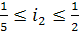
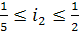 . (1.5)
. (1.5)
Произведём
подбор числа зубьев N1 и N2 путём перебора значений передаточного отношения 
 в
найденном диапазоне, подстановки его в целевую функцию для получения смежных
значений передаточного отношения
в
найденном диапазоне, подстановки его в целевую функцию для получения смежных
значений передаточного отношения 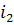
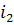 и
получения соответственно чисел зубьев N3 и N4. Перебор
значений передаточного отношения
и
получения соответственно чисел зубьев N3 и N4. Перебор
значений передаточного отношения 
 будем
производить с шагом 0,1 в знаменателе. Для удобства результаты расчётов сведём
в таблицу 1.1.
будем
производить с шагом 0,1 в знаменателе. Для удобства результаты расчётов сведём
в таблицу 1.1.
Таблица
1.1 Результаты комбинаторного решения
|
Передаточное отношение
первой ступени i1
|
Число зубьев первого колеса
N1
|
Число зубьев второго колеса
N2
|
Передаточное отношение
второй ступени i2 в
сопряжённой паре
|
Число зубьев третьегоколеса
N3
|
Число зубьев четвёртого
колеса N4
|
Общее передаточное
отношение передачи i
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|

|
20
|
100
|
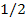
|
20 21 … 50
|
40 42 … 100
|

|
|
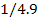
|
20
|
98
|

|
49
|
100
|

|
|
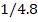
|
20
|
96
|
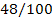
|
48 24
|
100 50
|

|
|
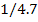
|
20
|
94
|
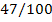
|
47
|
100
|

|
|

|
20
|
92
|

|
46 23
|
100 50
|

|
|
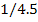
|
20 22
|
90 99
|
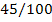
|
45
|
100
|

|
|
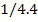
|
20
|
88
|

|
44 22
|
100 50
|

|
|
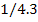
|
20
|
86
|
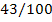
|
43
|
100
|

|
|

|
20
|
84
|
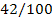
|
42 21
|
100 50
|

|
|
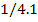
|
20
|
82
|
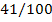
|
41
|
100
|

|
|

|
20 21 … 25
|
80 84 … 100
|
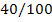
|
40 20
|
100 50
|

|
|

|
20
|
78
|
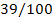
|
39
|
100
|

|
|

|
20
|
76
|

|
38
|
100
|

|
|
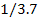
|
20
|
74
|
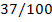
|
37
|
100
|

|
|
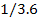
|
20
|
72
|
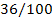
|
36
|
100
|

|
|
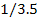
|
20 22 24 26 28
|
70 77 84 91 98
|
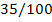
|
35
|
100
|

|
|
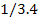
|
20 25
|
68 85
|
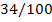
|
34
|
100
|

|
|
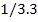
|
20
|
66
|
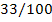
|
33
|
100
|

|
|
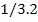
|
20 25 30
|
64 80 96
|
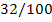
|
32
|
100
|

|
|
Продолжение таблицы 1.1
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
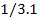
|
20
|
62
|
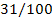
|
31
|
100
|

|
|
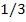
|
20 21 … 33
|
60 63 … 99
|
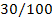
|
30
|
100
|

|
|
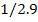
|
20
|
58
|
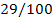
|
29
|
100
|

|
|
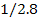
|
20 25 30 35
|
56 70 84 98
|

|
28
|
100
|

|
|
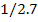
|
20
|
54
|
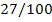
|
27
|
100
|

|
|

|
20 25 30 35
|
52 65 78 91
|
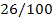
|
26
|
100
|

|
|
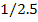
|
20 22 … 40
|
50 55 … 100
|

|
20 21 … 25
|
80 84 … 100
|

|
|

|
20 25 … 40
|
48 60 … 96
|
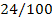
|
24
|
100
|

|
|
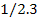
|
20 30 40
|
43 69 92
|

|
23
|
100
|

|
|
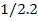
|
20 25 30 35 40
|
44 55 66 77 88
|
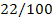
|
22
|
100
|

|
|
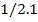
|
20 30 40
|
42 61 84
|
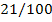
|
21
|
100
|

|
|
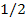
|
20 21 50
|
40 42 100
|

|
20
|
100
|

|
Существует множество допустимых решений. Чтобы определиться с оптимальным
решением, следует привлечь дополнительные критерии. В качестве дополнительных
критериев для обоснования оптимального решения можно принять:
желание уменьшить концентрацию напряжений;
желание уменьшить габариты редуктора.
После применения дополнительных критериев значение целевой функции может
незначительно отличаться от заданного, но стремиться к нему из-за учета
сопряжённости передаточных отношений ступеней.
2. Решения задачи линейного программирования графическим
методом
Предприятие содержит в подсобном хозяйстве коров, используя для этого два
вида корма - сено и концентраты. Определить оптимальный суточный рацион
кормления животных по минимуму себестоимости, пользуясь данными таблицы 2.1.
Таблица 2.1 - Исходные данные
|
Вид корма
|
Содержание в 1 кг корма
|
Себестоимость 1 кг корма,
коп
|
Ресурсы на 1 рацион
|
Предельные нормы суточной
дачи
|
|
Корм. един.
|
Белок, г
|
Кальций, г
|
|
|
|
|
Сено
|
0,5
|
40
|
5
|
20
|
35
|
45
|
|
Концентраты
|
1,0
|
200
|
4
|
40
|
25
|
20
|
|
Нормы потребления
|
30
|
2500
|
400
|
|
|
|
Пусть х - масса сена в рационе, а у - масса концентратов в рационе.
Пользуясь исходными данными, составим следующие неравенства-ограничения
,5х+1,0у≥30,
х+200у≥2500,
х+4у≥400,
0,2х≤35, (2.1)
0,4у≤25,
х≥45,
у≥20.
Выбрав в качестве критерия эффективности оптимальность суточного рациона
кормления животных по минимуму себестоимости, запишем целевую функцию
W=0,2х+0,4у
→ min. (2.2)
Перед графическим решением, представленным на рисунке 3, целесообразно
обозначить буквами неравенства-ограничения (2.1)
,5х+1,0у≥30 - (прямая a),
х+200у≥2500 - (прямая b),
х+4у≥400 - (прямая c),
0,2х≤35 - (прямая d),
0,4у≤25 - (прямая e),
х≥45 - (прямая f),
у≥20 - (прямая g).
На рисунке 2.1 дадим геометрическую интерпретацию полученной модели,
построив прямые, соответствующие неравенствам-ограничениям (2.1), и градиент
функции. Для этого продифференцируем целевую функцию (2.2) по переменным х и у.
Получим выражения
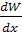
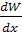 =0,2 и
=0,2 и 
 =0,4.
(2.3)
=0,4.
(2.3)

Рисунок
2.1 - Геометрическое решение задачи
Мысленно
проводя линии уровня перпендикулярно градиенту, приближаясь к нулю, находим,
что наименьшего значения целевая функция (2.2) достигает в точке D.
Координаты этой точки являются элементами решения задачи. Они определяются
совместными решением граничных уравнений, соответствующих прямым c и g, т.
е.
х+4у=400,
(2.4)
у=20.
Решая
систему (2.4), получаем х=64, у=20.
Проведем
проверку, подставив полученные значения х и у в неравенства-ограничения (2.1)
,5*64+1,0*20≥30,
*64+200*20≥2500,
*64+4*20≥400,
0,2*64≤35,
0,4*20≤25,
≥45,
≥20.
Получаем
≥2500,
≥400,
12,8≤35,
8≤25,
≥45,
≥20.
Неравенства-ограничения выполняются.
Таким образом, оптимальный суточный рацион кормления животных по минимуму
себестоимости составит 64 кг сена и 20 кг концентратов, а сумма затрат на
суточный рацион по формуле (2.2) составит
Wmin=0,2*64+0,4*20=20,8
руб.
3.Двойственная задача линейного программирования
Фирма «Транзистор» выпускает радиоприёмники трёх различных моделей: А, В,
С. Каждое изделие приносит доход в размере 80,150 и 250 руб соответственно.
Необходимо, чтобы фирма выпускала за неделю не менее 100 приёмников модели А,
150 приёмников В и 75 приёмников С.
На производство деталей, сборку и упаковку 10-ти приёмников требуется
определённое время, указанное в таблице 3.1.
Таблица 3.1 - Затраты времени на производство приёмников
|
Приёмники
|
Затраты ресурсов на
|
|
производство
|
сборку
|
упаковку
|
|
А
|
3
|
4
|
1
|
|
В
|
3,5
|
5
|
1,5
|
|
С
|
5
|
8
|
3
|
|
Ресурсы времени, ч. в
неделю
|
150
|
200
|
60
|
Определить оптимальный план производства. Сформулировать экономически и
решить двойственную задачу, выполнить экономический анализ производственной
программы. Целесообразно ли принять к производству новый приёмник с расходом
ресурсов 4, 3 и 2 ч и приносящий доход 120 руб.
Составим ММ задачи. Для этого обозначим Х1, Х2 и Х3
- объём производства приёмников моделей А, В и С соответственно. Ограничения по
ресурсам и по плану производства 10-ти приёмников выражаются системой
неравенств
3х1+3,5х2+5х3 ≤150,
х1+5х2+8х3≤200,
х1+1,5х2+3х3≤60, (3.1)
х1≥100,
х2≥150,
х3≥75.
Перепишем ограничения по ресурсам и плану производства с учётом (3.1) для
одного приёмника и приведём неравенство к одному знаку (≤)
,3х1+0,35х2+0,5х3≤ 150,
,4х1+0,5х2+0,8х3≤200,
,1х1+0,15х2+0,3х3≤60, (3.2)
х1≤-100,
х2≤-150,
х3≤-75.
Тривиальные ограничения (требования неотрицательности элементов решения)
х1>0; х2>0; х3>0. (3.3)
Для нахождения первоначального базисного решения разобьем переменные ММ
на две группы - основные (базисные) и неосновные (свободные). Воспользуемся
следующим правилом: в качестве основных переменных на первом шаге следует
выбрать (если возможно) такие m переменные, каждая из которых входит только в
одно из m уравнений системы ограничений; при этом нет таких уравнений системы,
в которые не входит ни одна из этих переменных.
Дополнительные переменные х4, х5, х6, х7,
х8, х9 >0 удовлетворяют этому правилу.
ЦФ является суммарный доход от реализации вех приёмников, который
составит
W=80 х1+150
х2+250 х3→max. (3.4)
Итак, ММ состоит из системы ограничений, записанных в общем виде, условия
не отрицательности и ЦФ.
С помощью дополнительных неотрицательных переменных перейдем к системе
уравнений
,3х1+0,35х2+0,5х3 +1х4+0х5+0х6+0х7+0х8+0х9=
150,
,4х1+0,5х2+0,8х3+0х4+1х5+0х6+0х7+0х8+0х9=
200,
,1х1+0,15х2+0,3х3+0х4+0х5+1х6+0х7+0х8+0х9=
60, (3.5)
х1-0х2-0х3 +0х4+0х5+0х6+1х7+0х8+0х9=-100,
х1-1х2-0х3 +0х4+0х5+0х6+0х7+1х8+0х9=-150,
х1-0х2-1х3+0х4+0х5+0х6+0х7+0х8+1х9=-75.
Балансные переменные равны
х4=150-(0,3х1+0,35х2+0,5х3 +0х5+0х6+0х7+0х8+0х9),
х5=200-(0,4х1+0,5х2+0,8х3+0х4+0х6+0х7+0х8+0х9),
х6=60-(0,1х1+0,15х2+0,3х3+0х4+0х5+0х7+0х8+0х9),
(3.5)
х7=-100-(-1х1-0х2-0х3 +0х4+0х5+0х6+0х8+0х9),
х8 =-150-(-0х1-1х2-0х3 +0х4+0х5+0х6+0х7+0х9),
х9=-75-(-0х1-0х2-1х3+0х4+0х5+0х6+0х7+0х8).
Целевую функцию (критерий эффективности) представим в виде
W=0-(-80
х1-150 х2-250 х3). (3.6)
Заполним первую симплексную таблицу 3.2.
Таблица 3.2
|
БП
|
СЧ
|
Переменные
|
Оценочное отношение
|
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
х8
|
х9
|
|
|
х4
|
150
|
0,3
|
0,35
|
0,5
|
1
|
0
|
0
|
0
|
0
|
0
|
300
|
|
х5
|
200
|
0,4
|
0,5
|
0,8
|
0
|
1
|
0
|
0
|
0
|
0
|
250
|
|
х6
|
60
|
0,1
|
0,15
|
0,3
|
0
|
0
|
1
|
0
|
0
|
0
|
200
|
|
х7
|
-100
|
-1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
∞
|
|
х8
|
-150
|
0
|
-1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
∞
|
|
х9
|
-75
|
0
|
0
|
-1
|
0
|
0
|
0
|
0
|
0
|
1
|
75
|
|
W
|
0
|
-80
|
-150
|
-250
|
0
|
0
|
0
|
0
|
0
|
0
|
max
|
Дальнейшее решение представим в таблицах 3.3 - 3.6.
Таблица 3.3 х9↔ х3
|
БП
|
СЧ
|
Переменные
|
Оценочное отношение
|
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
х8
|
х9
|
|
|
х4
|
112,5
|
0,3
|
0,35
|
0
|
1
|
0
|
0
|
0
|
0
|
0,5
|
225
|
|
х5
|
140
|
0,4
|
0,5
|
0
|
0
|
1
|
0
|
0
|
0
|
0,8
|
175
|
|
х6
|
37,5
|
0,1
|
0,15
|
0
|
0
|
0
|
1
|
0
|
0
|
0,3
|
125
|
|
х7
|
-100
|
-1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
∞
|
|
х8
|
-150
|
0
|
-1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
∞
|
|
х3
|
75
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
-1
|
∞
|
|
W
|
18750
|
-80
|
-150
|
0
|
0
|
0
|
0
|
0
|
0
|
-250
|
max
|
Таблица 3.4 х6↔ х9
|
БП
|
СЧ
|
Переменные
|
Оценочное отношение
|
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
х8
|
х9
|
|
|
х4
|
50
|

|
0,1
|
0
|
1
|
0
|
|
0
|
0
|
0
|
500
|
|
х5
|
40
|

|
0,1
|
0
|
0
|
1
|
|
0
|
0
|
0
|
400
|
|
х9
|
125
|
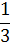
|
0,5
|
0
|
0
|
0
|
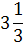
|
0
|
0
|
1
|
250
|
|
х7
|
-100
|
-1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
∞
|
|
х8
|
-150
|
0
|
-1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
150
|
|
х3
|
200
|
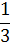
|
0,5
|
1
|
0
|
0
|
0
|
0
|
0
|
400
|
|
W
|
50000
|
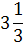
|
-25
|
0
|
0
|
0
|
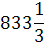
|
0
|
0
|
0
|
max
|
Таблица 3.5 х8↔ х2
|
БП
|
СЧ
|
Переменные
|
Оценочное отношение
|
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
х8
|
х9
|
|
|
х4
|
35
|

|
0
|
0
|
1
|
0
|
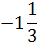
|
0
|
0,1
|
0
|
350
|
|
х5
|
25
|

|
1
|
0
|
0
|
1
|
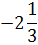
|
0
|
0,1
|
0
|
250
|
|
х9
|
50
|
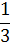
|
0
|
0
|
0
|
0
|
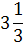
|
0
|
0,5
|
1
|
100
|
|
х7
|
-100
|
-1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
∞
|
|
х2
|
150
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
-1
|
0
|
∞
|
|
х3
|
125
|
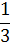
|
0
|
1
|
0
|
0
|
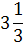
|
0
|
0,5
|
0
|
250
|
|
W
|
53750
|
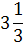
|
0
|
0
|
0
|
0
|
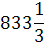
|
0
|
-25
|
0
|
max
|
Таблица 3.6 х9↔ х8
|
БП
|
СЧ
|
Переменные
|
Оценочное отношение
|
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
х8
|
х9
|
|
|
х4
|
25
|

|
0
|
0
|
1
|
0
|
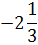
|
0
|
0
|
-0,2
|
375
|
|
х5
|
15
|

|
0
|
0
|
0
|
1
|
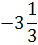
|
0
|
0
|
-0,2
|
225
|
|
х8
|
100
|
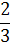
|
0
|
0
|
0
|
0
|
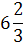
|
0
|
1
|
2
|
150
|
|
х7
|
-100
|
-1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
100
|
|
х2
|
250
|
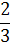
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
2
|
375
|
|
х3
|
75
|
0
|
0
|
1
|
0
|
0
|
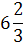
|
0
|
0
|
-1
|
∞
|
|
W
|
56250
|
20
|
0
|
0
|
0
|
0
|
1000
|
0
|
0
|
50
|
max
|
Полученное решение является оптимальным, т. к. все коэффициенты ЦФ
положительные, но не является допустимым, поскольку х7=-100<0.
Поэтому продолжим поиск оптимального допустимого решения и представим его в
таблице 3.7.
Таблица 3.7 х7↔ х1
|
БП
|
СЧ
|
Переменные
|
Оценочное отношение
|
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
х8
|
х9
|
|
|
х4
|
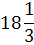
|
0
|
0
|
0
|
1
|
0
|
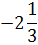
|

|
0
|
-0,2
|
|
|
х5
|
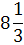
|
0
|
0
|
0
|
0
|
1
|
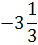
|

|
0
|
-0,2
|
|
|
х8
|
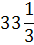
|
0
|
0
|
0
|
0
|
0
|
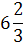
|
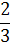
|
1
|
2
|
|
|
х1
|
100
|
1
|
0
|
0
|
0
|
0
|
0
|
-1
|
0
|
0
|
|
|
х2
|
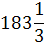
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
2
|
|
|
х3
|
75
|
0
|
0
|
1
|
0
|
0
|
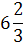
|
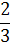
|
0
|
-1
|
|
|
W
|
54250
|
0
|
0
|
0
|
0
|
0
|
1000
|
20
|
0
|
50
|
max
|
Критерий
оптимальности выполнен, значит Wmax=54250, оптимальный план производства
составляет Х* =(100; 183; 75; 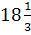
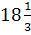 ;
; 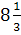
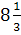 ; 0; 0;
33; 0).
; 0; 0;
33; 0).
Действительно,
подставляя полученные значения в (3.4), получаем
W= 80x1 + 150x2 + 250x3 = 80*100+183*150+75*250=54200.
Ресурсы
времени на сборку использованы полностью, осталось 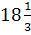
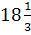 ч на
производство деталей и
ч на
производство деталей и 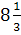
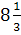 ч на
сборку приёмников. Перевыполнен план по выпуску приёмников модели В на 33 шт.
ч на
сборку приёмников. Перевыполнен план по выпуску приёмников модели В на 33 шт.
Решение
двойственной задачи. Используя три теоремы двойственности, значение
двойственных оценок у1 у2,..., уm
можно получить на основе решения исходной.
Сначала
составляем ММ двойственной задачи путем транспонирования расширенной матрицы
коэффициентов исходной задачи.

Основываясь
на свойствах взаимно двойственных задач, запишем ограничения, ЦФ из условия
неотрицательности двойственной задачи
,3у1+0,4у2+0,1у3-1у4+0у5+0у6≥80,
,35у1+0,5у2+0,15
у3+0у4-1у5+0 у6≥150, (3.7)
,5у1+0,8у2+0,3у3+0у4+0у5-1у6≥250.
ЦФ
принимает вид
Z=150 у1+200
у2+60 у3-100 у4-150 у5-75 у6→min.
(3.8)
Для преобразования ММ в ОЗЛП требуется ввести три дополнительные неотрицательные
переменные у7, у8, и у9.
,3у1+0,4у2+0,1у3-1у4+0у5+0у6
-1у7-0у8-0у9=80,
,35у1+0,5у2+0,15 у3+0у4-1у5+0
у6-0у7-1у8-0у9=150, (3.7)
,5у1+0,8у2+0,3у3+0у4+0у5-1у6-0у7-0у8-1у9=250.
Составляем таблицу 3.8 соответствия переменных ИсхЗ и ДвЗ.
Таблица 3.8 - Соответствие переменных ИсхЗ и ДвЗ
|
Исходная задача 1
|
|
Основные переменные
|
Дополнительные переменные
|
|
<j>
х1 х2 x3 ↕ ↕ ↕ у7
у8 у9 <m+1>
|
<n+1>
х4 х5 х6 х7 х8 х9
↕ ↕ ↕ ↕ ↕ ↕ у1 у2
у3 у4 у5 у6 <j>
|
|
Дополнительные переменные
|
Основные переменные
|
|
Двойственная задача 2
|
Согласно второй теореме двойственности, компоненты оптимального решения
ДвЗ равны абсолютным значениям коэффициентов при соответствующих переменных ЦФ
ИсхЗ, выраженной через неосновные переменные её оптимального решения. Из
таблицы 3.7 имеем
У*=(0; 0; 1000; 20; 0; 50; 0; 0; 0).
Вычисляем оптимальное значение ЦФ
Wmax=Zmin=150у1+200у2+60у3-100у4-150у5-75у6=
=150*0+200*0+60*1000-100*20-150*0-75 *50=54250.
W(x*)=Z(у*)=54250.
Получено подтверждение первой теоремы двойственности. Положительным
(ненулевым) компонентам оптимального решения одной из взаимно ДвЗ соответствуют
нулевые компоненты оптимального решения другой задачи, т. е.
если х*j >0, то
уm+j=0,
если х*n+I >0, то уi=0, (3.8)
если у*j >0, то хn+j=0,
если у*m+j >0, то хj=0.
Заполним таблицу 3.9 соответствия переменных элементами решения ИсхЗ и
ДвЗ.
Таблица 3.9 - Соответствие переменных элементами решения ИсхЗ и ДвЗ
|
Исходная задача 1
|
|
Число единиц продукции
|
Остатки ресурсов
|
Перевыполнение плана
|
|
х1=100 х2
=184 x3=75 ↕ ↕ ↕ у7=0
у8=0 у9=0
|
х4 =18,6 х5=8,6
х6=0 ↕ ↕ ↕ у1=0 у2=0 у3=1000
|
|
Превышение затрат на
ресурсы над ценой
|
Условие цены=ОбОбОц
ресурсов
|
|
Двойственная задача 2
|
Смысл объективно-обусловленных оценок. Третья теорема двойственности.
Компоненты оптимального решения ДвЗ называются оптимальными (двойственными)
оценками ИсхЗ, или объективно-обусловленными оценками (ОбОбОц). Смысл этих
оценок выясним по компонентам оптимального решения.
В таблице 3.8 дополнительные переменные ИсхЗ Х4, Х5
и Х6, представляющие разность между запасами ресурсов времени на
соответствующие операции и их использованием на соответствующие модели
приёмников, выражают остатки ресурсов времени, дополнительные переменные Х7,
Х8 и Х9, представляющие разность между выпуском и планом
выпуска соответствующих приёмников, выражают перевыполнение плана, а
дополнительные переменные ДвЗ у7, у8, и у9,
представляющие разность между затратами на ресурсы для производства из них
единицы продукции и прибылью от реализации ресурсов времени выражают превышение
затрат над прибылью.
Действительно, по формулам 3.5
х4= 150 - 0,3* 100 - 0,35*183 - 0,5*75 = 18,45,
х5= 200 - 0,4* 100 - 0,5*183 - 0,8*75 = 8,5,
х6= 60 - 0,1* 100 - 0,15*183 - 0,3*75 = 0,05,
х7=100-100=0,
х8=183-150=33,
х9=75-75=0.
Из формул 3.7 получаем
у7= 0,3*0+0,4*0+0,1*1000-1*20+0+0 -80=0,
у8= 0,35*0+0,5*0+0,15 *1000+0-1*0+0 *50-150=0,
у9= 0,5*0+0,8*0+0,3*1000+0+0-1*50-250=0.
Ресурсы
времени на упаковку по ОптПл полностью использованы (х6=0) и ОбОбОц
этих ресурсов ненулевые (у3 = 1000), ресурсы времени на производство
и сборку не полностью используются в ОптПл (х4=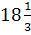
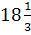 ; х5=
; х5=
 ) и
ОбОбОц этих ресурсов нулевые (у1 = 0; у2 = 0). План по
выпуску приёмников моделей А и С по ОптПл выполнен, но не перевыполнен (х7=0;
х9=0) и ОбОбОц этих ресурсов ненулевые (у4 = 20; у6
= 50), план по выпуску приёмников модели В по ОптПл перевыполнен (х8=33)
и ОбОбОц этого ресурса нулевая (у5 = 0).
) и
ОбОбОц этих ресурсов нулевые (у1 = 0; у2 = 0). План по
выпуску приёмников моделей А и С по ОптПл выполнен, но не перевыполнен (х7=0;
х9=0) и ОбОбОц этих ресурсов ненулевые (у4 = 20; у6
= 50), план по выпуску приёмников модели В по ОптПл перевыполнен (х8=33)
и ОбОбОц этого ресурса нулевая (у5 = 0).
Т.о.,
объективно обусловленные оценки ресурсов определяют степень дефицитности
ресурсов: дефицитные (т.е. полностью используемые) ресурсы получают ненулевые
оценки, а не дефицитные - нулевые оценки.
По
оптимальному плану в ИсхЗ следует производить приёмники в количестве х1=100,
х2=183 и х3=75 и превышение затрат на ресурсы над ценой
реализации равно нулю (у7=0, у8=0, у9=0).
Итак,
в оптимальный план производства могут попасть только рентабельные, неубыточные
виды продукции.
Появилась
возможность выпуска нового приёмника, приносящего доход 120 руб. Затраты
времени на 10 приёмников составляют 4, 3 и 2 ч соответственно на производство
деталей, сбору и упаковку, а на один приёмник соответственно 0,4, 0,3 и 0,2ч.
Оценим, целесообразно ли включение в план нового приёмника.
Можно
включить в условия задачи новый приёмник и заново решить задачу, но это
потребует новых (других) затрат ресурсов времени. Да и необходимости в этом нет
- ОбОбОц ресурсов известны. Действительно, сопоставим дополнительные затраты на
ресурсы в расчете на один новый приёмник с ценой его реализации
,4у1+0,3у2+0,2у3=0,4*0+0,3*0+0,2*1000=200
- больше цены приёмника (120 руб).
Следовательно,
включение в план нового приёмника нецелесообразно, т.к. затраты на его внедрение
превысят прибыль, принесенную им.
4.Оптимизация раскроя древесностружечных плит на заготовки
Составить оптимальный план раскроя ДСтП форматом С (2600*2235 мм) на
мебельные заготовки трёх типов 1 (70*37,5), 2 (75*37,5), 3 (90*40). Задание по
выпиливанию каждой из заготовок составляет Q1=350, Q1=400, Q1=350.
Провести оптимизацию по двум функциям цели:
) обеспечение минимума отходов, образующихся при раскрое;
) достижение минимального количества раскроенных плит.
Составить четыре (лучше смешанные) карты раскроя, определить
характеристики каждой из карт. Пропилы считать включёнными в размер заготовок.
Последовательность резов на картах должна соответствовать выбранному типу
форматно-раскроечного станка. Нормативный процент полезного выхода заготовок
принять равным 88.
Оптимизацию по минимуму отходов произвести на ПК, по минимуму раскроенных
плит симплекс-методом табличных преобразований («вручную»).
.1 Разработка карт раскроя
Площадь плиты составляет 2,6*2,235=5,811 м2 .
Площади заготовок:
первого типа
,7*0,375=0,2625 м2;
второго типа
,75*0,375=0,28125 м2;
- третьего типа
,8*0,4=0,36 м2.
Четыре наиболее оптимальные для условий задачи карты раскроя приведены на
рисунке 3.1 а) - г).
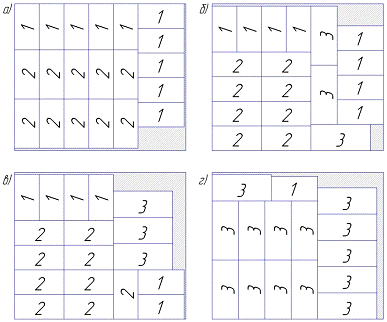
Рисунок 3.1 - Наиболее оптимальные карты раскроя
Площади отходов по соответствующим картам раскроя равны
а) 5,811-10*0,2625-10*0,28125=0,3735,
б) 5,811-8*0,2625-8*0,28125-3*0,36=0,381,
в) 5,811-6*0,2625-9*0,28125-3*0,36=0,62475,
г) 5,811-1*0,2625-14*0,36=0,5085.
Чтобы предотвратить перепроизводство одной из заготовок, соотношение
между числом заготовок q1:q2:q3 на всех картах раскроя должно
примерно соответствовать соотношению числа заготовок Q1:Q2:Q3 в плане производства. Для условия задачи имеем
q1:q2:q3 =25:27:20=1,25:1,35:1. (3.1)
Q1:Q2:Q3 =350:400:350=1:1,14:1. (3.2)
4.2Составление математической модели
Введем переменные х1, х2, х3 и х4,
под которыми будем понимать количество плит подлежащих раскрою по первой, второй,
третьей и четвертой картам раскроя, или частоту применения карт при раскрое
ДСтП на заготовки для мебели.
Целевая функция при минимизации количества раскраиваемых плит имеет вид
W=х1+х2+х3+х4
→ min. (3.3)
Система неравенств увязывающих возможности выпиливания заготовок 1-го,
2-го и 3-го типа по всем картам раскроя с плановым заданием
х1+8х2+6х3+1х4≥350,
х1+8х2+9х3+0х4≥400,
(3.4)
0х1+3х2+3х3+14х4≥350.
Условие не отрицательности переменных запишем в виде набора тривиальных
ограничений
х1≥ 0, х2≥0, х3≥0,
х4≥0. (3.5)
Чтобы неравенства в системе нетривиальных ограничений (3.4) преобразовать
в равенства введем дополнительные (балансные) переменные. Тогда математическая
модель в форме ОЗЛП будет записана следующей системой зависимостей
10х1+8х2+6х3+1х4 - х5=350,
х1+8х2+9х3+0х4 - х6=400,
(3.6)
0х1+3х2+3х3+14х4 - х7=350.
Тривиальные ограничения
хj ≥0 (i =1,…,7). (3.7)
Целевая функция
W=х1+х2+х3+х4+0
→ min. (3.8)
Для заполнения исходной таблицы балансные переменные выбираются в
качестве базисных, основных (БП) и выражаются из уравнений (3.6) через
свободные, независимые переменные следующим образом
х5=-350-(-10х1-8х2-6х3-1х4),
х6=-400-(-10х1-8х2-9х3-0х4),
х7=-350-(0х1-3х2-3х3-14х4).
Аналогично выражаем из (3.8) ЦФ
W2=0-(-1х1-1х2-1х3-1х4).
(3.9)
В исходную таблицу 4.1 переносим свободные члены (СЧ) и коэффициенты при
неизвестных из уравнений математической модели.
Таблица 4.1
|
БП
|
СЧ
|
Переменные
|
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
|
х5
|
-350
|
-10
|
-8
|
-6
|
-1
|
1
|
0
|
0
|
|
х6
|
-400
|
-10
|
-8
|
-9
|
0
|
0
|
1
|
0
|
|
х7
|
-350
|
0
|
-3
|
-3
|
-14
|
0
|
0
|
1
|
|
W
|
0
|
-1
|
-1
|
-1
|
-1
|
0
|
0
|
0
|
|
Оценочное отношение
|
0,1
|
0,125
|
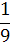
|
-
|
-
|
-
|
-
|
Дальнейшее решение представим в таблицах 4.2 - 4.5.
Таблица 4.2 х6↔х1
|
БП
|
СЧ
|
Переменные
|
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
|
х5
|
50
|
0
|
0
|
3
|
-1
|
1
|
-1
|
0
|
|
х1
|
40
|
1
|
0,8
|
0,9
|
0
|
0
|
-0,1
|
0
|
|
х7
|
-350
|
0
|
-3
|
-3
|
-14
|
0
|
0
|
1
|
|
W
|
40
|
0
|
-0,2
|
-0,1
|
-1
|
0
|
-0,1
|
0
|
|
Оценочное отношение
|
-
|

|
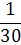
|
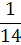
|
-
|
1
|
-
|
Таблица 4.3 х7↔х3
|
БП
|
СЧ
|
Переменные
|
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
|
х5
|
-300
|
0
|
-3
|
0
|
-15
|
1
|
-1
|
1
|
|
х1
|
-65
|
1
|
-0,1
|
0
|
-4,2
|
0
|
-0,1
|
0,3
|
|
х3
|
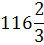
|
0
|
1
|
1
|
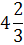
|
0
|
0
|
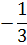
|
|
W
|
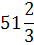
|
0
|
-0,1
|
0
|

|
0
|
-0,1
|

|
|
Оценочное отношение
|
-
|
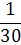
|
-
|
-
|
-
|
0,1
|
-
|
Таблица 4.4 х5↔х2
|
БП
|
СЧ
|
Переменные
|
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
|
х2
|
100
|
0
|
1
|
0
|
5
|
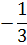
|
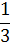
|
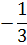
|
|
х1
|
-55
|
1
|
0
|
0
|
-3,7
|

|
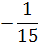
|
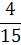
|
|
х3
|

|
0
|
0
|
1
|
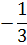
|
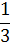
|
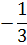
|
0
|
|
W
|
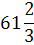
|
0
|
0
|
0
|

|

|
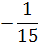
|

|
|
Оценочное отношение
|
-
|
-
|
-
|

|
1
|
1
|
-
|
Таблица 4.5 х1↔х5
|
БП
|
СЧ
|
Переменные
|
|
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
|
х2
|
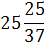
|
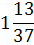
|
1
|
0
|
0
|
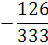
|
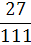
|

|
|
х4
|
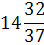
|

|
0
|
0
|
1
|

|

|
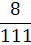
|
|
х3
|
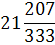
|
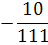
|
0
|
1
|
0
|
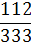
|
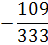
|
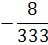
|
|
W
|
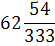
|
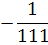
|
0
|
0
|
0
|
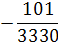
|

|

|
План раскроя в таблице 4.5 оказался оптимальным, так как все свободные
члены положительны, все коэффициенты при свободных переменных в строке W отрицательны.
Оптимальное решение может быть только целочисленным. С учётом округления
значения базисных переменных равны
х1*=0; х2*=26; х3*=22; х4*=15;
W=63.
4.3 Проверка и корректировка решения
Проверка и корректировка решения проводится и для оптимального плана
раскроя полученного при “ручном”, табличном, решении, и для плана, полученного
на ЭВМ. Если между этими решениями есть разница, то принимается в качестве
оптимального лучший план раскроя.
Для проверки на выполнение задания по заготовкам используем ограничения
(3.4). При этом будет обеспечен по каждой из заготовок следующий объем
производства:
- первого типа 10*0+8*26+6*22+1*15=355, т.е. план перевыполнен на 5
заготовок;
второго типа 10*0+8*26+9*22+0*15=406, т.е. план перевыполнен на 6
заготовок;
В приложении А приведен метод оптимизации раскроя плит при минимизации
количества отходов, образующихся при раскрое, выполненный на ЭВМ.
4.4Проверка полезного выхода заготовок при раскрое
Средневзвешенный процент полезного выхода по всей программе раскроя и с
учетом целочисленности элементов решения, получим как отношение площади
заготовок к площади раскроенных плит (в процентах):

 .
.
Т.е.
существенно выше нормативных 88%. Таким образом, план раскроя ДСтП на заготовки
для мебели по картам, представленным на рисунках 4.1 б), в), г), может быть
принят к исполнению как удовлетворяющий всем требованиям.
5.Транспортная задача и задачи транспортного типа
Некоторая фабрика производит рюкзаки для путешественников. Спрос на эту
продукцию есть только в марте - июне и составляет помесячно 100, 200, 180 и 300
шт. Объём производства рюкзаков меняется от месяца к месяцу в зависимости от
выпуска других изделий. В течение рассматриваемых четырёх месяцев фабрика может
выпустить 50, 180, 280 и 270 рюкзаков соответственно. В каждый месяц спрос
можно удовлетворить за счёт:
1) производства рюкзаков в течение текущего месяца;
2) избытка рюкзаков, произведённых в прошлом месяце;
3) избытка рюкзаков, произведённых в текущем месяце в счёт невыполненных
заказов.
В первом случае стоимость одного рюкзака составляет 700 руб. Во втором
случае возникают дополнительные расходы в расчёте 10 руб. на один рюкзак за
хранение в течение месяца. В третьем случае за просроченные заказы начисляются
штрафы в размере 40 руб. на один рюкзак за каждый просроченный месяц.
Постройте транспортную модель, позволяющую фабрике разработать
оптимальный план производства на эти четыре месяца.
Обозначим через ai - возможный объём выпуска рюкзаков в каждом рассматриваемом месяце, bj - спрос на рюкзаки в каждом
рассматриваемом месяце, хij - искомый объём выпуска рюкзаков, с ij - стоимость производства рюкзаков в
каждом месяце с учётом возможных дополнительных расходов на хранение продукции
в течение месяца и штрафов за просроченные заказы за каждый месяц. Транспортную
модель, позволяющую фабрике разработать оптимальный план производства на эти
четыре месяца, представим в виде таблицы 5.1.
Таблица 5.1 - Транспортная модель задачи
|
Месяцы
|
1 Март
|
2 Апрель
|
3 Май
|
4 Июнь
|
Возможный объём
производства
|
|
1 Март
|
700
|
710
|
720
|
730
|
50
|
|
2 Апрель
|
740
|
700
|
710
|
720
|
180
|
|
3 Май
|
780
|
740
|
700
|
710
|
280
|
|
4 Июнь
|
820
|
780
|
740
|
700
|
270
|
|
Спрос
|
100
|
200
|
180
|
300
|
|
Имеем следующие ограничения:
1) план производства должен быть полностью выполнен
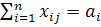
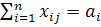 , (i=1,
2, 3, 4). (5.1)
, (i=1,
2, 3, 4). (5.1)
2) все произведённые рюкзаки должны быть реализованы, т. е.
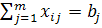
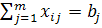 , (j=1,
2, 3, 4). (5.2)
, (j=1,
2, 3, 4). (5.2)
3) объёмы производства должны быть неотрицательны, т. е.
хij ≥0 (i=1, 2, 3, 4; j=1,
2, 3, 4). (5.3)
Требование минимума стоимости производства рюкзаков (ЦФ) реализуется
следующей функцией
W=
 →min
(5.4)
→min
(5.4)
Процесс
решения транспортной задачи состоит из двух этапов, как и для обычной задачи
линейного программирования:
1) отыскание опорного решения;
2) последовательное его улучшение с целью отыскания оптимального
решения задачи.
Отыскание опорного решения осуществляем по методу наименьшего элемента.
Вначале заполняется клетки с наименьшей стоимостью. Далее заполняются другие
аналогично. План является опорным, если число заполненных клеток равно m+n-1. Опорное решение представим в виде таблицы 5.2. В левом
верхнем углу ячейки записываем стоимость производства, а в правом нижнем -
объём производства в соответствующем месяце.
Таблицы 5.2 - Опорное решение задачи
|
Месяцы
|
1 Март
|
2 Апрель
|
3 Май
|
4 Июнь
|
Возможный объём
производства
|
|
1 Март
|
700 50
|
710
|
720
|
730
|
50
|
|
2 Апрель
|
740 50
|
700 130
|
710
|
720
|
180
|
|
3 Май
|
780
|
740 70
|
700 180
|
710 30
|
280
|
|
4 Июнь
|
820
|
780
|
740
|
700 270
|
270
|
|
Спрос
|
100
|
200
|
180
|
300
|
|
Значение целевой функции определяется по формуле (5.4)
W=50·700+50·740+130·700+70·740+180·700+30·710+270·700=551100.
Проверим, является ли полученное опорное решение оптимальным.
Перераспределим план производства методом потенциалов, который предполагает
выполнение нескольких этапов.
Каждому объёму производства аj ставится в соответствие некоторая переменная uj, называемая потенциалом
производства; каждому объёму спроса bj ставится в соответствие переменная vj - потенциал спроса (последний
столбец и последняя строка таблицы 5.3);
Для отыскания значений этих переменных, т. е. потенциалов производства и
спроса, составляется и решается система уравнений. При этом каждой занятой
клетке соответствует свое уравнение, имеющее вид
ui + vj=cij (5.5)
где сij -
стоимость производства для данной клетки;
uj и vj - соответственно потенциалы
производства и спроса.
Всего составляется m + n - 1 уравнений по числу занятых клеток. Число
переменных в системе равно m + n, т. е. на единицу больше числа уравнений.
Поэтому система решается следующим образом: одной из переменных придают
произвольное значение, обычно ноль, и тогда однозначно определяются значения
остальных переменных.
В соответствии с количеством месяцев, в которых осуществляется
производство и существует спрос на продукцию, рассмотрим четыре переменных u1, u2, u3, u4 - потенциалы производства и четыре
переменных v1, v2, v3, v4 -
потенциалы спроса. Для каждой занятой клетки в таблице 5.2 запишем уравнения
u1+v1=700,
u2+v1=740,2+v2=700,3+v2=740,
(5.6)3+v3=700,3+v4=710,4+v4=700.
Примем u3=0, после чего найдем из записанной системы уравнений
(5.6) значения остальных потенциалов: v2=740; v3=700; v4=710; u2=-40, v1=780, u1 =-80; u4 =-10.
На следующем этапе вычисляем суммы потенциалов, соответствующие каждой
свободной клетке. Эту сумму называют псевдостоимостью. Они приведены в левых
верхних углах этих клеток под соответствующей стоимостью производства (таблица
5.3).
Таблица 5.3 - Решение задачи методом потенциалов
|
Месяцы
|
1 Март
|
2 Апрель
|
3 Май
|
4 Июнь
|
Возможный объём
производства
|
Потенциал производства
|
|
1 Март
|
700 50
|
710 660
|
720 620
|
730 630
|
50
|
u1 =-80
|
|
2 Апрель
|
740 50
|
700 130
|
710 660
|
720 670
|
180
|
u2=-40
|
|
3 Май
|
780 780
|
740 70
|
700 180
|
710 30
|
280
|
u3=0
|
|
4 Июнь
|
820 770
|
780 730
|
740 690
|
700 270
|
270
|
u4 =-10
|
|
Спрос
|
100
|
200
|
180
|
300
|
|
|
|
Потенциал спроса
|
v1=780
|
v2=740
|
v3=700
|
v4=710
|
|
|
Получили элементы решения
Х*12=50, Х*21=50, Х*22=130, Х*32=70,
Х*33=180, Х*34=30, Х*44=270.
В полученном плане все псевдостоимости не превышают стоимости
производства рюкзаков, что свидетельствует об оптимальности уже полученного
решения, которому соответствует найденное выше минимальное значение целевой
функции, равное 551100 руб.
Таким образом, решение данной задачи методом наименьшего элемента
совпадает с ее оптимальным решением, что было определено с помощью метода
потенциалов.
6.Упорядочение последовательности запуска n деталей на m станках
Определить оптимальную последовательность (порядок запуска в обработку
шести деталей на четырёх станках графическим методом). Затраты времени на
обработку деталей, в минутах, приведены в таблице 6.1.
Таблица 6.1 - Затраты времени на обработку деталей
|
Станки
|
Затраты времени на
обработку деталей
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
9
|
10
|
8
|
12
|
10
|
6
|
|
2
|
10
|
7
|
9
|
5
|
13
|
11
|
|
3
|
11
|
10
|
12
|
8
|
7
|
13
|
|
4
|
8
|
11
|
6
|
14
|
4
|
3
|
|
Трудоёмкость обработки
|
38
|
38
|
35
|
39
|
34
|
33
|
После определения порядка запуска следует сделать вывод об эффективности
«работы» правил, по которым производилось упорядочение.
В данной задаче мы используем правила, базирующиеся на идее
программирования Джонсона.
Правило 1. Обрабатывать раньше те детали, у которых время обработки на
первом станке минимальное. По этому правилу получаем следующую
последовательность запуска деталей в обработку
→3→1→2→5→4;
→3→1→5→2→ 4.
Правило 2. Обрабатывать те детали раньше, у которых время обработки на
последнем станке максимальное. По этому правилу получаем следующую
последовательность запуска деталей в обработку
4→2→1→3→5→6.
Правило 3. Обрабатывать раньше те детали, для которых «узкое» место
находится дальше от начала процесса обработки. По этому правилу получаем следующую
последовательность запуска деталей в обработку
→4→1→ 3→6→5;
→2→1→ 3→6→5;
→4→3→1→ 6→5;
→2→3→1→6→5;
→4→6→1→3→5;
→2→6→1→3→5;
→4→1→6→ 3→5;
→2→1→6→3→5;
→4→3→6→1→5;
→2→3→6→1→5;
→4→6→3→1→5;
→4→6→3→1→5.
Правило 4. Пропускать вперёд те детали, для которых общая длительность
обработки на всех станках максимальная. По этому правилу получаем следующую
последовательность запуска деталей в обработку
→2→1→3→5→6;
→1→2→3→5→ 6.
По каждому из этих правил строится график Ганта. Графики приведены в
приложении В.
После построения графиков в качестве оптимальной последовательности
выбираем производительность по правилу 3 (4→2→3→1→6→5),
так как она обеспечивает наименьшую продолжительность производственного цикла Тц
(86 с) и наименьшее время пролёживания заготовок и простаивания оборудования (Тпз+Тпо=15+24=39
с).
После построения графиков также видно, что наиболее точно «работает»
третье правило, затем - четвёртое, затем - второе, и наименее точно - первое
правило.
7. Обоснование решений на моделях СПУ
Университет устанавливает компьютерную систему электронной почты, которая
позволит передавать сообщение между деканами восьми факультетов. Сеть возможных
электронных связей между деканатами показана ниже на рисунке 7.1.

Рисунок 7.1 - Сетевой график
Протяжённость коммуникаций в километрах отмечена на дугах. Предложим
проект системы связей, которая позволит всем восьми деканам обеспечить доступ к
системе.
Сетевая модель (СМ) представляет собой совокупность взаимосвязанных
операций и событий, отображающих процесс достижения определенной цели.
Временные взаимосвязи предстоящих работ могут быть заданы в виде сетевого
графика или таблицы.
Упорядоченный сетевой график нашего проекта, включающий 8 событий и 16
работ, представлен на рисунке 7.2.
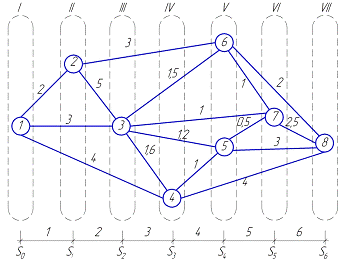
Рисунок 7.2 - Упорядоченный сетевой график
После построения сетевого графика (СГ) необходимо табличным способом
рассчитать временные параметры работ данной сетевой модели (таблица 7.1).
Перечень работ (i;j) и их продолжительность t(i;j) перенесем с СГ
во вторую и третью графы таблицы 7.1. При этом работы следует записать в графу
2 последовательно: сначала начинающиеся с номера 1, затем с номера 2 и т.д.
В первой графе поставим число, характеризующее количество непосредственно
предшествующих работ (Кпр) тому событию, с которого начинается
рассматриваемая работа. Для работ, начинающихся с номера «1», предшествующих
работ нет. Количество найденных работ записывается во все строчки, начинающиеся
с номера «К». Например, для работы (3,4) в графе 1 поставим «2», так как в
графе 2 на номер 3 оканчивается две работы: (1,3) и (2,3).
Таблица 7.1 - Временные параметры работ
|
Кпр
|
(i;j)
|
t(i;j)
|
tpн(i;j)= =tp(i)
|
tpo
(i;j)
|
tпн (i;j)
|
tпо(i;j)= =tп(j)
|
Rп(i;j)
|
Rн(i;j)
|
Kн(i;j)
|
|
0
|
(1,2)
|
2
|
0
|
2
|
0
|
2
|
0
|
0
|
1
|
|
0
|
(1,3)
|
3
|
0
|
3
|
4
|
7
|
4
|
4
|
0,58
|
|
0
|
(1,4)
|
4
|
0
|
4
|
4,6
|
8,6
|
4,6
|
4,6
|
0,47
|
|
1
|
(2,3)
|
5
|
2
|
7
|
2
|
7
|
0
|
0
|
1
|
|
1
|
(2,6)
|
3
|
2
|
5
|
6,1
|
9,1
|
4,1
|
3,5
|
0,61
|
|
2
|
(3,4)
|
1,6
|
7
|
8,6
|
7
|
8,6
|
0
|
0
|
1
|
|
2
|
(3,5)
|
1,2
|
7
|
8,2
|
8,4
|
9,6
|
1,4
|
1,4
|
0,75
|
|
2
|
(3,6)
|
1,5
|
7
|
8,5
|
7,6
|
9,1
|
0,6
|
0
|
0,89
|
|
2
|
(3,7)
|
1
|
7
|
8
|
9,1
|
10,1
|
2,1
|
2,1
|
0,63
|
|
2
|
(4,5)
|
1
|
8,6
|
9,6
|
9,6
|
0
|
0
|
1
|
|
2
|
(4,8)
|
4
|
8,6
|
12,6
|
8,6
|
12,6
|
0
|
0
|
1
|
|
2
|
(5,7)
|
0,5
|
9,6
|
10,1
|
9,6
|
10,1
|
0
|
0
|
1
|
|
2
|
(5,8)
|
3
|
9,6
|
12,6
|
9,6
|
12,6
|
0
|
0
|
1
|
|
1
|
(6,7)
|
1
|
8,5
|
9,5
|
9,1
|
10,1
|
0,6
|
0
|
0,89
|
|
1
|
(6,8)
|
2
|
8,5
|
10,5
|
10,6
|
12,6
|
2,1
|
1,5
|
0,63
|
|
3
|
(7,8)
|
2,5
|
10,1
|
12,6
|
10,1
|
12,6
|
0
|
0
|
1
|
Расчет параметров начинается с раннего срока начала работ tрн(i;j)=tp(i).
Для работ, имеющих цифру «ноль» в графе 4 также заносятся нули, а
значения в графе 5 получаются суммированием граф 3 и 4, т. е.
tро(i; j)= tp(i) +
t(i;j). (7.1)
В нашем случае таких работ три: (1,2), (1,3) и (1,4), поэтому в графе 4 в
соответствующей ей строке поставим «0», а в графе 5 для соответствующих работ
по формуле (7.1) получаем
tро (1,2)=0+2=2,
tро (1,3)=0+3=3,
tро (1,4)=0+4=4.
Для заполнения строк графы 4 просматриваются заполненные строки графы 5,
содержащие работы, которые оканчиваются на этот номер и максимальное значение
переносится в графу 4 обрабатываемых строк. Далее для каждой из этих работ
путем суммирования их значений граф 3 и 4 получаем значение графы 5. Этот
процесс повторяется до тех пор, пока не будет заполнена последняя строка
таблицы.
Графы 7 и 6 заполняются «обратным ходом», то есть снизу вверх. Для этого
просматриваются строки, оканчивающиеся на номер последнего события, и из графы
5 выбирается максимальная величина, которая записывается в графу 7 по все
строкам, оканчивающиеся на номер последнего события, т. е.
п(N)
= tр(N). (7.2)
В нашем случае из выражения (7.2) имеем
п(8)
= tр(8) = tпо(7,8) = 12,6.
Затем для этих строчек находится содержание графы 6 по формуле
tпн (i;j)= tп( j ) - t (i;j). (7.3)
По формуле (7.3) имеем
пн (7,8) = 12,6-2,5 = 10,1.
Далее просматриваются строки, оканчивающиеся на номер события, которое
предшествует завершающему событию. Для определения графы 7 этих строк
просматриваются все лежащие ниже строки графы 6, начинающиеся с этого номера. В
графе 6 среди них выбирается минимальная величина, которая переносится в графу
7. Процесс повторяется до тех пор, пока не будет заполнены все строки по графам
6 и 7.
Полный резерв времени работы Rп(i;j) рассчитывается по формуле
Rп(i;j) = tп(j) - tp(i) - t(i;j). (7.4)
По формуле (7.4) для работы (1;2) получаем
Rп(1,2) =2-0-2=0.
Полный резерв времени для остальных работ рассчитывается аналогично, и
его значение заносится в графу 8 таблицы 7.1.
Независимый резерв времени Rн(i;j) рассчитывается
по формуле
Rн(i;j) = tp(j) -
tп(i) - t(i;j). (7.5)
По формуле (7.5) для работы (1;2) получаем
Rн
= 2 - 0 - 2 = 0.
Независимый резерв времени для остальных работ рассчитывается аналогично,
и его значение заносится в графу 9 таблицы 7.1.
Учитывая, что нулевой резерв времени имеют только события и работы,
которые принадлежат критическому пути, получаем, что критическими являются
четыре равнозначных пути:
кр1= (123458);кр2= (1234578);кр3= (12348);кр4=
(123458);
tкр1=2+5+1,6+1+3=12,6 км;кр2=2+5+1,6+1+0,5+2,5=12,6
км,кр3=2+5+1,6+4=12,6 км,кр4=2+5+1,6+1+3=12,6 км.
После нахождения критического пути и резервов времени работ должен быть
проведен всесторонний анализ сетевой модели и приняты меры по ее оптимизации.
Величина полного времени поможет точно показать, насколько напряженным является
выполнение любой работы некритического пути, поэтому приходится дополнительно
определять коэффициент напряженности работ Кн(i;j), который рассчитывается по формуле
Kн(i:j) =
 , (7.6)
, (7.6)
где
tкр′ - продолжительность отрезка рассматриваемого пути,
совпадающего с критическим путём.
Коэффициент
напряженности может изменятся от нуля до единицы. Самыми напряженными являются
работы критического пути, для которых Кн=1. На основе коэффициента
напряженности все работы СМ могут быть разделены на три группы:
)
подкритические (Kн(i;j)>0,8);
)
напряженные (0,6< Kн(i;j)<0,8);
)
резервные (Kн(i;j)<0,6).
По
формуле (7.6) для работы (1;2) получаем
Kн(i:j) =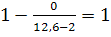
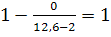 .
.
Коэффициент
напряженности для остальных работ рассчитывается аналогично, и его значение
заносится в графу 10 таблицы 7.1.
Анализируя
результаты вычисления Кн в данном случае, можно следующим образом
оценить перспективу реализации проекта в плановый срок. Из 16 работ, включенных
в СГ, 8 относятся к критическим, 2 - к подкритическим, 4 - к напряжённым, 2 - к
резервным.
Таким
образом, нет уверенности в том, что проект без особых трудностей будет выполнен
в намеченный срок, т.к. недостаточно резервных работ для сокращения времени
реализации проекта в случае появления непредвиденных обстоятельств,
препятствующих запланированному плану реализации проекта.
Распечатка результатов построения, упорядочения и расчёта временных
параметров сетевого графика для оптимизации комплекса работ на ЭВМ представлена
в приложении Г.
Заключение
В данной курсовой работе были рассмотрены методы решения задач
нелинейного и линейного программирования, транспортной и двойственной задач, а
также методы оптимизации решения задач сетевого планирования и управления.
Процесс решения транспортной задачи состоит из двух этапов: отыскания опорного
решения и последовательного его улучшения с целью отыскания опорного решения
задачи. Решение двойственной задачи содержит: формулировку прямой оптимальной
задачи на максимум общей стоимости продукции, определение оптимальной
производственной программы; формулировку двойственной задачи и ее оптимальный
план; анализ использования ресурсов в оптимальном плане; изменения общей
стоимости продукции и плана выпуска при определенных условиях.
Оптимизации решения задач сетевого планирования и управления включает в
себя: правила и приемы разработки сетевых моделей в детерминированной постановке;
табличный алгоритм расчета временных характеристик СМ; принципы и подходы к
оптимизации мероприятий (проектов, программ), требующих для реализации
привлечения многих исполнителей и разнообразных дефицитных ресурсов.
Список использованных источников
модель программирование раскрой древесная стружечная плита
1
Моделирование и оптимизация процессов деревообработки: Методические указания по
выполнению лабораторной и курсовой работы «Оптимизация раскроя
древесностружечных плит на мебельные заготовки» для студентов специальности
260200 «Технология деревообработки»/ Брян. ГИТА; Сост.: Э.В. Алендорф. -
Брянск, 1999. -15 с.
2
Моделирование и оптимизация процессов деревообработки: Учебно-методическое
пособие по решению оптимизационных задач методами сетевого планирования и
управления на детерминированной модели для студентов III курса специальности 260200 «Технология
деревообработки»/ Брян. ГИТА; Сост.: Э.В. Алендорф. - Брянск, 2000. -19 с.
3
Моделирование и оптимизация процессов деревообработки: Конспект лекций по
дисциплине «Математическое моделирование» двойственной задачи линейного
программирования для студентов специальности 260200 «Технология
деревообработки»/ Брян. ГИТА; Сост.: Э.В. Алендорф. - Брянск, 2004. -12 с.
Моделирование
и оптимизация процессов деревообработки: Методические указания по решению
«Транспортной задачи и задач транспортного типа» для студентов специальности
260200 «Технология деревообработки»/ Брян. ГИТА; Сост.: Э.В. Алендорф. -
Брянск, 2000. -20 с.
Моделирование
и оптимизация процессов деревообработки: Методические указания по
упорядочиванию последовательности запуска деталей в обработку для студентов
специальности 260200 «Технология деревообработки» / Брян. ГИТА; Сост.: Э.В.
Алендорф. - Брянск, 2001. -18 с.
Пижурин, А.А.
Моделирование и оптимизация процессов деревообработки: учебник/ А.А. Пижурин,
А.А. Пижурин. - М.: МГУЛ, 2004. - 375 с.