Изучение газодинамики в рабочем пространстве печи высокоточного нагрева при различном количестве загруженных заготовок
Аннотация
Данная выпускная квалификационная работа посвящена изучению нагрева
металла в печи высокоточного нагрева с применением математического
моделирования.
Моделирование осуществляется при помощи современного
программно-вычислительного комплекса FLUENT. Данный пакет предназначен для моделирования сложных течений жидкостей и
газов с широким диапазоном изменения теплофизических свойств.
Сравниваются случаи с разным количеством загруженных в печь заготовок при
одинаковой массе садки:
одна заготовка размерами 0,250х0,250х4 м;
две заготовки размерами 0,176х0,176х4 м;
четыре заготовки размерами 0,125х0,125х4 м.
Время нагрева составляет десять минут. Температура продуктов сгорания на
выходе из горелки 1273К. Массовый расход соответствует скорости продуктов
сгорания на выходе из горелки 100 м/с.
В результате получено распределение плотности теплового потока и
температуры по поверхности заготовок, распределение вектора скорости и
температуры в рабочем пространстве печи, а также зависимость изменения температурного
поля во времени.
Пояснительная записка к выпускной квалификационной работе изложена на 111
страницах, содержит 89 рисунков, 5 таблиц, список использованных источников из
9 наименований.
Содержание
Введение
1 Методы моделирования в металлургии
.1 Эксперимент
.1.1 Физическое моделирование
.1.2 Математическое моделирование
.1.2.1 Типы математических моделей
.1.2.1.1 Статистические модели
.1.2.1.2 Детерминированные модели
.2 Современная вычислительная гидрогазодинамика (CFD)
.3 Математическое моделирование в ПВК FLUENT
Математическое моделирование нагрева металла в печи ВТН
.1 Постановка задачи и исходные данные
.1.1 Геометрия системы для трех вариантов загрузки печи
.1.2 Зависимости теплофизических характеристик от температуры
.3 Математическая постановка задачи
Результаты моделирования
.1 Распределение температурного поля в различных сечениях
рабочего пространства печи для трех вариантов загрузки
.2 Распределение температурного поля в различных сечениях
заготовок для трех вариантов загрузки печи
.3 Распределение вектора скорости в рабочем пространстве печи
для трех вариантов загрузки
.4 Распределение плотности теплового потока по поверхности
заготовок для трех вариантов загрузки печи
.5 Распределение температурного поля по поверхности заготовок
для трех вариантов загрузки печи
.6 Изменение температурного поля заготовок во времени для
трех вариантов загрузки печи
Выводы
Список использованных источников
Введение
металлургия гидрогазодинамика моделирование нагрев печь
Нагревательные и термические печи являются основным технологическим
звеном металлообрабатывающей, машиностроительной и других отраслей
промышленности. Нагрев металла перед обработкой давлением или при
термообработке металлических изделий является достаточно сложным процессом, при
котором одновременно протекают явления, связанные с течением жидкости, тепло- и
массообменном, химическими реакциями. В тоже время от правильного выбора
технологического режима нагрева зависит качество получаемых изделий.
Эффективность проектирования и эксплуатации печей в значительной степени
определяется уровнем наших знаний о происходящих в печи процессах и
совершенством методов их расчета. При этом возникает необходимость понимания и
исследования этих процессов для выбора наиболее безопасных и эффективных режимов
работы нагревательной печи.
Информацию о происходящих в печи теплофизических процессах можно получить
при проведении натурных или физических экспериментов, но в большинстве случаев
такие опыты чрезмерно дороги и часто невозможны.
Альтернативой является теоретическое исследование с применением
математического моделирования. Достоинствами теоретического исследования
являются низкая стоимость, быстрота исследования, возможность получения
значений всех переменных во всей исследуемой области, возможность моделирования
как реальных, так и идеальных условий.
Детерминированные математические модели теплофизических процессов давно и
широко применяются исследователями и проектировщиками для совершенствования
конструкций и режимов работы промышленных печей.
Однако такие модели не удовлетворительны с точки зрения качества
математического описания движения газов внутри печного пространства. Между тем,
без такого описания невозможно с достаточной точностью описать процессы
конвективного переноса тепла и массы, играющие важную роль в формировании поля
температур и концентраций компонентов продуктов сгорания.
Современное развитие математического моделирования и компьютерных
технологий привело к созданию мощных программно-вычислительных комплексов. Эти
программные продукты позволяют успешно и с высокой точностью решать довольно
сложные задачи вычислительной теплофизики и детально описывать все происходящие
при этом процессы.
Применение современных ПВК достаточно часто встречается в практике
зарубежных исследователей при совершенствовании и проектировании тепловых
технологических агрегатов металлургической и других отраслей промышленности.
Одним из таких программно-вычислительных комплексов является FLUENT - продукт, предоставляемый компанией
ANSYS Inc и обладающий широким набором моделей для расчета
процессов гидрогазодинамики, тепло- и массообмена, горения.
В данной дипломной работе с помощью ПВК FLUENT проведено моделирование нагрева одной, двух, четырех
заготовок в печи высокоточного нагрева
1 Методы моделирования в металлургии
.1 Эксперимент
Эксперимент занимает главенствующее место среди способов получения
информации о внутренних взаимосвязях явлений в природе и технике.
Экспериментальные поиски часто ведутся в таких областях, где теоретически
нельзя сделать каких-либо предвидений. С помощью экспериментальных данных,
получаемых непосредственно от изучаемых объектов, проверяется истинность
теоретических предпосылок.
По мере роста сложности исследуемых процессов и явлений возрастают
затраты на аппаратуру и проведение эксперимента. Для проведения некоторых
специальных экспериментов требуется такое количество энергии, которое было бы
достаточным для энергоснабжения города средней величины. При этом постоянно
возрастает сложность решаемых задач, а большой объем информации, необходимой
для выяснения внутренних взаимосвязей в природе и технике, заставляет применять
все более сложные многомашинные комплексы для обработки информации, а
характеристики объектов испытаний все чаще оказываются недоступными
непосредственному измерению. Вследствие этого совокупность
технико-экономических показателей, по которым проводится оценка испытуемого
объекта или принимаются важные организационные и инженерные решения, не
совпадает, как правило, с совокупностью параметров объекта, определяемых по
результатам натурного эксперимента.
Под экспериментом понимается система операций и наблюдений, направленных
на получение информации об объекте исследования. Составной частью эксперимента
является опыт - воспроизведение исследуемого явления в определенных условиях
при возможности регистрации и количественной оценки состояния или результатов
функционирования исследуемого объекта [1]. Эксперимент проводится на
промышленном оборудовании, лабораторной установке, физической или
математической модели. При этом механизм изучаемого процесса известен лишь
частично или совсем не известен. В таких случаях объект исследования можно
представить в виде «черного ящика» - системы внутренних связей, недоступных
исследователю. Известны лишь переменные величины, воздействующие на объект
исследования, и величины, характеризующие его состояние или результаты
функционирования. Первые называют входными величинами, или факторами, вторые
выходными, или откликом (Рисунок 1).
Все факторы делятся на три группы:
- группа управляемых факторов X,
значения которых выбираются и целенаправленно изменяются в ходе исследования. В
каждом конкретном случае количество этих факторов и их числовые значения
определены (либо изначально, либо при планировании эксперимента);
группа неуправляемых факторов W, значения
которых известны (температура окружающей среды и т.п.);
- группа неуправляемых случайных факторов Z, значения которых неизвестны
(неоднородность материала, колебания скорости потока и т.п.).

Рисунок 1 - Модель объекта исследования
В связи с наличием третьей группы факторов отклик - случайная величина,
ее математическое ожидание как функция от управляемых факторов называется
функцией отклика Y.
Для получения значимых результатов экспериментального исследования важно:
грамотно сформулировать цель эксперимента;
определить управляемые и случайные факторы, отклик - величину,
характеризующую результат исследования, оценить диапазоны их изменения;
составить схему экспериментальной установки, определить необходимую
точность измерения, как следствие - приборную базу;
составить план эксперимента, то есть определить количество экспериментов,
уровни (значения) управляемых факторов;
провести статистическую обработку результатов эксперимента, опираясь на
рекомендации теории;
наглядно оформить и провести анализ результатов.
От правильности формулирования цели эксперимента в значительной степени
зависит успех самого эксперимента. Для грамотного формулирования необходимо
четко представлять себе основные виды экспериментов. Их три:
задачи, связанные с проверкой статистических гипотез, дисперсионный анализ и
регрессионный анализ.
В задачах, связанных с проверкой статистических гипотез, формулируются
основная (нулевая) Ho и конкурирующая H1
гипотезы. Далее
планируется эксперимент, обрабатываются его результаты, с помощью
статистических критериев с заданным уровнем надежности (то есть, вероятности
правильного ответа) принимается одна из двух гипотез.
При дисперсионном анализе имеется один или несколько управляемых факторов
и одна функция отклика. Необходимо установить, значимо ли (в статистическом
смысле) влияние каждого фактора на функцию отклика, и упорядочить факторы (если
их несколько) по степени влияния на функцию отклика.
При регрессионном анализе ставится задача отыскания функциональной
зависимости математического ожидания отклика M(Y) от значений одного или нескольких
факторов: M(Y)=f(X1) или M(Y)=f(X1,X2) и т.д. Это необходимо для прогнозирования значения функции
отклика при некотором наборе значений факторов и для решения различных
оптимизационных задач, связанных с данным процессом.
Объект исследования в эксперименте может представлять собой реально
существующий процесс или явление. В этом случае эксперименты проводятся в
реальном масштабе времени и пространства. В качестве функций отклика, как
правило, стараются выбирать не абсолютные, а относительные величины. Часто
проводятся модельные эксперименты на физических моделях объектов или процессов.
По характеру организации и методам обработки результатов эксперимент
может быть пассивным или активным. В пассивном
эксперименте исследователь наблюдает за объектом, не вмешиваясь в процесс его
функционирования. В активном эксперименте исследователь сам
изменяет уровень факторов.
К контролируемым факторам предъявляются следующие требования:
- управляемость - возможность поддерживать выбранный уровень в течение
необходимого для измерения отрезка времени;
- достаточно высокая точность, с которой
поддерживается и измеряется уровень фактора;
независимость - возможность задать любой уровень данного фактора вне
зависимости от уровней других факторов;
совместимость - безопасность функционирования объекта исследования и
возможность измерения отклика в любой точке той части факторного пространства,
которая является областью экспериментирования [1].
Отклик оценивается по результатам прямых или косвенных измерений.
Желательно, чтобы его можно было оценить количественно, в
противном случае следует прибегнуть к ранжированию по заранее выбранной шкале
(например, отлично - 80, хорошо - 60, удовлетворительно - 40, плохо - 20).
Способ оценки отклика зависит от природы отклика (случайная или
неслучайная величина) и точности измерений.
Если отклик является неслучайной величиной и ошибки измерения малы по
сравнению со значениями отклика, то при i-ом измерении получаем:
 (1)
(1)
где
 - истинное значение отклика,
- истинное значение отклика,  - измеренное значение отклика,
- измеренное значение отклика,  - по грешность измерения.
- по грешность измерения.
Если
 то погрешностью измерения можно пренебречь и
полученное после первого измерения значение
то погрешностью измерения можно пренебречь и
полученное после первого измерения значение  принять за истинное.
принять за истинное.
Если
отклик является неслучайной величиной, а погрешностями измерений нельзя
пренебречь, то для уменьшения влияния погрешностей производится многократное
измерение отклика в одинаковых условиях (при одних и тех значениях уровней
факторов).
За
истинное значение отклика в данном случае принимают среднее арифметическое
значение результатов параллельных измерений:
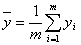 (2)
(2)
где
m - количество проведенных экспериментов,  -
измеренное значение отклика.
-
измеренное значение отклика.
Точность
соответствия 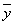 истинному значению тем выше, чем больше m.
истинному значению тем выше, чем больше m.
1.1.1
Физическое моделирование
В
настоящее время физическое моделирование применяется весьма широко, особенно
для процессов, протекающих в сложных геометрических системах, а также для
решения задач, связанных с движением жидкостей и газов. С помощью физического
моделирования исследуют и ряд сложных процессов в металлургии, таких как
взаимодействие газовой струи с жидким металлом и шлаком, разбрызгивание металла
и шлака, горение и движение газов в металлургических печах и т.д.
Физическая
модель характеризуется тем, что основные процессы, протекающие в ней и в
оригинале, имеют одинаковую физическую природу, однако, это не означает
тождественность обоих объектов. Процесс в физической модели обычно
схематизирован по сравнению с процессом в оригинале и может протекать в иных по
абсолютной величине пространственных и временных границах. Например, процесс
движения горючих газов в промышленной печи можно изучить на модели, размещенной
на столе. При этом внутренние границы оригинала и модели могут быть подобны
лишь приблизительно, а вместо высокотемпературных продуктов сгорания в модели
может двигаться обычный воздух.
Для
построения моделей всех типов желательно располагать максимальной информацией
об оригинале, однако, физическое моделирование позволяет ограничиться
незначительными знаниями, например, перечнем физических величин, существенных
для этих явлений. Кроме этого, физическое моделирование не требует знания
математических связей между этими величинами, в отличие от математического
моделирования. В этом заключается большое преимущество физического
моделирования перед другими способами. Другое преимущество этого способа -
наглядность получаемых результатов.
Недостатком
физического моделирования, по сравнению с математическим, является
необходимость изготовления моделей, подбора и комплектации оборудования и
измерительных приборов, проведения экспериментов [2].
Широкое
распространение вычислительной техники в настоящее время привело к тому, что
значительная область задач, решавшихся раньше на физических моделях, отошла к
математическому моделированию.
В
основе физического моделирования лежит теория подобия, которая утверждает, что
абсолютное подобие может иметь место лишь при замене одного объекта другим
точно таким же. В случае же исследования масштабных физических моделей
необходимо обеспечивать равенство безразмерных критериев подобия (определяющих
критериев). Основные критерии подобия, применяемые в исследованиях по
гидрогазодинамике и теплопередаче, приведены в таблице 1.
Таблица
1 - Основные критерии подобия
|
Критерий
|
Наименование
|
Физический смысл и область
применения
|
|
1
|
2
|
3
|
|
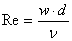 Критерий режима течения (Рейнольдса)Характеризует
гидродинамический режим потока и определяет соотношение в нем сил инерции и
молекулярного трения. Применяется при изучении вынужденных течений. Критерий режима течения (Рейнольдса)Характеризует
гидродинамический режим потока и определяет соотношение в нем сил инерции и
молекулярного трения. Применяется при изучении вынужденных течений.
|
|
|
|
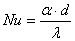 Безразмерный коэффициент теплоотдачи (Критерий
Нуссельта)Характеризует соотношение между интенсивностями конвективной
теплоотдачи и теплопроводности в пограничном слое потока. Применяется в
исследованиях теплообмена при конвекции. Безразмерный коэффициент теплоотдачи (Критерий
Нуссельта)Характеризует соотношение между интенсивностями конвективной
теплоотдачи и теплопроводности в пограничном слое потока. Применяется в
исследованиях теплообмена при конвекции.
|
|
|
|
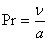 Критерий подобия температурных и скоростных полей
(Прандтля)Характеризует меру подобия скоростных и температурных полей.
Характеризует также свойства теплоносителей. Применяется в исследованиях
теплообмена при конвекции. Критерий подобия температурных и скоростных полей
(Прандтля)Характеризует меру подобия скоростных и температурных полей.
Характеризует также свойства теплоносителей. Применяется в исследованиях
теплообмена при конвекции.
|
|
|
|
 Критерий гравитационного подобия
(Фруда)Характеризует соотношение сил инерции и тяжести в однородном потоке. Критерий гравитационного подобия
(Фруда)Характеризует соотношение сил инерции и тяжести в однородном потоке.
|
|
|
|
В
приведенных в таблице 1 формулах:  -
коэффициент теплоотдачи, a -
коэффициент температуропроводности,
-
коэффициент теплоотдачи, a -
коэффициент температуропроводности,
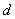 - диаметр,
- диаметр,
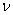 - коэффициент кинематической вязкости,
- коэффициент кинематической вязкости, 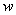 - скорость,
- скорость,
 - длина,
- длина, 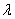 -
коэффициент теплопроводности,
-
коэффициент теплопроводности, 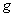 - ускорение свободного падения.
- ускорение свободного падения.
Основная
идея физического моделирования гидродинамических и тепловых процессов в
следующем: точное воспроизведение в модели численных значений всех определяющих
критериев практически невозможно, поэтому достаточно выбрать хотя бы один,
самый важный для данного процесса определяющий критерий [1].
В
зависимости от цели исследования выбирается наиболее важный критерий подобия,
затем выполняется построение физической модели, подбор параметров среды и
других факторов с тем, чтобы в максимальной степени обеспечить равенство
критериев подобия в модели и моделируемом процессе (устройстве).
При
уменьшенных размерах модели рабочее число Рейнольдса достигается увеличением
скорости, уменьшением кинематической вязкости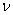 , например,
за счет применения другой жидкости. При уменьшении размера модели следует иметь
в виду, что при этом, как правило, увеличивается относительная шероховатость,
уменьшаются эффекты, связанные с естественной конвекцией и т.д.
, например,
за счет применения другой жидкости. При уменьшении размера модели следует иметь
в виду, что при этом, как правило, увеличивается относительная шероховатость,
уменьшаются эффекты, связанные с естественной конвекцией и т.д.
Нередко
значения критериев подобия выбираются в качестве контролируемых факторов при
построении модели. Это часто позволяет сократить количество факторов.
Например,
при экспериментальном исследовании процессов теплообмена ищут зависимость
величины критерия Нуссельта от величины критерия Рейнольдса в виде:
 (3)
(3)
Для большинства физических процессов теоретически нет ограничений на
выбор константы геометрического подобия. В этих случаях константу подобия нужно
выбирать исходя из условий удобства изготовления модели и проведения опытов.
Использование установок слишком больших размеров может привести к
нежелательному усложнению их изготовления и удорожанию, а также увеличению
количества расходуемых материалов. В то же время, применение установок слишком
малых размеров может затруднить наблюдение за процессом и проведение опытов
вследствие малости зоны процесса, а также усложнить изготовление отдельных
мелких узлов.
Необходимо учитывать, что любой эксперимент сопровождается погрешностями
(методическими, измерений) и содержит элементы неопределенности (случайности).
Проведение повторных опытов не дает полностью совпадающих результатов. Поэтому
процедура обработки должна учитывать эти обстоятельства. Обработка результатов
включает предварительную обработку результатов экспериментов, вычисление оценок
коэффициентов функции отклика и проведение ряда проверок: однородности
дисперсии воспроизводимости, адекватности модели и значимости коэффициентов.
1.1.2 Математическое моделирование
Понятие «математическое моделирование» в последние два - три
десятилетия является едва ли не самым распространенным в научной литературе, по
крайней мере, в естественнонаучной и технической. Сегодня трудно представить
себе проектную или конструкторскую организацию, не использующую в своей
практике в той или иной мере математические модели. Все более распространенным
и эффективным становится применение математического моделирования в научных
исследованиях. Интенсивно разрабатываются математические модели в экономике,
управлении, истории, биологии и многих других областях знаний.
С процессом моделирования и различными моделями человек начинает
сталкиваться с раннего детства. Так большинство игрушек в большей или меньшей
степени воспроизводят (моделируют) отдельные свойства и форму реально существующих
предметов и объектов.
Чтобы в дальнейшем четко представлять, о чем идет речь, введем
определения некоторых наиболее важных терминов, таких как модель,
математическая модель и математическое моделирование.
Чаще всего термин «модель» используют для обозначения устройства,
воспроизводящего строение или действие какого-либо другого устройства
(уменьшенное, увеличенное или в натуральную величину) или для обозначения
аналога (чертежа, графика, плана, схемы, описания и т.д.) какого-либо явления,
процесса или предмета.
К недостаткам термина «модель» следует отнести его многозначность. В
словарях можно найти до восьми различных значений данного термина, из которых в
научной литературе наиболее распространены два:
модель как аналог реального объекта;
модель как образец будущего изделия.
Если выделять функции моделей, то основными можно считать следующие
четыре:
а) модели как средство познания реального мира;
б) модели как средство передачи информации и средство общения;
в) модели как средство обучения;
г) модели как средство прогнозирования состояния объекта и постановки
математических экспериментов [3].
Модели как средство познания реального мира выявляют характеристики
объекта, его внутренние и внешние связи. Уже сама попытка составления модели
позволяет обнаружить и устранить нелогичности и противоречия наших
представлений, наметить пути дальнейших исследований. Модели как средство
обучения обеспечивают приобретение надежных профессиональных навыков без риска
возникновения критической ситуации
Таким образом, самым важным и наиболее распространенным предназначением
моделей является их применение при изучении и прогнозировании сложных процессов
и явлений. Другое, не менее важное, предназначение - выявление наиболее
существенных факторов, формирующих те или иные свойства объекта.
Математическая модель - это описание натурного образца, его свойств и
поведения с необходимой степенью приближения и подробности в виде формул,
уравнений или систем уравнений. Уравнения могут быть алгебраическими,
дифференциальными, интегральными или интегрально-дифференциальными.
Под математическим моделированием в технике понимают адекватную замену
исследуемого технического устройства или процесса соответствующей
математической моделью и ее последующее изучение методами вычислительной
математики с привлечением средств современной вычислительной техники. Поскольку
такое изучение математической модели можно рассматривать как проведение
эксперимента на компьютере при помощи вычислительно-логических алгоритмов, то в
научно-технической литературе термин вычислительный эксперимент часто
выступает как синоним термина «математическое моделирование»[4].
На сегодняшний день математическое моделирование тепловых процессов,
происходящих в промышленных печах, широко используется в металлургической теплотехнике.
Это обусловлено рядом преимуществ, которыми обладает математическое
моделирование.
Во-первых, высокая точность и объем получаемой с их помощью информации,
во-вторых, возможность исследования сложных процессов и, в-третьих,
экономическая эффективность по сравнению с исследованием процессов,
происходящих в реальных металлургических агрегатах, на стендах или на
физических моделях.
Предварительный расчет, основанный на адекватных математических моделях,
позволяет избежать ошибок при проектировании узлов и устройств и, таким
образом, значительно сократить расходы ресурсов на создание и опытную отработку
образцов новой техники. А также, математическое моделирование делает возможным
получение сравнительных оценок для агрегатов (машин), различающихся по
структуре, что редко достижимо при физическом моделировании.
Применение математического моделирования целесообразно, в частности, при
выборе рациональных параметров и схемы нового агрегата, формировании эталонных
рабочих характеристик, выявлении предельных возможностей и поиске путей
модернизации.
Практический опыт, накопленный к настоящему времени в области разработки
и использования математических моделей позволяет сформулировать основные
принципы моделирования, к которым относят принцип информационной достаточности,
принцип осуществимости, принцип множественности, принцип агрегирования и
принцип параметризации.
Принцип информационной достаточности говорит о том, что при полном
отсутствии информации об исследуемом объекте построение его модели невозможно.
При наличии полной информации об объекте его моделирование лишено смысла.
Должен существовать некоторый критический уровень априорных сведений об объекте
(уровень информационной достаточности), при достижении которого может быть
построена адекватная модель.
Создаваемая модель должна обеспечивать достижение поставленной цели
исследования с вероятностью, существенно отличающейся от нуля, и за конечное
время. Обычно задается некоторое пороговое значение вероятности достижения цели
моделирования, а также приемлемая граница времени достижения этой цели. В этом
и заключается принцип осуществимости.
Принцип множественности является ключевым. Создаваемая модель должна
отражать в первую очередь те свойства реального объекта, системы, явления,
которые влияют на выбранный показатель эффективности. Соответственно, при
использовании любой конкретной модели исследуются лишь некоторые стороны
реального объекта. Для более полного исследования необходим ряд моделей,
позволяющих отражать исследуемый объект с разных сторон и с разной степенью
детальности.
В большинстве случаев сложную систему можно представить в виде нескольких
подсистем, для адекватного описания которых оказываются пригодными некоторые
стандартные математические схемы - принцип агрегирования. Также данный принцип
позволяет достаточно гибко перестраивать модель в зависимости от задач
исследования.
В ряде случаев моделируемая система имеет в своем составе некоторые
относительно изолированные подсистемы, характеризующиеся определенным
параметром, в том числе векторным. Такие подсистемы можно заменять в модели
соответствующими числовыми величинами, а не описывать процесс их
функционирования. При необходимости зависимость значений этих величин от
ситуации может задаваться в виде таблицы, графика или аналитического выражения
(формулы). Принцип параметризации позволяет сократить объем и продолжительность
моделирования. Однако надо иметь в виду, что параметризация снижает
адекватность модели [5].
Каждая математическая модель должна обладать рядом таких свойств, как:
Полнота;
Адекватность;
Экономичность;
Продуктивность;
Наглядность.
Полнота позволяет отразить в достаточной мере именно те характеристики и
особенности исследуемого объекта, которые интересуют нас с точки зрения
поставленной цели проведения вычислительного эксперимента.
Способность математической модели отражать свойства объекта с
относительной погрешностью не хуже заданной, называют адекватностью. Если
результаты моделирования удовлетворяют исследователя и могут служить основой
для прогнозирования поведения или свойств исследуемого объекта, то говорят, что
модель адекватна (от лат. adaequatus - приравненный) объекту. Адекватность модели в наибольшей степени
зависит от целей моделирования и принятых критериев, поэтому модель, адекватная
при выборе одних характеристик, может быть неадекватной при выборе других
характеристик объекта.
Экономичность математической модели оценивается затратами на
вычислительные ресурсы (машинное время, память) необходимые для реализации
математической модели на компьютере. Эти затраты зависят от числа
арифметических операций при использовании модели, от особенностей применяемого
компьютера и многих других факторов. Свойство экономичности часто связывают с
простотой математической модели. Очевидно, что из двух моделей, позволяющих достичь
желаемой цели и получить требуемые результаты с заданной точностью,
предпочтение будет отдано более простой.
Продуктивность связана с достоверностью исходных данных. Если они
являются результатом измерений, то точность их измерения должна быть выше, чем
для тех параметров, которые получаются при использовании математической модели.
В противном случае модель будет непродуктивной и ее применение для анализа
конкретного объекта теряет смысл.
Использование математической модели упрощается, если ее составляющие
(например, отдельные члены уравнений) имеют ясный содержательный смысл, что
позволяет предвидеть результаты вычислительного эксперимента и облегчить
контроль их правильности [6].
В качестве еще одного свойства модели можно рассматривать потенциальность
модели или предсказательность с позиций возможности получения новых знаний об
объекте. В научных исследованиях модели, не обладающие определенной
предсказательностью, едва ли могут считаться удовлетворительными. Известно
немало случаев, когда изучение или использование моделей позволило сделать
открытия. В качестве примера можно привести открытие планеты Нептун астрономом
Лекселем, который выявил неправильность в движении Урана, воспользовавшись
моделью движения этой планеты, основанной на законе всемирного тяготения, что
означало наличие притяжения от неизвестной планеты, вращающейся на более
далеком расстоянии от Солнца.
Разработка любой математической модели начинается с ее формулировки, т.е.
с постановки задачи. При этом математическая модель должна охватывать важнейшие
для данной задачи стороны исследуемого процесса.
Наиболее сложной и ответственной задачей при разработке модели является
выбор связей и характеристик процесса, существенных для данной задачи и
подлежащих формализации и включению в математическую модель. Если
математическая модель будет проработана недостаточно тщательно, то все выводы
будут ненадежными, какие бы методы не применялись для расчета.
Следующий этап - математическое исследование. В зависимости от сложности
модели применяются различные математические подходы. Для грубых и несложных
моделей зачастую удается получить аналитическое решение. Что касается более
точных и сложных моделей, такое решение получают достаточно редко, поэтому для
их решения используют численные методы, позволяющие добиться достаточно высокой
математической точности. Надо отметить, что введение в модель упрощений снижает
точность расчета.
Заключительной стадией разработки математической модели является анализ
полученного математического решения и его сравнение с экспериментальными
результатами. Если расчеты хорошо согласуются с контрольными экспериментами, то
это свидетельствует о правильности выбранной модели. Если же модель и
эксперимент не согласуются - модель необходимо пересмотреть и уточнить.
Таким образом, систематизировав вышесказанное, делаем вывод о том, что
построение математической модели включает в себя следующие этапы:
а) формулировка законов, связывающих основные объекты модели;
б) исследование математической задачи;
в) проверка адекватности модели;
г) анализ модели и ее модификация.
Сегодня термины математическое моделирование и компьютерное моделирование
стали почти синонимами, так как большинство математических моделей требует
проведения расчетов на компьютере (компьютерных экспериментов).
Компьютерное моделирование можно разделить на три вида: численное,
имитационное и статистическое. При численном моделировании для построения
компьютерной модели используются методы вычислительной математики, а
вычислительный эксперимент заключается в численном решении некоторых
математических уравнений при заданных значениях параметров. Имитационное
моделирование - это вид компьютерного моделирования, для которого характерно
воспроизведение (имитация) процесса функционирования исследуемой системы. При
этом имитируются элементарные явления, составляющие процесс, с сохранением их
логической структуры, последовательности протекания во времени, что позволяет
получить информацию о состоянии системы в заданные моменты времени.
Статистическое моделирование - это вид компьютерного моделирования, позволяющий
получить статистические данные о процессах, протекающих в моделируемом объекте
[5].
Компьютерное моделирование незаменимо в тех случаях, когда натурный
эксперимент провести невозможно или затруднительно по тем или иным причинам.
Например, невозможно поставить натурный эксперимент, чтобы проверить
правильность той или иной космологической теории, однако, это вполне можно
выполнить при помощи компьютерного моделирования.
Однако между проведением физического и компьютерного эксперимента
существует много общего (Таблица 2).
Таблица 2 - Сравнение физического и компьютерного эксперимента.
|
Физический эксперимент
|
Компьютерный эксперимент
|
|
Образец
|
Математическая модель
|
|
Физический прибор
|
Программа
|
|
Калибровка
|
Тестирование программы
|
|
Измерения
|
Расчеты
|
|
Анализ данных
|
Анализ данных
|
С другой стороны, эксперимент, несомненно, является единственным методом
исследования новых фундаментальных явлений. В этом смысле расчет следует за
экспериментом. Однако расчет более эффективен для изучения проблемы, включающей
несколько взаимодействующих известных явлений. Но и в этом случае необходимо
обосновать результаты расчета путем сравнения их с экспериментальными данными.
Таким образом, исследование должно разумно сочетать расчет и
эксперимент. Доля каждого из двух компонентов будет зависеть от существа
проблемы, от целей исследования и от имеющихся экономических и других
ограничений.
1.1.2.1 Типы математических моделей
Математические модели (ММ) различают в основном по характеру отображаемых
свойств системы, степени детализации, способам получения и формального
представления.
В зависимости от способа получения различают функциональные
(стохастические), детерминированные и смешанные математические модели.
Функциональные математические модели получают в результате
экспериментальных исследований натурного образца. При этом исследуют лишь
реакцию системы на подаваемые на вход возмущения. Главное достоинство таких
моделей - это их простота, которая делает возможным применение таких моделей в
системах автоматического управления различными объектами. Но кроме достоинств
есть и свои недостатки - для анализа стохастических ММ необходимо использовать
выводы теории вероятностей, случайных процессов и математической статистики.
Однако основная трудность в их применении обычно связана с тем, что
вероятностные характеристики случайных величин (математические ожидания,
дисперсии, законы распределения) часто не известны или известны с не высокой
точностью, т.е. ММ не удовлетворяет требованию продуктивности. В таких случаях
эффективнее использовать ММ, более грубую по сравнению со стохастической, но и
более устойчивую по отношению к недостоверности исходных данных. Также
существенно ограничена универсальность данного типа моделей, поэтому приходится
строить свою функциональную модель для каждого индивидуального объекта. Это
происходит из-за того, что в функциональных моделях не вскрываются свойственные
объекту глубокие причинно-следственные связи, поэтому не учитывается все
многообразие проявлений процессов, протекающих в объекте, и влияние внешних
факторов на эти процессы [7].
Детерминированные математические модели строятся на основе
дифференциальных, интегральных или интегрально-дифференциальных уравнений,
описывающих каждый из существующих для данного натурного образца процессов и
полученных в рамках теории соответствующего процесса. В отличие от
функциональных математических моделей, детерминированные являются
универсальными, так как в них заложены не формальные связи между входными и
выходными переменными и параметрами, а информация о физических механизмах
соответствующих процессов, отражающая важнейшие причинно-следственные связи. В
силу универсальности детерминированных моделей их можно использовать для
различных объектов одного типа, поскольку специфические черты этих объектов
могут быть учтены в моделях с достаточной точностью. Недостатком
детерминированных моделей является их сложность [7].
Смешанные математические модели представляют собой нечто среднее между
функциональными и детерминированными моделями. Они строятся на основе одного
уравнения или небольшого числа уравнений, описывающих механизм лишь наиболее
существенных для данного натурного образца процессов. Влияние всех других
процессов учитывается с помощью настроечных коэффициентов. Эти коэффициенты
находят в результате сопоставления данных, полученных с помощью математической
модели, и данных, полученных в результате измерений, выполненных на образце.
Если ММ отражает элементы и их связи в системе, то ее называют
структурной математической моделью. Структурные ММ делят на
топологические и геометрические. Первые отображают состав системы и связи между
его элементами и чаще всего применяются на начальной стадии исследования
сложной системы. Такая ММ имеет форму графов, таблиц, матриц, списков и т.п., и
ее построению обычно предшествует разработка структурной схемы системы.
Геометрическая ММ дополнительно к информации, представленной в
топологический ММ, содержит сведения о форме и размерах системы и ее элементов,
об их взаимном расположении. В геометрическую ММ обычно входят совокупность
уравнений линий и поверхностей и алгебраические соотношения, определяющие
принадлежность областей пространства системе или ее элементам. Геометрические
ММ находят применение при проектировании элементов технических систем,
разработке технической документации и технологических процессов изготовления
изделий.
Функционирование сложных систем нередко удается описать лишь при помощи
совокупности ее реакций на некоторые известные (или заданные) входные
воздействия. Такую разновидность функциональной ММ относят к типу черного ящика
и обычно называют имитационной математической моделью, имея в виду, что она
лишь имитирует внешние проявления функционирования, не раскрывая и не описывая
существа протекающих в системе процессов. Имитационные ММ находят широкое
применение в исследовании сложных систем.
По форме представления имитационная ММ является примером алгоритмической
ММ, поскольку связь в ней между входными и выходными параметрами системы
удается описать лишь в форме алгоритма, пригодного для реализации в виде
программы. Если связи между параметрами системы можно выразить в аналитической
форме, то говорят об аналитических математических моделях. При создании
иерархии ММ одной и той же системы обычно стремятся к тому, чтобы упрощенный
вариант ММ был представлен в аналитической форме, допускающей точное решение,
которое можно было бы использовать для сравнения при тестировании результатов,
полученных при помощи более полных и поэтому более сложных вариантов ММ.
Ясно, что ММ конкретной системы по форме представления может включать
признаки как аналитической, так и алгоритмической ММ. Более того, в процессе
моделирования аналитическую ММ преобразуют в алгоритмическую.
Математические модели могут быть теоретическими или эмпирическими. Первые
получают в результате изучения свойств системы, протекающих в ней процессов на
основе использования известных фундаментальных законов сохранения, а также
уравнений равновесия, а вторые являются итогом обработки результатов внешних
наблюдений за проявлением этих свойств и процессов. Один из способов построения
эмпирических ММ заключается в проведении экспериментальных исследований,
связанных с измерением фазовых переменных системы, и в последующем обобщении
результатов этих измерений в алгоритмической форме или в виде аналитических
зависимостей. Поэтому по форме представления эмпирическая ММ может содержать
признаки как алгоритмической, так и аналитической ММ. Таким образом, построение
эмпирической ММ сводится к решению задачи идентификации.
Существенным признаком классификации ММ является их возможность описывать
изменение параметров системы во времени. Если при этом в ММ отражено влияние
инерционных свойств системы, то ее обычно называют динамической. В
противоположность этому ММ, которая не учитывает изменение во времени
параметров системы, называют статической.
Стационарные ММ описывают системы, в которых протекают так называемые
установившиеся процессы, т.е. процессы, в которых интересующие нас выходные
параметры постоянны во времени. К установившимся относят и периодические
процессы, в которых некоторые выходные параметры остаются неизменными, а
остальные претерпевают колебания.
Если выходные параметры системы изменяются медленно и в рассматриваемый
фиксированный момент времени этими изменениями можно пренебречь, то ММ считают
нестационарной.
Важным с точки зрения последующего анализа свойством ММ является ее
линейность, в смысле связи параметров системы линейными соотношениями. Это
означает, что при изменении какого-либо внешнего (или внутреннего) параметра
системы линейная ММ предсказывает линейное изменение зависящего от него
выходного параметра, а при изменении двух или более параметров - сложение их
влияний, т.е. такая ММ обладает свойством суперпозиции. Если ММ не обладает
свойством суперпозиции, то ее называют нелинейной.
Для количественного анализа линейных ММ разработано большое число
математических методов, тогда как возможности анализа нелинейных ММ связаны в
основном с методами вычислительной математики. Чтобы для исследования нелинейной
ММ системы можно было использовать аналитические методы, ее обычно линеаризуют,
т.е. нелинейные соотношения между параметрами заменяют приближенными линейными
и получают так называемую линеаризованную ММ системы. Так как линеаризация
связана с внесением дополнительных погрешностей, то к результатам анализа
линеаризованной модели следует относиться с определенной осторожностью, так как
линеаризация ММ может привести к утрате ее адекватности. Учет в ММ нелинейных
эффектов особенно важен, например, при описании смены форм движения или
положений равновесия, когда малые изменения входных параметров могут вызвать
качественные изменения в состоянии системы [5].
Каждый параметр системы может быть двух типов - непрерывно изменяющимся в
некотором промежутке своих значений или принимающим только некоторые дискретные
значения. Возможна и промежуточная ситуация, когда в одной области параметр
принимает все возможные значения, а в другой - только дискретные. В связи с
этим выделяют непрерывные дискретные и смешанные математические модели. В
процессе анализа ММ этих типов могут быть преобразованы одна в другую, но при
таком преобразовании следует контролировать выполнение требования адекватности
ММ рассматриваемой системе.
При математическом моделировании сложной системы описать ее поведение
одной ММ, как правило, не удается, а если такая ММ и была бы построена, то она
оказалась бы слишком сложной для количественною анализа, поэтому к таким
системам обычно применяют принцип декомпозиции. Он состоит в условном разбиении
системы на подсистемы, допускающие их независимое исследование с последующим
учетом их взаимного влияния друг на друга [5]. В свою очередь, принцип
декомпозиции можно применить и к каждой выделенной подсистеме вплоть до уровня
достаточно простых элементов. В таком случае возникает иерархия ММ связанных
между собой подсистем.
Иерархические уровни выделяют и для отдельных типов ММ. Например, среди
структурных ММ систем к более высокому уровню иерархии относят топологические
ММ, а к более низкому уровню, характеризующемуся большей детализацией, -
геометрические ММ. Среди функциональных ММ иерархические уровни отражают
степень детализации описания процессов, протекающих в системе и ее элементах. С
этой точки зрения обычно выделяют три основных уровня: микро- макро- и
мета-уровень.
Математические модели микроуровня описывают процессы в системах с
распределенными параметрами, а математические модели макроуровня - в системах с
сосредоточенными параметрами. В первых из них фазовые переменные могут зависеть
как от времени, так и от пространственных координат, а во-вторых - только от
времени [5].
Если
в ММ макроуровня число фазовых переменных имеет порядок  , то количественный анализ такой ММ становится громоздким
и требует значительных затрат вычислительных ресурсов. Кроме того, при столь
большом числе фазовых переменных трудно выделить существенные характеристики
системы и особенности ее поведения. В таком случае путем объединения и
укрупнения элементов сложной системы стремятся уменьшить число фазовых
переменных за счет исключения из рассмотрения внутренних параметров элементов,
ограничиваясь, лишь описанием взаимных связей между укрупненными элементами.
Такой подход характерен для ММ метауровня.
, то количественный анализ такой ММ становится громоздким
и требует значительных затрат вычислительных ресурсов. Кроме того, при столь
большом числе фазовых переменных трудно выделить существенные характеристики
системы и особенности ее поведения. В таком случае путем объединения и
укрупнения элементов сложной системы стремятся уменьшить число фазовых
переменных за счет исключения из рассмотрения внутренних параметров элементов,
ограничиваясь, лишь описанием взаимных связей между укрупненными элементами.
Такой подход характерен для ММ метауровня.
ММ
микроуровня называют одномерной, двумерной или трехмерной, если искомые фазовые
переменные зависят от одной, двух или трех пространственных координат
соответственно. Два последних типа ММ объединяют в многомерные математические
модели микроуровня.
1.1.2.1.1
Статистические модели
Далеко
не всегда можно построить аналитическую модель, как функциональную зависимость
выходного параметра системы от входных параметров. В этих случаях пользуются
построением статистических моделей.
Суть
метода заключается в замене эксперимента с реальной системой экспериментом с ее
математическим аналогом и имитацией работы системы (имитационное
моделирование).
В
первую очередь выбирается определенная модель, описывающая исследуемый процесс,
явление, систему. Затем, на основании математического описания модели и
численных методов разрабатывается внешние воздействия на систему, поведение ее
элементов, их взаимодействие и последовательное изменение состояний всей
системы во времени. После этого осуществляется одна случайная реализация моделируемого
явления. В конечном итоге, эксперимент многократно повторяется, и по
результатам моделирования определяются различные характеристики модели. При
этом полнота и достоверность полученной путем моделирования информации о
свойственных системе закономерностях зависят от того, насколько точно
использованная математическая модель описывает реальную систему, от точности
вычислительных методов, использованных при разработке моделирующего алгоритма,
и от числа проведенных испытаний.
В
основе статистического эксперимента лежит метод статистических испытаний (метод
Монте-Карло) - метод решения всевозможных задач, основанных на моделировании
случайных величин при помощи компьютера. В результате проведения серии
испытаний, получают множество частных значений наблюдаемой характеристики
(выборку). Полученные статистические данные обрабатываются и представляются в
виде численных оценок интересующих исследователя величин (характеристик
системы).
Отметим
две особенности метода статистического моделирования. Первая - относительная
простота вычислительного алгоритма. Как правило, составляется программа для
отслеживания одной реализации, а затем повторяется N раз. Вторая -
погрешность вычислений обычно пропорциональна  , т.е.
метод целесообразно применять там, где требуется очень высокая точность
вычислений.
, т.е.
метод целесообразно применять там, где требуется очень высокая точность
вычислений.
Метод
статистических испытаний применяется для моделирования сложных систем, в
которых не возможно или не целесообразно получить аналитические модели,
описывающие протекающие процессы, а также в случаях, когда реальные испытания
системы оказываются дорогостоящими или их невозможно проводить [5].
Данный
метод является универсальным, поскольку применим и к детерминированным задачам.
В этом случае производится замена детерминированной задачи эквивалентной схемой
некоторой вероятностной системы, выходные характеристики которой совпадают с
решением детерминированной задачи. В результате точное решение задачи
заменяется приближенным. Однако с ростом числа испытаний погрешности оценок
уменьшаются. При достаточно большом числе испытаний полученные результаты
приобретают статистическую устойчивость и с определенной точностью могут быть
приняты в качестве оценок неизвестных характеристик системы.
Имитационное
моделирование удобно для исследования практических задач: определение
показателей эффективности, сравнение вариантов построения и алгоритмов
функционирования систем, проверки устойчивости режимов системы при малых
отклонениях входных переменных от расчетных значений. Полнота имитации может
быть проверена путем построения серии последовательно уточняемых моделей. Если
дальнейшая детализация свойств модели не влияет на конечные показатели, то
усложнение модели можно прекратить. Как правило, моделируются те свойства
процесса, которые могут влиять на выбранный показатель эффективности или
критичны к наложенным ограничениям. Промежуточные результаты имитационного
моделирования имеют четкий физический смысл и позволяют обнаружить ошибки
программы.
Для
любого имитационного эксперимента независимо от физической природы и типа
моделируемой системы справедливы следующие утверждения:
с
увеличением продолжительности прогона (то есть наблюдения или объема испытаний)
отклонение измеряемой величины от ее точного значения уменьшается, поскольку
наблюдаемая система переходит в стационарное состояние;
влияние переходных условий можно уменьшить, если
увеличить количество прогонов модели (то есть количество экспериментов);
существует предел, за которым увеличение продолжительности прогона модели уже
не дает существенного повышения точности результата, измеряемой дисперсией.
Имитационное
моделирование не ограничивается разработкой модели и написанием соответствующей
программы, а требует подготовки и проведения статистического эксперимента. В
связи с этим результаты имитационного моделирования следует рассматривать как
экспериментальные данные, требующие специальной обработки и анализа.
1.1.2.1.2
Детерминированные модели
С
точки зрения содержательности детерминированные модели значительно превосходят
статистические, поскольку в них заложена глубоко содержательная информация о
физических механизмах соответствующих процессов, отражающая важнейшие
причинно-следственные связи.
Детерминированные
модели могут быть использованы для следующих целей:
исследование влияния различных переменных и параметров
на протекание процессов в образце;
расчета конструктивных и режимных параметров агрегата
на стадии его проектирования;
многовариантных расчетов агрегата с целью проверки
различных способов его конструктивного оформления и различных режимов работы;
численных экспериментов с последующей обработкой
результатов методами теории подобия или статистическими методами с целью
построения упрощенных математических моделей;
в какой-либо процедуре оптимизации с целью определения
оптимальных значений конструктивных, либо режимных параметров;
включения в банк моделей системы автоматизированного
проектирования (САПР) агрегатов; при этом модель может использоваться как для
однократного либо многовариантного расчета, так и для оптимизации параметров;
создание на их основе (с использованием ЭВМ)
тренажеров для обучения персонала методам правильной эксплуатации агрегатов
[7].
Процесс
разработки детерминированной математической модели, численно реализуемой на компьютере,
включает несколько этапов, которые одновременно представляют собой составляющие
структуры модели:
а)
математическая формулировка задачи;
б)
система алгебраических уравнений;
в)
выбор и применение численного метода решения;
г)
составление алгоритма решения задачи на компьютере;
д)
программная реализация математической модели.
Результат
качественного анализа представляют в виде системы уравнений, обычно
дифференциальных, интегральных, либо интегро-дифференциальных уравнений. При
этом часто исходную сложную систему уравнений упрощают на основе обоснованных
допущений о характере протекания процесса. В математическую формулировку задачи
входят кроме того краевые, т.е. начальные и граничные условия, а также
геометрические и физические параметры задачи.
Система
алгебраических уравнений - это представление исходных уравнений в вид, удобный
для применения численных методов. Для этого используется какой-либо метод
дискретизации, т.е. замены непрерывных изменений аргументов и функций
множествами их дискретных значений. Краевые условия при этом также записываются
в виде алгебраических соотношений.
Получив
систему алгебраических уравнений, выбирают метод ее решения. Если система
оказывается нелинейной, в процессе ее решения приходится использовать
какой-либо итерационный метод, т.е. метод последовательных приближений,
реализуемый в программе в виде цикла.
После
выбора численного метода решения, следует составление алгоритма решения задачи
на компьютер, причем численные методы обычно представляют в виде структурной
схемы. Далее составляют программу на одном из алгоритмических языков.
Программная
реализация математической модели включает отладку и тестирование программы.
Иногда
некоторые из указанных этапов опускают. После того, как разработка модели
закончена, проверяют ее качество, т.е. выполняют проверку ее адекватности путем
сопоставления расчетных результатов либо с экспериментальными данными, либо с
результатами точного аналитического решения простой задачи, называемой
модельной. Если результаты такого сопоставления оказываются
неудовлетворительными, это означает, что либо несправедливы принятые допущения,
либо имеются ошибки в численном методе решения. Последовательно изменяя либо
формулировку задачи, либо процедуру численного решения, добиваются адекватности
разработанной математической модели.
Математическое
моделирование тепловой работы промышленных печей является достаточно сложной
задачей, т.к. включает в себя задачи внутреннего и внешнего теплообмена.
Внутренние задачи обычно формулируются в виде уравнений теплопроводности с
соответствующими краевыми (начальными и граничными условиями), т.к. в
нагревательных и термических печах рассматривается распространение тепла в
твердом металле. Математическая модель внешнего теплообмена в
высокотемпературных печах включает в себя описание совместного
радиационно-конвективного переноса тепла (сложный теплообмен), турбулентного
движении газов и горения в турбулентном потоке.
Наибольшее
распространение получили комплексные математические модели тепловой работы
промышленных печей, объединяющие задачи как внутреннего, так и внешнего
теплообмена. Соответствующие задачи называются сопряженными задачами
теплообмена и требуют одновременного, совместного численного расчета
внутреннего и внешнего теплообмена. Именно эти модели позволяют получить
наиболее достоверную информацию о тепловой работе агрегатов и должны
использоваться для их исследования, многовариантных расчетов и оптимизации.
Для
решения сопряженной задачи теплообмена могут быть использованы два различных
итерационных алгоритма. В первом алгоритме вначале задают температуру (точнее,
ее распределение) на поверхности обрабатываемого в печи материала, затем, эту
температуру используют в качестве граничного условия для решения задачи
внешнего теплообмена, и в результате получают плотность теплового потока на
этой поверхности. После этого решают задачу внутреннего теплообмена, задавая на
поверхности полученную величину плотности теплового потока, что позволяет найти
новое значение температуры на поверхности, которое сравнивают с заданным. Если
расхождение превышает некоторую допустимую величину, вновь решают задачу
внешнего теплообмена, используя новое значение температуры на поверхности. Этот
итерационный процесс продолжают до тех пор, пока разность между значениями температуры
для двух последовательных итераций не окажется приемлемой.
Второй
вариант итерационного алгоритма отличается от предыдущего тем, что сопряжение
внутренней и внешней задач производят не по температуре, а по плотности
теплового потока на поверхности. При этом задачу внешнего теплообмена решают
при задании на поверхности металла плотности теплового потока, а найденное в
результате значение температуры на поверхности используют в качестве граничного
условия для решения внутренней задачи. Полученное в результате этого решения
значение плотности теплового потока на поверхности сопоставляют с тем, которое
использовали на предыдущей итерации, добиваясь, в конце концов, приемлемого
расхождения этих величин.
1.2 Современная вычислительная гидрогазодинамика (CFD)
В последнее время стремительно возрастает интерес к математическому
моделированию физических явлений и промышленных процессов. Этому способствует
развитие численных методов решения всех типов задач и усовершенствование
компьютерной техники. Вследствие этого, разработан целый ряд программных
комплексов, позволяющих моделировать различные физические процессы.
Моделирование в программных комплексах и анализ полученных данных в некоторых
областях промышленности позволяет избежать дорогостоящих и длительных циклов
разработки типа «проектирование - изготовление - испытания».
Вычислительная гидрогазодинамика (англ. Computational Fluid Dynamic - CFD)
возникла на стыке вычислительной математики и теоретической гидромеханики и к
настоящему времени оформилась как обособленный раздел науки, предметом которого
является численное моделирование различных течений жидкости и газа и решение
возникающих при этом задач при помощи методов, основанных на использовании
компьютерных систем [8].
Современная вычислительная гидродинамика занимается разработкой таких
актуальных направлений, как расчет движений вязкой жидкости, численное
исследование течений газа с физико-химическими превращениями, изучение
распространения ударных волн в различных средах, решение газодинамических задач
при наличии излучения, связанные задачи типа «прочность - газовая динамика»,
«акустика - газовая динамика» и пр.
Бурному росту CFD-расчетов,
безусловно, способствуют совершенствование компьютерных технологий, создание
универсальных, удобных в использовании и доступных широкому кругу
исследователей программных CFD-комплексов,
уверенно справляющихся с разнообразными типами задач. Подобные программы
обладают неоспоримым преимуществом перед физическим экспериментом и иногда
являются единственной возможностью ответить на интересующие вопросы.
Среди несомненных достоинств компьютерного моделирования можно отметить
следующие:
сокращение
времени при проектировании и отработке модели;
моделирование
условий, невозможных при натурных испытаниях;
получение
более полной и широкой информации об объекте исследования;
экономическая
эффективность компьютерных расчетов;
возможность быстрой корректировки расчетной модели;
эффективное
использование времени исследователя.
В настоящее время широкое распространение получили пакеты вычислительной
гидродинамики, тепломассообмена, прочности и электродинамики для проведения
инженерных расчетов. Среди них можно упомянуть такие, как CFX, FLUENT, STAR-CD, LS-DYNA,
ANSYS, ABAQUS, FlowVision, MSC/NASTRAN, MSC/MARC, MAGMASOFT, SolidWorks и др.
Газодинамика - это раздел механики сплошных сред, описывающий движение
жидкостей в рамках модели сплошной среды. Последнее означает, что
рассматриваются масштабы явлений, значительно превосходящие длину свободного
пробега молекул. В рамках данного подхода все физические законы, а также
свойства являются общими как для макрообъектов, так и бесконечно малых объемов.
Система уравнений газодинамики для турбулентного течения реальной
сжимаемой жидкости включает:
а) Уравнение неразрывности
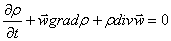 (4)
(4)
б)
Уравнение Навье-Стокса
 (5)
(5)
в) Уравнение энергии
 (6)
(6)
 -
эффективный коэффициент температуропроводности (с учетом турбулентного
переноса)
-
эффективный коэффициент температуропроводности (с учетом турбулентного
переноса)
г) Уравнение состояния
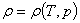 (7)
(7)
Система
уравнений Навье-Стокса образует законченную математическую модель поведения
жидкости, которая детально и строго описывает практически весь спектр течений.
Однако на практике к ней необходимо добавить уравнения модели турбулентности,
представляющие собой совокупность эмпирических и иных соотношений, чтобы
система в целом могла быть решена.
Получение точного математического решения для системы уравнений
Навье-Стокса является основной проблемой. Возможным способом ее преодоления
становятся численные методы.
На первом этапе построения численного решения, который принято называть
дискретизацией - дифференциальные уравнения в частных производных, описывающие
непрерывный процесс, а также вспомогательные (граничные и начальные) условия,
преобразуются в систему дискретных алгебраических уравнений.
Чтобы преобразовать исходное уравнение в частных производных (или систему
таких уравнений) в систему алгебраических уравнений, можно выбрать один из
нескольких вариантов. Способ осуществления дискретизации зависит также от того,
рассматриваются ли производные по времени (в применении к нестационарным
задачам), или же уравнения, которые содержат только пространственные
производные.
На практике дискретизация производных по времени осуществляется почти
исключительно с использованием разностных методов. При дискретизации
пространственных производных используются, как правило, методы конечных
разностей, конечных элементов, конечных объемов [8].
При применении данных методов алгебраические уравнения связывают между
собой значения искомых переменных в группе соседних узловых точек (сеточных
узлов). Также подразумевается, что сетка, состоящая из дискретных точек,
распределена по всей вычислительной области во времени и в пространстве.
В процессе замены отдельных членов исходных уравнений, представляющих
собой частные производные, алгебраическими выражениями, связывающими узловые
значения на конечной сетке, вносится некоторая ошибка аппроксимации. Ее
суть заключается в том, что при переходе от непрерывных функций к их дискретным
аналогам используется разложение в ряды с удержанием определенного числа
значимых членов и отбрасыванием малых высокого порядка, а также замене
дифференциалов переменных их приращениями.
Говорят, что система алгебраических уравнений, полученная в результате процесса
дискретизации, согласуется с первоначальным дифференциальным уравнением в
частных производных, если в пределе, когда размеры ячеек сетки и величина шага
по времени стремятся к нулю, система алгебраических уравнений эквивалентна
дифференциальному уравнению в частных производных в каждой из узловых точек
сетки.
Решение алгебраических уравнений называют сходящимся, если данных
уравнений приближается к точному решению дифференциального уравнения в частных
производных для любого значения независимой переменной, по мере того как
размеры ячеек сетки и шаг по времени приближаются к нулю.
Если учесть, что для большинства задач гидрогазодинамики определяющие
уравнения являются нелинейными, процесс построения численного решения обычно
ведется посредством итераций. Для этого используются методы Ньютона,
многосеточные методы, метод сопряженных градиентов.
Следует отметить, что наиболее востребованным численным методом решения
уравнений гидрогазодинамики является метод контрольного объема, обладающий
значительными преимуществами в сравнении с остальными.
Основная идея метода контрольного объема (МКО)
заключается в разбиении расчетной области на некоторое число непересекающихся
контрольных объемов и интегрировании дифференциального уравнения по каждому
контрольному объему [8]. Для вычисления интегралов внутри контрольного объема
используют функции формы, которые описывают изменение некоторой интересующей
переменной  между расчетными узловыми точками. В результате находят
дискретный аналог дифференциального уравнения, в который входят значения
между расчетными узловыми точками. В результате находят
дискретный аналог дифференциального уравнения, в который входят значения  в нескольких расчетных узловых
точках. В качестве расчетного узла в МКО принимается центр контрольного объема.
в нескольких расчетных узловых
точках. В качестве расчетного узла в МКО принимается центр контрольного объема.
Полученный подобным образом дискретный аналог выражает закон сохранения  для конечного контрольного объема
точно так же, как дифференциальное уравнение выражает закон сохранения для
бесконечно малого контрольного объема.
для конечного контрольного объема
точно так же, как дифференциальное уравнение выражает закон сохранения для
бесконечно малого контрольного объема.
В методе контрольного объема, центрированного по узлу,
грани расположены посередине между узловыми точками сетки, узел геометрической
сетки является центром контрольного объема. Таким образом, базовым является
положение узлов, вокруг которых располагаются контрольные объемы. Указанный
подход удобен при использовании структурированных (регулярных) сеток при
дискретизации расчетной области.
Тем не менее, при использовании МКО, центрированного
по узлу, возникает ряд затруднений:
расчетная сетка и исходная геометрическая не
совпадают;
расположение центров контрольного объема (или узлов
геометрической сетки) прослеживается без затруднений, однако, формирование
ячеек контрольных объемов представить гораздо сложнее;
контрольные объемы могут иметь форму значительно
сложнее, чем элементы геометрической сетки;
расположение контрольных объемов на границах требует
отдельного рассмотрения (Рис. 2, слева).
Преимуществом расположения контрольного объема вокруг
узла геометрической сетки является высокая точность нахождения градиентов и
производных, поскольку грани, на которых они вычисляются, расположены точно
посередине между двумя соседними узлами геометрической сетки. При этом точность
величин, полученных для расчетного узла интегрированием по контрольному объему,
оказывается ниже [8].
В методе контрольного объема, центрированного по
ячейке, для построения расчетной сетки используется уже имеющаяся
геометрическая сетка. Грани контрольного объема совпадают с гранями ячейки
исходной сетки, расчетным узлом является центр геометрической ячейки.
Указанная формулировка позволяет использовать уже готовые ячейки,
созданные на этапе дискретизации расчетной области, в качестве контрольных.

Рисунок 2 - Расположение центров контрольного объема
(или узлов геометрической сетки)
В этом виде МКО нет необходимости введения дополнительных условий при
рассмотрении граничных областей (рис. 2, справа). С другой стороны, контроль за
формированием расчетных узлов и их распределением по расчетной области
становится весьма затруднительным.
Наибольшую точность при использовании ячеек геометрической сетки в
качестве контрольных объемов имеют величины, полученные интегрированием по
объему. Градиенты и производные, вычисляемые на гранях, будут иметь меньший
порядок точности.
Численные методы, применяемые для решения задач газовой динамики,
являются инструментом, позволяющим использовать имеющуюся математическую модель
- систему Навье-Стокса [8]. Их использование в известном смысле расширило
возможности исследователей, однако число пользователей до сих пор
ограничивается узким кругом специалистов, непосредственно занимающихся
вычислительной газовой динамикой.
Вычислительные комплексы для проведения расчетов по газовой динамике
принято характеризовать по уровню сложности решаемых задач (поддерживаемое
число узлов расчетной сетки, степень учета нелинейностей), по количеству
моделей поведения жидкостей и газов. На сегодняшний день CFD-пакеты условно делятся на три
класса.
«Тяжелые» - комплексы высокого класса, подходящие как для научных, так и
инженерных расчетов, способные решать самые сложные задачи с учетом большого
количества эффектов и использованием широкого набора математических подходов, в
том числе специфических. К классу «тяжелых» относятся лидеры среди коммерческих
CFD-пакетов - ANSYS CFX (ANSYS,
Inc.), Star-CD (CD-adapco), FLUENT
(ANSYS, Inc.совместно с Fluent, Inc.). Все они содержат большое число
моделей турбулентности, способны решать задачи различной сложности с учетом
горения, химических реакций, многофазных потоков, поддерживают различные типы сеток
и т. д.
Среднего класса предназначены, главным образом, для расчетов инженерного
уровня сложности. Набор используемых моделей также может быть достаточно
широким. К этому разряду можно отнести COSMOSFloWorks (Solid Works Co.), STAR-CCM+ (CD-adapco), ANSYS FLOTRAN (ANSYS, Inc.).
«Легкие» - CFD-комплексы,
использующие алгоритмы невысокой точности (используются, например, в качестве
учебно-методических), либо имеющие узкую направленность расчета (специально
созданные под определенную проблематику).
Подавляющее большинство CFD-решателей,
реализованных в программах, основано на использовании МКО в различных
вариациях.
Несмотря на разницу в возможностях программ разных классов,
принципиальный порядок проведения расчета в них одинаков и представляет собой
следующие действия:
а) подготовка расчетной модели. Она включает в себя:
) создание геометрической модели, описывающей расчетную область;
) генерацию сеточной модели на основе созданной геометрии;
) задание граничных и начальных условий;
) выбор физической модели расчета (например, модели турбулентности,
теплопроводности, горения и т. д.) - препроцессинг.
б) Решение задачи в решателе;
в) Просмотр и оценка результатов - постпроцессинг;
г) Коррекция расчетной модели при необходимости (изменение геометрии,
сеточной, физической модели).
д) Проведение решения с учетом изменений [9].
Коррекция расчетной модели становится необходимой после получения
неудовлетворительных результатов в ходе решения. Однако к изменению параметров
может привести желание проследить влияние сеточной модели (количество и
параметры ячеек) на конечный результат, сходимость расчета, продолжительность
расчета или же желание выявить адекватность применения выбранной физической
модели.
Подготовка расчетной модели является основной стадией при проведении
численного эксперимента. Это связано, прежде всего, с тем, что дальнейшее
решение (его характер, точность, сходимость, устойчивость) во многом
определяются теми походами и оценками реальной физической проблемы, которые
затем были использованы при подготовке численного эксперимента.
Расчетная модель включает в себя:
геометрическую модель;
сеточную модель (сетка);
модель газа;
модели турбулентности;
граничные условия.
Основополагающим шагом при проведении численного эксперимента в области
гидрогазодинамики является выбор модели турбулентности. От этого выбора зависит
то, какие эффекты будут учтены в решении, а какие нет. Все модели
турбулентности не являются универсальными и имеют границы применимости, внутри
которых результаты будут наиболее близки к реальным. Кроме того, различные
подходы по моделированию турбулентности накладывают разные требования к сеткам.
Требования могут содержать условия для минимального размера ячейки, находящейся
на поверхности обтекаемой стенки, ограничения на тип используемого элемента при
дискретизации, на соотношения размеров сторон ячеек, уровень детализации
сеточной модели.
После выбора модели турбулентности следует построение сетки. Основой
сеточной модели является геометрическая 3D-модель, от качества которой зависит качество будущей
сеточной модели.
Необходимо помнить, что численные методы позволяют решить математическую
модель, отражающую с определенной степенью достоверности некоторый физический
процесс, наблюдаемый в реальности, поэтому результаты численного моделирования
нуждаются в анализе и, в лучшем случае, сравнении с результатом физических
наблюдений. При исследовании влияния характеристик расчетной модели на
численные результаты наличие данных физического эксперимента обязательно.
1.3 Математическое моделирования в ПВК FLUENT
FLUENT - это современный, универсальный программный комплекс,
предназначенный для решения задач механики жидкостей и газов. Пакет
предназначен для моделирования сложных течений жидкостей и газов с широким
диапазоном изменения теплофизических свойств посредством обеспечения различных
параметров моделирования и использования многосеточных методов с улучшенной
сходимостью. Он дает оптимальную эффективность и точность решения для широкого
диапазона моделируемых скоростных режимов [9].
Изобилие физических моделей в пакете FLUENT позволяет с хорошей точностью
предсказывать ламинарные и турбулентные течения, различные режимы
теплопереноса, химические реакции, многофазные потоки и другие явления на
основе гибкого построителя сеток и их адаптации к получаемому решению.
Разработка пакета FLUENT началась в 1980 году, когда проблемы
вычислительной гидрогазодинамики (CFD) интересовали весьма узкий круг
специалистов. Инженеры компании Creare, Inc. (США) совместно с группой ученых
из Шеффилдского университета (Sheffield University, Великобритания) под
руководством доктора Ферита Бойсана решили создать простой в использовании
интерактивный CFD-код для инженерных расчетов. Этот проект оказался столь
успешным, что в 1990 году для продолжения его реализации была создана
специализированная компания FLUENT, Inc. В 1997 году компания FLUENT дополнила
свою линейку продуктов новым пакетом POLYFLOW, ориентированным в первую очередь
на потребности химической промышленности (производство изделий из полимеров,
пластмасс, резины и т.п.), цветной и черной металлургии. В сентябре 2000 года
компания получила сертификаты ISO 9001 и TickIT.
FLUENT включает в себя несколько типов решателей, в том
числе сопряженный решатель с алгоритмом на основе давления, расщепленный
решатель с алгоритмом на основе давления и два решателя с алгоритмами на основе
плотности, что позволяет получать точные результаты для практически любого
течения.
Данный программно-вычислительный комплекс помимо
ламинарного течения, имеет широкий набор моделей турбулентности: несколько
распространенных k-epsilon и k-omega моделей, модель турбулентных напряжений
Рейнольдса для сильных вихревых или анизотропных потоков, модели турбулентности
для расчета больших вихрей (LES-модели) и модели изолированных вихрей (DES).
FLUENT также предлагает инженерам полный набор инструментов для моделирования
конвективного и радиационного теплообмена, теплопроводности. Доступны модели
для анализа излучений в оптически плотной среде - модель Розеланда, а также
модель «поверхность-поверхность» (основанная на коэффициентах излучения) для
лучепрозрачной среды. Модель дискретных ординат, дискретная модель переноса
излучения и Р-1 модель охватывают весь спектр оптических толщин, тем самым
подходят для любых сред. Кроме того существует возможность учета тепловой
нагрузки от солнечного излучения. позволяет моделировать горение топлива, в том
числе с частичным или полным предварительным смешением, процессы при наличии
реакций между газами и твердыми поверхностями, а также прогнозирование образования
NOx, SOx и других загрязняющих веществ.
FLUENT
использует самые современные модели для описания химических реакций. База
данных содержит свойства множества газообразных, твердых, угольных и жидких
топливных материалов.
Все это позволяет использовать данный
программно-вычислительный комплекс для моделирования сложных металлургических
процессов. Кроме того, FLUENT используют в аэродинамике, нефтегазовой
промышленности, медицине и других отраслях.
Постпроцессор FLUENT отображает результаты расчета в векторном и контурном видах, а
также способен отображать траектории движения частиц. Встроенный модуль
создания анимации позволяет обрабатывать результаты нестационарных расчетов.
Возможность использования динамической сетки существенно
расширяют область применения FLUENT. Динамические сетки могут рассматриваться совместно с
моделями горения, многофазного потока и др.
В программе используется неструктурированная сеточная технология, т.е.
сетка может состоять из элементов разнообразной формы: четырехугольников и
треугольников для 2-мерных моделей и гексаэдров, тетраэдров, призм и пирамид
для трехмерных моделей. Точные результаты расчетов гарантируют сложные
численные схемы и мощный решатель [9].
Адаптация расчетной сетки позволяет получить точное решение для областей
с большими градиентами потока, например для пограничных слоев. Данная
возможность также позволяет значительно сократить время на построение
качественной сетки, решение численной задачи и обработку результатов.
Процесс генерации сетки является неотъемлемой частью любого инженерного
расчета, в котором используются программные продукты. От качества сетки
напрямую зависят точность, сходимость и скорость решения. И зачастую время,
потраченное на построение геометрии расчетной области и сетки, является лимитирующим
фактором для всего процесса расчета.
Для создания расчетной сетки используется программный продукт GAMBIT. Данная программа позволяет
создавать различные типы сеток: структурированную гексаидальную,
неструктурированную гексаидальную и тетраидальную сетки, пограничные слои с
комбинированными сетками. В GAMBIT возможно импортирование геометрии из других
САD систем с поиском и исправлением возникающих при этом проблем нестыковки
объектов.
GAMBIT обладает мощными возможностями для создания двухмерных
и трехмерных расчетных областей непосредственно внутри программы, начиная от
построения линий и кончая созданием твердотельных объектов. Программа имеет единый интерфейс для
создания геометрических моделей и построения сетки. Кроме того, в процессе
использования производится запись всех операций построения в текстовый файл
(журнал событий), что дает возможность пользователю легко отслеживать путь
создания геометрической модели, исправлять ошибки, перестраивать модели и
сетки, а также интегрировать результаты в другие программы [9].
Математические модели, базирующиеся на ПВК FLuent (для исследования, совершенствования
и проектирования тепловых технологических аппаратов металлургической и других
отраслей промышленности) подтверждают факт, что численное компьютерное
моделирование в наши дни успешно заменяет физическое моделирование, а во многих
случаях и натурные исследования на промышленных агрегатах.
Еще одним продуктом компании ANSYS является модуль CFX, который в течение
долгого времени является лидером в области вычислительной гидрогазодинамики
вращающихся машин. Комплекс ANSYS CFX имеет полный набор моделей для расчета
взаимодействия между вращающимися и статичными компонентами, обладает
специальной рабочей средой для препроцессинга, постпроцессинга турбин и
полностью соответствует требованиям специалистов в области гидрогазодинамики
турбин.CD является многоцелевым единым CFD-пакетом, предоставляющим
пользователю возможности моделирования стационарных и нестационарных,
ламинарных и турбулентных течений, сжимаемые и несжимаемые потоки, тепло- и
массоперенос, химические реакции и горение, многокомпонентные течения и
многофазные потоки. Однако спектр моделей несколько уже, чем у продуктов
компании ANSYS. Решение в Star-CD основано на применении метода конечных
объемов.
Еще одним из «законченных» и известных CFD-пакетов, предназначенных для
вычислений на основе метода конечных элементов, является пакет OpenFOAM, пакет с открытым кодом. OpenFOAM позволяет решать задачи
гидродинамика ньютоновских и неньютоновских вязких жидкостей как в несжимаемом,
так и сжимаемом приближении с учётом конвективного теплообмена и действием сил
гравитации.
Для моделирования турбулентных течений возможно
использование RANS-моделей, LES- и DNS-моделей. Возможно решение дозвуковых, околозвуковых
и сверхзвуковых задач; задач теплопроводности в твёрдом теле; многофазных
задач, в том числе с описанием химических реакций компонент потока; задач,
связанных с деформацией расчётной сетки и сопряжённых задач.
Наиболее распространенным CFD-комплексом,
разработанным в России, является FlowVision, выпускаемый компанией ТЕСИС. На
данный момент FlowVision не обладает таким широким набором моделей. Основными
недостатками являются автоматическая генерация только прямоугольной сетки,
среди моделей турбулентности доступны только k-ε модели (стандартная,
низкорейнольдсовая, квадратичная), SST k-ω модель и модель Спаларта-Аллмараса.
В работе представлена разработанная на базе ПВК FLuent трехмерная нестационарная модель
теплообмена в печи высокоточного нагрева, включающая блок расчета нагрева
металла.
К сожалению, в России в области металлургии и, в частности, при
разработке нагревательных печей, ПВК в области вычислительной
гидрогазодинамики, в том числе ПВК FLUENT, не получили достаточного распространения.
2 Математическое моделирование нагрева металла в печи ВТН
.1 Постановка задачи и исходные данные
Модель представляет собой упрощенную модель печи высокоточного нагрева
(ВТН) с выкатным подом ОАО «Машиностроительный завод «ЗиО-Подольск»,
предназначенной для нагрева и термообработки особо ответственных изделий.
В модели сделаны допущения о том, что в рабочее пространство печи
поступают продукты сгорания, а не газо-воздушная смесь. Данное допущение
возможно благодаря тому, что печь оснащена скоростными рекуперативными
горелками полного предварительного смешения.
К недостаткам печей высокоточного нагрева относятся: значительный расход
топлива, наличие выбросов оксидов азота и диоксида углерода в атмосферу,
большой угар металла. Решение данных проблем может быть найдено при помощи
программно-вычислительного комплекса FLUENT. Компьютерное моделирование с использованием ПВК FLUENT позволит выбрать необходимые для
обеспечения однородности температурного поля заготовок и минимализации
энергетических затрат параметры конструкции и режима печи.
Исходные данные:
Температура продуктов сгорания на входе - 1273К;
Начальная температура заготовки - 293К;
Температура наружной поверхности кладки - 300К;
Время нагрева - 10 мин;
Материал заготовки - сталь среднеуглеродистая;
Материал кладки - шамот.
Сравниваются результаты моделирования при разном количестве загруженных
заготовок в печи:
одна заготовка с размерами 0,25х0,25х4 м;
две заготовки с размерами 0,176х0,176х4 м;
четыре заготовки с размерами 0,125х0,125х4 м.
Заготовки располагаются на расстоянии 15мм от пода печи, расстояние между
заготовками равно толщине. Масса садки одинаковая.
Из горелки в рабочее пространство поступают продуты сгорания заданного
состава: 13 % СО2 и 11% Н2О. Массовый расход равен 0,30308 кг/с.
Газовая смесь рассматривается как идеальный газ, но принято допущение,
что зависимость теплофизических параметров от температуры имеет
кусочно-линейный вид.
Геометрия печи для разного количества заготовок представлена на рисунках
3-8.
Горелка имеет следующие размеры:
диаметр входного отверстия 120 мм;
наружный диаметр 500 мм;
внутренний диаметр выходного отверстия 470 мм.
2.1.1 Геометрия системы для трех вариантов загрузки печи

Рисунок 3 - Геометрия печи с одной заготовкой
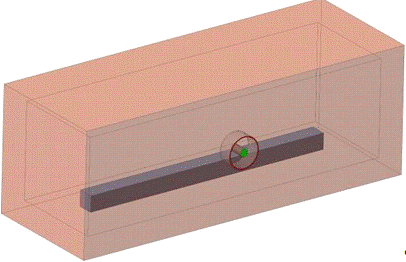
Рисунок 4 - Объемная геометрия печи с одной заготовкой

Рисунок 5 - Геометрия печи с двумя заготовками
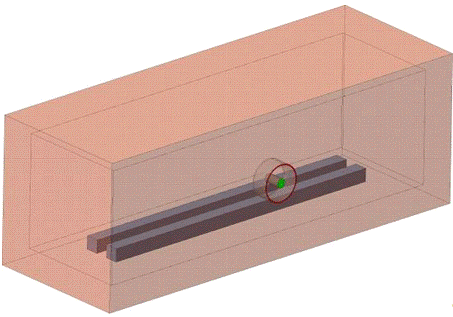
Рисунок 6 - Объемная геометрия печи с двумя заготовками

Рисунок 7 - Геометрия печи с четырьмя заготовками

Рисунок 8 - Объемная геометрия печи с четырьмя заготовками
2.1.2 Зависимости теплофизических характеристик от
температуры
Зависимости теплофизических характеристик продуктов сгорания от
температуры представлены в таблице 3.
Таблица 3 - Зависимости теплофизических характеристик продуктов сгорания
от температуры
Температура
Т, К Теплоемкость Ср,  кДж/(м3·К)Плотность
кДж/(м3·К)Плотность
ρ, кг/м3Теплопровод-
|
ность λ, Вт/(м·К)Динамич. коэфф. вязкости μ, кг/(м·с)
|
|
|
|
|
|
273
|
1,049
|
1, 295
|
2,26·10-2
|
1,58·10-5
|
|
573
|
1, 078
|
0, 617
|
4,85·10-2
|
2,83·10-5
|
|
973
|
1, 127
|
0, 363
|
8,29·10-2
|
4,07·10-5
|
|
1273
|
1, 156
|
0, 275
|
10,09·10-2
|
4,79·10-5
|
Изменение теплофизических свойств стали и огнеупорного материала (шамот)
также имеют кусочно-линейный вид. Зависимости теплофизических характеристик
шамота и стали от температуры представлены в таблицах 4, 5.
Таблица 4 - Зависимости теплофизических характеристик шамота от
температуры.
|
Температура, ºС
|
Теплоемкость Ср, Дж/(кг·К)
|
Теплопроводность λ, Вт/(м·К)
|
|
0
|
865
|
0,7
|
|
1500
|
1180
|
1,66
|
Зависимость теплоемкости и теплопроводности огнеупорных материалов от
температуры в действительности имеют линейный вид, и для их описания достаточно
двух значений.
Таблица 5 - Зависимости теплофизических характеристик стали от
температуры
|
Температура Т, К
|
Теплоемкость Ср, Дж/(кг·К)
|
Теплопроводность λ, Вт/(м·К)
|
|
273
|
486
|
51,9
|
|
373
|
486
|
51,1
|
|
473
|
502
|
48,5
|
|
573
|
519
|
44,4
|
|
673
|
540
|
42,7
|
|
773
|
561
|
39,3
|
|
873
|
590
|
35,6
|
|
973
|
628
|
31,9
|
|
1073
|
703
|
25,9
|
|
1173
|
703
|
26,4
|
|
1273
|
695
|
27,7
|
2.3 Математическая постановка задачи
Рассматриваемая задача описывается уравнением энергии для продуктов
сгорания, уравнением теплопроводности в области заготовки и слое футеровки,
уравнением Навье-Стокса для трех координат, уравнением неразрывности.
Описываемая система уравнений дополнена уравнениями переноса субстанции для
кинетической энергии турбулентности k и скорости ее диссипации ε
(эпсилон), поскольку
используется стандартная k-ε модель турбулентности.
Уравнение неразрывности:
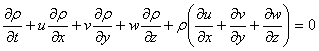 (8)
(8)
Уравнения
Навье-Стокса:
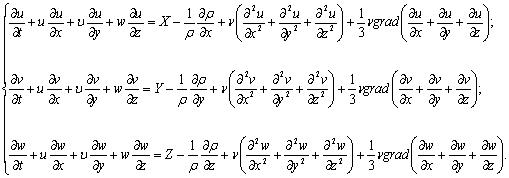 (9)
(9)
Уравнение
энергии:
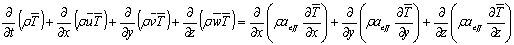 (10)
(10)
где
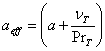 - эффективный коэффициент температуропроводности (с
учетом турбулентного переноса)
- эффективный коэффициент температуропроводности (с
учетом турбулентного переноса)
Уравнение
переноса субстанции для кинетической энергии турбулентности k и
скорости ее диссипации ε через объемные плотности:
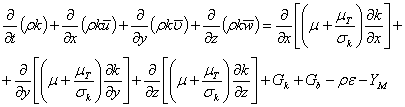 (11)
(11)
 (12)
(12)
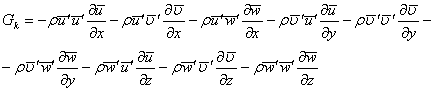 (13)
(13)
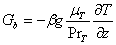 (14)
(14)
где
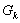 - слагаемое, описывающее генерацию кинетической
энергии турбулентности,
- слагаемое, описывающее генерацию кинетической
энергии турбулентности,  - слагаемое, описывающее генерацию турбулентности за
счет плавучести.
- слагаемое, описывающее генерацию турбулентности за
счет плавучести.
 (15)
(15)
где
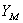 - величина, характеризующая затухание деформации
(растяжения/сжатия),
- величина, характеризующая затухание деформации
(растяжения/сжатия),  - турбулентное число Маха.
- турбулентное число Маха.
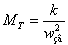 (16)
(16)
Константы:


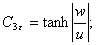

Уравнение
переноса излучения для Р-1 модели:
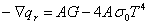 (17)
(17)
где
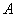 - коэффициент поглощения среды,
- коэффициент поглощения среды, 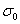 - постоянная Стефана-Больцмана, G -
падающее излучение.
- постоянная Стефана-Больцмана, G -
падающее излучение.
3 Результаты расчета
.1 Распределение температурного поля
в различных сечениях рабочего пространства печи для трех вариантов загрузки

Рисунок 9 - Температурное поле в рабочем пространстве печи в поперечном
сечении в плоскости горелки для одной заготовки

Рисунок 10 - Температурное поле в рабочем пространстве печи в поперечном
сечении в плоскости горелки для двух заготовок

Рисунок 11 - Температурное поле в рабочем пространстве печи в поперечном
сечении в плоскости горелки для четырех заготовок

Рисунок 12 - Температурное поле в рабочем пространстве печи в продольном
горизонтальном сечении для одной заготовки

Рисунок 13 - Температурное поле в рабочем пространстве печи в продольном
горизонтальном сечении для двух заготовок

Рисунок 14 - Температурное поле в рабочем пространстве печи в продольном
горизонтальном сечении для четырех заготовок

Рисунок 15 - Температурное поле в рабочем пространстве печи в продольном
вертикальном сечении для одной заготовки
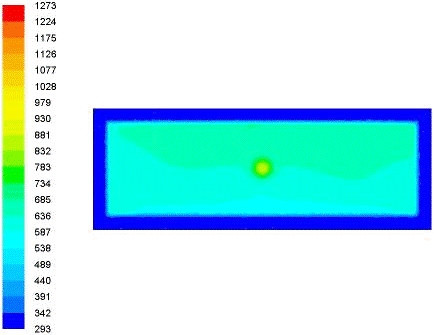
Рисунок 16 - Температурное поле в рабочем пространстве печи в продольном
вертикальном центральном сечении для двух заготовок

Рисунок 17 - Температурное поле в рабочем пространстве печи в продольном
вертикальном центральном сечении для четырех заготовок
Таким образом, с увеличением числа заготовок в печи, область, занятая
высокотемпературными продуктами сгорания, уменьшается, что приводит к ухудшению
прогрева заготовок, расположенных ближе к горелке. Это хорошо видно на рисунках
9, 10, 11.
3.2 Распределение температурного поля в различных сечениях
заготовок для трех вариантов загрузки печи

Рисунок 18 - Температурное поле для одной заготовки в поперечном сечении
в плоскости горелки

Рисунок 19 - Температурное поле для одной заготовки в поперечном сечении
на расстоянии 1,5 м от центра заготовки
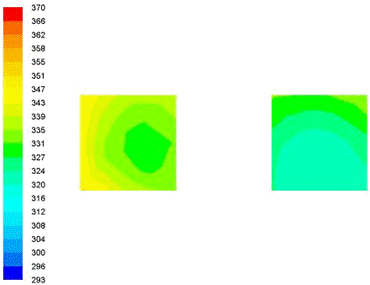
Рисунок 20 - Температурное поле для двух заготовок в поперечном сечении в
плоскости горелки

Рисунок 21 - Температурное поле для двух заготовок в поперечном сечении
на расстоянии 1,5 м от центра заготовок

Рисунок 22 - Температурное поле для четырех заготовок в поперечном
сечении в плоскости горелки

Рисунок 23 - Температурное поле для четырех заготовок в поперечном
сечении на расстоянии 1,5 м от центра заготовок

Рисунок 24 - Температурное поле для одной заготовки в продольном
горизонтальном сечении

Рисунок 25 - Температурное поле для двух заготовок в продольном
горизонтальном сечении

Рисунок 26 - Температурное поле для четырех заготовок в продольном
горизонтальном сечении

Рисунок 27 - Температурное поле для одной заготовки в продольном
вертикальном сечении

Рисунок 28 - Температурное поле для двух заготовок в продольном вертикаль
ном сечении

Рисунок 29 - Температурное поле для четырех заготовок в продольном
вертикальном сечении
Так как с увеличением количества заготовок в печи уменьшаются их размеры,
в случае с четырьмя заготовками наблюдается самая высокая температура прогрева
(рисунки 22, 26, 29). Кроме этого, в поперечном сечении, расположенном на
расстоянии 1,5 м от центра заготовок (рисунки 19, 21, 23), видно, что заготовки
прогреваются более равномерно, чем в поперечном сечении, расположенном в
плоскости горелки (рисунки 18, 20, 22).
3.3 Распределение вектора скорости в
рабочем пространстве печи для трех вариантов загрузки
Рисунок 30 - Вектор скорости в рабочем пространстве печи в поперечном
сечении в плоскости горелки для одной заготовки

Рисунок 31 - Локальные зоны циркуляции в рабочем пространстве печи в
поперечном сечении в плоскости горелки для одной заготовки

Рисунок 32 - Вектор скорости в рабочем пространстве печи в поперечном
сечении в плоскости горелки для двух заготовок

Рисунок 33 - Локальные зоны циркуляции в рабочем пространстве печи в
поперечном сечении в плоскости горелки для двух заготовок

Рисунок 34 - Вектор скорости в рабочем пространстве печи в поперечном
сечении в плоскости горелки для четырех заготовок

Рисунок 35 - Локальные зоны циркуляции в рабочем пространстве печи в
поперечном сечении в плоскости горелки для четырех заготовок

Рисунок 36 - Вектор скорости в рабочем пространстве печи в продольном
горизонтальном сечении для одной заготовки

Рисунок 37 - Локальная зона циркуляции №1 в рабочем пространстве печи в
продольном горизонтальном сечении для одной заготовки

Рисунок 38 - Локальная зона циркуляции №2 в рабочем пространстве печи в
продольном горизонтальном сечении для одной заготовки

Рисунок 39 - Локальная зона циркуляции №3 в рабочем пространстве печи в
продольном горизонтальном сечении для одной заготовки

Рисунок 40 - Вектор скорости в рабочем пространстве печи в продольном
горизонтальном сечении для двух заготовок
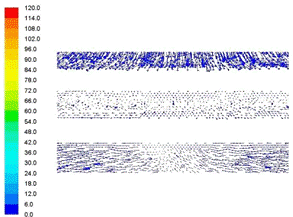
Рисунок 41 - Локальная зона циркуляции в рабочем пространстве печи в
продольном горизонтальном сечении для двух заготовок

Рисунок 42 - Вектор скорости в рабочем пространстве печи в продольном
горизонтальном сечении для четырех заготовок

Рисунок 43 - Локальная зона циркуляции в рабочем пространстве печи в
продольном горизонтальном сечении для четырех заготовок

Рисунок 44 - Вектор скорости в рабочем пространстве печи в продольном
вертикальном сечении для одной заготовки

Рисунок 45 - Локальная зона циркуляции №1 в рабочем пространстве печи в
продольном вертикальном сечении для одной заготовки
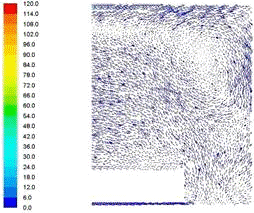
Рисунок 46 - Локальная зона циркуляции №2 в рабочем пространстве печи в
продольном вертикальном сечении для одной заготовки

Рисунок 47 - Вектор скорости в рабочем пространстве печи в продольном
вертикальном центральном сечении для двух заготовок

Рисунок 48 - Локальная зона циркуляции №1 в рабочем пространстве печи в
продольном вертикальном центральном сечении для двух заготовок
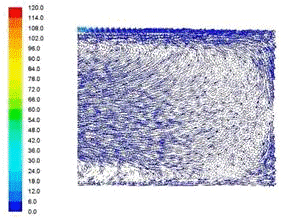
Рисунок 49 - Локальная зона циркуляции №2 в рабочем пространстве печи в
продольном вертикальном центральном сечении для двух заготовок

Рисунок 50 - Вектор скорости в рабочем пространстве печи в продольном
вертикальном центральном сечении для четырех заготовок

Рисунок 51 - Локальная зона циркуляции в рабочем пространстве печи в
продольном вертикальном центральном сечении для четырех заготовок.
Самая большая зона циркуляции, примыкающая к заготовке, образуется в
нижней части печи с противоположной от горелки стороны. Это хорошо видно на
поперечных сечениях (рисунки 30, 32, 34). Также наблюдаются зоны циркуляции
меньшего размера, расположенные между заготовками, причем, их размеры
уменьшаются по мере приближения к горелке (рисунки 32-35).
Для случая с одной заготовкой можно наблюдать зоны циркуляции на
продольном горизонтальном сечении слева и справа от заготовки (рисунки 37, 39),
а также вблизи центральной части грани, расположенной ближе к горелке (рисунок
38). Циркуляционные зоны образуются не только в нижней части печи, но и в
верхней. Примером тому служат рисунки 45, 46.
На продольном горизонтальном и вертикальном сечениях зоны циркуляции для
случаев с двумя и четырьмя заготовками в печи слабо выражены или отсутствуют
вовсе (рисунки 41, 43, 48, 49, 51).
3.4 Распределение плотности теплового потока по поверхности
заготовок для трех вариантов загрузки печи
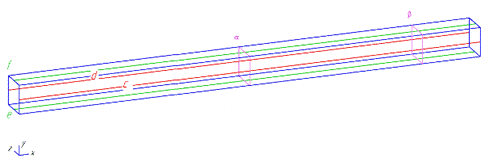
Рисунок 52 - отрезки c, d, e, f на поверхности
заготовки и плоскости α, β, взятые за основу при изучении
изменения искомых величин
α - плоскость, расположенная в
поперечном сечении по центру заготовки;
β - плоскость, расположенная в
поперечном сечении, сдвинутом на 1,5 м от центра заготовки;
c -
отрезок, расположенный по центру ближней к горелке торцевой грани заготовки;
d -
отрезок, расположенный по центру дальней от горелки торцевой грани заготовки;
e -
отрезок, расположенный по центру нижней грани заготовки;
f -
отрезок, расположенный по центру верхней грани заготовки.

Рисунок 53 - Распределение плотности теплового потока по поверхности
заготовки для случая с одной заготовкой
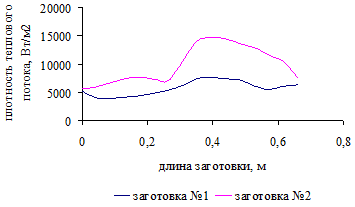
Рисунок 54 - Распределение плотности теплового потока по поверхности
заготовок в плоскости α для случая с двумя заготовками
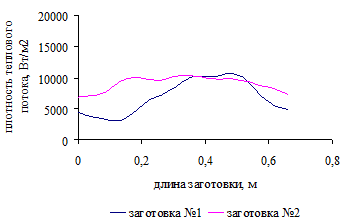
Рисунок 55 - Распределение плотности теплового потока по поверхности
заготовок в плоскости β для случая с двумя заготовками
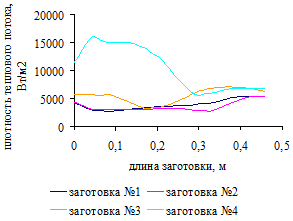
Рисунок 56 - Распределение плотности теплового потока по поверхности
заготовок в плоскости α для случая с четырьмя заготовками

Рисунок 57 - Распределение плотности теплового потока по поверхности
заготовок в плоскости β для случая с четырьмя заготовками

Рисунок 58 - Распределение плотности теплового потока для случая с одной
заготовкой
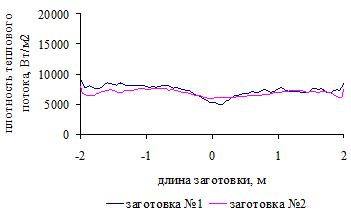
Рисунок 59 - Распределение плотности теплового потока по длине отрезка c для случая с двумя заготовками
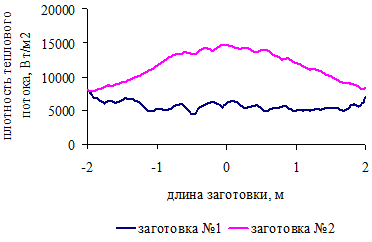
Рисунок 60 - Распределение плотности теплового потока по длине отрезка d для случая с двумя заготовками

Рисунок 61 - Распределение плотности теплового потока по длине отрезка с
для случая с четырьмя заготовками
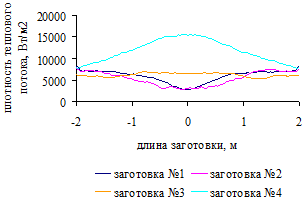
Рисунок 62 - Распределение плотности теплового потока по длине отрезка d для случая с четырьмя заготовками

Рисунок 63 - Распределение плотности теплового для случая с одной
заготовкой

Рисунок 64 - Распределение плотности теплового потока по длине отрезка f для случая с двумя заготовками
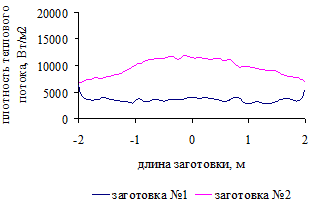
Рисунок 65 - Распределение плотности теплового потока по длине отрезка e для случая с двумя заготовками
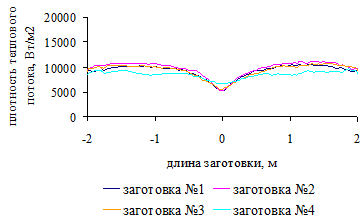
Рисунок 66 - Распределение плотности теплового потока по длине отрезка f для случая с четырьмя заготовками

Рисунок 67 - Распределение плотности теплового потока по длине отрезка e для случая с четырьмя заготовками
На графиках распределения плотности теплового потока видно, что самая
большая плотность теплового потока наблюдается для заготовок, расположенных
дальше всего от горелки. Для случая с двумя заготовками в печи - это заготовка
№2, для случая с четырьмя заготовками в печи - №4, 3. Судя по графикам
распределения плотности теплового потока по поверхности заготовок, для
поперечного сечения α существует большая неоднородность распределения
плотности теплового потока, имеются сильно выраженные максимумы (рисунки 53,
54, 56). Можно сделать вывод, что они приходятся на дальнюю по отношению к
горелке торцевую грань заготовки.
В поперечном сечении β неоднородность распределения
плотности теплового потока для дальних по отношению к горелке заготовок
уменьшается (рисунки 53, 55, 57).
Плотность теплового потока оказывается большей для отрезка d, расположенного по центру дальней от
горелки торцевой грани заготовки. Максимумы наблюдаются для заготовки №2, в
случае для двух заготовок в печи, и для заготовки №4, в случае с четырьмя
заготовками в печи (рисунки 60, 62). Для заготовок №1 и №2, в случае с четырьмя
заготовками в печи, минимумы плотности теплового потока наблюдаются как на
отрезке c, так и на отрезке d (рисунки 61, 62). Также минимум
наблюдается на отрезке c, для
заготовки №2, в случае для двух заготовок в печи (рисунок 59).
В продольном вертикальном сечении видно, что максимумы плотности
теплового потока приходятся на отрезок е заготовки №2 (рисунок 65), для случая
с двумя заготовками, и заготовки №4 (рисунок 67), для случая с четырьмя
заготовками. Ярко выраженные минимумы плотности теплового потока расположены
посередине отрезка f для всех
заготовок, кроме заготовки №4.
3.5 Распределение температурного поля
по поверхности заготовок для трех вариантов загрузки печи

Рисунок 68 - Распределение температуры по поверхности для случая с одной
заготовкой
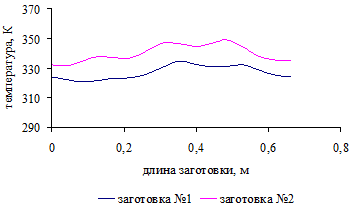
Рисунок 69 - Распределение температуры по поверхности в плоскости α для случая с двумя заготовками
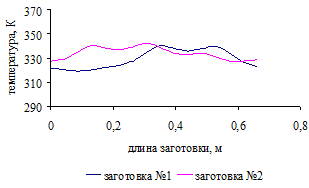
Рисунок 70 - Распределение температуры по поверхности в плоскости β для случая с двумя заготовками
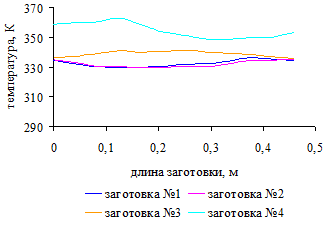
Рисунок 71 - Распределение температуры по поверхности в плоскости α для случая с четырьмя заготовками в
печи

Рисунок 72 - Распределение температуры по поверхности в плоскости β для случая с четырьмя заготовками в
печи

Рисунок 73 - Распределение температуры для случая с одной заготовкой

Рисунок 74 - Распределение температуры по длине отрезка с для случая с
двумя заготовками

Рисунок 75 - Распределение температуры по длине отрезка d для случая с двумя заготовками

Рисунок 76 - Распределение температуры по длине отрезка с для случая с
четырьмя заготовками
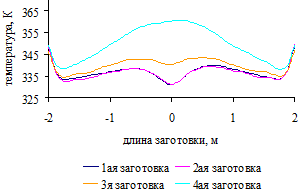
Рисунок 77 - Распределение температуры по длине отрезка d для случая с четырьмя заготовками
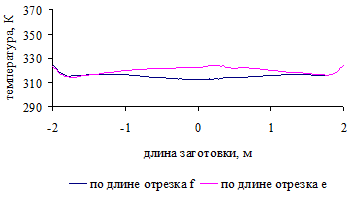
Рисунок 78 - Распределение температуры для случая с одной заготовкой
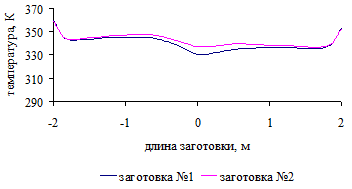
Рисунок 79 - Распределение температуры по длине отрезка f для случая с двумя заготовками

Рисунок 80 - Распределение температуры по длине отрезка е для случая с
двумя заготовками

Рисунок 81 - Распределение температуры по длине отрезка f для случая с четырьмя заготовками
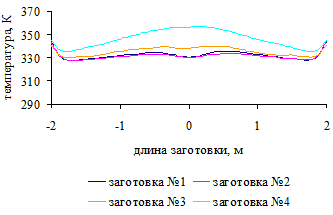
Рисунок 82 - Распределение температуры по длине отрезка е для случая с
четырьмя заготовками
В поперечном сечении α температура выше для заготовок,
расположенных дальше от горелки - заготовка №2 для случая с двумя заготовками в
печи (рисунок 69), заготовки №3 и №4 для случая с четырьмя заготовками в печи
(рисунок 71). В сечении β наблюдается уменьшение неоднородности распределения
температуры по поверхности по сравнению с сечением α.
На графиках видно, что распределение температуры на отрезке с имеет
одинаковый вид, с минимумом по центру отрезка, для заготовок №1 и №2 случая с
двумя заготовками в печи (рисунок 74). Для случая с четырьмя заготовками для
этого же отрезка, температурный минимум наблюдается для заготовок №1-3, а
максимум - для заготовки №4 ( рисунок 76).
На отрезке d максимальное
значение температуры наблюдается для заготовки №2, в случае с двумя заготовками
(рисунок 75), и для заготовки №4, в случае с четырьмя заготовками в печи
(рисунок 77). Температурный минимум наблюдается для заготовок №1 и №2 случая с
четырьмя заготовками (рисунок 77).
На отрезке f графики
распределения температуры также имеют одинаковый вид для заготовок №1 и №2
случая с двумя заготовками в печи с минимумом температуры, приходящимся на центр
отрезка (рисунок 79). В случае с четырьмя заготовками в печи наблюдается
температурный максимум для заготовки №4 и минимум для всех остальных (рисунок
81).
На отрезке e для случая с
двумя заготовками температура выше для заготовки №2 (рисунок 80). В случае с
четырьмя заготовками максимум температуры приходится на заготовку №4, а минимум
- №1 и №2 (рисунок 82).
Таким образом, по всем рассматриваемым отрезкам и плоскостям,
неоднородность распределения температуры меньше всего для случая с одной
заготовкой. В случаях с двумя и четырьмя заготовками в печи видно, что разные
стороны заготовок прогреваются по-разному, причем для дальних от горелки
заготовок наблюдаются температурные максимумы по поверхностям, содержащим
отрезки d, f, e. По мере
приближения к горелке максимальная температура поверхностей заготовок
уменьшается и, кроме этого, образуются температурные минимумы в центральных
частях граней, содержащих отрезки с, d, f.
С увеличением количества заготовок, неоднородность распределения
температуры в сечении α увеличивается.
3.6 Изменение температурного поля заготовок во времени для
трех вариантов загрузки печи
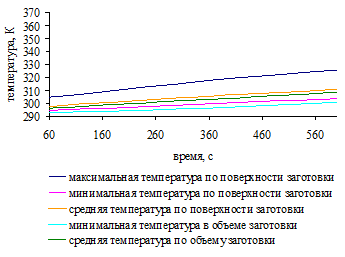
Рисунок 83 - Изменение температурного поля во времени для одной заготовки

Рисунок 84 - Изменение температурного поля во времени для заготовки №1
задачи с двумя заготовками в печи
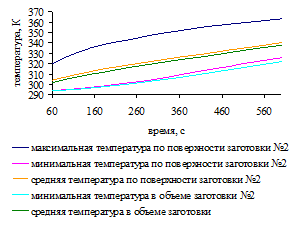
Рисунок 85 - Изменение температурного поля во времени для заготовки №2
задачи с двумя заготовками в печи
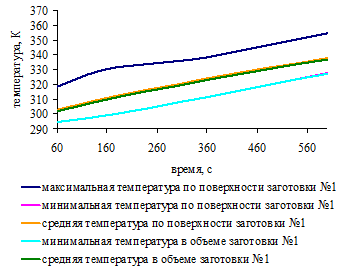
Рисунок 86 - Изменение температурного поля во времени для заготовки №1
задачи с четырьмя заготовками в печи

Рисунок 87 - Изменение температурного поля во времени для заготовки №2
задачи с четырьмя заготовками в печи

Рисунок 88 - Изменение температурного поля во времени для заготовки №3
задачи с четырьмя заготовками в печи
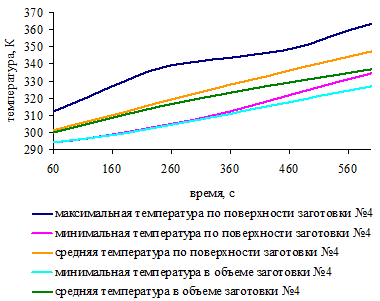
Рисунок 89 - Изменение температурного поля во времени для заготовки №4
задачи с четырьмя заготовками в печи
На всех графиках видно, что температура со временем растет. Минимальная и
средняя температура по поверхности заготовки и в объеме практически не
отличаются для случая с двумя заготовками и для заготовок №1 и №3 случая с четырьмя
заготовками в печи, а для заготовок №2 и №4 появляются расхождения с ростом
времени. Кроме этого видно, что максимальная и минимальная температура сильно
отличаются друг от друга, то есть имеет место высокая неоднородность нагрева
заготовок.
Выводы
В результате проведенного математического моделирования были получены
распределения плотности теплового потока и температуры по поверхности
заготовок, распределения вектора скорости и температуры в рабочем пространстве
печи, а также зависимость изменения температурного поля во времени.
Выявлено, что наибольшая по размеру зона циркуляции, образуются с
противоположной от горелки стороны между стенкой печи и заготовкой, а с
увеличением количества заготовок ее размеры уменьшаются.
Образование зон циркуляции, приводит к неравномерности прогрева по садке,
т.к. поверхность дальней по отношению к горелке заготовки попадает в более
высокотемпературную область. Соответственно, сильнее всего прогревается
центральная часть заготовки №2, в случае с двумя заготовками в печи, и
заготовки №4, в случае с четырьмя заготовками.
С увеличением количества заготовок также увеличивается неоднородность
распределения температуры по садке, о чем свидетельствуют графики распределения
температурного поля. По мере приближения к горелке, нагрев заготовок
ухудшается, причем минимум плотности теплового потока и температуры приходится
на центральную часть заготовок, так как в этой области продукты сгорания
движутся с наименьшей скоростью.
Кроме этого, сильному нагреву подвергаются края заготовок. Это связано с
тем, что площадь теплообмена в углах больше по отношению к прогреваемому
объему.
С точки зрения равномерности прогрева рекомендуется нагревать в данной
печи одну заготовку. Если же основной упор делается на производительность, то для
каждого случая следует провести математическое моделирование с целью выявления
наилучшего соотношения количества заготовок и однородности прогрева по садке.
Для улучшения равномерности нагрева при расположении в печи нескольких
заготовок рекомендуется установить две симметрично расположенные горелки вместо
одной центральной. Интенсивность перемешивания продуктов сгорания в рабочем
пространстве печи увеличится, что повлечет за собой выравнивание поля
температур в объеме печи и на поверхности заготовок.
Список использованных источников
1 Грин В. М.
Основы инженерного эксперимента: Учебное пособие. - Барнаул: АлтГТУ, 2007. -
44с
2 Марков Б.
Л., Кирсанов А. А. Физическое моделирование в металлургии. - М.: Металлургия,
1984. - 119 с.
Крюков А. Ю.,
Потапов Б. Ф. Математическое моделирование процессов в машиностроении: Учебное
пособие. - Пермь: ПГТУ, 2007. - 322с.
Зарубин В. С.
Математическое моделирование в технике: Учебник для вузов. - М.: МГТУ им. Н. Э.
Баумана, 2003. - 496 с.
Паничев В.
В., Соловьев Н. А. Компьютерное моделирование: учебное пособие. - Оренбург: ГОУ
ОГУ, 2008. - 130 с.
Трусов П. В.
Введение в математическое моделирование: Учебное пособие. - М.: Логос, 2005. -
440 с.
Арутюнов В.
А., Бухмиров В. В., Крупенников С. А. Математическое моделирование тепловой
работы промышленных печей: Учебник для вузов. - М.: Металлургия, 1990. - 239 с.
8 ANSYS FLUENT
12.1 in Workbench User’s guide// АНСИС. - URL:
<http://www1.ansys.com/customer/content/documentation/121/fluent/flwb.pdf>
(дата
обращения 4.06.12)
9 ANSYS
FLUENT// CAE-эксперт. - URL:
<http://www.cae-expert.ru/product/ansys-fluent> (дата обращения 7.06.12)