Теоретические распределения данных

КУРСОВАЯ РАБОТА

по дисциплине:

«Эконометрическое моделирование»

Теоретические распределения данных

Введение

В данной курсовой работе раскрывается тема «Теоретическое распределение данных»: демонстрируется зависимость функций плотности вероятности, кумулятивного и обратного кумулятивного распределений от их параметров. Представлены примеры вычисления вероятностей и доверительных интервалов. Рассмотрены нормальное и логнормальное распределения, распределения Пуассона и бинарное распределение.

Целью работы является изучить различные распределения данных, а также ознакомиться с программой MATLAB.

вероятность распределение доверительный интервал

1. Теоретические распределения данных

Для численного и графического представления теоретических распределений данных в MATLAB имеются 3 типа файл-функций, включающих в свое имя аббревиатуры pdf, cdf или inv, расшифровка и перевод которых даны в следующей таблице:

Файл-функции с указанными аббревиатурами оперируют числовыми переменными среды MATLAB и потому эквивалентны в представлении как непрерывных, так и дискретных распределений. Для дискретных распределений файл-функции pdfs (Probability density functions) вычисляют вероятности значений случайной переменной, для непрерывных - плотность вероятности значений случайной переменной. Еще заметим, в Help MATLAB при повторных или безальтернативных ссылках на файл-функции pdf, cdf и inv чаще используется одно слово distribution, т.е. «распределение».

1.1 Непрерывные распределения

.1.1 Общие положения

Если задана функция плотности вероятности f (x| а, b,…), где х - случайная переменная, принимающая непрерывный ряд значений, а, b,… - параметры распределения, то функция кумулятивного распределения

F (x|a, b,…)=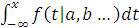

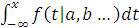
определяет вероятность того, что случайная переменная принимает значение, меньшее х.

Аналогично определяются вероятности того, что случайная переменная принимает значение, большее x, и значение, находящееся в интервале [x₁, x₂]. В краткой форме все три вероятности записывают так:

P (y<x) = F(x), P (y>x) = l-F(x), P(x₁≤y<x₂) = F(x₂) - F(x₁).

Дифференцирование функции кумулятивного распределения приводит к функции плотности вероятности

f (x|a, b,…)=F (x|a, b,…).

Вероятность попадания случайной переменной в интервал [x₁, x₂] определяется интегралом от функции плотности вероятности:

Р(x₁≤у<x₂) = x|a, b.) dx.

Нормировка плотности вероятности:

В Help MATLAB принята символическая форма записи функции обратного кумулятивного распределения

x = F^-1(p|a, b,…), где p = F (x|a, b,…).

Обратное кумулятивное распределение используется для оценок такого значения x_q случайной переменной, при котором функция кумулятивного распределения принимает значение, равное q, т.е.

F(x_q,|a, b.)=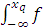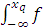(x|a, b,…) dx=q.

Из этого уравнения следует, что величина уровня q = P (x≤x_q) определяет вероятность того, что случайная переменная примет значение, меньшее или равное x_q. Величина x_q имеет называние «quantile». По-русски слово «квантиль» женского рода с ударением на втором слоге.

Для вычисления квантилей решают интегральное уравнение

x_q=F^-1(q|a, b,…).

Квантиль x_0,5 называется медианой (median), квантили x_0,25 и x_0,75 - соответственно нижняя квартиль и верхняя квартиль (quartile). Например, медиана вычисляется решением интегрального уравнения

.

Наряду с квантилями используют процентили (percentiles)

x_p=x_q*100%.

Процентиль х_50% также называется медианой, процентили х_25% и х_75% -соответственно нижняя и верхняя квартиль.

Модой х_m случайной величины называют ее значение, при котором функция распределения достигает максимума. Вычисляют моду решением уравнения

.

Еще раз обратим внимание, слова «квантиль», «квартиль», «процентиль», «медиана», «мода» женского рода.

Среднее значение (центр) распределения случайной переменной:

µ=.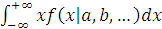

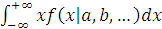Дисперсия (мера рассеяния) случайной переменной определяется как среднее значение квадрата отклонения значений случайной переменной от ее среднего значения,

D_σ.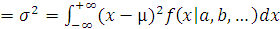

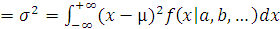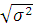
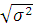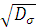
Величину σ = = 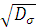называют стандартным отклонением. При интерпретации статистических результатов предпочтительнее обращаться именно к σ, а не к σ², в связи с тем, что величина стандартного отклонения σ имеет размерность исследуемой случайной переменной и потому легче воспринимается в качестве количественной характеристики.

Третий центральный момент

M₃=

определяет величину

A=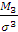

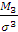
коэффициента асимметрии распределения относительно его среднего. Для значений А<0 данные распределены в большей мере слева от среднего, для А>0 - справа. Для распределений, симметричных относительно среднего, например, нормального, А = 0.

Четвертый центральный момент

M₄=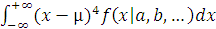

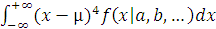
определяет величину

E=-3

коэффициента эксцесса (меру островершинности) распределения.

1.1.2 Нормальное (гауссово) распределение

Функция плотности вероятности

Базовая роль нормального распределения N (µ, σ) в анализе статистических данных связана с тем, что если результаты наблюдений определяются большим числом факторов, влияние каждого из которых пренебрежимо мало, то такой массив данных хорошо аппроксимируется нормальным распределением с соответствующим образом подобранными величинами среднего и стандартного отклонения.

Нормальное распределение находит применение в анализе

·   результатов большинства физических измерений,

·   финансово-экономических данных и маркетинговых исследованиях,

Функция плотности вероятности нормального распределения

f (x|µ, σ)=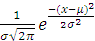

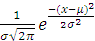
со средним значением µ случайной переменной х и стандартным отклонением σ представлена в MATLAB файл-функциями normpdf (x, mu, sigma) или pdf ('Normal', x, mu, sigma).

Построить графики плотностей нормальных распределений со средним значением

µ= 0 и стандартными отклонениями σ= 1,2,3 (рис. 1.1).

x=-4:0.1:4;=0; sigma=1;sigma<=3=normpdf (x, mu, sigma);

%f = pdf ('Normal', x, mu, sigma);(x, f, 'k', 'LineWidth', 1.5)on=sigma+1;('Плотность нормального распределения,\mu=0, \sigma=var')(' x ')(' f ')(-0.25, 0.38, '\sigma_1=1');(-0.25, 0.18, '\sigma_2=2');(-0.25, 0.12, '\sigma_3=3');

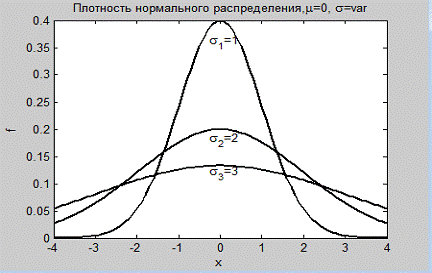
Из рис. 1.1 следует, что увеличение стандартного отклонения приводит к расплыванию плотности распределения случайной переменной.

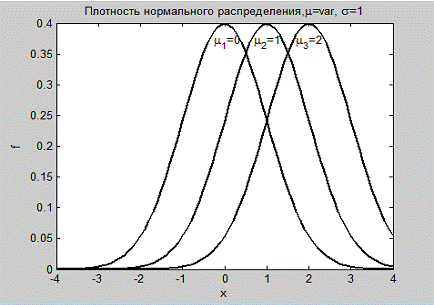
Построить графики плотностей нормальных распределений со средними значениями µ= 0,1,2 и стандартным отклонением σ= 1 (рис. 1.2).

x=-4:0.1:4;=0; sigma=1;mu<=2=normpdf (x, mu, sigma);(x, f, 'k', 'LineWidth', 1.5)on=mu+1;

%

title ('Плотность нормального распределения,\mu=var, \sigma=1 ')

xlabel (' x ')(' f ')(-0.25, 0.38, '\mu_1=0');(0.7, 0.38, '\mu_2=1');

text (1.7, 0.38, '\mu_3=2');

Из рис. 1.2 следует, что увеличение среднего значения сдвигает плотность распределения случайной переменной в положительном направлении оси абсцисс.

Вычислить среднее значение, дисперсию, 3-й и 4-й моменты, коэффициенты асимметрии и эксцесса нормального распределения случайной величины.

clear, clcpix mu sigma positive=1/2*exp (-1/2*(x-mu)^2/sigma^2)/sigma*2^(1/2)/pi^(1/2);=int (x*f, x, - inf, inf)=int((x-mu)^2*f, x, - inf, inf)=int((x-mu)^3*f, x, - inf, inf)=M3/sigma^3=int((x-mu)^4*f, x, - inf, inf)=M4/sigma^4-3=mu=sigma^23=0

A=3*sigma^4

E=0

Перепишем полученные результаты в аналитической форме

µ=µ, D=σ², M₃=0, A=0, M₄=3σ⁴, E=0.

Найти вероятности P₁(-∞, 0), P₂(-∞;+∞), P₃(1,2) попадания значений случайной переменной с распределением N (µ, σ) в интервалы значений (-∞, 0), (-∞,+∞) и [1,2].

clearx pi=0; sigma=1;=1/2*exp (-1/2*(x-mu)^2/sigma^2)/sigma*2^(1/2)/pi^(1/2);=int (f, x, - inf, 0),=int (f, x, - inf, inf),=int (f, x, 1,2), P3=vpa (P3,5)=1/2=1=erf (2^(1/2))/2 - erf (2^(1/2)/2)/23 =0.13591

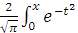
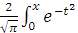Вероятность P₃(1,2)=erf() - erf() выражена через функцию ошибок erf(x)=dt.

Построить график функции ошибок erf(x)=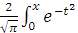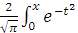dt.

x=-3:0.1:3;(x, erf(x), 'k', 'LineWidth', 1.5)(' x ')(' erf(x) ')

title (' Функция ошибок')

Результат показан на 1.3

Рис. 1.3

В аналитической форме интегралы, определяющие искомые вероятности, имеют следующий вид:

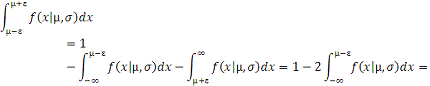
=1-2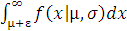

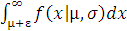
, clcx pi=5; sigma=1; epsilon=1;=1/2*exp (-1/2*(x-mu)^2/sigma^2)/sigma*2^(1/2)/pi^(1/2);=int (f, x, - inf, mu-epsilon);=simplify(P1), P1=vpa (P1,5)=int (f, x, mu-epsilon, mu+epsilon);=simplify(P2), P2=vpa (P2,5)=int (f, x, mu+epsilon, inf);=simplify(P3), P3=vpa (P3,5)=int (f, x, - inf, inf);=P1+P2+P3, P=vpa (P, 5)=P-P1-P3; P2=vpa (P2,5)=P-2*P1; P2=vpa (P2,5)=P-2*P3; P2=vpa (P2,5)

% График плотности вероятности=3*sigma;

hh=ezplot (f, [mu-xLim, mu+xLim]);on(hh, 'LineWidth', 2)(' x ')(' f(x) ')

title (' Симметричный интервал')

% Закраска площади трапеции PI

x=mu-xLim:2*epsilon*10^-3:mu-epsilon;=[.1.1.1]; F=normpdf (x, mu, sigma);=[x, mu-epsilon, mu-xLim]; fp=[F, 0,0]; patch (xp, fp, C);

% Закраска площади трапеции Р2=mu-epsilon:2*epsilon*10^-3:mu+epsilon;=[.7.7.7]; F=normpdf (x, mu, sigma);=[x, mu+epsilon, mu-epsilon];=[F, 0,0]; patch (xp, fp, C);

% Закраска площади трапеции РЗ=mu+epsilon:2*epsilon*10^-3:mu+xLim;=[.1.1.1]; F=normpdf (x, mu, sigma);=[x, mu+xLim, mu+epsilon]; fp=[F, 0,0]; patch (xp, fp, C);(gcf, 'Position', [35 35 750 650])=1/2 - erf (2^(1/2)/2)/2=0.15866=erf (2^(1/2)/2)=0.68269=1/2 - erf (2^(1/2)/2)/23 =0.15866

P =1

P =1.00000

P2 =0.68268

P2 =0.68268

P2 =0.68268

Создать файл-функцию для графической иллюстрации и оценок вероятностей попадания значений случайной переменной, подчиняющейся нормальному распределению с параметрами µ и σ, в интервал значений от x₁ до x₂. Используя файл-функцию, найти: 1) вероятность попадания нормально распределенной случайной величины с параметрами µ=0 и σ=1 в интервал значений от x₁= -1 до x₂= 2; 2) вероятность попадания случайно переменной с распределением N (µ= 2,σ= l) в интервал значений от x₁=µ-3σ= -1 до х₂= µ+3σ=5.

function NormFig (mu, sigma, x1, x2)

% Построение графика плотности вероятности=3*sigma;

x=mu-tsigma: (x2-x1)*10^-2:mu+tsigma;=normpdf (x, mu, sigma);(x, f, 'k', 'Linewidth', 1.5)on(' x ')(' f ')(' P')

% Закраска площади трапеции=x1: (x2-x1)*10^-2:x2;

C=[.7.7.7]; f=normpdf (x, mu, sigma);=[x, x2, x1]; fp=[f, 0,0];(xp, fp, C); alpha(.5)

% Оценка вероятности'x=normpdf (x, mu, sigma);=subs (f, x, mu); P=int (f, x, x1, x2); P=vpa (P, 5)

Вероятность попадания нормально распределенной случайной величины c параметрами µ= 0 и σ= 1 в интервал значений от х₁= -1 до x₂= 2 (рис. 1.5):

clear, clc, close(0,1, - 1,2)=0.81859

Далее используем файл-функцию NormFig для иллюстрации правила трех сигм, которое говорит о том, что если случайная переменная имеет нормальное распределение N (µ, σ), то практически достоверно попадание ее значений в интервал от µ-3σ до µ+3σ.

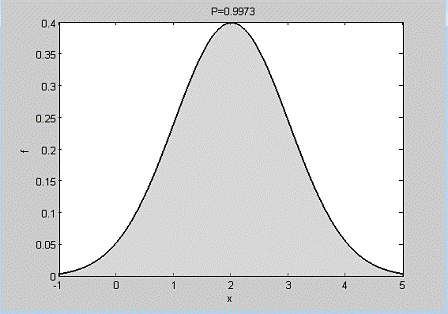
Вероятность попадания случайной переменной с распределением N (µ=2, σ=1) в интервал значений от х₁= µ-3σ= -1 до х₂ =µ+3σ= 5 (рис. 1.6):

clear, clc, close(2,1, - 1,5)=0.9973

Вычислить моду нормального распределения с параметрами µ= 2 и σ= 1.

clear, clcpix mu sigma positive= 1/2*exp (-1/2*…

(x-mu)^2/sigma^2)/sigma*2^(1/2)/pi^(1/2);_f=diff (f, x)=solve (diff_f)(2,1,1)=subs (f, {'mu', 'sigma'}, {2,1})=ezplot(f); hold on,(' x ')(' f(x) ')(2,1,2)_f=subs (diff_f, {'mu', 'sigma'}, {2,1})=ezplot (diff_f);(' x ')(' f(x) ')(gcf, 'position', [300 35 550 680])_f =(2^(1/2)*(2*mu - 2*x))/(4*pi^(1/2)*sigma^3*exp((mu - x)^2/(2*sigma^2)))=mu=2^(1/2)/(2*pi^(1/2)*exp((x - 2)^2/2))_f = - (2^(1/2)*(2*x - 4))/(4*pi^(1/2)*exp((x - 2)^2/2))

Мода нормального распределения совпадает со средним значением случайной переменной: 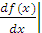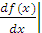_x=µ =0.

На рис. 1.7 помимо функции плотности нормального распределения, показанного в первом подокне, во втором подокне показана производная функции распределения, которая обращается в ноль при значении х=2.

Численное решение этой задачи связано с использованием М-функции [fmax, k]=max(f) обработки числовых массивов, где fmax - имя наибольшего элемента массива f, k - номер наибольшего элемента в массиве f.

clear, clc=2; sigma=1;=-3*sigma:0.1:3*sigma;

f=normpdf (x, mu, sigma);

% Определение максимального элемента массива х и номера этого элемента

[fmax, k]=max(f)

% Определение моды по номеру элемента массива х

mode=x(k)=0.3989= 51

mode =2.

Нормальное кумулятивное распределение

Функция кумулятивного нормального распределения

F (x|µ, σ)=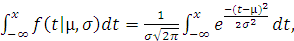

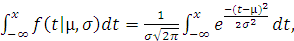
определяющая вероятность того, что случайная переменная примет значение, меньшее x, представлена в MATLAB файл-функциями normcdf (x, mu, sigma) и cdf (‘Normal’, x, mu, sigma).

Дифференцирование функции кумулятивного распределения приводит к функции плотности вероятности

f (x|µ, σ)=F (x|µ, σ).

clear, clct x mu sigma pi=int (exp(- (t-mu)^2/2/sigma^2), t, - inf, x)/sigma/(2*pi)^(1/2);=diff (F, x)=1/(sigma*exp((mu - x)^2/(2*sigma^2))*(2*pi)^(1/2))

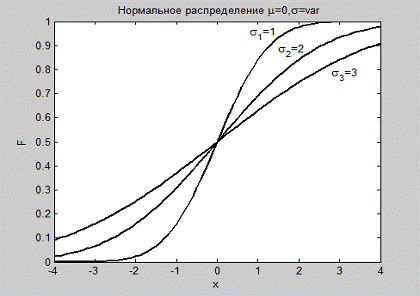
Построить график кумулятивных функций нормального распределения со средним значением µ=0 и стандартными отклонениями σ=1,2,3 (рис. 1.8)

x=-4:0.1:4;=0; sigma=1;sigma<=3=normcdf (x, mu, sigma);(x, F, 'k', 'LineWidth', 1.5), hold on=sigma+1;

%(' Нормальное распределение \mu=0,\sigma=var')(' x ')(' F ')(0.8, 0.95, '\sigma_1=1');(1.5, 0.88, '\sigma_2=2');(2.8, 0.78, '\sigma_3=3');

Установить связь функции ошибок erf(x)=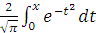 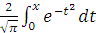с нормальным распределением F(x)=, имеющим параметры µ=0 и σ=.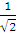

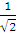Так как F()=+,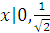

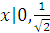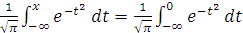
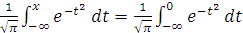то, вычисляя первый интеграл

clear, clct(exp(-t^2), t, - inf, 0) =pi^(1/2)/2

и подставляя найденное значение в формулу для F, получим

erf(x)=2F(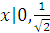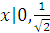) - 1.

Проверим эту связь:

clear, clct x mu sigma pi=int (exp(- (t-mu)^2/2/sigma^2), t, - inf, x)/sigma/(2*pi)^(1/2);=2*subs (F, {mu, sigma}, {0,1/2^(1/2)}) - 1;=simplify(erf)(F, 'k', 'LineWidth', 1.5), hold on =erf(x).

Сначала решим задачу аналитически. Для этого используем определение величины P через интеграл

P=

Так как

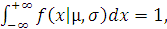
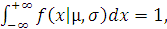
то разбивая диапазон изменения переменной интегрирования на 3 области (-∞, µ-ɛ),

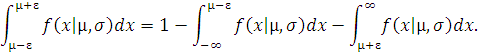
Учитывая, что

и следовательно

-

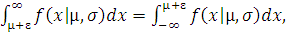
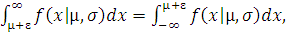
находим

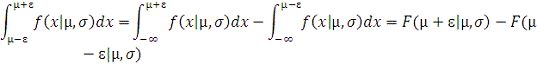
Решим задачу численно, полагая, например, µ=5, σ=1, ɛ=1.

clear, clcx pi=5; sigma=1; epsilon=1;=1/2*exp (-1/2*(x-mu)^2/sigma^2)/sigma*2^(1/2)/pi^(1/2);

disp ('Прямое вычисление исходного интеграла')

P=int (f, x, mu-epsilon, mu+epsilon), P=vpa (P, 5)

disp ('Вычисление интегралов, определяющих кумулятивную функцию')

P=int (f, x, - inf, mu+epsilon) - int (f, x, - inf, mu-epsilon);=simplify(P), P=vpa (P, 5)

disp ('Вычисление разности значений кумулятивной функции')

P=normcdf (mu+epsilon, mu, sigma) - normcdf (mu-epsilon, mu, sigma)

Прямое вычисление исходного интеграла

P =erf (2^(1/2)/2)

P =0.68269

Вычисление интегралов, определяющих кумулятивную функцию

P =erf (2^(1/2)/2)

P =0.68269

Вычисление разности значений кумулятивной функции

P =0.6827

Используя кумулятивную функцию распределения, найти вероятность того, что значения случайной переменной X=N (µ, σ) лежат в интервале [µ-ɛ, µ+ɛ]. Дать численное решение для случаев: а) X=N (0,1), [-0. 5,0.5]; b) X=N (3,1), [-0. 5,0.5]; c) X=N (0,2), [-0. 5,0.5]; d) X=N (0,2), [-3,3].

Для решения задачи напишем файл-функцию, основанную на обращении к высокоуровневой функции normcdf. В качестве выходной величины сформируем вектор с компонентами значений кумулятивной функции на краях заданных интервалов и их разности, определяющей искомую вероятность.

function epsilonM (mu, sigma, epsilon)

%=mu-epsilon; x2=mu+epsilon;=normcdf (x1, mu, sigma); p2=normcdf (x2, mu, sigma);=p2-p1;=[p1, p2, p]=x1-3*sigma:10^-1:x2+3*sigma; F=normcdf (x, mu, sigma);(x, F, 'k', 'LineWidth', 1.5), hold on('\mu=0, \sigma=1, \epsilon=0.5')(' x ')(' F ')

% Закраска площади трапеции=mu-epsilon:2*epsilon*10^-2:mu+epsilon;=[.7.7.7]; F=normcdf (x, mu, sigma);=[x, mu+epsilon, mu-epsilon];=[F, 0,0]; patch (xp, fp, C); alpha(.5)=normcdf (mu-epsilon, mu, sigma);(mu-epsilon, F1, num2str(F1));=normcdf (mu+epsilon, mu, sigma);(mu+epsilon, F2, num2str(F2));

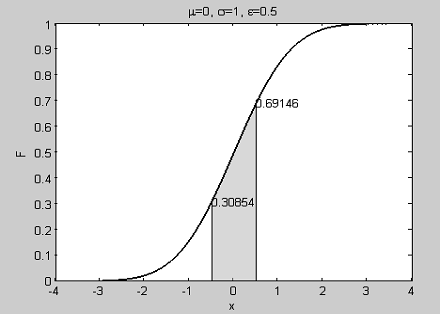
В случае а) обращение к файл-функции(0,1,0.5)=0.3085 0.6915 0.3829

дает величину 0.3829 вероятности попадания значений случайной переменной X=N (0,1) в интервале [-0. 5,0.5]. Рис. 1.9 иллюстрирует эти вычисления.

Вычисления для случая b) показывают, что изменение среднего значения случайной величины не изменяет значений вычисляемых вероятностей (рис. 1.10).

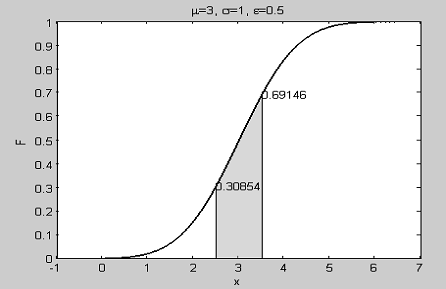
clear, clc, close(3,1,0.5)

P = 0.3085 0.6915 0.3829

В случае с) увеличение стандартного отклонения приводит к увеличению вероятности получить значение случайной переменной X=N (0,2) меньшее, чем нижняя граница заданного интервала [-0. 5,0.5], и к уменьшению вероятности получить значение случайной величины меньшее, чем верхняя граница интервала. Связано это с уменьшением крутизны кумулятивной функции. В результате этих изменений вероятность получить значение случайной переменной X=N (0,2) в заданном интервале уменьшается (рис. 1.11).

clear, clc, close(0,2,0.5)

P =0.4013 0.5987 0.1974

В случае d) увеличение интервала от [-0. 5,0.5] до [-3,3] приводит к увеличению вероятности обнаружить значения случайной переменной в пределах интервала.

clear, clc, close(0,2,3)

Проверим последний результат обращением к файл-функции NormFig, которая вычисляет вероятности на основании использования высокоуровневой функции normpdf

clear, clc, close(0,2, - 3,3)

P =0.86639

2. Обратная кумулятивная функция нормального распределения

Обратная кумулятивная функция нормального распределения, являющаяся решением интегрального уравнения

х=F^-1 (p|µ, σ), где р=F (x|µ, σ),

определена файл-функцией norminv (F, mu, sigma):

Квантиль x_q уровня q, вычисляют решением уравнения

F(x_q|µ, σ)=.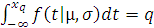

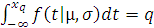Построить графики функций обратных кумулятивных нормальных распределений с параметрами µ=0 и σ=1,2,3 (рис. 1.14).

F=0:0.001:1;=0; sigma=1;sigma<=3=norminv (F, mu, sigma);(F, x, 'k', 'LineWidth', 1.5), hold on=sigma+1;

end

%(' Обратное нормальное распределение, \mu=0, \sigma=var')

xlabel (' F ')(' x(F) ')(0.88, 0.35, '\sigma_1=1');(0.85, 1.8, '\sigma_2=2'); (0.8, 3.5, '\sigma_3=3');

Связь функций кумулятивного и обратного кумулятивного распределений иллюстрируется следующими двумя алгоритмами.

x=-4:0.1:4;=0; sigma=1;sigma<=3=norminv (normcdf(x, mu, sigma), mu, sigma);(x, xnew, 'k', 'LineWidth', 1.5), hold on=sigma+1;

%(' x ')(' x ')('x=norminv (normcdf(x, mu, sigma), mu, sigma)')=0:0.1:1;=0; sigma=1;sigma<=3=normcdf (norminv(F, mu, sigma), mu, sigma);(F, Fnew, 'k', 'LineWidth', 1.5), hold on=sigma+1;

%(' F ')

ylabel (' F ')

title (' F=normcdf (norminv(F, mu, sigma), mu, sigma)')

Построить файл-функцию для вычисления и графической иллюстрации квантилей нормального распределения с параметрами µ и σ. Уровни квантилей задать вектором q= [q, q₂, q₃…].

function quantileMy (mu, sigma, q)

%('Уровни квантилей'), q('Квантили, вычисленные функцией norminv')

xq=norminv (q, mu, sigma)

%=0:10^-5:1; x=norminv (F, mu, sigma);

disp ('Квантили, вычисленные функцией quantile')=quantile (x, q)('Уровни процентилей')=q*100('Процентили, вычисленные функцией prctile')

xp=prctile (x, p100)(F, x, 'k', 'LineWidth', 1.5);(gca, 'XTick', q)(gca, 'YTick', xq)([0 1 mu-4 mu+4])(' x(F) ')

ylabel (' F ')('Квантили распределения N (\mu=5, \sigma=1)')

Например:

mu=5; sigma=1; q=[.05 0.25 0.5 0.75 0.95](mu, sigma, q)

Уровни квантилей

q =0.0500 0.2500 0.5000 0.7500 0.9500

Квантили, вычисленные функцией norminv

xq =3.3551 4.3255 5.0000 5.6745 6.6449

Квантили, вычисленные функцией quantile

xq =3.3551 4.3255 5.0000 5.6745 6.6449

Уровни процентилей

p100 =5 25 50 75 95

Процентили, вычисленные функцией prctile

xp =3.3551 4.3255 5.0000 5.6745 6.6449

Например, квантиль x_0.25 распределения N (5,1) говорит о том, что значению F=0.25 кумулятивной функции распределения соответствует значение случайной величины, равное х_0.25=4.3255.

Для нормального распределения с параметрами µ=0 и σ=1, используя высокоуровневую функцию disttool, предоставляющую графический интерфейс для интерактивной работы с функциями pdf и cdf, вычислить: 1) значение функции распределения (плотности вероятности, pdf) для значения случайной величины х=0.75; 2) значение кумулятивной функции (cdf) распределения для значения    случайной величины х=0.75;

) значение случайной величины x_0.75 для значения F=0.75 обратной кумулятивной функции

(т.е. квантили уровня q=0.75).

Вводя в командное окно MATLAB оператор

disttool

Сравнивая значение квантили х_0.75=0.67449=0.6745 распределения N (µ=0,σ=1), полученное в окне на рис. 1.20, со значением квантили 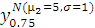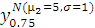=5.6745, найденной в предыдущей задаче, нетрудно заметить, что они связаны простым соотношением:

=5.6745-5 = 0.6745,

где символом у обозначено, что взята квантиль распределения другой переменной.

Примечание. Графический интерфейс disttool позволяет работать только с функциями pdf и cdf. Но в графическом окне для функции, cdf предоставлена возможность изменения значений как аргумента, так и функции, что делает избыточным построение графика обратного кумулятивного распределения (inv).

Инструмент disttool является чрезвычайно эффективным средством в освоении характерных черт различного рода статистических распределений.

Подойдем к вопросу связи квантилей разных распределений более подробно и одновременно для разнообразия воспользуемся идеей файл-функции disttool вычислять квантили с их графической иллюстрацией на основании функции cdf.

Построить файл-функцию для вычисления и графической иллюстрации с помощью функции cdf квантилей двух нормальных распределений N(µ₁, σ₁) и N(µ₁, σ₁). Уровни квантилей задать векторами q₁=[q_11,q_12,q₁₃…] и q₂=[q_21,q_22,q₂₃…].

function quantileMy2 (mu1, sigma1, q1, mu2, sigma2, q2)

%(2,1,1)=norminv (q1, mu1, sigma1)=mu1-3*sigma1:10^-5:mu1+3*sigma1;=normcdf (x1, mu1, sigma1);(x1, F1,'k', 'LineWidth', 1.5);(gca, 'XTick', xq1), set (gca, 'YTick', q1)([mu1-3*sigma1 mu1+3*sigma1 0 1])(' x ')(' F(x) ')

title ('Квантили распределения N (\mu_1, \sigma_1)')

subplot (2,1,2)=norminv (q2, mu2, sigma2)=mu2-3*sigma2:10^-5:mu2+3*sigma2;=normcdf (x2, mu2, sigma2);(x2, F2,'k', 'LineWidth', 1.5);(gca, 'XTick', xq2), set (gca, 'YTick', q2)([mu2-3*sigma2 mu2+3*sigma2 0 1])(' x ')(' F(x) ')

title ('Квантили распределения N (\mu_2, \sigma_2)').

Заключение

В заключение главы отметим, что представленные алгоритмы решений задач по темам непрерывных и дискретных распределений, в которых мы ограничились нормальным, логнормальным распределениями, распределением Пуассона и биномиальным распределением, задают основу для анализа произвольного статистического распределения.