Оптимизационные методы минимизации и максимизации
Введение
Оптимизация как раздел математики существует
достаточно давно. Оптимизация - это выбор, т.е. то, чем постоянно приходится
заниматься в повседневной жизни. Термином "оптимизация" в литературе
обозначают процесс или последовательность операций, позволяющих получить
уточненное решение. Хотя конечной целью оптимизации является отыскание
наилучшего или "оптимального" решения, обычно приходится
довольствоваться улучшением известных решений, а не доведением их до
совершенства. Поэтому под оптимизацией понимают скорее стремление к
совершенству, которое, возможно, и не будет достигнуто.
Необходимость принятия наилучших решений так же
стара, как само человечество. Испокон веку люди, приступая к осуществлению
своих мероприятий, раздумывали над их возможными последствиями и принимали
решения, выбирая тем или другим образом зависящие от них параметры - способы
организации мероприятий. Но до поры, до времени решения могли приниматься без
специального математического анализа, просто на основе опыта и здравого смысла.
Вообще, чем сложнее организуемое мероприятие,
чем больше вкладывается в него материальных средств, чем шире спектр его
возможных последствий, тем менее допустимы так называемые "волевые"
решения, не опирающиеся на научный расчет, и тем большее значение получает
совокупность научных методов, позволяющих заранее оценить последствия каждого
решения, заранее отбросить недопустимые варианты и рекомендовать те, которые
представляются наиболее удачными.
Практика порождает все новые и новые задачи
оптимизации причем их сложность растет. Требуются новые математические модели и
методы, которые учитывают наличие многих критериев, проводят глобальный поиск
оптимума. Другими словами, жизнь заставляет развивать математический аппарат
оптимизации.
Реальные прикладные задачи оптимизации очень
сложны. Современные методы оптимизации далеко не всегда справляются с решением
реальных задач без помощи человека. Нет, пока такой теории, которая учла бы
любые особенности функций, описывающих постановку задачи. Следует отдавать предпочтение
таким методам, которыми проще управлять в процессе решения задачи.
Оптимизационные методы минимизации и
максимизации приобретают всё большую ценность и востребованность.
Применение оптимизационных задач имеет особый
успех при проектировании и анализе больших технических систем. Кроме того,
интенсивное развитие средств вычислительной техники стимулирует ускорение
темпов внедрения теоретических разработок в инженерную практику. В настоящее
время для инженера знание методов оптимизации столь же необходимо, как знание
основ математического анализа, физики, радиоэлектроники и других дисциплин.
.
Нахождение стационарной точки
Целевая функция:
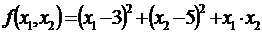
Для того, чтобы в точке 
 функция f(x) имела
безусловный локальный экстремум необходимо, чтобы все её частные производные
обращались в точке
функция f(x) имела
безусловный локальный экстремум необходимо, чтобы все её частные производные
обращались в точке 
 в нуль.
в нуль.
Найдем для данной целевой функции 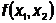 частные
производные по
частные
производные по 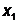 и
и 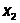 :
:

Приравняв полученные выражения к нулю, получим
систему уравнений:
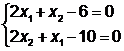
Решение системы уравнений даёт
результат:
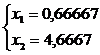
Таким образом, экстремум целевой
функции является точка с координатами х* = Т, значение целевой функции, в
которой:
Т, значение целевой функции, в
которой: 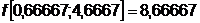 .
.
Для определения характера
стационарной точки составим определитель матрицы Гессе. Под определителем Гессе
понимается определитель, составленный из вторых производных исходной целевой
функции.
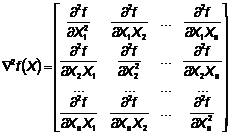
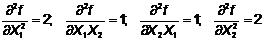

Так как гессиан функция -
положительно определенная матрица (выполняются условия Сильвестра: все
диагональные элементы матрицы Гесса - положительные величины, все ведущие
главные определители положительные величины), стационарная точка является
точкой минимума.

Рис 1. Линии уровня функции и стационарная точка
2.
Нахождение безусловного экстремума методами прямого поиска
Задача безусловной оптимизации состоит в
нахождении минимума или максимума функции в отсутствие каких-либо ограничений.
Несмотря на то что большинство практических задач оптимизации содержит
ограничения, изучение методов безусловной оптимизации важно с нескольких точек
зрения. Многие алгоритмы решения задачи с ограничениями предполагают сведение
ее к последовательности задач безусловной оптимизации. Другой класс методов
основан на поиске подходящего направления и последующей минимизации вдоль этого
направления. Обоснование методов безусловной оптимизации может быть
естественным образом распространено на обоснование процедур решения задач с
ограничениями.
2.1 Метод поиска по симплексу
Описание алгоритма:
Суть метода заключается в исследовании целевой
функции в вершинах некого "образца", построенного в пространстве
вокруг "базовой" точки. Вершина, давшая наибольшее значение целевой
функции отображается относительно двух других вершин и таким образом становится
новой базовой точкой, вокруг которой строится новый образец и снова выполняется
поиск. В случае двух переменных симплексом является равносторонний треугольник,
в трёхмерном пространстве - тетраэдр.
Работа алгоритма начинается с построения
регулярного симплекса в пространстве независимых переменных и оценивания
значений целевой функции в каждой точке. Затем определяется вершина с
максимальным значением целевой функции и проектируется через центр тяжести
оставшихся вершин в новую точку.
Процедура продолжается до тех пор, пока не будет
накрыта точка минимума.
Некоторые правила:
. Если вершина с максимальным значением целевой
функции построена на предыдущем шаге, то отбрасывается вершина со следующим по
величине значением целевой функции.
. Если вокруг одной из вершин начинается
циклическое движение, то необходимо уменьшить размеры симплекса.
Поиск заканчивается тогда, когда размеры
симплекса или разность значений целевой функции становятся достаточно малыми.
При заданной начальной точке  и
масштабном множителе
и
масштабном множителе 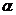 , координаты
остальных
, координаты
остальных  вершин
симплекса в
вершин
симплекса в  - мерном
пространстве вычисляются по формуле:
- мерном
пространстве вычисляются по формуле:

Приращения 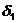 и
и  определяется
по формулам:
определяется
по формулам:
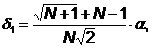
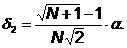
Величина 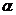 выбирается
исследователем, исходя из характеристики решаемой задачи. При
выбирается
исследователем, исходя из характеристики решаемой задачи. При 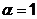 ребро
симплекса имеет единичную длину.
ребро
симплекса имеет единичную длину.
Вычисление центра тяжести:
Если 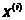 - точка, подлежащая отражению, то
координаты центра тяжести определяются по формуле:
- точка, подлежащая отражению, то
координаты центра тяжести определяются по формуле:

Координаты новой вершины удовлетворяют
уравнению:
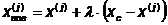
Для того чтобы симплекс обладал
свойством регулярности, отображение должно быть симметричным, т.е. 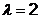

Если некоторая вершина симплекса не
исключается на протяжении нескольких итераций, то необходимо уменьшить размер
симплекса и построить новый симплекс, выбрав в качестве базовой точку с
минимальным значением целевой функции.
Алгоритм метода:
Шаг 1. Задать: 1. Начальную точку х(0) ;
. Масштабный множитель α;
3. Приращения δ1 и
δ2
;
.Условие окончания поиска. Перейти к шагу 2.
Шаг 2. Вычислить координаты вершин х(1) и х(2)
симплекса. Перейти к шагу 3.
Шаг 3. Определить значения целевой функции в
вершинах симплекса. Перейти к шагу 4.
Шаг 4. Вершина, которой соответствует наибольшее
значение целевой функции , построена на предыдущей итерации?
Да: отображается вершина, которой соответствует
следующее по величине значение целевой функции
Нет: отображается точка с наибольшим значением
целевой функции относительно двух других вершин симплекса. Перейти к шагу 5.
Шаг 5. Проверка на условие окончания.
Да: закончить поиск; результат- точка с
наименьшим значением целевой функции;
Нет: перейти к шагу 3.
Ход решения :
Исходные данные:
 - целевая функция;
- целевая функция;
Шаг 1.  - начальная
точка;
- начальная
точка;
 - масштабный множитель;
- масштабный множитель;
Минимизируем целевую функцию до
первого уменьшения размера симплекса:
Пусть масштабный множитель - 
 ;
;
 ;
;
Шаг 2-3.
-я итерация:
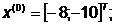
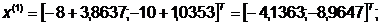

 - максимально, следовательно,
заменяем
- максимально, следовательно,
заменяем
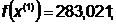
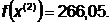

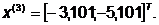
Шаг 3-5.
-я итерация:
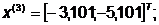

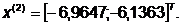

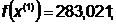 - максимально, следовательно,
заменяем
- максимально, следовательно,
заменяем
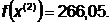
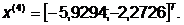
-я итерация:
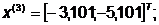
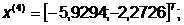
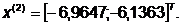


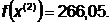 - максимально, следовательно,
заменяем
- максимально, следовательно,
заменяем

-я итерация:
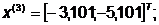
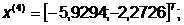

 - максимально, следовательно,
заменяем
- максимально, следовательно,
заменяем


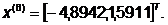
-я итерация:
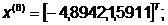
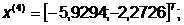

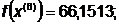
 - максимально, следовательно,
заменяем
- максимально, следовательно,
заменяем


-я итерация:
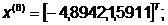


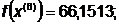

 - максимально, следовательно,
заменяем
- максимально, следовательно,
заменяем
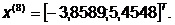
-я итерация:
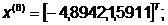

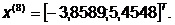
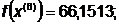 - максимально, следовательно,
заменяем
- максимально, следовательно,
заменяем

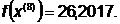

8-я итерация:
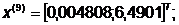

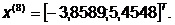


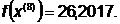 - максимально, следовательно,
заменяем
- максимально, следовательно,
заменяем

-я итерация:
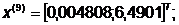



 - максимально, следовательно,
заменяем
- максимально, следовательно,
заменяем
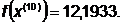
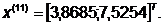
-я итерация:
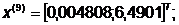
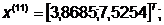


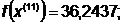
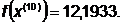
Так как наибольшее значение целевой
функции соответствует  , которое
получено на предыдущей итерации, отбрасываем
, которое
получено на предыдущей итерации, отбрасываем 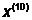 .
.
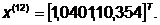
11-я итерация:
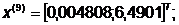
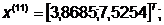
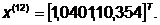

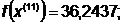

Так как наибольшее значение целевой
функции соответствует  , которое
получено на предыдущей итерации, отбрасываем
, которое
получено на предыдущей итерации, отбрасываем  .
.
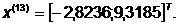
-я итерация:
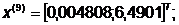
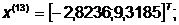
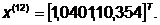

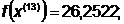
 - максимально, следовательно,
заменяем
- максимально, следовательно,
заменяем

-я итерация:
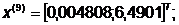
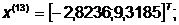


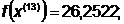 - максимально, следовательно,
заменяем
- максимально, следовательно,
заменяем
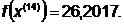
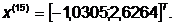
Симплекс сделал один оборот в
области расположения точки  , то есть точку
, то есть точку  при
заданных условиях можно считать точкой минимума целевой функции
при
заданных условиях можно считать точкой минимума целевой функции 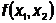 (для
получения более точного решения необходимо уменьшить размер симплекса).
(для
получения более точного решения необходимо уменьшить размер симплекса).
Таким образом, точка  - точка
минимума, значение функции в которой
- точка
минимума, значение функции в которой  .
.
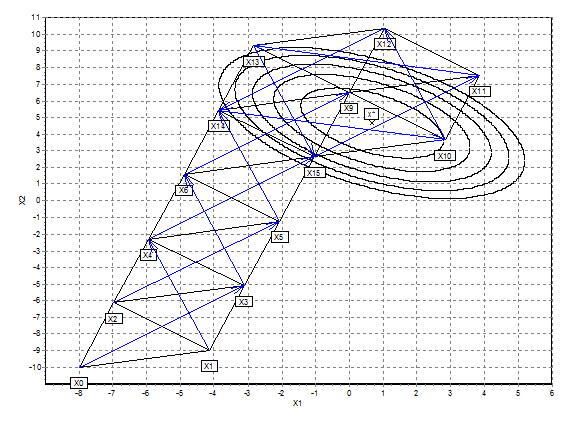
Рис 2. Графическое пояснение метода равномерного
симплекса
2.2 Метод поиска Хука-Дживса
Описание алгоритма:
Процедура Хука-Дживса представляет собой
комбинацию "исследующего" поиска с циклическим изменением переменных
и ускоряющего поиска по найденному образцу. Исследующий поиск ориентирован на
выявление направления вдоль "оврагов". Полученная в результате
исследующего поиска информация используется затем в процессе поиска по образцу
при движении по "оврагам".
Исследующий поиск:
Для проведения исследующего поиска
необходимо задать величину шага, которая может быть различна для разных
координатных направлений, и изменяться в процессе поиска. Поиск начинается в
некоторой исходной точке. Делается пробный шаг вдоль одного из координатных
направлений. Если значение целевой функции в пробной точке меньше, чем в
исходной, то шаг считается удачным. В противном случае возвращаются в исходную
точку и делают шаг в противоположном направлении. После перебора всех  координат
исследующий поиск заканчивается. Полученную в результате исследующего поиска
точку называют базовой.
координат
исследующий поиск заканчивается. Полученную в результате исследующего поиска
точку называют базовой.
Поиск по образцу:
Поиск по образцу в заключается в
реализации единственного шага из полученной базовой точки вдоль прямой,
соединяющей эту точку с предыдущей базовой точкой. Новая точка определяется по
формуле:

Как только движение по образцу не
приводит к уменьшению целевой функции, точка 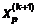 фиксируется в качестве временной
базовой точки и выполняется исследующий поиск. При уменьшении значения целевой
функции эта точка рассматривается как базовая точка. Если же исследующий поиск
не дал результата, необходимо вернуться в предыдущую точку и провести
исследующий поиск заново. Если такой поиск не приводит к успеху, то необходимо
уменьшить величину шага. Поиск завершается, когда величина шага приращения
становится достаточно малой.
фиксируется в качестве временной
базовой точки и выполняется исследующий поиск. При уменьшении значения целевой
функции эта точка рассматривается как базовая точка. Если же исследующий поиск
не дал результата, необходимо вернуться в предыдущую точку и провести
исследующий поиск заново. Если такой поиск не приводит к успеху, то необходимо
уменьшить величину шага. Поиск завершается, когда величина шага приращения
становится достаточно малой.
Алгоритм метода:
Шаг 1. Задать: 1. Начальную точку  ;
;
. Приращение 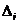 ,
,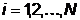 ;
;
. Коэффициент уменьшения шага  ;
;
. Параметр окончания поиска 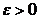 .
.
Шаг 2. Произвести исследующий поиск.
Шаг 3. Поиск удачный:
Да: перейти к шагу 5;
Нет: продолжить.
Шаг 4. Проверка на окончание поиска:
 ?
?
Да: прекратить поиск;
Нет: уменьшить приращение по
формуле:
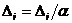 ,
,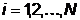 ; Перейти к шагу 2.
; Перейти к шагу 2.
Шаг 5. Провести поиск по образцу: 
Шаг 6. Провести исследующий поиск,
используя 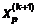 в качестве
базовой точки:
в качестве
базовой точки:  -
полученная в результате точка
-
полученная в результате точка
Шаг 7. Выполняется ли условие 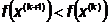 ?
?
Да: продолжить 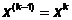 ;
; 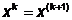 ;
;
перейти к шагу 5; Нет: перейти к
шагу 4.
Ход решения: Исходные данные:
 - целевая функция;
- целевая функция;
Шаг 1.
 - начальная точка;
- начальная точка;
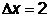 - векторная величина приращения;
- векторная величина приращения;
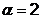 - масштабный множитель;
- масштабный множитель;
Минимизируем значение целевой
функции до первого сокращения шага поиска
1.

Шаг 2. Исследующий поиск вокруг
базовой точки  :
:
фиксируя 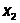 , даём
приращение переменной
, даём
приращение переменной 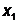 :
:
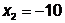 ;
;  ;
; 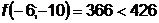 - поиск удачен;
- поиск удачен;
фиксируя 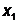 , даём
приращение переменной
, даём
приращение переменной 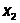 :
:
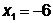 ;
; 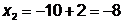 ;
;  - поиск удачен;
- поиск удачен;
Шаг 3.
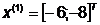
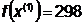
Так как поиск удачен, то переходим к
поиску по образцу (Шаг 5):
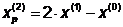
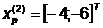
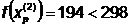
Шаг 6. 2. Исследующий поиск вокруг
точки 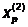 (Шаг 2.):
(Шаг 2.):
фиксируя 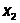 , даём
приращение переменной
, даём
приращение переменной 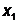 :
:
 ;
;  ;
; 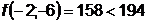 - поиск удачен;
- поиск удачен;
фиксируя 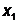 , даём
приращение переменной
, даём
приращение переменной 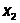 :
:
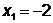 ;
; 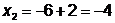 ;
; 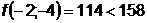 - поиск удачен;
- поиск удачен;
Шаг 7.
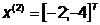
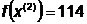
Шаг 5. Так как поиск удачен, то
переходим к поиску по образцу (Шаг 5.):

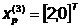
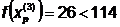
Шаг 6. 3.Исследующий поиск вокруг
точки  :
:
фиксируя 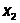 , даём
приращение переменной
, даём
приращение переменной 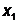 :
:
 ;
; 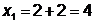 ;
;  - поиск неудачен;
- поиск неудачен;
 ;
;  ;
;  - поиск неудачен;
- поиск неудачен;
фиксируя 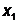 , даём
приращение переменной
, даём
приращение переменной 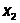 :
:
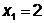 ;
;  ;
;  - поиск удачен;
- поиск удачен;
Шаг 7.

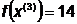
Так как поиск удачен, то переходим к
поиску по образцу (Шаг 5.):
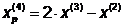
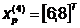

Значение целевой функции
увеличилось, поэтому возьмём последнюю точку за временную базовую и проведём
исследующий поиск.
.
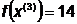
Шаг 6. Исследующий поиск вокруг
базовой точки  :
:
фиксируя 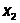 , даём
приращение переменной
, даём
приращение переменной 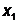 :
:
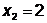 ;
; 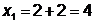 ;
;  - поиск неудачен;
- поиск неудачен;
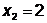 ;
;  ;
; 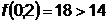 - поиск неудачен;
- поиск неудачен;
фиксируя 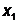 , даём
приращение переменной
, даём
приращение переменной 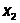 :
:
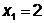 ;
; 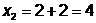 ;
;  - поиск удачен;
- поиск удачен;
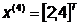

Так как поиск удачен, то переходим к
поиску по образцу (Шаг 5.) :

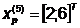

Значение целевой функции
увеличилось, поэтому возьмём последнюю точку за временную базовую и проведём
исследующий поиск (Шаг 6.).
.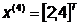

Исследующий поиск вокруг базовой
точки  :
:
фиксируя 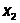 , даём
приращение переменной
, даём
приращение переменной 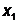 :
:
 ;
; 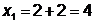 ;
;  - поиск неудачен;
- поиск неудачен;
 ;
;  ;
; 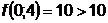 - поиск неудачен;
- поиск неудачен;
фиксируя 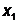 , даём
приращение переменной
, даём
приращение переменной 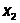 :
:
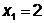 ;
;  ;
;  - поиск неудачен;
- поиск неудачен;
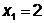 ;
; 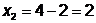 ;
; 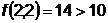 - поиск неудачен;
- поиск неудачен;
В результате исследующего поиска не
было достигнуто уменьшение значения целевой функции, то есть значение шага
(векторной величины приращения) уменьшить в 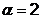 раз, до величины
раз, до величины 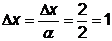 , затем
необходимо произвести исследующий поиск вокруг точки
, затем
необходимо произвести исследующий поиск вокруг точки 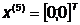 , используя
новое значение приращения
, используя
новое значение приращения 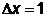 .
.
Итерации продолжаются, пока величина
шага не укажет на окончание поиска в окрестности точки минимума.
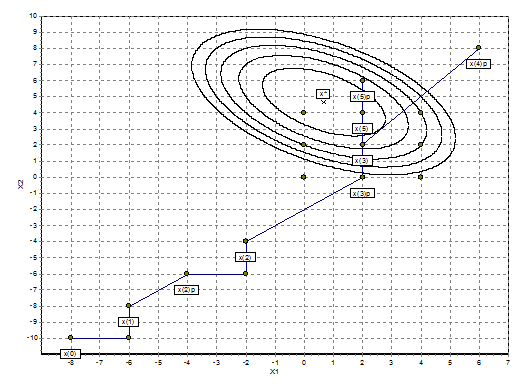
Рис 3. Графическое пояснение метода Хука-Дживса
2.3 Метод сопряженных направлений
Пауэлла
Описание алгоритма:
Метод ориентирован на решение задач с
квадратичными целевыми функциями. Основная идея алгоритма заключается в том,
что если квадратичная функция:
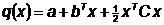
приводится к виду сумма полных
квадратов

то процедура нахождения оптимального
решения сводится к  одномерным
поискам по преобразованным координатным направлениям.
одномерным
поискам по преобразованным координатным направлениям.
В методе Пауэлла поиск реализуется в
виде:

вдоль направлений 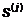 ,
, 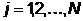 , называемых
, называемых
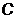 -сопряженными
при линейной независимости этих направлений.
-сопряженными
при линейной независимости этих направлений.
Сопряженные направления определяются
алгоритмически. Для нахождения экстремума квадратичной функции  переменных
необходимо выполнить
переменных
необходимо выполнить 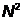 одномерных
поисков.
одномерных
поисков.
Алгоритм метода:
Шаг 1. Задать исходные точки 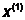 ,
, 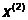 и
направление
и
направление  . В
частности, направление
. В
частности, направление  может
совпадать с направлением координатной оси;
может
совпадать с направлением координатной оси;
Шаг 2. Произвести одномерный поиск
из точки 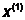 в
направлении
в
направлении  получить
точку
получить
точку 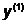 , являющуюся
точкой экстремума на заданном направлении;
, являющуюся
точкой экстремума на заданном направлении;
Шаг 3. Произвести одномерный поиск
из точки 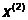 в
направлении
в
направлении  получить
точку
получить
точку 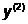 ;
;
Шаг 4. Вычислить направление 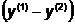 ;
;
Шаг 5. Провести одномерный поиск из
точки 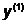 (либо
(либо 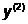 ) в
направлении
) в
направлении 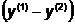 с выводом в
точку
с выводом в
точку  .
.
Ход решения:
Исходные данные:

Шаг 1.
 - начальная точка
- начальная точка

 ,
, 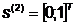 .
.
Шаг 2.
а) Найдем значение  , при
котором
, при
котором 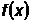 минимизируется
в направлении
минимизируется
в направлении  :
:
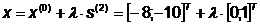
Откуда 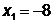 ;
; 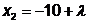 .
.
Значение функции в этой точке:  ;
;
Продифференцируем полученное
выражение по  , получим:
, получим:
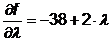 .
.
Приравняв его к нулю, находим 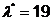 ;
;
Получили 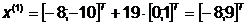

б) Аналогично находим значение  минимизирующее
функцию
минимизирующее
функцию
в направлении 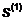 :
:
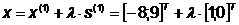
Откуда 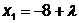 ;
;  .
.
Значение функции в этой точке:  ;
;
Продифференцируем полученное
выражение по  , получим:
, получим:
 .
.
Приравняв его к нулю, находим 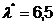 ;
;
Получили 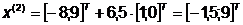
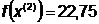
в) Найдем значение  минимизирующее
минимизирующее
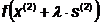 :
:

Откуда 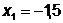 ;
; 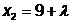 .
.
Значение функции в этой точке:  ;
;
Продифференцируем полученное
выражение по  , получим:
, получим:
 . Приравняв его к нулю, находим
. Приравняв его к нулю, находим 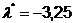 ;
;
Получили 
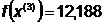
Шаг 3. 
Шаг4. Найдем такое значение  , при
котором
, при
котором  минимизируется
в направлении
минимизируется
в направлении 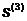 .
.

Откуда  ;
;  .
.
Значение функции в этой точке:  ;
;
Продифференцируем полученное
выражение по  , получим:
, получим:
 .
.
Приравняв его к нулю, находим  ;
;
Получили 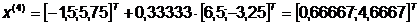
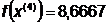
Таким образом, получили точку  , значение
функции в которой равно
, значение
функции в которой равно  , что совпадает
со стационарной точкой.
, что совпадает
со стационарной точкой.

Рис 4. Графическое пояснение метода сопряженных
направлений Пауэлла
3.
Нахождение безусловного экстремума градиентными
методами
В отличии от методов прямого поиска градиентные
методы поиска используют информацию о производных функции. Это позволяет
уменьшить
количество необходимых вычислений значений
функции. Эти методы делятся на две группы: методы, использующие информацию
только о первых производных , и методы, учитывающие информацию и первых, и
вторых производных.
3.1 Метод
Коши
Описание алгоритма:
В методе Коши или методе наискорейшего спуска в
качестве направления поиска выбирается направление антиградиента.
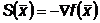
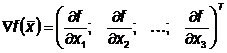 - градиент функции
- градиент функции 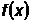
Алгоритм метода выглядит следующим
образом:
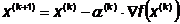 ,
,
где  - градиент.
- градиент.
Значение  на каждой
итерации вычисляется путем решения задачи одномерного поиска экстремума
на каждой
итерации вычисляется путем решения задачи одномерного поиска экстремума 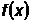 вдоль
направления градиента
вдоль
направления градиента  . Если в
качестве
. Если в
качестве  взять
некоторое положительное число, то получится простейший градиентный алгоритм:
взять
некоторое положительное число, то получится простейший градиентный алгоритм:
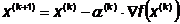
Одно из главных достоинств метода
Коши является его устойчивость, так как всегда выполняется условие:

Однако вблизи экстремума скорость
сходимости алгоритма становится недопустимо низкой, так как вблизи экстремума
значение градиента стремится к нулю.
Алгоритм метода:
Шаг 1. Задать: 1. Начальную точку х(0) ;
. Условие окончания поиска. Перейти к шагу 2.
Шаг 2. Вычислить направление поиска в виде
антиградиента функции
s(x(k)
) = - ∇f(x(k)
);
Перейти к шагу 3.
Шаг 3. Найти новое приближение
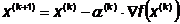 ,
,
где  - величина шага относительно
текущего приближения. Перейти к шагу4.
- величина шага относительно
текущего приближения. Перейти к шагу4.
Шаг 4. Проверка условия окончания
поиска.
Да: закончить поиск;
Нет: перейти к шагу 2.
Ход решения:
Исходные данные:

Шаг 1.
 - начальная точка (начальное
приближение);
- начальная точка (начальное
приближение);
Вычислим компоненты градиента:
Шаг 2.
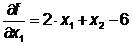
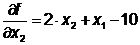
Шаг 3. Начальное приближение 
. Новое приближение определим по
формуле:
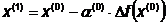
Шаг 2.
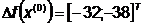
Выбираем 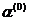 такое,
чтобы минимизировать функцию
такое,
чтобы минимизировать функцию 
Шаг 3.
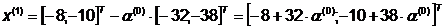
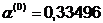

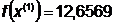
. Далее найдем точку:
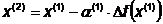
Шаг 2.
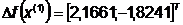
Шаг 3.
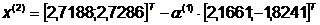
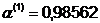


. Далее найдем точку:
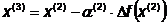
Шаг 2.

Шаг 3.

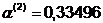
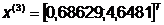
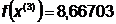
. Далее найдем точку:
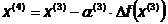
Шаг 2.

Шаг 3.
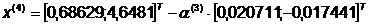
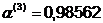
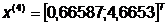
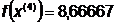
После 4 итераций найдено достаточно
точное значение минимума, при котором значение целевой функции в точке 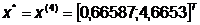 ,
, 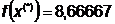 .
.
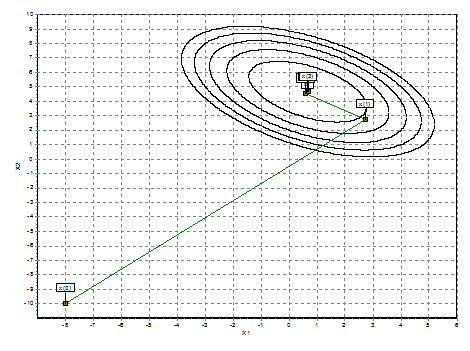
Рис 5. Графическое пояснение метода Коши
3.2 Метод Ньютона
Описание алгоритма:
Этот метод использует информацию о вторых
производных целевой функции. Эта информация появляется при квадратичной
аппроксимации целевой функции, когда при её разложении в ряд Тейлора
учитываются члены ряда до второго порядка включительно. Алгоритм метода
выглядит следующим образом:
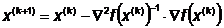 ,
,
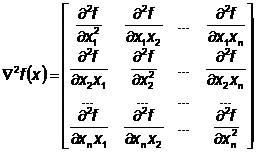 - гессиан (матрица Гессе)
- гессиан (матрица Гессе)
В случае, когда гессиан положительно
определён, направление по методу Ньютона оказывается направлением спуска.
Алгоритм метода:
Шаг 1. Задать: начальную точку х(0). Перейти к
шагу 2.
Шаг 2. Вычислить направление поиска в виде
s(x(k)) = - 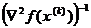 ×
×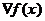 .
.
Шаг 3. Найти новое приближение (являющееся
решением задачи для квадратичной функции)
x(k+1) =
x(k) + s(x(k)) = x(k) -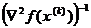 ×
×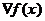 .
.
Шаг 4. Проверка на
условие окончания вычислений.
Да: закончить процесс;
Нет: перейти к шагу 2.
Ход решения:
Исходные данные:

- целевая функция;
Шаг 1.
 - начальная точка;
- начальная точка;
Шаг 2.
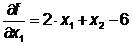
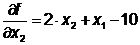
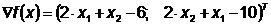
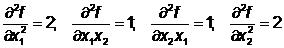
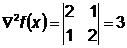

Шаг 3.
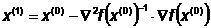 ;
;


Таким образом, точка минимума 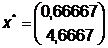 , значение
функции в которой
, значение
функции в которой 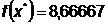 найдена за
одну итерацию.
найдена за
одну итерацию.
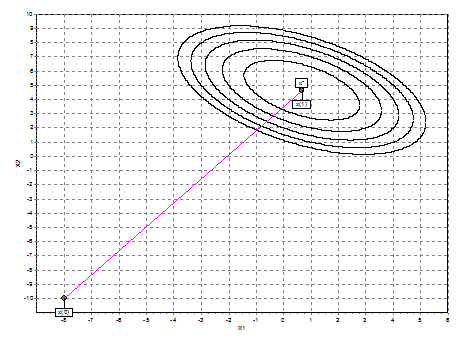
Рис 6. Графическое пояснение метода Ньютона
3.3
Метод сопряженных градиентов
Описание алгоритма:
Данный метод обладает положительными
свойствами методов Коши и Ньютона. Кроме того, этот метод использует информацию
только о первых производных исследуемой функции. Метод сопряженных градиентов
позволяет получить решение за  шагов в
шагов в  -мерном
пространстве и обладает квадратичной сходимостью. В основе метода лежит
организация поиска вдоль сопряженных направлений, причем для получения
сопряженных направлений используется квадратичная аппроксимация целевой функции
и значения компонент градиента.
-мерном
пространстве и обладает квадратичной сходимостью. В основе метода лежит
организация поиска вдоль сопряженных направлений, причем для получения
сопряженных направлений используется квадратичная аппроксимация целевой функции
и значения компонент градиента.
Операции аргумента проводятся по
формуле:
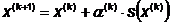
Направление поиска на каждой
итерации определяется с помощью формулы:
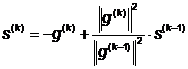
В этом случае направление  будет
будет 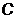 -сопряжено
со всеми ранее построенными направлениями поиска.
-сопряжено
со всеми ранее построенными направлениями поиска.
Если функция 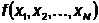 квадратичная,
то для нахождения точки экстремума требуется определить
квадратичная,
то для нахождения точки экстремума требуется определить  таких
направлений и провести поиски вдоль каждой прямой. Если
таких
направлений и провести поиски вдоль каждой прямой. Если 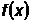 не является
квадратичной, то количество поисков возрастёт.
не является
квадратичной, то количество поисков возрастёт.
Используемые в методе формулы:

Изменение градиента при переходе от
точки  к точке
к точке 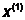 :
:


Изменения аргумента:
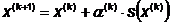
Направление поиска:
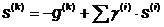 ,
, 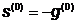 ,
, 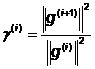 .
.
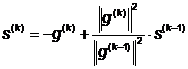
(рекуррентная формула
Флетчера-Ривса).
Алгоритм метода:
Шаг 1. Задать: начальную точку х(0).
Перейти к шагу 2.
Шаг 2. Вычислить направление поиска.
Произвести поиск вдоль прямой 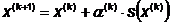 .
.
Шаг 3. Вычислено ли N-1
направлений.
Да: закончить поиск;
Нет: перейти к шагу 2.
Ход решения:
Исходные данные:

экстремум функция
симплекс программный
Шаг 1.
 - начальная точка;
- начальная точка;
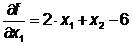
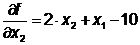
Шаг 2.
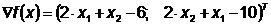


Поиск вдоль прямой:

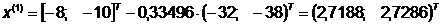
Шаг 2.
Определим направление 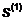 :
:
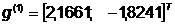
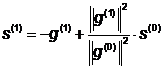
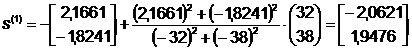
Поиск вдоль прямой:
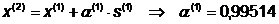
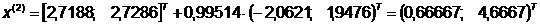
Таким образом, решение (точка
минимума) 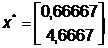 , значение
функции в которой
, значение
функции в которой 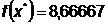 , получено в
результате двух одномерных поисков, поскольку целевая функция квадратична.
, получено в
результате двух одномерных поисков, поскольку целевая функция квадратична.
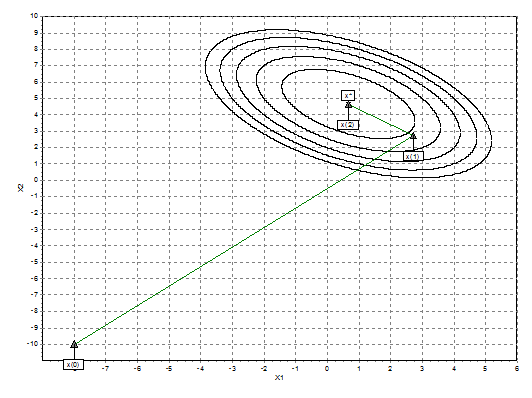
Рис 7. Графическое пояснение метода сопряженных
градиентов
3.4 Квазиньютоновский метод
Описание алгоритма:
Данный метод обладает положительными чертами
метода Ньютона, однако, использует информацию только о первых производных. В
этом методе приближение к очередной точке в пространстве оптимизируемых
параметров задается формулой:

Направление поиска определяется
выражением:
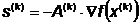 ,
,
где  - матрица порядка
- матрица порядка 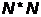 (метрика).
(метрика).
Матрица 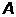 -
вычисляется по формуле.
-
вычисляется по формуле.
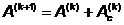 ,
,
где:
 (1)
(1)
Где  изменение градиента на предыдущем
шаге.
изменение градиента на предыдущем
шаге.
Данный алгоритм отличается
устойчивостью, так как обеспечивает убывание целевой функции от итерации к
итерации.
Алгоритм метода:
Шаг 1. Задать: начальную точку х(0). Перейти к
шагу 2.
Шаг 2. Вычислить направление поиска s(k).
Перейти к шагу 3.
Шаг 3. Произвести поиск вдоль прямой
 . Перейти
. Перейти
к шагу 4.
Шаг 4. Проверка условия окончания
поиска.
Да: закончить поиск;
Нет: перейти к шагу2.
Ход решения:
Исходные данные:

- целевая функция;
Шаг 1.
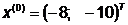
начальная точка;
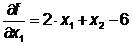
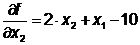
Шаг 2.


Положим

Шаг 3.
Поиск вдоль прямой:
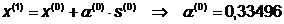
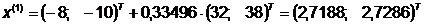
Шаг 2.
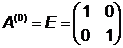
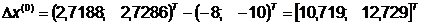
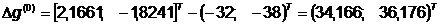
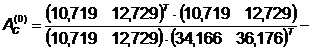
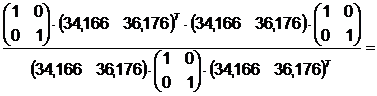

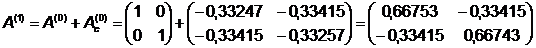
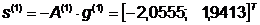
Шаг 3.
Поиск вдоль прямой:
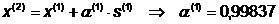

Таким образом, точка минимума  , значение
функции в которой
, значение
функции в которой 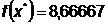 найдена за
одну итерацию.
найдена за
одну итерацию.
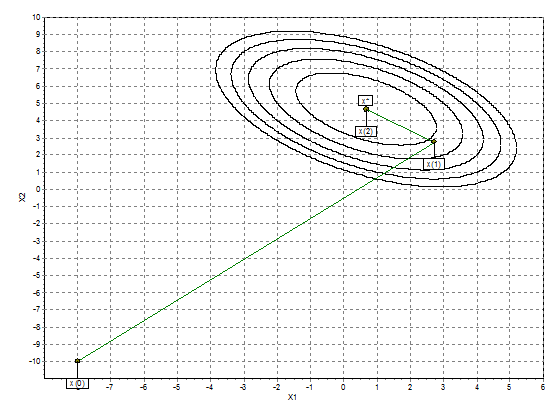
Рис 8. Графическое пояснение квазиньютоновского
метода
4.
Нахождение условного экстремума методом штрафных функций
Все предыдущие методы поиска оптимума функции
были предназначены для задач безусловной оптимизации. Ниже будет разобран метод
штрафных функций, один из многих, предназначенных для решения более сложных
задач, в которых область поиска ограничена из каких-либо практических
соображений.
Суть метода заключается в преобразовании
исходной целевой функции посредством включения в неё функции от ограничений,
получая, таким образом, задачу безусловной оптимизации, для решения которой
можно использовать рассмотренные в первой части методы. Переход от задачи
условной оптимизации к задаче безусловной оптимизации осуществляется
посредством включения в исходную функцию "штрафов" за нарушение
ограничений задачи.
Пусть исходная задача имеет следующий вид:
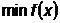
 при ограничениях:
при ограничениях:
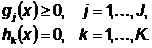
Тогда преобразованная задача
определится выражением:

где 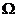 - штрафная функция от ограничений
задачи, а
- штрафная функция от ограничений
задачи, а  - штрафной
параметр. Наличие штрафного параметра
- штрафной
параметр. Наличие штрафного параметра  вызвано тем, что введение штрафной
функции сильно деформирует поверхность целевой функции, что, в свою очередь,
приводит к ухудшению обусловленности преобразованной задачи. Поэтому параметр
вызвано тем, что введение штрафной
функции сильно деформирует поверхность целевой функции, что, в свою очередь,
приводит к ухудшению обусловленности преобразованной задачи. Поэтому параметр  служит
"регулятором" веса штрафной составляющей в целевой функции, и процесс
решения задачи разбивается на ряд вспомогательных задач с различными значениями
параметра
служит
"регулятором" веса штрафной составляющей в целевой функции, и процесс
решения задачи разбивается на ряд вспомогательных задач с различными значениями
параметра  и контролем
сходимости их решений.
и контролем
сходимости их решений.
Виды штрафов:
Квадратичный штраф имеет вид:  . Этот вид
штрафов используется для учёта ограничений - равенств. Функция
. Этот вид
штрафов используется для учёта ограничений - равенств. Функция 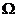 непрерывна
и имеет непрерывную производную, откуда следует, что если непрерывны и
дифференцируемы
непрерывна
и имеет непрерывную производную, откуда следует, что если непрерывны и
дифференцируемы 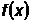 и
и 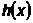 , то
стационарную точку можно найти аналитически.
, то
стационарную точку можно найти аналитически.
Логарифмический штраф.
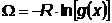
Этот штраф положителен для всех  таких, что
таких, что  , и
отрицателен при
, и
отрицателен при 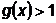 .
Логарифмический штраф - это барьерная функция, неопределенная в точках, где
.
Логарифмический штраф - это барьерная функция, неопределенная в точках, где 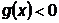 . Поэтому на
начальном этапе поиска, когда значение шага поиска невелико, необходимо
обеспечить защиту процедуры от попадания рабочей точки в недопустимую область.
. Поэтому на
начальном этапе поиска, когда значение шага поиска невелико, необходимо
обеспечить защиту процедуры от попадания рабочей точки в недопустимую область.
Штраф, заданный обратной функцией.

Как и предыдущий штраф, является
барьерным. В допустимой области вблизи границы значение штрафа быстро убывает
при продвижении внутрь допустимой области. На самой границе значение 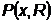 не
определено, как и в предыдущем случае возможно появление недопустимых точек.
не
определено, как и в предыдущем случае возможно появление недопустимых точек.
Штраф типа квадрата срезки.
 ,
,
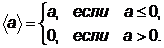
Этот штраф является внешним, и
недопустимые точки не создают проблем по сравнению с допустимыми. Различие
заключается том, что в допустимых точках штраф равен нулю. Этот вид штрафа
удобен тем, что 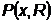 непрерывна
и определена всюду. Параметр
непрерывна
и определена всюду. Параметр  положителен и увеличивается от
итерации к итерации.
положителен и увеличивается от
итерации к итерации.
Алгоритм метода:
Шаг 1. Задать начальные данные:
 - начальная точка
- начальная точка
 - начальное значение штраф
параметра
- начальное значение штраф
параметра
 - параметр окончания работы
алгоритма
- параметр окончания работы
алгоритма
Шаг 2. Построить штрафную функцию:
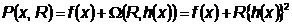
Шаг 3. Находим 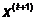 ,
доставляющее экстремум
,
доставляющее экстремум 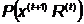 , методом
Ньютона.
, методом
Ньютона.
Шаг 4. Выполняется ли условие:
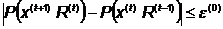
Да: 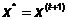 , процесс решения закончен.
, процесс решения закончен.
Нет: перейти к шагу 5. Шаг 5. 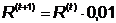 , перейти к
шагу 2.
, перейти к
шагу 2.
Нахождение минимума целевой функции
:
Исходные данные:

Шаг 1.
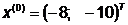 - начальная точка;
- начальная точка;
Ограничение на решение:
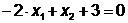
Преобразуем целевую функцию 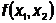 введением в
неё заданного квадратичного штрафа:
введением в
неё заданного квадратичного штрафа: 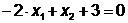
Шаг 2.
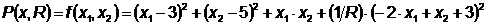
Шаг 3. Найдем минимум целевой
функции 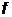 с заданным
квадратичным штрафом:
с заданным
квадратичным штрафом:

Совместное решение даёт:
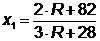

Устремляя  к нулю,
получаем
к нулю,
получаем 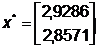
То есть, при изменении  от нуля до
бесконечности, решение будет изменяться от минимума задачи с учётом ограничений
до минимума функции без учёта ограничений.
от нуля до
бесконечности, решение будет изменяться от минимума задачи с учётом ограничений
до минимума функции без учёта ограничений.
Исследуем функцию при различных
значениях параметра 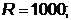
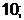

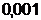 , то есть
, то есть 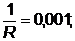

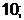
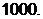
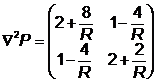
Шаг 5,2-3.
1. 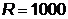
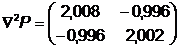
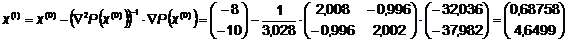
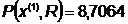
. 
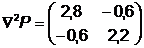

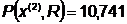
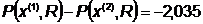
. 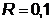
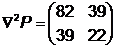
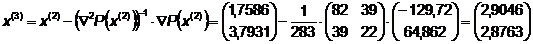

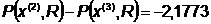
. 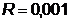


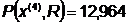
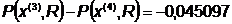
Сведем все данные в таблицу:
Решением задачи условной оптимизации
является точка:  , значение
функции в которой равно:
, значение
функции в которой равно:  . Мы
подтвердили, что при увеличении штрафного параметра все ограничения
уменьшаются, что доставляет минимум задачи безусловной оптимизации. Наоборот,
при уменьшении штрафного параметра до нуля вес ограничения возрастает, что
доставляет минимум задачи условной оптимизации.
. Мы
подтвердили, что при увеличении штрафного параметра все ограничения
уменьшаются, что доставляет минимум задачи безусловной оптимизации. Наоборот,
при уменьшении штрафного параметра до нуля вес ограничения возрастает, что
доставляет минимум задачи условной оптимизации.
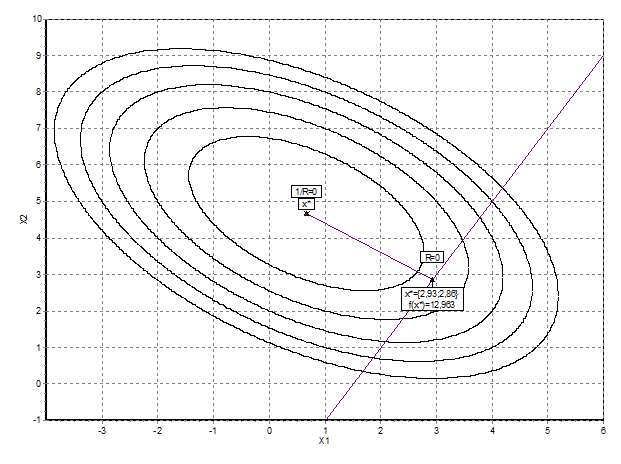
Рис 9. Графическое пояснение метода штрафных
функций
Вывод: метод штрафных функций служит для решения
задач условной оптимизации путем перевода их в задачу безусловной оптимизации.
Как видно их рисунка, величина штрафного параметра сильно влияет на вид
функции. При его увеличении "вес" ограничения в целевой функции
уменьшается, и функция принимает свой обычный вид (без штрафной составляющей).
5. Разработка программного модуля
Цель работы: разработка программного
продукта, находящего оптимум функции вида 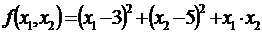
при помощи метода Коши.
Требования к программе:
1. Возможность изменения исходных данных с
клавиатуры.
2. Графическое отображение решения.
. Занесение результатов в таблицу.
Описание программы:
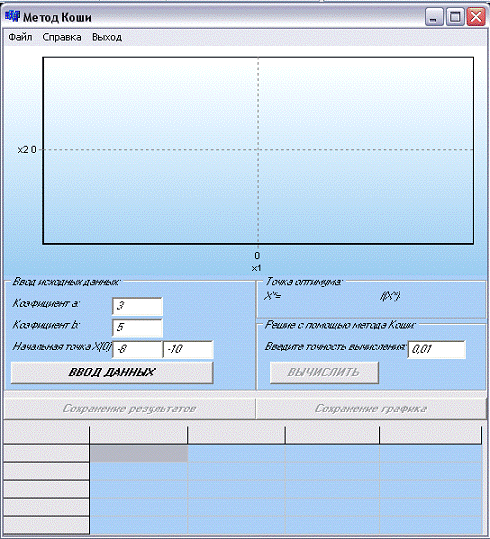
Рис 10.
Пользователю предоставляется возможность ввести
начальные параметры. После ввода данных с помощью кнопки «вычислить» мы
получаем решение. Результаты представлены в таблице, а так же ход решения можно
пронаблюдать на графике. В пункте меню Справка можно получить информацию о
методе и о разработчике программы. Для выхода из программы используется пункт
меню Выход.

Рис 11.
Вывод: Представленный модуль удовлетворяет
поставленным требованиям. Программа разработана в среде С++Builder
6.0. Код программы находится в приложении 2.
Заключение
Анализируя результаты исследования (сравнения)
всех рассмотренных выше методов, можно прийти к выводу о том, что каждый из них
имеет свои достоинства и недостатки и более применим для задач одних видов и
менее - для других. Однако, пользователь всегда сможет найти подходящий
алгоритм для решения своей конкретной проблемы, выбирая как из вышеприведенного
множества методов, так и из огромного спектра их модифицированных,
усовершенствованных и комбинированных вариантов.
Однако, есть целый класс проблем, где найти
оптимум либо крайне сложно, либо вообще невозможно получить точное решение с
помощью алгоритмов данных категорий. К таким задачам относится, например,
моделирование глобальных социально-экономических процессов.
Мощным инструментом теоретического исследования
алгоритмов являются теоремы о сходимости методов. Однако, как правило,
формулировки таких теорем абстрактны, при их доказательстве используется
аппарат современного функционального анализа. Кроме того, зачастую непросто
установить связь полученных математических результатов с практикой вычислений.
Дело в том, что условия теорем труднопроверяемы в конкретных задачах, сам факт
сходимости мало что дает, а оценки скорости сходимости неточны и неэффективны.
При реализации алгоритмов также возникает много дополнительных обстоятельств,
строгий учет которых невозможен (ошибки округления, приближенное решение
различных вспомогательных задач и т.д.) и которые могут сильно повлиять на ход
процесса.
Поэтому на практике часто сравнение алгоритмов
проводят с помощью вычислительных экспериментов при решении так называемых
специальных тестовых задач. Эти задачи могут быть как с малым, так и с большим
числом переменных, иметь различный вид нелинейности. Они могут быть составлены
специально и возникать из практических приложений, например задача минимизации
суммы квадратов, решение систем нелинейных уравнений и т.п.
Библиографический список
1. Микрокова В.И. «Методы
оптимизации». - Киров, 2004.
2. Пантелеев А.В. «Методы
оптимизации в примерах и задачах».- Высшая школа ,2002.
. Интернет.
Приложение
Листинг программы
Для программной реализации был предложен метод
Коши. Алгоритм метода описан в пояснительной записке.
//---------------------------------------------------------------------------
#include <vcl.h>
#include <math.h>
#include <string.h>
#include <io.h>
#include <stdio.h>
#pragma hdrstop
#include "Unit1.h"
#include "Unit2.h"
#include "Unit4.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource
"*.dfm"*Form1;N=1;
//---------------------------------------------------------------------------
__fastcall
TForm1::TForm1(TComponent* Owner)
: TForm(Owner)
{ lin_ur=new TStringList;}
//---------------------------------------------------------------------------__fastcall
TForm1::saveris()
{
if(Form1->SaveDialog1->Execute())
{Form1->Chart1->SaveToBitmapFile(Form1->SaveDialog1->FileName);}}
//---------------------------------------------------------__fastcall
TForm1::saverez()
{int k=0;str1="";="Метод
Коши
Уравнение
имеет
вид:
f(X1,X2)=(X1-"+FloatToStrF(a,ffGeneral,6,0)+")^2+(X2-"+FloatToStrF(b,ffGeneral,6,0)+")^2+X1*X2;
Точка
поиска:["+FloatToStrF(x110,ffGeneral,6,0)+";"+FloatToStrF(x210,ffGeneral,6,0)+"]\n";(int
j=0;j<N;j++)
{ for(int i=0;i<5;i++)
{k=StrLen(Form1->StringGrid1->Cells[i][j].c_str());+=("
"+Form1->StringGrid1->Cells[i][j]+" ");(int
p=0;25-k>p;p++)+=(" ");+=("|");}+='\n';}(Form1->SaveDialog2->Execute())
{String
save=Form1->SaveDialog2->FileName;*fp;=fopen(save.c_str(),"w");(str1.c_str(),fp);(fp);}
}
//-----------------------------------------------------------__fastcall
TForm1::zadanie()
{
Button2->Enabled=true;->Enabled=false;->Enabled=false;->Enabled=true;->Clear();->Clear();=StrToInt(Edit1->Text.c_str());=StrToInt(Edit2->Text.c_str());=atof(Edit3->Text.c_str());=atof(Edit4->Text.c_str());=x11;=x21;_pred=funk(x11,x21);=(-8*b+4*a)/3.0+2*b;=(4*b-2*a)/3.0;->Caption="["+FloatToStrF(q1,ffGeneral,6,0)+";"+FloatToStrF(q2,ffGeneral,6,0)+"]";
Label11->Caption="Данная точка является
минимумом функции";
fq=funk(q1,q2);->Caption=FloatToStrF(fq,ffGeneral,6,0);
//Label5->Caption="f(X1,X2)
= (X1-"+FloatToStrF(a,ffGeneral,6,0)+")^2+(X2-"+FloatToStrF(b,ffGeneral,6,0)+")^2+X1*X2";
//Form1->StatusBar1->Panels->Items[3]->Text="*******Введите
точность
метода
и
нажмите
\"ВЫЧИСЛИТЬ\"*******";
}
//----------------------------------------__fastcall
TForm1::vi4()
{Button1->Enabled=true;->Enabled=false;->Enabled=false;->Enabled=true;->Enabled=true;->Enabled=true;->Enabled=true;->Enabled=true;_lin_ur();_ur=new
TStringList;();();
//
Form1->StatusBar1->Panels->Items[3]->Text="*******Введите
новые
исходные
данные
и
нажмите
\"ВВОД
ДАННЫХ\"*******";}
//---------------------------------------------------------------------------__fastcall
TForm1::poisk()
{float
XX1,XX2,YY1,YY2;>Clear();>AddXY(q1,q2,"",clBlue);->StringGrid1->Cells[0][0]="N";->StringGrid1->Cells[1][0]="Производная";->StringGrid1->Cells[2][0]="Коэфициент
альфа";->StringGrid1->Cells[3][0]="Текущая
точка";->StringGrid1->Cells[4][0]="Значение
функции";->Clear();->Clear();i=0;=StrToFloat(Edit5->Text);_pred=9999;->AddXY(x11,x21,"",clBlue);->AddXY(x11,x21,"",clBlue);=1000;(fabs(tmp1)>eps)
{ N=i+2;->Cells[0][i+1]=i;=df_x1(x11,
x21);=df_x2(x11,
x21);((tmp1!=0)&(tmp2!=0))->Cells[1][i+1]="["+FloatToStrF(tmp1,ffGeneral,4,4)+";"+FloatToStrF(tmp2,ffGeneral,4,4)+"]";_v=
2*tmp1*(x11-a)+2*tmp2*(x21-b)+x11*tmp2+x21*tmp1;_z=
2*(tmp1*tmp1+tmp2*tmp2+tmp1*tmp2);(alpha_z!=0)
{alpha=alpha_v/alpha_z;->Cells[2][i+1]=FloatToStrF(alpha,ffGeneral,6,0);
}break;_pred=temp_tek;=x11-tmp1*alpha;=x21-tmp2*alpha;->AddXY(x11,x21,"",clBlue);->AddXY(x11,x21,"",clBlue);->Cells[3][i+1]="["+FloatToStrF(x11,ffGeneral,6,0)+";"+FloatToStrF(x21,ffGeneral,6,0)+"]";_tek=funk(x11,x21);->Cells[4][i+1]=FloatToStrF(temp_tek,ffGeneral,6,0);++;}}
//---------------------------------------------------------------------------__fastcall
TForm1::funk(float x11, float x21)
{return (pow(x11-a,2)+pow(x21-b,2)+x11*x21);}
//------------------------------------------------------__fastcall
TForm1::df_x1(float x11,float x21)
{return (2*x11-2*a+x21);}
{return (2*x21-2*b+x11);}__fastcall
TForm1::line()
{ double DD=0 ; // дискриминант 1D=0; //
дискриминант 2x_n; // начало сканированияx_k; // конец сканированияh=0.01; //
шаг построенияxx21,xx22,xx11,fx; // переменные и функция
Chart1->UndoZoom(); // отмена
Zoom'a->Clear();11=x11;
// точка оптимума
xx21=x21;
Series4->AddXY(xx11,xx21,"",clBlue);
fx=temp_tek; // значение функции в точке
опт.(int i=0;i<8;i++)
{fx+=10;
// шаг построения линий уровня
TLineSeries *Series2=new
TLineSeries(Form1);->ParentChart=Chart1;_ur->AddObject("",Series2);*Series3=new
TLineSeries(Form1);->ParentChart=Chart1;_ur->AddObject("",Series3);->Clear();->Clear();=pow((8*a-4*b),2)-16*(fx-a*a)*(1-4);_n=(4*b-8*a+sqrt(DD))/(2*(1-4));_k=(4*b-8*a-sqrt(DD))/(2*(1-4));=x_n;(xx11<x_k)
{D=(1-4)*xx11*xx11+(8*a-4*b)*xx11+4*(fx-a*a);(D<0)
D=0;=0.5*(2*b-xx11+sqrt(D));=0.5*(2*b-xx11-sqrt(D));->AddXY(xx11,xx21,"",clBlack);->AddXY(xx11,xx22,"",clBlack);+=h;}=x_k;=(1-4)*xx11*xx11+(8*a-4*b)*xx11+4*(fx-a*a);(D<0)
D=0;=0.5*(2*b-xx11+sqrt(D));=0.5*(2*b-xx11-sqrt(D));->AddXY(xx11,xx21,"",clGreen);->AddXY(xx11,xx22,"",clGreen);}
}
//--------------------------------------------------------------------__fastcall
TForm1::del_lin_ur()
{for (int
i=lin_ur->Count-1;i>=0;i--)lin_ur->Objects[i];lin_ur;}__fastcall
TForm1::N7Click(TObject *Sender)
{Close();}
//---------------------------------------------------------------------------__fastcall
TForm1::Button1Click(TObject *Sender)
{ zadanie();}
//---------------------------------------------------------------------------__fastcall
TForm1::Button2Click(TObject *Sender)
{ vi4();}
//---------------------------------------------------------------------------__fastcall
TForm1::N2Click(TObject *Sender)
{ zadanie();}
//---------------------------------------------------------------------------__fastcall
TForm1::N3Click(TObject *Sender)
{vi4();}
//---------------------------------------------------------------------------__fastcall
TForm1::Button4Click(TObject *Sender)
{ saveris();}
//---------------------------------------------------------------------------__fastcall
TForm1::Button3Click(TObject *Sender)
{saverez();}
//---------------------------------------------------------------------------__fastcall
TForm1::N4Click(TObject *Sender)
{saverez(); }
//---------------------------------------------------------------------------__fastcall
TForm1::N5Click(TObject *Sender)
{saveris();}
//---------------------------------------------------------------------------__fastcall
TForm1::PageControl1Change(TObject *Sender)
{//Form1->RichEdit1->Lines->LoadFromFile("metod.rtf");
}
//---------------------------------------------------------------------------__fastcall
TForm1::N8Click(TObject *Sender)
{Form1->Enabled=false;->Enabled=true;->Visible=true;->RichEdit2->Lines->LoadFromFile("metod.rtf");->Enabled=true;}
//---------------------------------------------------------------------------__fastcall
TForm1::N9Click(TObject *Sender)
{Form1->Enabled=false;->Enabled=true;->Visible=true;->RichEdit2->Lines->LoadFromFile("help.rtf");->Enabled=true;}