Нахождения минимума функции n переменных. Метод Гольдфарба
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ
ОБРАЗОВАНИЯ
БЕЛОРУССКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И
РАДИОЭЛЕКТРОНИКИ
Факультет
информационных технологий и управления
Кафедра
вычислительных методов и программирования
Дисциплина:
Основы алгоритмизации и программирования
ПОЯСНИТЕЛЬНАЯ
ЗАПИСКА
к
курсовой работе на тему
“Нахождения
минимума функции n переменных.
Метод Гольдфарба”
Студент: гр.120603 Нарчук А. С.
Руководитель: д.ф-м.н., профессор Синицын А.К.
Минск,2012
Содержание
Введение.
Описание
алгоритма и решения задачи
Описание
тестовой задачи и результатов работы программы
Заключение
Литература
Текст
программы
Приложение
Введение
Задачей оптимизации в математике, информатике и
исследовании операций называется задача нахождения экстремума (минимума или
максимума) целевой функции в некоторой области конечномерного векторного
пространства, ограниченной набором линейных и нелинейных равенств и неравенств.
Минимум- один из видов экстремума, наименьшее
значение функции на заданном интервале.
Пусть в пространстве задана функция
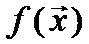
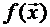
Говорят,
что
имеет локальный минимум в точке ,если
существует некоторая e-окрестность точки
,
в которой выполняется:
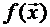
Будем полагать, что непрерывная
дважды дифференцируемая функция.
Локальный минимум:
Классификация методов оптимизации
Методы оптимизации классифицируют в
соответствии с задачами оптимизации:
Локальные методы: сходятся к
какому-нибудь локальному экстремуму целевой функции. В случае унимодальной
целевой функции, этот экстремум единственен, и будет глобальным
максимумом/минимумом.
Глобальные методы: имеют дело с
многоэкстремальными целевыми функциями. При глобальном поиске основной задачей
является выявление тенденций глобального поведения целевой функции.
По критерию размерности допустимого множества,
методы оптимизации делят на методы одномерной оптимизации и методы многомерной
оптимизации.
По виду целевой функции и
допустимого множества, задачи оптимизации и методы их решения можно разделить
на следующие классы:
1) Задачи
оптимизации, в которых целевая функция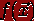 
и
ограничения 
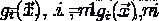являются линейными
функциями, разрешаются так называемыми методамилинейного программирования.
2) В
противном случае имеют дело с задачей нелинейного программирования и применяют
соответствующие методы. В свою очередь из них выделяют две частные задачи:
1. есл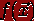и
и
-
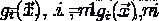выпуклые функции, то такую задачу называют задачей выпуклого программирования;
2. если
,
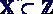то имеют дело с задачей целочисленного (дискретного) программирования.
Практически все методы минимизации функции n
переменных основаны на многократном повторении следующих двух действий:
1. выбор в области параметров некоторого
направления спуска;
2.
спуск к минимуму вдоль выбранного направления.
Если - единичный вектор выбранного направления в
точке , то уравнение прямой, проходящей через эту точку в
направлении , записывается в виде:
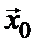
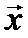
где параметр z
, соответствующий точкам на прямой (модуль z есть расстояние от текущей
точки до ).
Значения функции вдоль этой прямой можно описать
функцией одной переменной :
Изменяя z
двигаемся вдоль этой прямой, находим точку , в которой функция имеет меньшее
значение, чем в точке
Обычно находим минимум функции одной переменной:
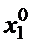
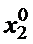
Все многообразие методов минимизации
функции n переменных определяется множеством способов выбора направлений и
методов спуска в выбранном направлении.
Классификация методов многомерной оптимизации
1. МЕТОДЫ НУЛЕВОГО ПОРЯДКА - при выборе
направления спуска требуют вычисления только значений функции
(методы:Гаусса-Зейделя, Пауэлла, ДСК, Розенброка, Хука-Дживса, Нелдера-Мида).
2. МЕТОДЫ ПЕРВОГО ПОРЯДКА - требуют
вычисления (точного или приближенного) градиента функции (методы: градиентный,
сопряженных градиентов, Давидона-Флетчера-Пауэлла (ДФП), Флетчера-Ривса идр.).
3. МЕТОДЫ ВТОРОГО ПОРЯДКА - требуют
вычисления как градиента, так и матрицы вторых производных (методы: Ньютона,
Ньютона-Рафсона).
4. МЕТОДЫ С ПЕРЕМЕННОЙ МЕТРИКОЙ - занимают
промежуточное место между методами 1-го и 2-го порядка.
Описание алгоритма и решение задачи
Методами с переменной метрикой
называется широкий класс эффективных градиентных методов, в которых направление
очередного спуска вычисляется по формуле:
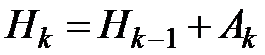
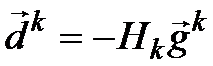
Н - положительно определенная симметричная
матрица.
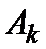-корректирующая
матрица, рассчитываемая по результатам предыдущих спусков таким образом, чтобы
обеспечить сходимость:
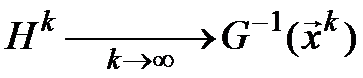
Последовательность вычислений
1. На 1-м шаге следует положить Н0=Е
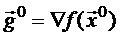
2. Делаем очередной одномерный спуск в направлении
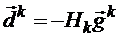
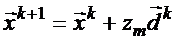
3. Делается пересчет корректирующей матрицы
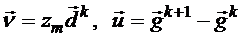
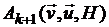
4. Если , то производится вычисление нового
направления спуска Нk+1=Нk+Аk+1;
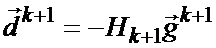
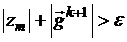
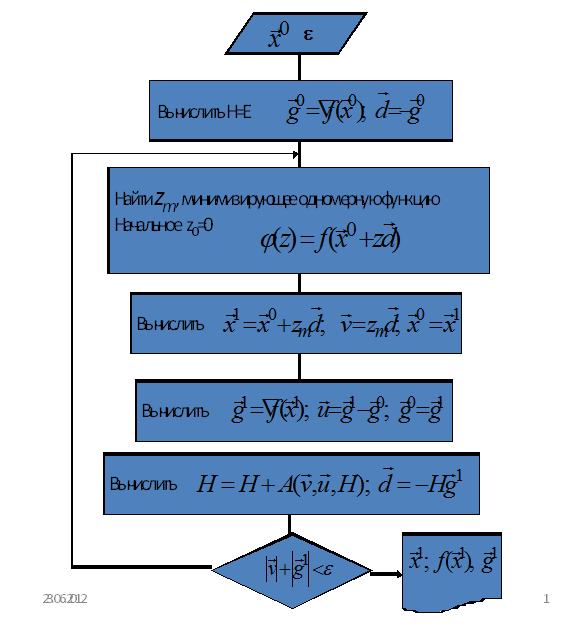
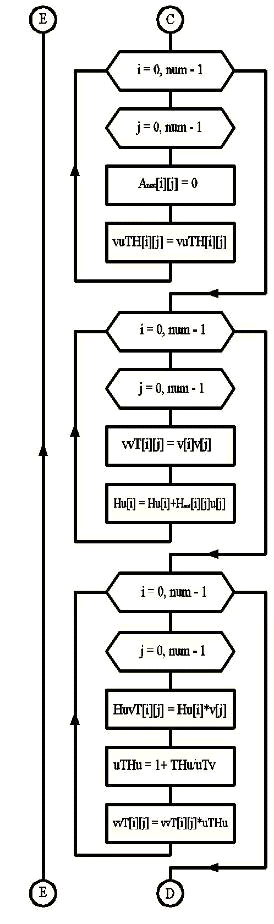
Общая схема алгоритма
В 1979г. Гринсдадт Дж. предложил
общее выражение, задающее в зависимости от выбираемой произвольной симметричной
матрицы М семейство методов с переменной метрикой
В последствии исходя из него
были предложены различные методы с переменной метрикой, наиболее эффективным
зарекомендовал себя метод Гольдфарба
Метод Гольдфарба:
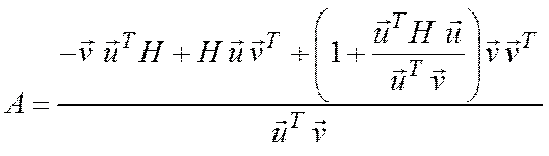
Описание тестовой задачи и
результатов работы программы
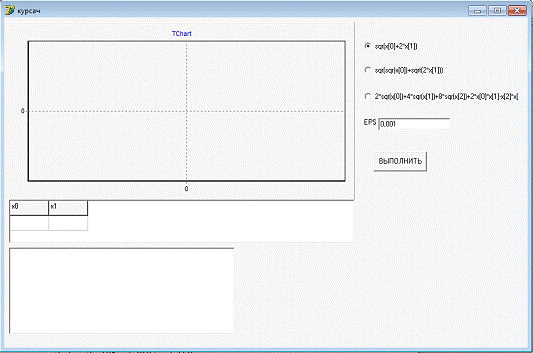
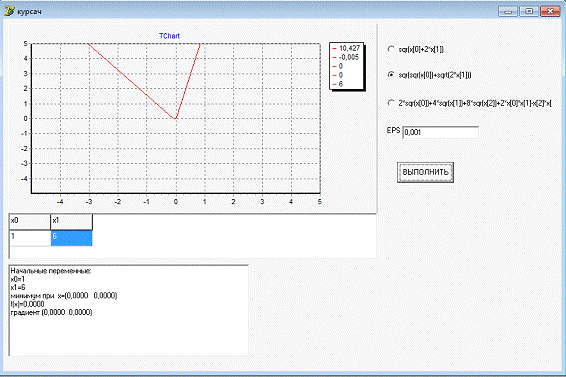
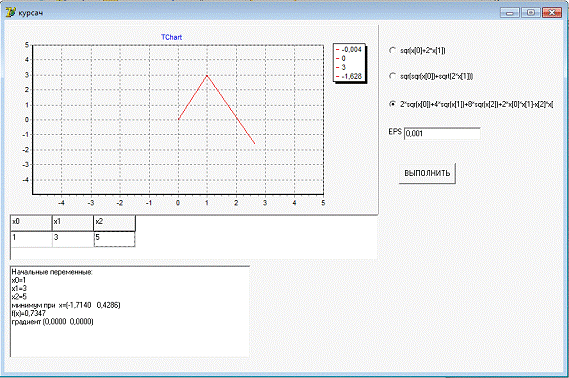
Данная программа выполняет
оптимизацию функции n переменных методом Гольдфарба.
Тестовая задача включает в себя поиск минимума следующих функций:
1. func1:=sqr(x[0]+2*x[1]);
2. func2:=10*sqr(x[0])+sqr(x[1]);
. func3:=2*sqr(x[0])+4*sqr(x[1])+8*sqr(x[2])+2*x[0]*x[1]-x[2]*x[2]+2*x[2]+6*x[0]-7*x[2];
В программу вводятся следующие начальные
условия:
. начальные координаты точки (x).
. эпселент.
В результате работы программы находиться минимум
функции, количество заходов в функцию и происходит прорисовка графика функции.
. func1:=sqr(x[0]+2*x[1]);
. func2:=10*sqr(x[0])+sqr(x[1]);
. func3:=2*sqr(x[0])+4*sqr(x[1])+8*sqr(x[2])+2*x[0]*x[1]-x[2]*x[2]+2*x[2]+6*x[0]-7*x[2];
оптимизация минимум
функция переменный
Заключение
Методы с переменной метрикой имеют превосходство
при решении задач с функциями общего вида. На эти методы точность вычислений на
ЭВМ оказывает большее влияние, чем на методы сопряжённых градиентов. В
частности данная программа находит минимум для тестовых функций быстрее, чем
методы спуска по градиенту и метод Гаусса-Зейделя.На самом деле многое зависит
от вида конкретной оптимизируемой функции. Особенно если количество оптимизируемых
переменных больше 4-5 нужно иметь в запасе несколько разнообразных методов, а
процесс оптимизации строить на основе интерактивных программ.
Литература
· Конспект
лекций д.ф-м.н., профессор Синицын А.К.
· <#"551300.files/image035.gif">
