Компьютерное моделирование графического решения матричных игр
Компьютерное моделирование
графического решения матричных игр
СОДЕРЖНИЕ
1. Принятие решений в условиях неопределенности
. Классические критерии принятия решений
.1 Минимаксный критерий
.2 Критерий Байеса-Лапласа
.3 Критерий Сэвиджа
.4 Пример и выводы
. Производные критерии принятия решений
.1 Критерий Гурвица
.2 Критерий Ходжа-Лемана
.3 Критерий Гермейра
.4 BL (MM) - Критерий
.5 Критерий произведений
. Теория игр
.1 Матричные игры
.2 Графоаналитический метод решения матричных игр 2×N и M×2
.2.1 Пример решения игры вида 2хN
.2.2 Пример решения игры вида Mх2
. Листинг программы
. Результаты тестирования программы
. Список использованной литературы
1. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
Будем предполагать, что лицу, принимающему решение не противостоит
разумный противник.
Данные, необходимо для принятия решения в условии неопределенности,
обычно задаются в форме матрицы, строки которой соответствуют возможным
действиям, а столбцы - возможным состояниям системы.
Пусть, например, из некоторого материала требуется изготовить изделие,
долговечность которого при допустимых затратах невозможно определить. Нагрузки
считаются известными. Требуется решить, какие размеры должно иметь изделие из
данного материала.
Варианты решения таковы:
Е1 - выбор размеров из соображений максимальной долговечности ;
Еm- выбор размеров из соображений минимальной долговечности ;-
промежуточные решения.
Условия требующие рассмотрения таковы :- условия, обеспечивающие
максимальной долговечность;- условия, обеспечивающие min долговечность;-
промежуточные условия.
Под результатом решения eij = е(Ei ; Fj ) здесь можно понимать оценку,
соответствующую варианту Ei и условиям Fj и характеризующие прибыль, полезность
или надёжность. Обычно мы будем называть такой результат полезностью решения.
Тогда семейство (матрица) решений имеет вид :
имеет вид :
|
F1
|
F2
|
. . .
|
Fn
|
|
E1
|
e11
|
e12
|
. . .
|
e1n
|
|
E2
|
e21
|
e22
|
. . .
|
e2n
|
|
. . .
|
. . . . . . . .
. . . . . . . .
|
|
|
|
|
Em
|
em1
|
em2
|
. . .
|
emn
|
Чтобы прийти к однозначному и по возможности наивыгоднейшему варианту
решению необходимо ввести оценочную (целевую) функцию. При этом матрица решений
 сводится к одному столбцу. Каждому
варианту Ei приписывается, т.о., некоторый результат eir, характеризующий, в
целом, все последствия этого решения. Такой результат мы будем в дальнейшем
обозначать тем же символом eir.
сводится к одному столбцу. Каждому
варианту Ei приписывается, т.о., некоторый результат eir, характеризующий, в
целом, все последствия этого решения. Такой результат мы будем в дальнейшем
обозначать тем же символом eir.
2.
КЛАССИЧЕСКИЕ КРИТЕРИИ ПРИНЯТИЯ РЕШЕНИЙ
.1
МИНИМАКСНЫЙ КРИТЕРИЙ
Правило выбора решения в соответствии с минимаксным критерием (ММ-критерием)
можно интерпретировать следующим образом:
матрица решений дополняется ещё одним столбцом из наименьших результатов
eir каждой строки. Необходимо выбрать те варианты в строках которых стоят
наибольшее значение eir этого столбца.
Выбранные т.о. варианты полностью исключают риск. Это означает, что
принимающий решение не может столкнуться с худшим результатом, чем тот, на
который он ориентируется. Это свойство позволяет считать ММ-критерий одним из
фундаментальных.
Применение ММ-критерия бывает оправдано, если ситуация, в которой
принимается решение следующая:
o. О возможности появления внешних состояний Fj ничего не известно;
o. Приходится считаться с появлением различных внешних состояний Fj;
o. Решение реализуется только один раз;
o. Необходимо исключить какой бы то ни было риск.
.2 КРИТЕРИЙ
БАЙЕСА-ЛАПЛАСА
Обозначим через qi - вероятность появления внешнего состояния Fj.
Соответствующее правило выбора можно интерпретировать следующим образом:
матрица решений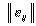 дополняется ещё одним столбцом содержащим математическое
ожидание значений каждой из строк. Выбираются те варианты, в строках которых
стоит наибольшее значение eir этого столбца.
дополняется ещё одним столбцом содержащим математическое
ожидание значений каждой из строк. Выбираются те варианты, в строках которых
стоит наибольшее значение eir этого столбца.
При этом предполагается, что ситуация, в которой принимается решение,
характеризуется следующими обстоятельствами:
о. Вероятности появления состояния Fj известны и не зависят от времени.
о. Решение реализуется (теоретически) бесконечно много раз.
о. Для малого числа реализаций решения допускается некоторый риск.
При достаточно большом количестве реализаций среднее значение постепенно
стабилизируется. Поэтому при полной (бесконечной) реализации какой-либо риск
практически исключён.
Т.о. критерий Байеса-Лапласа (B-L-критерий) более оптимистичен, чем
минимаксный критерий, однако он предполагает большую информированность и
достаточно длительную реализацию.
.3 КРИТЕРИЙ
СЭВИДЖА
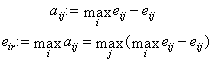
Соответствующее критерию Сэвиджа правило выбора теперь трактуется так:
). Каждый элемент матрицы решений 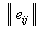 вычитается из наибольшего результата
max eij соответствующего столбца.
вычитается из наибольшего результата
max eij соответствующего столбца.
). Разности aij образуют матрицу остатков . Эта матрица пополняется столбцом
наибольших разностей eir. Выбирают те варианты, в строках которых стоит
наименьшее для этого столбца значение.
. Эта матрица пополняется столбцом
наибольших разностей eir. Выбирают те варианты, в строках которых стоит
наименьшее для этого столбца значение.
Требования, предъявляемые к ситуации, в которой принимается решение,
совпадают с требованием к ММ-критерию.
.4 ПРИМЕР И
ВЫВОДЫ
Из требований, предъявляемых к рассмотренным критериям становится ясно, что
в следствии их жёстких исходных позиций они применимы только для
идеализированных практических решений. В случае, когда возможна слишком сильная
идеализация, можно применять одновременно поочерёдно различные критерии. После
этого среди нескольких вариантов ЛПР волевым методом выбирает окончательное
решение. Такой подход позволяет, во-первых, лучше проникнуть во все внутренние
связи проблемы принятия решений и, во-вторых, ослабляет влияние субъективного
фактора.
Пример. При работе ЭВМ необходимо периодически приостанавливать обработку
информации и проверять ЭВМ на наличие в ней вирусов. Приостановка в обработке
информации приводит к определённым экономическим издержкам. В случае же если
вирус вовремя обнаружен не будет, возможна потеря и некоторой части информации,
что приведёт и ещё к большим убыткам.
Варианты решения таковы:
Е1- полная проверка;
Е2- минимальная проверка;
Е3- отказ от проверки.
ЭВМ может находиться в следующих состояниях:- вирус отсутствует;- вирус
есть, но он не успел повредить информацию;- есть файлы, нуждающиеся в
восстановлении.
Результаты, включающие затраты на поиск вируса и его ликвидацию, а также
затраты, связанные с восстановлением информации имеют вид:
Таблица 1.
|
|
|
|
ММ-критерий
|
критерий B-L
|
|
|
F1
|
F2
|
F3
|
eir=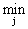 eij eij
|
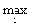 eir eir
|
eir =
|
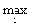 eir eir
|
|
E1
|
-20.0
|
-22.0
|
-25.0
|
-25.0
|
-25.0
|
-22.33
|
|
|
E2
|
-14.0
|
-23.0
|
-31.0
|
-31.0
|
|
-22.67
|
|
|
E3
|
0
|
-24.0
|
-40.0
|
-40.0
|
|
-21.33
|
-21.33
|
Согласно ММ-критерию следует проводить полную проверку. Критерий
Байеса-Лапласа, в предположении, что все состояния машины равновероятны.
(Fj) = qj = 0.33,
рекомендуется отказаться от проверки. Матрица остатков для этого примера
и их оценка (в тысячах) согласно критерию Сэвиджа имеет вид:
|
|
|
|
Критерий Сэвиджа
|
|
|
F1
|
F2
|
F3
|
eir=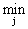 aij aij
|
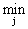 eir eir
|
|
E1
|
+20.0
|
0
|
0
|
+20.0
|
|
|
E2
|
+14.0
|
+1.0
|
+6.0
|
+14.0
|
+14.0
|
|
E3
|
0
|
+2.0
|
+15.0
|
+15.0
|
|
Пример специально подобран так, что каждый критерий предлагает новое
решение. Неопределённость состояния, в котором проверка застаёт ЭВМ,
превращается в неясность, какому критерию следовать.
Поскольку различные критерии связаны с различными условиями, в которых
принимается решение, лучшее всего для сравнительной оценки рекомендации тех или
иных критериев получить дополнительную информацию о самой ситуации. В
частности, если принимаемое решение относится к сотням машин с одинаковыми
параметрами, то рекомендуется применять критерий Байеса-Лапласа. Если же число
машин не велико, лучше пользоваться критериями минимакса или Севиджа.
3.
ПРОИЗВОДНЫЕ КРИТЕРИИ
.1 КРИТЕРИЙ
ГУРВИЦА
Стараясь занять наиболее уравновешенную позицию, Гурвиц предположил
оценочную функцию, которая находится где-то между точкой зрения крайнего
оптимизма и крайнего пессимизма:
где С- весовой множитель.
Правило выбора согласно критерию Гурвица, формируется следующим образом:
матрица решений 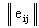 дополняется столбцом, содержащим среднее взвешенное
наименьшего и наибольшего результатов для каждой строки. Выбираются только те
варианты, в строках которых стоят наибольшие элементы eir этого столбца.
дополняется столбцом, содержащим среднее взвешенное
наименьшего и наибольшего результатов для каждой строки. Выбираются только те
варианты, в строках которых стоят наибольшие элементы eir этого столбца.
При С=1 критерий Гурвица превращается в ММ-критерий. При С = 0 он
превращается в критерий “азартного игрока”
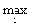 eir =
eir = 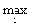
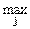 eij ,
eij ,
т.е. мы становимся на точку зрения азартного игрока, делающего ставку на
то, что «выпадет» наивыгоднейший случай.
В технических приложениях сложно выбрать весовой множитель С, т.к. трудно
найти количественную характеристику для тех долей оптимизма и пессимизма,
которые присутствуют при принятии решения. Поэтому чаще всего С := 1/2.
Критерий Гурвица применяется в случае, когда :
о вероятностях появления состояния Fj ничего не известно;
с появлением состояния Fj необходимо считаться;
реализуется только малое количество решений;
допускается некоторый риск.
.2 КРИТЕРИЙ
ХОДЖА-ЛЕМАНА
Этот критерий опирается одновременно на ММ-критерий и критерий
Баеса-Лапласа. С помощью параметра n выражается степень доверия к используемому
распределений вероятностей. Если доверие велико, то доминирует критерий
Баеса-Лапласа, в противном случае - ММ-критерий, т.е. мы ищем
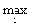 eir =
eir = 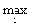 {n
{n  + (1-n)
+ (1-n) 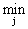 eir}, 0 £ n £ 1.
eir}, 0 £ n £ 1. 
Правило выбора, соответствующее критерию Ходжа-Лемана формируется
следующим образом:
матрица решений 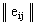 дополняется столбцом, составленным из средних взвешенных (с
весом n º const) математическое ожиданиями и
наименьшего результата каждой строки (*). Отбираются те варианты решений в
строках которого стоит набольшее значение этого столбца.
дополняется столбцом, составленным из средних взвешенных (с
весом n º const) математическое ожиданиями и
наименьшего результата каждой строки (*). Отбираются те варианты решений в
строках которого стоит набольшее значение этого столбца.
При n = 1 критерий Ходжа-Лемана переходит в критерий Байеса-Лапласа, а
при n = 0 становится минимаксным.
Выбор n субъективен т. к. Степень достоверности какой-либо функции
распределения - дело тёмное.
Для применения критерия Ходжа-Лемана желательно, чтобы ситуация в которой
принимается решение, удовлетворяла свойствам:
вероятности появления состояния Fj неизвестны, но некоторые предположения
о распределении вероятностей возможны;
принятое решение теоретически допускает бесконечно много реализаций;
при малых числах реализации допускается некоторый риск.
.3 КРИТЕРИЙ
ГЕРМЕЙРА
Этот критерий ориентирован на величину потерь, т.е. на отрицательные
значения всех eij. При этом
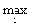 eir =
eir = 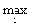
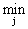 eij qj.
eij qj.
решение неопределенность матрица игра
Т.к. в хозяйственных задачах преимущественно имеют дело с ценами и
затратами, условие eij 0. При этом оптимальный вариант решения зависит от а.
Правило выбора согласно критерию Гермейера формулируется следующим
образом :
матрица решений 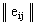 дополняется ещё одним столбцом содержащим в каждой строке
наименьшее произведение имеющегося в ней результата на вероятность
соответствующего состояния Fj. Выбираются те варианты в строках которых
находится наибольшее значение eij этого столбца.
дополняется ещё одним столбцом содержащим в каждой строке
наименьшее произведение имеющегося в ней результата на вероятность
соответствующего состояния Fj. Выбираются те варианты в строках которых
находится наибольшее значение eij этого столбца.
В каком-то смысле критерий Гермейера обобщает ММ-критерий: в случае
равномерного распределения qj = 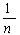 , j =
, j =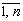 , они становятся идентичными.
, они становятся идентичными.
Условия его применимости таковы :
вероятности появления состояния Fj неизвестны;
с появлением тех или иных состояний, отдельно или в комплексе, необходимо
считаться;
допускается некоторый риск;
решение может реализоваться один или несколько раз.
Если функция распределения известна не очень надёжно, а числа реализации
малы, то, следуя критерию Гермейера, получают, вообще говоря, неоправданно
большой риск.
.4 BL (MM) - КРИТЕРИЙ
Стремление получить критерии, которые бы лучше приспосабливались к
имеющейся ситуации, чем все до сих пор рассмотренные, привело к построению так
называемых составных критериев. В качестве примера рассмотрим критерий,
полученный путем объединения критериев Байеса-Лапласа и минимакса.
Правило выбора для этого критерия формулируется следующим образом:
матрица решений 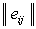 дополняется еще тремя столбцами. В первом из них
записываются математические ожидания каждой из строк, во втором - разность
между опорным значением
дополняется еще тремя столбцами. В первом из них
записываются математические ожидания каждой из строк, во втором - разность
между опорным значением

и наименьшим значением
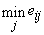
соответствующей строки. В третьем столбце помещаются разности между
наибольшим значением

каждой строки и наибольшим значением 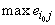 той строки, в которой находится
значение
той строки, в которой находится
значение  . Выбираются те варианты, строки
которых (при соблюдении приводимых ниже соотношений между элементами второго и
третьего столбцов) дают наибольшее математическое ожидание. А именно,
соответствующее значение
. Выбираются те варианты, строки
которых (при соблюдении приводимых ниже соотношений между элементами второго и
третьего столбцов) дают наибольшее математическое ожидание. А именно,
соответствующее значение

из второго столбца должно быть или равно некоторому заранее заданному
уровню риска 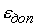 . Значение же из третьего столбца должно быть больше значения
из второго столбца.
. Значение же из третьего столбца должно быть больше значения
из второго столбца.
Применение этого критерия обусловлено следующими признаками ситуации, в
которой принимается решение:
вероятности появления состояний Fj неизвестны, однако имеется некоторая
априорная информация в пользу какого-либо определенного распределения;
необходимо считаться с появлением различных состояний как по отдельности,
так и в комплексе;
допускается ограниченный риск;
принятое решение реализуется один раз или многократно.(MM)-критерий
хорошо приспособлен для построения практических решений прежде всего в области
техники и может считаться достаточно надежным. Однако заданные границы риска 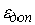 и, соответственно, оценок риска
и, соответственно, оценок риска 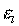 не учитывает ни число применения
решения, ни иную подобную информацию. Влияние субъективного фактора хотя и
ослаблено, но не исключено полностью.
не учитывает ни число применения
решения, ни иную подобную информацию. Влияние субъективного фактора хотя и
ослаблено, но не исключено полностью.
Условие
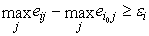
существенно в тех случаях, когда решение реализуется только один или
малое число раз. В этих условиях недостаточно ориентироваться на риск,
связанный только с невыгодными внешними состояниями и средними значениями.
Из-за этого, правда, можно понести некоторые потери в удачных внешних
состояниях. При большом числе реализаций это условие перестает быть таким уж
важным. Оно даже допускает разумные альтернативы. При этом не известно, однако,
четких количественных указаний, в каких случаях это условие следовало бы
опускать.
.5 КРИТЕРИЙ
ПРОИЗВЕДЕНИЙ
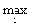 eir: =
eir: = 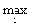
 eij
eij
Правило выбора в этом случае формулируется так :
Матрица решений 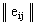 дополняется новым столбцом, содержащим произведения всех
результатов каждой строки. Выбираются те варианты, в строках которых находятся
наибольшие значения этого столбца.
дополняется новым столбцом, содержащим произведения всех
результатов каждой строки. Выбираются те варианты, в строках которых находятся
наибольшие значения этого столбца.
Применение этого критерия обусловлено следующими обстоятельствами :
вероятности появления состояния Fj неизвестны;
с появлением каждого из состояний Fj по отдельности необходимо считаться;
критерий применим и при малом числе реализаций решения;
некоторый риск допускается.
Критерий произведений приспособлен в первую очередь для случаев, когда
все eij положительны. Если условие положительности нарушается, то следует
выполнять некоторый сдвиг eij + а с некоторой константой а > ï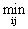 eijï. Результат при этом будет,
естественно зависеть от а. На практике чаще всего
eijï. Результат при этом будет,
естественно зависеть от а. На практике чаще всего
а := ï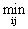 eijï+1.
eijï+1.
Если же никакая константа не может быть признана имеющей смысл, то
критерий произведений не применим.
4. ТЕОРИЯ ИГР
Теория игр, раздел математики, изучающий формальные модели принятия
оптимальных решений в условиях конфликта. При этом под конфликтом понимается
явление, в котором участвуют различные стороны, наделённые различными
интересами и возможностями выбирать доступные для них действия в соответствии с
этими интересами. Отдельные математические вопросы, касающиеся конфликтов,
рассматривались (начиная с 17 в.) многими учёными. Систематическая же
математическая теория игр была детально разработана американскими учёными Дж.
Нейманом и О. Моргенштерном (1944) как средство математического подхода к
явлениям конкурентной экономики. В ходе своего развития Теория игр переросла
эти рамки и превратилась в общую математическую теорию конфликтов. В рамках
Теория игр в принципе поддаются математическому описанию военные и правовые
конфликты, спортивные состязания, «салонные» игры, а также явления, связанные с
биологической борьбой за существование.
В условиях конфликта стремление противника скрыть свои предстоящие
действия порождает неопределённость. Наоборот, неопределённость при принятии
решений (например, на основе недостаточных данных) можно интерпретировать как
конфликт принимающего решения субъекта с природой. Поэтому Теория игр
рассматривается также как теория принятия оптимальных решений в условиях
неопределённости. Она позволяет математизировать некоторые важные аспекты
принятия решений в технике, сельском хозяйстве, медицине и социологии.
Перспективен подход с позиций Теория игр к проблемам управления, планирования и
прогнозирования.
Основным в Теория игр является понятие игры, являющееся формализованным
представлением о конфликте. Точное описание конфликта в виде игры состоит
поэтому в указании того, кто и как участвует в конфликте, каковы возможные
исходы конфликта, а также кто и в какой форме заинтересован в этих исходах.
Участвующие в конфликте стороны называются коалициями действия; доступные для
них действия - их стратегиями; возможные исходы конфликта - ситуациями (обычно
каждая ситуация понимается как результат выбора каждой из коалиций действия
некоторой своей стратегии); стороны, заинтересованные в исходах конфликта, -
коалициями интересов; их интересы описываются предпочтениями тех или иных
ситуаций (эти предпочтения часто выражаются численными выигрышами).
Конкретизация перечисленных объектов и связей между ними порождает
разнообразные частные классы игр.
Примером нестратегической (кооперативной) игры может служить простая
игра, состоящая в следующем. Множеством ситуаций являются в ней всевозможные
распределения (дележи) между игроками некоторого количества однородной
полезности (например, денег). Каждый делёж описывается теми суммами, которые
при этом получают отдельные игроки. Коалиция интересов называется выигрывающей,
если она может даже в условиях противодействия со стороны всех остальных
игроков присвоить и разделить между своими членами всю имеющуюся полезность.
Все коалиции, не являющиеся выигрывающими, совсем не могут присвоить какой-либо
доли полезности. Такие коалиции называются проигрывающими. Естественно считать,
что выигрывающая коалиция предпочитает один делёж другому, если доля каждого из
её членов в условиях первого дележа больше, чем в условиях второго.
Проигрывающие же коалиции не могут сравнивать дележи по предпочтительности (это
условие также вполне естественно: коалиция интересов, которая сама не в состоянии
добиться ничего, вынуждена соглашаться на любой делёж и лишена возможности
выбора между дележами).
Если в игре имеется более одной коалиции действия, то игра называется
стратегической. Важный класс стратегических игр составляют бескоалиционные игры,
в которых коалиции действия совпадают с коалициями интересов (они называются
игроками), а предпочтения для игроков описываются их функциями выигрыша: игрок
предпочитает одну ситуацию другой, если в первой ситуации он получает больший
выигрыш, чем во второй.
Одним из простейших примеров бескоалиционной игры может служить «морра» в
следующем своём варианте. Три игрока показывают одновременно 1 или 2 пальца
каждый. Если все три игрока показывают одно и то же число, то выигрыш каждого
равен нулю. В противном случае один из игроков показывает a ( = 1 или 2) и
получает b из некоторого источника (например, из банка, образованного
предварительными взносами), а два других игрока, показывающие одно и то же b (¹ a), не получают ничего.
Если в бескоалиционной игре участвуют два игрока, а значения их функций
выигрыша в любой ситуации отличаются только знаками, то игра называется
антагонистической игрой в ней выигрыш одного из игроков в точности равен
проигрышу другого. Если в антагонистической игре множества стратегий обоих
игроков конечны, то игра называется матричной игрой ввиду некоторой
специфической возможности её описания.
В качестве другого примера бескоалиционной игры можно привести шахматы. В
этой игре участвуют два игрока (белые и чёрные). Стратегия каждого из игроков
есть мыслимое (хотя практически и не поддающееся детальному описанию) правило
выбора в каждой возможной позиции некоторого хода, допускаемого движениями
фигур. Пара таких правил (за белых и за чёрных) составляет ситуацию, которая
полностью определяет протекание шахматной партии и в том числе её исход.
Функция выигрыша белых имеет значение 1 на выигрываемых партиях, 0 на ничейных
и - 1 на проигрываемых (такой способ начисления очков практически ничем не
отличается от принятого в турнирной и матчевой практике). Функция выигрыша
чёрных отличается от функции выигрыша белых лишь знаком. Из сказанного видно,
что шахматы относятся к числу антагонистических и притом матричных игр. В
шахматах стратегии не выбираются игроками до начала игры, а реализуются постепенно,
ход за ходом. Это значит, что шахматы принадлежат к позиционным играм
Теория игр является нормативной теорией, тоесть предметом её изучения
являются не столько сами модели конфликтов (игры), как таковые, сколько
содержание принимаемых в играх принципов оптимальности, существования ситуаций,
на которых эти принципы оптимальности реализуются (такие ситуации или множества
ситуаций называются решениями в смысле соответствующего принципа
оптимальности), и, наконец, способы нахождения таких ситуаций. Рассматриваемые
в Теория игр объекты - игры - весьма разнообразны, и пока не удалось установить
принципов оптимальности, общих для всех классов игр. Практически это означает,
что единого для всех игр истолкования понятия оптимальности ещё не выработано.
Поэтому прежде чем говорить, например, о наивыгоднейшем поведении игрока в
игре, необходимо установить, в каком смысле эта выгодность понимается. Все
применяемые в Теория игр принципы оптимальности при всём их внешнем
разнообразии отражают прямо или косвенно идею устойчивости ситуаций или
множеств ситуаций, составляющих решения. В бескоалиционных играх основным
принципом оптимальности считается принцип осуществимости цели, приводящий к
ситуациям равновесия. Эти ситуации характеризуются тем свойством, что любой игрок,
который отклонится от ситуации равновесия (при условии, что остальные игроки не
изменят своих стратегий), не увеличит этим своего выигрыша.
В частном случае антагонистических игр принцип осуществимости цели
превращается в так называемый принцип максимина (отражающий стремление
максимизировать минимальный выигрыш).
Принципы оптимальности (первоначально выбиравшиеся интуитивно) выводятся
на основании некоторых заранее задаваемых их свойств, имеющих характер аксиом.
Существенно, что различные применяемые в Теория игр принципы оптимальности
могут противоречить друг другу.
Теоремы существования в Теория игр доказываются преимущественно теми же
неконструктивными средствами, что и в других разделах математики: при помощи
теорем о неподвижной точке, о выделении из бесконечной последовательности
сходящейся подпоследовательности и т. п., или же, в весьма узких случаях, путём
интуитивного указания вида решения и последующего нахождения решения в этом
виде.
Фактическое решение некоторых классов антагонистических игр сводится к
решению дифференциальных и интегральных уравнений, а матричных игр - к решению
стандартной задачи линейного программирования. Разрабатываются приближённые и
численные методы решения игр. Для многих игр оптимальными оказываются так
называемые смешанные стратегии, то есть стратегии, выбираемые случайно
(например, по жребию).
Теория игр, созданная для математического решения задач экономического и
социального происхождения, не может в целом сводиться к классическим
математическим теориям, созданным для решения физических и технических задач.
Однако в различных конкретных вопросах Теория игр широко используются весьма
разнообразные классические математические методы. Кроме этого, Теория игр
связана с рядом математических дисциплин внутренним образом. В Теория игр
систематически и по существу употребляются понятия теории вероятностей. На
языке Теория игр можно сформулировать большинство задач математической
статистики. Необходимость при анализе игры количественного учёта
неопределённости предопределяет важность и тем самым связь Теория игр с теорией
информации и через её посредство - с кибернетикой. Кроме того, Теория игр,
будучи теорией принятия решений, может рассматриваться как существенная
составная часть математического аппарата операций исследования. Теория игр
применяется в экономике, технике, военном деле и даже в антропологии. Основные
трудности практического применения Теория игр связаны с экономической и
социальной природой моделируемых ею явлений и недостаточным умением составлять
такие модели на количественном уровне.
К 70-м гг. 20 в. число публикаций по научным вопросам Теория игр достигло
многих сотен (в том числе несколько десятков монографий). Курсы по Теория игр
читаются во многих высших учебных заведениях для студентов математических и
экономических специальностей (в СССР - с 1956).
Международные конференции по Теория игр проходили в Принстоне (1961),
Иерусалиме (1965), Вене (1967) и Беркли (1970). Всесоюзные конференции по
Теория игр состоялись в Ереване (1968) и Вильнюсе (1971).
.1 МАТРИЧНЫЕ ИГРЫ
Матричные игры, понятие теории игр. Матричные игры - игры, в которых
участвуют два игрока (I и II) с противоположными интересами, причём каждый
игрок имеет конечное число чистых стратегий Если игрок I имеет m стратегий, а
игрок II - n стратегий, то игра может быть задана (m n)-maтрицей А =
||aij||, где aij есть выигрыш игрока I, если он выберет стратегию i (i = -1,
..., m), а игрок II - стратегию j (j = 1, ..., n). Следуя общим принципам
поведения в антагонистических играх (частным случаем которых являются Матричные
игры), игрок I стремится выбрать такую стратегию i0, на которой достигается
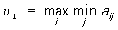 ;
;
игрок II стремится выбрать стратегию jo, на которой достигается
 ;
;
Если u1 = u2,, то пара (i0, j0) составляет седловую точку игры, то
есть выполняется двойное неравенство
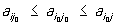 ; i = 1, …, m; j = 1, …, n.
; i = 1, …, m; j = 1, …, n.
Число 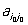 называется значением игры; стратегии i0, j0 называются
оптимальным и чистыми стратегиями игроков I и II соответственно. Если u1 ¹ u2, то всегда u1
< u2; в этом случае в игре седловой точки нет, а
оптимальные стратегии игроков следует искать среди их смешанных стратегий (то
есть вероятностных распределений на множестве чистых стратегий). В этом случае
игроки оперируют уже с математическими ожиданиями выигрышей.
называется значением игры; стратегии i0, j0 называются
оптимальным и чистыми стратегиями игроков I и II соответственно. Если u1 ¹ u2, то всегда u1
< u2; в этом случае в игре седловой точки нет, а
оптимальные стратегии игроков следует искать среди их смешанных стратегий (то
есть вероятностных распределений на множестве чистых стратегий). В этом случае
игроки оперируют уже с математическими ожиданиями выигрышей.
Основная теорема теории Матричные игры (теорема Неймана о минимаксе)
утверждает, что в любой Матричные игры существуют оптимальные смешанные
стратегии х*, у*, на которых достигаемые «минимаксы» равны (общее их значение
есть значение игры). Например, игра с матрицей  имеет седловую точку при i0 = 2, j0
= 1, а значение игры равно 2; игра с матрицей
имеет седловую точку при i0 = 2, j0
= 1, а значение игры равно 2; игра с матрицей  не имеет седловой точки. Для неё
оптимальные смешанные стратегии суть х* = (3/4, 1/4), y* = (1/2, 1/2); значение
игры равно 1/2.
не имеет седловой точки. Для неё
оптимальные смешанные стратегии суть х* = (3/4, 1/4), y* = (1/2, 1/2); значение
игры равно 1/2.
Для фактического нахождения оптимальных смешанных стратегий чаще всего
используют возможность сведения Матричные игры к задачам линейного
программирования Можно использовать так называемый итеративный метод Брауна -
Робинсон, состоящий в последовательном фиктивном «разыгрывании» данной игры с
выбором игроками в каждой данной партии своих чистых стратегий, наилучших против
накопленных к этому моменту стратегий оппонента. Игры, в которых один из
игроков имеет только две стратегии, просто решить графически.
Матричные игры могут служить математическими моделями многих простейших
конфликтных ситуаций из области экономики, математической статистики, военного
дела, биологии. Нередко в качестве одного из игроков рассматривают «природу»,
под которой понимается вся совокупность внешних обстоятельств, неизвестных
принимающему решения лицу (другому игроку).
4.2 Графоаналитический метод решения матричных
игр 2×n и m× 2
Для некоторых классов матричных игр практический интерес представляет
графоаналитический метод. Этот метод состоит из двух частей. Вначале в
матричной игре графически выявляются качественные особенности решения, затем
полная характеристика решения находится аналитически. В основе метода лежит
утверждение, которое остаётся верным и в смешанном расширении игры. Седловая
точка в матричной игре существует тогда и только тогда, когда выполняется
равенство
max min f (x,y) min max f (x,y)= 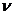 *
*
причём
седловую точку составляют стратегии, доставляющие внешние экстремумы в
последнем равенстве.
4.2.1 Пример решения игры вида 2хN:
Рассмотрим следующую игру 2х4.
Таблица 1
Эта игра не имеет седловой точки. Ожидаемые выигрыши игрока А,
соответствующие чистым стратегиям В, представлены в таблице 2.
|
Чистые стратегии игрока В
|
Ожидаемый выигрыш игрока А
|
|
1
|
-2х1+4
|
|
2
|
-х1+3
|
|
3
|
х1+2
|
|
4
|
-7х1+6
|
Таблица 2
На рисунке 1 изображены четыре прямые, являющиеся графиками этих функций
от х1. Максимин достигается при х1*=1/2. В этой точке пересекаются любые две из
прямых 2,3 и 4. Следовательно, оптимальной стратегией игрока А является
(х1*=1/2, х2*=1/2) и значение игры находится подстановкой х1 в уравнение любой
из прямых, проходящих через максиминную точку. Это дает
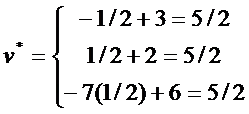
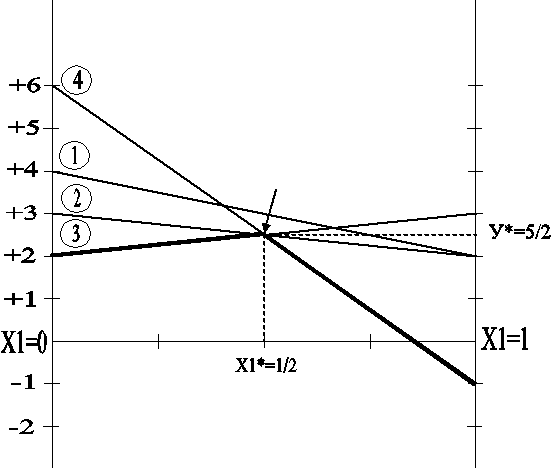
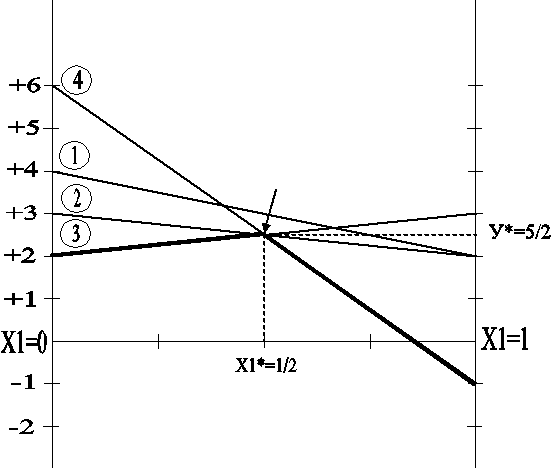
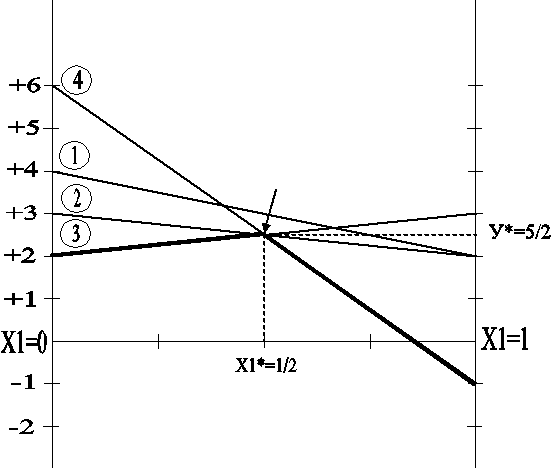
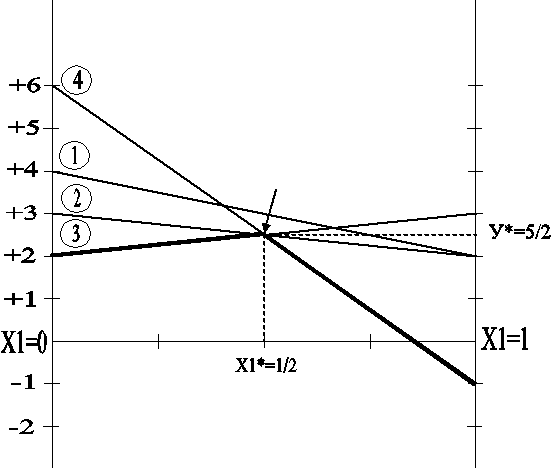
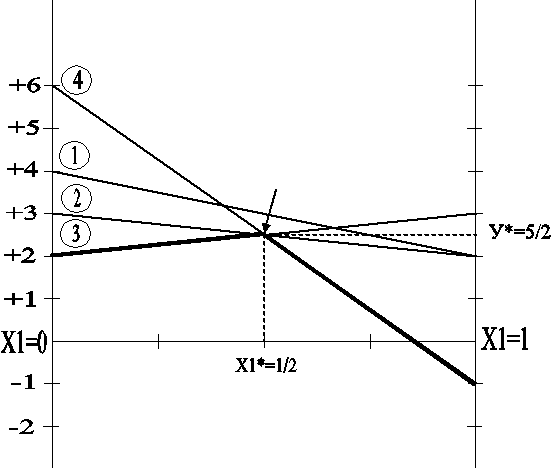
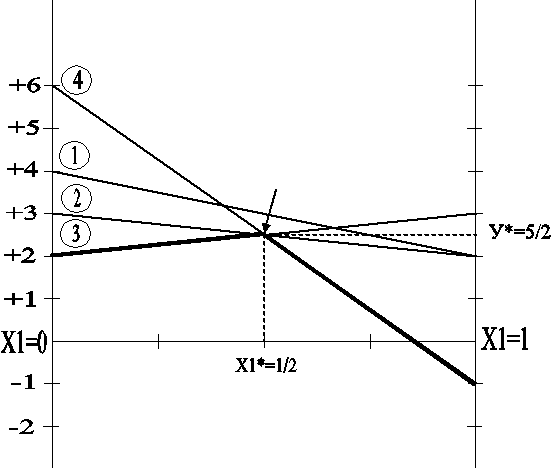
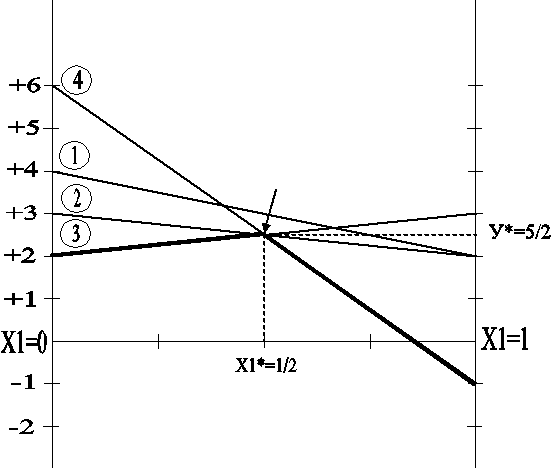
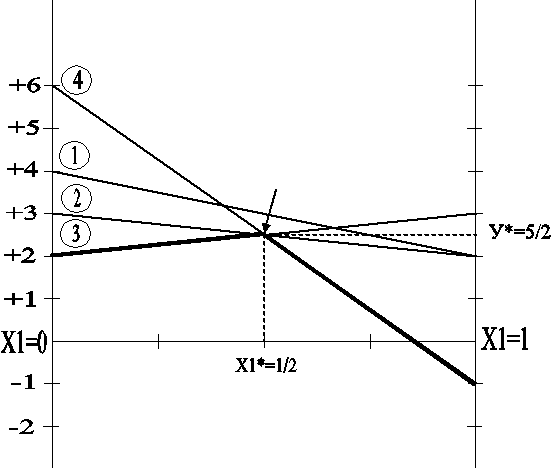
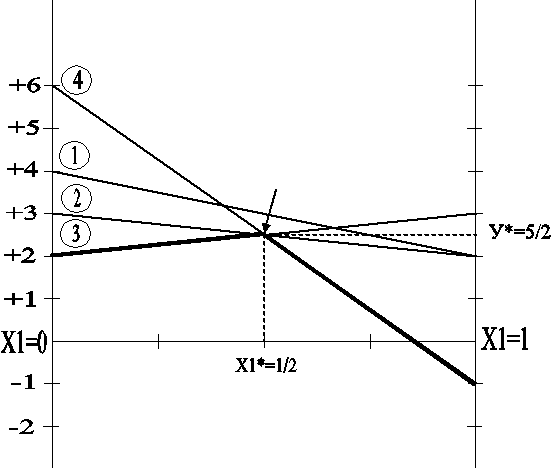
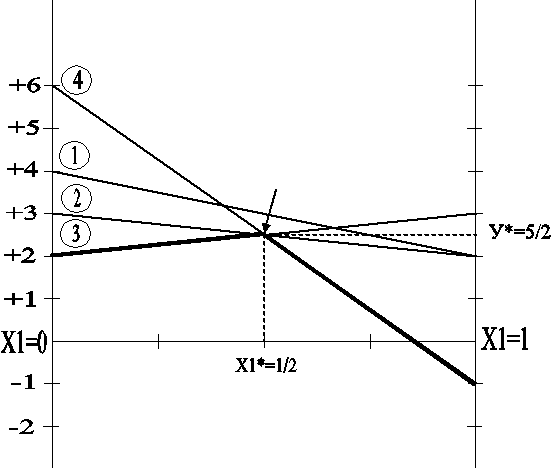
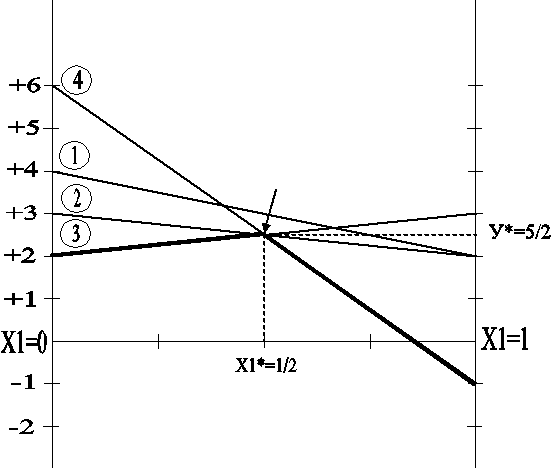
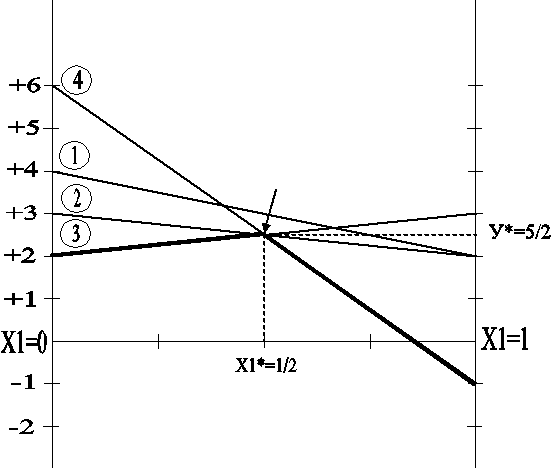
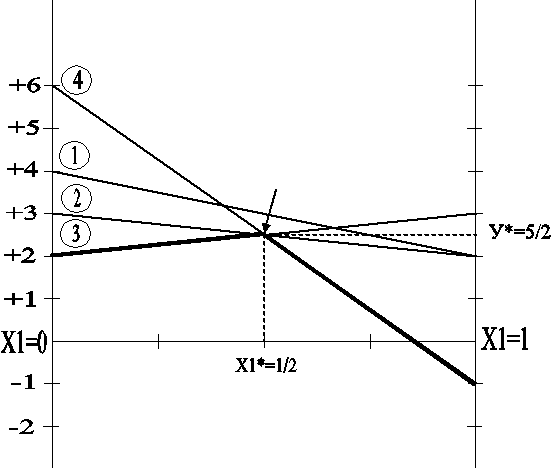
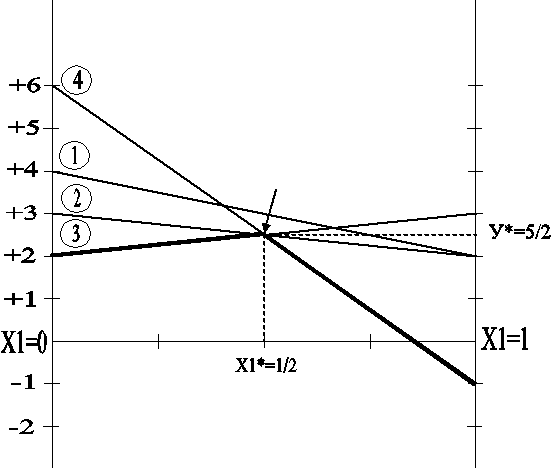
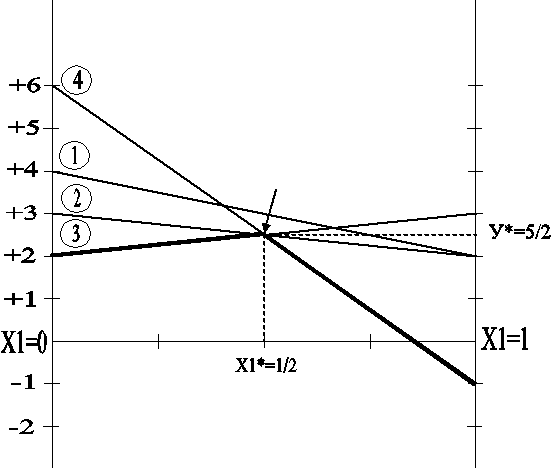

Рис. 1
4.2.2 Пример решения игры вида Mх2:
Рассмотрим следующую игру вида 4х2.
Таблица 3
Эта игра не имеет седловой точки. Пусть у1 и у2=(1-у1) - смешанные
стратегии игрока В. Тогда
|
Чистые стратегии игрока А
|
Ожидаемый выигрыш игрока В
|
|
1
|
-2у1+4
|
|
2
|
-у1+3
|
|
3
|
У1+2
|
|
4
|
-8у1+6
|
Таблица 4
Эти
четыре прямые изображены на рисунке 2. В данном случае минимаксная точка
определяется как самая нижняя точка на огибающей сверху. Значение у1*
получается как точка пересечения прямых 1 и 3. Это дает у1*=2/3 и  *=8/3.
*=8/3.
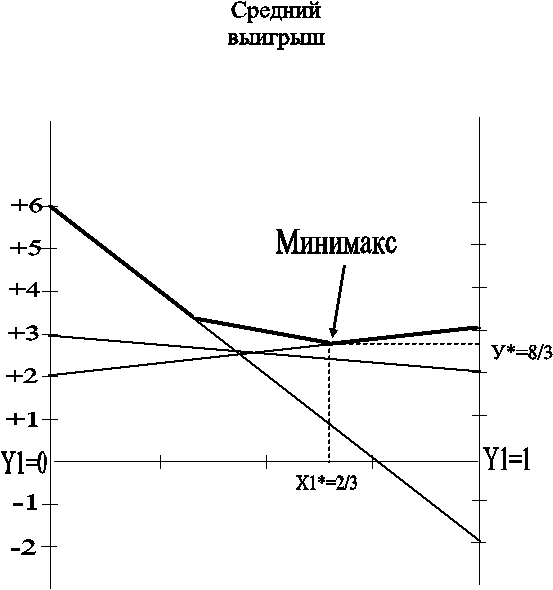














Рис. 2
. ЛИСТИНГ ПРОГРАММЫ
uses crt,Graph;
var, Gm : Integer;:array [1..10,1..10] of
integer;,y,k1,k2,z0,z1:array [1..10] of
integer;,q0,a,yy,wx,wy:integer;,j,n,m,c,minZ0,minZ1,zj0,zj1:integer;,yyy,aa:real;:string[15];[1]:='9';st[2]:='8';st[3]:='7';st[4]:='6';[5]:='5';st[6]:='4';st[7]:='3';st[8]:='2';[9]:='1';st[10]:='
';st[11]:='1';st[12]:='2';[13]:='3';st[14]:='4';;('‚›Ѓ€ђ€’… ђЂ‡Њ…ђЌЋ‘’њ ‡Ђ„Ђ-€: 1 - 2xN, 2 - Mx2');('1 -> 2 x N');('2 -> M x 2');(c);;c=1
then('‚‚€„€’… N :');read(n); clrscr;('‚‚€„€’… Џ‹Ђ’…†„“ћ ЊЂ’ђ€-“ :');i:=1 to 2 doj:=1 to n
do('a[',i,',',j,']='); readln(Mat[i,j]);;;j:=1 to n
do[j]:=mat[1,j]-mat[2,j];[j]:=mat[2,j];;(' €ѓђЋЉ B | €ѓђЋЉ A
');('-----------------------------------');j:=1 to n do(' ',j,' | ',k1[j],' X1
+(',k2[j],')' );;j:=1 to n do[j]:=k2[j];[j]:=k1[j]+k2[j];;:=z0[1];zj0:=1;j:=2
to n dominZ0>z0[j] then begin minZ0:=z0[j] ; zj0:=j;end;;:=z1[1];zj1:=1;j:=2
to n dominZ1>z1[j] then begin minZ1:=z1[j] ; zj1:=j;end;;(k2[zj0]<>k2[zj1])
or (k1[zj0]<>k1[zj1])
then:=((k2[zj1])-(k2[zj0]))/((k1[zj0])-(k1[zj1]));:=k1[zj1]*XXX+k2[zj1];minz1>minz0
then xxx:=1xxx:=0;;:=k1[zj1]*XXX+k2[zj1];yyy<minz0
then:=0;:=minz0;;yyy<minz1 then:=1;:=minZ1;;(' ');(' x1* = ',XXX:2:2);(' x2*
= ',(1-xxx):2:2);(' -Ґ ЁЈал : ',YYY:2:2);('');('Ќ ¦¬ЁвҐ «оЎго Є®ЇЄг ¤«п Їа®¤®«¦ҐЁп'); readkey;:=Detect;(Gd, Gm, '');GraphResult <> grOk Then
Halt(1);(2);(168,305, 'X1=0');(352,305,
'X1=1');(200,100,200,400);(350,100,350,400);(190,300,360,300);:=120;i:=1 to 14
do(345,yy,355,yy);(195,yy,205,yy);yy>300 then OutTextXY(358,yy-3,
'-');(366,yy-3, st[i]);yy>300 then OutTextXY(180,yy-3, '-');(187,yy-3,
st[i]);:=yy+20;;:=abs(trunc(150*xxx));:=abs(trunc(20*yyy));(5);j:=1 to n
do:=20*z0[j];:=20*z1[j];(200,300-q0,350,300-q1);(5+j);;(2);i:=1 to 3
do(200+wx,300-wy,i);n>=1 then begin setcolor(5); OutTextXY(10,100, 'line -
1'); end;n>=2 then begin setcolor(6); OutTextXY(10,110, 'line - 2');
end;n>=3 then begin setcolor(7); OutTextXY(10,120, 'line - 3'); end;n>=4
then begin setcolor(8); OutTextXY(10,130, 'line - 4'); end;n>=5 then begin
setcolor(9); OutTextXY(10,140, 'line - 5'); end;n>=6 then begin
setcolor(10); OutTextXY(10,150, 'line - 6'); end;n>=7 then begin
setcolor(11); OutTextXY(10,160, 'line - 7'); end;(3); OutTextXY(10,30,
'Exit-[Esc] ');(255,50, '2 x N'); readkey;;;c=2 then;('‚‚…„€’… M :');read(n);
clrscr;('‚‚€„€’… Џ‹Ђ’…†Ќ“ћ ЊЂ’ђ€-“ :'); clrscr;i:=1 to n
doj:=1 to 2 do('a[',i,',',j,']='); readln(Mat[i,j]);;;i:=1 to n
do[i]:=mat[i,1]-mat[i,2];[i]:=mat[i,2];;(' €ѓђЋЉ B | €ѓђЋЉ A
');('-----------------------------------');i:=1 to n do(' ',i,' | ',k1[i],' Y1
+(',k2[i],')' );;i:=1 to n do[i]:=k2[i];[i]:=k1[i]+k2[i];;('Ќ ¦¬ЁвҐ «оЎго Є®ЇЄг ¤«п Їа®¤®«¦ҐЁп');;:=z0[1];zj0:=1;j:=2 to n dominZ0<z0[j] then begin minZ0:=z0[j] ;
zj0:=j;end;;:=z1[1];zj1:=1;j:=2 to n dominZ1<z1[j] then begin minZ1:=z1[j] ;
zj1:=j;end;;(k2[zj0]<>k2[zj1]) or (k1[zj0]<>k1[zj1])
then:=((k2[zj1])-(k2[zj0]))/((k1[zj0])-(k1[zj1]));:=k1[zj1]*XXX+k2[zj1];minz1<minz0
then xxx:=1xxx:=0;;:=k1[zj1]*XXX+k2[zj1];yyy>minz0
then:=0;:=minz0;;yyy>minz1 then:=1;:=minZ1;;(' ');(' y1* = ',XXX:2:2);(' y2*
= ',(1-xxx):2:2);(' -Ґ ЁЈал : ',YYY:2:2);('');('Ќ ¦¬ЁвҐ «оЎго Є®ЇЄг ¤«п Їа®¤®«¦ҐЁп'); readkey;:=Detect;(Gd, Gm, '');GraphResult <> grOk Then
Halt(1);(2);(168,305, 'Y1=0');(352,305,
'Y1=1');(200,100,200,400);(350,100,350,400);(190,300,360,300);:=120;(2);i:=1 to
14 do(345,yy,355,yy);(195,yy,205,yy);yy>300 then OutTextXY(358,yy-3,
'-');(366,yy-3, st[i]);yy>300 then OutTextXY(180,yy-3, '-');(187,yy-3, st[i]);:=yy+20;;(5);i:=1
to n
do:=20*z0[i];:=20*z1[i];(200,300-q0,350,300-q1);(5+i);;:=abs(trunc(150*xxx));:=abs(trunc(20*yyy));(2);i:=1
to 3 do(200+wx,300-wy,i);n>=1 then begin setcolor(5); OutTextXY(10,100,
'line - 1'); end;n>=2 then begin setcolor(6); OutTextXY(10,110, 'line - 2');
end;n>=3 then begin setcolor(7); OutTextXY(10,120, 'line - 3'); end;n>=4
then begin setcolor(8); OutTextXY(10,130, 'line - 4'); end;n>=5 then begin
setcolor(9); OutTextXY(10,140, 'line - 5'); end;n>=6 then begin setcolor(10);
OutTextXY(10,150, 'line - 6'); end;n>=7 then begin setcolor(11);
OutTextXY(10,160, 'line - 7'); end;(3); OutTextXY(10,30, 'Exit-[Esc] ');
OutTextXY(255,50, 'M x 2'); readkey;
End;;.
6. РЕЗУЛЬТАТ ТЕСТИРОВАНИЯ ПРОГРАММЫ
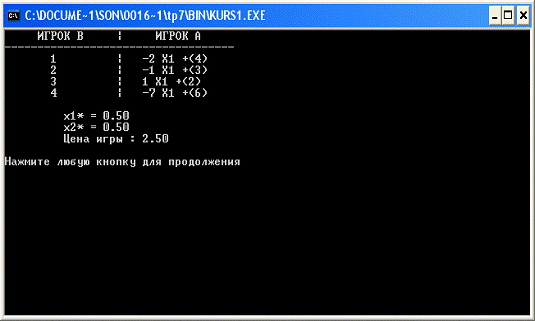
Рис.
1.1

Рис.
1.2
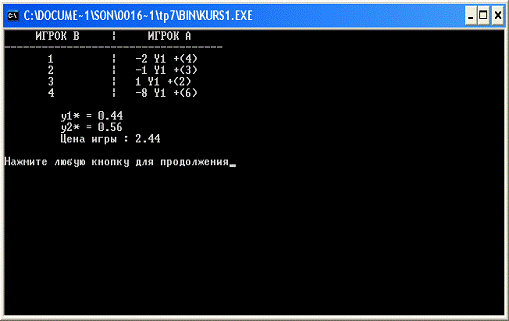
Рис.
2.1
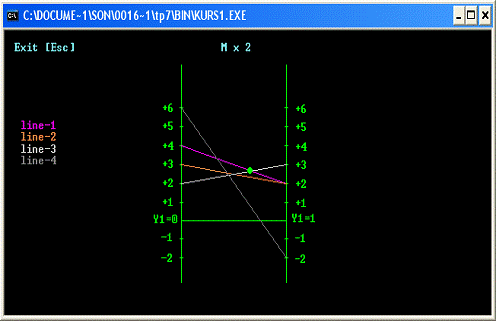
Рис.
2.2
7.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1 Сухарев
А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. - М.: Наука, Главная
редакция физико-математической литературы, 1986
. Таха Х.
Ведение в исследование операций: В 2-х книгах. Кн. 1. Пер. с англ. - М.: Мир,
1985
Таха Х.
Ведение в исследование операций: В 2-х книгах. Кн. 2 Пер. с англ. - М.: Мир,
1985
. Капустин
В.Ф. Практические занятия по курсу математического программирования. Л., Изд-во
Ленингр. Ун-та, 1976
. Современное
состояние теории исследования операций. Под. Ред. Н.Н. Моисеева. - М.: Наука.
Главная редакция физико-математической литературы, 1979