Исследование временных характеристик работы кодера кода Рида-Соломона в частотной области в зависимости от типа ДПФ параметров кода
Введение
Современная цивилизация немыслима
без использования разнообразных средств передачи информации. По мере
технического и социального прогресса требования к объемам передаваемых данных,
качеству и широте охвата информационного сервиса непрерывно возрастают,
стимулируя исследовательскую и инженерную активность и пополняя новыми людскими
ресурсами контингент информационного сообщества.
Надежность передачи сообщений в
реальных линиях связи критически зависит от помех и искажений в канале, так что
проблема помехоустойчивости оказывается центральной при разработке большинства
информационных систем. Современная теория связи, базирующаяся на статистических
методах, включает множество ветвей и направлений, среди которых следует
упомянуть теорию оптимального приема, теорию информации и теорию кодирования.
Содержание теории оптимального
приема сообщений составляют статистический синтез приемных устройств, анализ
эффективности различных видов модуляции, расчет показателей помехоустойчивости
линии связи и др. Теория информации занимается статистическим описанием
источников сообщений и каналов связи, методами экономного представления
информации, а также выяснением предельных возможностей каналов с учетом
энергетических и спектральных ограничений. Важным разделом теории информации,
выделившимся в самостоятельную дисциплину, является теория кодирования,
основной задачей которой является разработка методов отображения сообщений в
некоторые абстрактные эквиваленты с целью повышения достоверности передачи
данных по зашумленным каналам.
Суть кодирования состоит во введении
в информационный поток специальным образом дополнительных символов, в
результате чего каждому блоку из k информационных символов сопоставляется n символьная
последовательность символов из какого-нибудь алфавита.
Основное внимание в данной работе
уделяется кодам Рида-Соломона, которые являются оптимальными кодами,
исправляющими не только одиночные искажения, но и пачки ошибок и стираний.
Разработаны разные методы кодирования этими кодами.
В дипломной работе рассмотрен
спектральный метод кодирования кодов Рида-Соломона над полем GF(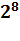
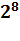 ). В основе
спектрального описания РС-кодов лежит дискретное преобразование Фурье (ДПФ над
конечным полем.
). В основе
спектрального описания РС-кодов лежит дискретное преобразование Фурье (ДПФ над
конечным полем.
Существует закон Гроша,
устанавливающий связь между стоимостью и скоростью обработки информации в
вычислительных сетях. Согласно этому закону, стоимость вычислений
пропорциональна корню квадратному из скорости вычислений. Так, например, для
снижения стоимости вычисления в 10 раз скорость вычислений должна быть
увеличена в 100 раз.
Цель работы - исследование временных
характеристик работы кодера кода Рида-Соломона в частотной области в
зависимости от типа ДПФ параметров кода.
Для выполнения этой цели был разработан
программный комплекс, реализующий ДПФ, трехмерное ДПФ, БПФ-преобразования и их
укорочения. На основе этих программ реализован кодер кодов Рида-Соломона в
частотной области и проведены вычислительные эксперименты для исследования
временных характеристик алгоритма кодирования.
1. Основы теории
помехоустойчивого кодирования
.1 Основные определения
кодирование программный алгоритм преобразование
Повышение требований к
скорости и достоверности передачи информации, увеличение протяженности линий
связи приводит к необходимости принятия специальных мер, направленных на
уменьшение вероятности возникновения ошибок в процессе передачи. Одним из
возможных решений указанной задачи служит помехоустойчивое кодирование. Под помехоустойчивыми
понимаются коды, позволяющие обнаруживать и исправлять ошибки, возникающие при
передаче из-за воздействия помех. Суть данной процедуры состоит во введении в
информационный поток специальным образом дополнительных символов, в результате
чего каждому блоку из k
информационных бит сопоставляется n
символьная последовательность 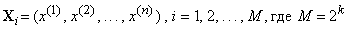 - число возможных
сообщений. Поскольку
- число возможных
сообщений. Поскольку 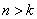 ,
то не все последовательности длины n
используются при кодировании M
сообщений. Комбинации символов, используемые для отображения информационных
блоков или сообщений, называют разрешенными комбинациями или кодовыми
последовательностями (словами), тогда как остальные - запрещенными. Вся
совокупность кодовых слов
,
то не все последовательности длины n
используются при кодировании M
сообщений. Комбинации символов, используемые для отображения информационных
блоков или сообщений, называют разрешенными комбинациями или кодовыми
последовательностями (словами), тогда как остальные - запрещенными. Вся
совокупность кодовых слов 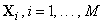 образует
код, для обозначения которого обычно говорят «код объема
образует
код, для обозначения которого обычно говорят «код объема 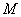 длины
длины
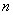 ».
Множество символов, из которых составляются кодовые слова, называется алфавитом
кода, а число различных символов в алфавите - основанием кода, или
объемом (мощностью) алфавита.
».
Множество символов, из которых составляются кодовые слова, называется алфавитом
кода, а число различных символов в алфавите - основанием кода, или
объемом (мощностью) алфавита.
Именно введение
дополнительных символов и позволяет осуществить нейтрализацию влияния канальных
помех. Появление указанной способности объясняется введением добавочных (проверочных)
символов в кодовом слове, т.е. за счет введения избыточности.
1.2 Классификация кодов
Существует несколько
подходов к классификации кодов, мы приведем основные из них:
В зависимости от
позиций, с которых рассматривается процедура кодирования, классификация кодов
может осуществляться различным образом. Простейшим вариантом может служить
классификация по размеру алфавита кода. Если символы кода  или
или
 ,
то код называется двоичным или бинарным соответственно. Если же
алфавит кода содержит
,
то код называется двоичным или бинарным соответственно. Если же
алфавит кода содержит  символов,
соответствующий ему код носит наименование
символов,
соответствующий ему код носит наименование  -ичного. В данной
работе основное внимание будет концентрироваться на двоичных или бинарных
кодах.
-ичного. В данной
работе основное внимание будет концентрироваться на двоичных или бинарных
кодах.
Классификация кодов
может быть осуществлена и по возможности выделения информационных символов
в кодовом слове. Коды, в которых, как правило, первые 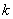 позиций
занимают информационные символы, называются систематическими кодами. В
противном случае - несистематическимими.
позиций
занимают информационные символы, называются систематическими кодами. В
противном случае - несистематическимими.
Коды можно
классифицировать и по способу противодействия искажениям в канале
распространения. Коды, позволяющие исправлять ошибки, получили наименование исправляющих
ошибки, тогда как коды только их фиксирующие, называются кодами, обнаруживающими
ошибки. Нередко коды, обнаруживающие и исправляющие ошибки, называют контролирующими
ошибки.
В заключении также
отметим, что часто термину код предшествует слово, определяющее либо алгоритм
его конструирования, либо имя ученого, открывшего правило формирования:
линейные, циклические, полиномиальные коды, коды Хэмминга и др.
1.3 Принципы обнаружения
и исправления ошибок
Пусть для передачи
сообщений используется некоторый код длины 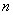 и объема
и объема 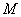 .
Это означает, что на вход дискретного канала поступает одна из
последовательностей
.
Это означает, что на вход дискретного канала поступает одна из
последовательностей ,
называемая кодовым словом. На приемной стороне наблюдается некоторая выходная
последовательность (вектор наблюдений)
,
называемая кодовым словом. На приемной стороне наблюдается некоторая выходная
последовательность (вектор наблюдений)  . Процедуру решения о
том, произошла ли ошибка при передаче кодовой последовательности или нет, можно
описать следующим алгоритмом. Все множество
. Процедуру решения о
том, произошла ли ошибка при передаче кодовой последовательности или нет, можно
описать следующим алгоритмом. Все множество 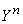 разбивается на две
области
разбивается на две
области 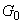 и
и
 ,
причем область
,
причем область 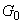 образована
кодовыми последовательностями, а
образована
кодовыми последовательностями, а  - запрещенными
комбинациями. Очевидно, что если наблюдаемая последовательность
- запрещенными
комбинациями. Очевидно, что если наблюдаемая последовательность 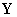 ,
полученная в результате трансформации каналом некоторой кодовой комбинации
,
полученная в результате трансформации каналом некоторой кодовой комбинации  ,
оказывается в области
,
оказывается в области  ,
то принимается решение об обнаружении ошибок в принятой последовательности.
Если же наблюдаемая последовательность окажется в области
,
то принимается решение об обнаружении ошибок в принятой последовательности.
Если же наблюдаемая последовательность окажется в области 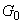 ,
то принимается решение о безошибочной передаче информации.
,
то принимается решение о безошибочной передаче информации.
Естественно возникает
вопрос о том, а все ли ошибки могут быть обнаружены? Предположим, что алфавит
входных 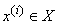 и
выходных
и
выходных  символов
одинаков, и его объем равен
символов
одинаков, и его объем равен  . Тогда объем кода, а
значит и мощность множества
. Тогда объем кода, а
значит и мощность множества 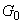 , составляют величину
, составляют величину 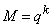 ,
а число запрещенных комбинаций (или мощность множества
,
а число запрещенных комбинаций (или мощность множества  )
определится как
)
определится как  .
При передаче по каналу связи M
кодовых комбинаций возможны
.
При передаче по каналу связи M
кодовых комбинаций возможны  их переходов в принятые
наблюдения
их переходов в принятые
наблюдения 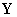 ,
из которых только
,
из которых только  будут
правильными, тогда как остальные
будут
правильными, тогда как остальные  переходов
сопровождаются искажениями. Как уже указывалось, решение об обнаружение ошибок
в принятой последовательности принимается всякий раз, когда она оказывается в
области
переходов
сопровождаются искажениями. Как уже указывалось, решение об обнаружение ошибок
в принятой последовательности принимается всякий раз, когда она оказывается в
области  .
Подобной ситуации отвечают
.
Подобной ситуации отвечают  переходов и, значит,
общее число обнаруживаемых ошибок составляет величину
переходов и, значит,
общее число обнаруживаемых ошибок составляет величину 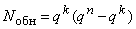 ,
что еще раз свидетельствует о возможности обнаружения ошибок только при условии
,
что еще раз свидетельствует о возможности обнаружения ошибок только при условии
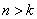 ,
т.е. при введении избыточных символов. Сравнение же общего количества ошибок
,
т.е. при введении избыточных символов. Сравнение же общего количества ошибок с числом обнаруживаемых
с числом обнаруживаемых 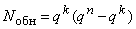 демонстрирует,
что не все ошибки удается зафиксировать. Последнее объясняется тем, что переход
одной кодовой комбинации в другую под действием канальных помех невозможно
обнаружить, причем общее количество подобных переходов составит величину
демонстрирует,
что не все ошибки удается зафиксировать. Последнее объясняется тем, что переход
одной кодовой комбинации в другую под действием канальных помех невозможно
обнаружить, причем общее количество подобных переходов составит величину 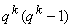 .
.
Аналогичным образом
реализуется и процедура исправления ошибок. Отличие заключается лишь в том, что
все множество 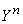 разбивается
теперь на
разбивается
теперь на 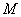 (по
числу передаваемых сообщений) решающих областей
(по
числу передаваемых сообщений) решающих областей 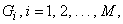
 , причем
, причем 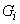 и
и
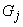 при
при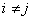 не пересекаются, а в каждую область решения
не пересекаются, а в каждую область решения 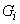 включается только одна
кодовая последовательность. Если оказывается, что вектор наблюдений
включается только одна
кодовая последовательность. Если оказывается, что вектор наблюдений 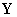 принадлежит
j-й области, т.е.
принадлежит
j-й области, т.е.  , то принимается решение
о том, что было передано слово
, то принимается решение
о том, что было передано слово 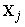 и, значит, канальные
ошибки, вызвавшие трансформацию
и, значит, канальные
ошибки, вызвавшие трансформацию 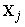 в
в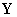 ,
будут исправлены. Поскольку области решений не перекрываются, то общее число
исправляемых ошибок определяется числом запрещенных комбинаций, распределяемых
между M решающими областями. Следовательно,
,
будут исправлены. Поскольку области решений не перекрываются, то общее число
исправляемых ошибок определяется числом запрещенных комбинаций, распределяемых
между M решающими областями. Следовательно,  и,
значит, как и в случае обнаружения ошибок, их исправление возможно лишь при
и,
значит, как и в случае обнаружения ошибок, их исправление возможно лишь при 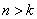 ,
т.е. при введении избыточности.
,
т.е. при введении избыточности.
1.4 Корректирующая
способность кода
Для того, чтобы дать
наглядное, геометрическое толкование процедуры различения сигналов, введем
понятие расстояния Хэмминга.
Расстояние Хэмминга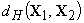 ,
определяется как число позиций, в которых кодовые символы двух слов отличаются
друг от друга.
,
определяется как число позиций, в которых кодовые символы двух слов отличаются
друг от друга.
Данная характеристика
показывает, насколько удалены сигналы друг от друга, что играет определяющую
роль в теории информации в целом. Чем больше расстояние между сигналами, тем
меньше вероятность перепутывания переносимой ими информации.
Для расстояния Хэмминга
выполняются следующие три аксиомы:
симметрии -  ;
;
неотрицательности - 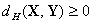 ,
причем если
,
причем если  ,
то
,
то 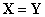 ;
;
неравенства треугольника
-  .
.
Наряду с расстоянием
Хэмминга широко используется такая характеристика, как вес Хэмминга .
Весом Хэмминга вектора
.
Весом Хэмминга вектора  называется
число его ненулевых компонент. Очевидно, что
называется
число его ненулевых компонент. Очевидно, что 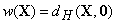 и
и 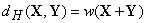 ,
где под суммированием векторов понимается покомпонентное сложение.
,
где под суммированием векторов понимается покомпонентное сложение.
Пример 1.4.1. Для
двух двоичных векторов 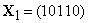 и
и
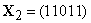 расстояние
Хэмминга
расстояние
Хэмминга  ,
поскольку символы, стоящие на второй, третьей и пятой позиций различаются, а на
первой и четвертой - совпадают. В свою очередь вес Хэмминга для указанных
векторов составляет величину
,
поскольку символы, стоящие на второй, третьей и пятой позиций различаются, а на
первой и четвертой - совпадают. В свою очередь вес Хэмминга для указанных
векторов составляет величину  и
и  .
.
Теорема 1.4.1. Код
исправляет любые ошибки кратности 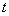 и менее в том и только
в том случае, если кодовое расстояние удовлетворяет неравенству
и менее в том и только
в том случае, если кодовое расстояние удовлетворяет неравенству
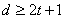 . (*)
. (*)
Доказательство:
Достаточность: Пусть
имеется код 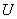 с
кодовым расстоянием
с
кодовым расстоянием 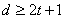 .
Предположим, что произошла ошибка кратности
.
Предположим, что произошла ошибка кратности 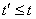 , и что найдутся два
кодовых вектора
, и что найдутся два
кодовых вектора  и
и
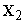 такие,
что
такие,
что
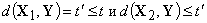 ,
,
а значит, не позволяющие
исправить ошибку кратности  . Однако, как следует из
аксиом расстояния,
. Однако, как следует из
аксиом расстояния,
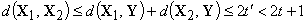 ,
,
что противоречит условию
теоремы. Следовательно, неравенство (*) определяет достаточное условие
исправление ошибок кратности 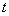 и менее.
и менее.
Необходимость: С
другой стороны, если 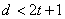 ,
то обязательно возникнет ситуация, при которой произойдет неверное
декодирование. Например, если
,
то обязательно возникнет ситуация, при которой произойдет неверное
декодирование. Например, если 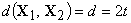 , то существует такой
вектор наблюдения
, то существует такой
вектор наблюдения 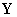 ,
для которого
,
для которого 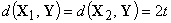 ,
и, следовательно, наблюдается неопределенность в принятии решения. Таким
образом, условие (*) является необходимым.
,
и, следовательно, наблюдается неопределенность в принятии решения. Таким
образом, условие (*) является необходимым.
Полезной иллюстрацией
приведенного доказательства может служить диаграмма, представленная на рис. 1.
На ней изображены сферы Хэмминга радиуса 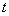 c центром
c центром 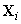 ,
представляющие собой множество точек (векторов), расположенных от
,
представляющие собой множество точек (векторов), расположенных от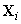 на
расстоянии Хэмминга
на
расстоянии Хэмминга 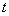 или
ближе. Если все сферы Хэмминга радиуса
или
ближе. Если все сферы Хэмминга радиуса 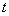 , окружающие кодовые
вектора
, окружающие кодовые
вектора 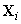 ,
не перекрываются, декодер воспримет любой вектор внутри i-ой сферы, как i-ый
кодовый вектор
,
не перекрываются, декодер воспримет любой вектор внутри i-ой сферы, как i-ый
кодовый вектор 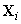 .
Это означает, что любая ошибка кратности
.
Это означает, что любая ошибка кратности 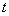 и менее в кодовом слове
будет исправлена. Вместе с тем, при условии исправления любых ошибок кратности
и менее в кодовом слове
будет исправлена. Вместе с тем, при условии исправления любых ошибок кратности 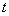 избежать
перекрытия сфер можно только в том случае, если минимальное расстояние Хэмминга
между кодовыми векторами не меньше, чем
избежать
перекрытия сфер можно только в том случае, если минимальное расстояние Хэмминга
между кодовыми векторами не меньше, чем 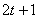 .
.
Из представленной
диаграммы легко увидеть, что обнаружение ошибок кратности 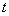 в
принятых векторах возможно тогда, когда выполняется условие
в
принятых векторах возможно тогда, когда выполняется условие
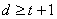 .
.
Из рассмотренного видно,
что основными параметрами блокового кода являются: кодовое расстояние 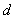 ,
его объем
,
его объем 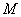 и
длина
и
длина 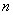 .
Часто при описании характеристик кода вместо объема
.
Часто при описании характеристик кода вместо объема 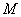 используют
либо число информационных символов в кодовом слове
используют
либо число информационных символов в кодовом слове 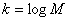 ,
либо скорость кода
,
либо скорость кода 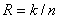 .
Именно с этими параметрами связаны два основных варианта задач, рассматриваемых
теорией кодирования. Первая из них связана с максимизацией
.
Именно с этими параметрами связаны два основных варианта задач, рассматриваемых
теорией кодирования. Первая из них связана с максимизацией 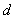 при
заданных значениях
при
заданных значениях 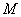 (
(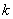 или
или 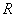 )
и
)
и 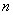 для
достижения хорошей корректирующей способности кода. Дуальной задачей является
максимизация
для
достижения хорошей корректирующей способности кода. Дуальной задачей является
максимизация 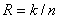 (
( или
или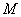 )
при минимуме
)
при минимуме 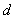 и
длины
и
длины 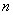 .
.
2. Арифметика и
структура конечных полей Галуа. Многочлены над полями Галуа
.1 Введение в теорию
конечных полей
кодирование программный алгоритм преобразование
Математическое понятие конечного
поля является ключевой категорией теории кодирования, и знакомство с ним начнем
с определения поля.
Полем называется множество элементов, замкнутое относительно двух операций,
называемых сложением и умножением (обозначаемых привычными знаками «+» и «
называется множество элементов, замкнутое относительно двух операций,
называемых сложением и умножением (обозначаемых привычными знаками «+» и «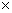 »
(или точкой)). Замкнутость операций означает, что результаты сложения или
умножения также являются элементами поля
»
(или точкой)). Замкнутость операций означает, что результаты сложения или
умножения также являются элементами поля  : если
: если 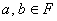 ,
то
,
то 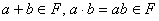 .
.
Операции сложения и
умножения удовлетворяют следующим аксиомам:
. Сложение и умножение
коммутативно:
 ;
;
. Сложение и умножение
ассоциативно:
 ;
;
. Существует нейтральный
элемент по сложению и умножению, не изменяющий значения любого элемента
поля в этих операциях. Нейтральный элемент по сложению называется нулем
и обозначается символом «0», а нейтральный элемент по умножению - единицей
и обозначается как «1»:
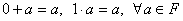 ;
;
4. Для любого элемента  существует
единственный обратный или противоположный по сложению
(обозначаемый, как «
существует
единственный обратный или противоположный по сложению
(обозначаемый, как «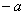 »)
элемент такой, что
»)
элемент такой, что
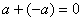 ;
;
. Для любого элемента  (за
исключением 0) существует единственный обратный элемент (обозначаемый, как
(за
исключением 0) существует единственный обратный элемент (обозначаемый, как 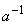 )
по умножению такой, что
)
по умножению такой, что
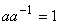 ;
;
. Сложение и умножение
подчиняется дистрибутивному закону:
 .
.
Непосредственно из
вышеприведенных аксиом следует, что в любом поле наряду со сложением определена
операция вычитания, а с умножением - деление:
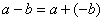 , а для
, а для 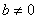 -
-
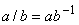 .
.
Простейшими примерами
полей являются числовые поля (поле рациональных и вещественных чисел), имеющих
бесконечной число элементов.
Теория кодирования в
основном оперирует с конечными полями, состоящими из конечного числа
элементов. Общепринятым обозначением конечного поля является 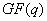 (Galois field - в честь французского математика Эвариста Галуа), где
(Galois field - в честь французского математика Эвариста Галуа), где  -
порядок конечного поля, т.е. число элементов поля. Нетрудно доказать,
что существуют конечные поля только порядка, равного целой степени простого
числа:
-
порядок конечного поля, т.е. число элементов поля. Нетрудно доказать,
что существуют конечные поля только порядка, равного целой степени простого
числа:  ,
где
,
где 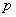 -
простое, а
-
простое, а  -
натуральное числа. Конечное поле простого порядка
-
натуральное числа. Конечное поле простого порядка 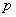 называется
простым полем и обозначается
называется
простым полем и обозначается 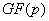 . Любое подобное поле
может трактоваться как множество остатков от деления натуральных чисел на
. Любое подобное поле
может трактоваться как множество остатков от деления натуральных чисел на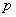
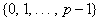 с операциями сложения и умножения по модулю
с операциями сложения и умножения по модулю 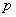 .
.
Расширенные конечные
поля (порядка  ,
где
,
где  )
не могут быть построены на основании арифметики по
)
не могут быть построены на основании арифметики по 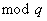 ,
и их более сложная структура будет рассмотрена несколько позже.
,
и их более сложная структура будет рассмотрена несколько позже.
2.2 Векторное
пространство над конечными полями. Линейная зависимость и независимость
Пусть  -
конечное поле, элементы которого будем называть скалярами.
-
конечное поле, элементы которого будем называть скалярами.
Векторным пространством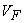 над полем
над полем  называется
множество элементов (векторов), замкнутое относительно двух операций: сложения
векторов и умножения вектора на скаляр, обозначаемых привычными символами «+» и
«•», т.е. если
называется
множество элементов (векторов), замкнутое относительно двух операций: сложения
векторов и умножения вектора на скаляр, обозначаемых привычными символами «+» и
«•», т.е. если  ,
то
,
то 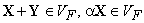 .
.
Операции сложения и
умножения удовлетворяют следующим аксиомам:
. Сложение коммутативно
и ассоциативно:
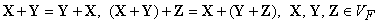 ;
;
. Существует нулевой
(нейтральный) вектор 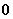 по
сложению, не изменяющий любой вектор, сложенный с ним:
по
сложению, не изменяющий любой вектор, сложенный с ним:
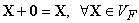 ;
;
3. Для любого вектора
существует единственный противоположный (обратный) вектор  такой,
что:
такой,
что:
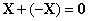 ;
;
. Умножение на скаляр
ассоциативно:
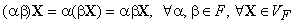 ;
;
. Умножение любого
вектора на единичный скаляр (всегда существующий в  )
не меняет его значения:
)
не меняет его значения:
 ;
;
. Выполняется
дистрибутивный закон
 .
.
Модель векторного
пространства, используемая в теории кодирования, есть ничто иное, как
пространство 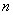 -мерных
векторов (кодовых слов)
-мерных
векторов (кодовых слов) 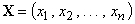 с
компонентами, принадлежащими заданному конечному полю:
с
компонентами, принадлежащими заданному конечному полю: 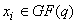 .
Операции с векторами в этом пространстве выполняются по следующим простым правилам:
.
Операции с векторами в этом пространстве выполняются по следующим простым правилам:
 и
и 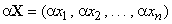 ,
,
где сложение и умножение
скаляров осуществляется в соответствии с правилами поля 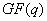 .
Пространство такого типа может содержать до
.
Пространство такого типа может содержать до 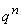 векторов. В двоичном
пространстве
векторов. В двоичном
пространстве 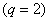 максимальное
число векторов не превосходит величины
максимальное
число векторов не превосходит величины 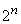 и согласно правилам
поля
и согласно правилам
поля 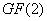
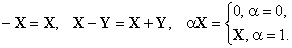
Пусть в пространстве 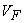 имеется
набор из
имеется
набор из  векторов
векторов
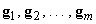 .
Эти вектора называются линейно зависимыми, если хотя один представим в
виде линейной комбинацией других
.
Эти вектора называются линейно зависимыми, если хотя один представим в
виде линейной комбинацией других
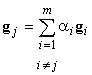 ,
,
где все  -
скалярные коэффициенты. Напротив, если ни один из векторов
-
скалярные коэффициенты. Напротив, если ни один из векторов 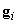 не
является линейной комбинацией других, то вектора называются линейно независимыми.
не
является линейной комбинацией других, то вектора называются линейно независимыми.
Максимальное число
линейно независимых векторов  в данном пространстве
называется размерностью пространства (пространство размерности
в данном пространстве
называется размерностью пространства (пространство размерности  также
называют
также
называют  -мерным).
Любое множество
-мерным).
Любое множество  линейно
независимых векторов в
линейно
независимых векторов в  -мерном
пространстве образует его базис. Если
-мерном
пространстве образует его базис. Если 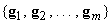 - базис пространства
- базис пространства 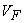 ,
то любой вектор
,
то любой вектор 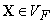 может
быть получен в виде линейной комбинации
может
быть получен в виде линейной комбинации 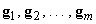 :
:
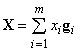 ,
,
где 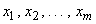 -
компоненты или координаты
-
компоненты или координаты  в
базисе
в
базисе 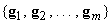 ,
а само выше приведенное соотношение называют представлением
,
а само выше приведенное соотношение называют представлением  в
базисе
в
базисе 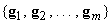 .
.
Если в векторном
пространстве 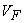 существует
подмножество
существует
подмножество 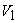 ,
являющееся пространством над полем
,
являющееся пространством над полем  с такими же операциями
сложения векторов и умножения на скаляр, то
с такими же операциями
сложения векторов и умножения на скаляр, то 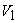 называется подпространством
называется подпространством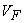
2.3 Арифметика
полиномов, заданных над конечным полем
Рассмотрим полином
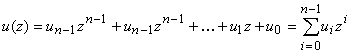 ,
,
в котором коэффициенты 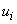 являются
элементами поля
являются
элементами поля 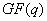 .
.
Введем основные правила
арифметических действий с формальными полиномами, коэффициенты которого
принадлежат полю 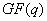 (подобные
полиномы обычно называют полиномами над
(подобные
полиномы обычно называют полиномами над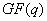 ).
).
1. Суммой
двух полиномов  и
и
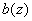 называется
полином, определяемый соотношением:
называется
полином, определяемый соотношением:
 .
.
2. Умножение
полинома  на
скаляр
на
скаляр 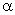 (где
(где
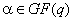 )
осуществляется как
)
осуществляется как
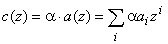 .
.
Установив операции
сложения полиномов и умножения полинома на скаляр, можно сказать, что множество
полиномов 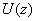 кодовых
слов обладает структурой векторного пространства и для него справедливы
утверждения:
кодовых
слов обладает структурой векторного пространства и для него справедливы
утверждения:
если 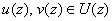 ,
то
,
то  ;
;
если 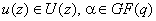 ,
то
,
то 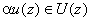 .
.
Рассмотрим некоторые
определения, связанные с полиномами, заданными над конечным полем.
Пусть имеется многочлен  .
.
Приведенным
(или нормированным) полиномом называется полином, старший коэффициент
которого 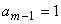 .
.
Нулевым полиномом
называется полином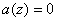 .
.
Степенью
ненулевого полинома  называется
наибольшая степень формальной переменной
называется
наибольшая степень формальной переменной 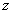 при ненулевом
коэффициенте
при ненулевом
коэффициенте  и
обозначается как
и
обозначается как 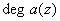 .
.
Важную роль играет операция
умножения полиномов, которая не определена для векторного пространства. Считая,
что для формальных полиномов выполняется обычный дистрибутивный закон и что  ,
произведение полиномов задается соотношением, ничем не отличающимся от обычного
произведения полиномов, изучаемого в школьной алгебре.
,
произведение полиномов задается соотношением, ничем не отличающимся от обычного
произведения полиномов, изучаемого в школьной алгебре.
Если  и
и
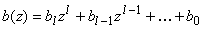 ,
то
,
то
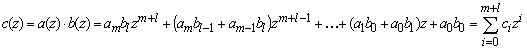 ,
,
где  .
.
В современной алгебре
структура, отличающаяся от поля только отсутствием обратимости ненулевых
элементов, т.е. отсутствием операции деления, называется кольцом.
Очевидно, что множество полиномов над полем 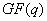 образуют кольцо.
образуют кольцо.
Другим, более известным
примером кольца является множество целых чисел. Однако в кольце целых чисел
операция умножения порождает еще одну, называемую делением с остатком.
Возьмем некоторое положительное целое число 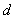 . Тогда любое целое
число
. Тогда любое целое
число 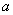 может
быть представлено в виде
может
быть представлено в виде
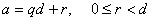 ,
,
где неотрицательное
целое  ,
меньшее
,
меньшее 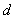 ,
называется остатком (от деления
,
называется остатком (от деления 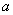 на
на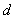 ),
),
 называется
частным от деления,
называется
частным от деления, 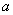 - делимым, а
- делимым, а 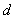 -
делителем.
-
делителем.
Поскольку в кольце
полиномов определена операция умножения, то, поступая аналогично, можно ввести операцию
деления полиномов с остатком. Однако, для полиномов сравнение в терминах
«больше-меньше» невозможно, поэтому для получения остатка сравниваются степени
полиномов. Возьмем полином 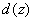 и представим
произвольный полином
и представим
произвольный полином  как
как
 .
.
В данном соотношении,
возможном для любых  и
и
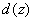 ,
назовем полиномы
,
назовем полиномы  ,
,
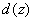 ,
,
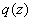 и
и
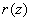 делимым,
делителем, частным и остатком соответственно.
Операция деления полиномов известна под названием алгоритма Евклида.
Определение частного и остатка от деления полиномов осуществляется «в столбик»,
как и при делении целых чисел.
делимым,
делителем, частным и остатком соответственно.
Операция деления полиномов известна под названием алгоритма Евклида.
Определение частного и остатка от деления полиномов осуществляется «в столбик»,
как и при делении целых чисел.
В теории кодирования
особая роль принадлежит остатку от деления, который часто называют вычетом
многочлена  по
модулю многочлена
по
модулю многочлена 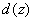 .
Данному определению соответствует запись
.
Данному определению соответствует запись
 ,
,
которая символизирует,
что полиномы  и
и
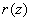 имеют
один и тот же остаток от деления на
имеют
один и тот же остаток от деления на 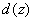 . Действительно,
. Действительно, 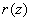 является
остатком от деления
является
остатком от деления  на
на
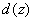 .
С другой стороны, поскольку
.
С другой стороны, поскольку  , то
, то 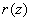 сразу
же является остатком от деления на
сразу
же является остатком от деления на 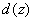 .
.
Если  ,
т.е.
,
т.е. 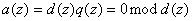 ,
то говорят, что
,
то говорят, что  делится
на
делится
на 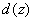 ,
или
,
или 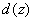 делит
делит ,
или
,
или 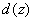 является
множителем
является
множителем .
Используется также выражение, что
.
Используется также выражение, что  раскладывается на
множители меньшей степени.
раскладывается на
множители меньшей степени.
Полином, который не
может быть разложен на множители меньшей степени, называется неприводимым.
Наибольшим общим
делителем двух полиномов  и
и 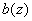 ,
обозначаемым как
,
обозначаемым как 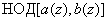 ,
называется приведенный полином наибольшей степени, делящий одновременно оба из
них.
,
называется приведенный полином наибольшей степени, делящий одновременно оба из
них.
Наименьшим общим кратным
двух полиномов  и
и
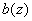 ,
обозначаемым как
,
обозначаемым как  ,
называется приведенный полином наименьшей степени, делящийся на оба из них.
,
называется приведенный полином наименьшей степени, делящийся на оба из них.
Если наибольший общий
делитель двух полиномов равен единицы, т.е. 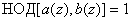 , то они называются взаимно
простыми.
, то они называются взаимно
простыми.
2.4 Расширенные конечные
поля
Теперь у нас есть все
необходимые сведения, чтобы расширить поле 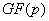 до поля
до поля (
(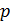
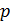 - простое число). Как
уже известно, существуют конечные поля только порядка
- простое число). Как
уже известно, существуют конечные поля только порядка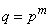 (
(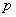 - простое,
- простое,  -
натуральное числа). Простое поле
-
натуральное числа). Простое поле 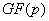 порядка
порядка 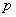 может
трактоваться как множество остатков от деления целых чисел на
может
трактоваться как множество остатков от деления целых чисел на 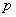 :
:
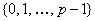 с
операциями сложения и умножения по модулю
с
операциями сложения и умножения по модулю 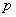 . Аналогичным образом
расширенное поле
. Аналогичным образом
расширенное поле  порядка
порядка
 ,
может трактоваться как множество остатков от деления полиномов над
,
может трактоваться как множество остатков от деления полиномов над 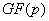 на
некоторый неприводимый полином
на
некоторый неприводимый полином 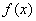 степени
степени  с
операциями сложения и умножения по модулю
с
операциями сложения и умножения по модулю 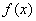 . Другими словами, поле
. Другими словами, поле  содержит
все полиномы над полем
содержит
все полиномы над полем 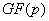 степени
не выше
степени
не выше 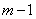 с
общепринятыми операциями сложения и умножением, осуществляемым в два этапа -
вначале производится обычное умножение полиномов, а затем удерживается только
остаток от деления полученного произведения на полином
с
общепринятыми операциями сложения и умножением, осуществляемым в два этапа -
вначале производится обычное умножение полиномов, а затем удерживается только
остаток от деления полученного произведения на полином 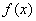 .
.
Отметим, что среди
полиномов степени не выше 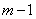 присутствуют
и полиномы нулевой степени, т.е. элементы простого поля
присутствуют
и полиномы нулевой степени, т.е. элементы простого поля 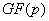 ,
сложение и умножение которых, осуществляются по правилам
,
сложение и умножение которых, осуществляются по правилам 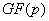 .
Это означает, что простое поле
.
Это означает, что простое поле 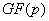 полностью содержится в
расширенном
полностью содержится в
расширенном  ,
или, другими словами,
,
или, другими словами, 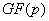 является
подполем
является
подполем .
Для поля
.
Для поля  порядок
его простого подполя
порядок
его простого подполя 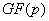 называется
характеристикой поля
называется
характеристикой поля  . Например, любое
расширенное поле
. Например, любое
расширенное поле  является
полем характеристики 2, вследствие чего вычисление коэффициентов полиномов,
рассматриваемых как элементы поля
является
полем характеристики 2, вследствие чего вычисление коэффициентов полиномов,
рассматриваемых как элементы поля  , осуществляется по
модулю два. В частности, для любого
, осуществляется по
модулю два. В частности, для любого 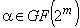 ,
, ,
поскольку
,
поскольку 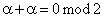 .
.
2.5 Мультипликативный
порядок элементов поля. Примитивные элементы. Другой подход к построению
расширения поля Галуа
В любом поле 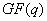 ,
является ли оно простым или расширенным, определена операция
,
является ли оно простым или расширенным, определена операция 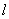 -кратного
умножения элемента
-кратного
умножения элемента 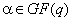 .
Естественно назвать такое произведение
.
Естественно назвать такое произведение 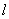 -ой степенью элемента
-ой степенью элемента 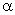 ,
обозначив его как
,
обозначив его как
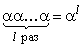 .
.
Тогда
 ,
,
и для любого ненулевого 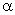
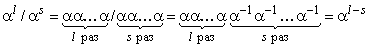 .
.
Следовательно, в
конечных полях действуют те же самые правила обращения с целочисленными
степенями элементов, что и в обычной арифметике.
Возьмем некоторый
ненулевой элемент 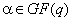 и
рассмотрим его степени вида
и
рассмотрим его степени вида 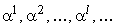 . Поскольку все они
являются элементами поля
. Поскольку все они
являются элементами поля 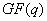 ,
то вследствие его конечности лишь ограниченное число подобных степеней будет
различными, т.е. для некоторых
,
то вследствие его конечности лишь ограниченное число подобных степеней будет
различными, т.е. для некоторых 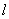 и
и 
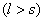 будет справедливо
будет справедливо 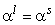 ,
а значит,
,
а значит, 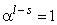 .
Назовем минимальное натуральное число
.
Назовем минимальное натуральное число 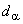 , для которого
, для которого
 ,
,
мультипликативным
порядком элемента 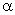 .
Очевидно, что только единичный элемент любого конечного поля обладает
мультипликативным порядком, равным единице, т.е.
.
Очевидно, что только единичный элемент любого конечного поля обладает
мультипликативным порядком, равным единице, т.е.  .
.
Следующая теорема,
приводимая без доказательства, утверждает, что значения мультипликативных
порядков элементов поля подчиняются достаточно строгому ограничению.
Теорема 2.5.1. Мультипликативный
порядок любого ненулевого элемента 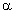 поля
поля 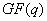 делит
делит
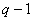 ,
т.е. число ненулевых элементов поля
,
т.е. число ненулевых элементов поля 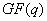 .
.
Элемент  поля
поля
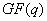 ,
имеющий максимальный мультипликативный порядок
,
имеющий максимальный мультипликативный порядок 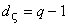 , называется примитивным
элементом поля.
, называется примитивным
элементом поля.
В любом конечном поле 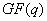 всегда
существует хотя бы один примитивный элемент
всегда
существует хотя бы один примитивный элемент  . Отличительной
особенностью данного элемента является то, что все его
. Отличительной
особенностью данного элемента является то, что все его 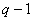 последовательных
степеней
последовательных
степеней 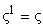 ,
,
 различны
и пробегают все ненулевые элементы поля
различны
и пробегают все ненулевые элементы поля 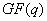 .
.
Утверждение 2.5.1. Если
мультипликативный порядок элемента  равен
равен 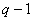 ,
то порядок элемента
,
то порядок элемента 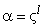 определяется
как
определяется
как
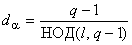 ,
,
где 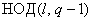 -
наибольший общий делитель
-
наибольший общий делитель 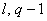 .
.
Утверждение 2.5.2. В
любом поле 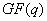 содержится
содержится
 примитивных
элементов, где
примитивных
элементов, где 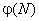 -
функция Эйлера, указывающая число целых чисел из диапазона от 1 до
-
функция Эйлера, указывающая число целых чисел из диапазона от 1 до 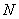 ,
взаимно простых с
,
взаимно простых с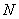 .
.
Расширенное поле,
построенное как множество полиномов по модулю некоторого неприводимого
полинома, всегда содержит в качестве элемента поля полином 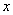 .
Если окажется, что
.
Если окажется, что 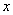 -
примитивный элемент, то соответствующий неприводимый полином называется примитивным
полиномом. Примитивные полиномы произвольной степени
-
примитивный элемент, то соответствующий неприводимый полином называется примитивным
полиномом. Примитивные полиномы произвольной степени  определены
над любым конечным полем. Они являются полезным инструментом для построения
расширенных полей, поскольку позволяют реализовать очень простой вариант
таблицы умножения элементов поля. Действительно, любые ненулевые элементы
определены
над любым конечным полем. Они являются полезным инструментом для построения
расширенных полей, поскольку позволяют реализовать очень простой вариант
таблицы умножения элементов поля. Действительно, любые ненулевые элементы 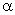 и
и
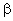 расширенного
поля
расширенного
поля 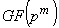 могут
быть выражены как некоторые
могут
быть выражены как некоторые 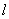 -я и
-я и  -я
степени примитивного элемента
-я
степени примитивного элемента  :
: 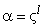 ,
,
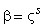 .
Тогда
.
Тогда 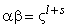 и,
значит, таблица умножения двух элементов поля
и,
значит, таблица умножения двух элементов поля 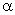 и
и 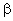 представляет
собой ни что иное, как все не нулевые степени примитивного элемента.
представляет
собой ни что иное, как все не нулевые степени примитивного элемента.
Таким образом,
построение расширенного поля 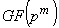 в виде степеней
примитивного элемента предполагает следующий алгоритм действий. На первом этапе
выбирается некоторый примитивный полином степени
в виде степеней
примитивного элемента предполагает следующий алгоритм действий. На первом этапе
выбирается некоторый примитивный полином степени  над основным полем
над основным полем 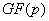 ,
которые содержатся в специальных таблицах:
,
которые содержатся в специальных таблицах:  . Тогда
. Тогда  -я
степень
-я
степень 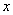 по
модулю
по
модулю 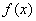 определится
как
определится
как 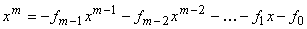 .
Предположение о примитивности
.
Предположение о примитивности 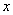 позволяет задать
позволяет задать  в
виде
в
виде 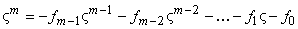 .
Отсюда
.
Отсюда
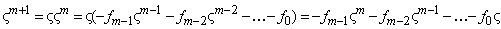 .
.
Учитывая, что 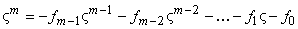 и
подставляя его в последнее соотношение, получаем в явном виде выражение для
и
подставляя его в последнее соотношение, получаем в явном виде выражение для 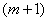 -й
степени
-й
степени  .
Последовательное возведение в степень
.
Последовательное возведение в степень  позволяет, таким образом,
определить все ненулевые элементы расширенного поля в виде линейной комбинации
первых
позволяет, таким образом,
определить все ненулевые элементы расширенного поля в виде линейной комбинации
первых  степеней
степеней
 :
:
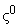 ,
,
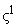 ,
…,
,
…,  с
коэффициентами из основного поля
с
коэффициентами из основного поля 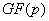 .
.
2.6 Некоторые свойства
расширенных конечных полей
Теорема 2.6.1. Среди
всех элементов расширенного поля  только для элементов
основного подполя
только для элементов
основного подполя 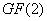 ,
т.е. для 0 и 1, выполняется соотношение
,
т.е. для 0 и 1, выполняется соотношение
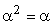 .
.
Доказательство: Справедливость
указанного соотношения для нулевого элемента поля очевидна. Среди всех
ненулевых элементов поля мультипликативный порядок, равный единице, имеет лишь 1, что и завершает
доказательство теоремы.
мультипликативный порядок, равный единице, имеет лишь 1, что и завершает
доказательство теоремы.
Теорема 2.6.2. Пусть
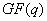 -
конечной поле характеристики
-
конечной поле характеристики  . Тогда для любых
элементов
. Тогда для любых
элементов 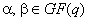 ,
,
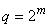 ,
выполняется соотношение
,
выполняется соотношение
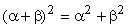 .
.
Доказательство: Поскольку
поле 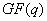 имеет
характеристику, равную 2, то сомножитель
имеет
характеристику, равную 2, то сомножитель 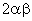 в разложении бинома
обращается в нуль. Следовательно
в разложении бинома
обращается в нуль. Следовательно
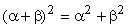 .
.
Данная теорема может
быть обобщена на случай любого натурального 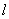 и произвольного числа
и произвольного числа  элементов
элементов
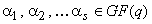 :
:
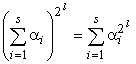 .
.
Познакомимся теперь с
еще одним важным определением.
Пусть 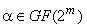 .
Тогда элементы поля
.
Тогда элементы поля  вида
вида
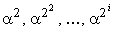
называются 2 -
сопряженными с элементом 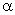 .
.
Вследствие конечности
поля  последовательность,
составленная из
последовательность,
составленная из 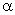 и
2 - сопряженных с ним элементов, имеет ограниченный набор отличающихся друг от
друга элементов. Так, если все элементы вида
и
2 - сопряженных с ним элементов, имеет ограниченный набор отличающихся друг от
друга элементов. Так, если все элементы вида

различны, а продолжение
последовательности приводит к повторению какого-либо уже содержащегося в ней
элемента, то
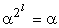 .
.
Можно доказать, что
длина 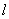 любой
последовательности (цикла) 2-сопряженных элементов поля
любой
последовательности (цикла) 2-сопряженных элементов поля  всегда
делит степень расширения
всегда
делит степень расширения  .
.
Следует отметить, что
приведенные выше результаты могут быть обобщены на случай расширения любого
недвоичного основного поля 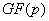 .
.
3. Линейные блоковые
коды
3.1 Линейные коды
Рассмотрим множество 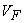 ,
состоящее из
,
состоящее из 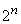 всех
возможных
всех
возможных 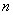 -компонентных
векторов
-компонентных
векторов 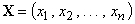 ,
элементы которого
,
элементы которого 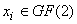 .
Очевидно, что
.
Очевидно, что 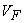 образует
образует
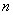 -мерное
векторное пространство. Выберем в этом пространстве
-мерное
векторное пространство. Выберем в этом пространстве  линейно
независимых векторов
линейно
независимых векторов 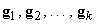 ,
что всегда возможно, поскольку в
,
что всегда возможно, поскольку в 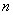 -мерном пространстве
всегда существуют
-мерном пространстве
всегда существуют 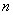 линейно
независимых векторов. Построим множество
линейно
независимых векторов. Построим множество 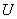 , содержащее
, содержащее 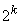 векторов,
образованных как линейная комбинация
векторов,
образованных как линейная комбинация  вида:
вида:
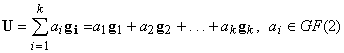 .
.
Непосредственной
проверкой легко убедиться, что множество 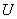 замкнуто по сложению
векторов и умножению их на скаляр из
замкнуто по сложению
векторов и умножению их на скаляр из 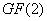 , и, следовательно,
, и, следовательно, 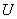 является
векторным пространством, т.е. подпространством
является
векторным пространством, т.е. подпространством 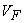 . Это подпространство
имеет размерность
. Это подпространство
имеет размерность 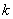 и
непосредственно является той конструкцией, которую назовем линейным кодом.
и
непосредственно является той конструкцией, которую назовем линейным кодом.
Двоичным  линейным
кодом является любое
линейным
кодом является любое 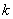 -мерное подпространство
пространства векторов длины
-мерное подпространство
пространства векторов длины 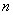 .
.
Поскольку
подпространство содержит  кодовых
слов, то
кодовых
слов, то 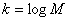 есть
ни что иное, как число информационных символов, переносимых кодом, а
есть
ни что иное, как число информационных символов, переносимых кодом, а 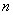 -
длина кода. Наряду с обозначением кода как
-
длина кода. Наряду с обозначением кода как  код, встречается и
другое, в котором используется еще один его параметр - кодовое расстояние:
код, встречается и
другое, в котором используется еще один его параметр - кодовое расстояние: 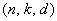 .
.
3.2 Определение
циклического кода. Порождающий полином
Циклические коды
являются подклассом линейных кодов, удовлетворяющие дополнительному
структурному требованию. В силу этого требования поиск хороших помехоустойчивых
кодов оказался наиболее продуктивным. При этом в качестве математического аппарата
используется теория полей Галуа. Вне класса циклических кодов теория полей
Галуа не столь эффективна.
Важность циклических
кодов обусловлена также тем, что заложенные в основу их построения идеи теории
конечных полей приводят к процедурам кодирования и декодирования, эффективным
как с алгоритмической, так и вычислительной точек зрения.
Линейный блоковый код 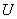 длины
длины
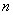 называется
циклическим, если наряду с любым своим кодовым словом
называется
циклическим, если наряду с любым своим кодовым словом  он
содержит также циклический сдвиг
он
содержит также циклический сдвиг  этого слова. Иными
словами, циклический код содержит все циклические сдвиги всех своих кодовых
слов.
этого слова. Иными
словами, циклический код содержит все циклические сдвиги всех своих кодовых
слов.
Лемма 3.2.1. Пусть
некоторому слову  циклического
кода
циклического
кода 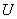 сопоставлен
полином
сопоставлен
полином 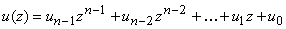 .
Тогда его циклическому сдвигу
.
Тогда его циклическому сдвигу  будет соответствовать
полином
будет соответствовать
полином 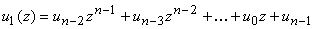 ,
являющийся вычетом полинома
,
являющийся вычетом полинома 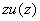 по модулю бинома
по модулю бинома  ,
т.е.
,
т.е. 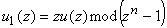 .
.
Доказательство:
Добавим и вычтем  в
соотношении для
в
соотношении для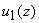 и сгруппируем его слагаемые следующим образом
и сгруппируем его слагаемые следующим образом
 .
.
Откуда непосредственно
следует утверждение леммы 3.2.1.
На основании леммы
3.2.1. не составляет труда показать, что 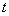 -кратному циклическому
сдвигу
-кратному циклическому
сдвигу 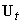 слова
слова
 будет
соответствовать полином
будет
соответствовать полином  ,
определяемый как
,
определяемый как
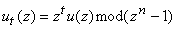 . (**)
. (**)
Лемма 3.2.2. Если
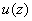 -
кодовый полином слова
-
кодовый полином слова 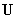 циклического
кода
циклического
кода 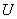 ,
то для произвольного полинома
,
то для произвольного полинома  вычет произведения
вычет произведения 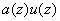 по
модулю биномa
по
модулю биномa также является кодовым
полиномом.
также является кодовым
полиномом.
Доказательство:
Пусть  ,
где
,
где 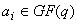 .
Тогда
.
Тогда
 .
.
Отсюда на основании
леммы 3.2.1, ясно, что каждое слагаемое последнего выражения является кодовым
полиномом, отвечающим некоторому циклическому сдвигу исходного слова 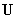 .
Учитывая же свойства линейного подпространства, т.е. тот факт, что умножение на
скаляр и сложение кодовых слов вновь дают кодовое слово, следует, что вычет
.
Учитывая же свойства линейного подпространства, т.е. тот факт, что умножение на
скаляр и сложение кодовых слов вновь дают кодовое слово, следует, что вычет 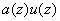 по
модулю
по
модулю  также
соответствует кодовому слову.
также
соответствует кодовому слову.
Следствие. Если
степень полинома  удовлетворяет
неравенству
удовлетворяет
неравенству
 ,
,
то само произведение 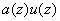 отвечает
полиному некоторого слова циклического кода.
отвечает
полиному некоторого слова циклического кода.
Рассмотрим множество
полиномов 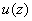 ,
образующих циклический код
,
образующих циклический код 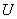 и найдем среди них
ненулевой полином наименьшей степени.
и найдем среди них
ненулевой полином наименьшей степени.
Ненулевой нормированный
кодовый полином  циклического
кода
циклического
кода 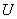 наименьшей
степени называется порождающим многочленом циклического кода.
наименьшей
степени называется порождающим многочленом циклического кода.
Следовательно, если  ,
то
,
то
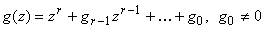 .
.
Теорема 3.2.1. Любой
кодовый полином 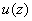 циклического
кода
циклического
кода 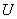 делится
без остатка на порождающий многочлен
делится
без остатка на порождающий многочлен  этого кода, т.е.
этого кода, т.е. 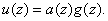
Доказательство:
Предположим противное, т.е. что существует некоторый кодовый многочлен, который
представим в виде
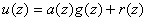 ,
,
где 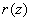 остаток
от деления
остаток
от деления 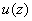 на
на .
.
Так как 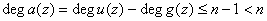 ,
то, согласно следствию из леммы 3.2.2, многочлен
,
то, согласно следствию из леммы 3.2.2, многочлен  является кодовым.
Тогда, с учетом линейности кода,
является кодовым.
Тогда, с учетом линейности кода, 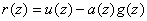 также является кодовым
многочленом. Но поскольку
также является кодовым
многочленом. Но поскольку  ,
то в циклическом коде
,
то в циклическом коде 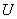 содержится
кодовый полином, имеющий меньшую степень, чем порождающий, что противоречит
определению порождающего полинома, а значит, наше предположение неверно, и
порождающий многочлен делит без остатка любой кодовый полином, т.е.
содержится
кодовый полином, имеющий меньшую степень, чем порождающий, что противоречит
определению порождающего полинома, а значит, наше предположение неверно, и
порождающий многочлен делит без остатка любой кодовый полином, т.е.  .
.
Таким образом, любой
кодовый полином циклического кода 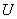 может быть представлен
в виде произведения
может быть представлен
в виде произведения
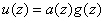 ,
,
в котором  -
порождающий многочлен, а
-
порождающий многочлен, а  -
некоторый информационный полином. Иными словами, отличие всех кодовых полиномов
-
некоторый информационный полином. Иными словами, отличие всех кодовых полиномов
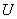 друг
от друга определяется только информационными полиномами. Поскольку
друг
от друга определяется только информационными полиномами. Поскольку
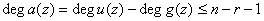 ,
,
то для двоичных кодов
может существовать 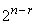 различных
информационных полиномов
различных
информационных полиномов  ,
т.е.
,
т.е.  различных
кодовых слов. Отсюда число информационных символов в каждом кодовом слове
различных
кодовых слов. Отсюда число информационных символов в каждом кодовом слове 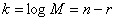 ,
и, значит,
,
и, значит, 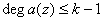 ,
тогда как степень порождающего многочлена
,
тогда как степень порождающего многочлена

соответствует числу
проверочных символов.
Порождающий многочлен  циклического
кода
циклического
кода 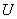 обладает
характерными чертами, которые устанавливается следующей теоремой.
обладает
характерными чертами, которые устанавливается следующей теоремой.
Теорема 3.2.2. Порождающий
многочлен  циклического
кода
циклического
кода 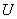 длины
длины
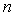 обязательно
делит бином
обязательно
делит бином  .
.
Доказательство:
Из леммы 3.2.1 следует, что вычет из произведения 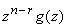 по
модулю
по
модулю  является
кодовым полиномом. Учитывая, что
является
кодовым полиномом. Учитывая, что  , то
, то
 ,
,
и значит, как кодовый
полином, делится без остатка на . Следовательно, и
. Следовательно, и  делится
на
делится
на  .
.
3.3 Систематический
циклический код
Построение кодового
полинома путем перемножения информационного и порождающего полиномов приводит к
не систематическому кодовому слову, в котором отсутствует явное разделение
информационных и проверочных символов.
Для того чтобы прийти к
систематической форме кодового слова необходимо осуществить некоторое
согласование между информационным и кодовым полиномами. Пусть  -
информационный полином, а
-
информационный полином, а 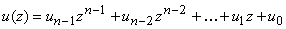 -
кодовый. Систематическое правило кодирование предполагает получение кодового
полинома в таком виде, чтобы коэффициенты при старших степенях полинома
-
кодовый. Систематическое правило кодирование предполагает получение кодового
полинома в таком виде, чтобы коэффициенты при старших степенях полинома 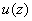 соответствовали
информационным символам. Данное требование достигается путем умножения
информационно полинома на многочлен
соответствовали
информационным символам. Данное требование достигается путем умножения
информационно полинома на многочлен 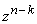 :
:
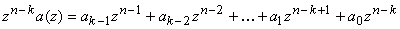 ,
,
что эквивалентно сдвигу
информационного слова на 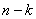 позиций вправо и добавления слева
аналогично числа нулей.
позиций вправо и добавления слева
аналогично числа нулей.
Поскольку любой кодовый
полином 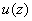 должен
делиться на порождающий полином
должен
делиться на порождающий полином  , из последнего
соотношения необходимо вычесть остаток
, из последнего
соотношения необходимо вычесть остаток 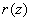 , получаемый в
результате деления
, получаемый в
результате деления  на
на
 ,
т.е.
,
т.е. 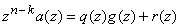 .
В итоге, кодовое слово в систематической форме представимо в виде
.
В итоге, кодовое слово в систематической форме представимо в виде
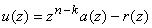 .
.
3.4 Коды Рида-Соломона
Остановимся здесь на
важном частном случае циклического кода - коде Рида-Соломона (РС).
Коды РС являются
недвоичными циклическими кодами, символы кодовых слов которых берутся из
конечного поля 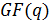
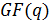 . Здесь
. Здесь 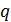
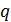 степень некоторого
простого числа,
степень некоторого
простого числа, 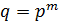
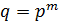 ,
, 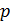
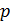 -простое.
-простое.
Кодовые слова РС-кода
отображаются в виде многочленов
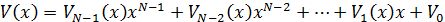
где 
 - длина кода;
- длина кода; 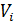
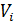 -
- 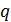
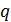 -ичные коэффициенты
(символы кодовых слов), которые могут принимать любое значение из
-ичные коэффициенты
(символы кодовых слов), которые могут принимать любое значение из 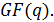
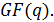 Коды РС являются
максимальными, т.к. при длине кода
Коды РС являются
максимальными, т.к. при длине кода 
 и информационной
последовательности
и информационной
последовательности 
 они обладают наибольшим
кодовым расстоянием
они обладают наибольшим
кодовым расстоянием 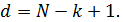
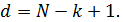
Порождающим многочленом 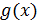
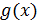 РС-кода является
делитель двучлена xN+1 степени меньшей
РС-кода является
делитель двучлена xN+1 степени меньшей 
 с коэффициентами из
с коэффициентами из 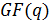
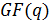 при условии, что
элементы
при условии, что
элементы 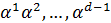
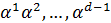 этого поля являются
корнями
этого поля являются
корнями 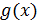
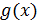 . Здесь
. Здесь 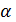
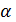 - примитивный элемент
- примитивный элемент 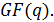
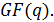
На основе этого
определения, а также теоремы Безу, выражение для порождающего многочлена
РС-кода будет иметь вид
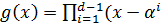
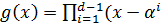 )
)

В РС-кодах
принадлежность кодовых слов данному коду определяется выполнением d-1 уравнений
в соответствии с выражением,

где 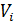
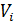 - символы-коэффициенты
из
- символы-коэффициенты
из 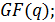
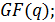 0,
z1… zN-1 - ненулевые элементы
0,
z1… zN-1 - ненулевые элементы 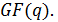
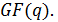
Элементы z0,
z1… zN-1 называются локаторами, т.е. указывающими
на номер позиции символа кодового слова. Например, указателем 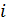
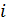 - позиции является
локатор
- позиции является
локатор 
 или элемент i
или элемент i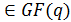
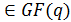 . Так как все локаторы
должны быть различны и причем ненулевыми, то их число в
. Так как все локаторы
должны быть различны и причем ненулевыми, то их число в 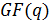
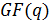 равно
равно 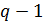
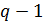 . Следовательно, такое
количество символов должно быть в кодовых словах кода. Поэтому обычно длина
РС-кода определяется из выражения
. Следовательно, такое
количество символов должно быть в кодовых словах кода. Поэтому обычно длина
РС-кода определяется из выражения 
 .
.
Приведем основные
свойства РС-кодов.
. Циклический
сдвиг кодовых слов, символы которых принимают значение из 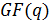
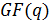 , порождает новые
кодовые слова этого же кода.
, порождает новые
кодовые слова этого же кода.
. Сумма по 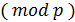
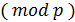 двух и более кодовых
слов дает кодовое слово, принадлежащее этому же коду.
двух и более кодовых
слов дает кодовое слово, принадлежащее этому же коду.
. В РС-коде,
исправляющем tu ошибок, порождающий многочлен определяется из
выражения. 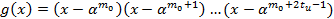
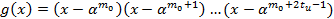
Обычно m0 принимают
равным 1. Однако, с помощью разумного выбора значения m0, иногда
можно упростить схему кодера.
4. Спектральное описание
циклических кодов
.1 Дискретное
преобразование Фурье
В данном разделе мы
рассмотрим один из способов описания циклических кодов, основанный на
использовании дискретного преобразования Фурье (ДПФ) кодовых
последовательностей, заданных над конечным полем 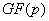 . Данный подход
позволяет в ряде случаев найти альтернативные методы кодирования и
декодирования циклических кодов.
. Данный подход
позволяет в ряде случаев найти альтернативные методы кодирования и
декодирования циклических кодов.
В поле комплексных чисел
ДПФ вектора 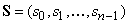 с
комплексными компонентами определяется как вектор
с
комплексными компонентами определяется как вектор  ,
компоненты которого вычисляются согласно соотношению
,
компоненты которого вычисляются согласно соотношению
 .
.
Ядром преобразования
Фурье является 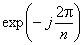 ,
которое является корнем n-й
степени из единицы в поле комплексных чисел. В конечном поле
,
которое является корнем n-й
степени из единицы в поле комплексных чисел. В конечном поле  элемент
элемент
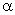 порядка
порядка
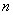 также
является корнем n-й степени из
единицы. Тогда, проводя аналогию между
также
является корнем n-й степени из
единицы. Тогда, проводя аналогию между 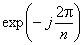 и
и 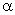 ,
можно ввести следующее определение.
,
можно ввести следующее определение.
Пусть 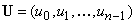 -
вектор над
-
вектор над 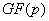 ,
где n делит
,
где n делит 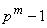 при
некотором m и пусть
при
некотором m и пусть 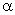 -
элемент мультипликативного порядка n
в расширенном поле
-
элемент мультипликативного порядка n
в расширенном поле  .
Тогда ДПФ над полем
.
Тогда ДПФ над полем 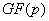 вектора
вектора
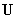 является
вектор
является
вектор  с
элементами
с
элементами 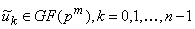 ,
задаваемыми равенствами
,
задаваемыми равенствами
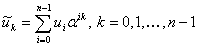 ,
,
или в матричном
представлении
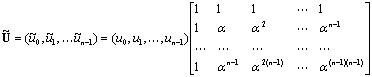 .
.
Учитывая ранее указанную
аналогию, дискретный индекс i
естественно назвать дискретным временем, а вектор 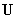 -
временной функцией (последовательностью) или сигналом.
Аналогично, индекс k
можно назвать дискретной частотой, а вектор
-
временной функцией (последовательностью) или сигналом.
Аналогично, индекс k
можно назвать дискретной частотой, а вектор 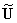 -
частотной функцией (последовательностью) или спектром.
-
частотной функцией (последовательностью) или спектром.
 называется ядром
преобразования, а матрица в правой части равенства - матрицей Фурье.
называется ядром
преобразования, а матрица в правой части равенства - матрицей Фурье.
Если спектр определяется
прямым ДПФ, то с помощью обратного ДПФ по спектру может быть определен сам
сигнал, т.е. компоненты вектора 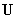
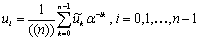 .
.
Следует также отметить,
что если ДПФ 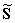 вещественнозначной
временной функции
вещественнозначной
временной функции 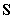 является
комплексным, то аналогично при преобразовании в поле Галуа временной функции
является
комплексным, то аналогично при преобразовании в поле Галуа временной функции 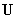 ,
элементы которой принадлежат полю
,
элементы которой принадлежат полю 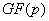 , ее спектр
, ее спектр 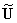 лежит
в расширенном поле
лежит
в расширенном поле  .
.
Преобразование Фурье
обладает рядом замечательных свойств, которые переносятся и на случай
преобразования в конечных полях.
Теорема 4.1.1. (Теорема
о свертке) Пусть 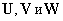 -
временные последовательности, причем
-
временные последовательности, причем 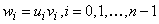 . Тогда компоненты ДПФ
. Тогда компоненты ДПФ 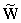 могут
быть определены как
могут
быть определены как
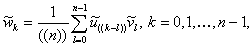
где двойные скобки
означают, что индекс вычисляется в арифметике по модулю n.
Доказательство:
Вычислим преобразование Фурье вектора 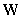 с компонентами вида
с компонентами вида 
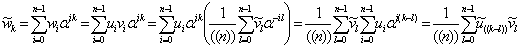 .
.
Можно сформулировать и
обратную теорему, поменяв местами временную и частотную области.
Теорема 4.1.2. Пусть
 -
частотные последовательности, причем
-
частотные последовательности, причем 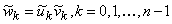 . Тогда компоненты
вектора
. Тогда компоненты
вектора 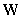 могут
быть определены как
могут
быть определены как
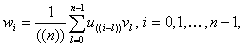
где двойные скобки
означают, что индекс вычисляется в арифметике по модулю n.
Отметим также, что выбор
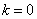 в
теореме о свертке приводит к формуле типа равенства Парсеваля
в
теореме о свертке приводит к формуле типа равенства Парсеваля
 .
.
Замечание.
Основываясь на этом свойстве ДПФ, возможен альтернативный вариант описания
циклических кодов. Любое кодовое слово циклического кода может быть
представлено в несистематическом виде как
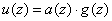 ,
,
где  -
информационный, а
-
информационный, а  -
проверочный полиномы. Во временной области коэффициенты кодового полинома
определяются циклической сверткой коэффициентов информационного и порождающего
полиномов
-
проверочный полиномы. Во временной области коэффициенты кодового полинома
определяются циклической сверткой коэффициентов информационного и порождающего
полиномов
 ,
,
так что в частотной
области, согласно теореме 4.1.2, операция кодирования может быть осуществлена
покомпонентным перемножением спектров 
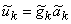
и последующим
вычислением обратного ДПФ для спектра кодового слова.
Теорема 4.1.3. (Свойство
сдвига) Если последовательности  и
и 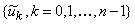 являются
парой преобразования Фурье, то парами преобразований Фурье являются также
являются
парой преобразования Фурье, то парами преобразований Фурье являются также 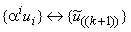 и
и
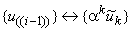 .
.
Доказательство
осуществляется непосредственной подстановкой.
В том случае, когда
кодовому вектору 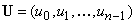 сопоставляется
полином
сопоставляется
полином 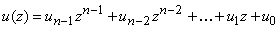 ,
он может быть преобразован в полином
,
он может быть преобразован в полином 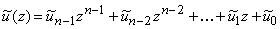 , коэффициенты которого
отвечают спектральным компонентам ДПФ в поле Галуа вектора
, коэффициенты которого
отвечают спектральным компонентам ДПФ в поле Галуа вектора 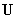 ,
а сам полином называется спектральным (или ассоциированным) с
,
а сам полином называется спектральным (или ассоциированным) с 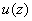 многочленом.
Следующая теорема устанавливает, что свойства спектра тесно связана с корнями
многочленов.
многочленом.
Следующая теорема устанавливает, что свойства спектра тесно связана с корнями
многочленов.
Теорема 4.1.4.
(i). Элемент  является корнем
полинома
является корнем
полинома 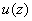 тогда
и только тогда, когда k-й
частотный компонент
тогда
и только тогда, когда k-й
частотный компонент 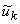 равен
нулю.
равен
нулю.
(ii). Элемент  является корнем
многочлена
является корнем
многочлена 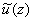 тогда
и только тогда, когда i-й
временной компонент
тогда
и только тогда, когда i-й
временной компонент 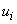 равен
нулю.
равен
нулю.
Доказательство
утверждения (i) очевидно, поскольку из непосредственной подстановки корня в
полином 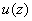 имеем
имеем
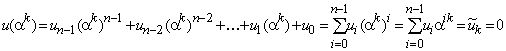 .
.
Аналогичным образом
доказывается и утверждение (ii).
На основании приведенной
теоремы можно сделать следующее заключение. Поскольку любой кодовый многочлен
содержит в качестве множителя порождающий многочлен, то корни порождающего
полинома являются и корнями кодового. Тогда, согласно теореме 4.1.4, корням
порождающего многочлена 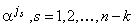 будут
соответствовать нулевые спектральные компоненты кодовых слов на позициях
будут
соответствовать нулевые спектральные компоненты кодовых слов на позициях 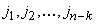 .
Следовательно, можно дать следующее альтернативное определение циклического
кода. Циклическим кодом
.
Следовательно, можно дать следующее альтернативное определение циклического
кода. Циклическим кодом 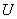 называется
множество таких слов над конечным полем
называется
множество таких слов над конечным полем 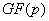 , у которых все
спектральные компоненты, принадлежащие заданному множеству т.н. проверочных
частот
, у которых все
спектральные компоненты, принадлежащие заданному множеству т.н. проверочных
частот 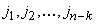 равны
нулю
равны
нулю
Кодовое слово кода Р-С
длины 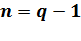
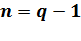 и его спектр лежат в
одном поле
и его спектр лежат в
одном поле 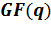
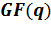 .Кодирование кода
Рида-Соломона в частной области можно осуществить следующим образом: какие либо
.Кодирование кода
Рида-Соломона в частной области можно осуществить следующим образом: какие либо
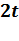
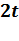 последовательных
координат полагаются равными нулю, в остальных
последовательных
координат полагаются равными нулю, в остальных 
 координатах
записываются информационные символы. Например, информационный вектор может быть
такой:
координатах
записываются информационные символы. Например, информационный вектор может быть
такой: 
 .Кодовый
вектор, соответствующий информационному вектору, определяется как ДПФ вектора
.Кодовый
вектор, соответствующий информационному вектору, определяется как ДПФ вектора 
 с ядром α.
Координаты кодового вектора задаются по правилу
с ядром α.
Координаты кодового вектора задаются по правилу
 так как каждая
компонента
так как каждая
компонента 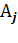
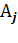 вычисляется как значение
многочлена a(x) в точке
вычисляется как значение
многочлена a(x) в точке 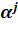
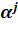 :
: 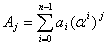 .
Если a(x) - многочлен из информационной области, A(x) - многочлен из кодовой области, тогда дискретное преобразование
Фурье с ядром α (прямое) переводит многочлен из информационной области в кодовую, а
дискретное преобразование Фурье с ядром
.
Если a(x) - многочлен из информационной области, A(x) - многочлен из кодовой области, тогда дискретное преобразование
Фурье с ядром α (прямое) переводит многочлен из информационной области в кодовую, а
дискретное преобразование Фурье с ядром 
 (обратное) переводит
многочлен из кодовой области в информационную а(х)
(обратное) переводит
многочлен из кодовой области в информационную а(х) 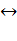
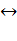 А(х),
А(х), 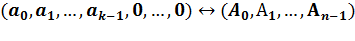
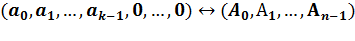 .
.
4.2 Китайская теорема об
остатках
Рассмотрим более
детально формулу (4.1), задающую ДПФ над полем  . Например, для того,
чтобы вычислить ДПФ над полем
. Например, для того,
чтобы вычислить ДПФ над полем  вектора длины
вектора длины
 , требуется
, требуется 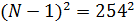
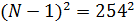 умножений в поле. Как
известно, умножение является одной из наиболее затратных по времени операций, т.е.
алгоритм ДПФ имеет сложность порядка O(
умножений в поле. Как
известно, умножение является одной из наиболее затратных по времени операций, т.е.
алгоритм ДПФ имеет сложность порядка O(
 . Известные алгоритмы
многомерного преобразования Фурье, а так же БПФ (быстрое преобразование Фурье)
позволяют снизить эту цифру до N*logN умножений. Данные алгоритмы основаны на следующей китайской
теореме об остатках.
. Известные алгоритмы
многомерного преобразования Фурье, а так же БПФ (быстрое преобразование Фурье)
позволяют снизить эту цифру до N*logN умножений. Данные алгоритмы основаны на следующей китайской
теореме об остатках.
Теорема 4.2.1.
(Китайская теорема об остатках, единственность)
Для заданного множества
целых положительных попарно взаимно-простых чисел
 и множества
неотрицательных целых чисел
и множества
неотрицательных целых чисел 

при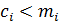
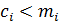 , система сравнений
, система сравнений

имеет не более одного
решенияc в интервале 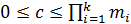
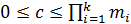
Теорема 4.2.2.
(Китайская теорема об остатках, существование)
Пусть 
 -произведение целых
положительных попарно взаимно-простых положительных чисел, пусть
-произведение целых
положительных попарно взаимно-простых положительных чисел, пусть 
 и пусть
и пусть 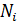
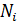 удовлетворяют равенству
удовлетворяют равенству 
 , тогда единственным
решением системы сравнений
, тогда единственным
решением системы сравнений

будет

Эта теорема позволяет каждое число n,
0≤n<M однозначно задать системой остатков по модулям 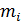
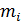 , i=1, k.
, i=1, k.
4.3 Трехмерное
преобразование Фурье в поле 
Рассмотрим ДПФ длины N=255, ядром которого является примитивный элемент поля  .
.
В этом случае, М=255=3
 5
5
 17,
17, 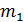
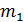 =3,
=3, 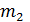
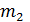 = 5,
= 5, 
 =17, так что n
=17, так что n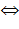
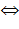 (
(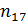
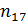 ,
, 
 ,
, 
 ), где
), где
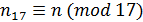
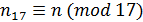 ,
, 
 ,
, 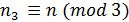
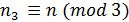
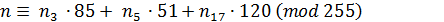
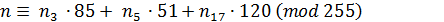
Произвольный ненулевой
элемент 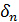
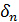 поля
поля 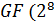
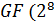 ) задается как степень
примитивного элемента
) задается как степень
примитивного элемента 
 поля:
поля: 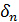
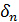 =
= 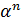
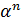 ,
, 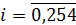
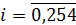
Согласно (2)
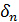
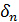 =
= 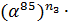
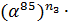 (
(
 ,
,
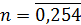
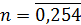 ,
, 
 =
=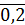
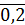 ,
, 
 =
=
 =
=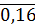
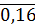 ,
,
Где приняты обозначения:
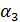
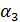 =
=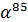
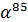 ,
, 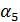
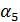 =
=
 ,
,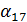
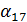 =
=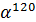
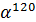
Более того, в силу
попарной взаимной простоты модулей 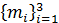
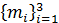 , если i
, если i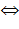
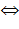 (
(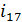
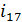 ,
, 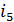
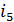 ,
,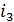
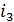 ) и j
) и j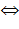
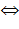 (
(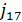
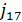 ,
, 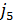
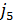 ,
, 
 ), то ij
), то ij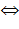
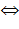 (
(
 ,
, 
 ,
, 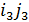
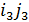 ). Таким образом,
формулу (4.1) определяющую ДПФ, можно переписать в виде:
). Таким образом,
формулу (4.1) определяющую ДПФ, можно переписать в виде:



 ,
, 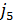
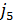 =
=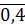
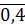 ,
, 
 =
=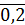
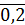
Это сразу подсказывает
следующий алгоритм вычисления вектора 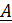
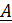 по вектору
по вектору 
 . Сначала разбиваем
координаты вектора
. Сначала разбиваем
координаты вектора 
 на тройки чисел
(прификсированных
на тройки чисел
(прификсированных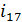
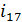 и
и 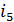
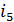 ) и к каждой из них
применяем 3-точечное преобразование с ядром
) и к каждой из них
применяем 3-точечное преобразование с ядром 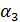
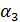 =
=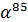
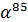 ; это дает набор из 255
величин
; это дает набор из 255
величин
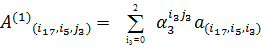
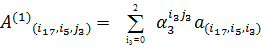
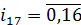
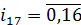 ,
, 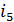
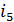 =
=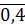
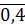 ,
, 
 =
=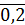
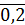 .
.
Затем к этому вектору 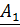
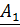 длины 255 применяется
5-точечное ДПФ с ядром
длины 255 применяется
5-точечное ДПФ с ядром 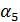
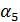 =
=
 по правилу: координаты
вектора
по правилу: координаты
вектора 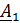
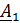 группируются по 5 чисел
(по фиксированным
группируются по 5 чисел
(по фиксированным 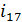
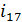 и
и 
 ) и для каждой такой
совокупности вычисляется 5-мерный вектор
) и для каждой такой
совокупности вычисляется 5-мерный вектор 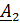
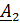 ,
,


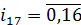
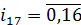 ,
, 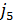
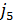 =
=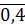
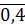 ,
, 
 =
=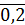
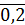 .
.
Наконец, к вектору 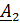
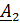 длины 255 применяется
17-точечное ДПФ с ядром
длины 255 применяется
17-точечное ДПФ с ядром 
 =
=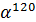
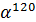 , приводящее к искомому
255-мерному вектору
, приводящее к искомому
255-мерному вектору 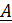
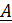 :
:
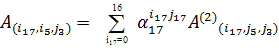
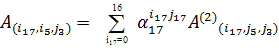
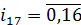
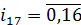 ,
, 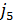
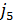 =
=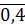
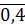 ,
, 
 =
=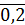
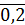 .
.
Описанный алгоритм
вместо 
 умножений при прямом
вычислении по формуле (4.1) требует
умножений при прямом
вычислении по формуле (4.1) требует
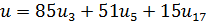
умножений, где 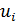
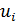 - число умножений,
необходимое для выполнения i-точечного
ДПФ, i=3,5,17. Аналогично выписывается и формула для числа сложений
(кстати, напомним, что характеристика рассматриваемого поля равна 2, так что
вычитание совпадает со сложением)
- число умножений,
необходимое для выполнения i-точечного
ДПФ, i=3,5,17. Аналогично выписывается и формула для числа сложений
(кстати, напомним, что характеристика рассматриваемого поля равна 2, так что
вычитание совпадает со сложением)
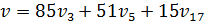
Экспериментально
установлено, что переход от одномерной структуры к трехмерной, уменьшает время,
требуемое на вычисление ДПФ примерно в 10 раз.
Таким образом, переход
от ДПФ длины 255 к ДПФ длин 3, 5 и 17, каждое из которых вычисляется 255 раз в
цикле, очень существенно понижает вычислительную сложность алгоритма.
Следующий наш шаг -
полностью избавиться от ДПФ внутри циклов, заменив их на БПФ (быстрое
преобразование Фурье) длин 3, 5 и 17, которые основаны как на свойствах поля  ,
так и на свойствах алгоритмов быстрого умножения многочленов, заданных над
конечным полем.
,
так и на свойствах алгоритмов быстрого умножения многочленов, заданных над
конечным полем.
4.4 Быстрое
преобразование Фурье БПФ длины 3
3-точечное ДПФ с ядром β для вектора a=,
a-0., a-1., a-2. задается формулой
Так как ядро β
удовлетворяет тождеству 1+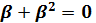
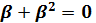 , то легко проверить
непосредственно, что числа
, то легко проверить
непосредственно, что числа 
 могут быть вычислены по
правилу:
могут быть вычислены по
правилу:
s-1.=,
a-1.+, a-2., m-1.=β∙, s-1.,
A-1.=, s-2.+,
a-1., 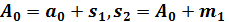
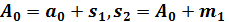
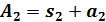
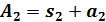 ,
,
которое содержит только
одно умножение и 5 сложений (вместо 4 умножений и 6 сложений). Если 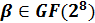
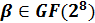 ,
, 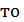
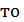 β=,
α-3.=,
α-85.
β=,
α-3.=,
α-85.
4.5 Быстрое
преобразование Фурье длины 5
5-точечное ДПФ с ядром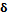
 задается равенством
задается равенством
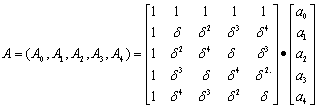 ,
,
непосредственное
вычисление по которому требует 16 умножений и 20 сложений. Использование только
тождества на ядре (которое в данном случае имеет вид 1+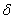 +
+ +
+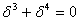 )
дает 9 умножений и 21 сложение. Это достигается, например, следующим образом:
)
дает 9 умножений и 21 сложение. Это достигается, например, следующим образом:
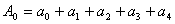 ,
,

Аналогично,
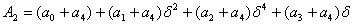 ,
,
 ,
,
и, наконец,

Дальнейшего уменьшения
числа умножений можно добиться за счет перехода к циркулянту и использования
полиномиальной свертки (ПС). Приведем необходимые сведения:
Утверждение 4.5.1. Два
двучлена 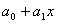 и
и
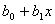 ,
,
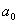 ,
,
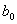 ,
,
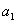 ,
,
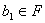 ,
можно перемножить, выполняя не более трех умножений чисел в поле F.
,
можно перемножить, выполняя не более трех умножений чисел в поле F.
Действительно, (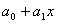 )(
)(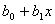 )?
)? ,
где
,
где  ,
,
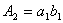 и
и
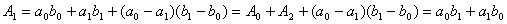
Если умножение
происходит в поле F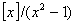 ,
то
,
то 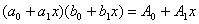 ,
где
,
где 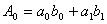 ,
,

Следствие 4.5.1.
Два многочлена степени m
над полем F
можно перемножить, выполняя не более  умножений чисел в поле F.
умножений чисел в поле F.
Например, для m=3 (с учетом, что char GF(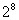 )=2)
имеем:
)=2)
имеем:
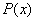 ?
?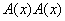 ?
?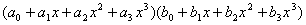 =
=
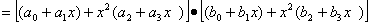 ?
?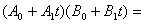
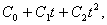
где t?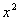 (так что при вычислении по модулю многочлена
(так что при вычислении по модулю многочлена 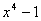 надо делать редукцию по
модулю
надо делать редукцию по
модулю  );
согласно утверждению 4.5.1:
);
согласно утверждению 4.5.1:
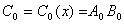 ?
?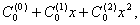
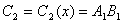 ?
?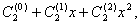
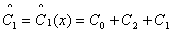
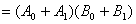 ?
?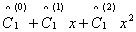
Для вычисления 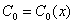 ,
,
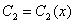 ,
,
 опять
воспользуемся утверждением 4.5.1. Имеем
опять
воспользуемся утверждением 4.5.1. Имеем
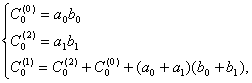


Таким образом, для
вычисления коэффициентов 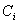 многочлена
многочлена

 необходимо только 9
(вместо 16) умножений. Точные формулы для коэффициентов многочлена
необходимо только 9
(вместо 16) умножений. Точные формулы для коэффициентов многочлена  (при
(при
 )
имеют вид:
)
имеют вид:
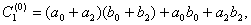

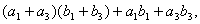
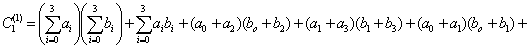

Для коэффициентов 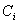 при
при ,
согласно (10) - (12)
,
согласно (10) - (12)
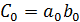
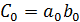 ,
,
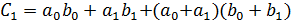
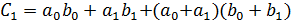 ,
,

 ,
,
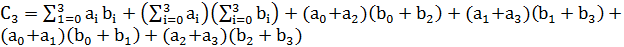
 ,
,
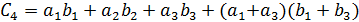
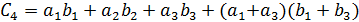 ,
,
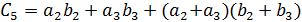
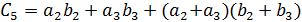 ,
,
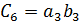
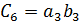 ,
,
Если произведение 
 вычисляется в кольце F
вычисляется в кольце F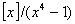 (так
что
(так
что 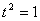 ),
то формулы (10) - (12) принимают вид:
),
то формулы (10) - (12) принимают вид:
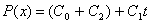 ≜
≜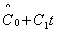 ,
(10а)
,
(10а)
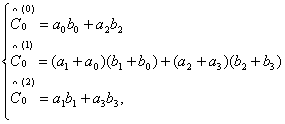
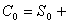
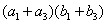 ,
, 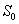 ≜
≜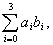
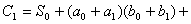
 ,
,


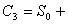
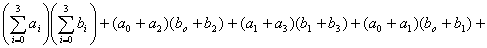
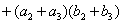 .
.
Вычисление вектора 
 где
где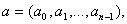 а
а
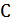 - циркулянт, первая
строка которого задается вектором
- циркулянт, первая
строка которого задается вектором 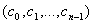 , равносильно вычислению
в F
, равносильно вычислению
в F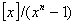 произведения
произведения 

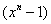 , где
, где
 и
и 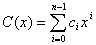 .
.
Подчеркнем, что
преобразуемая последовательность 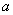 , за исключением первого
элемента, дает реверсивный порядок коэффициентов многочлена
, за исключением первого
элемента, дает реверсивный порядок коэффициентов многочлена 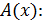
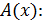 при
при  координате
стоит коэффициент
координате
стоит коэффициент 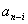 .
.
Утверждение 4.5.2. Для
ДПФ простой длины n
всегда существует такая перестановка строк и столбцов матрицы Фурье, что она
может быть превращена в окаймленный циркулянт.
Этот результат
принадлежит Рейдеру. Мы подробно проиллюстрируем соответствующий алгоритм в
следующем пункте, посвященному БПФ длины 17, а сейчас вернемся к БПФ длины 5.
Прежде всего избавимся
от единичного окаймления матрицы Фурье:
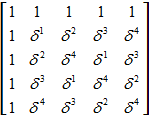


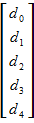
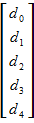 =
= 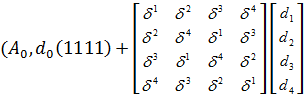
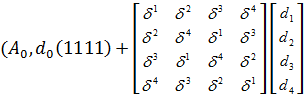 )
)
В столбцах и строках
матрицы, стоящей в правой части равенства выполним перестановку 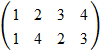
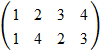 . Если выполним такую же
перестановку координат у векторов d
и его спектра А, получаем
. Если выполним такую же
перестановку координат у векторов d
и его спектра А, получаем

 )
)
 (14)
(14)
Циркулярная матрица 
 для БПФ длины 5
получается, если задать нумерацию ненулевого элемента поля GF(5) с образующей 3:
для БПФ длины 5
получается, если задать нумерацию ненулевого элемента поля GF(5) с образующей 3: 
 1 (mod5), 3
1 (mod5), 3
 3 (mod5),
3 (mod5), 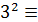
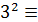 4 (mod5),
4 (mod5), 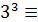
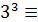 2 (mod5):
2 (mod5): 
 .
.
Этим задача свелась,
согласно утверждения 4.5.2, к вычислению многочлена c(x)=d(x) w(x) mod(x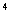 -1),
где d(x)=
-1),
где d(x)=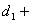
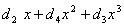 или, иначе, циклической
свертки с=с
или, иначе, циклической
свертки с=с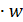
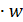
Для вычисления этой
циклической свертки длины 4, перепишем формулы (13) в более удобном для
организации экономного вычисления виде:

 ,
, 
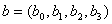 ;
;
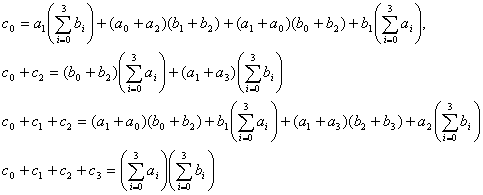 (15)
(15)
Этот алгоритм содержит 9
умножений и 17 сложений. Но если появляются какие-то условия на коэффициенты 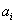 или
или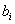 ,
то число вычислений уменьшается. Например, если
,
то число вычислений уменьшается. Например, если  =0 или 1, то число
умножений равно только 5. В нашем случае
=0 или 1, то число
умножений равно только 5. В нашем случае 

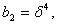
 и так как
и так как 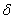 -
ядро БПФ длины 5, то
-
ядро БПФ длины 5, то =1.
Учитывая это, из формул (13) - (14) окончательно приходим к следующему
алгоритму:
=1.
Учитывая это, из формул (13) - (14) окончательно приходим к следующему
алгоритму:
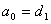 ,
, 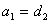 ,
,
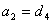 ,
,
 ,
,
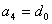 ,
,
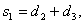
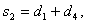

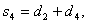

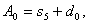
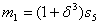 ,
, 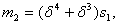
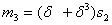 ,
, 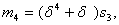
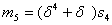 ,
, 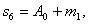
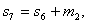

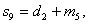

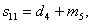
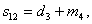
 ,
, 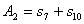 ,
,
 ,
,
 .
(16)
.
(16)
Так что алгоритм БПФ
длины 5 в поле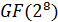
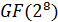 в нашем случае содержит
5 умножений и 11 сложений.
в нашем случае содержит
5 умножений и 11 сложений.
4.6 Быстрое
преобразование Фурье длины 17
-точечное ДПФ с ядром  задается
равенством
задается
равенством

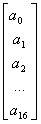 (17)
(17)
В 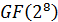
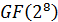
 =
= .
.
Для уменьшения числа
умножений, как и для 5-точечного ДПФ, воспользуемся переходом к циклической
свертке с последующей редукцией по следствию из утверждения 4.5.1. Сначала воспользуемся
алгоритмом Рейдера для перехода к циркулянту. Так как 5 является примитивным
элементом поля GF(17),
то имеем:
|
i
|
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16
|
|
N=5 5
8 6 13 14 2 10 16 12 9 11 4 3 15 7 1 5
8 6 13 14 2 10 16 12 9 11 4 3 15 7 1
|
|
Таким образом, без учета
в нумерации одиночного окаймления, к циклической свертке приводит, например,
такая перестановка строки столбцов матрицы Фурье в (17) (соответствующих
координат преобразуемого вектора а и спектра А), которая дается
второй строкой этой таблицы: единичное окаймление остается на месте, а первая
строка циркулянта  соответственно
имеет вид:
соответственно
имеет вид:
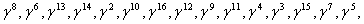
получаем,

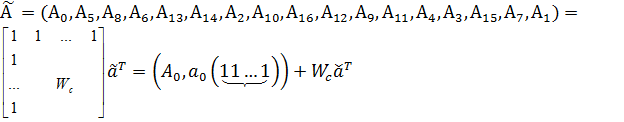
 , (18)
, (18)
где 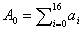 ,
,
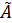
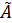 - вектор, полученный из
спектра А указанной перестановкой координат, а
- вектор, полученный из
спектра А указанной перестановкой координат, а 
 - вектор
столбец, определяемый вторым равенством в (18).
- вектор
столбец, определяемый вторым равенством в (18).
Согласно утверждению
4.5.2, задача вычисления (18) эквивалентна задаче вычисления циклической
свертки
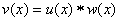
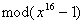 (19)
(19)
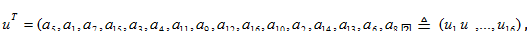

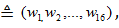
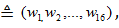
Вычислять свертку (19)
будем следующим образом. Пусть  (так что
(так что  )
и пусть
)
и пусть
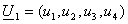
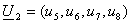
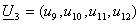
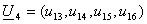
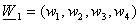

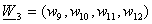
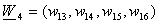
Так что
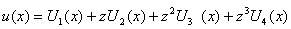

 ,
,

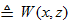
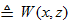 ,
,
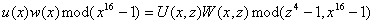
Сначала будем полагать
переменную х параметром и найдем циклическую свертку по модулю  .
Обозначая
.
Обозначая 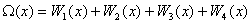 ,
согласно равенствам (15) имеем:
,
согласно равенствам (15) имеем:




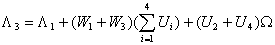 (20)
(20)

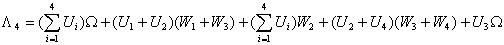
В поле 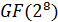
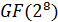 для элемента
для элемента 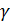
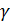 выполняется тождества:
выполняется тождества:
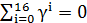
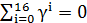 ;
;  ;
;

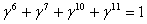 (21)
(21)
Эти тождества позволяют
упростить вычисления величин, входящих в (20). Например,
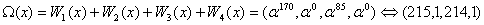
Aлгоритм
вычисления R(x)=r(x) 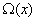 для
произвольного многочлена
для
произвольного многочлена 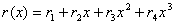 содержит
4 умножения и 12 сложений. А именно, воспользуемся равенством (12) и учтем, что
в поле
содержит
4 умножения и 12 сложений. А именно, воспользуемся равенством (12) и учтем, что
в поле 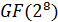
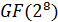 согласно второму из
тождеств в (20) выполняется равенство
согласно второму из
тождеств в (20) выполняется равенство 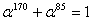 , char
, char
 =2. Имеем:
=2. Имеем:

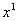
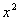
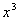

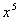


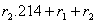
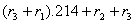

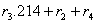

При табличной реализации
умножения необходимо иметь только один массив длины 256 произведений всех
элементов поля на элемент  .
Алгоритм:
.
Алгоритм:
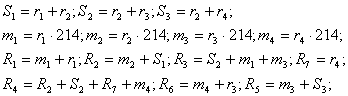 (22)
(22)
Для остальных 5 умножений вида R(x)=r(x) b(x) число умножений не уменьшается, равно 9, и алгоритм, согласно
(12), можно записать в виде:
Алгоритм: 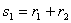 ,
,
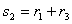 ,
,
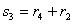 ,
,
 ,
,
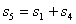 ,
,
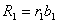 ,
,
 ,
, 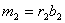 ,
,
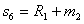 ,
,
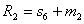 ,
,
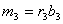 ,
,
 ,
(23)
,
(23)
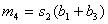 ,
, 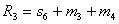 ,
,
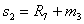 ,
,
 ,
,
 ,
,
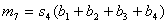 ,
,
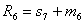 ,
,
 ,
,
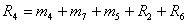 .
.
Так как суммы
коэффициентов 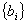 ,
естественно, вычисляются заранее и вводятся в алгоритм фиксированными
константами, то всего имеем 9 умножений и 17 сложений. Для входящих в (20)
коэффициентов, величины
,
естественно, вычисляются заранее и вводятся в алгоритм фиксированными
константами, то всего имеем 9 умножений и 17 сложений. Для входящих в (20)
коэффициентов, величины
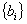 соответственно равны:
соответственно равны:
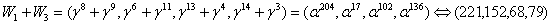
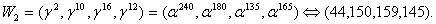
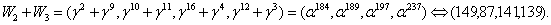
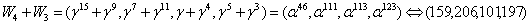
Полное число сложений и
умножений для этой реализации равно соответственно 129 и 61. Для полного БПФ по
длине 255 имеем 1935 сложений и 1255 умножений.
4.7 БПФ-укороченные коды
Рида-Соломона
В 4.2 было дано
спектральное описание циклического кода. Согласно этому описанию, кодовое слово
находится спектре кодового слова информационного вектора, содержащего 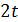
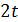 подряд идущих нулей.
При таком подходе код способен исправлять не более
подряд идущих нулей.
При таком подходе код способен исправлять не более 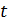
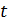 ошибок. Были построены
эффективные алгоритмы вычисления ДПФ длин 3, 5, 17 над полем
ошибок. Были построены
эффективные алгоритмы вычисления ДПФ длин 3, 5, 17 над полем  и
быстрый алгоритм вычисления ДПФ длины 255.
и
быстрый алгоритм вычисления ДПФ длины 255.
На практике, однако, не
всегда возможно (или целесообразно) применять кодовые слова длины 255 над 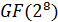
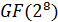 . Одним из путей
уменьшения требуемых вычислительных ресурсов и снижения времени обработки
данных при кодировании и декодировании применение так укороченных РС-кодов.
. Одним из путей
уменьшения требуемых вычислительных ресурсов и снижения времени обработки
данных при кодировании и декодировании применение так укороченных РС-кодов.
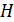
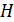 -укороченный РС-код
-укороченный РС-код 
 представляет собой
подпространство полного
представляет собой
подпространство полного 
 кода. При этом все
кодовые слова длины
кода. При этом все
кодовые слова длины 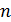
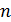 укороченного кода
заканчиваются
укороченного кода
заканчиваются 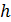
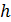 нулями. Такой код можно
записать
нулями. Такой код можно
записать 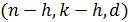
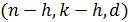 . Работают с ним так же,
как и с полным
. Работают с ним так же,
как и с полным 
 кодом, просто он имеет
не
кодом, просто он имеет
не 
 , а
, а 
 информационных позиций.
информационных позиций.
Алгоритмы кодирования при
прямом способе укорочения РС-кода совпадают с алгоритмами для полного кода.
Поэтому временные характеристики несистематического кодера, основанного на
спектральной технологии кодирования остаются такими же, как и для полного кода.
Объясняется это тем, что при несистематическом кодировании, когда к
информационному вектору применяется быстрое преобразование Фурье (БПФ), весь
массив данных (все 255 координат) обрабатываются одновременно и вычисления
проводятся сразу для нескольких групп точек. При этом обнуляемые позиции
кодового слова равномерно распределяются по всему трехмерному кубу,
реализующему БПФ, и автоматически включаются в вычисления на полной длине
кодового слова. Поэтому целесообразно сделать укорочение кодового слова таким
образом, чтобы сократить вычисления в алгоритмах БПФ.
4.8 Несистематические
БПФ-укорочения
Порядок
мультипликативной группы поля  является составным
числом n=255=3*5*17. Группа
является составным
числом n=255=3*5*17. Группа  является циклической и
порождается примитивным элементом α; она
содержит 255 элементов:
является циклической и
порождается примитивным элементом α; она
содержит 255 элементов: 
 . Эта группа имеет
циклические подгруппы порядка
. Эта группа имеет
циклические подгруппы порядка 
 (
(
 делят
делят 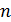
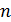 ).
).
В таблице 1 приведены
циклические подгруппы мультипликативной группы поля  .
.
Таблица 1. Циклические
подгруппы мультипликативной группы поля 
|
Порядок подгруппы
|
Порождающий элемент
|
Подгруппа
|
|
3
|
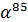
|
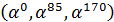
|
|
5
|

|
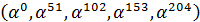
|
|
15
|
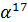
|
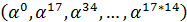
|
|
17
|
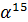
|

|
|
51
|
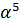
|

|
|
85
|

|
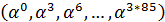
|
В основе несистематического
кодирования укороченных РС-кодов лежит дискретное преобразование Фурье (ДПФ) на
группе, образуемой ненулевыми элементами поля.
Кодовое слово 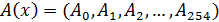
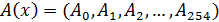 задается как ДПФ
информационного вектора
задается как ДПФ
информационного вектора 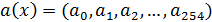
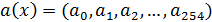 c
c
 информационными
символами и
информационными
символами и 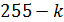
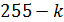 нулями, где
нулями, где 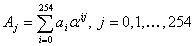 ,
а в качестве примитивного элемента
,
а в качестве примитивного элемента 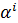
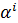 выбран корень
неприводимого многочлена
выбран корень
неприводимого многочлена 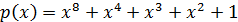
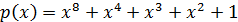 .
.
Aлгоритм
трехмерного ДПФ позволяет вычислить элементы 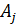
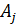 кодового вектора по
формуле:
кодового вектора по
формуле:

 (24)
(24)
Рассмотрим
преобразование Фурье длины 
 в поле
в поле  .
Элементами этого преобразование
.
Элементами этого преобразование 
 должны быть элементы
подгруппы, образованной примитивным элементом
должны быть элементы
подгруппы, образованной примитивным элементом 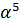
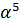 (в соответствии с
таблицей 1). Перекодируем укороченный вектор
(в соответствии с
таблицей 1). Перекодируем укороченный вектор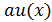
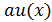 (вектор длины 51) в
полный вектор
(вектор длины 51) в
полный вектор 
 (длины 255) таким
образом, чтобы все координаты
(длины 255) таким
образом, чтобы все координаты 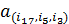
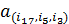 , для которых
, для которых 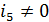
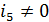 , были нулевыми.
Практически это означает, что мы разместим укороченный вектор
, были нулевыми.
Практически это означает, что мы разместим укороченный вектор 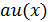
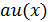 только в одной плоскости
БПФ-куба там, где
только в одной плоскости
БПФ-куба там, где 
 . Тогда формулу (24)
можно переписать в виде:
. Тогда формулу (24)
можно переписать в виде:

 (25)
(25)
А это означает переход к
ДПФ с ядром 
 для вектора
для вектора 
 . Преобразование Фурье
вычисляется как значение многочлена
. Преобразование Фурье
вычисляется как значение многочлена 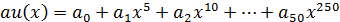
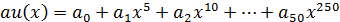 в точках поля:
в точках поля: 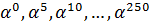
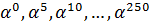 , что эквивалентно работе
в подгруппе с ядром
, что эквивалентно работе
в подгруппе с ядром 
 :
: 
 .
.
Очевидно, что для
реализации БПФ-укорочения длины 85 с порождающим элементом 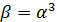
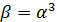 из формулы (24)
необходимо исключить суммирование по
из формулы (24)
необходимо исключить суммирование по 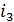
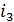 , что достигается путем
размещения укороченного вектора в плоскости БПФ-куба там, где
, что достигается путем
размещения укороченного вектора в плоскости БПФ-куба там, где 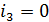
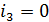 . Это означает переход к
ДПФ с ядром
. Это означает переход к
ДПФ с ядром 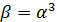
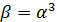 для мультипликативной
подгруппы порядка 85 с шагом 3.
для мультипликативной
подгруппы порядка 85 с шагом 3.

 (26)
(26)
Проводя аналогичные
рассуждения можно построить формулы вычисления ДПФ для всех циклических
подгрупп, указанных в таблице 1. Эти БПФ-укорочения можно применить для
кодирования укороченными кодами Рида-Соломона над полем длин n=85,51,17,15,5,3.
длин n=85,51,17,15,5,3.
Заключение
На основании китайской
теоремы об остатках получен результат, существенно понижающий вычислительную
сложность ДПФ. Приведены формулы для трехмерного преобразования Фурье поле 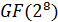
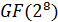 . Построены алгоритмы
быстрого преобразование Фурье (БПФ) длин 3, 5 и 17 на основе алгоритма Рейдера
и алгоритма Винограда вычисления циклической свертки. Показана эквивалентность
между вычислением ДПФ простой длины и вычислением циклической свертки.
. Построены алгоритмы
быстрого преобразование Фурье (БПФ) длин 3, 5 и 17 на основе алгоритма Рейдера
и алгоритма Винограда вычисления циклической свертки. Показана эквивалентность
между вычислением ДПФ простой длины и вычислением циклической свертки.
На основании трехмерного
преобразования Фурье построены укороченные преобразования длин 15, 51, 85,
которые рационально применять, когда не требуется кодировать слова длины 255.
Показана эквивалентность между укорочением преобразования и переходом на
соответствующую ему подгруппу мультипликативной группы поля.
В приложении представлен
программный комплекс, реализующий построение поля 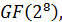
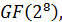 основные операции в
этом поле, вычисление значения произвольного многочлена в любой точке поле,
вычисление ДПФ, ОДПФ, трехмерного преобразования Фурье и БПФ длин 255,85,51,15,17,5,3,
кодирование кодом Рида-Соломона в частотной области.
основные операции в
этом поле, вычисление значения произвольного многочлена в любой точке поле,
вычисление ДПФ, ОДПФ, трехмерного преобразования Фурье и БПФ длин 255,85,51,15,17,5,3,
кодирование кодом Рида-Соломона в частотной области.
Проведенные
вычислительные эксперименты показали практическую эффективность перехода от ДПФ
к трехмерному преобразованию: если на вычисление ДПФ длины 255 затрачивается
примерно 300-350 мс машинного времени, то трехмерное преобразование занимает от
20 до 35 мс. При этом на вычисление БПФ длины 255 затрачивается всего 13-17 мс.
Разработанный
программный комплекс можно применять при создании систем хранения и передачи
данных с повышенной надежностью. Удобный и наглядный пользовательский интерфейс
интуитивно понятен и не вызовет проблем у разработчиков этих систем.
Языком реализации выбран
Borland Delphi Enterprise 2007.
Список использованной
литературы
1. Берлекэмп Э.Р. Алгебраическая теория кодирования. М.: Мир,
1971
2. Nussbaumer H.J. Fast Fourier Transform and Convolution
Algorithms. - Springer-Verlag: Berlin, Heidelberg, New York, 1981.
3. Помехоустойчивое кодирование и надежность ЭВМ. М.: Наука,
1987.
. Макмеллан Дж.Х., Рейдер Ч.М. Применение теории чисел в
цифровой обработке сигналов. М.: Радио и связь, 1983.
. Блейхут Р. Теория и практика кодов, контролирующих
ошибки. М.: Мир, 1986.
6. Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория
передачи сигналов. М: Радио и связь, 2001 г.
. Золотарев В.В. Помехоустойчивое кодирование. Методы и
алгоритмы:
справочник / В.В. Золотарев, Г.В. Овечкин. - М.: Горячая линия -
Телеком, 2004. - 126 с.
. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов.
М.: Мир, 1989.
9. Лидл Р., Нидеррайтер Г. Конечные поля, т. 1. М.: Мир,
1988
. Волошина В.Н., Руднева И.В. Надежное хранение информации
с помощью кодов Рида-Соломона: Препр. Владивосток: ИАПУ ДВНЦ АН СССР, 1987, 13
с.
. Волошина В.Н., Герасимов В.В., Руднева И.В.,
Программно-технологическая система хранения информации с повышенной
надежностью: Препр. Владивосток: ИАПУ ДВО АН СССР, 1989, 22 с.