Дифференциальное уравнение
1. Решить уравнение

Решение:
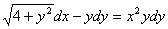 - уравнение с разделяющимися
переменными
- уравнение с разделяющимися
переменными
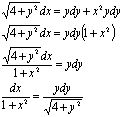
Проинтегрируем обе части полученного
уравнения:
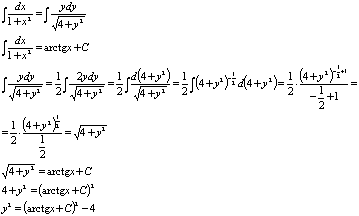
 - общее решение уравнения
- общее решение уравнения
Ответ: 
2. Решить однородное дифференциальное
уравнение
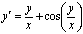
Решение:
Сделаем замену
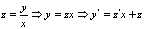
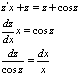
Проинтегрируем обе части полученного
уравнения:
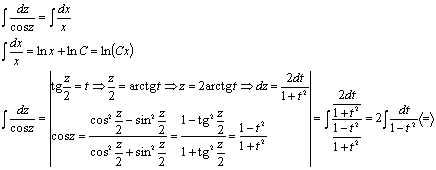
Разложим подынтегральную дробь на
сумму простейших дробей:

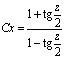
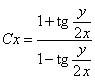 - общий интеграл дифференциального
уравнения
- общий интеграл дифференциального
уравнения
Ответ: 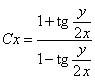
3. Найти частное решение линейного
дифференциального уравнения
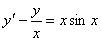 ,
, 
Решение:
Решаем уравнение методом Бернулли:
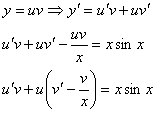
Для решения исходного уравнения
необходимо решить систему уравнений
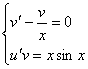 (*)
(*)
Решим первое уравнение системы (*):

Проинтегрируем обе части полученного
уравнения
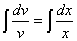
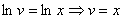
Подставим найденное выражение для
функции  во второе
уравнение системы (*) и решим его.
во второе
уравнение системы (*) и решим его.
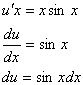
Проинтегрируем обе части полученного
уравнения.
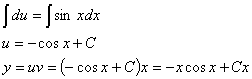
 - общее решение дифференциального
уравнения
- общее решение дифференциального
уравнения
Найдем частное решение уравнении при
условии  .
.

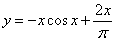 - частное решение дифференциального
уравнения
- частное решение дифференциального
уравнения
Ответ: 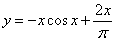
4. Найти общий интеграл уравнения
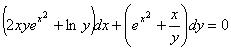 ,
, 
Решение:
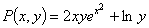 ,
, 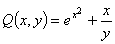
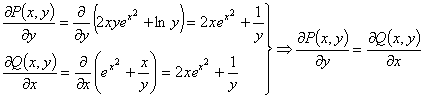
Таким образом, данное уравнение -
уравнение в полных дифференциалах.
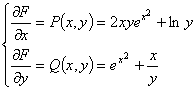
Решим второе уравнение системы:
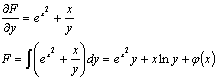
Найдем  от
найденной функции и подставим в первое уравнение полученной выше системы:
от
найденной функции и подставим в первое уравнение полученной выше системы:


 - общий интеграл дифференциального
уравнения
- общий интеграл дифференциального
уравнения
Ответ: 
5. Найти решение уравнения,
удовлетворяющее начальным условиям
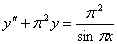 ,
,  ,
,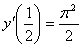
Решение:
Найдем общее решение однородного
уравнения, соответствующего данному неоднородному. Для этого составим
характеристическое уравнение:
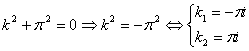
Тогда общее решение однородного
уравнения запишем в виде
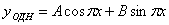
Для нахождения частного решения
неоднородного уравнения составим систему

Решим полученную систему методом
Крамера. Вычислим главный определитель:

Вычислим побочные определители:

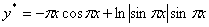
Тогда общее решение неоднородного
уравнения имеет вид:

Найдем частное решение, отвечающее
начальным условиям.

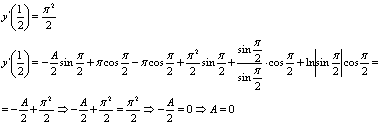
 - решение задачи Коши
- решение задачи Коши
Ответ: 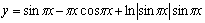
6. Решить уравнение
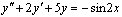
Решение:
Найдем общее решение однородного
уравнения, соответствующего данному неоднородному. Для этого составим
характеристическое уравнение:
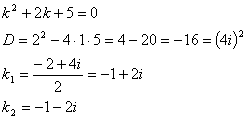
Тогда

Найдем частное решение неоднородного
уравнения. Поскольку  не является
корнем характеристического уравнения, то искать его будем в виде
не является
корнем характеристического уравнения, то искать его будем в виде

Подставим найденные значении
производных в исходное уравнение:

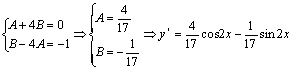
Тогда общее решение неоднородного
уравнения имеет вид:

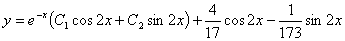
общее решение неоднородного
уравнения
Ответ:
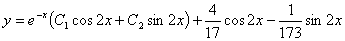
7. Исследовать сходимость ряда
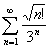
Решение:
Для исследования ряда на сходимость
применим признак Даламбера.
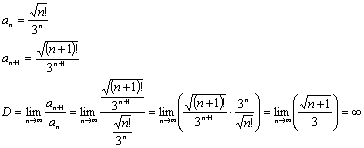
Поскольку 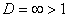 , то ряд
, то ряд 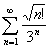 расходится
расходится
Ответ: ряд 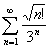 расходится
расходится
8. Найти область сходимости
функционального ряда
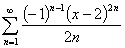 (1)
(1)
Решение:
Найдем радиус сходимости ряда (1):
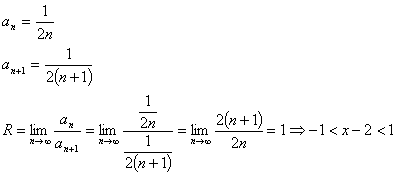
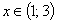 - интервал сходимости ряда (1)
- интервал сходимости ряда (1)
Исследуем сходимость ряда в
граничных точках:
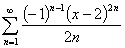 :
: 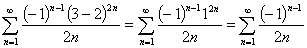 (2)
(2)
Исследуем ряд (2)на сходимость:
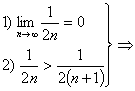 условия теоремы Лейбница выполнены,
т.е. ряд (2) сходится
условия теоремы Лейбница выполнены,
т.е. ряд (2) сходится
Рассмотрим ряд из модулей 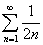 (3)
(3)
Данный ряд расходится как
геометрический.
Поскольку ряд (2) сходится, а ряд
(3) из модулей расходится, то ряд (2)сходится условно.
 :
: 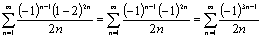 (4)
(4)
Исследуем ряд (4)на сходимость:
 условия теоремы Лейбница выполнены,
т.е. ряд (4) сходится
условия теоремы Лейбница выполнены,
т.е. ряд (4) сходится
Рассмотрим ряд из модулей  (5)
(5)
Данный ряд расходится как
геометрический.
Поскольку ряд (4) сходится, а ряд
(5) из модулей расходится, то ряд (4) сходится условно.
Таким образом, окончательно получаем
интервал сходимости 
Ответ: ряд 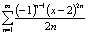 сходится
при
сходится
при  ; причем,
при
; причем,
при 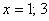 соответствующие
знакочередующиеся ряды сходятся условно
соответствующие
знакочередующиеся ряды сходятся условно
. Разложить в степенной ряд
функцию 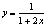 в
окрестности точки
в
окрестности точки  и найти
интервал сходимости ряда.
и найти
интервал сходимости ряда.
Решение:
Вычислим несколько производных указанной
функции:
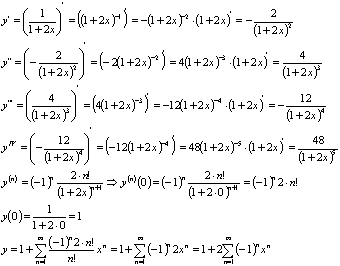
Найдем радиус сходимости полученного
ряда:
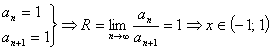
Исследуем граничные точки.
 :
:  (1)
(1)
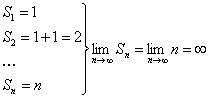 , т.е. не существует предела
частичных сумм ряда (1), следовательно, этот ряд расходится
, т.е. не существует предела
частичных сумм ряда (1), следовательно, этот ряд расходится
 :
: 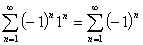 (2)
(2)

т.е. не существует предела частичных
сумм ряда (2), следовательно, этот ряд расходится
Ответ: 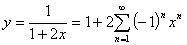 , данный ряд
сходится при
, данный ряд
сходится при 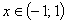
. Разложить в ряд Фурье периодическую
функцию  с периодом
с периодом 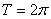 , заданную
на отрезке
, заданную
на отрезке 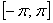 .
.
Решение:
Поскольку  - нечетная
функция на
- нечетная
функция на 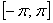 , то ее ряд
Фурье будет содержать только синусы.
, то ее ряд
Фурье будет содержать только синусы.

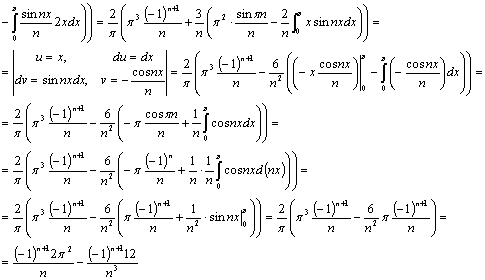
Тогда ряд Фурье исходной функции
имеет вид:
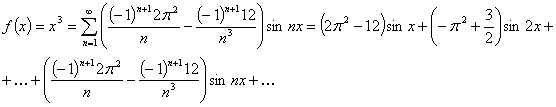
1.
На книжной полке случайным образом расставлены 4 учебника и 3 задачника. Найти
вероятность того, что все учебники окажутся рядом.
Решение:
Событие 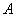 : все
учебники окажутся рядом
: все
учебники окажутся рядом
Для решения задачи воспользуемся
классическим определением вероятности.
Общее число исходов равно числу
перестановок семиэлементного множества:
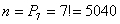
Благоприятствующее число исходов
определим следующим образом как квадрат числа перестановок четырех элементного
множества. Поскольку все учебники должны оказаться рядом, то рассмотрим их как
единый элемент. Тогда с учетом еще трех задачников получаем 4 элемента. Число
всех возможных размещений таких элементов - число перестановок
четырехэлементного множества. Но "внутри" единого элемента учебники
тоже могут меняться местами (при этом они все равно будут рядом), поэтому
 .
.
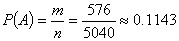
Ответ: 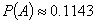
. Вероятность отказа каждого
элемента в течение времени 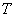 равна
равна 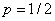 . Элементы
работают независимо и включены в цепь по приведенной схеме.
. Элементы
работают независимо и включены в цепь по приведенной схеме.

Пусть событие 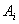 означает
отказ элемента с номером
означает
отказ элемента с номером 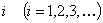 , а событие
, а событие 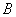 - отказ
цепи за время
- отказ
цепи за время 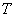 (прекращение
тока в цепи). Требуется написать формулу, выражающую событие
(прекращение
тока в цепи). Требуется написать формулу, выражающую событие 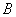 через все
события
через все
события 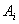 . Найти
вероятность события
. Найти
вероятность события 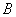 при
при 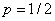 .
.
Решение:
Поскольку событие 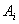 - отказ
элемента с номером
- отказ
элемента с номером 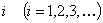 , тогда
, тогда 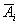 -
нормальная работа элемента с номером
-
нормальная работа элемента с номером 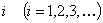 . Для наступления события
. Для наступления события 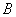 необходимо,
чтобы
необходимо,
чтобы
· отказали все три элемента с номерами
1, 2, 3, но мог работать хотя бы один из элементов 4, 5;
· отказали оба элемента с номерами 4,
5, но мог работать хотя бы один из элементов 1, 2, 3;
· отказали все элементы в цепи.
В формульном виде это можно записать следующим
образом:
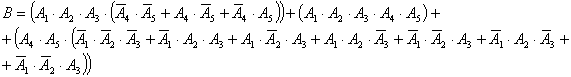
Найдем вероятность события 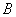 на
основании теорем сложения и умножения вероятностей.
на
основании теорем сложения и умножения вероятностей.
Поскольку
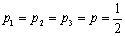 , то
, то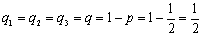
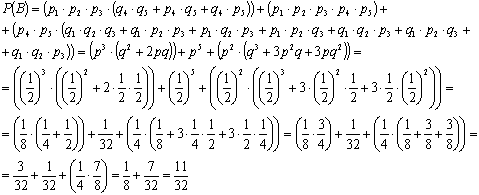
Ответ:
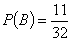
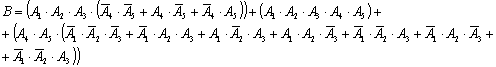
3. Противник может применить в
налете самолеты одного из двух типов 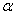 и
и 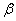 с вероятностями соответственно 0,7
и 0,3. Самолет типа
с вероятностями соответственно 0,7
и 0,3. Самолет типа 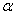 сбивается
ракетой с вероятностью 0,7, типа
сбивается
ракетой с вероятностью 0,7, типа 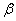 - с вероятностью 0,9. По
появившемуся самолету выпущены одновременно две ракеты. Найти вероятность того,
что сбитый самолет был типа
- с вероятностью 0,9. По
появившемуся самолету выпущены одновременно две ракеты. Найти вероятность того,
что сбитый самолет был типа 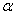 .
.
Решение:
Событие 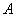 : самолет
сбит
: самолет
сбит
Событие 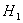 : самолет
типа
: самолет
типа 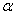
Событие 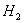 : самолет
типа
: самолет
типа 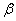
Событие 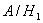 : самолет
типа
: самолет
типа 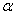 сбит
сбит
Событие 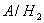 : самолет
типа
: самолет
типа 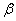 сбит
сбит
Событие 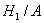 :
оказавшийся сбитым самолет был типа
:
оказавшийся сбитым самолет был типа 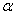
 ,
, 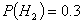 ,
, 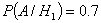 ,
, 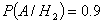
По формуле полной вероятности

По формуле Байеса

Ответ: 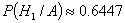
. Каждый прибор проходит два
независимых испытания. Вероятность выхода из строя прибора при первом испытании
равна  , при втором
-
, при втором
- 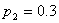 . Испытано
независимо 5 приборов. Найти вероятность выхода из строя не более одного
прибора.
. Испытано
независимо 5 приборов. Найти вероятность выхода из строя не более одного
прибора.
Решение:
Событие 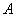 : при
независимом испытании 5 приборов из строя вышло не более одного прибора
: при
независимом испытании 5 приборов из строя вышло не более одного прибора
Вероятность для одного прибора
пройти оба испытания
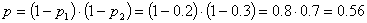 ,
,
тогда вероятность того, что прибор
испытания не пройдет равна

Вероятность события 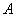 определим
по формуле Бернулли:
определим
по формуле Бернулли:
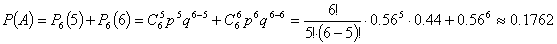
Ответ: 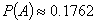
5. Самолеты испытываются при перегрузочных
режимах. Вероятность каждого самолета пройти испытание равна 0,8. Испытания
заканчиваются после первого самолета, не выдержавшего испытания. Составить
закон распределения и функцию распределения числа испытаний самолетов.
Решение:
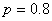 - вероятность того, что самолет
пройдет испытание
- вероятность того, что самолет
пройдет испытание
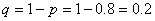 - вероятность того, что самолет не
пройдет испытание
- вероятность того, что самолет не
пройдет испытание
Пусть  - случайная величина - число
самолетов, прошедших испытание
- случайная величина - число
самолетов, прошедших испытание
Данная случайная величина
распределена по биномиальному закону. Составим закон распределения данной
случайной величины:
Составим функцию распределения:
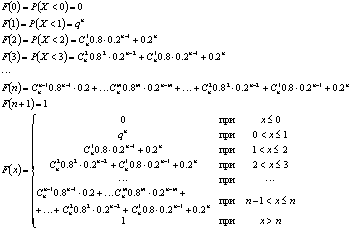
6. Дана плотность вероятности  случайной
величины
случайной
величины  :
:
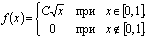
Найти  ,
, 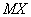 ,
,  ,
, 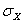 ,
,  .
.
Решение:
Вычислим данный интеграл:

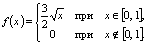
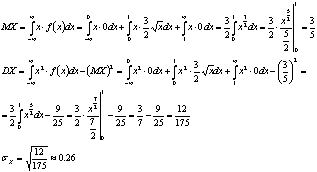
Оценим вероятность 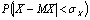 с помощью
неравенства Чебышева:
с помощью
неравенства Чебышева:
переменная
дифференциальный неравенство гистограмма
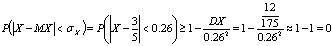
Ответ:
 ,
,  ,
, 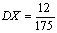 ,
,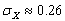 ,
, 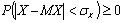 .
.
7. Случайная величина  распределена
по закону Гаусса с
распределена
по закону Гаусса с 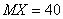 и
и  . Найти
вероятность попадания
. Найти
вероятность попадания  в интервал
в интервал  .
.
Решение: Поскольку 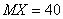 и
и  , то
, то 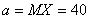 ,
, 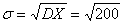
Для нахождения искомой вероятности воспользуемся
формулой

Ответ: 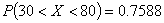
8. Ряд наблюдений для отклонения
воздушного судна от заданной высоты полета (в м) имеет вид:
+27; +38; -5; -36; -62; -77;
-85; -54; -8; +25; +34; +73; +112; +90; +61; +37; -15; -29; -62; -33; -44; -17;
+20; +40; +47; +61; +10; -8.
Построить интервальный вариационный
ряд. Дать статистические оценки среднего значения 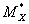 , дисперсии
, дисперсии 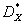 и среднего
квадратичного отклонения
и среднего
квадратичного отклонения 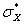 генеральной
совокупности, а так же интервальную оценку
генеральной
совокупности, а так же интервальную оценку 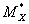 с доверительной вероятностью 0,99.
Построить статистические графики - гистограмму (вместе с плотностью нормального
распределения с параметрами
с доверительной вероятностью 0,99.
Построить статистические графики - гистограмму (вместе с плотностью нормального
распределения с параметрами 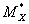 и
и 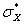 ) и выборочную функцию
распределения.
) и выборочную функцию
распределения.
Решение: Упорядочим
данный ряд по убыванию:
+112; +90; +73; +61; +61; +47; +40; +38; +37;
+34; +27; +25; +20; +10; -5; -8; -8; -15; -17; -29; -33; -36; -44; -54; -62;
-62; -77; -85.
Тогда  ,
, 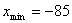
Число интервалов определим по
формуле Стерджеса:
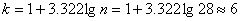
Длина каждого частичного интервала

Построим интервальный вариационный
ряд:
|
Интервал
|
-85
-52,17
|
-52,17
-19,34
|
-19,34
13,49
|
13,49
46,32
|
46,32
79,15
|
79,15
112
|
|
Частота
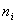 546742 546742
|
|
|
|
|
|
|
|
Середина
интервала 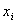 -68,585-35,755-2,92529,90562,73595,575 -68,585-35,755-2,92529,90562,73595,575
|
|
|
|
|
|
|
Найдем статистические оценки

Найдем интервальную оценку  . Поскольку
доверительная вероятность
. Поскольку
доверительная вероятность 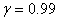 , то
, то 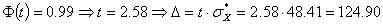
Тогда искомый доверительный интервал
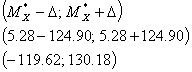
Плотность нормального распределения
с параметрами 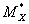 и
и 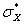 имеет вид:
имеет вид:
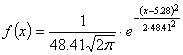
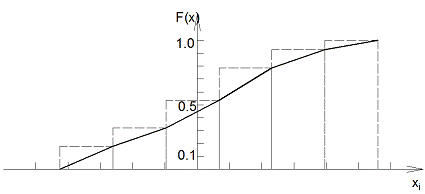
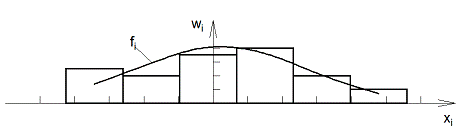
Построим гистограмму и функцию
плотности на одном графике:
|
№
интервала
|
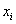 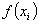  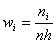 
|
|
|
|
|
|
1
|
-68,585
|
0,0028
|
0,178
|
0,005
|
0,178
|
|
2
|
-35,755
|
0,0058
|
0,143
|
0,004
|
0,321
|
|
4
|
-2,925
|
0,0081
|
0,214
|
0,007
|
0,535
|
|
3
|
29,905
|
0,0072
|
0,250
|
0,008
|
0,785
|
|
5
|
62,735
|
0,143
|
0,004
|
0,928
|
|
6
|
95,575
|
0,0014
|
0,072
|
0,002
|
1,000
|
Построим выборочную функцию распределения