Кратные интегралы
КУРСОВАЯ
РАБОТА
По
дисциплине Математика
На
тему Кратные интегралы
СОДЕРЖАНИЕ
1. КРАТНЫЕ КРИВОЛИНЕЙНЫЕ И
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
.1 Определенный интеграл
.2 Двойной интеграл
.3 Тройной интеграл
.4 Кратные интегралы в криволинейных
координатах
.5 Криволинейные интегралы
.6 Поверхностные интегралы
ПРАКТИЧЕСКАЯ ЧАСТЬ
ПРИЛОЖЕНИЯ
СПИСОК ЛИТЕРАТУРЫ
1 КРАТНЫЕ, КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ
ИНТЕГРАЛЫ
1.1 Определенный
интеграл
Пусть функция y=ƒ(x)
определена на отрезке [a;b],a<b.
Выполним следующие действия.
1. С помощью точек a=x0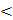 x1
x1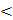 x2
x2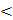 …
…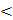 xn=b(i=
xn=b(i=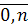 ) разобьем
отрезок [a,b] на n частичных
отрезков [x0;x1],[x1,x2],…,[xn-1;xn],обозначим
) разобьем
отрезок [a,b] на n частичных
отрезков [x0;x1],[x1,x2],…,[xn-1;xn],обозначим  xi= xi - xi-1 (см. рис.
1).
xi= xi - xi-1 (см. рис.
1).
c1 ci cn
a=x0 x1 xi-1 xi b=xn
Рис.1
. В каждом частичном отрезке [xi-1;xi], i =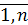 произвольным образом выберем точку ci
произвольным образом выберем точку ci 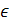 [xi-1;xi] и вычислим
значение рассматриваемой функции в ней ƒ(ci).
[xi-1;xi] и вычислим
значение рассматриваемой функции в ней ƒ(ci).
.Составляем интегральную сумму
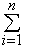 ƒ(ci)*
ƒ(ci)* xi
xi
.Находим предел интегральной суммы
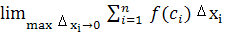
Если предел интегральных сумм
конечен (существует),не зависит от способа разбиения отрезка АВ на участки,не
зависит от выбора точки на каждом из отрезков ,то он определяет определенный
интеграл, то есть:
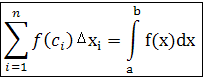
1.2 Двойной
интеграл
Рассмотрим в плоскости Оху замкнутую
область D,
ограниченную линией L. Разобьем эту область какими-нибудь
линиями на п частей 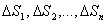 , а
соответствующие наибольшие расстояния между точками в каждой из этих частей
обозначим d1, d2, ..., dn. Выберем в
каждой части
, а
соответствующие наибольшие расстояния между точками в каждой из этих частей
обозначим d1, d2, ..., dn. Выберем в
каждой части 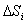 точку Рi.
точку Рi.
Пусть в области D
задана функция z = f(x,
y). Обозначим через f(P1),
f(P2),…,
f(Pn)
значения этой функции в выбранных точках и составим сумму произведений вида f(Pi)ΔSi
:
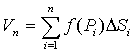 , (1)
, (1)
называемую интегральной суммой для
функции f(x, y) в области D.
Если существует один и тот же предел
интегральных сумм (1) при 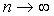 и
и 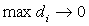 , не
зависящий ни от способа разбиения области D на части,
ни от выбора точек Pi в них, то он называется двойным
интегралом от функции f(x, y) по области
D и
обозначается
, не
зависящий ни от способа разбиения области D на части,
ни от выбора точек Pi в них, то он называется двойным
интегралом от функции f(x, y) по области
D и
обозначается
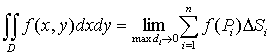 . (2)
. (2)
Вычисление двойного интеграла по
области D,
ограниченной линиями 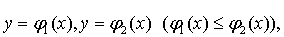 x = a, x = b ( a < b ), где φ1(х) и φ2(х)
непрерывны на [a, b] (рис. 1)
сводится к последовательному вычислению двух определенных интегралов, или так
называемого двукратного интеграла:
x = a, x = b ( a < b ), где φ1(х) и φ2(х)
непрерывны на [a, b] (рис. 1)
сводится к последовательному вычислению двух определенных интегралов, или так
называемого двукратного интеграла:
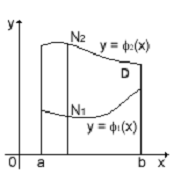
Рис. 1
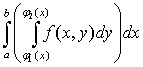 =
= 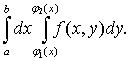 (3)
(3)
.3
Тройной интеграл
Понятие тройного интеграла вводится по аналогии
с двойным интегралом.
Пусть в пространстве задана некоторая область V,
ограниченная замкнутой поверхностью S.
Зададим в этой замкнутой области непрерывную функцию f(x,
y, z).
Затем разобьем область V
на произвольные части Δvi
, считая объем каждой части равным Δvi
, и составим интегральную сумму вида
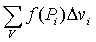 , (4)
, (4)
Предел при 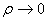 интегральных
сумм (11), не зависящий от способа разбиения области V и выбора
точек Pi в каждой
подобласти этой области, называется тройным интегралом от функции f(x, y, z) по области
V:
интегральных
сумм (11), не зависящий от способа разбиения области V и выбора
точек Pi в каждой
подобласти этой области, называется тройным интегралом от функции f(x, y, z) по области
V:
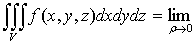
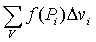 . (5)
. (5)
Тройной интеграл от функции f(x,y,z)
по области V равен трехкратному
интегралу по той же области:
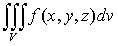
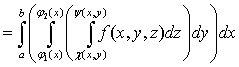 . (6)
. (6)
.4 Кратные
интегралы в криволинейных координатах
Введем на плоскости криволинейные
координаты, называемые полярными. Выберем точку О (полюс) и выходящий из нее
луч (полярную ось).
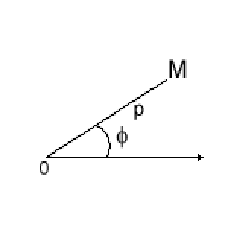
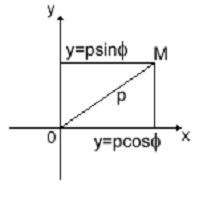
Рис. 2 Рис. 3
Координатами точки М (рис. 2) будут
длина отрезка МО - полярный радиус ρ и угол φ между МО и
полярной осью: М(ρ,φ). Отметим,
что для всех точек плоскости, кроме полюса, ρ > 0, а полярный
угол φ будем
считать положительным при измерении его в направлении против часовой стрелки и
отрицательным - при измерении в противоположном направлении.
Связь между полярными и декартовыми
координатами точки М можно задать, если совместить начало декартовой системы
координат с полюсом, а положительную полуось Ох - с полярной осью (рис. 3).
Тогда x=ρcosφ, у=ρsinφ . Отсюда 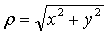 , tg
, tg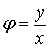 .
.
Зададим в области D,
ограниченной кривыми ρ=Φ1
(φ)
и ρ=Φ2
(φ),
где φ1
<
φ < φ2 , непрерывную функцию z
= f(φ, ρ) (рис.
4).
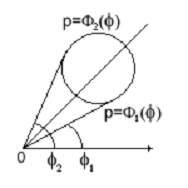
Рис. 4
Тогда
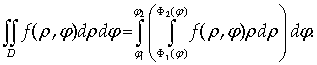 (7)
(7)
В трехмерном пространстве вводятся
цилиндрические и сферические координаты.
Цилиндрические координаты точки Р(ρ,φ,z) - это
полярные координаты
ρ, φ
проекции этой точки на плоскость Оху и аппликата данной точки z (рис.5).
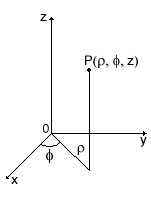
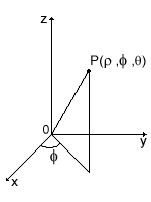
Рис.5 Рис.6
Формулы перехода от цилиндрических координат к
декартовым можно задать следующим образом:
x = ρ
cosφ,
y = ρ
sinφ,
z = z.
(8)
В сферических координатах положение точки в
пространстве определяется линейной координатой r
- расстоянием от точки до начала декартовой системы координат (или полюса
сферической системы), φ - полярным
углом между положительной полуосью Ох и проекцией точки на плоскость Оху, и
θ
- углом между положительной полуосью оси Оz
и отрезком OP (рис.6).
При этом
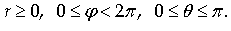
Зададим формулы перехода от
сферических координат к декартовым:
x = r sinθ cosφ, y = r sinθ sinφ, z = r cosθ. (9)
Тогда формулы перехода к
цилиндрическим или сферическим координатам в тройном интеграле будут выглядеть
так:
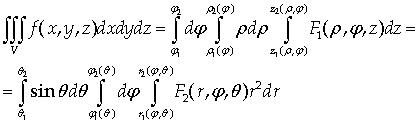 , (10)
, (10)
1.5
Криволинейные интегралы
Рассмотрим на плоскости или в
пространстве кривую L и функцию f,
определенную в каждой точке этой кривой. Разобьем кривую на части Δsi длиной Δsi и выберем
на каждой из частей точку Mi. Назовем d длину
наибольшего отрезка кривой: 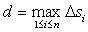 .
.
Криволинейным интегралом первого
рода от функции f по кривой L называется
предел интегральной суммы 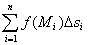 , не
зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi:
, не
зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi:
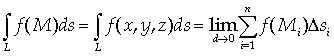 (24)
(24)
Если кривую L
можно задать параметрически:
x = φ(t),
y = ψ(t),
z = χ(t),
t0 ≤ t
≤
T,
то способ вычисления криволинейного интеграла
первого рода задается формулой
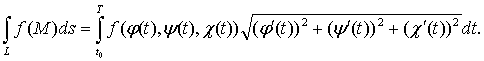 (25)
(25)
В частности, если кривая L задана на
плоскости явным образом:
у=φ(х),
где х1 ≤ х ≤ х2, формула
(40) преобразуется к виду:
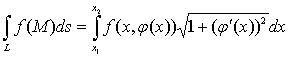 . (26)
. (26)
Теперь умножим значение функции в
точке Mi не на длину
i-го отрезка,
а на проекцию этого отрезка, скажем, на ось Ох, то есть на разность xi - xi-1 = Δxi.
Если существует конечный предел при 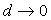 интегральной
суммы
интегральной
суммы 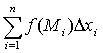 , не
зависящий от способа разбиения кривой на отрезки и выбора точек Mi, то он
называется криволинейным интегралом второго рода от функции f(M) по кривой L и
обозначается
, не
зависящий от способа разбиения кривой на отрезки и выбора точек Mi, то он
называется криволинейным интегралом второго рода от функции f(M) по кривой L и
обозначается
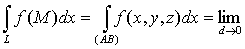
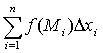 . (27)
. (27)
Подобным образом можно определить и
криволинейные интегралы 2-го рода вида
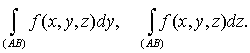
Если вдоль кривой L определены
функции
P(M)=P(x, y, z), Q(M) = Q(x, y, z), R(M) = R(x, y, z),
которые можно считать компонентами
некоторого вектора 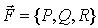 , и
существуют интегралы
, и
существуют интегралы
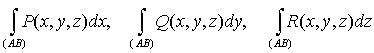 ,
,
тогда их сумму называют
криволинейным интегралом второго рода (общего вида) и полагают
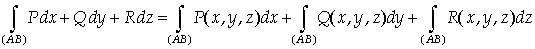
Если кривая L задана
параметрическими уравнениями
x = φ(t), y = ψ(t), z = χ(t), α ≤ t ≤ β ,
где φ, ψ, χ - непрерывно
дифференцируемые функции, то
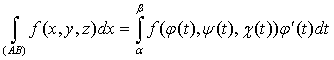 . (28)
. (28)
Связь между двойным интегралом и
криволинейным интегралом 2-го рода задается формулой Грина:
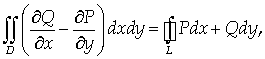 (29)
(29)
где L - замкнутый
контур, а D - область,
ограниченная этим контуром.
Необходимыми и достаточными условиями
независимости криволинейного интеграла
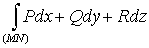
от пути интегрирования являются:
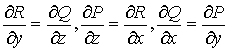 . (30)
. (30)
При выполнении условий (30) выражение Pdx
+ Qdy +Rdz
является полным дифференциалом некоторой функции и. Это позволяет свести
вычисление криволинейного интеграла к определению разности значений и в
конечной и начальной точках контура интегрирования, так как
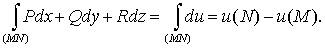
При этом функцию и можно найти по
формуле
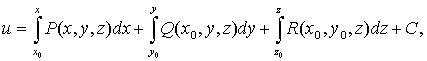 (31)
(31)
где (x0,
y0, z0)
- точка из области D, a
C - произвольная
постоянная.
1.6 Поверхностные
интегралы
Рассмотрим некоторую поверхность S,
ограниченную контуром L,
и разобьем ее на части S1,
S2,…, Sп
(при этом площадь каждой части тоже обозначим Sп).
Пусть в каждой точке этой поверхности задано значение функции f(x,
y, z).
Выберем в каждой части Si
точку
Mi (xi,
yi, zi)
и составим интегральную сумму
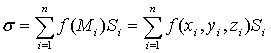 .
.
Если существует конечный предел при 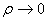 этой
интегральной суммы, не зависящий от способа разбиения поверхности на части и
выбора точек Mi, то он
называется поверхностным интегралом первого рода от функции f(M) = f(x, y, z) по
поверхности S и
обозначается
этой
интегральной суммы, не зависящий от способа разбиения поверхности на части и
выбора точек Mi, то он
называется поверхностным интегралом первого рода от функции f(M) = f(x, y, z) по
поверхности S и
обозначается
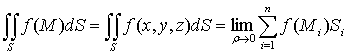 . (32)
. (32)
Если поверхность S
задается явным образом, то есть уравнением вида z
= φ(x, y),
вычисление поверхностного интеграла 1-го рода сводится к вычислению двойного
интеграла:
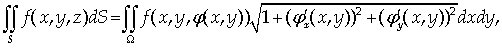 (33)
(33)
где Ω - проекция
поверхности S на
плоскость Оху.
Разобьем поверхность S на части S1, S2,…, Sп, выберем в
каждой части Si точку Mi(xi, yi, zi), и умножим
f(Mi) на площадь
Di проекции
части Si на
плоскость Оху. Если существует конечный предел суммы
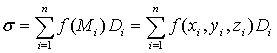 ,
,
не зависящий от способа разбиения поверхности и
выбора точек на ней, то он называется поверхностным интегралом второго рода от
функции f(M)
по выбранной стороне поверхности S
и обозначается
интеграл предел координата
декартовый
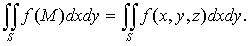 (34)
(34)
Подобным образом можно проектировать части
поверхности на координатные плоскости Оxz
и Оyz. Получим два
других поверхностных интеграла 2-го рода:
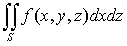 и
и 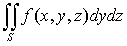 .
.
Рассмотрев сумму таких интегралов по одной и той
же поверхности соответственно от функций P(x,
y, z),
Q(x,
y, z),
R(x,
y, z),
получим поверхностный интеграл второго рода общего вида:
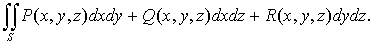 (35)
(35)
Если D, D΄ и D΄΄ - проекции
поверхности S на
координатные плоскости Оху, Oxz и Oyz, то
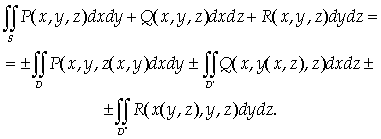 (36)
(36)
Связь между тройным интегралом по
трехмерной области V и поверхностным интегралом 2-го
рода по замкнутой поверхности S, ограничивающей тело V, задается
формулой Гаусса-Остроградского:

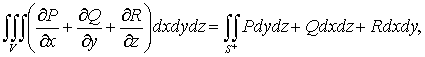 (37)
(37)
где запись «S+» означает,
что интеграл, стоящий справа, вычисляется по внешней стороне поверхности S.
Формула Стокса устанавливает связь между поверхностным
интегралом 1-го рода по поверхности σ
и криволинейным интегралом 2-го рода по ограничивающему ее контуру
λ
с учетом ориентации поверхности:
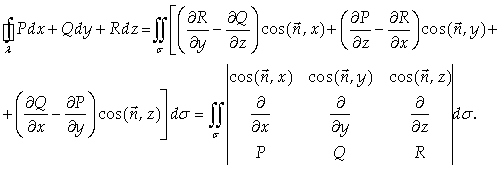 (38)
(38)
ПРИЛОЖЕНИЯ
Геометрические и физические приложениякратных
интегралов
) Площадь плоской области S:
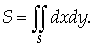 (11)
(11)
Пример 1.
Найти площадь фигуры D,
ограниченной линиями
у = 2, у = 5.
Решение.

Эту площадь удобно вычислять, считая у внешней
переменной. Тогда границы области задаются уравнениями
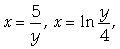 и
и
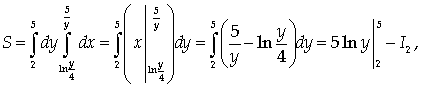
где 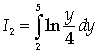 вычисляется с помощью
интегрирования по частям:
вычисляется с помощью
интегрирования по частям:
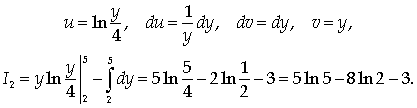
Следовательно,
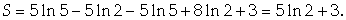
) Объем цилиндроида, то есть тела,
ограниченного частью поверхности S: z = f(x,y) ,
ограниченной контуром L, проекцией D этой
поверхности на плоскость Оху и отрезками, параллельными оси Оz и
соединяющими каждую точку контура L с
соответствующей точкой плоскости Оху:
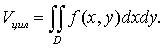 (12)
(12)
) Площадь части криволинейной
поверхности S, заданной
уравнением z = f(x,y),
ограниченной контуром L:
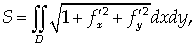 (13)
(13)
где D - проекция S на
плоскость Оху.
) Момент инерции относительно начала
координат О материальной плоской фигуры D:
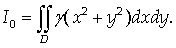 (14)
(14)
Пример 2.
Найти момент инерции однородной
круглой пластинки
(x - a)2 + (y - b)2 < 4b2
относительно начала координат.
Решение.
В силу однородности пластинки
положим ее плотность γ(х,у) = 1.

Центр круга расположен в точке C(a,
b), а его радиус
равен 2b.
Уравнения границ пластинки имеют вид
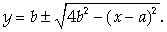
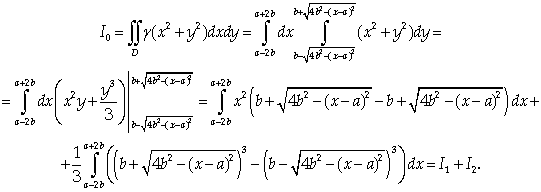
Вычислим каждый из полученных
интегралов отдельно.
Для вычисления интеграла I1 сделаем
замену: 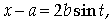
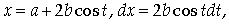 при x = a - 2b
при x = a - 2b 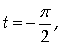 при
x = a + 2b
при
x = a + 2b 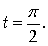
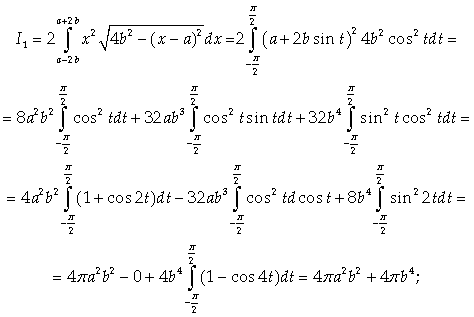
Для вычисления интеграла I2
преобразуем подынтегральную функцию по формуле разности кубов:
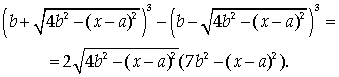
Тогда
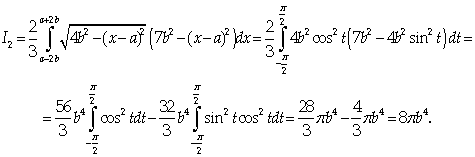
Следовательно, 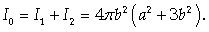
Моменты инерции фигуры D
относительно осей Ох и Оу:
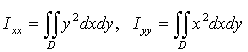 (15)
(15)
) Масса плоской фигуры D переменной
поверхностной плотности γ
= γ (х,
у):
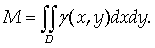 (16)
(16)
Пример 3.
Найти массу пластинки D плотности γ = ух3, если 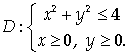
Решение.

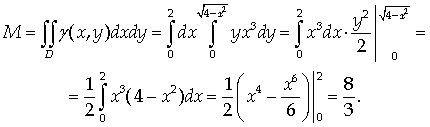
Координаты центра масс плоской
фигуры переменной поверхностной плотности γ = γ (х, у):
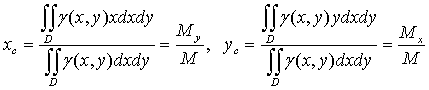 (17)
(17)
Пример 4.
Найти центр тяжести однородной
пластины D,
ограниченной кривыми
у2 = ах и 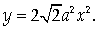
Решение.
Так как пластина однородна, т.е. ее
плотность постоянна, то можно принять ее за единицу.

Тогда 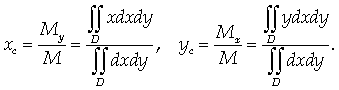
Найдем массу пластины, а для этого определим
абсциссу точки пересечения ограничивающих ее линий:
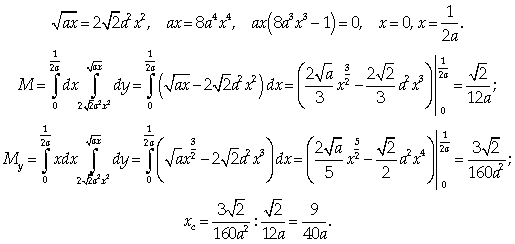
Соответственно
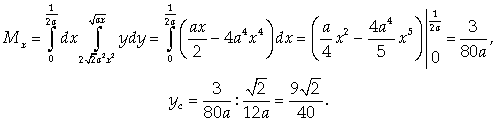
) Объем тела V:
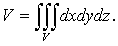 (18)
(18)
Пример 5.
Найти объем тела V,
ограниченного поверхностями 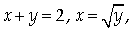
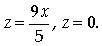
Решение.
Найдем проекцию тела на плоскость
Оху (при этом заметим, что плоскость 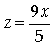 проектируется на эту плоскость в
виде прямой
проектируется на эту плоскость в
виде прямой
х = 0):

Определим абсциссу точки пересечения кривых
у = х2 и х + у = 2:
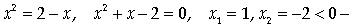 посторонний корень.
посторонний корень.
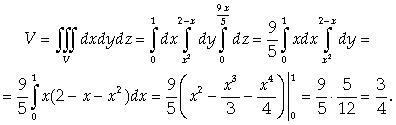
7) Масса тела V
плотности γ = γ (x,
y, z):
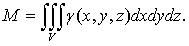 (19)
(19)
) Моменты инерции тела V
относительно координатных осей и начала координат:
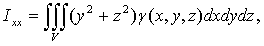
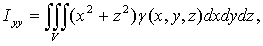 (20)
(20)
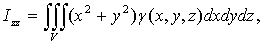
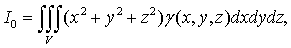 (21)
(21)
где γ (х,
y, z)
- плотность вещества.
Статические моменты тела относительно
координатных плоскостей Oyz,
Oxz, Oxy:
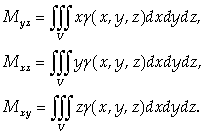 (22)
(22)
) Координаты центра масс тела:
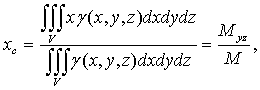
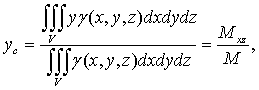 (23)
(23)
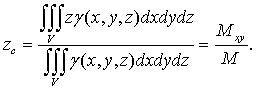
Геометрические и физические приложения
1) Длина кривой.
Если подынтегральная функция f(x,
y, z)
≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в
этом случае он равен длине кривой, по которой ведется интегрирование:
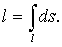 (39)
(39)
2) Масса кривой.
Считая, что подынтегральная функция γ
(x, y,
z) определяет
плотность каждой точки кривой, найдем массу кривой по формуле
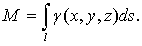 (40)
(40)
Пример 6.
Найти массу кривой с линейной
плотностью 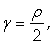 заданной в
полярных координатах уравнением ρ = 4φ, где
заданной в
полярных координатах уравнением ρ = 4φ, где 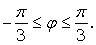
Решение.
Используем формулу (40) с учетом
того, что кривая задана в полярных координатах:
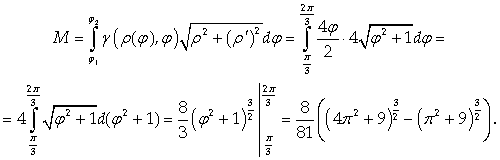
3) Моменты кривой l:
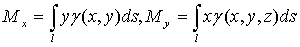 - (41)
- (41)
- статические моменты плоской кривой l
относительно осей Ох и Оу;
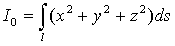 - (42)
- (42)
- момент инерции пространственной кривой
относительно начала координат;
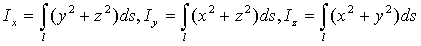 - (43)
- (43)
- моменты инерции кривой относительно
координатных осей.
) Координаты центра масс кривой вычисляются по
формулам
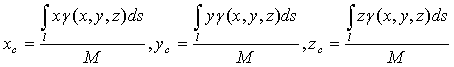 . (44)
. (44)
) Работа силы 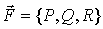 ,
действующей на точку, движущуюся по кривой (АВ):
,
действующей на точку, движущуюся по кривой (АВ):
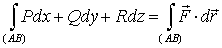 , (45)
, (45)
Пример 7.
Вычислить работу векторного поля 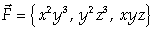 вдоль
отрезка прямой от точки А(-2;-3;1) до точки В(1;4;2).
вдоль
отрезка прямой от точки А(-2;-3;1) до точки В(1;4;2).
Решение.
Найдем канонические и
параметрические уравнения прямой АВ:
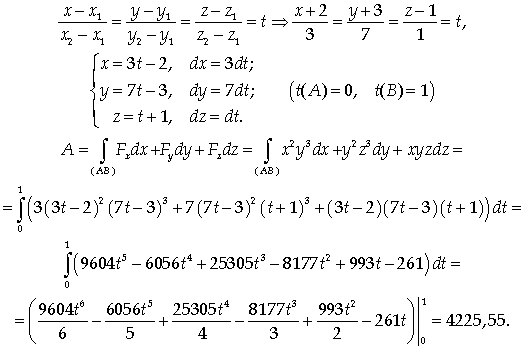
6) Площадь криволинейной поверхности,
уравнение которой
z = f(x,
y), можно найти в
виде:
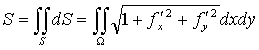 (46)
(46)
(Ω - проекция S на
плоскость Оху).
7) Масса поверхности
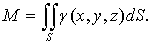 (47)
(47)
Пример 8.
Найти массу поверхности
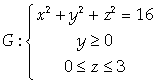
с поверхностной плотностью γ = 2z2 + 3.
Решение.

На рассматриваемой поверхности
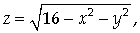
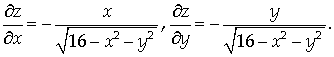 Тогда
Тогда

Проекцией D этой
поверхности на координатную плоскость Оху является полукольцо с границами в
виде дуг концентрических окружностей радиусов 3 и 4.

Применяя формулу (47) и переходя к полярным
координатам, получим:
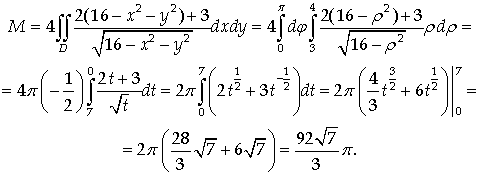
8) Моменты поверхности:
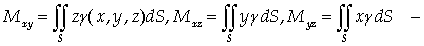 (48)
(48)
статические моменты поверхности
относительно координатных плоскостей Oxy, Oxz, Oyz;
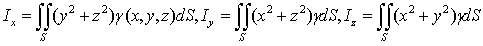 (49)
(49)
- моменты инерции поверхности
относительно координатных осей;
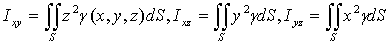 - (50)
- (50)
- моменты инерции поверхности
относительно координатных плоскостей;
- момент инерции поверхности относительно
начала координат.
9) Координаты центра масс поверхности:
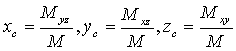 .
.
СПИСОК ЛИТЕРАТУРЫ:
1. Выгодский
М.Я. Справочник по высшей математике. - М.: Наука, 1966
. Письменный
Д.Т. - Ч.2 - 4-е изд. - М.: Айрис-пресс, 2006
. Кузнецов
Л.А. Сборник задач по высшей математике. - М.:1994