Нахождение переходных процессов в электрических цепях первого и второго порядка
СУРГУТСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ
АВТОМАТИКИ И ТЕЛЕКОММУНИКАЦИЙ
КАФЕДРА
ИНФОРМАТИКИ И КОМПЬЮТЕРНЫХ СИСТЕМ
Курсовое
проектирование по дисциплине
«Общая
электротехника»
расчёт
переходных процессов в электрических цепях
Выполнил: студент группы.12-91
Банишевский Р.Ю.
Проверила: доцент кафедры РЭ
Попова А.И.
Сургут 2011
г.
Содержание
электрический цепь ток
переходной
Введение
. Расчет переходных процессов классическим методом
.1 Определение начальных условий
.2 Определение установившейся составляющей
.3 Определение свободной составляющей
.4 Нахождение постоянных интегрирования
.5 Построение графика полученного аналитического выражения
. Расчет переходных процессов операторным методом
.1 Определение начальных условий
.2 Составление операторной схемы замещения
.3 Нахождение изображения искомой функции
.4 Нахождение оригинала искомой функции
.5 Построение графика полученного аналитического выражения
. Расчет переходных процессов с использованием интеграла
Дюамеля
.1 Нахождение переходной характеристики
.2 Аналитическое описание функции входного напряжения
.3 Запись интеграла Дюамеля
.4 Построение графика полученного аналитического выражения
Вывод по работе
Введение
Данная курсовая работа является частью курса по предмету «Теоретические
основы электротехники» и выполняется на основе индивидуального задания для
более глубокого изучения материала, более детального рассмотрения методик
расчетов при решении задач.
Работа предусматривает выполнение расчётов переходных процессов в электрических
цепях классическим и операторным методами, а также с помощью интеграла Дюамеля.
Параллельно этого студентом исследуются преимущества и недостатки каждого из
перечисленных методов расчета, производятся соответствующие выводы,
сравниваются полученные результаты.
В процессе решения данных задач применяются изученные законы и алгоритмы
нахождения неизвестных величин. Все расчёты и построения графических объектов
осуществляются по действующим методикам и стандартам.
1. Расчет переходных процессов классическим методом
1.1 Определение начальных условий
Для того чтобы найти ток через катушку индуктивности найдем протекающий в
цепи ток. Для определения независимых начальных условий перерисовываем схему до
коммутации.

Рис. 1.1: Схема исследуемой цепи до коммутации
Поскольку
в цепи находится источник постоянной ЭДС, то все токи и напряжения в ней будут
постоянными. Тогда, поскольку постоянный ток через конденсатор протекать не
может, ток, токи 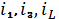
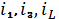 равны.
Заменим конденсатор разрывом, а катушку индуктивности - проводником.
равны.
Заменим конденсатор разрывом, а катушку индуктивности - проводником.
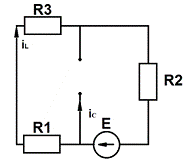
Рис. 1.2: Преобразованная схема исследуемой цепи до коммутации

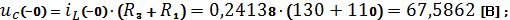
Таким
образом, начальные условия для тока на катушке 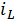
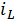 и
напряжения на конденсаторе
и
напряжения на конденсаторе 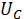
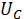 по
законам коммутации:
по
законам коммутации:

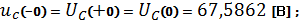
.2 Определение установившейся составляющей
Определим
сначала установившуюся составляющую. Будем считать, что система находится в
установившемся режиме. Перерисуем схему цепи для момента времени 
 .
.

Рис.
1.3: Схема исследуемой цепи в установившемся режиме.
Поскольку
в цепи находится источник постоянной ЭДС, то все токи и напряжения в ней будут
постоянными. Тогда, поскольку постоянный ток через конденсатор протекать не
может, ток 
 .
Преобразуем схему: объединим два параллельных резистора R1 и R4 в R5, заменим конденсатор разрывом, а катушку
индуктивности - проводником.
.
Преобразуем схему: объединим два параллельных резистора R1 и R4 в R5, заменим конденсатор разрывом, а катушку
индуктивности - проводником.

Рис. 1.4: Преобразованная схема исследуемой цепи в установившемся режиме.

Таким
образом, ток на катушке 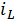
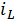 и
напряжение на конденсаторе
и
напряжение на конденсаторе 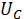
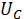 в
установившемся режиме:
в
установившемся режиме:
.3 Определение свободной составляющей
Перерисуем схему электрической цепи после коммутации, объединив два
параллельных резистора R1 и R4 в R5 . Обозначим направления обходов
выбранных контуров и направления токов.
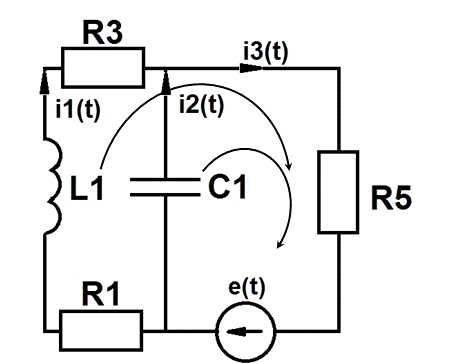
Рис. 1.5: Схема исследуемой цепи в момент коммутации.
Составим
систему уравнений по методу уравнений Кирхгофа и сведем ее к одному
интегро-дифференциальному уравнению относительно искомой величины - ток через
катушку индуктивности 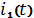
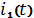 :
:
Из
уравнения 1 выразим ток 
 и
подставим в уравнения 2 и 3:
и
подставим в уравнения 2 и 3:
Выразим
из (5) уравнения ток 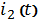
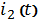 и
подставим в 6:
и
подставим в 6:
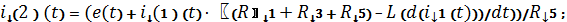
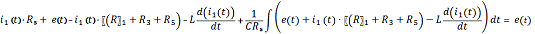
Приведем
подобные слагаемые и продифференцируем обе части уравнения:
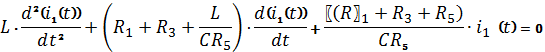
Мы
получили неоднородное дифференциальное уравнение второго порядка. По однородной
части данного уравнения составим характеристический полином, произведя
следующую замену:
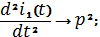

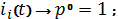
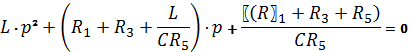
Получили
квадратное уравнение вида:
Переходя
к числовым значениям, получим:
a=0,038; b=371,761364;
с=698863,636;
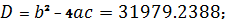

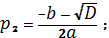
Т.к.
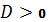
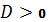 , и
корни характеристического полинома - действительные отрицательные, то,
следовательно, процесс - апериодический и решение для свободной составляющей
тока
, и
корни характеристического полинома - действительные отрицательные, то,
следовательно, процесс - апериодический и решение для свободной составляющей
тока 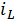
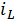 имеет
вид:
имеет
вид:

Аналитическое выражение процесса имеет вид:
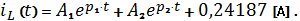
1.4 Нахождение постоянных интегрирования
Для нахождения постоянных интегрирования воспользуемся начальными
условиями для катушки индуктивности:
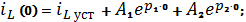
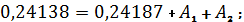

Для нахождения второго уравнения воспользуемся тем условием, что при
постоянном токе напряжении на зажимах катушки равно нулю:


В момент времени t=0:
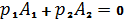
Итого,
получено два уравнения для нахождения постоянных интегрирования 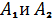
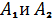 :
:
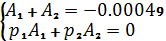
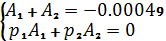 ;
; 

Отсюда
получаем: 

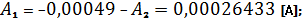
После
того как найдены постоянные интегрирования, запишем окончательное аналитическое
выражение переходного процесса:

.5 Построение графика полученного аналитического выражения.
Построим
график изменения 
 в
функции времени на интервале от
в
функции времени на интервале от
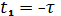
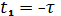 до
до 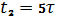
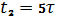 ,
,
где


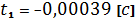
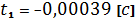 ;
;

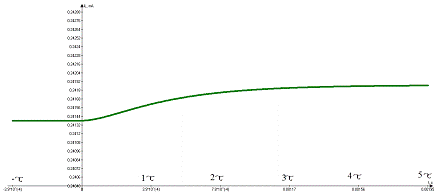
Рис.1.6: График полученного аналитического выражения.
2. Расчет переходных процессов операторным методом
.1 Определение начальных условий
Для того чтобы найти ток через катушку индуктивности найдем протекающий в
цепи ток. Для определения независимых начальных условий перерисовываем схему до
коммутации.

Рис. 2.1: Схема исследуемой цепи до коммутации
Поскольку
в цепи находится источник постоянной ЭДС, то все токи и напряжения в ней будут
постоянными. Тогда, поскольку постоянный ток через конденсатор протекать не
может, ток  , токи
, токи 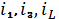
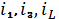 равны.
Заменим конденсатор разрывом, а катушку индуктивности - проводником.
равны.
Заменим конденсатор разрывом, а катушку индуктивности - проводником.

Рис. 2.2: Преобразованная схема исследуемой цепи до коммутации

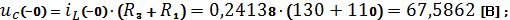
Таким
образом, начальные условия для тока на катушке 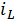
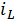 и
напряжения на конденсаторе
и
напряжения на конденсаторе 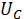
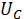 по
законам коммутации:
по
законам коммутации:

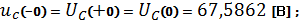
.2 Составление операторной схемы замещения
Перерисуем операторную схему замещения после коммутации, добавляя при
необходимости операторные источники, учитывающие энергии, накопленную в
конденсаторе и катушке индуктивности до коммутации.
Операторная ЭДС источника, связанного с энергией, накопленной в магнитном
поле катушки индуктивности:
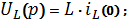
Операторная ЭДС источника, связанного с энергией, накопленной в
электрическом поле конденсатора:
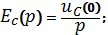
Операторная ЭДС источника с постоянной ЭДС:
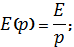
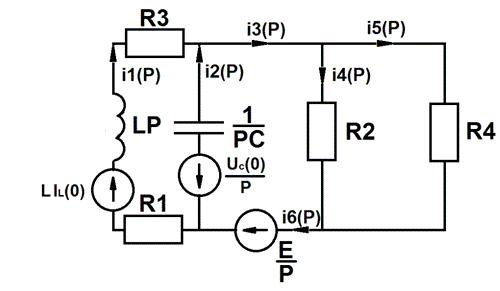
Рис. 2.3: Операторная схема замещения исследуемой цепи.
Преобразуем схему: объединим два параллельных резистора R1 и R4 в R5:

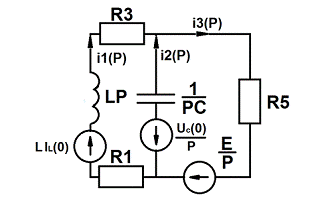
Рис. 2.4: Преобразованная операторная схема замещения исследуемой цепи.
2.3 Нахождение изображения искомой функции
В преобразованной операторной схеме замещения обозначим направления
обходов контуров и составим систему уравнений по методу уравнений Кирхгофа.
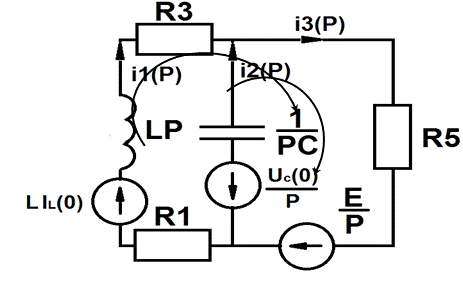
Рис. 2.5: Операторная схема замещения исследуемой цепи с обозначенными
направлениями обходов контуров.
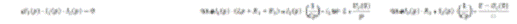
Выразим
из (1) уравнения ток 
 и
подставим в (3) уравнение:
и
подставим в (3) уравнение:
Выразим
из (6) уравнения 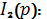
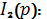
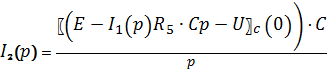
Подставим
получившееся уравнение в (5):
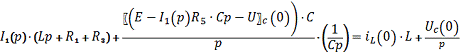
Выразим
из получившегося выражения ток 
 , это и
будет изображением тока, проходящего через катушку индуктивности:
, это и
будет изображением тока, проходящего через катушку индуктивности:
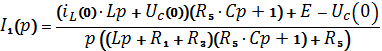
Упростим
выражение и, раскрыв скобки, приведем подобные слагаемые:

Получили
выражение вида:

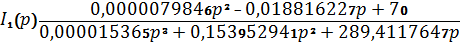
.4 Нахождение оригинала искомой функции.
Изображение тока через катушку индуктивности:
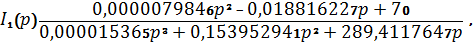
где:
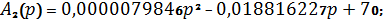
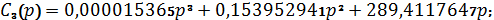
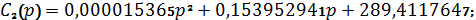
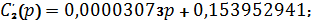
Для использования формулы разложения, найдем полюса изображения тока:
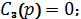
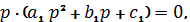
где
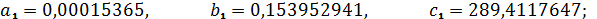
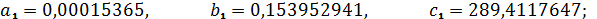
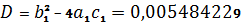



Т.к.
корни действительные, разные и один из них - нулевой, то используем следующую
формулу обратного преобразования Лапласа:
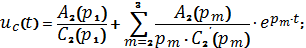
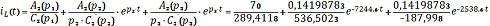
Окончательное аналитическое выражение переходного процесса:
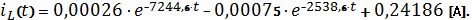
2.5 Построение графика полученного аналитического выражения.
Построим
график изменения 
 в
функции времени на интервале от
в
функции времени на интервале от 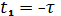
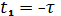 до
до 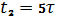
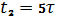 , где
, где 
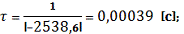
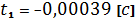
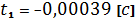 ;
;

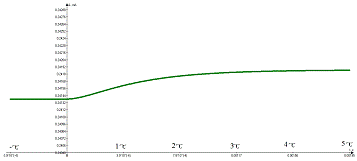
Рис.2.6: График полученного аналитического выражения.
3. Расчет переходных процессов с использованием интеграла
Дюамеля
.1 Нахождение переходной характеристики
Найдем
переходную характеристику цепи 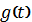
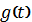 через
операторную передаточную функцию, для чего составим операторную схему замещения
цепи.
через
операторную передаточную функцию, для чего составим операторную схему замещения
цепи.
Поскольку
до коммутации в цепи отсутствовал источник ЭДС, то начальные условия для
катушки индуктивности будут нулевыми: 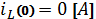
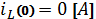 , и
операторная ЭДС источника, связанная с энергией, накопленной в магнитном поле
катушки индуктивности, в операторной схеме замещения будет отсутствовать.
, и
операторная ЭДС источника, связанная с энергией, накопленной в магнитном поле
катушки индуктивности, в операторной схеме замещения будет отсутствовать.
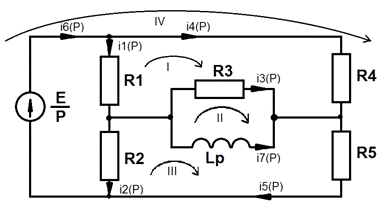
Рис.3.1:
Операторная схема замещения исследуемой цепи.
Учитывая
направления обходов контуров, составим систему уравнений по методу уравнений
Кирхгофа:
Искомое
напряжение 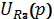
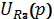 будем
находить методом Краммера. Для этого составим матрицу:
будем
находить методом Краммера. Для этого составим матрицу:

Далее,
находим ток через резистор R3:
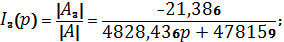
Изображение
напряжения на резисторе:

Запишем
операторную передаточную функцию:
Переходная
характеристика в операторном виде будет равна:
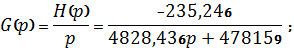
Используя
обратное преобразование Лапласа, переходим от изображения к функции времени:

Введем
обозначения:


Найдем
корни полинома знаменателя:


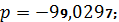
Для
нахождения переходной характеристики используем следующую формулу разложения:

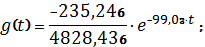
Окончательно
получаем:
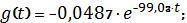
3.2 Аналитическое описание функции входного напряжения
Функция входного напряжения имеет следующий вид:

Рис.3.2: Функция входного напряжения.
Из
предыдущего пункта найдем постоянную времени 
 :
:
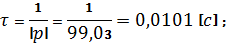
И
зададим значение времени 
 :
:
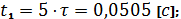
3.3 Запись интеграла Дюамеля
Общий вид интеграла Дюамеля:
Запишем интеграл Дюамеля для первого промежутка:
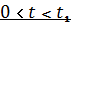
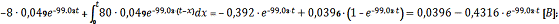
Для второго промежутка интеграл Дюамеля выглядит следующим образом:

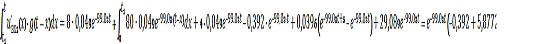
3.4 Построение графика полученного аналитического выражения
Для
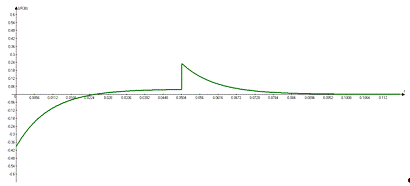
двух временных промежутков, используя полученные аналитические выражения,
построим график зависимости 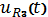
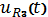 .
.
Вывод по работе
В ходе выполнения курсовой работы были изучены переходные процессы и
определена неизвестная величина (ток через катушку индуктивности) двумя
методами: операторным и классическим. С использованием интеграла Дюамеля
находили напряжение на резисторе, параллельно соединенного с катушкой
индуктивности.
В классическом и операторном методе полученные аналитические выражения
для переходного процесса полностью совпадают, совпадают также графики в
математическом пакете Advanced Grapher, выполняется
закон коммутации для катушки индуктивности - в начальный момент времени после
коммутации ток скачком не меняется.
Так же хочется отметить, что применение классического метода расчёта к
цепям более высокого порядка встречает определённые трудности. Главная из них -
возрастающий объём необходимых вычислений, связанных с решением уравнений
высокого порядка. В этой связи операторный метод имеет преимущество.
Существенно упрощает процесс вычисления неизвестной величины в операторном
методе - это преобразование Лапласа, которое позволяет перенести решение из
области функций действительного переменного в область комплексного. Далее,
дифференцирование и интегрирование заменяются соответствующими операциями
умножения и деления, т.е. система интегро-дифференциальных уравнений сводится к
системе алгебраических.
Важнейшим моментом при этом в практическом плане является необходимость
определения только независимых начальных условий, что существенно облегчает
расчет переходных процессов в цепях высокого порядка по сравнению с
классическим методом. Так же отпадает необходимость определения постоянных
интегрирования. В классическом метода тоже есть свои преимущества, например,
хорошо объясняет физический смысл того или иного процесса, тогда как
операторный метод формализован.
Интеграл Дюамеля удобно применять в цепях с входным сигналом, имеющим
сложную форму. Единственная сложность этого метода в нахождении переходной
характеристики цепи. Использование такой характеристики позволяет свести расчёт
реакции цепи от действия непериодического сигнала произвольной формы к
определению реакции цепи на простейшее воздействие типа импульсной функции, с
помощью которой аппроксимируется исходный сигнал.
Вычисления, произведённые в данной работе с использованием различных
способов расчётов, и применением различных пакетов инженерных и математических
программ позволяют легче освоить, углубить и закрепить знания.