Численные методы решения обыкновенных дифференциальных уравнений и систем
КУРСОВАЯ РАБОТА
Тема: Численные методы решения
обыкновенных дифференциальных уравнений и систем
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1.
ЧИСЛЕННОЕ РЕШЕНИЕ МЕТОДОМ ЭЙЛЕРА
1.1
Постановка задачи
1.2
Математическая модель задачи (метод Эйлера)
1.3
Исходные данные
1.4
Численное решение уравнения методом Эйлера в Excel
2.
ЧИСЛЕННОЕ РЕШЕНИЕ МЕТОДОМ РУНГЕ-КУТТА В EXCEL И TURBO PASCAL 7.0
2.1
Постановка задачи
2.2
Математическая модель задачи (метод Рунге-Кутта)
2.3
Исходные данные
2.4
Численное решение уравнения методом Рунге-Кутта в Excel
2.5
Блок-схема алгоритма
2.6
Программа на языке Turbo Pascal
2.7
Выполнение расчетов
2.8
Результаты расчетов
2.9
Представление результатов в виде графиков
2.10
Анализ результатов
3.
МЕТОД РУНГЕ-КУТТА ДЛЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
3.1
Постановка задачи
3.2
Математическая модель задачи
3.3
Исходные данные
3.4
Расчет контрольного варианта в Excel для тестирования
3.5
Блок-схема алгоритма
3.6
Численное решение задачи с использованием Turbo Pascal 7.0.
3.7
Выполнение расчетов
3.8
Результаты расчетов
3.9
Представление результатов в виде графиков
3.10
Анализ результатов
4.
МОДЕЛЬ ТИПА «ХИЩНИК-ЖЕРТВА» С УЧЕТОМ ВНУТРИВИДОВОГО ВЗАИМОДЕЙСТВИЯ
4.1
Постановка задачи
4.2
Математическая модель задачи
4.3
Исходные данные
4.4
Расчет контрольного варианта в Excel для тестирования
4.5
Блок-схема алгоритма
4.6
Численное решение задачи с использованием Turbo Pascal 7.0.
4.7
Выполнение расчетов
4.8
Результаты расчетов
4.9
Представление результатов в виде графиков
4.10
Анализ результатов
ЗАКЛЮЧЕНИЕ
СПИСОК
ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
В программе подготовки инженеров, как правило, включен ряд дисциплин,
изучающих сложные физические и химические процессы. Многие из них могут
описываться дифференциальными уравнениями. Математические модели реальных
процессов могут быть достаточно сложными, и соответствующие задачи не решаться
аналитически. В этом случае требуется решение с помощью приближенной модели или
приближенных (численных) методов. Вычислительная мощность современных ЭВМ, а
также их внедрение в научную и инженерную деятельность позволило решать
достаточно сложные уравнения, довольно точно описывающие рассматриваемые
явления, а также моделировать различные системы. Таким образом, изучение
изложенных методик является важной составляющей при освоении технической
специальности.
1. ЧИСЛЕННОЕ РЕШЕНИЕ МЕТОДОМ ЭЙЛЕРА
.1 Постановка задачи
Решить численно указанную задачу Коши для уравнения первого порядка
методом Эйлера, используя табличный процессор Excel.
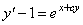
Исследовать поведение решения на отрезке [0,1.5] с начальным условием y(0)=0, числом отрезков разбиения n=15. Параметр c=0.2.
1.2 Математическая модель задачи (метод Эйлера).
По
условию выполнено соотношение: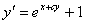 
Пусть начальное значение искомой функции y(x0) =y0. Можно приближенно
вычислить следующие значения, находя приращение функции через дифференциал:
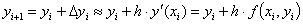
Для
проведения расчетов сначала вычисляется добавка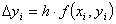 
к
текущему значению функции для вычисления следующего: Для вычислений
используются формулы:
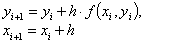
где
i = 0,1,…, n-1, x0, y0
определено из начальных условий, а f(xi, yi) -
функция правой части уравнения, вычисленная в узловой точке.
1.3 Исходные данные
Отрезок изменения аргумента: [0,1.5].
Начальное условие y(a): y(0)=0.
Число отрезков разбиения: 15. Тогда шаг h=0.1.
Параметр c=0.2.
1.4 Численное решение уравнения методом Эйлера в Excel
Рассмотрим
расчетную таблицу в Excel, содержащую три столбца для значений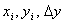 
. Дадим им заголовки x, y, 
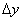, расположив их в ячейках A2:C2.
Для постоянных величин h, c отведем отдельные ячейки E2 и E3.
Их заголовки помещены в ячейки D2 и D3.
Расчеты
в таблице Excel выполняются по следующему алгоритму:
1. Вычисление первого столбца: первые два значения x = x0 и x1 = x0+h
вводятся в ячейки A3 и A4, затем, выделив две эти ячейки, заполняем столбец
значений x до достижения конечного значения x=1,5.
2.
Затем заполним первую строку расчетной таблицы: в столбце y введем y0 в ячейку
B3, в столбце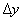 
введем в ячейку C3 формулу: =$E$2*(A3^2-B3^2)
(вычисляется приращение функции y для текущего значения x в соответствии с формулой ).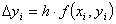
3. Вычисление второго столбца:
вводим
формулу =В3+С3 в ячейку B4 и копируем ее в ячейки B5:B18 (вычисляется новое
значение функции y при изменении x на один шаг с помощью линейного приращения
по формуле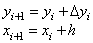 
).
копируем формулу из ячейки C3 в ячейки C4:C18
Рис. 1.1. Фрагмент рабочего листа с решением примера по методу Эйлера
2. ЧИСЛЕННОЕ РЕШЕНИЕ МЕТОДОМ РУНГЕ-КУТТА В EXCEL И TURBO
PASCAL 7.0
2.1 Постановка задачи
Решить численно указанную задачу Коши для уравнения первого порядка
методом Рунге-Кутта, используя табличный процессор Excel и с помощью программы на языке Турбо Паскаль 7.0.
Построить графики решений в Excel,
с помощью Мастера диаграмм. Провести анализ полученных результатов.
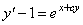
Исследовать поведение решения на отрезке [0,1.5] с начальным условием y(0)=0, числом отрезков разбиения n=15. Параметр c=0.2.
2.2 Математическая модель задачи (метод Рунге-Кутта).
Приводим
уравнение к виду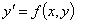 
.
По
условию выполнено соотношение: .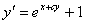
Расчетные
формулы для конкретного примера записываются, исходя из общих формул:
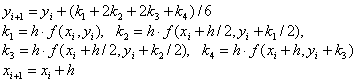
где
i = 0,1,…, n-1.
2.3 Исходные данные.
Отрезок изменения аргумента: [0,1.5].
Начальное условие y(a): y(0)=1.
Число отрезков разбиения: 15. Тогда шаг h=0.1.
2.4 Численное решение уравнения методом Рунге-Кутта в Excel
Заполняем таблицу Excel
в следующем порядке:
1. Первая строка заполнена именами переменных.
. Ячейка H21 отводится под значения константы h, ячейка G21 - под ее имя.
. Первый столбец заполняется значениями x.
. В ячейку B22 вводим значение y0.
. В ячейки С22, D22, E22, F22 вводим соответственно формулы:
=$H$21*(A22^2-B22^2)
=$H$21*((A22+$H$21/2)^2-(B22+C22/2)^2)
=$H$21*((A22+$H$21/2)^2-(B22+D22/2)^2)
=$H$21*((A22+$H$21)^2-(B22+E22)^2)
. В ячейку B23 вводим
формулу:
=B22+(C22+2*D22+2*E22+F22)/6
. В ячейки B24:B37 копируем формулу из ячейки B23.
. В ячейки C22:F36 копируем формулы из ячеек C22:F22.
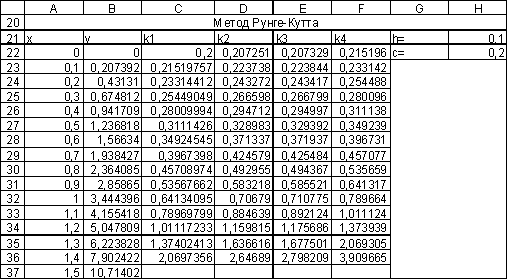
Рис. 2.1. Фрагмент рабочего листа с решением примера по методу
Рунге-Кутта
.5 Блок-схема алгоритма
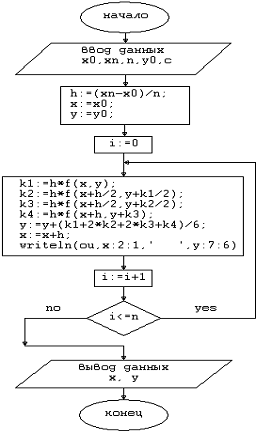
Рис. 2.2. Блок-схема алгоритма Рунге-Кутта для дифференциального
уравнения 1-го порядка
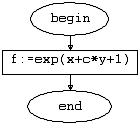
Рис.
2.3. Функция f(x,y:real):real
2.6.Программа на языке Turbo Pascal
Текст программы:
program rungekutt1_v3;
var,xn,y0,h,x,y,k1,k2,k3,k4:real;,i:integer;,ou:text;f(x,y:real):real;:=exp(x+c*y)+1;(inp,'inp1.txt');(inp);(inp,x0,xn,n,y0);(inp);:=(xn-x0)/n;:=x0;:=y0;(ou,'ou1.txt');(ou);(ou,'
x',' ','y');(ou,x:2:1,' ',y:7:6);i:=0 to n-1
do:=h*f(x,y);:=h*f(x+h/2,y+k1/2);:=h*f(x+h/2,y+k2/2);:=h*f(x+h,y+k3);:=y+(k1+2*k2+2*k3+k4)/6;:=x+h;(ou,x:2:1,'
',y:7:6);
close(ou)
end.
2.7 Выполнение расчетов
Исходные значения должны находиться в файле inp1.txt в
следующем порядке: левая граница промежутка, правая граница промежутка, число
отрезков разбиения, начальное значение функции, параметр.
2.8 Результаты расчетов
Результаты расчетов пишутся в файл ou1.txt.y
.0 0.000000
.1 0.207392
.2 0.431310
.3 0.674812
.4 0.941709
.5 1.236818
.6 1.566340
.7 1.938427
.8 2.364085
.9 2.858650
.0 3.444396
.1 4.155418
.2 5.047809
.3 6.223828
.4 7.902422
.5 10.714022
2.9 Представление результатов в виде графиков
Построим графики численного решения данного уравнения в Excel методами Эйлера и Рунге-Кутта.
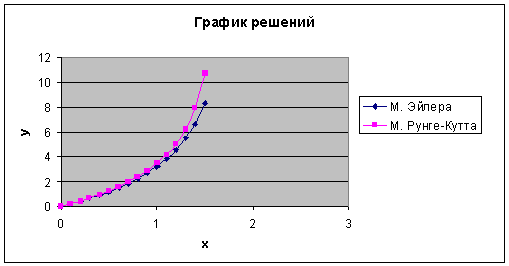
Рис.
2.4. График зависимости у(х).
На графике видно, что численные решения задачи различными способами
незначительно различаются.
Результаты, полученные при расчете с использованием Turbo Pascal 7.0 совпадают с расчетами (методами Эйлера и
Рунге-Кутта) в Excel, что
является косвенным признаком правильности решения задачи.
3. МЕТОД РУНГЕ-КУТТА ДЛЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
3.1 Постановка задачи
1) Решить численно указанную задачу Коши для уравнения второго порядка
методом Рунге-Кутта, с помощью программы на языке Turbo Pascal 7.0.
) Построить графики решения и его производной в Excel с помощью мастера диаграмм.
) Провести анализ полученных результатов.
3.2 Математическая модель задачи
Рассмотрим уравнение второго порядка, разрешенное относительно второй
производной:
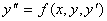(1.12)
на
отрезке [a, b] с начальными условиями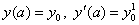 
.
Это
уравнение легко свести к системе уравнений первого порядка с помощью замены
переменных: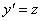 
. Тогда 
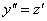и
уравнение (1.12) сводится к системе первого порядка
(1.13)
с
начальными условиями y(a)=y0, z(a)=z0 , где за z0 обозначено y10.
Данная
система может решаться как система двух уравнений первого порядка (1.8)-(1.9),
где 
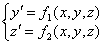(1.8)
на
отрезке [a, b] с начальными условиями
, (1.9)
Формулы метода Рунге - Кутта для системы двух уравнений имеют вид:
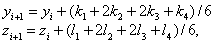(1.10)
Где
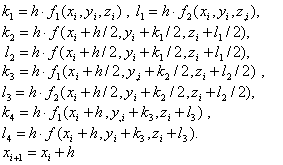(1.11)
Последовательно
вычисляются на каждом шаге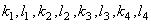 
, а затем
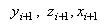, где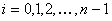 
.
3.3 Исходные данные
Уравнение:
.
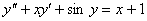Аргумент:
[0.5,1.5].
Начальные
условия: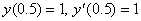 
.
Число
отрезков разбиения n: 10.
3.4 Расчет контрольного варианта в Excel для тестирования
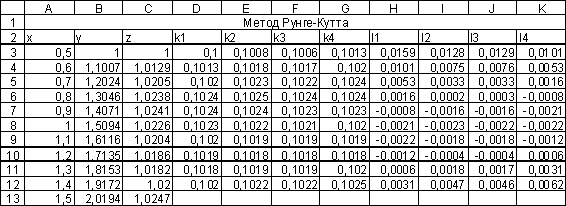
Рис.
3.1. Расчет контрольного варианта в режиме отображения данных.
3.5 Блок-схема алгоритма
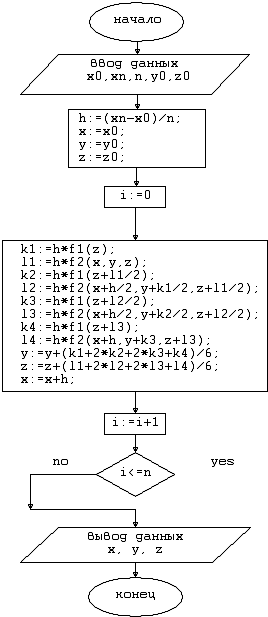
Рис. 3.2. Блок-схема алгоритма Рунге-Кутта для дифференциального
уравнения 2-го порядка.
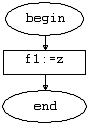
Рис.
3.3 Функция f1(z:real):real.
Рис.
3.4. Функция f2(x,y,z:real):real.
3.6 Численное решение задачи с использованием Turbo Pascal
7.0
Текст программы:
program rungekutt2_v3;
var,xn,y0,z0,h,x,y,z,k1,k2,k3,k4,l1,l2,l3,l4,c:real;,i:integer;,ou:text;f1(z:real):real;:=z;f2(x,y,z:real):real;:=x-x*z-sin(y)+1;(inp,'inp2.txt');(inp);(inp,x0,xn,n,y0,z0);(inp);:=(xn-x0)/n;:=x0;:=y0;:=z0;(ou,'ou2.txt');(ou);(ou,'
x',' ','y',' ','z');(ou,x:2:1,' ',y:7:6,' ',z:7:6);i:=0 to n-1
do:=h*f1(z);:=h*f2(x,y,z);:=h*f1(z+l1/2);:=h*f2(x+h/2,y+k1/2,z+l1/2);:=h*f1(z+l2/2);:=h*f2(x+h/2,y+k2/2,z+l2/2);:=h*f1(z+l3);:=h*f2(x+h,y+k3,z+l3);:=y+(k1+2*k2+2*k3+k4)/6;:=z+(l1+2*l2+2*l3+l4)/6;:=x+h;(ou,x:2:1,'
',y:7:6,' ',z:7:6);
close(ou)
end.
3.7 Выполнение расчетов
Исходные значения должны находиться в файле inp2.txt в
следующем порядке:
левая
граница промежутка, правая граница промежутка, число отрезков разбиения,
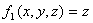начальное значение функции 
,
начальное значение функции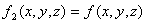 
.
3.8 Результаты расчетов
Результаты расчетов пишутся в файл ou2.txt.
x y z
.5 1.000000 1.000000
.6 1.100693 1.012891
.7 1.202401 1.020476
.8 1.304646 1.023823
.9 1.407064 1.024112
.0 1.509408 1.022562
.1 1.611554 1.020359
.2 1.713494 1.018593
.3 1.815320 1.018223
.4 1.917212 1.020041
.5 2.019422 1.024669
.9 Представление результатов в виде графиков
Построим графики численного решения данного уравнения в Excel методом
Рунге-Кутта.
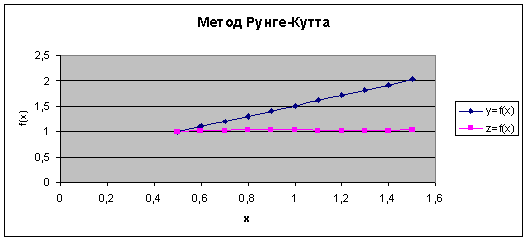
Рис.
3.5. График решения уравнений системы.
3.10 Анализ результатов
Результаты, полученные при расчете с использованием Turbo Pascal 7.0, совпадают с контрольным вариантом расчета по
методу Рунге-Кутта, произведенном в Excel, что является косвенным признаком правильности решения.
4. МОДЕЛЬ ТИПА «ХИЩНИК-ЖЕРТВА» С УЧЕТОМ ВНУТРИВИДОВОГО ВЗАИМОДЕЙСТВИЯ
.1 Постановка задачи
1) Решить численно задачу Коши для системы дифференциальных уравнений
первого порядка, являющейся моделью “хищник - жертва” при различных начальных
условиях и различных значениях параметров системы. Величину интервала решения и
шаг подобрать самостоятельно, так чтобы решение не выходило за пределы сотен
единиц и давало картину поведения траекторий. Решить задачу на отрезке [0,T] .
) Контрольный вариант рассчитать самостоятельно вручную или с помощью Excel.
) Построить траектории системы и графики зависимости искомых функций от
времени. Показать траектории при различных начальных данных в одной системе
координат.
) Провести анализ поведения решений.
4.2 Математическая модель задачи
Система уравнений, описывающая динамику популяций двух видов,
взаимодействующих между собой по типу «хищник-жертва» и с учетом внутривидового
взаимодействия:
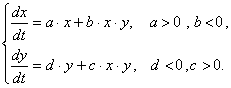
Заданные начальные условия при t=0
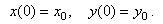
4.3 Исходные данные
Начальное и конечное значение аргумента t: t0, tn.
Начальные
значения неизвестных функций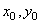 
.
Число
отрезков разбиения области интегрирования n.
t0=0, tn= 15, n=30, x0=100,
x0=90, x0=85, y0=30.
Параметры:
a=0.25,
b=-0.01, c=0.01, d=-1.0
Начальные данные: (100,30), (90,30), (85,30).
Таким образом, получаем систему:
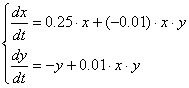
4.4 Расчет контрольного варианта в Excel для тестирования.
Рис.
4.1. Расчет контрольного варианта для тестирования (для демонстрации приведено
только 3 точки; специальная вставка).
4.5 Блок-схема алгоритма
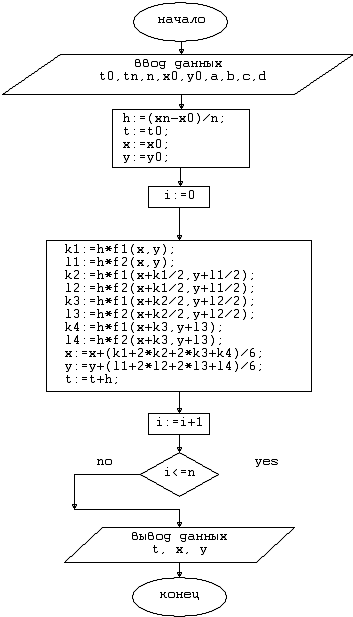
Рис. 4.2. Блок-схема алгоритма решения уравнения второго порядка.
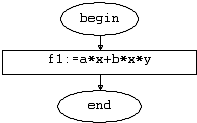
Рис.
4.3. Функция f1(x,y:real):real
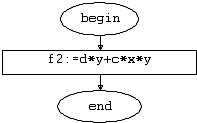
Рис.
4.4. Функция f2(x,y:real):real
4.6 Численное решение задачи с использованием Turbo Pascal
7.0
Текст программы:
program rungekutt3_v3;
var,tn,x0,xi,y0,yi,h,t,x,y,k1,k2,k3,k4,l1,l2,l3,l4,a,b,c,d:real;,i:integer;,ou:text;f1(x,y:real):real;:=a*x+b*x*y;f2(x,y:real):real;:=d*y+c*x*y;(inp,'inp3.txt');(inp);(inp,t0,tn,n,x0,y0,a,b,c,d);(inp);:=(tn-t0)/n;:=t0;:=x0;:=y0;(ou,'ou3.txt');(ou);(ou,'
t',' ','x',' y');(ou,t:2:1,' ',x:7:6,' ',y:7:6);i:=0 to n-1 do:=h*f1(x,y);:=h*f2(x,y);:=h*f1(x+k1/2,y+l1/2);:=h*f2(x+k1/2,y+l1/2);:=h*f1(x+k2/2,y+l2/2);:=h*f2(x+k2/2,y+l2/2);:=h*f1(x+k3,y+l3);:=h*f2(x+k3,y+l3);:=x+(k1+2*k2+2*k3+k4)/6;:=y+(l1+2*l2+2*l3+l4)/6;:=t+h;(ou,t:2:1,'
',x:7:6,' ',y:7:6);
close(ou)
end.
4.7 Выполнение расчетов
Исходные значения должны находиться в файле inp3.txt в
следующем порядке:
t0, tn, n, x0, y0, a, b, c, d.
4.8 Результаты расчетов
Результаты расчетов пишутся в файл ou3.txt.
t x y
.0 100.000000 30.000000
.5 97.561239 29.815776
.0 95.353243 29.288566
.5 93.509932 28.479413
.0 92.123606 27.469108
.5 91.246723 26.344787
.0 90.897734 25.189133
.5 91.068114 24.073624
.0 91.728650 23.055723
.5 92.834069 22.179046
.0 94.325805 21.475262
.5 96.133177 20.966690
.0 98.173439 20.668779
.5 100.351315 20.591967
.0 102.558763 20.742577
.5 104.675808 21.122501
.0 106.573439 21.727539
.5 108.119585 22.544379
.0 109.188919 23.546528
.5 109.676451 24.690050
.0 109.513570 25.910610
.5 108.683393 27.123941
.0 107.230929 28.231615
.5 105.263667 29.132734
.0 102.940443 29.739682
.5 100.450388 29.993707
.0 97.987412 29.875306
.5 95.726963 29.406092
.0 93.810121 28.642112
.5 92.336705 27.661622
t x y
.0 90.000000 30.000000
.5 88.124156 28.394467
.0 87.012742 26.674766
.5 86.658548 24.967828
.0 87.024499 23.371275
.5 88.055005 21.953894
.0 89.682440 20.760590
.5 91.829580 19.818959
.0 94.409030 19.145673
.5 97.320635 18.751745
.0 100.447745 18.646266
.5 103.653281 18.838414
.0 106.776833 19.337464
.5 109.634518 20.150400
.0 112.023954 21.276600
.5 113.737034 22.699264
.0 114.582555 24.374201
.5 114.418204 26.218489
.0 113.186582 28.104125
.5 110.944203 29.863405
.0 107.869782 31.310759
.5 104.242954 32.278633
.0 100.396886 32.655897
.5 96.660823 32.413057
.0 93.312336 31.604059
.5 90.551709 30.346190
.0 88.499048 28.788864
.5 87.206469 27.083737
.0 86.676001 25.363928
.5 86.876414 23.734166
.0 87.755735 22.269710
t x y
.0 85.000000 30.000000
.5 83.375891 27.708055
.0 82.724512 25.446600
.5 82.981548 23.347415
.0 84.068146 21.494220
.5 85.900092 19.933744
.0 88.390379 18.688092
.5 91.447368 17.765652
.0 94.970044 17.169616
.5 98.841344 16.904054
.0 102.920315 16.977785
.5 107.034024 17.406067
.0 110.970899 18.209699
.5 114.478409 19.410485
.0 117.269715 21.021441
.5 119.045257 23.030314
.0 119.534328 25.376914
.5 118.555694 27.929736
.0 116.083872 30.474461
.5 112.293600 32.730777
.0 107.552495 34.405945
.5 102.352137 35.271435
.0 97.202394 35.227990
.5 92.534733 34.326265
.0 88.649307 32.736884
.5 85.710787 30.691654
.0 83.775361 28.425558
.5 82.827091 26.138116
.0 82.809436 23.977472
.5 83.646711 22.041294
.0 85.255835 20.386485
4.9 Представление результатов в виде графиков.
Построим графики в Excel
численного решения данного уравнения.
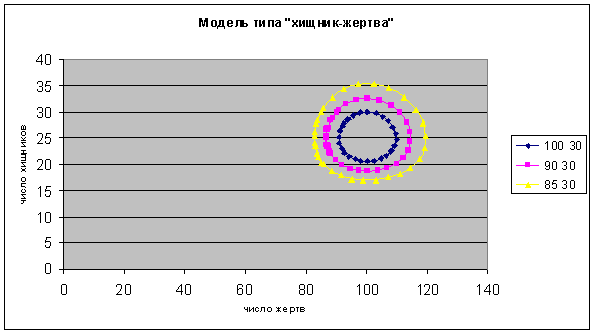
Рис. 4.1. Траектория решения при различных исходных данных.
4.10 Анализ результатов
Из графического представления решения системы дифференциальных уравнений
первого порядка, описывающей динамику популяций двух видов, взаимодействующих
между собой по типу «хищник-жертва» и с учетом внутривидового взаимодействия,
видно, что поведение системы изменяется при разных параметрах. В данном случае
при изменении y (начального количества хищников)
изменяется амплитуда колебаний численности обоих популяций в системе. Тем не
менее, во всех трех случаях система ведет себя стабильно.
ЗАКЛЮЧЕНИЕ
В данной работе рассмотрены методы решения дифференциальных уравнений и
систем. Закреплены навыки решения дифференциальных уравнений и систем первого
порядка методом Рунге-Кутта, которые могут быть применены в будущем при
построении различных математических моделей и в прикладных задачах. В ходе
решения использовались программы: Turbo Pascal 7.1.
процессор MS Excel. Отчет оформлен в Microsoft Word.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
численный метод
дифференциальное уравнение
1.
Н.С. Пискунов.
Дифференциальное и интегральное исчисление.
2.
Лабораторные
работы по курсу “Вычислительная математика и применение ЭВМ”, методическое
пособие. - Ленинград, 1987. - 160 с.
3.
Турчак Л.И.
Основы численных методов. - М.: ”Наука”, 1987. -
4.
Воробьева Г.Н.,
Данилова А.Н.. Практикум по вычислительной математике, М.:“Высшая школа”, 1991.
208 с.
5.
Информатика.
Программирование в среде Турбо Паскаль 7.0. Лабораторные работы 1-3, 4-6, 7-9.
СПб.: СПГГИ, 2003.
6.
Турбо Паскаль
7.0. Киев, Торгово-издательское бюро BHV, 1997.
7.
Вычислительная
техника и программирование. Практикум по программированию. - М.:“Высшая школа”,
1990 / Под ред. А.В. Петрова - 400 с.