Введение в исследование и дифференциальное исчисление функции одного переменного
РОССИЙСКАЯ
ФЕДЕРАЦИЯ
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ
ФЕДЕРАЛЬНОЕ
АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ТЮМЕНСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
ИНСТИТУТ
ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
Специальность
« Менеджмент организации »
КОНТРОЛЬНАЯ
РАБОТА
По
дисциплине: Высшая математика
На
тему: ВВЕДЕНИЕ В АНАЛИЗ И ДИФФЕРЕНЦИАЛЬНОЕ ИСЧЕСЛЕНИЕ ФУНКЦИИ ОДНОГО
ПЕРЕМЕННОГО
Выполнил:
Студент __1__ курса
______1_____ семестр
Шошина Екатерина Анатольевна
№ зачетки- 32091031
Тюмень,
2010
«ВВЕДЕНИЕ В АНАЛИЗ И ДИФФЕРЕНЦИАЛЬНОЕ ИСЧЕСЛЕНИЕ
ФУНКЦИИ ОДНОГО ПЕРЕМЕННОГО»
1. Вычислить
предел
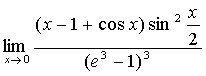
Решение.
При 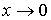 имеем
имеем
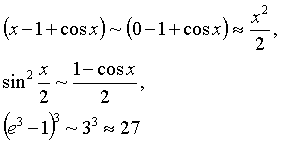
Следовательно,
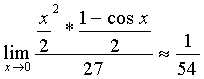
1. Найти
асимптоты функции
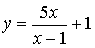
Решение.
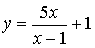 =
=
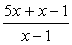

Очевидно, что функция при  .
.
Отсюда получаем, что
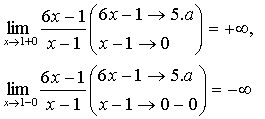
Следовательно,  -
вертикальная асимптота.
-
вертикальная асимптота.
Теперь найдем горизонтальные
асимптоты.
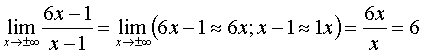
Следовательно,  -
горизонтальная асимптота при
-
горизонтальная асимптота при  .
.
1. Определить
глобальные экстремумы
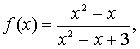 при хÎ[1,2]
при хÎ[1,2]
Найдем производную 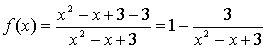
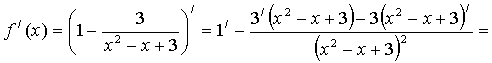
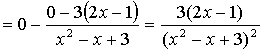
Для нахождения локальных экстремумов
решим уравнение 

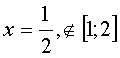 ,
,
значит для нахождения глобальных
экстремумов наибольшего и наименьшего значения на отрезке надо взять значения
функции в концах отрезка. 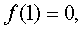 наименьшее
наименьшее  наибольшее
наибольшее
1. Исследовать
на монотонность, найти локальные экстремумы и построить эскиз графика функции

Найдем производную
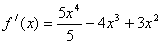
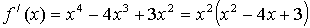
Решим уравнение

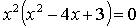
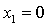
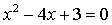



|
x
|
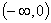 0 0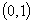 1(1,3)3 1(1,3)3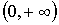
|
|
|
|
|
|
|
|
 +0+0-0+ +0+0-0+
|
|
|
|
|
|
|
|
|
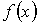 возрастаетт.перегибавозрастаетmaxубываетminвозрастает возрастаетт.перегибавозрастаетmaxубываетminвозрастает
|
|
|
|
|
|
|
|
Локальные экстремумы:  т. max
т. max
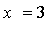 т. min
т. min
Точка перегиба 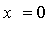
Промежутки монотонности:
возрастает при 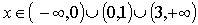 ,
,
убывает при 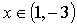 .
.
Точка  - локальный минимум.
- локальный минимум.
|
x
|
-2
|
-1
|
0
|
2
|
3
|
4
|
5
|
|
y
|
-30.4
|
-2.2
|
0
|
0.2
|
-1.6
|
-5.4
|
12.8
|
125
|

1. Найти
промежутки выпуклости и точки перегиба функции

Решение:
Требуется найти вторую производную 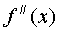
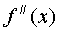 =
= =
=
Точки перегиба
 6x-12=0
6x-12=0
x=2
выпуклость вверх (выгнутость)
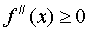

Выпуклость вниз (выпуклость)
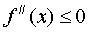
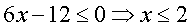
Отсюда следует, что функция выпуклая
при 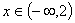 ; вогнутая
при
; вогнутая
при 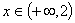 ; точка
перегиба x =2
; точка
перегиба x =2
«ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ И ЕГО
ПРИЛОЖЕНИЕ»
. Провести полное исследование свойств и
построить эскиз графика функции
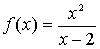 .
.
Решение.
1) Область определения функции
 .
.
) Функция не является четной или
нечетной, так как
 .
.
) Теперь найдем точки пересечения с
осями:
а) с оx:  , б) с oy
, б) с oy  .
.
) Теперь найдем асимптоты.
а) 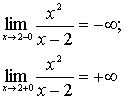
А значит, 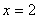 является
вертикальной асимптотой.
является
вертикальной асимптотой.
б) Теперь найдем наклонные асимптоты

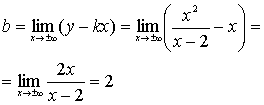
Отсюда следует, что
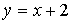 является наклонной асимптотой при
является наклонной асимптотой при 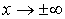 .
.
) Теперь найдем критические точки
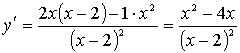
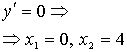
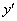 не существует при
не существует при 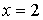 .
.
) 
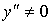
 не существует при
не существует при 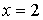
|
x
|
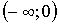 0 0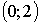 2 2 4 4
|
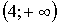
|
|
|
|
|
|
|
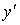 +0-Не
сущ.-0+ +0-Не
сущ.-0+
|
|
|
|
|
|
|
|
|
 ---Не
сущ.+++ ---Не
сущ.+++
|
|
|
|
|
|
|
|
y возрастает выпуклая max 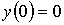 убывает
убывает
выпуклаяне
сущ.убывает
вогнутаяmin
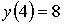 возрастает
возрастает
Построим эскиз графика функции 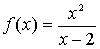

1. Найти
локальные экстремумы функции

Решение.
Решим систему
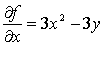
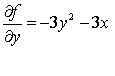
Известно, что необходимым условием
существования экстремума является равенство нулю частных производных.

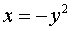 ,
, 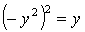 ,
, 
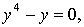

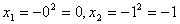
Две точки подозрительны на экстремум
(0,0), (-1,1)
Для анализа характера экстремума
найдем вторые производные
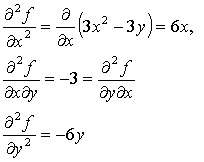
Найдем знаки выражений в
подозрительных точках, т.е
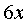 и
и 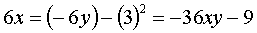
В точке (0,0) получим 0 и - 9
В точке (-1,1) получим - 6 и - 27
Вывод: в точке (0,0) экстремума нет,
в точке (-1,1) знаки - + это точка
максимума
1. Определить
экстремумы функции
 ,
,
если ху=100, х>0, у>0
Решение.
Сначала запишем функцию Лагранжа
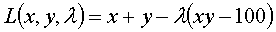 .
.
И исследуем ее

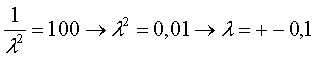
При  ,
,  ,
, 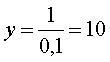
При 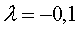 ,
, 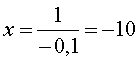 ,
, 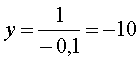
Т.к. 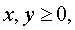 то получаем одну точку (10,10).
то получаем одну точку (10,10).
Это точка минимума 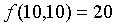

«ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОГО
ПЕРЕМЕННОГО»
1. Найти неопределенный интеграл

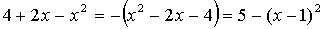
Поэтому сделаем замену y=x-1
Тогда x=y+1, dx=dy
Получим
 =
=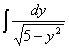 =
=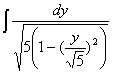 =
=
функция интеграл деление
асимптота
Сделаем замену 
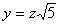

 =
=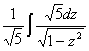 =
=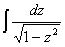
=arcsinz+C (табличный
интеграл)
=arcsin (возврат к y,x)
(возврат к y,x)
= arcsin 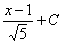
2. Найти неопределенный интеграл
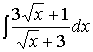
Решение:
Сделаем замену 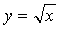 , тогда
, тогда 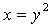 , dx=2ydy
, dx=2ydy
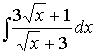 =
= =
=
Выполним деление с остатком:
 на
на  получим
получим 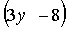 , остаток 24
, остаток 24
 =
= =
=
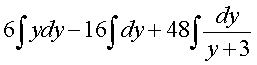
Первые два интеграла табличные, в
последнем - замена
Y+3=z, y=z-3, dy=dz

= =
=
3. Найти неопределенный интеграл
Решение:
Применим замену


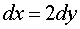
=
Так как 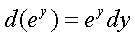 , то =
, то = 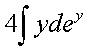
По формуле интегрирования по частям

= 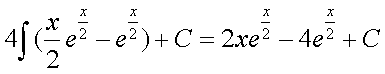
Вычислить 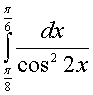
Решение:
Сделаем замену
 ;
; 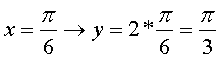
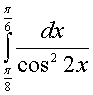 =
=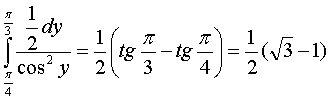
. Определить площадь плоской фигуры,
ограниченной кривыми
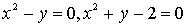
Решение:
) 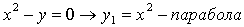

2) 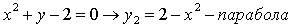

Найдем точки пересечения.
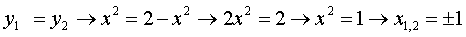
Точки пересечения (-1,1), (1,1)
Фигура располагается по x от -1 до 1

Требуется найти площадь заштрихованной области
При 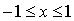 видим, что
видим, что 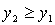 , поэтому
, поэтому

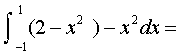
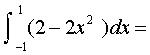
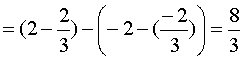
Список используемой литературы
1.Кругликов
В.И.Основы высшей математики: Учебное пособие. Тюмень: Мздательство Тюменского
государственного университета,2004.
.
Артемьева Е. Ю. Сборник задач по теории вероятностей и математической
статистике для психологов. - Издательство МГУ, 1969.
.
Макаров И. П. Дополнительные главы математического анализа. - М., «Просвещение»,
1968.
.
Мацкевич И. П., Свирид Г. П., Булдык Г. М. Сборник задач и упражнений по высшей
математике. - Минск,
«Высшая
школа», 1996.
.
Пугачев И. С. Теория вероятностей и математическая статистика. - М.: Наука,
1979.
.
Столл Р. Множества. Логика. Аксиоматические теории. - Москва, «Просвещение»,
1968.
.
Столяр А. А. Логическое введение в математику. - Минск, «Высшая школа», 1971.
.
Чистяков В. П. Курс теории вероятностей. -М.: Наука, 1978.
.
Шрейдер Ю. А. Равенство, сходство, порядок. -М.: Наука, 1971.