Совершенствование методики обучения решению геометрических задач на построение
Введение
В последние годы в связи с дифференциацией
обучения, появлением школ и классов различной профильной направленности, в том
числе гуманитарных, технических, экономических, естественно-математических и
других, по-новому встают вопросы о целях, содержании, формах и методах обучения
математике в школе, о месте и роли каждого школьного предмета.
Цели обучения обусловлены структурой личности,
общими целями образования, концепцией предмета математики, её статусом и ролью
в науке, культуре и жизнедеятельности общества, ценностями математического
образования, новыми образовательными идеями, среди которых важное место
занимают гуманизация и гуманитаризация образования.
Образование на современном этапе характеризуется
усилением внимания к ученику, к его саморазвитию и самопознанию, вниманием
ученика к окружающему миру и к себе, к воспитанию умения искать и находить свое
место в жизни. Целью современного образования является полное достижение
развития тех способностей личности, которые нужны ей и обществу. Включение ее в
социально ценную активность и обеспечение возможности эффективного
самообразования за пределами институционализированных образовательных систем.
Развитие логического мышления является одним из
важнейших элементов воспитания личности. Этому служит математика, и в первую
очередь - геометрия. Круг задач, рассматриваемых в геометрии, очень широк.
Среди них особое место занимают задачи на построение, которые способствуют
развитию у учащихся определенности, последовательности, обоснованности мышления.
На этих задачах учитель может научить учащихся таким методам познания как
анализ и синтез. Задачи на построение являются важным средством формирования у
учащихся геометрических представлений в целом. В процессе геометрических
построений учащиеся в практическом плане знакомятся со свойствами
геометрических фигур и отношений, учатся пользоваться чертежными инструментами,
приобретают графические навыки. В правильности многих математических
утверждений в большинстве случаев школьники убеждаются также в процессе
геометрических построений.
Задачи на построение еще в Древней Греции
приобрели важную роль, поскольку любые математические задачи, будь то
доказательство свойств или нахождение корней уравнений, решались
геометрическими способами. К построениям предъявлялись высокие требования
точности, простоты и экономности. Самой совершенной линией на плоскости
является окружность, а самой простой - прямая. Наиболее ценными считались
построения, использующие только эти две линии. Поскольку прямую можно провести
при помощи линейки (без делений), а окружность построить циркулем, то мы теперь
говорим о задачах на построение с помощью циркуля и линейки. циркуль позволяет
не только построить окружность с указанным радиусом, но и отложить отрезок
равный данному, и выяснить, какой из имеющихся отрезков длиннее. С помощью
линейки можно провести прямую через две данные точки. (Линейка с делениями,
которой мы пользуемся, не годится для измерений длин отрезков, она дает
приближенный результат - этого античные математики не могли допустить). А в
школе Платона при решении задач на построение не разрешалось использовать
никакие другие инструменты, кроме циркуля и линейки. Такое ограничение сыграло
большую роль в развитии геометрии, а в дальнейшем в установлении ее связей с
алгеброй.
Задачи на построение - это задачи, которые
значительно чаще других поражают красотой, оригинальностью и во многих случаях
простотой найденного решения, что вызывает к ним повышенный интерес.
Все вышесказанное, говорит об актуальности
выбранной темы, кроме того, тема методически недостаточно разработана и
вызывает трудности в обучении учащихся.
Гипотеза: предложенная система обучения решению
задач на построение, будет способствовать развитию наиболее прочных
конструктивных умений и навыков.
Объект исследования: процесс обучения геометрии
в основной школе.
Предмет исследования: методика обучения решению
задач на построение.
Цель исследования -совершенствование методики
обучения решению задач на построение, реализующей в достаточной мере
формирование конструктивных умений и навыков учащихся.
Для достижения данной цели планируется
реализовать следующие задачи:
1. Изучить теоретические основы и практическую
часть темы «Задачи на построение»
2. Рассмотреть различные виды задач на
построение;
. Разработать методические рекомендации к
изучению темы «Задачи на построение».
В исследовании планируется использовать
следующие методы:
. Изучение математических источников, в том
числе публикаций по данной теме в периодической печати;
. Анализ математической, методической и психолого
- педагогической литературы по данной теме;
. Систематизация и обобщение теоретического и
практического материала изученного материала.
Глава I.
Теоретические основы изучения темы «Задачи на построение»
Простейшие задачи на построение
. Построение угла равного данному
Задача. Отложить от данного луча угол, равный
данному.

Решение. Данный угол с вершиной А и луч ОМ
изображены на рисунке 1. Требуется построить угол, равный углу А, так, чтобы
одна из сторон совпала с лучом ОМ. Проведем окружность произвольного радиуса с
центром в вершине А данного угла. Эта окружность пересекает стороны угла в
точках В и С (Рис 2, а). Затем проведем окружность того же радиуса с центром в
начале данного луча ОМ. Она пересекает луч в точке D
(Рис. 2, б). После этого построим окружность с центром D,
радиус которой равен ВС. Окружности с центрами О и D
пересекаются в двух точках. Одну из этих точек обозначим буквой Е. Докажем, что
угол МОЕ - искомый.
Рассмотрим треугольники АВС и ОDЕ.
Отрезки АВ и АС являются радиусами окружности с центром А, а ОD
и ОЕ - радиусами окружности с центром О. Так как по построению эти окружности
имеют равные радиусы, то АВ=ОD
, АС=ОЕ. Также по построению ВС= DЕ.
Следовательно, DАВС=D ОDЕ
по трем сторонам. Поэтому Ð DОЕ=ÐВАС,
т.е. построенный угол МОЕ равен данному углу А.

Рис. 2

. Построение биссектрисы данного угла
Задача. Построить биссектрису данного угла.
Решение. Проведем окружность произвольного
радиуса с центром в вершине А данного угла. Она пересечет стороны угла в точках
В и С. Затем проведем две окружности одинакового радиуса ВС с центрами в точках
В и С (на рисунке 3 изображены лишь части этих окружностей). Они пересекутся в
двух точках. Ту из этих точек, которая лежит внутри угла ВАС, обозначим буквой
Е. Докажем, что луч АЕ является биссектрисой данного угла.
Рассмотрим треугольники АСЕ и АВЕ. Они равны по
трем сторонам. В самом деле, АЕ - общая сторона; АС и АВ равны, как радиусы
одной и той окружности; СЕ=ВЕ по построению. Из равенства треугольников АСЕ и
АВЕ следует, что ÐСАЕ=ÐВАЕ, т.е.
луч АЕ - биссектриса данного угла.

Рис. 3
. Построение середины отрезка
Задача. Построить середину данного отрезка.

Решение. Пусть АВ - данный отрезок. Построим две
окружности с центрами А и В радиуса АВ (рис. 4). Они пересекаются в точках Р и Q.
Проведем прямую РQ. Точка О
пересечения этой прямой с отрезком АВ и искомая середина отрезка АВ.
В самом деле, треугольники АРQ
и ВРQ равны по трем
сторонам, поэтому Ð1=Ð2.
Следовательно, отрезок РО - биссектриса
равнобедренного треугольника АРВ, а значит, и медиана, т.е. точка О - середина
отрезка АВ.
4. Построение перпендикулярных прямых
Задача. Через данную точку О провести прямую,
перпендикулярную данной прямой а.
Решение. Возможны два случая:1) точка О лежит на
прямой а; 2) точка О не лежит на прямой а.

Рассмотрим первый случай (рис. 5). Из точки О
проводим произвольным радиусом окружность. Она пересекает рямую а в двух
точках: А и В. из точек А и В проводим окружности радиусом АВ. Пусть С - точка
их пересечения. Искомая прямая проходит через точки О и С.
Перпендикулярность прямых ОС и АВ следует из
равенства углов при вершине О треугольников АСО и ВСО. Эти треугольники равны
по третьему признаку равенства треугольников.
Рассмотрим построение и доказательство

для второго случая (рис. 6).
Из точки О проводим окружность,
пересекающую прямую а. Пусть А и В - точки ее пересечения с прямой а. Из точек
А и В тем же радиусом проводим окружности. Пусть О - точка их
пересечения, лежащая в полуплоскости, отличной от той, в которой лежит точка О.
Искомая прямая проходит через точки О и О
- точка их
пересечения, лежащая в полуплоскости, отличной от той, в которой лежит точка О.
Искомая прямая проходит через точки О и О . Докажем это.
. Докажем это.
Обозначим через С точку пересечения
прямых АВ и ОО .
Треугольники АОВ и АО
.
Треугольники АОВ и АО В равны по
третьему признаку. Поэтому угол ОАС равен углу О
В равны по
третьему признаку. Поэтому угол ОАС равен углу О АС. А тогда треугольники ОАС и О
АС. А тогда треугольники ОАС и О АС равны по
первому признаку. Значит, их углы АСО и АСО
АС равны по
первому признаку. Значит, их углы АСО и АСО равны. А так как они смежные, то
они прямые. Таким образом, ОС - перпендикуляр, опущенный из точки О на прямую
а.
равны. А так как они смежные, то
они прямые. Таким образом, ОС - перпендикуляр, опущенный из точки О на прямую
а.
Построение треугольника по трем
элементам
Задача 1. Построить треугольник по
двум сторонам и углу между ними.
Решение. Прежде всего уточним, как
нужно понимать эту задачу, т. е. что здесь дано и что нужно построить. Даны
отрезки Р Q
Q , Р
, Р Q
Q и угол hk (рис. 7а).
Требуется с помощью циркуля и линейки (без масштабных делений) построить такой
треугольник АВС, у которого две стороны, скажем АВ и АС, равны данным отрезкам
Р
и угол hk (рис. 7а).
Требуется с помощью циркуля и линейки (без масштабных делений) построить такой
треугольник АВС, у которого две стороны, скажем АВ и АС, равны данным отрезкам
Р Q
Q и Р
и Р Q
Q , а угол А
между этими сторонами равен данному углу hk.
, а угол А
между этими сторонами равен данному углу hk.

Проведем прямую а и на ней с помощью
циркуля отложим отрезок АВ, равный отрезку Р Q
Q (рис. 7б). Затем построим угол ВАМ,
равный данному углу hk. На луче АМ отложим отрезок АС,
равный отрезку Р
(рис. 7б). Затем построим угол ВАМ,
равный данному углу hk. На луче АМ отложим отрезок АС,
равный отрезку Р Q
Q , и проведем
отрезок ВС. Треугольник АВС - искомый.
, и проведем
отрезок ВС. Треугольник АВС - искомый.
В самом деле, по построению АВ= Р Q
Q , АС= Р
, АС= Р Q
Q ,
,  А=
А= hk. описанный
ход построения показывает, что при любых данных отрезках Р
hk. описанный
ход построения показывает, что при любых данных отрезках Р Q
Q , Р
, Р Q
Q и
неразвернутом угле hk искомый треугольник построить
можно. Так как прямую а и точку А на ней можно выбрать произвольно, то
существует бесконечно много треугольников удовлетворяющих условиям задачи. Все
эти треугольники равны друг другу (по первому признаку равенства
треугольников), поэтому принято говорить , что данная задача имеет единственное
решение.
и
неразвернутом угле hk искомый треугольник построить
можно. Так как прямую а и точку А на ней можно выбрать произвольно, то
существует бесконечно много треугольников удовлетворяющих условиям задачи. Все
эти треугольники равны друг другу (по первому признаку равенства
треугольников), поэтому принято говорить , что данная задача имеет единственное
решение.
Задача 2. Построить треугольник по
стороне и двум прилежащим к ней углам.
Решение. Дан отрезок КМ и углы mp и rs (рис.8а).
Требуется с помощью циркуля и линейки построить такой треугольник АВС, у которого
сторона АВ, равна отрезку КМ, а углы А и В равны соответственно углам mp и rs.
Проведем прямую а и на ней с помощью
циркуля отложим отрезок АВ, равный отрезку КМ (рис. 8б). Затем построим угол ВАN, равный
данному углу mp. Построим
угол АВН равный углу rs. Обозначим точку пересечения
АN и BH как С.
Треугольник АВС - искомый.

В самом деле, по построению КМ=АВ,  ВАN=
ВАN= mp,
mp,
 АВН=
АВН= rs.
rs.
Описанный ход построения показывает, что при
любом данном отрезке КМ и условии  mp+
mp+ rs<180º
данный треугольник построить можно. Так как прямую а и точку А на ней можно
выбрать произвольно, то существует бесконечно много треугольников,
удовлетворяющих условиям задачи. Все эти треугольники раны друг другу (по
второму признаку равенства треугольников), поэтому принято говорить, что данная
задача имеет единственное решение.
rs<180º
данный треугольник построить можно. Так как прямую а и точку А на ней можно
выбрать произвольно, то существует бесконечно много треугольников,
удовлетворяющих условиям задачи. Все эти треугольники раны друг другу (по
второму признаку равенства треугольников), поэтому принято говорить, что данная
задача имеет единственное решение.
Задача 3. построить треугольник по трем
сторонам.
Решение. Пусть даны отрезки Р Q
Q , Р
, Р Q
Q и P
и P Q
Q (рис. 9а).
Требуется построить треугольник АВС, в котором АВ= Р
(рис. 9а).
Требуется построить треугольник АВС, в котором АВ= Р Q
Q , ВС= Р
, ВС= Р Q
Q , СА= P
, СА= P Q
Q .
.
Проведем прямую и на ней с помощью
циркуля отложим отрезок АВ, равный отрезку Р Q
Q (рис. 9б). Затем построим две
окружности: одну - с центром А и радиусом P
(рис. 9б). Затем построим две
окружности: одну - с центром А и радиусом P Q
Q , а другую -
с центром В и радиусом P
, а другую -
с центром В и радиусом P Q
Q . Пусть точка С - одна из точек
пересечения двух окружностей. Проведя отрезки АС и ВС, получим искомый
треугольник АВС. В самом деле, по построению АВ=P
. Пусть точка С - одна из точек
пересечения двух окружностей. Проведя отрезки АС и ВС, получим искомый
треугольник АВС. В самом деле, по построению АВ=P Q
Q , ВС= Р
, ВС= Р Q
Q , СА= P
, СА= P Q
Q , т.е.
стороны треугольника АВС равны данным отрезкам.
, т.е.
стороны треугольника АВС равны данным отрезкам.

Задача 3 не всегда имеет решение. Действительно,
во всяком треугольнике сумма любых двух сторон больше третьей стороны, поэтому
если какой-нибудь из данных отрезков больше или равен сумме двух других, то
нельзя построить треугольник, стороны которого равнялись бы данным отрезкам.
Теорема Фалеса
Теорема. Если на одной из двух прямых отложить
последовательно несколько равных отрезков и через их концы провести
параллельные прямые, то они отсекут на второй прямой равные между собой
отрезки.
Доказательство. Пусть на прямой  отложены
равные отрезки А
отложены
равные отрезки А А
А , А
, А А
А , А
, А А
А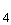 , … и через
их концы проведены параллельные прямые, которые пересекают прямую
, … и через
их концы проведены параллельные прямые, которые пересекают прямую  в точках В
в точках В , В
, В ,В
,В ,В
,В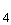 ,…(рис. 10).
Требуется доказать, что отрезки В
,…(рис. 10).
Требуется доказать, что отрезки В В
В , В
, В В
В , В
, В В
В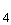 ,… равны друг другу. Докажем,
например, что В
,… равны друг другу. Докажем,
например, что В В
В = В
= В В
В .
.
Рассмотрим сначала случай, когда
прямые  и
и  параллельны
(рис. 10а). Тогда А
параллельны
(рис. 10а). Тогда А А
А = В
= В В
В и А
и А А
А = В
= В В
В как
противоположные стороны параллелограммов А
как
противоположные стороны параллелограммов А В
В В
В А
А и А
и А В
В В
В А
А . Так как А
. Так как А А
А = А
= А А
А , то и В
, то и В В
В =В
=В В
В ,
,
Если прямые  и
и  не
параллельны, то через точку В
не
параллельны, то через точку В проведем прямую
проведем прямую 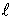 ,
параллельную прямой
,
параллельную прямой  (рис. 10б).
Она пересечет прямые А
(рис. 10б).
Она пересечет прямые А В
В и А
и А В
В в некоторых
точках С и D. Так как А
в некоторых
точках С и D. Так как А А
А = А
= А А
А , то по
доказанному В
, то по
доказанному В С=СD. Отсюда
получаем В
С=СD. Отсюда
получаем В В
В = В
= В В
В .
Аналогично, В
.
Аналогично, В В
В =В
=В В
В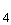 и т.д.
и т.д.

Геометрическое место точек и метод
геометрических мест
Геометрическое место точек
Одним из методов решения задач на построение
является метод геометрических мест.
Геометрическим местом точек называется фигура, которая
состоит из вех точек плоскости, обладающих определенным свойством.
Например, окружность можно определить как
геометрическое место точек, равноудаленных от данной точки. Важное
геометрическое место дает следующая теорема:

Теорема. Геометрическое место точек,
равноудаленных от двух данных точек, есть прямая, перпендикулярная к отрезку,
соединяющему эти точки, и проходящая через его середину.
Доказательство. Пусть А и В - данные точки, а -
прямая, проходящая через середину О отрезка АВ перпендикулярно к нему (рис.
11). Докажем, что:
1) каждая точка прямой а равноудалена от
точек А и В;
2) каждая точка D
плоскости, равноудаленная от точек А и В, лежит на прямой а.
То, что каждая точка С прямой а находится на
одинаковом расстоянии от точек А и В, следует из равенства треугольников АОС и
ВОС. У этих треугольников углы при вершине О прямые, сторона ОС общая, а АО=ОВ,
так как О - середина отрезка АВ.
Покажем теперь, что каждая точка D
плоскости, равноудаленная от точек А и В, лежит на прямой а. Рассмотрим
треугольник АDВ. Он
равнобедренный, так как АD=ВD.
В нем DO - медиана.
По свойству равнобедренного треугольника медиана, проведенная к основанию,
является высотой. Значит, точка D
лежит на прямой а. Теорема доказана.
Метод геометрических мест
Сущность метода геометрических мест,
используемого при решении задач на построение, состоит в следующем. Пусть,
решая задачу на построение, нам надо найти точку Х, удовлетворяющую двум
условиям. Геометрическое место точек, удовлетворяющих первому условию, есть
некоторая фигура F , а геометрическое место точек,
удовлетворяющих второму условию, есть некоторая фигура F
, а геометрическое место точек,
удовлетворяющих второму условию, есть некоторая фигура F . Искомая
точка Х принадлежит F
. Искомая
точка Х принадлежит F и F
и F , т. е.
является их точкой пересечения. Если эти геометрически места простые (скажем,
состоят из прямых и окружностей), то мы можем их построить и найти интересующую
нас точку Х. Приведем пример.
, т. е.
является их точкой пересечения. Если эти геометрически места простые (скажем,
состоят из прямых и окружностей), то мы можем их построить и найти интересующую
нас точку Х. Приведем пример.

Задача. Даны три точки: А, В, С. Постройте точку
Х, которая одинаково удалена от точек А и В и находится на данном расстоянии от
точки С.
Решение. Искомая точка Х удовлетворяет двум
условиям: 1) она одинаково удалена от точек А и В; 2) она находится на данном
расстоянии от точки С. Геометрическое место точек, удовлетворяющих
первому условию, есть прямая, перпендикулярная
отрезку АВ и проходящая через его середину (рис. 12). Геометрическое место
точек, удовлетворяющих второму условию, есть окружность данного радиуса с
центром в точке С. Искомая точка Х лежит на пересечении этих геометрических
мест.
Преобразования плоскости
Отображение плоскости на себя
Отображением плоскости на себя называется такое
преобразование, что каждой точке исходной плоскости сопоставляется какая-то
точка этой же плоскости, причем любая точка плоскости оказывается
сопоставленной другой точке. Если при отображении плоскости на себя фигура F
преобразовывается в фигуру F', то говорят, что фигура F' - образ фигуры F, а
фигура F - прообраз фигуры F'. Если одним отображением фигура F переводится в
фигуру F', а затем фигура F' переводится в фигуру F'', то отображение,
переводящее F в F'' называется композицией двух отображений. Неподвижной точкой
отображения называется такая точка A которая этим отображением переводится сама
в себя. Отображение, все точки которого неподвижные называется тождественным
отображением. Если при данном отображении разным точкам фигуры соответствуют
разные образы, то такое отображение называется взаимно однозначным. Пусть
фигура F' получена из фигуры F взаимно однозначным отображением f, то можно
задать отображение обратное отображению f, которое определяется так: композиция
отображения f и отображения, обратного f является тождественным отображением.
Существует множество видов отображения плоскости на себя, рассмотрим некоторые
из них:
1. Движения
1 Симметрия
относительно прямой (осевая симметрия)
2 Параллельный
перенос
3 Поворот
4 Центральная
симметрия
1. Подобие
1 Гомотетия
Движение
Движением называется отображение плоскости на
себя при котором сохраняются все расстояния между точками. Движение имеет ряд
важных свойств:
1. Три
точки, лежащие на одной прямой, при движении переходят в три точки, лежащие на
одной прямой, и три точки, не лежащие на одной прямой, переходят в три точки,
не лежащие на одной прямой.
Доказательство: пусть движение переводит точки
A, B, C в точки A', B', C'. Тогда выполняются равенства'B'=AB , A'C'=AC ,
B'C'=BC (1)
Если точки A, B, C лежат на одной прямой, то
одна из них, например точка B лежит между двумя другими. В этом случае
AB+BC=AC, и из равенств (1) следует, что A'C'+B'C'=A'C'. А из этого следует,
что точка B' лежит между точками A' и C'. Первое утверждение доказано. Второе
утверждение докажем методом от противного: Предположим, что точки A', B', C'
лежат на одной прямой даже в том случае, если точки A, B, C не лежат на одной
прямой, то есть являются вершинами треугольника. Тогда должны выполнятся
неравенства треугольника:
<AC+BC<AB+BC<AB+AC
но из равенств (1) следует, что те же
неравенства должны выполнятся и для точек A', B', C' следовательно точки A',
B', C' должны быть вершинами треугольника, следовательно точки A', B', C' не
должны лежать на одной прямой.
. Отрезок движение переводится в отрезок.
2. При
движении луч переходит в луч, прямая в прямую.
3. Треугольник
движением переводится в треугольник.
4. Движение
сохраняет величины углов.
5. При
движении сохраняются площади многоугольных фигур.
6. Движение
обратимо. Отображение, обратное движению является движением.
7. Композиция
двух движений также является движением.
Используя определение движения можно дать такое
определение равенства фигур:
Две фигуры называются равными, если одну из них
можно перевести в другую некоторым движением.
Виды движений
На плоскости существуют четыре типа движений:
1. Параллельный
перенос.
2. Осевая
симметрия
3. Поворот
вокруг точки
4. Центральная
симметрия
Рассмотрим подробнее каждый вид.
Симметрия относительно прямой
Определение. Симметрией S относительно прямой
относительно прямой 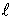 называется
преобразование плоскости, при котором образом точки А
называется
преобразование плоскости, при котором образом точки А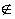
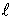 является такая точка А' (этой же
плоскости), что: 1) АА'
является такая точка А' (этой же
плоскости), что: 1) АА'
 ; 2) точка А
; 2) точка А = АА'
= АА'
 - середина
отрезка АА' (рис. 13)
- середина
отрезка АА' (рис. 13)

Прямая 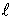 называется
осью симметрии. Если точка К
называется
осью симметрии. Если точка К
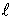 , то К'= К, т. е. каждая точка,
принадлежащая
, то К'= К, т. е. каждая точка,
принадлежащая 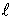 , является
двойной точкой преобразования симметрии; других точек плоскости, обладающих
этим свойством, нет. Докажем с помощью метода координат, что симметрия
относительно прямой: 1) преобразует прямую в прямую; 2) сохраняет расстояние
между точками.
, является
двойной точкой преобразования симметрии; других точек плоскости, обладающих
этим свойством, нет. Докажем с помощью метода координат, что симметрия
относительно прямой: 1) преобразует прямую в прямую; 2) сохраняет расстояние
между точками.
Примем ось симметрии за ось ОХ прямоугольной
декартовой системы координат. Тогда образом точки А(х; у) при этой симметрии
служит точка А'(х; -у) (рис. 14).

Если прямая g
определяется уравнением ах+ by
+ с= 0, то образом этой прямой будет множество точек {(х'; у')}, где х = х, у'
= -у, определяемое уравнением ах - bу'
+ с = 0, т. е. некоторая прямая g'.
Пусть А (х ; y
; y ), В(х
), В(х ; y
; y ) - две
произвольные точки плоскости, а точки А' (х
) - две
произвольные точки плоскости, а точки А' (х ; -y
; -y ), В' (х
), В' (х ; -y
; -y ) - их
образы. Тогда
) - их
образы. Тогда
А'В'= 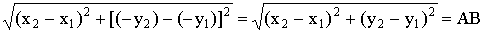 .
.
Определение. Если при симметрии относительно
прямой 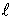 некоторая
фигура F
отображается на себя, то прямая
некоторая
фигура F
отображается на себя, то прямая 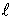 называется осью симметрии этой
фигуры.
называется осью симметрии этой
фигуры.
Так каждый диаметр окружности
является осью симметрии этой окружности; каждая прямая, перпендикулярная данной
прямой, является осью симметрии этой прямой; каждая высота правильного
треугольника является его осью симметрии.
Параллельный перенос
Определение. Пусть 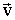 - некоторый
вектор плоскости. Преобразование, при котором каждой точке А плоскости ставится
в соответствие такая точка А' этой же плоскости, что АА' =
- некоторый
вектор плоскости. Преобразование, при котором каждой точке А плоскости ставится
в соответствие такая точка А' этой же плоскости, что АА' =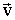 , называется
параллельным переносом и обозначается: Т
, называется
параллельным переносом и обозначается: Т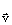 или же
или же 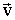 .
.
При параллельном переносе: 1) прямая
отображается на параллельную ей прямую; 2) сохраняются расстояния между
точками. Докажем это.
Если А' (х'; у') - образ точки А (х;
у), то по определению, АА' = у. Но вектор АА' имеет при наших обозначениях
координаты х' - x и у' - у. Следовательно, если 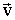 = (m; n), то х' - х
= m, у' - у = n. Значит,
координаты х', у' образа выражаются через координаты х, у прообраза при
параллельном переносе
= (m; n), то х' - х
= m, у' - у = n. Значит,
координаты х', у' образа выражаются через координаты х, у прообраза при
параллельном переносе 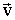 = (m; n) следующими
формулами:
= (m; n) следующими
формулами:
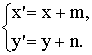
Пусть g - некоторая
прямая, заданная уравнением ax + bу + с = 0.
Подставляя в это уравнение х' - m вместо х и у' - n вместо у,
получим:
а (х' - m)
+ b(y'
- n) + с = 0.
Следовательно, координаты x',
y' связаны
зависимостью, выражаемой уравнением первой степени:
ax' + by' + (с - am - bn) = 0.
Это и означает, что множество образов точек
прямой g есть также некоторая прямая g'.
При этом коэффициенты при переменных в уравнениях прямых соответственно равны,
так что прямые g и g' параллельны.
Если А (х ; y
; y ), В (х
), В (х ; y
; y ) -две
произвольные точки и А'(х'
) -две
произвольные точки и А'(х' ; y'
; y' ) и В'(х'
) и В'(х' ; y'
; y' ) - их
образы, то
) - их
образы, то
х' =x
=x + m, y'
+ m, y' = y
= y + n, х'
+ n, х' =x
=x + m, y'
+ m, y' = y
= y + n, так что
+ n, так что
А'В'= 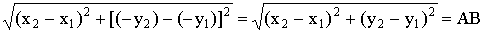 .
.
Поворот
Определение. Пусть заданы точка О -
центр поворота и некоторый ориентированный угол а. Тогда поворотом вокруг точки
О на угол  называется
преобразование, при котором каждой точке А плоскости ставится в соответствие
такая точка А' этой плоскости, что: 1) ОА'=ОА; 2) угол АОМ конгруэнтен углу
называется
преобразование, при котором каждой точке А плоскости ставится в соответствие
такая точка А' этой плоскости, что: 1) ОА'=ОА; 2) угол АОМ конгруэнтен углу  и
ориентирован так же, как угол
и
ориентирован так же, как угол  . Поворот на угол
. Поворот на угол  обозначается
R
обозначается
R . С помощью
метода координат можно убедиться, что при повороте прямая отображается на
прямую и сохраняются расстояния между точками.
. С помощью
метода координат можно убедиться, что при повороте прямая отображается на
прямую и сохраняются расстояния между точками.
Выберем начало координат
прямоугольной декартовой системы в центре поворота (рис. 11) и ориентируем угол
( ) так же,
как данный угол
) так же,
как данный угол  .
.

Пусть А (х; у) А' (х'; у'). Если
обозначить угол (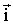 ,
, ) через Р,
то (рис. 15) угол (i, OA') будет
иметь такую же величину, как и угол
) через Р,
то (рис. 15) угол (i, OA') будет
иметь такую же величину, как и угол  +
+ . Поэтому
. Поэтому
х' = ОА'
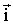 =ОА'cos
(
=ОА'cos
( +
+ ) = ОА'
(cos
) = ОА'
(cos  cos
cos  - sin
- sin  sin
sin  ).
).
Аналогично
y' = ОА'
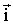 =ОА'
sin (
=ОА'
sin ( +
+ ) = ОА'
(sin
) = ОА'
(sin cos
cos + cos
+ cos sin
sin ).
).
А так как ОАcos =х, ОАsin
=х, ОАsin =y, то
=y, то
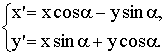 (2)
(2)
Решая уравнение системы (2)
относительно х и y получим:

Значит, образом прямой ах+by+c=0 будет
фигура, определяемая уравнением 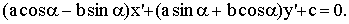
Нетрудно проверить, что если при
повороте АА', ВВ', то А'В'=АВ.
Центральная симметрия
Определение. Поворот вокруг точки О
на угол, величина которого равна 180°, называют симметрией относительно точки О
или центральной симметрией. Точку О называют центром симметрии.

Ясно, что в этом преобразовании центр симметрии
- точка О, а также точки А и А' (образ точки А) лежат на одной прямой (рис. 16)
и ОА =OА'.
Определение. Если какая-либо фигура при
симметрии относительно точки О отображается на себя, то точка О называется
центром симметрии этой фигуры.
Так, центр окружности является одновременно и ее
центром симметрии, точка пересечения диагоналей параллелограмма - центром
симметрии этого параллелограмма.
Подобие
Определение. Преобразование плоскости называется
подобием, если для любых двух точек А и В плоскости и их образов А' и В' имеет
место соотношение:
А'B'=kAB,
где k - положительное
число, называемое коэффициентом подобия,
Определение. Фигура Ф называется подобной фигуре
Ф' (Ф ~ Ф'), если существует преобразование подобия, при котором фигура Ф
преобразуется в фигуру Ф'.
Отметим некоторые важнейшие свойства
преобразования подобия.
. Преобразование подобия сохраняет
коллинеарность точек, а также порядок расположения точек на прямой.
Действительно, если, например, точка В лежит
между точками А и С, то AC=AB+BC.
При этом, согласно определению подобия, для образов А', В', С' точек А, В, С мы
получим следующее соотношение:
A'C'=kAC=k(AB+BC)=kAB+kBC=A'B'+B'C'.
Соотношение A'C'=A'B'+B'C'
показывает, что точки A',
B', C'
лежат на одной прямой, причем точка В' лежит между точками А' и С'.
Из сохранения порядка точек вытекает также
сохранение сорасположенности или противорасположенности двух точек относительно
некоторой прямой.
. Точки, не лежащие на одной прямой,
преобразуются в точки, не лежащие на одной прямой. Действительно, в противном
случае при обратном преобразовании нарушалась бы коллинеарность точек.
Из сказанного вытекает, что:
. Подобие преобразует прямую в прямую, отрезок
прямой - в отрезок, луч - в луч, угол - в угол, многоугольник - в одноименный
многоугольник, окружность - в окружность.
. Преобразование подобия сохраняет величину
угла, т.е. является конформным преобразованием. В частности, при преобразовании
подобия сохраняется перпендикулярность прямых.
. При подобии многоугольник преобразуется в
одноименный ему многоугольник, углы которого конгруэнтны соответственным углам,
а стороны пропорциональны соответственным сторонам данного многоугольника.
Докажем теперь теорему существования подобия.

Теорема. Если стороны треугольника А'В'С'
пропорциональны соответственным сторонам треугольника АВС, то существует и
притом единственное преобразование подобия, преобразующее вершины А, В, С
треугольника АВС соответственно в вершины А', В', С' треугольника А'В'С'.
. Доказательство существования
Пусть АВС и А'В'С' - два треугольника, причем
A'B'
: AB = A'C'
: AC = B'C'
: BC|= k.
Построим (рис. 17) на луче А'В' такую точку
В", что A'B''=AB,
и на луче А'С' такую точку С'', что A'C''=AC.
Углы треугольника А'В'С' имеют те же величины, что и соответственные углы
треугольника АВС. В частности,  В'А'С'=
В'А'С'= ВАС.
А так как углы В'А'С' и В''А'С'' совпадают, то
ВАС.
А так как углы В'А'С' и В''А'С'' совпадают, то  В''А'С''=
В''А'С''= ВАС.
ВАС.
Из соотношений A'B''=AB,
A'C''=AC
и  В''А'С'=
В''А'С'= ВАС
следует, как известно, что B''C''=BC.
ВАС
следует, как известно, что B''C''=BC.
Из соотношений A'B''=AB,
A'C''=AC,
B''C''=BC
следует, что существует перемещение L
преобразующее точки А, В, С, соответственно в точки А', В'', С''.
. Доказательство единственности
Если точка М на прямой АВ, то точка
М' - ее образ в подобии - однозначно определяется тем, что 1) М'  А'В', 2)A'M'=kAM, 3) точки
А', В', М' располагаются на прямой на прямой АВ.
А'В', 2)A'M'=kAM, 3) точки
А', В', М' располагаются на прямой на прямой АВ.
Если же М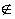 АВ, то ее
образ однозначно определяется следующими условиями: 1)
АВ, то ее
образ однозначно определяется следующими условиями: 1)  В'А'М'=
В'А'М'= ВАМ, 2) A'M'=kAM, 3) точка
М' сорасположена или противорасположена с точкой С' относительно прямой А'В'
соответственно тому, сорасположена ли или противорасположена точка М с точкой С
относительно прямой АВ.
ВАМ, 2) A'M'=kAM, 3) точка
М' сорасположена или противорасположена с точкой С' относительно прямой А'В'
соответственно тому, сорасположена ли или противорасположена точка М с точкой С
относительно прямой АВ.
Гомотетия
Определение. Гомотетией с центром О
и коэффициентом k 0 (Н
0 (Н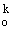 ) называется отображение плоскости
на себя, при котором образом произвольной точки М является такая точка М', что
) называется отображение плоскости
на себя, при котором образом произвольной точки М является такая точка М', что  =k
=k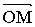 .
.
Исходя из этого определения, можно
установить ряд свойств гомотетии. Остановимся на некоторых из них.
1. Гомотетия есть взаимно однозначное
отображение.
Действительно, если задана точка М,
то при заданных центре О и коэффициенте k однозначно
определяется вектор  =k
=k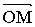 , а
следовательно, и точка М'. Обратно: если задана точка М', центр О и коэффициент
k, то
однозначно определяется вектор
, а
следовательно, и точка М'. Обратно: если задана точка М', центр О и коэффициент
k, то
однозначно определяется вектор  , а значит, и вектор
, а значит, и вектор 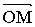 =
=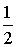
 , т.е. и точка М.
, т.е. и точка М.
. Точка и ее образ в данной
гомотетии лежат на одной прямой с центром гомотетии.
Это следует из коллинеарности
векторов  и
и 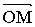 . При этом,
если k>0,
векторы
. При этом,
если k>0,
векторы  и
и 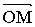 сонаправлены,
т.е. точка М и точка М' - ее образ - располагаются по одну сторону от центра
гомотетии; в этом случае гомотетию называют прямой. Если же k<0, то
точки М и М' располагаются по разные стороны от центра гомотетии; в этом случае
гомотетию называют обратной.
сонаправлены,
т.е. точка М и точка М' - ее образ - располагаются по одну сторону от центра
гомотетии; в этом случае гомотетию называют прямой. Если же k<0, то
точки М и М' располагаются по разные стороны от центра гомотетии; в этом случае
гомотетию называют обратной.
. Гомотетия сохраняет коллинеарность
точек.
Действительно, пусть точки А, В, С,
лежат на одной прямой, точки А', В', С' - образы точек А, В, С в некоторой
гомотетии Н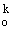 .
.
Так как, по определению,

то

Пусть 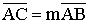 (векторы
(векторы 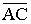 и
и  коллинеарны),
тогда из полученных выше равенств следует
коллинеарны),
тогда из полученных выше равенств следует
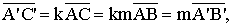
т. е. векторы 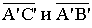 также
коллинеарны. Это означает, что точки А', В' и С' лежат на одной прямой.
также
коллинеарны. Это означает, что точки А', В' и С' лежат на одной прямой.
. Если гомотетия Н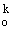 преобразует
точки А, В соответственно в точки А', B', то
преобразует
точки А, В соответственно в точки А', B', то
А'B'=kAB.
Это следует из того, что (как было
показано при доказательстве свойства 3),
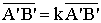 .
.
. Если гомотетия Н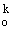 преобразует
точки А, В соответственно в точки А', B', то
преобразует
точки А, В соответственно в точки А', B', то
АВ || A'B'.
Это также непосредственно вытекает
из соотношения 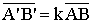 .
.
. Множество гомотетий с данным
центром О образуют группу.
Действительно:
) Композиция гомотетии Н и гомотетии
Н
и гомотетии
Н есть
гомотетия Н
есть
гомотетия Н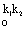 , потому что
из
, потому что
из 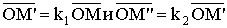 следует,
что
следует,
что 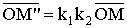 .
.
) В множестве гомотетий с данным
центром О имеется тождественное преобразование.
Действительно, при гомотетии Н получим:
получим: 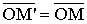 и,
следовательно, образ М' совпадает с прообразом М, т. е. Н
и,
следовательно, образ М' совпадает с прообразом М, т. е. Н -
тождественное преобразование.
-
тождественное преобразование.
) Преобразование, обратное гомотетии
Н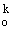 , есть
гомотетия Н
, есть
гомотетия Н , потому что
из соотношения
, потому что
из соотношения 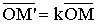 следует
соотношение
следует
соотношение 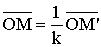 .
.
Методические рекомендации по
изучению данной темы
Простейшие задачи на построение
Набор простейших задач на построение
в различных пособиях для школы примерно одинаков, хотя порядок рассмотрения
этих задач может быть различным.
К простейшим обычно относятся
следующие задачи на построение:
1) Построение угла, равного данному;
2) Построение биссектрисы угла;
) Деление отрезка пополам;
) Построение прямой, проходящей через
данную точку и перпендикулярной данной прямой.
Эти задачи изучаются в 7 классе - глава II
«Треугольники». На изучение данной темы отводится 3 часа. В результате изучения
ученики должны научиться решать задачи на построение с помощью циркуля и
линейки, уметь доказывать правильность выполняемых операций.
На первом уроке предлагается рассмотреть задачи:
построение угла равного данному и построение биссектрисы угла. Второй урок
посвящен решению задач: деление отрезка пополам и построение перпендикулярных
прямых. Третий урок - решение задач, отрабатывающих умения и навыки построения
циркулем и линейкой.
Первоначально учителю необходимо выявить систему
условий, на которую должен опираться ученик для успешного овладения
практическим действием.
Для того чтобы научиться производить построения
с помощью циркуля и линейки, ученикам необходимо иметь знания о следующих
фактах: о данных геометрических фигурах - полупрямой, полуплоскости и угле,
отрезке, биссектрисе, перпендикуляре (определения, представления об их
изображении и обозначении); о цели действия; об инструментах построения; о
каждой из конструктивных операций и о последовательности их выполнения.
Учащиеся должны быть также подготовлены к обоснованиям возможности каждого шага
построения и доказательству правильности построения (аксиомы откладывания
отрезков и углов, определение равных треугольников, признаки равенства
треугольников). Нельзя обойтись и без навыков в выполнении элементарных
конструктивных операций: построение окружности произвольного или указанного
радиуса с центром в некоторой точке, построение полупрямой, имеющей данное
начало и проходящей через данную точку.
Рассмотрим несколько уроков изучения нового
материала темы «Задачи на построение».
Урок№1
Тема: Построение угла, равного данному.
Построение биссектрисы угла
Цели: 1. Познакомить учащихся с задачами на
построение, при решении которых, используются только циркуль и линейка.
. Научить выполнять построение угла, равного
данному, строить биссектрису угла.
. Развитие пространственного мышления, внимания.
. Воспитание трудолюбия и аккуратности.
Оборудование: таблицы с порядком решения задач
на построение.
Ход урока:
Актуализация основных теоретических понятий:
окружность, заданного радиуса с данным центром; признаки равенства
треугольников; через две точки на плоскости можно провести прямую и притом
только одну.
Для повторения признаков равенства треугольников
можно предложить задание: укажите на каком из рисунков (рис. 18) есть равные
треугольники.
Повторение понятия окружности и ее элементов
можно организовать, предложив классу следующее задание, с выполнением его одним
учеником на доске: дана прямая а и точка А, лежащая на прямой и точка В, не
лежащая на прямой. Провести окружность с центром в точке А, проходящую через
точку В. Отметьте точки пересечения окружности с прямой а. Назовите радиусы
окружности.

Для рассмотрения нового материала учителю
полезно иметь таблицу. (табл. 1). Работу с таблицей можно организовать
по-разному: она может иллюстрировать рассказ учителя или образец записи
решения; можно предложить учащимся, пользуясь таблицей, рассказать о решении
задачи, а затем самостоятельно его выполнить в тетрадях. Таблица может быть
использована при опросе учащихся и при повторении материала.
Учащимся можно предложить в указанном порядке
составить план решения задачи.
Таблица 1.
|
Построение
угла, равного данному
|
|
ДАНО:
|
ПОСТРОЕНИЕ:
|
ДОКАЗАТЕЛЬСТВО:
|
|
    АВС= АВС= ОDЕ по трем
сторонам, значит, ОDЕ по трем
сторонам, значит,  DOE= DOE= ВАС, то
есть построенный угол МОЕ равен данному углу А. ВАС, то
есть построенный угол МОЕ равен данному углу А.
|
|
|
Построение биссектрисы данного угла
Учитель может предложить учащимся по данной
таблице построить биссектрису угла.
Ученик у доски выполняет построение, обосновывая
каждый шаг выполняемых действий.
Доказательство показывает учитель, необходимо
подробно остановиться на доказательстве того факта, что в результате построения
действительно получатся равные углы.
Закрепление
Полезно предложить учащимся следующее задание
для закрепления пройденного материала:
Задача 1. Дан тупой угол АОВ. Постройте луч ОХ
так чтобы углы ХОА и ХОВ были равными тупыми углами.
Задача 2. Построить с помощью циркуля и линейки
углы в 30º и 60º
.
Задача 3. Постройте треугольник по стороне,
углу, прилежащему к его стороне, и биссектрисе треугольника, исходящей из
вершины данного угла.
Таблица 2.
|
Построение
биссектрисы угла
|
|
ДАНО:
|
ПОСТРОЕНИЕ:
|
ДОКАЗАТЕЛЬСТВО:
|
|
 АВС.
Построить биссектрису угла. АВС.
Построить биссектрису угла.
|
  АСЕ= АСЕ= АВЕ по трем сторонам, значит, АВЕ по трем сторонам, значит,  САЕ= САЕ= ВАЕ, т. е.
луч АЕ - биссектриса денного угла. ВАЕ, т. е.
луч АЕ - биссектриса денного угла.
|
|
Для домашней работы: №150-152.
Урок№2
Тема: Построение середины отрезка.Построение
перпендикулярных прямых
Цель: 1. Научить учащихся с помощью циркуля и
линейки выполнять деление отрезка пополам.
. Сформировать умения и навыки построения
перпендикулярных прямых.
. Актуализация внимания.
. Воспитание трудолюбия и аккуратности.
Ход урока:
Методом фронтального опроса повторить понятия:
окружность заданного радиуса с данным центром, признаки равенства
треугольников, свойства равнобедренного и равностороннего треугольников.
Далее предложить задание: с помощью циркуля и
линейки построить биссектрису, выходящую из вершины равнобедренного
треугольника. Перечислить ее свойства.
При изучении нового материала используется
таблица 3, по которой учащиеся составляют рассказ, как разделить данный отрезок
пополам. После этого в тетрадях выполняются соответствующие построения.
Таблица 3
|
Построение
середины отрезка
|
|
ДАНО:
|
ПОСТРОЕНИЕ:
|
ДОКАЗАТЕЛЬСТВО:
|
|
Отрезок
АВ. Построить точку О так чтобы О АВ, АО=ОВ. АВ, АО=ОВ.  АРQ= АРQ= ВРQ по трем
сторонам, поэтому ВРQ по трем
сторонам, поэтому  1= 1= 2. значит
РО - биссектриса равнобедренного 2. значит
РО - биссектриса равнобедренного  АРВ, следовательно, и медиана т.е.
АО=ОВ. АРВ, следовательно, и медиана т.е.
АО=ОВ.
|
|
|
Построение перпендикулярных прямых
Здесь необходимо обратить внимание, что возможны
два случая:
1. Точка принадлежит прямой;
2. Точка не принадлежит прямой.
После повторения учитель формулирует задачу и
объясняет построение для первого случая, при этом может быть использована
таблица 4.
При рассмотрении второго случая учащиеся при
помощи таблицы 4 проводят построение и доказательство самостоятельно.
|
Построение
перпендикулярной прямой
|
|
ДАНО:
|
ПОСТРОЕНИЕ:
|
1. О а. 2. О
а. 2. О а.
а.
|
Построить
ОС а а
|
|
Таблица 4
Закрепление
Задача. Постройте прямоугольный треугольник по
его катетам.
Данную задачу ученик решает у доски,
предварительно проведя ее анализ. Запись решения данной задачи может выглядеть
так:

ДОКАЗАТЕЛЬСТВО:
В  АВС ВС=а, СА= b, ВD
АВС ВС=а, СА= b, ВD АС,
следовательно, угол ВСА равен 90º . Значит треугольник АВС -
искомый.
АС,
следовательно, угол ВСА равен 90º . Значит треугольник АВС -
искомый.
Также для отработки умений и
навыков, можно использовать задачи №154 (а,б).
Для домашней работы: №153.
Урок№3
Тема: Решение задач на построение
Цель: 1. Отработка умений и навыков
выполнения элементарных построений с помощью циркуля и линейки.
.Актуализация внимания.
Ход урока:
Проверить выполнение задачи №153.
Проверку можно организовать так: у доски три ученика, они должны построить
прямую, проходящую через
точку А перпендикулярно прямой а.
Класс в это время может выполнить
задание: дан треугольник АВС. построить высоту АD. После
выполнения задания каждый шаг построения должен быть прокомментирован и
обоснован.
Самостоятельная работа.
1. Разделить отрезок на 4 равные части.
2. Дан  АВС.
Построить биссектрису ВК.
АВС.
Построить биссектрису ВК.
. Дан угол АОВ. Построить
угол, для которого луч ОВ является биссектрисой.
Построение треугольника по трем элементам
На изучение данной темы отводится 3 урока.
Урок№1
Тема: Построение треугольника по двум сторонам и
углу между ними. Построение треугольника по стороне и двум прилежащим к ней
углам.
Цель: 1. Познакомить учащихся с алгоритмом
построения треугольника по двум сторонам и углу между ними; по стороне и двум
прилежащим к ней углам.
. Формирование умений и навыков по применению
данного алгоритма к решению задач.
. Развитие математического мышления, творчества,
внимания.
Ход урока:
Необходимо повторить: откладывание на прямой
отрезка данной длины, построение угла, равного данному, признаки равенства
треугольников.
Организовать повторение можно в форме
практической работы, с комментариями учащихся:
1. Дан произвольный отрезок. На прямой а
от заданной точки отложить отрезок, равный данному.
2. Дан произвольный угол. Построить с
помощью циркуля и линейки угол, равный данному.
Изучение нового материала:
Задача1. Построить треугольник по двум сторонам
и углу между ними.
Задача2. Построить треугольник по стороне и двум
прилежащим к ней углам.
Учитель проводит анализ данных задач используя
решение приведенное в учебнике, а учащиеся у доски выполняют построение и
доказательство.
Закрепление №287, №290(а).
Для домашней работы: №290 (б), №291 (а).
Урок№2
Тема: Построение треугольника по трем сторонам.
Цель: 1. Познакомить с алгоритмом построения
треугольника по трем сторонам.
.Отработка умений и навыков применения данного
алгоритма при решении задач.
. Развитие гибкости математического мышления,
творчества, внимательности.
Ход урока:
Активизация необходимых теоретических понятий:
повторить неравенство треугольника. Учитель предлагает ответить на вопрос:
существует ли треугольник со сторонами: а) 1м, 2м, 3м; б) 1,2 см, 1см, 2,4см;
в)5дм, 3дм, 7дм; г)12,1см, 8см, 5,6см? Ответ обосновать.
Закрепление: №292, 294.
Урок№3
Тема: Решение задач на построение треугольника
по трем элементам.
Цель: 1. Отработка умений и навыков решать
задачи на построение треугольников по трем элементам.
. Развитие абстрактного мышления.
. Актуализация внимания.
Ход урока:
Задача 1. Построить прямоугольный треугольник по
катету и прилежащему углу.
При решении этой задачи учитель, в форме
эвристической беседы, проводит ее анализ. Анализ можно провести устно,
изобразив чертеж-набросок на доске (рис. 20а). Затем ученик решает задачу у
доски.

Дано:
Анализ:
Построение:
1. На прямой отметим точку С (рис. 20б) и
отложим отрезок СВ=а.
2. Построим  В=
В=

. Построим прямую, проходящую
через точку С перпендикулярно СВ.
. Сторона угла и прямая
перпендикулярная СВ пересекаются в точке А.
.  АВС -
искомый.
АВС -
искомый.
Доказательство:
В треугольнике АВС АС
перпендикулярна СВ, СВ=а,  СВА=
СВА= (по
построению).
(по
построению).
Задача 2. По катету и
противолежащему углу построить треугольник.

Решение этой задачи сводится к
решению предыдущей задачи, для этого ученики должны научиться строить угол
равный 90º -  . Учитель
ставит перед учащимися проблему: как построить угол 90º-
. Учитель
ставит перед учащимися проблему: как построить угол 90º- , если
, если 
 задан.
задан.

Дано:
Построить:  (90º -
(90º - )
)
Построение.
. Построим две перпендикулярные
прямые АВ и СD (рис. 21).
Обозначим точку пересечения прямых точкой О.
. Построим угол ВОК = 
 .
.
. Тогда угол КОС= (90º -  )
)
Решение задачи 2 учащиеся должны
осуществить самостоятельно.
Задача 3. Построить треугольник по
стороне, противолежащему углу и высоте, проведенной на одну из двух сторон
треугольника.

Анализ данной задачи учитель проводит вместе с
учениками. Построение и доказательство ученики выполняют самостоятельно.
Дано:
Построить
 АВС так, чтобы ВС=а, ВD=h
АВС так, чтобы ВС=а, ВD=h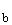 (ВD
(ВD АС),
АС),  ВАD=
ВАD= .
.
Анализ:
. Выполним чертеж - набросок (рис.
22)
. Рассмотрим треугольник АВD его мы
можем построить по катету и
противопо-
ложному углу ( ВDА=90º ,
ВDА=90º ,  ВАD=
ВАD= , ВD= h
, ВD= h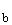 ).
).
. Построив треугольник АВD мы легко
можем его достроить до треугольника АВС, построив ВС=а.
Задачи на построение в курсе
геометрии 8 класса
На изучение данной темы отводится 2
урока.
Тема: Теорема Фалеса. Деление
отрезка на n равных
частей.
Цель: 1. Доказать теорему Фалеса.
. Познакомить с алгоритмом деления
отрезка на n равных
частей.
. Отработка умений и навыков
применения изученного материала при решении задач.
Ход урока: Доказать теорему Фалеса.
Учитель самостоятельно формулирует теорему и проводит ее доказательство.
Деление отрезка на n равных
частей. Этот материал можно предложить учащимся рассматривать самостоятельно,
опираясь на решение задачи №396. В данном случае учитель играет роль
консультанта.
Закрепление изученного материала
можно провести в форме самостоятельной работы, предложив учащимся разделить
отрезок на 5, 6, 7, и т.д. частей.
Урок№2
Тема: Построение четырехугольников.
Цель: 1. Отработка умений и навыков
построения четырехугольников по заданным элементам.
. Развитие математического мышления,
расширение кругозора.
. Актуализация внимания.
Ход урока: Актуализация знаний. На
доске заготовлены чертежи, на которых изображены: прямоугольник, ромб, квадрат,
параллелограмм, трапеция. К каждому чертежу приглашается ученик. Он должен
перечислить все известные свойства изображенной фигуры.
Следующие задачи решаются учащимися
у доски: 393, 397, 398.
Для домашнего изучения: №394, 395.
Геометрическое место точек
Работающим по учебнику Л. С.
Атанасяна можно предложить рассмотреть на факультативных занятиях следующие
темы: «Геометрическое место точек», «Метод геометрических мест».
Этот урок можно начать с рассказа учителя.
Приведем его примерное содержание.
На плоскости часто приходится рассматривать
точки, которые обладают одним и тем же свойством, например: удаленные от данной
точки О на расстояние 10 см, или удаленные от данной прямой а на 15 см, или
одинаково удаленные от концов данного отрезка АВ и т.д. По ходу объяснения на
доске открываются рисунки (рис. 23).
Рассматривая такие точки, выделяют фигуры,
которые состоят из всех точек плоскости, обладающим некоторым свойством.
Сначала объясняется слово «состоит». Фигура
состоит из точек, обладающих определенным свойством, это значит, что каждая
точка фигуры обладает этим свойством или иначе, если точка принадлежит фигуре,
то она обладает данным свойством. Затем объясняются слова: «состоит из всех
точек плоскости». Фигура может состоять из всех точек плоскости, обладающих
определенным свойством, но не включать все точки плоскости с данным свойством.
Когда же говорят, что фигура состоит из всех точек плоскости с данным
свойством, то это означает не только, что каждая точка фигуры обладает этим
свойством, но и что каждая точка плоскости, обладающая данным свойством,
принадлежит данной фигуре, или иначе, если точка плоскости обладает данным
свойством, то она принадлежит данной фигуре.
Делая вывод, что слова «фигура состоит из всех
точек плоскости, обладающих определенным свойством» означают:
. Если точка принадлежит фигуре, то она обладает
данным свойством.
. Если точка обладает данным свойством, то она
принадлежит фигуре.
Эти два условия - взаимно обратные утверждения.
Разъясним сказанное на примере. Рассмотрим три фигуры: окружность, часть
окружности и фигуру, состоящую из окружности и точек заштрихованной части
плоскости (табл. 5). (Рисунок помещен в таблице, на которой знаки «+», «-», ГМТ
пока не проставлены. Это будет сделано в процессе дальнейшей беседы с классом.)
Учитель обращает внимание учащихся на то, что
будут рассматриваться точки плоскости со свойством: точки удалены от данной
точки О на расстояние, равное R.
Классу предлагается выяснить, для каких из данных трех фигур выполняются два
указанных выше условия, т.е. какая из трех фигур состоит из всех точек
плоскости, удаленных от точки О на расстояние, равное R.
Заполняется таблица (ставятся знаки «+», «-»).
Необходимо объяснить, почему для второй фигуры не выполняется второе условие (фигуре
принадлежат не все точки с указанным свойством); почему для третьей фигуры не
выполняется первое условие (фигуре принадлежат и точки, не обладающие указанным
свойством).
Заполнив таблицу учащиеся должны сделать вывод
какая из фигур удовлетворяет двум поставленным условиям и дать определение
геометрического места точек.
Задание. Приведите примеры точек, так же
удовлетворяющих поставленным условиям ГМТ (серединный перпендикуляр,
биссектриса угла).
|
Фигуры
|
Условия
|
Название
Фигуры
|
|
если
точка принадлежит фигуре, то обладает данным свойством
|
Если
точка обладает данным свойством, то принадлежит фигуре
|
|
|
+
|
+
|
ГМТ
|
|
+
|
_
|
|
|
_
|
+
|
|
Закрепление
. Верно ли утверждение, что отрезок АВ,
параллельный данной прямой а и удаленный от нее на 5 см, является
геометрическим местом точек, удаленных от данной прямой на 5 см? [Нет, так как
хотя отрезок АВ и состоит из точек с данным свойством, но не все точки
плоскости с данным свойством ему принадлежат, или не выполняется условие: ели
точка обладает данным свойством, то она принадлежит отрезку АВ.]
Условие задачи можно варьировать: взять два
отрезка, отрезок и прямую и, наконец, две прямые (рис. 24).

2. Можно ли прямую АВ, где А и В - различные
точки прямой, считать геометрическим местом точек, лежащих между точками А и В?
[Нет, так как про прямую АВ нельзя сказать, что она состоит из точек, лежащих
между точками А и В, т.е. не выполняется условие: ели точка принадлежит прямой
АВ, то она лежит между точками А и В.]
Затем в условиях данной задачи заменяется прямая
лучом АВ, а луч отрезком АВ.
. Можно ли отрезок АВ, параллельный двум
параллельным прямым а и b
и одинаково отстоящий от них, считать геометрическим местом точек, одинаково
удаленных от двух параллельных прямых? [Нет, так как не выполняется условие:
если точка одинаково удалена от двух данных параллельных прямых, то она
принадлежит отрезку АВ.]
. Найдите геометрическое место точек, одинаково
удаленных от двух параллельных прямых а и b.
Решение. Проведем общий перпендикуляр DM
прямых а и b и найдем его
середину N (рис. 25). Через
точку N проведем прямую m,
параллельную прямой а (она будет параллельна и прямой b).
Докажем, что прямая m есть
искомое геометрическое место точек.

Доказательство. 1) Докажем, что если точка К
принадлежит прямой m, то она
удалена от прямых а и b
на расстояние, равное р, где р-длина отрезка DN
или MN. Так как
параллельные прямые равноотстоящие, то точка К удалена как от прямой а, так и
от прямой b на расстояние,
равное р.
2) Докажем, что точка S, одинаково
удаленная от прямых а и b, принадлежит прямой m. Так как
расстояние между прямыми а и b равно 2р, то точка S середина
отрезка СЕ, перпендикулярного к прямым а и b и равного
2р. Пусть S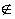 m, а СЕ
пересекает m в точке R. Тогда RC=RE=p по
доказанному в первой части, т.е. отрезок СЕ имеет две середины R и S, что
невозможно, значит, S
m, а СЕ
пересекает m в точке R. Тогда RC=RE=p по
доказанному в первой части, т.е. отрезок СЕ имеет две середины R и S, что
невозможно, значит, S m.
m.
Метод геометрических мест
Учитель разъясняет сущность метода
геометрических мест так, например, как это сделано в главе 1 (геометрическое
место точек и метод геометрических мест). Свой рассказ учитель может немного
конкретизировать, а именно: сказать, что точкой Х может быть центр окружности,
вершина треугольника и т.д.; точка Х может быть найдена и как точка пересечения
построенного геометрического места точек и данной в условии задачи фигуры (прямой,
угла и т. д.).
При решении задачи, особое внимание
обращается на проведение анализа: выделяется по условию задачи искомая точка;
выясняется, каким условиям она должна удовлетворять, а значит, каким
геометрическим местам точек она должна принадлежать (или геометрическому месту
точек и данной фигуре); делается вывод: искомая точка - точка пересечения
указанных геометрических мест точек. Учитель должен подвести учащихся к
самостоятельным выводам и алгоритму построения искомой точки. Для этого можно
задать следующие вопросы:
. Каким условиям удовлетворяет
искомая точка? [ 1) она одинаково удалена от т. А и В; 2) она находится на
заданном расстоянии от точки С].
. Что является ГМТ, удовлетворяющих
первому свойству? (прямая, перпендикулярная отрезку АВ и проходящая через его
середину).
. Что является ГМТ, удовлетворяющих
второму свойству? (окружность данного радиуса с центром в точке С).
. Где будет находиться искомая точка
Х? (на пересечении этих ГМТ).
Рассмотрим еще несколько задач,
которые можно предложить для закрепления пройденного материала.

. На данной прямой найдите точку. Которая
находится на данном расстоянии от другой данной прямой.
В задаче даны прямые а, m,
расстояние h (рис. 26). Искомая
точка должна удовлетворять двум условиям: 1) лежать на прямой m
(прямая дана); 2) находиться на прямой а на данном расстоянии, которое
обозначим через h.
Геометрическим местом точек, находящихся на прямой а на расстоянии h,
являются две прямые b и с,
параллельные а и отстоящие от а на расстоянии h.
Построим эти прямые. Искомая точка должна быть точкой пересечения прямых b
или с с прямой m. На нашем
рисунке две точки, удовлетворяющие этим условиям: А и В. (Если а||m,
то могут представиться два случая: прямая m
не пересекается с b и с и
задача не имеет решения; прямая m
совпадает с прямой b или прямой
с, в этом случае любая точка прямой m
является решением.)
. На данной прямой найдите точку, равноудаленную
от двух данных точек.
Искомая точка должна удовлетворять двум
условиям: 1) равноудаленную от точек А и В, т.е. лежит на серединном
перпендикуляре m к отрезку
АВ; 2) лежит на данной прямой а. значит искомая точка Х есть точка пересечения
прямых а и m (рис. 27). (Задача
может не иметь решения, иметь бесконечное множество решений.)

. Постройте окружность, которая касается сторон
данного угла, причем одной из них - в данной точке.
Предположим, что задача решена.

Пусть точка О - центр искомой окружности (рис.
28). Проведем ОА и ОС - радиусы окружности. прямоугольные треугольники АВО и
СВО равны по катету и гипотенузе (АО=СО=R,
ВО - общая). Из равенства треугольников следует, что  АВО=
АВО= СВО,
т.е. ВО - биссектриса угла АВС.
СВО,
т.е. ВО - биссектриса угла АВС.
Построение. Проведем биссектрису  АВС
и перпендикуляр к стороне ВА, проходящий через точку А. Точка О пересечения
биссектрисы и перпендикуляра является центром искомой окружности
АВС
и перпендикуляр к стороне ВА, проходящий через точку А. Точка О пересечения
биссектрисы и перпендикуляра является центром искомой окружности

угол отрезок треугольник
геометрический
4. Построить треугольник АВС по
периметру р, углу В, равному  , и высоте h, опущенной
из вершины А.
, и высоте h, опущенной
из вершины А.
Пусть задача решена и  АВС построен
(рис. 29). Отложив на прямой ВС отрезки DВ=АВ и
СЕ=АС, получим равнобедренные треугольники АВD и АСЕ.
АВС построен
(рис. 29). Отложив на прямой ВС отрезки DВ=АВ и
СЕ=АС, получим равнобедренные треугольники АВD и АСЕ.
Исходя из приведенных выше
рассуждений построение можно осуществить в следующей последовательности:
1) Проводим прямую и на ней откладываем
отрезок DE=р.
2) На расстоянии h от прямой DE проводим
прямую 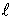 ,
параллельную DE.
,
параллельную DE.
) С вершиной в точке D строим угол
АDЕ, равный 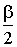 . Точка А -
одна из вершин искомого треугольника.
. Точка А -
одна из вершин искомого треугольника.
4) Проводим серединные перпендикуляры к
отрезкам AD и АЕ. Точки
В и С пересечения этих серединных перпендикуляров с прямой DE
- две другие вершины искомого треугольника.
Решение задач на построение с использованием
свойств движений
Тема «Движение», представленная в учебниках по
геометрии для основной школы, содержит немного задач на применение
преобразований фигур. Однако по данной теме можно найти интересные
геометрические задачи. Они могут быть разнообразны и по уровню сложности, и по
учебному материалу, необходимому для решения. Это разнообразие можно с успехом
использовать в ходе повторения темы «Движение». Опишем один урок повторения. Он
начинается с того, что учащиеся повторяют определения и построения, относящиеся
к центральной симметрии, осевой симметрии, повороту, параллельному переносу.
Для этого предлагаются следующие задания; которые выполняются у доски:
1) Построить отрезок, симметричный относительно
прямой; точки.
2) Выполнить параллельный перенос
треугольника на заданный вектор.
) Построить прямую, которая получается из
заданной прямой поворотом вокруг точки О на угол 80º
по часовой стрелке.
После повторения теоретической части
предлагаются задачи на построение, которые предлагается решать учащимися у
доски.
Задача1. Построить параллелограмм по двум
противоположным вершинам, лежащим на сторонах данного четырехугольника, причем
остальные вершины параллелограмма также должны принадлежать сторонам данного
четырехугольника.
Решение. 1. Анализ. Пусть искомый параллелограмм
построен. На рис. 30а, это параллелограмм АВСD,
который вписан в данный четырехугольник LMNK,
точки В и D - данные.

Проанализируем, что можно предпринять, чтобы
стала видна возможность построения. Пока видно только одно: можно провести
диагонали. Проводим диагонали BD
и СА ( рис. 30б) и тут же замечаем, что точка О их пересечения является центром
симметрии параллелограмма. А это значит, что она лежит на пересечении отрезка ML
с образом отрезка KN
при симметрии относительно точки О. Таким образом, мы нашли способ построения
третьей вершины искомого параллелограмма. А четвертую его вершину можно найти,
исходя из свойств этой фигуры.
. Построение. Проведем отрезок BD
и разделим его пополам точкой О.
Строим точки K и N
и N ,
симметричные относительно О точкам K и N
соответственно.
,
симметричные относительно О точкам K и N
соответственно.
Обозначим через А точку пересечения
отрезков ML и K N
N . Строим
точку С, симметричную относительно О точке А. Искомая фигура - АВСD (рис. 31).
. Строим
точку С, симметричную относительно О точке А. Искомая фигура - АВСD (рис. 31).
. Доказательство. Точки А и С, В и D - симметричны
относительно точки О по построению. А это значит, что диагонали BD и АС
четырехугольника АВСD пересекаются и точкой пересечения
делятся пополам. Отсюда следует (по определению), что построенный
четырехугольник - параллелограмм.
. Исследование. Успех построения
зависит от возможности найти точку А.

Если прямые KN и LM
пересекаются, то пересекаются и прямые K N
N , LM. Тогда
задача имеет единственное решение. Это значит, что данный четырехугольник не
должен быть ни параллелограммом, ни трапецией с основаниями KN и ML.
, LM. Тогда
задача имеет единственное решение. Это значит, что данный четырехугольник не
должен быть ни параллелограммом, ни трапецией с основаниями KN и ML.
Есть и еще одно ограничение. Стороны
KN и ML должны быть
такими, чтобы пересекались отрезки K N
N и ML. Иначе
пересечение прямых ML и K
и ML. Иначе
пересечение прямых ML и K N
N вне отрезка
ML привело бы
к видоизменению задачи.
вне отрезка
ML привело бы
к видоизменению задачи.
Если KN÷ïLM, то задача
имеет либо множество решений (когда прямые MN и K N
N оказываются
параллельными).
оказываются
параллельными).
Задача 2. Точки А и В лежат по
разные стороны от прямой d. Постройте на ней такую точку Х,
чтобы биссектриса угла АХВ лежала на прямой d.

Решение. 1. Анализ. Предположим, что
точка Х найдена (рис. 32). Тогда ÐАХЕ=ÐЕХВ. А это значит, что лучи
АХ и ВХ симметричны относительно луча ХЕ. Проведем перпендикуляры к прямой d из точек А
и В. они пересекут лучи угла АХВ в точках А и В
и В соответственно. Причем точки А и А
соответственно. Причем точки А и А , В и В
, В и В симметричны
друг другу относительно прямой d.
симметричны
друг другу относительно прямой d.
. Построение. Строим точку А ,
симметричную точке А относительно прямой d.
,
симметричную точке А относительно прямой d.
Строим точку В ,
симметричную точке В относительно прямой d.
,
симметричную точке В относительно прямой d.
Точки А и В (А
(А , В)
оказались в одной полуплоскости, а прямые В
, В)
оказались в одной полуплоскости, а прямые В А и ВА
А и ВА пересекаются в искомой точке Х.
пересекаются в искомой точке Х.
. Доказательство. Углы АХЕ и ВХЕ
равны по построению, следовательно, ХЕ - биссектриса, но луч ХЕ принадлежит
прямой d. Значит,
точка Х искомая.
. Исследование. Если точка А совпадает с
точкой В, то возможно только одно решение.
совпадает с
точкой В, то возможно только одно решение.
Если точка А совпадает с
точкой В, то задача имеет бесконечно много решений, так как любая точка прямой d
удовлетворяет условию.
совпадает с
точкой В, то задача имеет бесконечно много решений, так как любая точка прямой d
удовлетворяет условию.
Если отрезок А В
оказывается параллельным прямой d, то решений нет.
В
оказывается параллельным прямой d, то решений нет.
Задача 3. Постройте такой
равносторонний треугольник, чтобы одна его вершина совпадала с данной точкой О,
а две другие принадлежали двум данным окружностям.

Решение. 1. Анализ. Предположим, что
требуемый треугольник построен. Угол при данной вершине О равен 60°, причем ОА=ОВ. Это значит,
что при повороте на 60° вокруг
точки О против часовой стрелки вершина А перейдет в вершину В. значит, вторая
искомая вершина треугольника является точкой пересечения образа окружности с
центром О (при повороте на 60°
вокруг точки О) с данной окружностью, имеющей центр О .
.
. Построение. Построим образ одной
из окружностей при повороте на угол 60°
с центром в данной точке О. Точка пересечения полученной окружности и второй из
данных окружностей является второй вершиной треугольника. На рис. 33 это точка
В.
Доказательство и исследование
учащиеся должны провести дома самостоятельно.
Задача 4. Построить трапецию по
диагоналям d , d
, d и двум
параллельным сторонам а и b.
и двум
параллельным сторонам а и b.
Решение. 1. Анализ. Предположим, что
искомая трапеция построена и в ней проведены диагонали d и d
и d . Попробуем
построить фигуру, в которой диагонали присутствовали бы в «целом» виде, т.е.
без пересечения друг с другом. Оставим одну диагональ на месте, а другую
(допустим, АС) перенесем параллельно на расстояние АD (рис. 34а).
Получим треугольник ВЕ
. Попробуем
построить фигуру, в которой диагонали присутствовали бы в «целом» виде, т.е.
без пересечения друг с другом. Оставим одну диагональ на месте, а другую
(допустим, АС) перенесем параллельно на расстояние АD (рис. 34а).
Получим треугольник ВЕ D в котором
известны три стороны:
D в котором
известны три стороны:
ВЕ =а+b, BD= d
=а+b, BD= d , DE= d
, DE= d .
.

Точки В, Е , D позволяют
построить параллелограмм АСЕ
, D позволяют
построить параллелограмм АСЕ D, в котором диагональ СD служит
стороной искомой трапеции.
D, в котором диагональ СD служит
стороной искомой трапеции.
Для того чтобы найти другую сторону
трапеции (рис. 34б), построим сначала треугольник АСЕ , у которого
сторона АЕ
, у которого
сторона АЕ является
образом при параллельном переносе диагонали ВD на
расстояние АD.
является
образом при параллельном переносе диагонали ВD на
расстояние АD.
При таком анализе построение
оказывается совершенно очевидным. Поэтому все последующие этапы решения
целесообразно оставить учащимся для домашней работы.
Метод подобия
При решении многих задач на
построение применяется метод подобия. Суть которого заключается в следующем:
сначала строится фигура подобная данной, затем эта фигура увеличивается
(уменьшается) в нужном отношении (т.е. строится подобная фигура),
удовлетворяющая условию задачи.
Процесс обучения применению подобия
к решению задач на построение целесообразно разбить на четыре этапа:
подготовительный, ознакомительный, формирующий умение, совершенствующий умение.
Каждый этап имеет свою дидактическую цель, которая достигается, когда учащиеся
выполняют специально составленные задания.
Дидактическая цель подготовительного
этапа - сформировать у учащихся умения: выделять данные, определяющие форму
фигуры, множество пар подобных между собой фигур; строить фигуру по данным,
определяющим форму; переходить от построенной фигуры к искомой.

После изучения первого признака подобия
треугольников можно предложить следующий набор заданий:
Постройте треугольник по двум углам. Сколько
решений имеет задача? Какие элементы определяют форму построенных
треугольников?
Назовите подобные треугольники на рис.35.
Известны следующие элементы треугольника: а)
углы в 75°и 25°; б) высота 1,5 см;
в) углы в 75° и 25°, высота 1,5 см.
какие из этих данных определяют единственную фигуру на рис.35?
Подобны ли треугольники АВС и А ВС
ВС на рис.36,
если АС÷ïА
на рис.36,
если АС÷ïА С
С ? если они
подобны, то каков их коэффициент подобия?
? если они
подобны, то каков их коэффициент подобия?
Какие углы определяют форму
треугольников на рис.36?
Можно ли будет определить размеры
одного из треугольников на рис.36, если станут известны следующие данные: а)
углы при основании треугольника; б) высоты треугольника; в) сторона и углы при
основании?
На рис.31 равные углы помечены
одинаково. Кроме того, N Р
Р =N
=N P
P , М
, М Р
Р =МР
=МР . Как
расположены прямые NP и N
. Как
расположены прямые NP и N P
P ?
?
Каким отношением связаны треугольники
M N
N P
P и MN
и MN P
P и их
биссектрисы?
и их
биссектрисы?

Набор заданий, предъявляемых учащимся после
изучения 2 и 3 признаков подобия треугольников, составляются аналогично. Однако
при переходе от данного признака к следующему вопросы несколько усложняются, а
именно: расположение треугольников на рисунках меняется, удаляясь от
стандартного, варьируется набор элемента, определяющего единственную фигуру.
Задания, например, могут быть такими:
1. Подобны ли треугольники АВС
и А В
В С
С , если: а)
АВ=5см, ВС=7см,
, если: а)
АВ=5см, ВС=7см,

 В=30º, А
В=30º, А В
В =10см, В
=10см, В С
С =14см,
=14см,  В
В =60º; б) АВ=5см,
ВС=7см,
=60º; б) АВ=5см,
ВС=7см,  В=30º, А
В=30º, А В
В =10см, В
=10см, В С
С =14см,
=14см,  В
В =30º; в) АВ=3см,
ВС=5см, СА=7см, А
=30º; в) АВ=3см,
ВС=5см, СА=7см, А В
В =4,5см, В
=4,5см, В С
С =7,5см, С
=7,5см, С А
А =10,5см; г)
АВ=1,7см, ВС=3см, СА=4,2см, А
=10,5см; г)
АВ=1,7см, ВС=3см, СА=4,2см, А В
В =34дм, В
=34дм, В С
С =60дм, С
=60дм, С А
А =84дм?
=84дм?

2. В треугольнике АВС с острым углом
С проведены высоты АЕ и ВD (рис. 35). Докажите, что  АВС подобен
АВС подобен  ЕDC.
ЕDC.
. Докажите, что у подобных
треугольников периметры относятся как соответствующие стороны.
Дидактическая цель ознакомительного
этапа в том, чтобы разъяснить учащимся структуру процесса построения методом
подобия.
Объяснение начинается с задачи.
Задача 1. Построить треугольник по
двум данным углам 
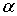 и
и  и биссектрисе длины d,
проведенной из вершины третьего угла.
и биссектрисе длины d,
проведенной из вершины третьего угла.
Анализируя задачу с учащимися,
учитель предлагает задания - вопросы, ответы на которые кратко фиксируются на
доске. Вопросы могут быть такими:
1. Какие данные определяют форму искомого треугольника?
2. Какие данные определяют размеры
искомого треугольника?
. Сколько треугольников можно построить
построение двум углам? Какими будут построение форме все построенные
треугольники?
. Какой отрезок нужно провести в
треугольнике, подобном искомому?
. Как построить искомый треугольник?
Ответы на вопросы сопровождаются выполнением на
доске чертежа от руки (рис. 38).

Далее составляется план построения и выполняется
само построение. Запись построения у учащихся в тетрадях может быть такой:
а) D А В
В С
С : ÐА
: ÐА =
=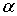 , ÐВ
, ÐВ =
=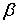 ;
;
б) построить биссектрису угла С в
треугольнике А
в
треугольнике А В
В С
С ,
,
в) построить С N=d, N
N=d, N C
C D
D ;
;
г) через точку N провести
прямую 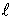 ,
, 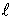 ÷ï А
÷ï А В
В ;
;
д) 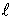
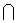 А
А C
C =А,
=А, 
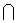 В
В С
С =В;
=В;
е) DАВС - искомый: ÐА=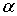 , ÐВ=
, ÐВ=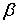 (так как DАВС¥D А
(так как DАВС¥D А В
В С
С по 1
признаку) и С
по 1
признаку) и С N=d по
построению.
N=d по
построению.
Дидактическая цель этапа,
формирующего умение решать задачи рассматриваемого вида, ясна уже из его
названия. Основная форма деятельности на этом этапе - индивидуально-поисковая.
Она завершается обобщающей беседой.
Приведем несколько примеров задач,
которые можно предложить на данном этапе.
Задача. Внутри угла АОВ задана точка
F. Построить
на стороне ОА точку М, одинаково удаленную от F и от
стороны ОВ
Решение. 1. Анализ. Обратимся к
рисунку 39. Пусть точка М построена, тогда MF=MP. Это
означает, что искомая точка М - есть центр окружности g радиуса МF с центром
М, касающуюся стороны ОВ в точке Р.

Если мы возьмем на ОА произвольную
точку М и опустим ^М Р
Р на СВ и
найдем F
на СВ и
найдем F пересечения
окружности g с центром М
пересечения
окружности g с центром М радиуса М
радиуса М Р
Р с прямой ОF, то DМ
с прямой ОF, то DМ F
F P
P будет
подобен DМFР. Отсюда
вытекает требуемое построение.
будет
подобен DМFР. Отсюда
вытекает требуемое построение.
. Построение. Проводим ОF, берем на
СА произвольную точку М и опускаем ^М
и опускаем ^М Р
Р на СВ.
Проводим окружность g
на СВ.
Проводим окружность g радиуса М
радиуса М Р
Р с центром в
точке М
с центром в
точке М . Пусть F
. Пусть F - точка
пересечения этой окружности с ОF. Проводим F
- точка
пересечения этой окружности с ОF. Проводим F M
M и затем
проводим прямую через точку F÷ïF
и затем
проводим прямую через точку F÷ïF M
M . Точка М
пересечения этой прямой с ОА - искомая.
. Точка М
пересечения этой прямой с ОА - искомая.
. Доказательство. Очевидно из
проведенного анализа.
. Исследование. Задача имеет 2
решения. Это следует из того, что окружность пересекается с ОF в 2-х точках.
Задача. Построить треугольник по 2
углам и периметру.
Решение. 1. Анализ. Пусть  и y - данные углы и Р - периметр
искомого треугольника (рис.40). Допустим, что искомый треугольник построен,
и y - данные углы и Р - периметр
искомого треугольника (рис.40). Допустим, что искомый треугольник построен,
тогда, если мы рассмотрим какой-либо
DАВ С
С , подобный
искомому, отношение периметра Р DАВС
к периметру Р
, подобный
искомому, отношение периметра Р DАВС
к периметру Р DАВ
DАВ С
С равно
отношению сторон
равно
отношению сторон
АС и АС .
.
. Построение. Построим DАВС подобный искомому. На
луче АВ, отложим отрезки АD=Р и АD =Р
=Р , затем
соединим точку D
, затем
соединим точку D и С
и С , и через точку D проведем
прямую ÷ï D
, и через точку D проведем
прямую ÷ï D C
C .
.
Пусть С - точка пересечения прямой с
лучом АС . Через
точку С проведем прямую ÷ï С
. Через
точку С проведем прямую ÷ï С В
В и обозначим
В точку пересечения этой прямой с AD, тогда DАВС - искомый.
и обозначим
В точку пересечения этой прямой с AD, тогда DАВС - искомый.

3. Доказательство. Очевидно, что DAС D подобен DАСD, поэтому
D подобен DАСD, поэтому 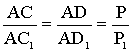 . По
соотношению сторон
. По
соотношению сторон  равно
отношению периметров подобных DАВС
и DАВ
равно
отношению периметров подобных DАВС
и DАВ С
С , поэтому
периметр DАВС=Р,
следовательно, DАВС -
искомый.
, поэтому
периметр DАВС=Р,
следовательно, DАВС -
искомый.
. Исследование. Так как сумма любых
двух углов треугольника <180°,
то условие  +y<180° является необходимым
условием для данного построения оно и достаточно. Затем указанным выше способом
строится искомый DАВС. Такой
треугольник единственный, ибо любой другой с такими же данными будет иметь
периметр Р и следовательно, будет подобен построенному с коэффициентом подобия
равным 1, а два подобных треугольника с одним коэффициентом равны.
+y<180° является необходимым
условием для данного построения оно и достаточно. Затем указанным выше способом
строится искомый DАВС. Такой
треугольник единственный, ибо любой другой с такими же данными будет иметь
периметр Р и следовательно, будет подобен построенному с коэффициентом подобия
равным 1, а два подобных треугольника с одним коэффициентом равны.
Задача. Дан ÐАОВ и точка М, расположенная
во внутренней области этого угла. Построить окружность g, проходящую через точку А
касающуюся сторон угла АОВ.
Решение. 1. Анализ. Пусть ÐАОВ - данный и точка М,
расположена во внутренней области угла (рис. 41). Проведем еще одну окружность g, касающуюся сторон ÐАОВ. Обозначим, М - точку
пересечения окружности g с прямой ОМ
и рассмотрим DОМN и ОМ
- точку
пересечения окружности g с прямой ОМ
и рассмотрим DОМN и ОМ N
N (N и N
(N и N центры
окружности g и g
центры
окружности g и g ). Эти треугольники подобны по двум
углам, поэтому построение искомой окружность можно провести следующим образом:
). Эти треугольники подобны по двум
углам, поэтому построение искомой окружность можно провести следующим образом:
. Построение. Так как центр искомой
окружности лежит на биссектрисе ÐАОВ,
то проводим биссектрису угла. Далее, возьмем здесь же точку N и построим
окружность g
и построим
окружность g с центром N
с центром N , касающуюся
, касающуюся

ÐАОВ.
Затем проводим прямую СМ и обозначим через М - точку пересечения прямой с
окружностью (таких точек две - М
- точку пересечения прямой с
окружностью (таких точек две - М и М
и М - берем одну из них). Проводим
прямую М
- берем одну из них). Проводим
прямую М N
N и ÷ïей прямую
через точку М. Тогда N -пересечение прямой с биссектрисой
угла и есть центр искомой окружности, а ее радиус равен МN. Проведем
ее.
и ÷ïей прямую
через точку М. Тогда N -пересечение прямой с биссектрисой
угла и есть центр искомой окружности, а ее радиус равен МN. Проведем
ее.
. Доказательство. По построению
окружность g подобна g , О - центр подобия. Это следует из
подобия треугольников ОМN и ОМ
, О - центр подобия. Это следует из
подобия треугольников ОМN и ОМ N
N ,поэтому раз окружность g касается сторон угла, то и
окружность g
,поэтому раз окружность g касается сторон угла, то и
окружность g будет
касаться сторон угла .
будет
касаться сторон угла .
. Исследование. Задача имеет два
решения, т.к. ОМ пересекается с окружностью g в двух
точках М
в двух
точках М и М
и М , каждой из
которых будет соответствовать своя окружность, проходящая через точку М и
, каждой из
которых будет соответствовать своя окружность, проходящая через точку М и
касающаяся сторон ÐАОВ.
Дидактической целью этапа,
совершенствующего умение решать задачи типа рассмотренных, является перенос
сформированного умения на более сложные задачи, в частности на следующие
ситуации: искомая фигура занимает определенное положение по отношению к данным
точкам или линиям, при этом устранение одного из условий задачи приводит к
системе подобных или гомотетичных фигур. Приведем пример такой задачи.
Задача. В данный треугольник впишите
квадрат так, чтобы две его вершины лежали на одной стороне треугольника, а две
другие - на двух других сторонах.
Задачи, соответствующие целям этого
этапа, исключены из числа задач обязательного уровня. Поэтому они предлагаются
только хорошо успевающим школьникам. Главное внимание на этом этапе уделяется
индивидуально-поисковой деятельности учащихся.
Заключение
Овладение практически любой
современной профессией требует определенных математических знаний.
Представление о роли математики в современном мире, математические знания стали
необходимым компонентом общей культуры. Для жизненной самореализации,
возможность продуктивной деятельности в информационном мире требуется
достаточно прочная математическая подготовка.
В процессе математической
деятельности учащихся в арсенал приемов и методов мышления включаются индукция
и дедукция, обобщение и конкретизация, анализ и синтез, классификация и
систематизация, абстрагирование, аналогия. Ведущая роль принадлежит математике
в формировании алгоритмического мышления, воспитании умения действовать по
заданному алгоритму и конструировать новые в ходе решения задач, основа учебной
деятельности на уроках математики. Развиваются творческая и прикладная стороны
мышления.
Данная работа имеет практическую
направленность. Учитель может использовать предложенную методику в своей
практической деятельности. Разнообразие рассматриваемых задач позволит учителю
применить их как для обязательного курса изучения геометрии, так и для
индивидуальной, факультативной работы и для работы в классах с углубленным
изучением математики.
Таким образом, цель поставленная в
данной дипломной работе выполнена, задачи реализованы.
Литература
1. Аргунов
Б. И., Балк М. Б. Геометрические построения на плоскости, второе издание - М.:
«Просвещение», 1975.
2. Базылев
В. Т., Дуничев К. И. Геометрия (часть 2) - М.: «Просвещение», 1975.
3. Белозеров
С. Е. Пять знаменитых задач древности (История и современная теория) -
издательство Ростовского университета, 1975.
4. Мельникова
Н. Б., Мищенко Т. М. Геометрия в 6 классе - М.: «Просвещение», 1986.
5. Карнацевич
Л. С., Грузин А. И., Изучение геометрии в 6 классе - М.: «Просвещение», 1983.
6. Аргунов
Б. И. Преобразования плоскости-М.: «Просвещение», 1976.
7. Кожарин
А. Ф., Лебедев В. К., Алгебра и геометрия. Методика преподавания в 9-11 классах
- Ростов-на-Дону, «Феникс», 2002.
8. Мухина
В. С. Возрастная психология - М.: «Академия», 1999.
9. Абрамова
Г. С. Возрастная психология - М.: «Академия», 1999.
10. Алферов
А. Д. Психология развития школьника - Ростов-на-Дону, «Феникс», 2000.
11. Рыбалко
Е. Ф. Возрастная и дифференциальная психология - СПб.: «Питер», 2001.
12. Белошистая
А. В. Задачи на построение в школьном курсе геометрии
//Математика
в школе. - 2002. - 9.
13. Чистякова
Л. С. Приемы формирования практических умений и навыков при обучении геометрии
//Математика в школе. - 1987. - 4.
14. Корнеева
В. Е. Решение задач на построение методом спрямления //Математика в школе. -
1995. - 5.
15. Фукс
Д. Б. Построения одним циркулем //Квант. - 1987. - 6.
16.
Нильме Д. В. Циркулем и линейкой //Квант. - 1975. - 6.
17.
Погорелов А. В. Геометрия 6-10 - М.: «Просвещение», 1982.
18.
Атанасян Л. С., Бутузов В. Ф. Геометрия 7-9 - М.: «Просвещение», 1994.
19.
Бевз Г. П., Бевз В. Г. Геометрия 7-11 - М.: «Просвещение», 1992.