Специальные вопросы электроснабжения промышленных предприятий
Основные понятия теории вероятностей
энергетика теория
вероятность энергосбережение
Вопрос № 3
Какие задачи энергетики решаются с помощью
методов теории вероятностей?
Ответ:
Развитие электроэнергетической отрасли в
настоящее время немыслимо без решения вопросов и расчётов надёжности элементов
и систем, входящих в комплексные функциональные устройства. Внезапные перерывы
электроснабжения влекут за собой значительные народно-хозяйственные ущербы, а
также при стечении ряда обстоятельств не исключают появление пожаров и
взрывоопасных ситуаций, связанных с угрозой здоровью и жизни людей. Поэтому
вопрос повышения надёжности систем электроснабжения приобретает важное
государственное значение. Расчёт надёжности систем электроснабжения проводится
с использованием математического аппарата теории вероятностей.
С помощью методов теории вероятностей можно:
ü анализировать рабочие и аварийные
режимы систем электроснабжения;
ü производить расчёты надёжности
систем электроснабжения;
ü оценивать ущерб предприятию из-за
отсутствия электропитания;
ü построить рациональную по надёжности
схему электроснабжения;
ü оценивать качество электрической
энергии и проводить мероприятия по его улучшению;
ü анализировать процессы смены
состояний системы, на которые влияют случайные отказы отдельных элементов.
Конечной целью расчёта надёжности систем
электроснабжения является количественная оценка комплексных показателей
надёжности:
вероятность безотказной работы (вероятность
того, что в пределах заданной
продолжительности работы объекта отказ не
возникает);
интенсивность отказов;
параметр потока отказов;
частота отказов;
наработка на отказ;
вероятность восстановления в заданное время;
среднее время восстановления;
продолжительность восстановления;
коэффициент готовности (вероятность нахождения
элемента в работоспособном состоянии);
коэффициент технического использования;
коэффициент оперативной готовности;
средний недоотпуск электроэнергии;
коэффициент необеспеченности электроэнергией;
экономический ущерб от надежности;
удельный ущерб
относительно конкретных узлов нагрузки и
разработать на основе полученных результатов мероприятий целенаправленного их
изменения.
Основные теоремы теории вероятностей
Вопрос № 7.
Объясните физический смысл формулы полной
вероятности.
Ответ:
Формула полной вероятности является следствием
обеих основных теорем - теоремы сложения вероятностей и теоремы умножения
вероятностей.
Пусть требуется определить вероятность
некоторого события А, которое может произойти вместе с одним из событий:
Н1, Н2, …, Нп,
образующих полную группу (несколько событий в
данном опыте образуют полную группу событий, если в результате опыта
непременно должно появиться хотя бы одно из них) несовместных событий
(несколько событий называются несовместными в данном опыте, если никакие
два из них не могут появиться вместе). Будем эти события называть гипотезами.
Так как гипотезы Н1, Н2, …, Нп образуют полную
группу, то событие А может появиться только в комбинации с какой-либо из этих
гипотез:
А=Н1∙А+Н2∙А+…+Нп∙А.
Так как гипотезы Н1, Н2, …, Нп несовместны, то и
комбинации Н1∙А+Н2∙А+…+Нп∙А также несовместны. Применяя к ним
теорему сложения вероятностей (Вероятность суммы двух несовместных событий
равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В) ), получаем:
Р(А)= Р(Н1∙А)+Р(Н2∙А)+…+Р(Нп∙А)= .
.
Применяя к событию Рi∙А
теорему умножения (Вероятность произведения двух событий равна произведению
вероятности одного из них на условную вероятность другого, вычисленную при
условии, что первое имело место: Р(А∙В)=Р(А)∙Р(В/А) ), получим:
Р(А)= Р(Н1)∙Р(А/Н1)+Р(Н2)∙Р(А/Н2)+…+Р(Нп)∙Р(А/Нп)
или 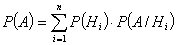 .
.
Полученная формула и есть формула
полной вероятности.
Пример. Вдоль линии
электропередач (ЛЭП) происходит три грозовых разряда. Вероятность попадания в
ЛЭП первого грозового разряда равна 0.4; второго - 0.5; третьего - 0.7. ЛЭП
выходит из строя при одном попадании молнии с вероятностью 0.2; при двух
попаданиях с вероятностью 0.6 и при трёх попаданиях с вероятностью 1.0.
Найти вероятность того, что в
результате грозовых разрядов ЛЭП вышла из строя.
Решение. Рассмотрим четыре гипотезы:
1. Н0 - в ЛЭП не попало ни одного
грозового разряда;
2. Н1 - в ЛЭП попал один разряд молнии;
. Н2 - в ЛЭП попало два разряда молнии;
. Н3 - в ЛЭП попало три разряда молнии.
Очевидно, что эти гипотезы имеют место при
следующих сочетаниях событий, образующих несколько несовместных вариантов:
 ;
;
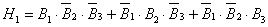 ;
;
 ;
;
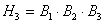 ,
,
где В1, В2, В3 - попадание молнии в
ЛЭП при первом, втором и третьем грозовом разряде, соответственно. 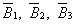 - события
противоположные событиям В1, В2, В3 соответственно, вычисленные как
- события
противоположные событиям В1, В2, В3 соответственно, вычисленные как 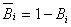 .
.
Пользуясь теоремами сложения,
умножения и свойством противоположных событий, находим вероятности этих
гипотез.
 ;
;
 ;
;
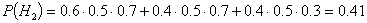 ;
;
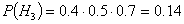 .
.
Условные вероятности события А
(выход из строя ЛЭП) при этих гипотезах равны:
 ;
; 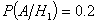 ;
;  ;
; 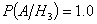 .
.
Применяя формулу полной вероятности,
получаем:
Р(А)= Р(Н0)∙Р(А/Н0)+Р(Н1)∙Р(А/Н1)+Р(Н2)∙Р(А/Н2)
+Р(Н3)∙Р(А/Н3)=
.09∙0+0.36∙0.2+0.41∙0.6+0.14∙1.0=0.458.
Данный пример наглядно показывает область
применения формулы полной вероятности, с помощью которой можно определить
вероятность некоторого события, которое может произойти вместе с одним из
событий, образующих полную группу несовместных событий.
Формула полной вероятности играет большую роль
при анализе надёжности сложных схем, поскольку позволяет свести любую сложную
схему к совокупности элементарных. Метод оценки надёжности, основанный на
формуле полной вероятности, достаточно удобен, прост и нагляден в расчётах даже
без применения ЭВМ относительно небольших по объёму схем с небольшим числом
ветвей и узлов, к которым можно отнести схемы внутризаводского
электроснабжения.
Случайные величины
Вопрос № 3.
Как определяется математическое ожидание
произведения и суммы нескольких независимых случайных величин?
Ответ:
Случайной величиной называется
величина, которая в результате опыта может принять то или иное значение, причём
неизвестно заранее, какое именно. Например, случайной величиной является
количество отказов системы электроснабжения за определённый промежуток времени
или время отыскания повреждения и ремонта вышедшего из строя кабеля и т. д.
Среднее значение случайной величины есть
некоторое число, являющееся как бы её «представителем» и заменяющее её при
ориентировочных расчётах. Когда мы говорим: «средняя нагрузка шинопровода равна
200 А», то этим указываем определённую числовую характеристику случайной
величины, описывающую её местоположение на числовой оси, т. е. «характеристику
положения».
Из характеристик положения важнейшую роль играет
математическое ожидание случайной величины, которое часто называют
просто средним значением случайной величины.
Рассмотрим дискретную случайную величину Х,
имеющую возможные значения х1, х2, х3, … хп с вероятностями Р1, Р2, Р3, … Рп.
Требуется охарактеризовать каким-то числом положение значений случайной
величины на оси абсцисс с учётом того, что эти значения имеют различные
вероятности. Для этой цели воспользуемся так называемым «средним взвешенным» из
значений хi, причём каждое
значение хi при осреднении
должно учитываться с «весом», пропорциональным вероятности этого значения.
Таким образом, мы вычислим среднее значение случайной величины Х, которое
обозначим М[X]:
 ,
,
или, учитывая, что 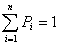 ,
,
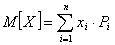 .
.
Это среднее взвешенное значение и
называется математическим ожиданием случайной величины. Другими словами, математическим
ожиданием дискретной случайной величины называется сумма произведений всех
возможных значений случайной величины на вероятности этих значений.
Выведенная формула для математического
ожидания соответствует случаю дискретной случайной величины. Для непрерывной
величины Х математическое ожидание, естественно, выражается уже не суммой, а
интегралом
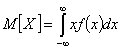 ,
,
где f(x) - плотность
распределения величины Х.
Отметим две теоремы о математическом
ожидании функций, представляющих практические формулы вычисления этой
характеристики:
ü Математическое ожидание суммы
независимых случайных величин
 ,
,
т. е. математическое ожидание суммы
нескольких случайных величин равно сумме их математических ожиданий.
ü Математическое ожидание произведения
независимых случайных величин
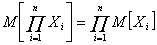 ,
,
т. е. математическое ожидание
произведения независимых случайных величин равно произведению их математических
ожиданий.
Виды законов распределения случайной
величины в задачах электроснабжения
Вопрос № 8.
При каких условиях
гамма-распределение превращается в показательное?
Ответ:
В процессе эксплуатации в материалах
элементов электрической сети вследствие термических и механических воздействий,
электромагнитных полей, агрессивной среды, снижения показателей качества
электрической энергии и др. накапливаются необратимые изменения, снижающие
прочность, нарушающие координацию и взаимодействие отдельных частей. Эти
изменения в случайные моменты времени могут приводить к отказу элемента.
Основной причиной постепенных
отказов является старение материалов и износ отдельных частей элементов.
Как бы ни совершенна была конструкция элемента и его частей, технология
производства и монтажа, со временем материалы, из которых изготовлен объект,
претерпевают необратимые изменения. Они возникают вследствие теплового,
вибрационного старения изоляции трансформаторов, кабельных линий, генераторов,
коррозии металлических частей проводов, оболочек кабельных линий, износа
дугогасительных камер коммутационных аппаратов, а также вследствие деформации
материалов, диффузии материала и других причин.
По мере эксплуатации
электротехнических изделий в изоляции вследствие влияния процессов нагревания,
обусловленных протеканием токов нагрузки, изменения условий внешней среды,
электродинамических сил, возникающих при резком изменении тока, вибрации,
повышения влажности и вредных примесей в среде, окружающей изоляцию,
воздействий электрического поля происходят сложные физико-химические процессы
старения. Изоляция становится хрупкой, ломкой, появляются трещины, в результате
чего уменьшается её электрическая прочность и при случайном повышении
напряжения сверх допустимого уровня происходит отказ.
Таким образом, постепенный износ
отдельных частей элемента представляет собой как бы накопление элементарных
повреждений в различных его частях и снижение общего предела прочности. После
достижения некоторого уровня, т. е. накопления определённого числа элементарных
повреждений (необходимо, например, многократное превышение температуры изоляции
сверх допустимой, многократное отключение токов коротких замыканий
выключателем, многократное воздействие неблагоприятных условий окружающей среды
и т. д.), происходит отказ элемента.
Для построения математического
описания этих явлений положим некоторые идеализированные условия. В случайные
моменты времени возникают единичные, элементарные повреждения и при накоплении
повреждений объект отказывает. Число элементарных повреждений зависит не от
момента времени, а лишь от его продолжительности (стационарность). Элементарное
повреждение состоит в том, что износ объекта увеличивается на некоторую
величину Δη за время Δt,
вероятность возникновения этого износа равна λΔt и не
зависит от того, насколько изношен объект за предшествующий период эксплуатации
(независимость), т. е. не зависит от его состояния. Выберем интервал времени
таким образом, чтобы вероятностью двух и более элементарных повреждений в этом
интервале можно было пренебречь (ординарность потока).
При указанных условиях несложно
определить вероятность появления k элементарных повреждений на
интервале времени (0, t).
Для начала найдём вероятность того,
что в произвольно выбранном интервале времени Δt произойдёт,
по крайней мере, одно повреждение. Согласно условию ординарности потока
элементарных повреждений вероятность появления, по крайней мере, одного
повреждения и только одного повреждения в указанных условиях численно совпадает
и равна λΔt, а
вероятность отсутствия такого повреждения равна 1- λΔt.
Разделим интервал времени (0, t) на п
равных отрезков (частей) Δt=t/n. Так как
вероятности возникновения элементарных повреждений в указанных отрезках
независимы, то вероятность появления k
элементарных повреждений на интервале времени (0, t) можно
определить, используя схему независимых испытаний (биноминальный закон
распределения):
 .
.
Предел этого выражения при
неограниченном увеличении числа интервалов (п → ∞), а
следовательно, при Δt → 0,
 ,
,
т. е. вероятность числа элементарных
повреждений на интервале (0, t) зависит от длины этого участка и
распределена по закону Пуассона с параметром λt.
Очевидно, объект не откажет, если
произойдёт менее k элементарных повреждений.
Вероятность того, что время
безотказной работы будет не менее Т (интегральная функция распределения):
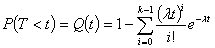 ,
,
где i - число
элементарных повреждений.
Дифференциальная функция
распределения, или плотность вероятности времени безотказной работы
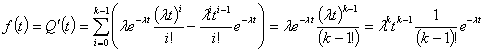 .
.
Так как для целых k
гамма-функция (k-1)! =Г(t) = , то в общем
виде
, то в общем
виде
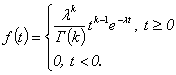
Это распределение называется гамма-распределением
времени безотказной работы. Вид этого распределения для различных значений k. При k=1 это
распределение превращается в показательное, т. е. одно повреждение приводит к
отказу элемента.
Методы расчёта показателей
надёжности систем электроснабжения
Вопрос № 3.
Какими параметрами определяется коэффициент
готовности и коэффициент вынужденного простоя?
Ответ:
Параметр потока отказов и наработка на отказ
характеризуют надёжность ремонтируемого изделия и не учитывают времени,
необходимого на его восстановление. Поэтому они не характеризуют готовность
изделия к выполнению своих функций в нужное время. Для этой цели вводятся такие
критерии, как коэффициент готовности и коэффициент вынужденного простоя.
Коэффициент готовности.
Он представляет собой отношение времени исправной работы к сумме времён
исправной работы и вынужденных простоев объекта, взятых за один и тот же
календарный срок. Эта характеристика обозначается КГ.
Согласно данному определению
 ,
,
где tp - суммарное
время исправной работы объекта; tn - суммарное время
вынужденного простоя.
Времена tp и tп
вычисляются по формулам
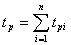 ,
, 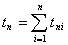 ,
,
где tpi - время
работы объекта между (i-1)-м и i-м отказом; tпi - время
вынужденного простоя после i-го отказа; п - число отказов
(ремонтов) объекта.
Выражение  является
статистическим определением коэффициента готовности. Для перехода к
вероятностной трактовке величины tp и tп заменяются
математическими ожиданиями времени между соседними отказами и времени восстановления,
соответственно.
является
статистическим определением коэффициента готовности. Для перехода к
вероятностной трактовке величины tp и tп заменяются
математическими ожиданиями времени между соседними отказами и времени восстановления,
соответственно.
Тогда
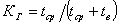 ,
,
где tср -
наработка на отказ; tв - среднее время восстановления.
Коэффициент вынужденного простоя. Он
определяется отношением времени вынужденного простоя к сумме времён исправной
работы и вынужденных простоев изделия, взятых за один и тот же календарный
срок.
Согласно определению
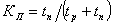
или, переходя к средним значениям
величин,
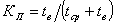 .
.
КП=1-КГ.
При анализе надёжности
восстанавливаемых систем коэффициент готовности обычно вычисляют по формуле
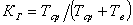 .
.
Эта формула справедлива только в том
случае , если поток отказов простейший, и тогда tср=Тср.
Рассмотрим элемент, который может
находиться в двух состояниях: 0 - безотказной работы, 1 -
состоянии отказа (восстановления). Определим соответствующие вероятности
состояний элемента Р0(t), Р1(t) в
произвольный момент времени t при различных начальных условиях.
Эту задачу решим при условии, что поток отказов простейший с интенсивностью
отказов λ=const и
восстановлении μ=const, закон
распределения времени между отказами (частота отказов) 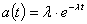 , время
восстановления описывается также показательным законом распределения с
параметром μ, т.
, время
восстановления описывается также показательным законом распределения с
параметром μ, т.
е. 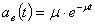 .
.
Для любого момента времени сумма
вероятностей Р0(t)+ Р1(t)=1 -
вероятность достоверного события. Зафиксируем момент времени t и найдём
вероятность Р0(t+Δt) того, что
в момент t+Δt элемент
находится в работе. Это событие осуществляется при выполнении двух условий.
. В момент t элемент
находился в состоянии 0 и за время Δt не
произошло отказа. Вероятность работы элемента определяется по правилу умножения
вероятностей независимых событий. Вероятность того, что в момент t элемент был
в состоянии 0, равна Р0(t). Вероятность того, что за время Δt он не
отказал, равна 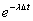 . С
точностью до величины высшего порядка малости можно записать
. С
точностью до величины высшего порядка малости можно записать
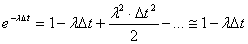 .
.
Поэтому вероятность этой гипотезы
будет равна произведению Р0(t)∙(1- λΔt).
. В момент времени t элемент
находился в состоянии 1 (в состоянии восстановления), за время Δt восстановление
закончилось и элемент перешёл в состояние 0. Эту вероятность также
определим по правилу умножения вероятностей независимых событий. Вероятность
того, что в момент времени t элемент находился в состоянии 1,
равна Р1(t).
Вероятность того, что восстановление закончилось, определим через вероятность
противоположного события, т. е. 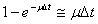 . Следовательно, вероятность второй
гипотезы равна Р1(t)∙ μΔt.
Вероятность рабочего состояния элемента в момент (t+Δt)
определяется вероятностью суммы независимых несовместимых событий при
выполнении обеих гипотез:
. Следовательно, вероятность второй
гипотезы равна Р1(t)∙ μΔt.
Вероятность рабочего состояния элемента в момент (t+Δt)
определяется вероятностью суммы независимых несовместимых событий при
выполнении обеих гипотез:

или
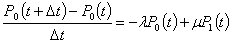 ;
;
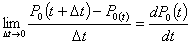 .
.
Следовательно, первое уравнение
состояния
 .
.
Проводя аналогичные рассуждения для
второго состояния элемента - состояние отказа (восстановления), можно записать
второе уравнение состояния
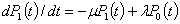 .
.
Таким образом, для описания
вероятностей состояния элемента получена система двух дифференциальных
уравнений. Необходимо отметить, что λdt и μdt выполняют
роль вероятностей перехода соответственно в отказовое и в рабочее состояние
элемента.
Систему дифференциальных уравнений
можно использовать для определения вероятностей безотказной работы системы
электроснабжения, функции и коэффициента готовности, вероятности нахождения в
ремонте (восстановлении), среднего времени пребывания системы в рабочем
состоянии, интенсивности отказов системы на относительно коротких интервалах
времени, когда необходим учёт начальных условий (состояний элементов).
Решением системы уравнений,
описывающих состояние одного элемента при начальных условиях [Р0(0)=1; Р1(0)=0],
будет:
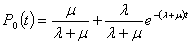 .
.
Вероятность состояния отказа
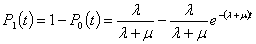 .
.
Если в начальный момент времени
элемент находился в состоянии отказа (восстановления) т. е. Р0(0)=0; Р1(0)=1,
то
 ;
;
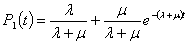 .
.
Для стационарного состояния (t→∞)
вероятность работы элемента равна стационарному коэффициенту готовности, а
вероятность отказа состояния - коэффициенту вынужденного простоя:
 ;
;
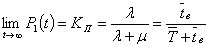 ,
,
где  - среднее время безотказной работы;
- среднее время безотказной работы;
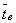 - среднее
время восстановления.
- среднее
время восстановления.
Коэффициент готовности и коэффициент
вынужденного простоя можно интерпретировать как среднюю вероятность нахождения
системы соответственно в рабочем состоянии и в состоянии отказа.
Математическая статистика в задачах
надёжности
Вопрос № 8.
Как определяется вероятность события
по его частоте в опытах?
Ответ:
Если произведена серия из п опытов,
в каждом из которых могло появиться или не появиться некоторое событие А, то частотой
события А, в данной серии опытов называется отношение числа опытов, в
которых появилось событие А, к общему числу произведённых опытов.
Частоту событий иногда называют его
статистической вероятностью. Если обозначить её знаком 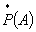 , то частота
события вычисляется на основании результатов опыта по формуле
, то частота
события вычисляется на основании результатов опыта по формуле
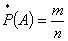 ,
,
где т - число появлений события А; п
- общее число произведённых опытов.
Частота события всегда правильная
дробь и изменяется в пределах 0≤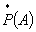 ≤1.
≤1.
При небольшом числе опытов частота
события носит в значительной мере случайный характер и может заметно изменяться
от одной группы опытов к другой. При увеличении числа опытов частота события
всё более теряет свой случайный характер, проявляет тенденцию
стабилизироваться, приближаясь с незначительными колебаниями к некоторой
средней, постоянной величине - его вероятности.
Это свойство «устойчивости
частот» есть одна из наиболее характерных закономерностей, наблюдаемых в
случайных явлениях.
Связь между частотой события и его
вероятностью - глубокая, органическая. Эти два понятия, по существу,
неразделимы. Численная оценка степени возможности события посредством
вероятности имеет практический смысл именно потому, что более вероятные события
происходят в среднем чаще, чем менее вероятные.
Требования и учёт надёжности систем
электроснабжения
Вопрос № 3.
Чем определяется ущерб от перерыва
электроснабжения?
Ответ:
При определении категорийности того или иного
электроприемника оцениваются последствия, к которым приводит внезапный перерыв
в электроснабжении того или иного электроприемника.
По характеру последствий внезапного перерыва в
электроснабжении все электроприемники можно разделить на две группы:
с экономическим характером последствий, случай,
когда эти последствия можно подсчитать в денежном выражении;
с неэкономическим характером последствий,
случай, когда оценка последствий в денежном выражении невозможна или полностью
не исчерпывает этих последствий. В этом случае руководствуются категорией
тяжести последствий, возникающих при перерывах в электроснабжении, определяемой
по имевшим место аналогиям, либо по прогнозам экспертов.
В различных отраслях народного хозяйства вводят
нормированные показатели, как правило, по продолжительности внезапного перерыва
в электроснабжении или величине разового ущерба, и на основании этих критериев
определяется категорийность электроприемников.
Наиболее эффективным способом обеспечения
электроприемников рациональным уровнем надежности электроснабжения является
проведение технико-экономической оценки надежности электроснабжения.
Технико-экономическая оценка уровня надежности
заключается в:
количественной оценке разовых ущербов от
внезапного перерыва электроснабжения потребителя;
количественной оценке характеристик таких
нарушений (чаще всего - в ожидаемой частоте и продолжительности перерывов) -
т.е. расчете надежности;
определении по первым двум вышеприведенным
оценкам величины ожидаемого ущерба в год при существующем в данной схеме уровне
надежности.
Слагаемые ущерба весьма многоплановы и не
поддаются точному математическому описанию. Однако не вызывает сомнений то, что
необходимо иметь нормативную документацию, регламентирующую выбор варианта схем
электроснабжения для различных электроприемников в зависимости от требуемой по
условиям технологического процесса надежности электроснабжения.
Многолетний опыт эксплуатации показал, что
перерывы электроснабжения приводят к аварийным ситуациям (аварийная остановка
оборудования, расстройство технологического процесса и т. д.).
Ущерб от перерыва электроснабжения определяется
такими показателями надёжности, как средний недоотпуск электроэнергии и экономический
ущерб от ненадёжности.
Средний недоотпуск электроэнергии.
Этот показатель характеризует не только все основные свойства надёжности
системы, но и режим её загрузки, и представляет собой математическое ожидание
недоотпуска электроэнергии потребителям за расчётный период времени. Его оценка
для узлов нагрузки и системы в целом является одной из конечных целей расчётов
надёжности.
Рассмотрим суть оценки недоотпуска
электроэнергии. Пусть в процессе эксплуатации объёкта в момент t
наступил отказ, в то время как нагрузка потребителя составляла величину Wн.
В общем случае отказ системы по отношению к рассматриваемому потребителю может
быть не полным, а частичным, когда система способна удовлетворять не всю
нагрузку, а только её часть WR.
Недоотпуск электроэнергии при этом может быть найден как
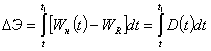 ,
,
где интервал времени (t÷t1) - время
дефицита энергии и интегрирование осуществляется только в области времени
положительных дефицитов, т. е. когда D(t)>0:
D(t)=Wн(t)-WR.
В практических расчётах интеграл
заменяется суммой
 ,
,
где Wн(t)час -
среднечасовая текущая нагрузка потребителя в момент t,
определяемая по ожидаемому графику нагрузки в день аварии, Δt=1 час.
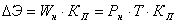 ,
,
где Рн, Wн -
соответственно математическое ожидание мощности и энергии, потребляемой узлом
нагрузки за время Т; КП - коэффициент вынужденного простоя системы относительно
узла нагрузки (средняя вероятность состояния отказа).
Экономический ущерб от ненадёжности. Этот
показатель надёжности является наиболее полным. Он характеризует интегрально
все свойства надёжности системы, включая режим её загрузки и значимость
потребителя энергии. Важность каждого потребителя с экономической точки зрения
характеризуется величиной удельного ущерба [У0, р./(кВт∙ч)].
Экономический ущерб при каждом
отказе k (k=1, 2, … n) за
некоторый период Т
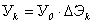 .
.
Практическое задание.
На рис. 2 приведена схема электроснабжения
завода. Завод питается от районной энергосистемы (Г1 и Г2) по двум линиям
электропередач. Коммутация линий и трансформаторов осуществляется
высоковольтными выключателями.
Параметры потоков отказов lо
и потоков преднамеренных отключений lп элементов системы
электроснабжения, средние времена восстановления tв
и длительности преднамеренных отключений tп
приведены в табл. 1.
Для упрощения расчетов коммутационные аппараты
на стороне 10 кВ - В110, на стороне 10 кВ - В10 и трансформаторы Т по
надежностным параметрам считать одинаковыми.
График нагрузки имеет две ступени: S1
= 80 МВА; S2 = 60 МВА.
Соответствующие вероятности этих значений РS1
= 0,4; РS2 = 0,6.

Рис. 2. Схема электроснабжения завода
Таблица 1. Статистические данные элементов схемы
|
Элемент
|
Л1
|
Л2
|
Л3
|
Л4
|
В110
|
В10
|
Т
|
|
lо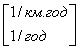 0,0230,0190,200,150,060,020.016 0,0230,0190,200,150,060,020.016
|
|
|
|
|
|
|
|
|
L, км
|
80
|
30
|
3
|
5
|
-
|
-
|
-
|
|
tв, час
|
30
|
30
|
40
|
40
|
15
|
10
|
280
|
|
lп, 1/год
|
2,2
|
1,8
|
0,25
|
0,2
|
3,5
|
1
|
0.33
|
|
tп, час
|
32
|
35
|
50
|
45
|
32
|
10
|
110
|
Допущения:
при расчете принять вероятность отказа сборных шин равной 0; время оперативных
переключений не учитывать; считать, что во время аварийного восстановления
преднамеренных отключений не производится; принять, что вероятности отказов
линий и подстанций не зависят от значений нагрузки; поток отказов простейший.
Расчеты выполнить для узла нагрузки А схемы
(рис. 2). Элементами, подлежащими преднамеренному отключению для ремонта
являются выключатель В3 и трансформатор Т1.
Требуется определить:
1)
параметр
потока отказов системы электроснабжения для указанного узла нагрузки;
2)
среднее
время безотказной работы;
3)
среднюю
вероятность отказа;
4)
среднее
время восстановления;
5)
недоотпуск
электроэнергии заводу за год.
Параметры по п. 1-5 должны быть определены без
учета и с учетом преднамеренных отключений. Результаты расчета сопоставить,
проанализировать и сделать выводы.
Решение.
Из принципиальной схемы, приведенной на рис. 2,
составляем схему электроснабжения, обеспечивающую питанием узел нагрузки А,
которая будет иметь вид, показанный на рис. 3.
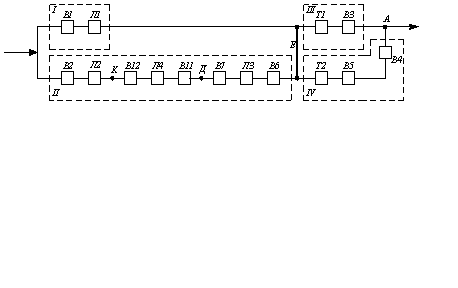
Полученную принципиальную схему заменяем на
расчетную по надежности. Для узла нагрузки А она будет иметь вид, показанный на
рис. 4. Для наглядности и удобства расчета группы последовательно соединенных
элементов выделены на расчетной схеме пунктирными прямоугольниками в
эквивалентные по надежности элементы I-IV.
В последовательные цепи
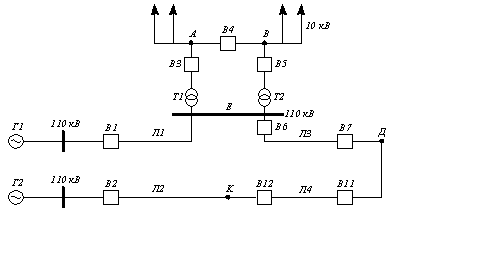
Рис. 3. Схема электроснабжения, обеспечивающая
питанием узел А.
расчётной схемы по надёжности, кроме элементов
последовательной электрической цепи (линии, выключатель, трансформатор и т.
д.), вводятся также смежные выключатели, отказ которых может привести к отказу
рассматриваемой цепи (например, выключатели всех присоединений, секционные
выключатели шин, к которым подключена анализируемая цепь).
Расчёт показателей надёжности системы
электроснабжения проводим по средним значениям вероятностей состояния
элементов.
Для всех элементов расчетной схемы
(выключателей, трансформаторов и линий электропередачи) определяем вероятности
отказового состояния (вероятности вынужденного простоя) q
по формулам:
 ;
;  ;
; 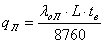
где, 8760 - число часов в году; lо - параметры потоков отказа;
tв - средние
времена восстановления. Т. е. средняя вероятность отказа равна произведению
параметра потока отказа на среднее время восстановления элемента после одного
отказа. Параметр потока отказов представляет собой плотность вероятности отказа
восстанавливаемого объекта, определяемую для рассматриваемого момента времени:  , где Р(t,t+Δt) -
вероятность безотказной работы на интервале времени Δt после
момента t.
, где Р(t,t+Δt) -
вероятность безотказной работы на интервале времени Δt после
момента t.
Тогда вероятности отказового
состояния для:
выключателей 110 кВ -  ;
;
выключателей 10 кВ -  ;
;
трансформаторов - 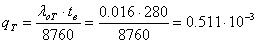 ;
;
линий электропередач - 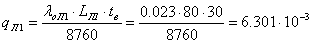 ;
;
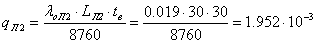 ;
;
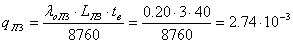 ;
;
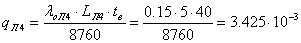 .
.
Последовательно включенные элементы
на расчетной схеме заменяем эквивалентным с соответствующим определением
параметров потока отказов и вероятностей отказового состояния.
параметры потоков отказов и
вероятности отказовых состояний для эквивалентных элементов I, II, III, IV
определяются соответственно:
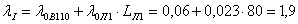 год-1;
год-1;
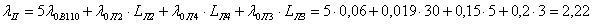
год-1;
 год-1;
год-1;
 год-1;
год-1;
 ;
;
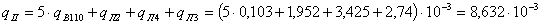 ;
;
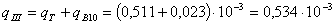 ;
;
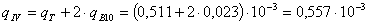 .
.
В результате проведенных расчетов схема на рис.
4.8 свелась к схеме, приведенной на рис. 5 с четырьмя эквивалентами элементами.
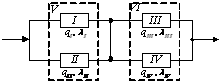
Рис. 5. Упрощенная расчетная схема
Эта схема состоит из параллельно включенных
элементов. При условии независимости отказов каждого элемента и пропускной
способности каждого, достаточной для обеспечения всей мощности, необходимой
потребителю, такая система будет в рабочем состоянии при условии работы хотя бы
одного из параллельно соединённых элементов. Вероятность надёжной работы
системы определим по вероятностям отказового состояния элементов. Система будет
в отказовом состоянии при условии, если все параллельные элементы откажут.
Вероятность отказового состояния определяется с использованием формулы для
произведения (совмещения) независимых событий - отказов каждого элемента
системы:
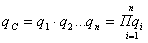
Схему с четырьмя эквивалентными
элементами приводим к виду, показанному на рис. 6, с двумя последовательными
эквивалентными элементами V и VI и
параметрами lV, qV и lVI, qVI:
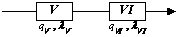
Рис. 6. Промежуточная схема
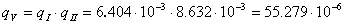 ;
;
 ;
;
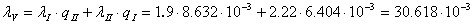 год-1;
год-1;
 год-1.
год-1.
Эта схема сводится к итоговой схеме
(рис. 7) для которой можно рассчитать параметры надежности системы в целом.
Элементы V и VI
объединяются в эквивалентный с параметрами потока отказов системы lс и вероятности отказового
состояния системы qс.

Рис. 7. Итоговая схема.
Параметр потока отказов lс
без учета преднамеренного отключения определится:
 год-1.
год-1.
Вероятность отказового состояния без учета
преднамеренного отключения qс:
 .
.
Среднее время восстановления системы
без учета преднамеренного отключения:
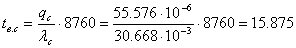 час.
час.
Среднее время безотказной работы:
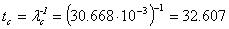 лет.
лет.
Недоотпуск энергии по заводу:
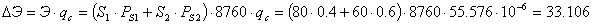 МВ∙А/ч.
МВ∙А/ч.
Определим эквивалентный параметр
потока отказов lVI, с учетом
преднамеренных отключений двух последовательно соединенных элементов В3 и Т1,
входящих в эквивалентный элемент III.
Расчетная формула будет иметь вид:
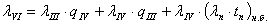
где, (lп·tп)н.б. - наибольшая вероятность
преднамеренного отключения одного из отключаемых элементов.
Это обусловлено тем, что для
уменьшения вероятности отключенного состояния и числа перерывов
электроснабжения в системе с последовательным соединением элементов
преднамеренные отключения для профилактических и капитальных ремонтов стремятся
совместить. В нашем случае наибольшей является вероятность преднамеренного отключения
трансформатора Т1.
С учетом преднамеренного отключения выключателя
В3 и трансформатора Т1, входящих в эквивалентный элемент III,
параметр потока отказов системы определится:
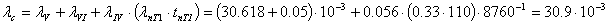 год-1.
год-1.
Эквивалентное время восстановления оставшейся
части схемы после преднамеренного отключения В3 и Т1:
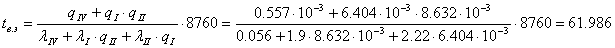 часа
часа
или по упрощенной формуле:
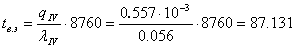 часа.
часа.
Из сравнения видно, что можно использовать
упрошенное выражение для определения tв.э
использовать нельзя.
Коэффициент понижения надежности системы в связи
с преднамеренным отключением выключателя В3 и трансформатора Т1(так как в нашей
схеме преднамеренно отключаются два последовательных элемента, входящих в
эквивалентный элемент III,
то учитываем только элемент с наибольшей вероятностью преднамеренного
отключения (lп·tп)н.б).:
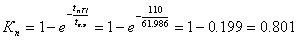 .
.
Средняя вероятность отказового состояния системы
с учетом преднамеренного отключения В3 и Т1:
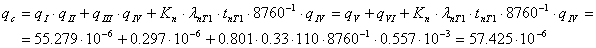 .
.
Среднее время восстановления системы с учетом
преднамеренного отключения В3 и Т1:
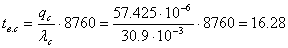 час.
час.
Среднее время безотказной работы системы с
учетом преднамеренного отключения В3 и Т1:
 лет.
лет.
Недоотпуск энергии заводу с учетом
преднамеренного отключения В3 и Т1:
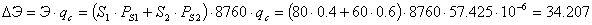 МВ∙А/ч.
МВ∙А/ч.
Литература
1.
Волков Н.Г. Надёжность функционирования систем электроснабжения: Учебное
пособие. - Томск: Изд-во ТПУ, 2005. - 157 с.