Обыкновенные дифференциальные уравнения
Обыкновенные
дифференциальные уравнения
Задание 1. Найти
решение дифференциальных уравнений с разделяющимися переменными
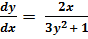 .
.
Решение:
Произведём разделение переменных:
(3y2 + 1)dy = 2xdx
Проинтегрируем левую и правую часть.
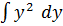 +
+  =
2
=
2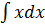 .
.
 + y + C = 2
+ y + C = 2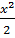 ,+ y + C = x2, или x =
,+ y + C = x2, или x = 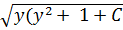 .
.
yy' = x.
Запишем уравнение в виде:
y = x и произведём
замену переменных:
= x и произведём
замену переменных:
ydy = xdx, тогда 3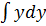 =
= 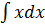
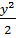 =
= 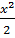 +
C/2 или 3y2 = x2 + C, тогда
+
C/2 или 3y2 = x2 + C, тогда
y =  .
.
Задание 2. Найти
решение однородных дифференциальных уравнений первого порядка
(2x - y)dx + (2y - x)dy = 0.
Разрешим уравнение относительно dy/dx:
' = 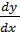 =
-
=
- 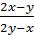 ,
,
поделив числитель и знаменатель правой части на
х, получим:
' = - 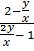 ,
,
т. е. у' есть функция отношения у/х. Это
означает, что данное уравнение однородное.
Для решения этого уравнения введём новую функцию
u = y/x. Тогда у = ux, y' = xdu/dx + u. Исходное уравнение запишется в виде
уравнения с разделяющимися переменными:
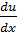 + u =
+ u = 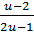 ;
;
x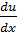 =
= 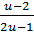 -
u =
-
u = 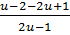 =
=
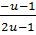 ,
,
 = -
= -  du
=
du
= 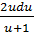 -
-
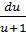 .
Проинтегрируем это уравнение:
.
Проинтегрируем это уравнение:
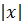 = 2
= 2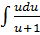 -
- 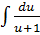 +
lnC.
+
lnC.
ln = 2(u - ln(u + 1)) - ln(u + 1) = 2u - l-2ln(u + 1) - ln(u + 1) = 2u - 3 ln(u +
1),
= 2(u - ln(u + 1)) - ln(u + 1) = 2u - l-2ln(u + 1) - ln(u + 1) = 2u - 3 ln(u +
1),
 + ln(u + 1)3 = 2u,
+ ln(u + 1)3 = 2u, (u + 1)3 = 2u,
(u + 1)3 = 2u,
 (u + 1)3 = e2u , и
окончательно получаем решение:
(u + 1)3 = e2u , и
окончательно получаем решение:
 (
( + 1)3 = exp (
+ 1)3 = exp (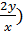 .
.
- ydx = ydy.
(x - y)dy = ydx y =
=  .
.
Для решения этого уравнения введём новую функцию
u = y/x. Тогда у = ux, y' = xdu/dx + u. Исходное уравнение запишется в виде
уравнения с разделяющимися переменными:
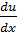 + u =
+ u =  ;
;
x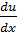 =
=  -
u =
-
u = 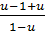 =
=
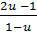 ,
,
 = -
= -  du
=
du
= 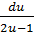 -
-
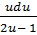 .
Проинтегрируем это уравнение:
.
Проинтегрируем это уравнение:
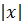 =
= 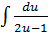 -
-
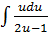 +
lnC.
+
lnC.
 = ln(2u - 1) - u -
ln(2u - 1) = - u, окончательно получаем:
= ln(2u - 1) - u -
ln(2u - 1) = - u, окончательно получаем:
x = Ce-u = Ce-y/x.
Задание 3. Найти
решение линейных дифференциальных уравнений первого порядка
 - y ctg x = 2x sin
x.
- y ctg x = 2x sin
x.
Положим y = uv, тогда y' = u'v + uv' и данное
уравнение принимает вид:'v + uv' - uv ctg x = 2x sin x,'v + u(v' - v ctg x) =
2x sin x.
Решая уравнение v' - v ctg x = 0, получим его
простейшее частное решение:
 = v ctg x;
= v ctg x; 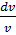 =
ctg x dx; ln
=
ctg x dx; ln = ln
= ln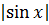 ;
откуда v = sin x.
;
откуда v = sin x.
Подставляя v в исходное уравнение получаем
уравнение: sin x = 2x sin x,
из которого находим u' = 2x, следовательно du = 2xdx u = x2 +C.
sin x = 2x sin x,
из которого находим u' = 2x, следовательно du = 2xdx u = x2 +C.
Итак, искомое решение y = (x2 + C) sin x.
' + 3y tg 3x = sin 6x, y(0) = 1/3.
Положим y = uv, тогда y' = u'v + uv' и данное
уравнение принимает вид:'v + uv' + 3uv tg 3x = sin 6x,'v + u(v' + 3v tg 3x) =
sin 6x.
Решая уравнение v' + 3v tg 3x = 0, получим его
простейшее частное решение:
 = 3v tg x;
= 3v tg x; 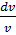 =
3tg 3x dx; ln
=
3tg 3x dx; ln = - ln
= - ln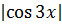 ;
откуда v = 1/cos 3x.
;
откуда v = 1/cos 3x.
Подставляя v в исходное уравнение получаем
уравнение:
 /cos 3x = sin 6x,
из которого находим u
/cos 3x = sin 6x,
из которого находим u
 =
= 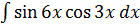 ,
,
= -  -
-
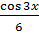 +
C, и окончательно получим решение
+
C, и окончательно получим решение
= uv = - 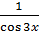 (
( + C).
+ C).
Найдём постоянную С, согласно заданным начальным
условиям у(0) = 1/3:
/3 = - 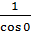 (
(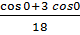 + C) = - 4/18 - C, C = - 1/3 - 4/18 = - 10/18 = - 5/9.
+ C) = - 4/18 - C, C = - 1/3 - 4/18 = - 10/18 = - 5/9.
Получаем решение:
у = - 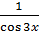 (
( - 5/9) = -
- 5/9) = - 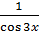 (
(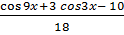 )
=
)
=
= - 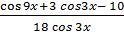 .
.
Задание 4. Найти решение дифференциального
уравнения, допускающего понижение порядка
''' = cos x, y(0) = 1, y'(0) = 0, y''(0) = 1.
Проводим последовательное интегрирование:
y'' = 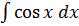 =
sin x + C1,
=
sin x + C1,
Из начального условия y (0)
= 1 найдём постоянную С1:
(0)
= 1 найдём постоянную С1:
1 + 0 = C1, C1 = 1, следовательно y'' = = sin x
+ 1,' = 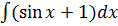 =
- cos x + x + C2,
=
- cos x + x + C2,
Из начального условия y (0)
= 0 найдём постоянную С2:
(0)
= 0 найдём постоянную С2:
= - 1 + 0 + C2, C2 = 1,
В итоге получаем y' = - cos x + x + 1.
Из начального условия y(0) = 1 найдём постоянную
С3:
= - 0 + 0 + 0 + C3, C3 = 1,
В итоге получаем y = - sin x + x2/2 + x + 1.
Задание 5.
Проинтегрировать следующие линейные неоднородные уравнения
'' + y' - 6y = 0
Запишем характеристическое уравнение. Для этого
заменим функцию у и её производные соответствующими степенями λ:
λ2 + λ
- 6 =
0
откуда λ1
= - 3 и λ2
= 2. Так
как корни характеристического уравнения действительные и различные, то общее
решение данного дифференциального уравнения имеет вид:
у = С1е-3х + С2е2х.
у'' - у' = 12х.
Составим характеристическое уравнение: λ2
- λ = 0, откуда λ1 = 0;
λ2
= 1, поэтому
λ1
= 0
есть простой корень ( r = 1) этого уравнения. В правой части многочлен первой
степени (m = 1), поэтому частное решение неоднородного дифференциального
уравнения следует искать в виде:
ỹ(x) = x(B0x + B1).
Подставляя ỹ(х) в уравнение и сравнивая
коэффициенты при одинаковых степенях х, найдём, что
ỹ'(x) = (B0x + B1) + хВ0 = 2В0х + В1.
ỹ''(x) = 2B0.
B0 - 2В0х - В1 = 12х
В0 = 12 и 2В0 - В1 = 0
В0 = - 6 и В1 = -12,
в итоге получаем ỹ(x) = x(- 6x - 12) = -
12х - 6х2.
у'' + 2у' + 5y = - 2sin 2x.
Найдём общее решение уравнения ỹ
соответствующего однородного уравнения:
у'' + 2у' + 5y = 0.
Решая отвечающее ему характеристическое
уравнение
λ2 + 2λ + 5 = 0,
получаем комплексные корни λ1
= - 1 - 2i;
λ2
=
- 1 + 2i, следовательно,
ỹ = e-x(C1 cos x + C2 sin 2x).
Будем теперь искать у*. Здесь правая часть f(x)
имеет вид:
(x) = a cos λx + b sin
λx , т. е. а = 0, b = - 2, λ = 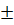 2i.
2i.
Числа 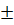 2i
не являются корнями характеристического уравнения, поэтому частное решение у*
следует искать в форме
2i
не являются корнями характеристического уравнения, поэтому частное решение у*
следует искать в форме
у* = А cos 2x + B sin 2x,
где А и В - неопределенные коэффициенты.
Найдём производные у*' и у*'':
у*' = - 2А sin 2x + 2B cos 2x;
у*'' = -4A cos 2x - 4B sin 2x.
подставляя теперь выражения для у*, у*', у*'' в
данное уравнение и группируя члены при cos 4x и sin 4x, в результате получим
(-4A
cos 2x
- 4B
sin 2x)
+ 2(- 2А sin 2x
+ 2B
cos 2x)
+ 5(А cos 2x
+ B
sin 2x)=
-2sin 2x
дифференциальный уравнение линейный интегрирование
Cos 2x(- 4A + 4B + 5A) + sin 2x( -4B - 4A + 5B)
= -2sin 2x.
Составим систему:

В = - 2 + 4А, А + 4(-2 + 4А) = А - 8 + 16А = 0.
А = 8/17 и В = - 2/17.
Таким образом,
у* = 8/17 cos 2x - 2/17 sin x.
Итак, общее решение данного уравнения имеет вид:
у = ỹ +
у*
= e-x(C1 cos2x + C2sin2x) + 8/17 cos 2x - 2/17sin 2x.