Теория графов

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕСИОНАЛЬНОГО ОБРАЗОВАНИЯ

"ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ"

ИНСТИТУТ НЕФТИ И ГАЗА

КАФЕДРА ИНФОРМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Курсовая работа

по дисциплине "Дискретная математика"

на тему "Теория графов"

Выполнил: студент группы

Проверил: ст.преподаватель

Гапанович И.В.

Тюмень 2009

Содержание

Введение

1. Постановка задачи

. Описание алгоритма решения задачи

3. Ручной просчёт задачи

. Тестирование программы

Закючение

Список литературы

Приложение

Введение

Существует большое количество практических задач, рассмотрение которых сводится к изучению совокупности объектов, существенные свойства которых описываются связями между ними. Интерес могут представлять различные экономические связи, связи и отношения между людьми, событиями, состояниями, и вообще, между любыми объектами.

В подобных случаях удобно рассматривать объекты точками, называя их вершинами, а связи между ними - линиями (произвольной конфигурации), называя их ребрами. Полученная при этом конфигурация называется графом.

Цель данной работы: рассмотреть решение задачи: "Задана система двусторонних дорог, причем для любой пары городов можно указать соединяющий их путь. Найти такой город, для которого сумма расстояний до остальных городов минимальна", составить алгоритм решения задачи, написать программу и проверить правильность работы программы.

Работа содержит следующие пункты: постановка задачи, описание алгоритма решения задачи, ручной подсчет решения задачи, тестирование программы, листинг программы.

1.      Постановка задачи

Задача. Найти минимальные пути от фиксированной вершины до произвольной вершины графа, используя алгоритм Дейкстры.

Решение задачи будет произведено по алгоритму Дейкстры.

Пусть в орграфе D из вершины v в вершину w, где v ¹ w, называется минимальным, если он имеет минимальную длину среди всех путей орграфа D из v в w.

Назовем орграф D = (V,X) нагруженным, если на множестве дуг X определена некоторая функция l : X ® R, которую часто называют весовой функцией. Значение l(x) будем называть длиной дуги x. Предположим, что l(x) ³ 0. Длиной пути П в нагруженном орграфе будем называть величину l(П), равную сумме длин дуг, входящих в П, при этом каждая дуга учитывается столько раз, сколько она входит в данный путь.

Нагруженный орграф можно задать с помощью матрицы весов С(D) = {cij}nxn с элементами

Рассмотрим алгоритм Дейкстры, который позволяет определить минимальный путь в орграфе между двумя заданными вершинами при условии, что этот путь существует.

Пусть s - начальная вершина, t - конечная вершина. На каждой итерации любая вершина v имеет метку l*(v), которая может быть постоянной или временной. Постоянная метка l*(v) - это длина кратчайшего пути от s к v, временная метка l(v) - это вес кратчайшего пути из s в v, проходящий через вершины с постоянными метками. Если на каком-то шаге метка становится постоянной, то она остается такой до конца работы алгоритма.

Вторая метка Q(v) - это вершина, из которой вершина v получила свою метку.

Алгоритм Дейкстры

Данные: матрица весов С(D) орграфа D, начальная вершина s.

Результат: расстояния от вершины s до всех вершин орграфа D: D[v] = d(s,v), v Î V, а также последовательность вершин, определяющая кратчайший путь из s в v .

1.       Положим l*(s) = 0 и будем считать эту метку постоянной. Для всех v ÎV, v ¹ s, положим l*(v) = ¥ и будем считать эти метки временными. Положим p = s.

.        Для всех vÎГp с временными метками выполним: если l*(v)>l*(p)+l(p,v), то l*(v)=l*(p)+l(p,v) и Q(v) =р. Иначе l*(v) и Q(v) не менять, т.е. l*(v) = min (l*(t), l*(p)+cpv). (Идея состоит в следующем: пусть p - вершина, получившая постоянную метку l^*(p) на предыдущей итерации. Просматриваем все вершины vÎГp, имеющие временные метки. Метка l^*(v) вершины vÎГp заменяется на l^*(p)+l(p,v), если оказывается, что ее метка l^*(v)>l^*(p)+l(p,v). В этом случае говорим, что вершина v получила свою метку из вершины p, поэтому положим Q(v) = p. С помощью этих дополнительных меток будем потом восстанавливать сам путь. Если l^*(v) £ l^*(p)+c_pv, то метки остаются прежними. путь вершина граф схема

3.       Пусть V* - множество вершин с временными метками. Найдем вершину v* такую, что l*(v*) = min l*(v), v ÎV*. Считать метку l*(v*) постоянной для вершины v*.

4.       Положим p = v*. Если p = t, то перейдем к п.5 ( l*(t) - длина минимального пути ). Иначе перейдем к п.2.

.        Найдем минимальный путь из s в t, используя метки Q(v): П = s…Q(t)t.

Заметим, что, если продолжить работу алгоритма Дейкстры до тех пор, пока все вершины не получат постоянные метки, то мы получим расстояния от начальной вершины s до произвольной вершины графа.

. Описание алгоритма решения задачи

Программа выводит минимальный путь между двумя указанными вершинами в графе и его длину.

При запуске программы на экран выводится запрос о вводе весов рёбер исследуемого графа. Данные, введённые пользователем, отображаются в виде матрицы смежности, в которой не существующие рёбра обозначаются нулями. После указанным рёбрам присваивается значение 65535, которое принимается за бесконечность. Следующим этапом выполнения программы является запрос о вводе номеров вершин, между которыми необходимо узнать путь. В случае, если начальная и конечная вершины совпадают, отображается соответствующее сообщение и работа программы завершается. В противном случае выполняется непосредственно алгоритм Дейкстры, схема которого приведена в приложении. Результатом программы является вывод на экран вершин, через которые проходит минимальный путь, а также вывод длины маршрута. Если пути между заданными точками не существует - выводится соответствующее сообщение.

Описание использованных программных средств

Кроме стандартных функций из библиотек iostream.h, string.h, stdio.h, conio.h были использованы также следующие функции.

·        word minim(word x, word y) - функция, которая возвращает минимальное из x и y.

·        int min(int n) - функция, которая возвращает номер элемента массива l[i] минимальной "неотмеченной" длиной пути(flag[i]=0).

3. Ручной просчёт задачи

Пусть дан граф, заданный матрицей весов:

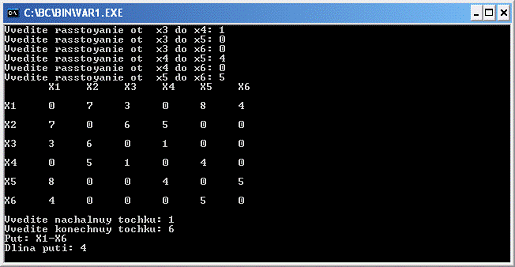
Получаем, что путь из точки А в точку В: А, F, а длина пути равна 4.

. Тестирование программы

Заключение

При рассмотрении теории графов можно сделать вывод: решая задачу о нахождении города, для которого сумма расстояний до остальных городов минимальна, удобно было использовать теорию графов.

Цель данной работы достигнута: алгоритм и программа решения задачи составлен, правильность работы программы проверена.

Список литературы

1.       Гапанович В.С., Гапанович И.В. Дискретная математика: Учебное пособие. Тюмень: ТюмГНГУ, 2002. - 187 с.

2.       Дискретная математика для программистов / Ф.А. Новиков - СПб: Питер, 2000. - 304 с.

.        Дискретная математика. Алгоритмы и программы: Учеб. пособие/Б.Н. Иванов. - М.: Лаборатория Базовых Знаний, 2003. - 288 с.

.        Кормен Алгоритмы: построение и анализ / 1990.

Приложение

#include<iostream.h>

#include<string.h>

#include<stdio.h>

#include<stdlib.h>

#include<conio.h>

#define word unsigned inti, j, n, p, xn, xk;flag[11];c[11][11], l[11];s[80], path[80][11];min(int n)

{i, result;(i=0;i<n;i++)(!(flag[i])) result=i;(i=0;i<n;i++)((l[result]>l[i])&&(!flag[i])) result=i;result;

}minim(word x, word y)

{(x<y) return x;y;

}main()

{<<"Vvedite kolichestvo tochek: ";>>n;(i=0;i<n;i++)(j=0;j<n;j++) c[i][j]=0;(i=0;i<n;i++)(j=i+1;j<n;j++)

{

cout<<"Vvedite rasstoyanie ot x"<<i+1<<" do x"<<j+1<<": ";

cin>>c[i][j];

}<<" ";(i=0;i<n;i++) cout<<" X"<<i+1;<<endl<<endl;(i=0;i<n;i++)

{("X%d",i+1);(j=0;j<n;j++)

{("%6d",c[i][j]);[j][i]=c[i][j];

}("\n\n");

}(i=0;i<n;i++)(j=0;j<n;j++)(c[i][j]==0) c[i][j]=65535; //бесконечность<<"Vvedite nachalnuy tochku: ";>>xn;<<"Vvedite konechnuy tochku: ";>>xk;-;-;(xn==xk)

{<<"Nachalnaya I konechnaya tochki sovpadayt."<<endl;();;

}(i=0;i<n;i++)

{[i]=0;[i]=65535;

}[xn]=0;[xn]=1;=xn;(xn+1,s,10);(i=1;i<=n;i++)

{(path[i],"X");(path[i],s);

}

{(i=0;i<n;i++)((c[p][i]!=65535)&&(!flag[i])&&(i!=p))

{(l[i]>l[p]+c[p][i])

{(i+1,s,10);(path[i+1],path[p+1]);(path[i+1],"-X");(path[i+1],s);

}[i]=minim(l[i],l[p]+c[p][i]);

}=min(n);[p]=1;

}(p!=xk);(l[p]!=65535)

{<<"Put: "<<path[p+1]<<endl;<<"Dlina puti: "<<l[p]<<endl;

}<<"takogo puti ne syshestvuet!"<<endl;

getch();

}