Практическая реализация принципа оптимальности в экономике
Федеральное агентство по
образованию
ГОУ ВПО
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Факультет:
Финансово-кредитный
Специальность:
080100 бакалавр экономики
КОНТРОЛЬНАЯ РАБОТА
по дисциплине:
Экономико-математические методы и прикладные модели
Выполнил:
Студент
Гребёнкин Игорь Андреевич
Курс
3
№
зачетной книжки 11ФЛД61185
Преподаватель:
проф.
Денисов Владимир Петрович
Омск
-
2011
Задание № 1
двойственная оценка
функционал временной ряд
Двойственные оценки как мера влияния ограничений
на функционал.
Выбор наилучшего решения
предполагает наличие некоторого критерия оптимальности, позволяющего оценить
эффективность принятых решений. В экономике такие задачи возникают при
практической реализации принципа оптимальности в планировании и управлении, при
этом в качестве критерия оптимальности могут выступать максимум прибыли,
минимум себестоимости, минимум трудовых затрат и др. Если записать критерий
оптимальности в виде математической функции 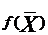 , то эта функция называется целевой
функцией (функция цели, функционал).
, то эта функция называется целевой
функцией (функция цели, функционал).
Любую задачу линейного
программирования в стандартной форме можно записать в виде соотношений:
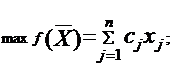 (1.1)
(1.1)
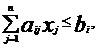
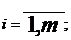 (1.2)
(1.2)
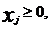
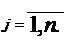 (1.3)
(1.3)
Ограничения (1.2) принято называть функциональными
ограничениями, а условия неотрицательности переменных (1.3) - прямыми ограничениями.
Если эту задачу назвать исходной (прямой), то ей можно поставить в
соответствие двойственную задачу. Построение двойственной ЗЛП основано
на следующих пяти правилах:
) если в исходной задаче надо найти
максимум целевой функции, то в двойственной -
минимум, и наоборот;
) коэффициентами целевой функции двойственной
задачи служат правые части системы ограничений исходной задачи в стандартной
форме;
) матрицы коэффициентов левых частей
систем функциональных ограничений исходной и двойственной задач являются
транспонированными по отношению друг к другу;
) если функциональные ограничения
исходной задачи в стандартной форме имеют вид неравенств типа £, то
аналогичные ограничения двойственной задачи являются неравенствами типа ³, и
наоборот;
) правыми частями системы
функциональных ограничений двойственной задачи служат коэффициенты целевой
функции исходной ЗЛП.
Таким образом, задача, двойственная
по отношению к задаче (1.1) -
(1.3), в стандартной форме имеет вид:
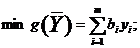 (1.4)
(1.4)
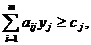
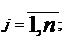 (1.5)
(1.5)

 (1.6)
(1.6)
Если рассматривать исходную ЗЛП
(1.1) - (1.3) как
задачу оптимального использования ресурсов предприятия, то можно дать следующую
экономическую интерпретацию двойственной задачи. Пусть некоторая фирма
обратилась к предприятию с предложением продать ее имеющиеся ресурсы, и встает
проблема установления объективно обусловленных цен этих ресурсов. Если эти цены
обозначить yi , то целевая
функция (1.4) будет выражать интересы фирмы, покупающей ресурсы (наименьшая
стоимость ресурсов), а функциональные ограничения (1.5) - интересы предприятия
(стоимость ресурсов не менее стоимости продукции, которую можно из этих
ресурсов выпустить). В связи с этой интерпретацией переменные двойственной
задачи называются объективно обусловленными оценками или двойственными
оценками (за рубежом принят термин «теневая цена»).
Слова «и наоборот» в первом и
четвертом правилах построения двойственной задачи свидетельствует о том, что
если в качестве исходной ЗЛП взять задачу (1.4) - (1.6), то построенная по тем же правилам
двойственная задача будет иметь вид задачи (1.1) - (1.3). Таким образом, рассматриваемые задачи
образуют пару взаимодвойственных задач. Следует оговориться, что здесь
рассматриваются только так называемые симметричные взаимодвойственные задачи
(ограничения обеих задач имеют вид неравенств).
Задание № 2
Финансовый консультант фирмы «ABC»
консультирует клиента по оптимальному инвестиционному портфелю. Клиент хочет
вложить средства (не более 25 000 долл.) в два наименования акций крупных
предприятий в составе холдинга «Дикси».
Анализируются акции «Дикси-Е»
и «Дикси-В».
Цены на акции: «Дикси-Е» - 5долл. за
акцию; «Дикси-В» - 3 долл. за акцию.
Клиент уточнил, что он хочет
приобрести максимум 6000 акций обоих наименований, при этом акций одного из
наименований должно быть не более 5000 штук.
По оценкам «ABC»,
прибыль от инвестиций в эти акции в следующем году составит: «Дикси-Е»
-
1,1 долл.; «Дикси-В» - 0,9 долл.
Задача консультанта состоит в
том, чтобы выдать клиенту рекомендации по оптимизации прибыли от инвестиций.
Построить экономико-математическую модель
задачи, дать необходимые комментарии к ее элементам и получить решение
графическим методом. Что произойдет, если решать задачу на минимум, и почему?
РЕШЕНИЕ:
Пусть х1 шт. - количество акций
«Дикси-Е»;
х2 шт. - количество акций «Дикси-В», тогда
количество приобретаемых акций:
х1 + х2 <= 6000;
причем х1 <= 5000; x2
<= 5000;
вложенные средства должны составить:
х1 + 3х2 <= 25 000
долл.;
а максимальная прибыль выразится функцией:
F = 1,1x1
+ 0,9x2
®max
Получили задачу оптимизации:
найти максимальное значение линейной функции
F = 1,1x1
+ 0,9x2 при
ограничениях:
х1 +х2 <= 6000
х1 + 3х2 <= 25000
≤ х1 ≤ 5000; 0 ≤ х2
≤ 5000
Построим многоугольник решений.
Для этого в системе координат х1Ох2 на плоскости
изобразим граничные прямые
х1 + х2 =
6000 (L1);
х1 + 3x2
= 25000 (L2);
х1+90х2 =
0 (F);
x1
= 5000 (L4);
х2 = 5000 (L3)
Установим, какую полуплоскость
определяет каждое неравенство относительно граничной прямой.
|
|
x1
|
x2
|
|
L1
|
0
|
6000
|
|
6000
|
0
|
|
L2
|
0
|
8333
|
|
5000
|
0
|
|
L3
|
0
|
5000
|
|
5000
|
5000
|
|
L4
|
5000
|
0
|
|
5000
|
5000
|
|
F
|
0
|
0
|
|
900
|
-1100
|
|
0
|
0
|
|
5500
|
4500
|

В результате имеем пятиугольник
АВСDO.
Построим вектор N = (5500; 4500) и прямую 1,1х1
+ 0,9х2 = 0 (F).
Перемещаем прямую F параллельно
самой себе в направлении вектора N. Из рис. следует, что она выйдет из
многогранника решений и станет опорной по отношению к нему в угловой точке С;
в точке С линейная функция принимает максимальное значение.
Точка С лежит на пересечении прямых L1
и L2;
для определения ее координат решим систему уравнений:
х1 + х2 = 6000
х1 + 3x2
= 25000 . Имеем: х1 = 3500; х2 = 2500.
Подставляя найденные значения в линейную
функцию, получаем:
Fmax
= 1,1×3500
+ 0,9×2500
= 3850 + 2250 = 6100.
Для того, чтобы обеспечить максимум прибыли
(6100 долл.), необходимо приобрести 3500 акций «Дикси-Е»
и 2500 акций «Дикси-В».
Если решить эту задачу на минимум, то получим,
что вообще ничего не надо приобретать, т.к. функция достигает своего
минимального значения в точке (0; 0).
Задание № 3
В течение девяти последовательных недель
фиксировался спрос Y(t)
(млн. руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t)
этого показателя приведен в таблице:
|
t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Y(t)
|
12
|
15
|
16
|
19
|
17
|
20
|
24
|
25
|
28
|
Требуется:
1) проверить наличие аномальных
наблюдений.
2) построить линейную
модель Ŷ(t) =  , параметры
которой оценить МНК (Ŷ(t) - расчетные, смоделированные
значения временного ряда);
, параметры
которой оценить МНК (Ŷ(t) - расчетные, смоделированные
значения временного ряда);
) оценить адекватность построенных
моделей, используя свойства независимости остаточной компоненты, случайности и
соответствия нормальному закону распределения (при использовании R/S-критерия
взять табулированные границы 2,7 - 3,7);
4) оценить точность моделей на основе
использования средней относительной ошибки аппроксимации;
5) по построенной модели осуществить
прогноз спроса на следующие две недели (доверительный интервал прогноза считать
при доверительной вероятности р = 70%);
) фактические значения показателя, результаты
моделирования и прогнозирования представить графически.
Вычисления провести с одним знаком в дробной
части. Основные промежуточные результаты вычислений представить в таблицах (при
использовании компьютера представить соответствующие листинги с комментариями).
РЕШЕНИЕ:
) Для выявления аномальных уровней временного
ряда используем метод Ирвина, который предполагает использование следующей
формулы:
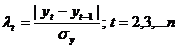 , где
, где
sу -
среднеквадратическое отклонение рассчитывается с использованием формул:
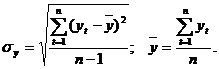
Таблица 1
|
t
|
Y
|
|yt-yt-1|
|
yt-yср
|
(yt-yср)2
|
λ
|
λтабл
|
|
1
|
12
|
|
-7,6
|
57,1
|
|
|
|
2
|
15
|
3
|
-4,6
|
20,8
|
1,7
|
>1,5
|
|
3
|
16
|
1
|
-3,6
|
12,6
|
0,6
|
1,5
|
|
4
|
19
|
3
|
-0,6
|
0,3
|
1,7
|
>1,5
|
|
5
|
17
|
2
|
-2,6
|
6,5
|
1,1
|
1,5
|
|
6
|
20
|
3
|
0,4
|
0,2
|
1,7
|
>1,5
|
|
7
|
24
|
4
|
4,4
|
19,8
|
2,3
|
>1,5
|
|
8
|
25
|
1
|
5,4
|
29,6
|
0,6
|
1,5
|
|
9
|
28
|
3
|
8,4
|
71,3
|
1,7
|
>1,5
|
|
Сумма
|
45
|
176
|
|
|
218,2
|
|
|
|
Ср.знач
|
5
|
19,6
|
|
|
24,2
|
|
|
|
|
|
|
|
3,0
|
|
|
|
|
|
|
|
1,7
|
|
|
Вывод:
видим, что значения у2, у4, у6, у7
и у8 являются аномальными, т.к. все, кроме них, вычисленные значения
λ
меньше
критического значения критерия Ирвина: n=10,
для уровня значимости 0,05, т.е. с 5%-ной ошибкой, λтабл=1,5.
) Результаты регрессионного анализа для
временного ряда представим в таблицах 2 и 3.
Таблица 2
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
|
Y-пересечение
|
10,30556
|
0,985152
|
10,46088
|
|
t
|
1,85
|
0,175066
|
10,56744
|
Таблица 3
|
Наблюдение
|
Предсказанное
Y
|
Остатки
|
|
1
|
12,15556
|
-0,15556
|
|
2
|
14,00556
|
0,994444
|
|
3
|
15,85556
|
0,144444
|
|
4
|
17,70556
|
1,294444
|
|
5
|
19,55556
|
-2,55556
|
|
6
|
21,40556
|
-1,40556
|
|
7
|
23,25556
|
0,744444
|
|
8
|
25,10556
|
-0,10556
|
|
9
|
26,95556
|
1,044444
|
|
Сумма
|
176,0
|
0,0
|
Во втором столбце табл. 2 содержатся
коэффициенты уравнения регрессии 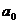 и
и 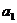 , в третьем столбце - стандартные
ошибки коэффициентов уравнения регрессии, а в четвертом - t-статистика,
используемая для проверки значимости коэффициентов уравнения регрессии.
, в третьем столбце - стандартные
ошибки коэффициентов уравнения регрессии, а в четвертом - t-статистика,
используемая для проверки значимости коэффициентов уравнения регрессии.
Уравнение регрессии зависимости уt (спроса на
кредитные ресурсы финансовой компании) от времени t имеет вид:
Y(t) = 10,3 +
1,9t.
При вычислении «вручную» получаем те
же результаты.
Промежуточные расчеты параметров
линейной модели приведем в таблице 4.
Таблица 4
|
t
|
y
|
t-tср
|
(t-tср)2
|
y-yср
|
(t-tср)(y-yср)
|
|
1
|
12
|
-4
|
16
|
-7,56
|
30,2
|
|
2
|
15
|
-3
|
9
|
-4,56
|
13,7
|
|
3
|
16
|
-2
|
4
|
-3,56
|
7,1
|
|
4
|
19
|
-1
|
1
|
-0,56
|
0,6
|
|
5
|
17
|
0
|
0
|
-2,56
|
0,0
|
|
6
|
20
|
1
|
1
|
0,44
|
0,4
|
|
7
|
24
|
2
|
4
|
4,44
|
8,9
|
|
8
|
25
|
3
|
9
|
5,44
|
16,3
|
|
9
|
28
|
4
|
16
|
8,44
|
33,8
|
|
Сумма
|
45
|
176
|
0
|
60
|
0,0
|
111
|
|
Ср.знач
|
5
|
19,6
|
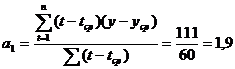 ;
;
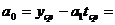 19,6- 1,9×5 = 10,3.
19,6- 1,9×5 = 10,3.
) Расчетное значение в момент
времени получается по формуле:
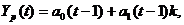
где k -
количество шагов прогнозирования (обычно k = 1).
Это значение сравнивается с
фактическим уровнем, и полученная ошибка прогноза:
Е(t) = Y(t) - Yp(t)
используется для корректировки модели.
Корректировка параметров
осуществляется по формулам:
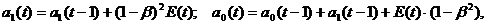
где β - коэффициент дисконтирования
данных, отражающих большую степень доверия к более поздним данным.
Процесс модификации модели (t = 1, 2,…,N) в
зависимости от текущих прогнозных качеств обеспечивает ее адаптацию к новым
закономерностям развития.
Для прогнозирования используется
модель, полученная на последнем шаге (при t=N).
Начальные оценки параметров получим
по первым пяти точкам при помощи МНК:
Таблица 5
|
t
|
Y(t)
|
t-tср
|
(t-tср)2
|
Y(t)-Yср
|
(t-tср)(Y(t)-Yср)
|
|
1
|
12
|
-2
|
4
|
-3,8
|
7,6
|
|
2
|
15
|
-1
|
1
|
-0,8
|
0,8
|
|
3
|
16
|
0
|
0
|
0,2
|
0
|
|
4
|
19
|
1
|
1
|
3,2
|
3,2
|
|
5
|
17
|
2
|
4
|
1,2
|
2,4
|
|
Сумма
= 15
|
79
|
0
|
10
|
0,0
|
14
|
|
Ср.знач
= 3
|
15,8
|
|
|
|
|
Используя эти результаты, получим:
 14 : 10 = 1,4;
14 : 10 = 1,4;
 15,8 - 1,4×3 = 11,6.
15,8 - 1,4×3 = 11,6.
Возьмем k = 1 и α = 0,4,
β = 1 - α = 0,6.
Подробно покажем расчет на первых
двух шагах, а остальные отразим в таблице 6.
t = 1 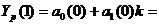 11,6 + 1,4×1
= 13,0;
11,6 + 1,4×1
= 13,0;
Е(1) = Y(1) -
Yp(1) = 12 - 13 = -1;
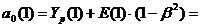 13,0 - 1×0,64 = 12,4;
13,0 - 1×0,64 = 12,4;
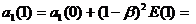 1,4 - 1×0,16 = 1,2.=
2
1,4 - 1×0,16 = 1,2.=
2  12,4 + 1,2×1 = 13,6;
12,4 + 1,2×1 = 13,6;
Е(2) = Y(2) - Yp(2)
= 15 - 13,6 = 1,4;
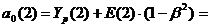 13,6 +1,4×0,64 = 14,5;
13,6 +1,4×0,64 = 14,5;
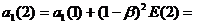 1,2 +1,4×0,16 = 1,4 и
т. д.
1,2 +1,4×0,16 = 1,4 и
т. д.
Таблица 6
|
a=0,4
|
|
t
|
Факт
Y(t)
|
a0(t)
|
a1(t)
|
Расчет
Yp(t)
|
E(t)
|
E2(t)
|
|
0
|
|
11,6
|
1,4
|
|
|
|
|
1
|
12
|
12,4
|
1,2
|
13,0
|
-1,0
|
1,0
|
|
2
|
15
|
14,5
|
1,5
|
13,6
|
1,4
|
2,0
|
|
3
|
16
|
16,0
|
1,5
|
16,0
|
0,0
|
0,0
|
|
4
|
19
|
18,4
|
1,7
|
17,5
|
1,5
|
2,4
|
|
5
|
17
|
18,1
|
1,2
|
20,2
|
-3,2
|
10,0
|
|
6
|
20
|
19,8
|
1,3
|
19,3
|
0,7
|
0,4
|
|
7
|
24
|
22,9
|
1,8
|
21,1
|
2,9
|
8,5
|
|
8
|
25
|
24,9
|
1,8
|
24,7
|
0,3
|
0,1
|
|
9
|
28
|
27,5
|
2,0
|
26,7
|
1,3
|
1,6
|
|
Сумма
|
176
|
|
|
172,1
|
3,9
|
25,97
|
|
|
|
|
|
|
|
|
a=0,7
|
|
t
|
Факт
Y(t)
|
a0(t)
|
a1(t)
|
Расчет
Yp(t)
|
E(t)
|
E2(t)
|
|
0
|
|
11,6
|
1,4
|
|
|
0
|
|
1
|
12
|
12,1
|
1,3
|
13,0
|
-1,0
|
1,0
|
|
2
|
15
|
14,9
|
1,5
|
13,4
|
1,6
|
2,6
|
|
3
|
16
|
16,0
|
1,4
|
16,3
|
-0,3
|
0,1
|
|
4
|
19
|
18,9
|
1,6
|
17,5
|
1,5
|
2,4
|
|
5
|
17
|
17,3
|
1,3
|
20,4
|
-3,4
|
11,7
|
|
6
|
20
|
19,9
|
1,4
|
18,6
|
1,4
|
2,1
|
|
7
|
24
|
23,8
|
1,6
|
21,3
|
2,7
|
7,5
|
|
8
|
25
|
25,0
|
1,6
|
25,4
|
-0,4
|
0,1
|
|
9
|
28
|
27,9
|
1,7
|
26,6
|
1,4
|
1,9
|
|
Сумма
|
176
|
|
|
172,4
|
|
29,39
|
Так как ∑Е2(t)
(α = 0,4) < ∑E2(t)
(α = 0,7), на последнем шаге получена модель:
Yp(N+k)
= 27,5 +2,0k.
Далее исследуем адекватность
модели. Модель является адекватной, если математическое ожидание значений
остаточного ряда близко или равно нулю и если значения остаточного ряда
случайны, независимы и подчинены нормальному закону распределения.
Проверка равенства нулю
математического ожидания уровней ряда остатков.
Проверка равенства
математического ожидания уровней ряда остатков нулю выполним с использованием t-критерия
Стьюдента:
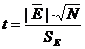 ,
,
где 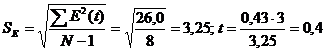 ;
;
t < tтабл.(1,05),
поэтому гипотеза о равенстве математического ожидания значений остаточного ряда
нулю выполняется.
При проверке независимости (отсутствие
автокорреляции) определяется отсутствие в ряду остатков систематической
составляющей, с помощью d-критерия
Дарбина-Уотсона по формуле. Численное значение коэффициента равно
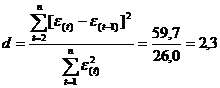 d`= 4 -
2,3=1,7.
d`= 4 -
2,3=1,7.
Попадает в интервал от d2 до 2 (для
линейной модели при 10 наблюдениях можно взять в качестве критических табличных
уровней величины d1 = 1,08, d2 = 1,36),
значит, гипотеза о независимости уровней остаточной последовательности, т.е. об
отсутствии в ней автокорреляции, принимается и модель адекватна по данному
признаку.
Таблица 7
|
Остатки
|
εt-εt-1
|
(εt-εt-1)2
|
ε2
|
Eотн
|
|
-1,0
|
|
|
1,0
|
8,3
|
|
1,4
|
2,4
|
5,8
|
2,0
|
9,3
|
|
0,0
|
-1,4
|
1,8
|
0,0
|
0,2
|
|
1,5
|
1,5
|
2,3
|
2,4
|
8,1
|
|
-3,2
|
-4,7
|
22,1
|
10,0
|
18,6
|
|
0,7
|
3,8
|
14,5
|
0,4
|
3,3
|
|
2,9
|
2,3
|
5,1
|
8,5
|
12,2
|
|
0,3
|
-2,7
|
7,0
|
0,1
|
1,1
|
|
1,3
|
1,0
|
1,0
|
1,6
|
4,5
|
|
3,9
|
2,3
|
59,7
|
26,0
|
65,7
|
|
|
|
|
|
7,3
|
Проверка случайности уровней ряда
остатков по критерию пиков дает положительный результат:
р = 6; 6>2 - неравенство выполняется, следовательно, свойство случайности
выполняется.
Соответствие ряда остатков
нормальному закону распределения определим при
помощи RS-критерия: RS=
[εmax
- εmin]:Sε
= [2,9+3,2]: 1,8 = 3,4 (для N=10
и 5%-го уровня значимости границы критерия (2,7 - 3,7)), 3,4 попадает в
указанный интервал, следовательно, свойство нормальности распределения
выполняется.
 .
.
Вывод: модель
статистически адекватна (выполняются все условия из четырех).
Средняя относительная ошибка:  %, т.к. 7,3%
< 15%, то точность модели считается приемлемой.
%, т.к. 7,3%
< 15%, то точность модели считается приемлемой.
) Для этого следует преобразовать
график подбора, который был получен с помощью инструмента Регрессия:
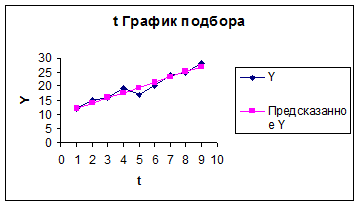
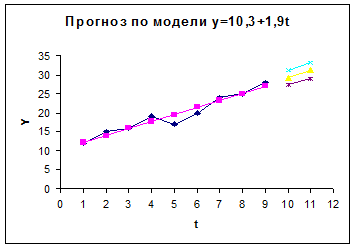
Результаты моделирования и
прогнозирования.
5) Построим точечный и интервальный
прогнозы спроса на следующие две недели (для вероятности 70% использовать t = 1,12):
Yp(10) = 27,5
+2,0k = 27,5 + 2×1 = 29,5;
Yp(11) = 27,5
+2,0k = 31,5.
Для построения интервального
прогноза рассчитаем доверительный интервал. Примем значение уровня значимости α
= 0,3 следовательно,
доверительная вероятность равна 70%, а критерий Стьюдента при v
= п - 2 = 7 равен 1,12. Ширину доверительного интервала вычислим по
формуле:
 , где
, где 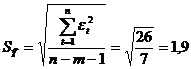 ;
;
m=1 -
количество факторов в модели (для линейной модели m=1).
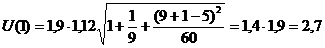 ;
;
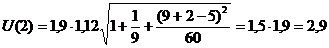 .
.
Таблица 8
|
Время
t
|
Шаг
k
|
Прогноз
|
Верхняя
граница
|
Нижняя
граница
|
|
10
|
1
|
29,5
|
32,2
|
26,8
|
|
11
|
2
|
31,5
|
34,4
|
28,6
|
Т.к. построенная модель адекватна, то можно
утверждать, что при сохранении сложившихся закономерностей развития,
прогнозируемая величина попадает в интервал, образованный нижней и верхней
границами.
)
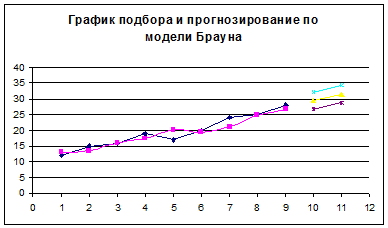
Задание № 4
Фирма может производить изделие или покупать
его. Если фирма сама выпускает изделия, то каждый запуск его в производство
обходиться в 20 тыс. руб. Интенсивность производства составляет 100 шт. в
день. Если изделие закупается, то затраты на осуществление заказа равны 1500
руб. Затраты на содержание изделия в запасе независимо от того, закупается оно
или производится, равны 20 руб. в день. Потребление изделия фирмой оценивается
в 30 тыс. шт. в год.
Предполагая, что фирма работает без дефицита,
определите, что выгоднее: закупать или производить изделия (в месяце 22 рабочих
дня). Построите график общих годовых затрат по наиболее выгодному способу.
Дано:
Количество рабочих дней в месяце -
22 раб. дн.;
M = 30 000 шт./год;
h = 0,02 тыс.руб×22
раб. дн.×12
мес. = 5,28 тыс.руб./ ед. в год;
K1
= 20 тыс. руб;
K2
= 1,5 тыс. руб.
Определить:
Сравнить Z1(Q)
по первому и второму способам, построить график Z1(Q)
наиболее выгодного способа.
РЕШЕНИЕ:
) Первый способ -
производства изделия.
. Экономичный размер производимой партии:
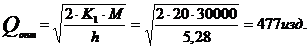
2. Совокупные издержки на
производство и хранение:
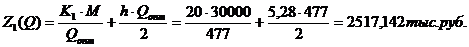
2) Второй способ - покупка изделия.
. Количество изделий в одном заказе:
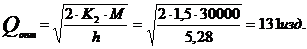
. Совокупные издержки на заказ и
хранение:
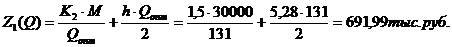
Вывод: второй
способ выгоднее, чем первый.
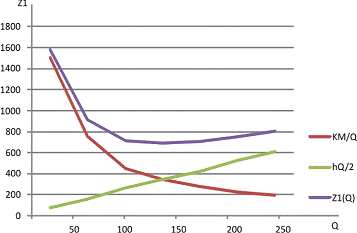
Строим график общих годовых затрат Z1(Q) по второму
способу с помощью таблицы:
|
Q
|
KM/Q
|
hQ/2
|
Z1(Q)
|
|
30
|
1500,00
|
79,20
|
1579,20
|
|
60
|
750,00
|
158,40
|
908,40
|
|
100
|
450,00
|
264,00
|
714,00
|
|
131
|
343,51
|
345,84
|
691,99
|
|
160
|
281,25
|
422,40
|
703,65
|
|
200
|
225,00
|
528,00
|
753,00
|
|
230
|
196,65
|
607,20
|
802,85
|
График общих годовых затрат