Исследование и прогноз величин, распределенных по закону Парето

Содержание

Введение

1. Теоретическая часть

1.1 Кривая Парето

1.2 Закон Парето

1.3 Распределение Парето

1.4 Применение распределения Парето в теории катастроф

1.5 Методы обработки данных, имеющих распределения с тяжелыми хвостами, предложенные Малинецким Г.Г.

2. Практическая часть

2.1 Программная реализация

2.2 Практические расчеты

Выводы

Список использованных источников

Приложения

Введение

Проблемы, связанные с неравномерным распределением доходов среди населения, интересовали человечество с очень давних пор. Наверное, можно сказать, что как только появилась частная собственность, отделенная от собственности первобытной общины, в тот же момент появились предпосылки к зарождению неравномерного распределения богатства и доходов среди людей, которые быстро переросли в такое неравномерное распределение.

История человечества претерпела значительное влияние от различных общественных процессов, основной движущей силой которых было неравномерное распределение доходов среди его членов. Из-за недовольства людей своим материальным благосостоянием происходило множество различных по масштабу восстаний, революций и им подобных движений, как известно, не прошли эти проблемы и мимо Украины. Причем можно сказать, что в современных условиях они вновь приобретают для нашего государства большую важность.

Между тем, несмотря на многовековую историю существования проблемы, научно к ней стали подходить только в конце ХIХ - начале XX вв. На вопрос, какой же величиной можно охарактеризовать неравномерность распределения доходов среди населения, дал ответ итальянский экономист, один из основоположников математической школы политэкономии, Вильфредо Парето (1948-1923). Он предложил уравнение, которое описывает зависимость между размером доходов и количеством людей получающих доходы не менее данного и сформулировал закон, описывающий подобные величин, который был назван его именем. Позже его идеи были интерпретированы с точки зрения теории вероятностей и математической статистики и соответствующее распределение названо именем Парето.

Кроме того, в наше время распределение Парето стали применять для анализа не только данных о доходах населения, но и некоторых других величин. В частности, одним из таких направлений является теория катастроф. В ней распределение Парето применяется для анализа динамики ущерба от катастроф с течением времени, вероятности появления редких, но чрезвычайно масштабных событий. Эти исследования становятся особенно важными в современное время, когда наука и техника развиваются очень быстрыми темпами, порой люди даже не могут представить себе какие последствия такое развитие может оказать в будущем. В связи с этим риск возникновения различных техногенных аварий и катастроф значительно возрастает. И здесь человечеству подготовиться к возможным проблемам может распределение Парето.

Настоящая работа посвящается возможностям анализа и прогноза величин, распределенных по закону Парето.

1. Теоретическая часть

1.1 Кривая Парето

В 1897 г. итальянский экономист Вильфредо Парето (1848 - 1923 гг.), ученик Леона Вальраса и его преемник на кафедре политэкономии Лозаннского университета, установил некоторую закономерность в распределении доходов в капиталистических странах, а также в странах, где преобладали феодальные и раннекапиталистические отношения. Опираясь на эту закономерность, Парето пытался сделать некоторые общие выводы экономического и социологического характера.

На материалах статистики различных стран В. Парето составлял кумулятивные ряды распределения, показывающие, сколько лиц имеет доход не ниже некоторых указанных в рядах величин. Затем он построил графики таких рядов распределения, откладывая на оси абсцисс величины доходов х, а на оси ординат - число лиц, имеющих доход, который равен или больше х.В. Парето обнаружил, что в большинстве исследовавшихся им случаев кривые, отражающие такого рода распределение дохода, похожи одна на другую - они являются гиперболами, уравнение которых может быть выражено формулой:

 (1.1)

где  - минимальный доход, от которого на графике начинается кривая;

а А,  - некоторые положительные параметры.

Такая кривая, называемая кривой Парето, изображена на рисунке 1.1 По уравнению кривой видно, что при , , а при , ; следовательно, кривая Парето имеет две асимптоты:  и . Если ось у перенести в точку , соответствующую минимальному из рассматриваемых нами доходов, то  и уравнение кривой Парето приобретает вид:

 или  (1.2)

_А_ х^а

Этой упрощенной разновидностью кривой Парето и пользуются обычно на практике, ибо, как правило, сведений о числе лиц, имеющих небольшие доходы, бывает недостаточно. Данные о доходах в капиталистических странах заимствуются обычно из налоговой статистики, а лица, имеющие небольшие доходы, не платят подоходного налога. Однако если бы мы имели сведения о лицах с минимальными доходами, то кривая (рисунок 1.1) отклонилась бы книзу и в определенной точке пересекла бы прямую . Для низких доходов формула Парето неприменима, так как исследования показали, что они распределены по логнормальному закону.

Рисунок 1.1 - Кривая Парето

Приведем два примера распределения доходов, из которых один основывается на американской, а второй - на английской статистике. В табл.1.1 дается кумулятивный ряд распределения частот доходов в США за 1919 г. и обычный ряд распределения доходов в Англии за 1911-1912 гг., относящийся к лицам с высокими доходами, причем в этой таблице, указаны как фактические данные, так и данные, полученные при помощи формулы Парето. Необходимо обратить внимание, что данные для Англии содержат неравные интервалы доходов, чем объясняется немонотонное изменение числа лиц, попадающих в такие интервалы.

Таблица 1.1 - Распределение доходов в США за 1919 г. и Англии за 1911-1912 гг.

Рассмотрим ближе приведенные примеры распределения доходов. Упрощенное уравнение кривой Парето (1.2) мы можем представить в логарифмах:

. (1.3)

Тогда, графическое изображение такой кривой в двойной логарифмической шкале представляет собой прямую линию с угловым коэффициентом, равным  (рисунок 1.2). Уравнение этой кривой, подобранной к данному ряду методом наименьших квадратов, имеет вид 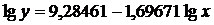, или в нелогарифмической форме .

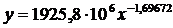Рисунок 1.2 - Кривая Парето в двойной логарифмической шкале, по оси абсцисс отложена величина дохода, тыс. долл. США, по оси ординат - число лиц, получающих доход не менее данного

По табл.1.1 видно, что вначале кривая Парето для данных по США не совсем соответствует статистическим данным, ибо фактическое число лиц, доход которых меньше 500 долл., значительно превосходит число, подсчитанное по уравнению кривой Парето. Для более крупных доходов кривая Парето уже значительно лучше согласуется с данным рядом распределения доходов.

Для данных по Англии параметры кривой Парето, также полученной методом наименьших квадратов, приблизительно таковы: 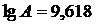, ; уравнение этой кривой в логарифмах имеет вид: .

В. Парето, исследуя данные, характеризующие доходы в разных странах и в разные периоды, установил, что величина параметра  кривой распределения доходов колеблется в пределах от 1,2 до 1,9, следовательно, в среднем .

Значение параметра  можно считать некоторой мерой неравенства в распределении доходов. Чем оно больше, тем больше вогнутость гиперболы и тем больше разрыв между доходами отдельных групп населения, эту зависимость видно на рисунке 1.3.

Рисунок 1.3 - Влияние параметра  на форму кривой Парето. По оси абсцисс отложены размеры доходов населения США тыс. долл. США по данным таблицы 1.1, а по оси ординат - количество лиц, получающих доход не меньше данного, А = 1925,8*10⁶

Рассмотрим подробнее свойства кривой Парето. Как указывалось выше, эта линия в двойной логарифмической шкале принимает вид прямой. Параметр  показывает угол наклона этой прямой и эластичность функции распределения доходов:

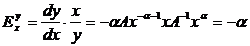. (1.4)

Таким образом, если принять  для распределения доходов среди населения Украины, а нижний предел дохода 1000 грн., тогда при увеличении этого предела на 10%, т.е. до 1100 грн., число лиц, получающих такой доход или больше уменьшится на 15% относительно первоначально взятого предела в 1000 грн.

Рассмотрим, произведение ху, характеризующее общий доход числа лиц, получающих доход х и более. Логично предположить, что с ростом х эта величина будет убывать. Найдем производную этого выражения по х:

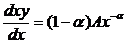. (1.5)

С учетом вышесказанного можно сделать вывод о том, что для распределения доходов 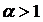, иначе с ростом х величина общего дохода будет также возрастать, что невозможно.

1.2 Закон Парето

Рассмотрим еще одно важное свойство кривой Парето. Из выражения (1.4) получаем:

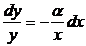. (1.6)

Если принять фиксированное значение dx, то с ростом величины дохода х, относительная величина отсева лиц, имеющих доход равный или больше х,  будет уменьшаться, так как она пропорциональна относительному увеличению дохода 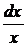, которое, естественно, уменьшается. Это свойство можно выразить следующим образом: переход в высший класс доходов легче для лиц, уже достигших высокого уровня доходов, чем для людей, имеющих низкий доход. Легкость перехода в высшую группу растет пропорционально имеющемуся доходу. Если представить себе ряд уровней дохода, разделенных "ситами", затрудняющими движение вверх, то эти "сита" задерживают тем меньше людей, чем выше доход, причем процент "отсева" падает пропорционально размерам дохода.

В этом случае наблюдается то же, что и на экзаменах на разных курсах обучения. Наиболее крупный процент "отсева" в ходе экзаменов имеет место на первом курсе, на втором он меньше, на третьем еще меньше и т.д.

Пропорциональное доходу уменьшение относительного спада ("отсева") числа лиц при переходе ко все большим и большим доходам составляет сущность закона Парето. Сам факт, выраженный законом Парето, не вызывает удивления. Если, например, переход к высшему классу доходов происходит путем накопления, то, действительно, при той же норме накопления, рост дохода будет пропорционален данному уровню дохода.

Из эмпирически установленной им закономерности В. Парето пытался вывести некий общий социологический закон, который он считал естественным законом, действующим во все времена и при любом общественном строе. Отсюда следовало, что всякие социальные реформы, направленные на устранение неравенства в распределении национального дохода, заранее обречены на неудачу, так как естественный закон о распределении доходов действует при любых условиях и доходы будут распределяться в соответствии с приведенной им формулой.В. Парето выразил эту мысль следующим образом:

"Поскольку существует тенденция к тому, что доходы среди населения распределяются по определенной форме, все изменения в одной части кривой отразятся на других участках кривой; в конечном итоге общество возвращается к своей нормальной форме так же, как раствор данной соли всегда дает однородные кристаллы".

Такая позиция В. Парето объясняется тем, что он был ярым консерватором и врагом всяких социальных реформ; он был и идеологическим предшественником итальянского фашизма (хотя и не являлся его сторонником, но фашисты активно использовали его идеи). В своем учебнике по политэкономии Парето выступал даже против борьбы с алкоголизмом, ибо, как он утверждал, алкоголизму подвержены люди слабые и лучше, если они будут устранены из общества.

В поддержку тезиса, что открытая им закономерность распределения дохода является всеобщим законом природы, В. Парето приводил тот факт, что его наблюдения основаны на статистике разных стран и разных периодов: им исследовалось, в частности, положение по этому вопросу в Англии, Пруссии и Саксонии в XIX в., во Флоренции эпохи Возрождения, в средневековом Базеле, в Аугсбурге XV-XVI вв., в Перу в конце XVIII в. и т.п., и всегда он получал одни и те же результаты. Социальные системы менялись, а закон распределения дохода, как утверждал Парето, оставался в силе.

В экономической литературе известны многочисленные социологические толкования закона Парето.

Гарольд Дэвис, современный американский эконометрик, считал, что если коэффициент 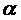 в формуле Парето для распределения национального дохода имеет значение, близкое к 1,5, то это общество находится в состоянии социального равновесия. Если значение коэффициента 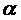 значительно отклоняется от 1,5, то равновесие нарушается, причем, когда 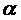 меньше 1,5, обществу угрожает фашизм или другая недемократическая форма правления, как это имело место в Испании и других странах. Значительное же отклонение коэффициента 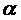 в противоположную сторону (свыше 1,5) ведет к социальной революции. Общество, по мнению Дэвиса, как бы привыкло к распределению дохода согласно кривой, имеющей уравнение (1.2) при 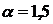. Если же неравномерность распределения дохода возрастает ( 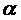>> 1,5), среди народа растет недовольство и он проявляет стремление к революции. В обратном случае, когда распределение дохода выравнивается (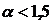), высшие классы в собственных интересах стремятся усилить свою власть и возникает недемократическая форма правления имущих классов.

Часто делались попытки толковать закон Парето таким образом, что распределение доходов является результатом распределения человеческих способностей в обществе. В частности, тот же Г. Дэвис приводит примеры, показывающие, что результаты экзаменов по математике, число работ, опубликованных в научных журналах, умение играть в гольф и т.п. распределяются аналогично распределению дохода по кривой Парето. Эти примеры означают, что дальнейший прогресс в развитии научных и физических способностей облегчается для тех, кто уже раньше достиг в этой области более высокого уровня. Отсюда один шаг до вывода, что распределение доходов соответствует распределению человеческих способностей и что существует какое-то определенное значение коэффициента 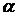, соответствующее нормальному условию социального равновесия.

Учитывая вышесказанное, следует отметить, что до налогообложения и предоставления льгот, социальной помощи и другой материальной поддержки со стороны государства, в современном обществе доходы несомненно распределяются согласно кривой Парето, начиная с некоторого уровня. Такие выводы подтверждены богатой статистикой. Но перераспределение национального дохода посредством налогов и различного рода материальной помощи может в значительной степени изменить первичное распределение доходов, особенно при применении прогрессивных ставок подоходного налога, в сторону его равномерности.

парето распределение закон доход

1.3 Распределение Парето

Перейдем от выражения для кривой Парето (1.2) к распределению Парето случайной величины х (в вышерассмотренных примерах - это величина доходов) в терминах теории вероятностей и математической статистики.

Сначала перейдем к вероятностной интерпретации величины лиц, имеющих доход Х не ниже данного х, представленный (1.2), поделив это выражение на общее количество Y населения, получающего доход не ниже х.

. (1.7)

Учитывая, что по закону Парето, как было указано ранее, доходы (или другая случайная величина) начинают распределяться, начиная с некоторого значения х₀, необходимо ввести эту переменную в (1.7), несмотря на то, что ранее мы от нее избавились для удобства. Это можно сделать проведя нормировку х на х₀:

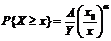. (1.8)

Проведем замену:

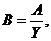 тогда: 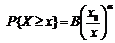. (1.9)

Но в теории вероятностей принято рассматривать не вероятность выраженную (1.9), а так называемую функцию распределения случайной величины, которая представляет собой дополнение (1.9) до единицы. Функция распределения F (x), определяющая вероятность того, что случайная величина Х примет значение меньше данного х, , для распределения Парето имеет вид:

. (1.10)

Соответствующая плотность вероятности р (х) находится как производная функции распределения и определяет вероятность того, что случайная величина примет значение равное х. Для распределения Парето плотность вероятности определяется выражением:

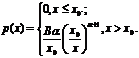. (1.11)

Распределения, подобные распределению Парето в том плане, что они ограничены с одной стороны значениями, которые может принимать случайная величина, называются усеченными распределениями. Обычно они применяются в исследованиях, когда важна динамика поведения не всей совокупности исследуемых объектов, а лишь некоторой ее части или даже хвоста распределения, либо если часть совокупности распределена по одному закону, а часть - по другому.

Рассмотрим важную характеристику распределения Парето, определяющую области его применения в исследованиях. Для этого найдем математическое ожидание данного распределения:

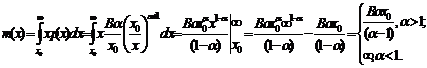. (1.12)

Таким образом, можно видеть, что математическое ожидание распределения Парето может быть конечно либо бесконечно в зависимости от параметра 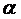. Как уже было указано ранее, в экономических исследованиях распределения доходов выполняется условие 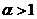, таким образом существует возможность найти математическое ожидание (средний уровень доходов, распределенных по закону Парето). Второй случай распределения Парето при  представляет собой распределение с тяжелым хвостом (понятие рассматривается далее) и нашел применение в теории катастроф в качестве распределения, по которому определяется вероятность наступления редких, но значительных по масштабам, событий.

Рассмотрим еще одну интересную характеристику, которая определяет сумму накопленных значений х случайной величины, обозначим ее , (в рассмотренных ранее примерах это общее количество дохода всех лиц, попадающих в заданный интервал по доходу) между значениями х₁ и х₂. Эту величину можно определить следующим образом:

. (1.13)

При этом она будет тем точнее отображать реальность, чем больше будет расстояние между х₁ и х₂. Понятно, что при  поведение этой функции будет зависеть от параметра  таким же образом, как и выше найденное математическое ожидание.

При использовании данной функции для расчета, например, суммарного дохода лиц, которые получают доход от некоторого значения х₁ до максимального дохода, получаемого в стране одним человеком, х_max, целесообразней принять в качестве х₂ это значение х_max которое можно выразить так:

, (1.14)

где 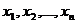 - значения, которые принимает случайная величина, в рассматриваемом примере - доход, в каждом конкретном случае.

Выражение (1.14) можно применять, если имеется необходимая информация о максимальном значении х_max. При этом суммарный эффект (1.13) будет конечным при любом значении параметра  и выражение (1.13) можно использовать для прогнозирования суммарных эффектов случайной величины х, распределенной по закону Парето, даже если это распределение имеет тяжелый хвост. Опишем, как можно сделать выражение (1.13) еще более эффективным при анализе указанных случайных величин. Предположим (а можно утверждать это с большой долей уверенности) что величина х_max зависит от количества произошедших событий или наблюдаемых объектов п. А оно в свою очередь, конечно, зависти от времени t, таким образом получаем:

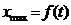. (1.15)

Логично было бы так же предположить, что от времени зависит и параметр  и A (это наверняка справедливо для экономических и социальных явлений, а, возможно, и для природных):

. (1.16)

Теперь можем переписать (1.13) для х_max и x₀ в виде:

. (1.17)

Имея достаточное количество статистических данных можно рассчитать вид и параметры (1.15) и (1.16). Таким образом мы получим динамическую модель, описывающую накопленный суммарный эффект случайной величины, распределенной по закону Парето

1.4 Применение распределения Парето в теории катастроф

При внимательном анализе статистических данных по крупнейшим катастрофам выясняется, что они проявляют весьма необычные особенности, плохо укладывающиеся в привычные представления. Так, при Тянь-Шанском землетрясении 28.07.1976 г. в Китае погибло (по разным источникам) от 240 до 650 тыс. чел., что в десятки тысяч раз превосходит число погибших при обычном, "рядовом" разрушительном землетрясении.

Эта же закономерность наблюдается для наводнений. При наводнении 1931 г. на реке Янцзы в Китае погибло около 1,3 млн чел. Наводнение 1970 г. в Бангладеш вызвало гибель более 500 тыс. чел. Гигантские экстраординарные значения наблюдаются и для стоимостных характеристик ущерба, что типично для наиболее экономически развитых стран. При этом перечисленные катастрофы (происшедшие в нашем столетии), по-видимому, не являются максимально возможными. Во всяком случае, летописные источники и древнейшие памятники человечества описывают еще более разрушительные катаклизмы.

Таким образом, в ряду ущербов от катастроф изредка встречаются суперэкстремальные значения, несоизмеримые по величине со значениями для подавляющей части событий. Ущерб от этих суперэкстремальных событий сравним с суммарным ущербом от всех катастроф за тот же период времени.

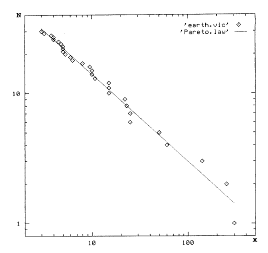
Рисунок 1.4 - Кумулятивная гистограмма распределения 30-ти природных катастроф за 1970-1995 гг. с наибольшим количеством жертв, подобранная кривая Парето с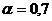

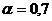На рисунке 1.4 приведена накопленная гистограмма хвоста выборочного распределения для 30 наихудших, в смысле количества человеческих жертв, природных катастроф (землетрясения, ураганы, наводнения) за 1970-1995 гг. Здесь N (x_i > x) - количество событий с числом жертв x_i, большим заданного аргумента x. На рисунке 1.3 изображена кривая Парето с , построенная по данным о катастрофах, по которой видно, что в логарифмическом масштабе хвост распределения хорошо приближается к прямой с угловым коэффициентом около - 0,7. Таким образом, количество событий с числом жертв, превышающим x, убывает очень медленно при x ® ¥. И если при анализе "привычных" статистических зависимостей мы обыкновенно пренебрегаем возможностью очень крупных событий, лежащих на быстро убывающем "хвосте" распределения, то здесь мы этого сделать не можем. Более того, по причинам, которые будут указаны далее, можно рассматривать только "хвост", отвлекаясь от поведения распределения при малых x. Подобные распределения называются распределениями с тяжелыми хвостами. В литературе можно найти различные трактовки этого термина, суть их всех состоит в следующем: распределение с тяжелым хвостом - это распределение, хвост которого нельзя "отрезать", т.е. нельзя пренебречь крупными, но редкими событиями. Основная проблема, связанная с такими распределениями, состоит в том, что моменты достаточно высокого порядка у них расходятся. Как было показано выше, для распределения Парето с , бесконечно уже математическое ожидание. Очевидно, что на расходимость моментов влияет только тяжелый хвост распределения, "перевешивающий голову", описывающую вероятность наиболее частых, но небольших событий. Вид "головы" при этом оказывается не очень существенным, а решающую роль играет только асимптотика хвоста.

Рассмотрим распределение Парето с  и . Сумма S_n накопленных эффектов событий с ростом n растет нелинейно как n^1/a. Этот вывод можно получить следующим способом. Рассмотрим максимальный член m_max выборки x₁, x₂,… x_n:

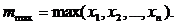 (1.18)

Распределение m_max выписывается следующим образом:

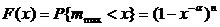. (1.19)

Уравнение для медианы med m_max (медианой распределения называется такое число, что ровно в половине случаев случайная величина принимает значения меньше него и, соответственно, ровно в половине случаев - больше) имеет вид F ⁿ (x) = 0,5. Отсюда находим:

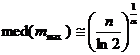. (1.20)

Из этого выражения следует, что характерная величина максимального члена m_max, если в качестве этой величины взять медиану med m_max, растет с точностью до множителя как n^1/a. Поскольку для неотрицательных величин S_n ³ m_max, то мы снова убеждаемся в том, что S_n должна возрастать с ростом n нелинейно, а именно, не медленнее, чем n^1/a.

На самом деле можно доказать что для распределений неотрицательных величин с тяжелыми хвостами величины S_n и m_max имеют одинаковый порядок и, более того, математическое ожидание их отношения:

 (1.21)

Это свойство распределений с тяжелыми хвостами выглядит парадоксально: сумма положительных эффектов с точностью до множителя порядка 1/ (1 - a) определяется одним, максимальным членом m_max, причем этот факт справедлив для сколь угодно больших выборок. В обычной ситуации, когда у случайной величины имеются конечные моменты, отношение S_n/m_max, естественно, стремится к бесконечности с ростом n. В этой ситуации вклад любого отдельного слагаемого (в том числе и максимального) в сумму S_n стремится к нулю.

Кроме приведенных ранее можно найти другие примеры распределений с тяжелыми хвостами. Они относятся к ущербам от ураганов и землетрясений, а также к максимальным расходам воды в реках. С большой долей уверенности можно предполагать, что распределения с тяжелыми хвостами характерны не только для потерь от природных катастроф, но также и для потерь от техногенных катастроф типа Чернобыльской аварии, разливов нефти в морях в результате аварий танкеров, аварий химических предприятий, пожаров, разрушений нефтепроводов, аварий глобальных компьютерных сетей и т.п. Этот вопрос требует дальнейшего тщательного изучения.

Ниже будет теоретически показано, что в случае распределений с тяжелыми хвостами выборочные средние неустойчивы и малоинформативны из-за неприменимости закона больших чисел. Покажем неустойчивость и слабую информативность средних значений ущерба на конкретных примерах. По данным ЮНЕСКО за 1947-1960 гг. от тайфунов, ураганов, наводнений погибло 900 тыс. чел., что за год в среднем составило 64300 жертв. Если сравнить это среднегодовое значение с числом жертв от отдельных катастроф, то оказывается, что эти последние могут быть в десятки раз больше. Так, при наводнениях в Китае в 1931 г. погибло около 1 300 тыс. чел., а в 1938 г. - 500 тыс. чел., в 1970 г. в Бангладеш жертвами наводнения стали более 500 тыс. чел. Ясно, что среднегодовые показатели не дают представления о возможности таких гигантских катастроф. О неустойчивости среднегодового значения числа жертв говорит следующий факт. По материалам каталога, подготовленного в рамках Международной программы Десятилетия борьбы со стихийными бедствиями, среднегодовое число жертв за 1962 - 1992 годы от тех же катастроф составило 36000. Уменьшение среднегодового числа жертв, по сравнению с периодом 1947-1960 гг., почти в два раза было бы большим успехом, если бы оно не носило случайного характера.

Случайность уменьшения числа жертв продемонстрируем на примере землетрясений - наиболее изученного вида катастроф. Согласно подборке данных проф. Н.В. Шебалина (Институт физики Земли РАН) в 1947-1970 гг. от землетрясений погибло 151 тыс. чел., что дает среднегодовое число жертв 6300. В то же время, по данным за 1962-1992 гг. число жертв от землетрясений составило 577 600 чел., т.е., несмотря на успехи сейсмостойкого строительства, среднегодовое число погибших увеличилось до 18600 чел. Таким образом, среднегодовые показатели разнятся втрое, причем оба показателя много меньше максимальных потерь от единичного события (при землетрясении 28.07.1976 в Китае погибло, по меньшей мере, 240 тыс. чел.). Из приведенных примеров безо всякого специального анализа видно, что среднегодовые значения весьма неустойчивы и потому неинформативны.

1.5 Методы обработки данных, имеющих распределения с тяжелыми хвостами, предложенные Малинецким Г.Г.

Один из общих подходов к обработке положительных величин, имеющих распределения с тяжелым хвостом, состоит в переходе от наблюдаемых величин x_i к их логарифмам y_i = ln x_i. В случае степенного убывания хвостов с любым показателем степени величины y_i уже будут иметь все статистические моменты и, таким образом, к ним можно применять стандартные методы статистической обработки. Следует отметить важный недостаток этого подхода. Если нас интересует суммарный эффект S_n, то переход к логарифмам не поможет, ибо связать поведение S_n и ln x₁ + ln x₂ +… + ln x_n в общем случае очень трудно. Остановимся подробнее на важном частном случае, когда можно считать априори известным, что хвост распределения удовлетворительно описывается степенной зависимостью при x, превышающем некоторый также известный порог x₀ (отметим, что для каждого типа природных и техногенных катастроф этот вопрос должен рассматриваться отдельно на основе известной статистики или результатов математического моделирования). При этом не обязательно, чтобы это приближение выполнялось для всего диапазона наблюдаемых значений, достаточно, чтобы оно выполнялось для хвоста распределения, т.е. при x > x₀. Действительно, для распределений с тяжелыми хвостами основной вклад в суммарный эффект S_n вносят наибольшие наблюдения. Поэтому указанное пороговое ограничение не скажется заметно на оценке вероятностных характеристик сумм S_n при достаточно больших значениях n. После перенормировки на известное значение порога можно считать, что нормированные величины x/x₀ имеют распределение Парето. Нужно только выбирать порог x₀ так, чтобы осталось достаточное для оценки параметра 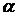 число наблюдений выше этого порога. Практика показывает, что следует оставлять не менее 25-30 наибольших наблюдений. Оценка максимального правдоподобия 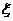 для параметра  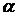имеет вид:

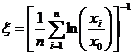 (1.22)

В качестве разброса этой оценки можно взять стандартное отклонение :

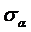. (1.23)

Если для медианы максимального члена med m_n использовать выражение (1.12) то в качестве оценки характерного значения суммы можно взять значение

, (1.24) где 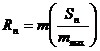. (1.25)

Для распределения Парето математическое ожидание (1.25) можно вычислить точно:

, (1.26)

где через  обозначена бета-функция. В табл.1.2 приведены величины R_n для некоторых значений  и n.

Таблица 1.2 - Средние значения отношений S_n/m_max

Неизвестный параметр  в (1.25), (1.26) необходимо заменить на его оценку 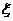. При этом погрешность такой замены можно проконтролировать, подставив в (1.25) и (1.26) значения 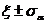. Оценку  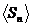по формуле (1.24) можно использовать для предсказания будущих характерных значений суммарного эффекта S_n. Как было отмечено ранее эта оценка растет нелинейно с увеличением n. Поскольку величина n обычно пропорциональна интервалу времени наблюдения, то можно сказать, что суммарный эффект растет нелинейно со временем. Необходимо отметить, что, хотя среднее значение отношения S_n/m_max согласно (1.21) при n ® ¥ стремится к константе 1/ (1 - ) в случае  < 1, дисперсия этого отношения не уменьшается до нуля; она также стремится к некоторой константе. Характерные значения сумм S_n растут согласно уравнению (1.24). Однако случайные отклонения весьма велики. Поэтому во многих прогноз суммарного эффекта целесообразней делать не в виде точечной оценки, а в виде доверительного интервала  такого, что:

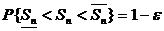, (1.27)

где  - задаваемое исследователем малое число, характеризующее уровень доверия. Можно дать следующую приближенную оценку для верхней доверительной границы:

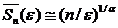. (1.28)

Оценка для нижней доверительной границы - соответственно:

. (1.29)

Таким образом в данном подразделе была рассмотрена методика расчета и прогноза теоретических значений суммы накопленных эффектов в зависимости от количества событий n при распределении таких эффектов по закону Парето с .

2. Практическая часть

2.1 Программная реализация

Для автоматических расчетов параметров кривой Парето и накопленной суммы эффектов, была разработана программа в табличном процессоре MS Excel 2000.

Рисунок 2.1 - Рабочее окно программы

Исходными данными для расчетов выступают эмпирические данные о значениях случайной величины х, которые принимают некоторые исследуемые объекты, причем предполагается, что эта величина распределена по закону Парето. Также исходной информацией являются значения х, для которых будет проводиться оценка количества объектов, для которых х не меньше данного.

Выходными данными программы являются рассчитанные значения параметров кривой Парето, посчитанные теоретические значения у для указанных х, графики теоретической кривой Парето и эмпирической ломаной линии, данные о промежуточных расчетах. Также рассчитывается теоретическая и фактическая величина суммы накопленных эффектов между х₂ и х₁, с применением выражения (1.13), что позволяет также сделать выводы о том, насколько правильна гипотеза распределении случайной величины по закону Парето. Рабочее окно программы приведено на рисунке 2.1.

Программа работает в следующей последовательности:

–              ввести данные о значениях х в столбец С. в., х (можно ввести до 10000 значений);

–              ввести значения х, для которых будет определяться количество объектов, для которых х принимает значения не меньше данного в столбец х (11 значений);

–              выполнить команду меню Сервис-Поиск решения-Выполнить-ОК, при этом будут рассчитаны параметры кривой Парето и они отобразятся в соответствующих ячейках, на которые указывают надписи А = и alpha =. Также при этом автоматически пересчитаются теоретические значения у, на графике отобразится поученная кривая Парето;

–              при желании получить точечный прогноз у для некоторого х, необходимо ввести значение такого х в колонку х и при этом в соответствующей ячейке колонки у теор. отразится прогнозное значение у;

–              при необходимости можно рассчитать сумму накопленных эффектов между заданными х₁ и х₂, для этого необходимо вбить интересующие значения в соответствующие ячейки. При этом в ячейке 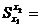 отразится посчитанное значение накопленной суммы эффектов. Можно принять в качестве верхней границы максимальное эмпирическое значение х, которое отражается в соответствующей ячейке;

–              в ячейке Сумм. факт = показывается значение 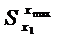 для сравнения с соответствующим расчетным значением.

2.2 Практические расчеты

В качестве примера для расчетов возьмем данные о величине убытков от пожаров в Украине за 2006 г, прямой ущерб от которых составил более 10 тыс. грн. Соответствующие данные приведены в приложении А.1. По рассчитанным в программе данным получаем следующее уравнение, количество пожаров у, ущерб от которых составил не менее х тыс. грн.:

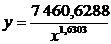. (2.1)

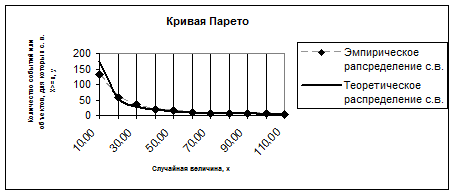
Рисунок 2.2 - Кривая Парето, показывающая распределение пожаров по нанесенному ущербу

Соответствующая кривая Парето и эмпирическое распределение показаны на рисунке 2.2 Как можно видеть по рисунку 2.2 теоретическая кривая довольно хорошо описывает эмпирические данные. Но при малых х наблюдается значительное расхождение, свидетельствующее о том, что для них соответствующее количество пожаров у распределено по другому закону. Также относительно невелико отклонение расчетной накопленной суммы эффектов на всем отрезке от ущерба в 10 тыс. грн. до максимальной суммы ущерба в 156,348 тыс. грн., которая составила 3720 тыс. грн., от фактической суммы прямого ущерба, которая составила для того же интервала значений х 3291 тыс. грн. Имеющиеся отклонения можно объяснить во-первых тем, что замечено ранее о несоответствии гипотезы о распределении Парето при малых х эмпирическим данным, а во-вторых тем, что количество исследуемых объектов (132) довольно невелико для вычислений по такому выражению, к тому же для таких распределений, как отмечается в литературе, характерны значительные случайные отклонения.

Выводы

В настоящей работе было рассмотрено распределение доходов по закону Парето. Было проанализировано влияние параметра  на степень неравномерности в распределении доходов и соответствующем ему поведении общества. На основании проработанного материала можно сделать выводы о том, что параметр  является мерой неравномерности распределения доходов в обществе.

Было осуществлено преобразование уравнения кривой Парето к вероятностному распределению Парето случайной величины. Показано, что при  математическое ожидание такой случайной величины бесконечно, что усложняет работу с ней, а при 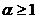 - конечно.

Также была выведена формула, позволяющая рассчитать накопленный суммарный эффект для всех объектов, попадающих в заданный отрезок по значению исследуемой случайной величины, в том числе до максимального эмпирического значения, которое принимает такая величина. Также было показано что эта зависимость является динамической и изменяется с течением времени. Но процесс определения ее вида и параметров трудоемок и требует значительного количества статистической информации.

В работе рассмотрено применение распределения Парето при анализе убытков от катастроф. При этом определено, что для такого распределения . В связи с этим в работе рассмотрена методика анализа такого распределения и накопленной суммы эффектов таких величин, предложенная Малинецким Г.Г. В результате также получены выводы о динамическом характере накопленной суммы эффектов.

Была проведена оценка возможности применения распределения Парето для определения количества пожаров в Украине за 2006 г., прямой ущерб от которых составил не менее 10 тыс. грн. Сделаны выводы, что данная величина распределена по закону Парето при больших х, причем для нее . Также проанализирована возможность применения уравнения (1.13), описывающего накопленную сумму эффектов от данных событий, сделаны выводы о том, что, несмотря на довольно большие случайные отклонения, это уравнение все же можно применять для анализа подобных данных.

В целом можно сказать, что распределение Парето и другие распределения с тяжелыми хвостами. Нашли свое применение в вопросах, связанных с моделированием катастроф и других подобных событий, что особенно актуально во время современного развития науки и техники и все усиливающегося давления человека на окружающий мир.

Список использованных источников

1.      Ланге О. Введение в эконометрику/ пер. с польск. под общ. ред.А.Я. Боярского - М.: "Прогресс", 1964. - 296 с.

2.      Крамер Г. Математические методы статистики/пер. с англ.А.С. Монина и А.А. Петрова под ред. ак. А.Н. Колмогорова - М.: гос-е изд-во иностранной лит-ры, 1918.

.        Управление риском / под ред. Г.Г. Малинецкого - М.: Российская академия наук, 2000.

.        http://kek. ksu.ru/EOS/Model/uchebnik/ - применение прикладных пакетов программ при исследовании распределения доходов.

Приложения

Приложение А

Таблица А.1 - Убытки от пожаров, тыс. грн., на территории Украины, прямые убытки по которым составили более 10 тыс. грн.