Особенности решения концептуальной модели задачи решающего комплекса
Оглавление
концептуальная модель задача программа
Введение
Концептуальное
модельное представление задачи как системы
Программная
реализация представления концептуальной модели задачи
Решение задач
посредством прямого расчёта
Судоку
Решение
судоку
Составление
судоку
Литература
Приложение.
Программный код
Введение
концептуальная модель задача программа
В настоящее время высокий уровень развития современных
электронно-вычислительных средств даёт возможность быстро и эффективно решать
вопросы, связанные с хранением и обработкой всевозможных видов информации,
представлением данных и знаний в удобных для пользователя и понятных для
компьютера формах. Подобные возможности реализуются посредством эффективного
применения баз данных и хранилищ данных, а также автоматизированных,
электронных и интеллектуальных систем. Растущие потребности человечества
порождают все более сложные в качественном и количественном аспектах задачи,
решение которых зачастую определяет прогресс общества.
В ходе данной работы будет рассмотрено представление концептуальной
модели задачи (КМЗ) на основе триады «Задача - Данные - Решатель» и работа
одного из компонентов подобной системы - генератора вспомогательных
концептуальных моделей.
В процессе выполнения данной работы была создана программа (на языке
Python), позволяющая решать любые задачи, связанные с вычислениями на основе
вводимых пользователем исходных данных и определяемых некоторой предметной
областью, для которой заданы действительные математические формулы. Программа
осуществляет поиск необходимых формул на основе вводимых пользователем данных,
а затем применяет данные формулы для получения конечного результата. Кроме
того, данная программа позволяет решать и составлять судоку - один из видов
японских кроссвордов, составляя вспомогательные концептуальные задачи и решая
их и исходную задачу на основе различных рекурсивных методов.
Особенность предлагаемого метода представления задачи как концептуальной
модели имеет отличительную особенность по сравнению с классической технологией,
так как исходная задача не разбивается на меньшие составные подзадачи, а
происходит генерация вспомогательных задач, решая которые можно решить исходную
задачу.
Далее в работе будет описано представление исходной задачи как
концептуальной модели задачи, формализация задачи, а также описана практическая
реализация составленной программы.
Концептуальное
модельное представление задачи как системы
Деятельность человека имеет две основные формы: умственную -
“деятельность мозга” и физическую - “деятельность рук”. Очевидно, что и
умственная и физическая деятельность сопряжены с постоянной необходимостью
решения разнообразных задач. Спектр таких задач определяется многочисленными
факторами, как существенными, так и малозначимыми. К существенным факторам,
прежде всего, следует отнести причины возникновения задачи. В качестве
первопричины, порождающей задачу, выступают потребности человека.
Удовлетворение потребностей осуществляется в процессе взаимодействия человека
не только с внешней, но и с собственной внутренней средой, т.е. с природой, с
другими людьми или самим собой. Реализация потребностей всегда связана с
решением соответствующих этим потребностям задач. Практически весь спектр
потребностей человека определяется тремя сферами его деятельности:
материальной, социальной и духовной. Следовательно, можно констатировать, что
возникновение задач обусловлено материальными, социальными и духовными
факторами. К существенным факторам, определяющим содержание и свойства задач,
следует также отнести: предметную область существования задачи, её размерность
и уровень сложности, степень определенности, возможности формализации, полноту
исходных данных, требования к конечному результату, а также ряд других свойств,
характеристик, параметров и особенностей.

На представленном выше рисунке отражена концептуальная архитектура
задачного решающего комплекса. Интеллектуальная решатель взаимодействует с
концептуальной моделью, которая, в свою очередь, взаимодействует с
интеллектуальными интерфейсами, посредством которых в решатель загружаются
пользовательские задачи.
Концептуальная модель задачи разрабатывалась на основе методов
системно-комплексного анализа (СК - анализа) “внутреннего устройства задачи”,
как целостной системы, и её внешнего окружения - среды существования задачи.
Для успешного разрешения проблемы создания КМЗ использовались:
·
системно-комплексный
подход и СК-анализ;
·
основы
теории концептуального моделирования;
·
методологические
аспекты метамоделирования;
·
технология
концептуального метамоделирования (КММ - технология), а также метод раскрытия
неопределённости системной задачи на уровне её концептуального представления,
основанный на метазадачной технологии и рекурсивных механизмах, приводящий к
рекурсивным и взаимнорекурсивным структурам системной КМЗ.
Изложенный подход к созданию и использованию КМЗ по своей сути может быть
определен как концептуальная метамодельная технология автоматизированного
описания, представления, постановки и решения системных задач.
Многоуровневое
представление концептуальной модели системной задачи 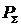 осуществляется на основе метода стратификации. Для
формирования страт - уровней организации задачи
осуществляется на основе метода стратификации. Для
формирования страт - уровней организации задачи 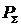 необходим
критерий или основание стратификации. В качестве такого критерия в
рассматриваемом случае целесообразно выбрать показатель неопределённости
системной задачи
необходим
критерий или основание стратификации. В качестве такого критерия в
рассматриваемом случае целесообразно выбрать показатель неопределённости
системной задачи 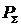 . В соответствие с указанным критерием введём
качественную шкалу неопределённости. На шкале неопределённости ранжируем
компоненты концептуальной модели, представленной системой кортежей (1), по
степени возрастания неопределённости. При этом будет иметь место следующая
последовательность страт - уровней неопределённости системной задачи:
. В соответствие с указанным критерием введём
качественную шкалу неопределённости. На шкале неопределённости ранжируем
компоненты концептуальной модели, представленной системой кортежей (1), по
степени возрастания неопределённости. При этом будет иметь место следующая
последовательность страт - уровней неопределённости системной задачи:
конечного
результата - решения -  ;
;
исходных
данных (начальной информации) -  ;
;
показателя
адекватности - 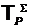 ;
;
программы
решения задачи - 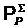 ;
;
алгоритма
решения задачи - 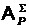 ;
;
метода
решения задачи - 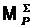 ;
;
цели
системной задачи - 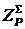 ;
;
среды
существования задачи - 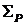 .
.
Графическая
интерпретация шкалы неопределённости имеет вид, представленный на рис.1. В
последовательности страт (см. рис. 1) определённость задачи 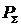 возрастает при движении по шкале сверху вниз. При
этом, каждый выделенный на шкале уровень - страта
возрастает при движении по шкале сверху вниз. При
этом, каждый выделенный на шкале уровень - страта 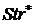 разбивает её на две части. Верхняя часть шкалы
включает все известные (определённые) компоненты, а нижняя - компоненты,
которые необходимо определить, т.е. неизвестные.
разбивает её на две части. Верхняя часть шкалы
включает все известные (определённые) компоненты, а нижняя - компоненты,
которые необходимо определить, т.е. неизвестные.

Рис.
2. Ранжированное представление компонентов системной задачи по шкале
неопределённости
Полное описание концептуальной модели задачи, а также методов и теорий их
возникновения и т. п. даны в статье [1]. В рамках данной работы мы рассмотрим
работу компонента генератора вспомогательной задачи.

На рисунке выше представлены компоненты концептуальной модели системной
задачи.
КМСЗ - концептуальная модель системной задачи
ПЦНД - критерии полноты, целостности, необходимости, достаточности
Ан-р - анализатор
ГВЗ - генератор вспомогательных задач
КМВЗ - концептуальная модель вспомогательной задачи
На основании концептуальной модели системной задачи, которая
представляется концептом 0го ранга (К) мы разворачиваем пирамиду, каждым
уровнем которой будут соответствующие концептуальные вспомогательные задачи
(В).

На рисунке выше представлена многоуровневая рекурсивная концептуальная
модель задачной системы. От компонента 0го ранга мы рекурсивно переходим вниз
на компоненты более низких рангов, причём каждый из них может быть рассмотрен
как вершина своей пирамиды. По достижению результата мы возвращаемся наверх к
первоначальной задаче.
Программная
реализация представления концептуальной модели задачи
Решение задач посредством прямого расчёта
Первая технология, которая реализуется в представленном программной
средстве - прямой расчёт. Сначала пользователь выбирает предметную область. Для
примера рассмотрим задачу на простое прямолинейное движение.

Рис.5. Окно программы - загрузка данных по предметной
области
Программа загружает исходные данные предметной области, которые
представляют собой формулы для вычисления всех возможных параметров. В нашем
случае эти формулы таковы:
Набор переменных:
x -
текущая координата
xs -
начальная координата
v -
текущая скорость
vs -
начальная скорость
astart
- начальное ускорение
t -
время
to -
время (1й корень решения уравнения движения относительно t)
tt -
время (2й корень решения уравнения движения относительно t)
Формулы для вычисления:
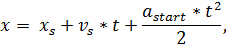
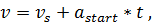

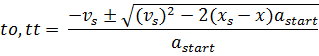
Затем пользователь загружает непосредственно задачу.
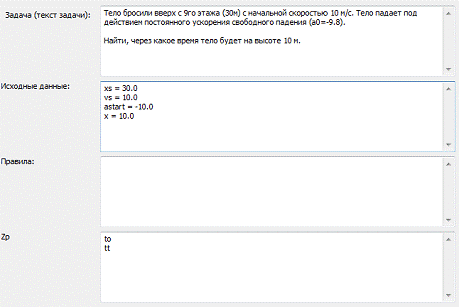
Ввод (exec) начальной информации: xs = 30.0
Ввод (exec) начальной информации: vs = 10.0
Ввод (exec) начальной информации: astart = -10.0
Ввод (exec) начальной информации: x = 10.00:
Применение шаблона to = ((-1)*(vs) + math.sqrt(((vs)**2) -
2*((xs)-(x))*(astart)))/(astart) для переменной to (to = ((-1)*(vs) +
math.sqrt(((vs)**2) - 2*((xs)-(x))*(astart)))/(astart))= -1.23606798
Переменная to не удовлетворяет параметрам внешней среды (to > 0)1:
Применение шаблона tt = ((-1)*(vs) - math.sqrt(((vs)**2) -
2*((xs)-(x))*(astart)))/(astart) для переменной tt (tt = ((-1)*(vs) -
math.sqrt(((vs)**2) - 2*((xs)-(x))*(astart)))/(astart))= 3.23606798
Таким образом, мы получаем решение задачи (подсчёт переменных посредством
прямого математического расчёта, то есть подстановки) и проверку на
удовлетворение полученного параметрам внешней среды.
Непосредственно рекурсия здесь не применяется, но если мы изменим условия
задачи следующим образом:

Рис.7. Окно программы - другие варианты исходных данных
То есть приведём задачу к виду «на какую максимальную высоту поднялось
тело», то получим следующий вывод:
Ввод (exec) начальной информации: xs = 30.0
Ввод (exec) начальной информации: vs = 10.0
Ввод (exec) начальной информации: astart = -9.80:
Применяем правило v=0
Применение шаблона x = (xs) + (vs)*t + (astart)*(t**2)/2 для переменной x
(x = (xs) + (vs)*t + (astart)*(t**2)/2)
Какая-то из переменных правой части правил не может быть найдена в
условиях и/или других правилах, ожидается name 't' is not defined
Поиск 't'
Применение шаблона t = (v-vs)/astart для переменной t (t = (v-vs)/astart)
t
t =
1.02040816
Step
1:
Применение шаблона x = (xs) + (vs)*t + (astart)*(t**2)/2 для переменной x
(x = (xs) + (vs)*t + (astart)*(t**2)/2)= 35.10204082
Таким образом видно, что программа попыталась применить искомый шаблон
для нахождения переменной x, но,
так как не смогла его найти, то начала рекурсивный поиск шаблонов для решения
концептуальной подзадачи - нахождения t как переменной, которая требуется для нахождения x. После того, как данная шаблон
(формула) для нахождения t была
найдена, идёт её применения. В случае ошибки программа бы рекурсивно перешла
дальше и так до тех пор, пока не кончились бы все формулы. После того, как
шаблон для t был найден, идёт вторая попытка
применения шаблона для x. В
случае успеха происходит вывод.
Следует отметить, что процесс поиска вспомогательных концептуальных задач
последовательный, так как интерпретатор языка выводит ошибку при нахождения
первого несоответствия и не просматривает строку дальше.
Таким образом, можно решать задачи практически любой сложности. Глубину
рекурсии также можно регулировать во избежание попадания в бесконечный цикл.
Можно выделить две базовые задачи эксперта по моделированию. Первая - это
наполнение базы данных и знаний (по сути - математических формул) для
предметной области. Вторая - правильное описание данных для нахождения решения
данной конкретной задачи.
Принципиальная схема решения:

Рис.8. Принципиальная схема
работы программы
Судоку
Судоку (яп. 数独 су:доку) - популярная
головоломка-пазл с числами. В переводе с японского «су» - «цифра», «доку» -
«стоящая отдельно». Иногда судоку называют «магическим квадратом», что в
общем-то не верно, так как судоку является латинским квадратом 9-го порядка.
Судоку активно публикуют газеты и журналы разных стран мира, сборники судоку
издаются большими тиражами. Решение судоку - популярный вид досуга.
Игровое поле представляет собой квадрат размером 9x9, разделённый на
меньшие квадраты со стороной в 3 клетки. Таким образом, всё игровое поле
состоит из 81 клетки. В них уже в начале игры стоят некоторые числа (от 1 до
9), так как незаполненное игровое поле не имеет смысла. В зависимости от того,
сколько клеток уже заполнены, конкретную судоку можно отнести к лёгким или
сложным.
Существует несколько методов решения судоку. Условно их можно разделить
на две категории - логические и вычислительные. К вычислительным методам
относится метод полного перебора (BruteForce). Логические - метод одиночного квадрата, закрытого
кандидата, голой и скрытой пары, крыло, slicing and dicing и методы предположений различного уровня.
Методы составления судоку начинаются с составления правильного латинского
квадрата. Дальнейшее составление идёт либо постепенным вычёркиванием чисел и
проверкой на возможность решения, с оценкой сложности по количеству итераций и
применяемому методы, либо открытием определённого числа закрытых клеток. Причём
как в первом, так и во втором случае вообще говоря судоку может получиться
недетерменированным (то есть допускающим несколько вариантов решения для одних
и тех же исходных данных).
Исходный вид разработанной программы при решении судоку такой:
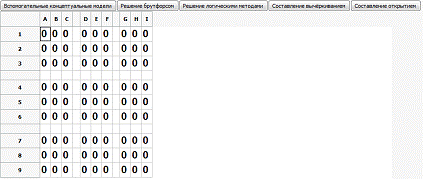
Рис.9. Вид окна программы в режиме решения судоку
Решение судоку
Сначала рассмотрим решение при помощи вспомогательных концептуальных
моделей. При нажатии на эту кнопку вызывается окно, в котором можно переключать
просмотр по столбцам, строкам или малым квадратам. Элементами вспомогательной
концептуальной модели являются непосредственно столбцы, строки или малые
квадраты.
Рассмотрим на примере простого судоку:

Рис.10.
Пример простого судоку
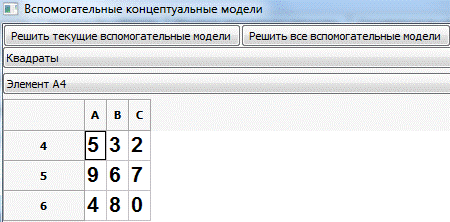
Рис.11. Одна из вспомогательных концептуальных моделей для простого
судоку
При нажатии на кнопку «Решить текущие вспомогательные модели» программа
выполнит решение для выделенной вспомогательной концептуальной модели, то есть
в нашем случае попытается разрешить все квадраты.
Разрешение вспомогательной модели возможно только в том случае, если в
данном конкретном элементе (в нашем случае это квадрат с левым верхним углом A4) отсутствует только одна цифра. В
данном случае это верно, поэтому после нажатия данной кнопки мы получим
результат:

Рис.12. Решение всех возможных концептуальных моделей для малых квадратов
В случае нажатия на кнопку «Разрешить все вспомогательные модели»
программа в бесконечном цикле будет проходить по всем возможным вспомогательным
моделям до тех пор, пока они имеют решение. Принципиально это выглядит
следующим образом:

Рис.13. Принципиальная схема разрешения вспомогательных концептуальных
моделей
Метод полного перебора действует следующим образом:
. Ведётся поиск первого вхождения 0 (то есть пустой клетки)
. Если вхождений нет, значит мы получили решение
. Определяются цифры, которые могут входить в данную клетку (с
учётом столбца, строки и малого квадрата). Определение осуществляется функцией:
c = [s[j] for j in range(81)not ((i-j)%9 * (i//9^j//9) *
(i//27^j//27 | (i%9//3^j%9//3)))]
1. (i-j)%9 - вхождение в столбец
. (i//9^j//9) - вхождение в строку
. (i//27^j//27 | (i%9//3^j%9//3))
- блок из трёх строк
. В случае вхождения получается 0
. Для всех чисел, которые могут стоять в данной строке рекурсивно
вызывается функция перебора, где на месте пустой клетке стоит некоторое число
. Если нет чисел, которые мы можем вставить в данную клетку,
значит метод зашёл в тупик и следует выход из рекурсии на шаг выше.
Несмотря
на то, что существует порядка 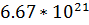
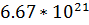 финальных
вариантов судоку (то есть всех возможных расположений), метод брутфорса может
быть полезен для решения задачи судоку на компьютере. Действительно, для
указанного простого судоку подобный метод перебора получил решения за 0.0163с.
финальных
вариантов судоку (то есть всех возможных расположений), метод брутфорса может
быть полезен для решения задачи судоку на компьютере. Действительно, для
указанного простого судоку подобный метод перебора получил решения за 0.0163с.
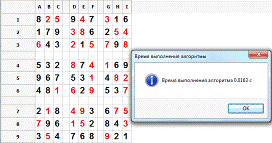
Рис.14. Пример работы алгоритма полного перебора для решения простого
судоку
Но существуют задачи, которые алгоритм полного перебора будет решать
очень долго. Возьмём для примера судоку под названием «Star Burst Leo»

Рис.9. Вид окна программы в
режиме решения судоку
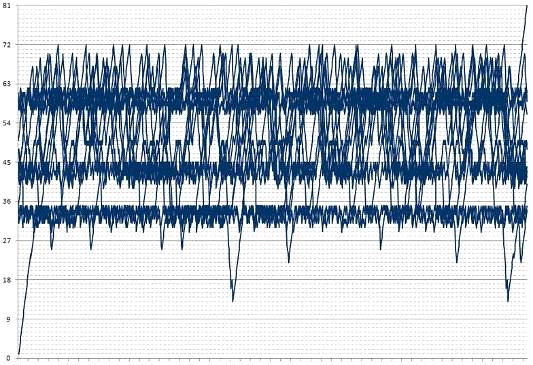
Рис.16. Распределение позиций
при решении судоку
Было оценено, что для решения данного судоку потребуется 641 580 331
итерация, причём в данном случае в итерации не входит процесс поиска цифр,
которые можно внести в данную клетку.
На рисунке 16 показано распределение числа заполненных клеток (ось
ординат) от уровня рекурсии (ось абсцисс). Таким образом можно оценить, что
процесс перебора доходит до 72 заполненных клеток, а затем встречает
несоответствие и ему приходится возвращаться, причём мы видим чёткие полосы в
районе 33, 43 и 60 заполненных клеток.
Логические методы решения
Очевидно, что предложенный выше метод хорош для компьютерного
моделирования. Но очевидно, что человек на практике никогда не будет
пользоваться таким методом. Для этого существуют другие методы.
Обычно решение судоку начинают с расставления чисел, которые могут стоять
в данной клетке. Первая часть метода аналогична методу полного перебора, но в
отличие от него, сначала мы просто оцениваем элементы, которые могут стоять в
клетках, а затем минимизируем количество вариантов. Пример подобного анализа
представлен на рисунке ниже:
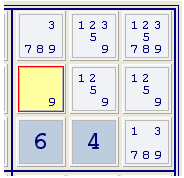
Рис.17. Пример анализа клеток
на предмет подбора кандидатов
Все методы рассматриваются в статье [2], но здесь я опишу несколько из
них.
Первый метод - Х-крыло.
«X-крыло» - позиция, когда один из кандидатов дважды (и только дважды)
встречается в двух строчках головоломки. Эти кандидаты должны входить в две
колонки, что обеспечивает формирование прямоугольного Х-крыла. Также две
колонки с двумя (и только с двумя) клетками, которые содержат одинаковых
кандидатов (входящие в две строки) также формируют X-крыло. Эти четыре клетки -
единственные возможные места расположения для «настоящих» кандидатов в этих
строках или колонках. Другие подобные кандидаты, расположенные по периметру
прямоугольника, образованного «настоящими» кандидатами, должны быть удалены.
Возможно эта комбинация была названа X-крылом потому, что
Рассмотрим пример решения Х-крыла (рисунок вверху). Как видим, для
легкости восприятия из кандидатов отображены только шестерки (был применен
фильтр кандидатов - программа Simple Sudoku это умеет делать).
Синие и ярко-зеленые ячейки формируют классическое «X-крыло» - первая и
девятая строчки имеют только по две ячейки с кандидатом 6, их разделяют две
колонки (седьмая и восьмая), кандидаты образуют прямоугольник. «Настоящих»
кандидатов представляют синие, или ярко-зеленые ячейки. Потому другие кандидаты
в шестой и девятой колонках нужно удалить (они выделены желтым контуром).

Рис.18. Использование метода
Х-крыло
Slicind and dacing
Рассмотрим метод slicing and dacing на примере:
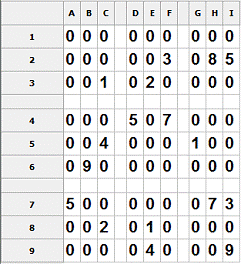
Рис.19. Пример судоку для
алгоритма slicing and dicing
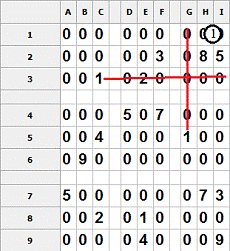
Рис.20.
Первый шаг алгоритма
На первом шаге рассматриваются пересечения столбца и строки для цифры 1 в
рамках квадрата G1-I3. Получается, что 1 может стоять
либо на позиции H1 либо на позиции
I1.

Рис.21. Второй шаг алгоритма
На основе полученного результата на первом шаге просматривается
полученная строка. В квадрате D1-F3 с учётом стоящей на позиции E8 единицы и полученной на первом шаге
строки остаётся только одна позиция - D2. Таким образом, после работы алгоритма получаем судоку:
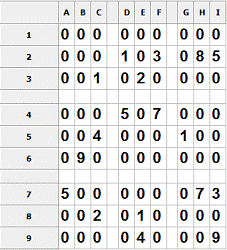
Рис.22. Результат работы алгоритма
Аналогичным образом можно получить единицы во всех остальных малых
клетках.
Метод предположений похож на метод полного перебора. Но применяется он
после применения вышеуказанных методов. Рассмотри на примере:
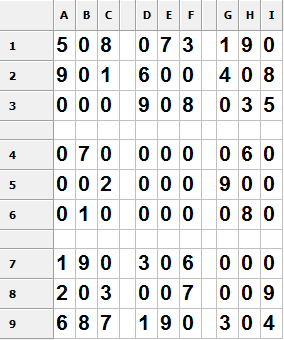
Рис.9. Вид окна программы в
режиме решения судоку
При решении стандартными логическими методами (скрытые пары, скрытые
квадраты и т. п.) решение не найдено:
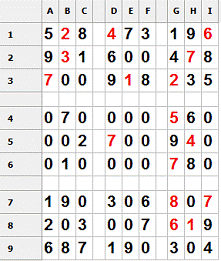
Рис.24. Судоку после
выполнения первых логических методов
Но мы видим, что в клетках B3 и C3 может стоять только пара 46.
Алгоритм делает предположение, что стоит в B3 стоит 4, доходит до несоответствия, ставит 6 и получает
результат:
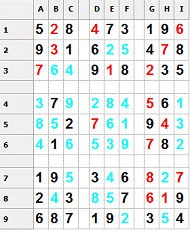
Рис.24. Судоку после выполнения предположений
Таким образом исходное судоку разрешено.
Блок-схема алгоритма выглядит следующим образом:

Рис.25. Блок-схема работы
алгоритма
Составление судоку
Составление судоку может осуществляться двумя методами - либо сокрытием
случайной ячейки после составления правильного латинского квадрата, либо
наоборот открытием случайных ячеек. В первом случае после каждого шага
выполняется решение и проверяется количество итераций и их сложность
(применение методов первичных, slicing and dicing, предположений).
Составление открытием

Рис.25. Блок-схема работы алгоритма составления
открытыием
Но несмотря на то, что цифры из доски выполняется в порядке, обратном
заполнению, всё равно возможно получение недетерменированного судоку и данную
проблему разрешить невозможно.
Решение вычёркиванием
Решение вычёркиванием состоит в получении правильного латинского квадрата.
Затем в полученном латинском квадрате рекурсивно осуществляются перестановки
строк, столбцов и малых квадратов в соответствие с требованиями. Затем
происходит вычёркивание случайного элемента и решение полученного судоку на
основе методов решения. Сложность алгоритма определяется количеством итераций,
которые необходимы для решения.
Переносимость
и интегрируемость
Так как программа написана на Python, программа является переносимой на любую платформу (Windows, Linux, MacOS).
В целях интегрируемости программа принимает параметры в командной строке.
Перечень параметров:
t, --type - [math | sudoku]
- тип шаблона, математические формулы по предметной области или судоку
a, --task - [solve | generate] - задание, решить или создать, для шаблона math по умолчанию - решить
m, --method - [[None] | [brute
| analytic] | [opening | cut]]
- метод, не применим для шаблона math,
принимает значения brute или analytic при задании solve или opening
или cut при задании generate
q, --template - шаблон для математических формул
i, --input - входной файл
o, --output - выходной файл
Литература
1. Нечаев
В.В. Концептуальное модельное представление задачи как системы. Информационные
технологии, № 2009.с.
2. http://www.angusj.com/sudoku/hints.php
Приложение
Программный
код
Решатель математических моделей
# -*- coding: cp1251 -*-mathcodecsresysstringgraphWindowcopy
solver():__init__(self, data, rules, goals,
**kwargs):._recursionLevel = 0.data =
(data.lower()).split("\n").rules =
(rules.lower()).split("\n").goals = (goals.lower()).split("\n").rawgoals
= self.goals.templateVars = kwargs.get('templateVars', {}).templateFull =
kwargs.get('templateFull', {}).sErrTxt = ''.sSolveTxt = ''.env = kwargs.get('env',
{}).__globals = {}.__locals = {}.fString = []
.parent = kwargs.get('parent', None)
.analyzeData().analyzeRules().analyzeGoals()
.makeSolveFor()
#for g in self.goals:
#self.makeSolveFor(g)
analyzeData(self):.definiedVariables = []q in self.data:=
q.split('=').definiedVariables.append(r[0].strip()).definiedVariablesFirst =
copy.copy(self.definiedVariables)
analyzeRules(self):self.rules.ruledVariablesLeft =
[].ruledVariablesRight = []= 0 q in self.rules:=
q.split('=').ruledVariablesLeft.append(r[0]):[1]IndexError:.solveErr =
31.solveErrExtend = { 'vString' : r}.solveErrorsText()= re.split('([A-Za-z]+)([0-9]*)',
r[1]).ruledVariablesRight.append([])splRulessId in range(len(splRules)-1):=
splRules[sId]= splRules[sId+1]re.match('^[A-Za-z]+$', sRule) and ('' ==
nsRule or re.match('^[0-9]+$', nsRule)):sRule+nsRule.ruledVariablesRight[l].append(str(sRule+nsRule))=
l + 1
'goalParts' : goalParts if goalParts[0] != '' else
goalParts[1:3]
})
makeSolveFor(self):'Solving'self.ruledVariablesLeftself.ruledVariablesRightself.goals.solveErr
= 0.solveErrExtend = {}.solution = 0.solutionString = 'крабе'
('import math', self.__globals, self.__locals)
cGoal in self.goals:cGoal['goalParts'][0] not in
self.templateVars['vars'].lower().split(','):.solveErr =
24.solveErrExtend = { 'vName' : cGoal['goalParts'][0], 'dVars' :
self.templateVars['vars']}
cGoal in self.goals:'definded: '+
''.join(self.definiedVariables)'goal:'+cGoal['goalLine']cGoal['goalLine'] in
self.definiedVariables:'Found'.solveErr = 14.solveErrExtend =
cGoal['goalLine'].solveErrorsText()self._recursionLevel == 0:iData in
self.data:iData.strip() == ''::(iData+';', self.__globals, self.__locals)
self.log("Ввод (exec) начальной информации:
%s"%(iData))
except NameError as err:'NameError %s' %(err).solveErr =
1.solveErrExtend = { 'vName' : err }:'Unknown exception
%s'%sys.exc_info()[0].solveErr = 3.solveErrExtend = {}
m in range(len(self.goals)):.log('Step %d:\n'%m)
iRule in self.rules:iRule.strip() == ''::
self.log('Применяем правило %s' %iRule)
exec(iRule+';', self.__globals, self.__locals)NameError as
err:'NameError %s' %(err).solveErr = 15.solveErrExtend = { 'vName' : err
}.solveErrorsText():'Unknown exception'.solveErr = 18.solveErrExtend =
{}.solveErrorsText()
= self.preFind()
#l = [0](l[0] not in (0, 2, 5, 13)):12 ==
l[0]:.solveErrorsText()self._recursionLevel < 2:._recursionLevel =
self._recursionLevel + 1.makeSolveFor():.solveErrorsText()2 ==
l[0]:.solveErrorsText()5 == l[0]::.solveErrorsText() (l[1]['ruleString'], self.__globals,
self.__locals).log(l[1]['varName']).log("%s = %2.8lf"
%(l[1]['varName'], eval(l[1]['varName'], self.__globals,
self.__locals)))NameError as s:'NameError in right solving %s' %s.solveErr =
21.solveErrExtend = l[1].solveErrorsText()
(key, val) in self.templateFull.iteritems():(key ==
self.goals[m]['goalParts'][0]):'Found %s'%key:-1 !=
self.goals[m]['goalParts'][1]:
# заменяем шаблон= val.lower()ctr in self.templateVars['vars'].lower().split(','):=
string.replace(lf, ctr, ctr+str(self.goals[m]['goalParts'][1]))IndexError as
s:'IndexError %s'%s= val.lower().log('Применение шаблона %s = %s для переменной %s (%s = %s)' % (key, val, self.goals[m]['goalLine'],
self.goals[m]['goalLine'], lf)):("%s=%s"%(self.goals[m]['goalLine'],
lf), self.__globals, self.__locals).fString.append((self.goals[m]['goalLine'],
lf)).log(self.goals[m]['goalLine'])= eval(self.goals[m]['goalLine'],
self.__globals, self.__locals).log("%s = %2.8lf"
%(self.goals[m]['goalLine'], r)).data.append(r).definiedVariables.append(self.goals[m]['goalLine'])
.checkEnv(self.goals[m]['goalLine'], r)
NameError as err:.solveErr = 36 .solveErrExtend = { 'line' :
"%s=%s"%(self.goals[m]['goalLine'], lf), 'err' : err}:.solveErr =
37.solveErrExtend = { 'line' : "%s=%s"%(self.goals[m]['goalLine'],
lf), 'err' : sys.exc_info()[0]}
# if (key == self.goals[m]['goalLine']):
preFind(self):'Analyzing'self.goals,
self._recursionLevelsGoal in self.goals:= sGoal['goalLine']sRule in
self.ruledVariablesRight:goalLine in sRule:.solveErr = 2.solveErrExtend =
{'vName' : goalLine}(2, {})goalLine in self.ruledVariablesLeft:.solveErr = 5=
self.retRuleStringByVal(goalLine).solveErrExtend = { 'vName' : goalLine,
'ruleString' : rS } (5, {'ruleString' : rS, 'varName' : goalLine})= 0sRule in
self.ruledVariablesRight:l in sRule:l in self.definiedVariables:= 1l in
self.ruledVariablesLeft:= 2
1 == err: (0, {})2 == err:.solveErr = 13(0, {}): =
self.analyzeGoalsNeeded()qq == '':(0, {}):.solveErr = 12=
self.analyzeGoalsNeeded().solveErrExtend = { 'vName' : line }
#self.goals = ('%s'
%(line)).split('\'')[1]+"\n".join(self.rawgoals).goals =
[].goals.append(('%s' %(line)).split('\'')[1])i in
self.rawgoals:.goals.append(i).log('Поиск \'%s\''%('%s' %(line)).split('\'')[1])'Поиск \'%s\''%('%s'
%(line)).split('\'')[1].analyzeGoals() (12, {})
analyzeGoalsNeeded(self):goalLine in self.goals:=
goalLine['goalLine']= goalLine['goalParts'](key, val) in
self.templateFull.iteritems():key == gP[0]::-1 != gP[1]:
# заменяем шаблон= val.lower()ctr in self.templateVars['vars'].lower().split(','):=
string.replace(lf, ctr, ctr+str(self.goals[m]['goalParts'][1]))IndexError as
s:'IndexError %s'%s= val.lower():lf(lf, self.__globals, self.__locals)NameError
as err:err''
simpleCheckEnv(self, varName, envVar, envParts,
envElem)::[1]:envVar == varName:= eval(envElem, self.__globals,
self.__locals)l:'TRUE':
self.log('Переменная %s не удовлетворяет параметрам
внешней среды (%s)'%(varName, envElem))
print 'FALSE'
checkEnv(self, varName, res):'Checking %s by %lf'%(varName,
res)self.env(envKey, envElem) in self.env.iteritems():= envElem.split('>=')=
envParts[0].lower().strip().simpleCheckEnv(varName, envVar, envParts, envElem)=
envElem.split('<=')= envParts[0].lower().strip().simpleCheckEnv(varName,
envVar, envParts, envElem)= envElem.split('>')= envParts[0].lower().strip().simpleCheckEnv(varName,
envVar, envParts, envElem)= envElem.split('<')=
envParts[0].lower().strip().simpleCheckEnv(varName, envVar, envParts, envElem)
retRuleStringByVal(self, val):i in self.rules:val == i.split('=')[0].strip():i
retSolving(self, **kwargs):= { 'err' : self.solveErr,
'errTxt' : self.sSolveTxt,
'sol' : self.solution,
'solStr' : self.sSolveTxt
}ret
solveErrorsText(self):.log({
: lambda q: 'ОК',
1 : lambda q: "Переменная %s используется, но не
задана" %(q['vName']),
: lambda q: "Переменная %s задана для поиска
и в то же время используется в правиле. Возможна
рекурсия"%(q),
: lambda q: 'Неизвестная ошибка при задании начальных
условий',
: lambda q: "Переменная %s прямо вычисляется по
правилу %s"%(q['vName'], q['ruleString']),
: lambda q: "Не задана переменная %s"
%(q['vName']),
: lambda q: 'Какая-то из переменных правой
части правил не может быть найдена в условиях
и/или других правилах, ожидается %s'%(q['vName']),
: lambda q: 'Переменная правой части условий найдена
в задании левой. Может вызвать ошибку',
: lambda q: 'Избыточные данные: переменная %s задана
и требуется найти'%(q),
: lambda q: "Попытка использовать незаданную переменную
%s в правилах" %(q['vName']),
: lambda q: 'Неизвестная ошибка при задании правил',
: lambda q: 'Ошибка прямого подсчёта, строка %s, переменная %s:
'%(q['ruleString'], q['varName']),
: lambda q:
"Переменная %s не найдена среди возможных (%s)" %(q['vName'],
q['dVars']),
: lambda q: 'Не заданы правило: строка должна быть формата A=(B) (дано:
%s'%(''.join(q['vString'])),
: lambda q: 'Ошибка обработки строки %s: %s'%(q['line'], q['str'])
}[self.solveErr](self.solveErrExtend), True)
log(self, txt, error=False, onlyError=False):error:.sErrTxt =
self.sErrTxt + "\n" + txtnot onlyError:.sSolveTxt = self.sSolveTxt +
"\n" + txt
graph(self,
event):self.definiedVariablesself.definiedVariablesFirst.graphWindow(self.parent,
globals=self.__globals,
locals=self.__locals,=self.definiedVariablesFirst,=self.data,=self.fString)
Решатель судоку методом полного перебора
def solve(s)::= s.index(0)ValueError:
# No empty cell left: solution founds
= [s[j] for j in range(81)not ((i-j)%9 * (i//9^j//9) *
(i//27^j//27 | (i%9//3^j%9//3)))]
v in range(1, 10):v not in c:= solve(s[:i]+[v]+s[i+1:])r is
not None:r
Sudoku(list):
'''Sudokus with nicer IO'''__init__(self,
content):.__init__(self, [int(i) for i in content.split()] isinstance(content,
str) else content)__str__(self):'\n'.join(
' '.join([(str(j) if j != 0 else '-') j in
self[i*9:(i+1)*9]]) for i in range(9))
Решатель судоку аналитическими методами
TRIPLETS = [[0,1,2],[3,4,5],[6,7,8]]
#Row/Col/3x3 iteration list, each is nine lists of
nine (row,col) pairs_ITER = [[(row,col) for col in range(0,9)] for row
in range(0,9)]_ITER = [[(row,col) for row in range(0,9)] for col in
range(0,9)]_ITER = [[(row,col) for row in rows for col in cols] for rows in
TRIPLETS for cols in TRIPLETS]
sudoku:__init__(self, start_grid=None) :
#Setup list of lists (the rows), each row is a list of 9
cells, which are each a list of integers 1-9 inclusive..squares =[ [range(1,10)
for col in range(0,9)] for row in range(0,9)]
start_grid is not None:len(start_grid)==81 :row in range(0,9)
:.set_row(row, start_grid[(row*9):((row+1)*9)]):len(start_grid)==9, "Bad
input!"row in range(0,9) :.set_row(row, start_grid[row])
#self.check()._changed=False
solved(self) :row in range(0,9) :col in range(0,9)
:len(self.squares[row][col]) > 1 :FalseTrue
copy(self) :_copy = sudoku(None)row in range(0,9) :col in
range(0,9) :_copy.squares[row][col] = self.squares[row][col][:]
#copy!_copy._changed=Falsesudoku_copy
#self.set_cell(row,col,x).set_cell(row,col,x)
set_cell(self,row,col,x):self.squares[row][col] == [x] :
#Already done!x not in range(1,9+1) :
#Set to unknown:x in self.squares[row][col], \
"Told to set square (%i,%i) to an impossible entry,
%i" % (row,col,x)
.squares[row][col] = [x].update_neighbours(row,col,x)._changed=True
cell_exclude(self, row,col,x) :x in range(1,9+1)x in
self.squares[row][col] :
#Remove it....squares[row][col].remove(x)
#Should be one or more entries
left...len(self.squares[row][col]) > 0, \
"Removed last possible entry for square (%i,%i) which
was %i" \
% (row, col, x)
#Now, has this confirmed the value for this
square?len(self.squares[row][col]) == 1 :
#This cell is now definate..
#Need to update its friends...
#print "After exluding %i, square (%i,%i) must be
%i" \
#% (x, self.row, self.col,
self[0])._changed=True.update_neighbours(row,col,self.squares[row][col][0]):
#Don't need to remove this, already done!
row_exclude(self, row, x) :x in range(1,9+1)col in range(0,9)
:.cell_exclude(row,col,x)
col_exclude(self, col, x) :x in range(1,9+1)row in range(0,9)
:.cell_exclude(row,col,x)
update_neighbours(self,set_row,set_col,x) :
"""Call this when the square is set to x,
either directly,as a side effect of an exclude leaving only one
entry"""
#print "Updating (%i,%i) to be %i..." % (self.row,
self.col, x)
#Update the possibilies in this row...row in
range(0,9) :row <> set_row :.cell_exclude(row,set_col,x)
#Update the possibilies in this col...col in
range(0,9) :col <> set_col :.cell_exclude(set_row,col,x)
#Update the possibilies in this 3x3 square...triplet
in TRIPLETS :set_row in triplet : rows = triplet[:]set_col in triplet : cols =
triplet[:]
#Only need to do four of the eight possibles (well, 9 if you
count the cell itself)
#as did two on the row, and two on the col.remove(set_row).remove(set_col)row
in rows :col in cols :row <> set_row or col <> set_col
#print "Updating (%i,%i) to be %i, excluding %i from
(%i, %i)" \
#% (self.row, self.col, x, x, row, col).cell_exclude(row,col,x)
get_cell_int(self,row,col) :len(self.squares[row][col])==1
:int(self.squares[row][col][0]):0
get_cell_str(self,row,col) :len(self.squares[row][col])==1
:"(%i,%i) = %i" % (row, col,
self.squares[row][col][0]):("(%i,%i) = " % (row, col)) +
",".join([str(x) for x in self.squares[row][col]])
get_cell_digit_str(self,row,col)
:len(self.squares[row][col])==1 :str(self.squares[row][col][0]):"0"
as_test_81(self) :
"""Return a string of 81
digits""""".join(self.as_test_list())
simple_text(self) :"\n".join(self.as_test_list())
as_test_list(self) :[ ("".join(
[self.get_cell_digit_str(row,col) for col in range(0,9)])) for row in
range(0,9) ]
"""=[]row in range(0,9) :=""col
in range(0,9) := line + self.get_cell_digit_str(row,col).append(line)answer
"""
__repr__(self):="[" + ",".join([ \
("[" + ",".join(
[self.get_cell_digit_str(row,col) for col in range(0,9)]) + "]") \row
in range(0,9) ])answer
__str__(self):= " 123 456 789\n"row in range(0,9)
:= answer + str(row+1) \
+ " [" +
"".join([self.get_cell_digit_str(row,col).replace("0","?")
for col in range(0,3)]) \
+ "] [" +
"".join([self.get_cell_digit_str(row,col).replace("0","?")
for col in range(3,6)]) \
+ "] [" +
"".join([self.get_cell_digit_str(row,col).replace("0","?")
for col in range(6,9)]) \
+ "]\n"row+1 in [3,6] : = answer + " --- ---
---\n"answer
retArr(self):= []row in range(0,9) :.append([])col in
range(0, 9):[row].append(self.get_cell_digit_str(row,col))data
check(self, level=0) :._changed=Trueself._changed:
#print
"checking..."._changed=False.check_for_single_occurances().check_for_last_in_row_col_3x3()level
>= 1 :.overlapping_3x3_and_row_or_col() #(aka slicing and
dicing)level >= 2 :.one_level_supposition()level >= 3
:.two_level_supposition()
#If nothing happened, then self.changed==False (still)
#and we break the loop
check_for_single_occurances(self):
#Want to see if x only occurs once in this row/col/3x3...check_type
in [ROW_ITER, COL_ITER, TxT_ITER]:check_list in check_type :x in range(1,9+1) :
#1 to 9 inclusive_in_list = [](row,col) in check_list :x in self.squares[row][col]
:_in_list.append((row,col))len(x_in_list)==1 :
(row,col) = x_in_list[0]
#This position MUST be be xlen(self.squares[row][col]) > 1
:.set_cell(row,col,x)
check_for_last_in_row_col_3x3(self):
#Now, for each row/col/3x3 want to see if there is a
single
#unknown entry...(type_name, check_type) in
[("Row",ROW_ITER),("Col",COL_ITER),("3x3",TxT_ITER)]:check_list
in check_type :_entries = []_values = range(1,9+1) #1-9 inclusive_values =
[](row,col) in check_list :len(self.squares[row][col]) == 1 :self.squares[row][col][0]
not in known_values, \
"Already have %i (%i,%i) in known list [%s] for %s"
% (self.squares[row][col][0],row,col,
",".join(map(str,known_values)), type_name)
_values.append(self.squares[row][col][0])
self.squares[row][col][0] in unassigned_values, \
"Expected %i (%i,%i) in list [%s] for %s" %
(self.squares[row][col][0],row,col,
",".join(map(str,unassigned_values)), type_name)
_values.remove(self.squares[row][col][0]):_entries.append((row,col))len(unknown_entries)
+ len(known_values) == 9len(unknown_entries) ==
len(unassigned_values)len(unknown_entries) == 1 :
#This cell must be the only number 1-9 not in known_values=
unassigned_values[0]
(row,col) = unknown_entries[0]
#assert x not in known_values
#print "Because its the last cell in its row/col/3x3
entry (%i,%i) must be %i" \
#% (row,col,x).set_cell(row,col,x)
"""row in range(0,9) : self.check_row(row)col
in range(0,9) : self.check_col(col)
#Check the 3x3 squares...rows in TRIPLETS :cols in
TRIPLETS :x in range(0,9) :_in_location=[]row in rows:col in cols
:x in self.squares[row][col] :_in_location.append((row,col))len(x_in_location)==1
:
(row,col) = x_in_location[0]
"""
diagnosis(self) :=""= long(1)row in range(0,9) :col
in range(0,9):len(self.squares[row][col]) > 1 := answer +
str(self.squares[row][col]) + "\n"= df * len(self.squares[row][col])=
answer + "Degrees of freedom: %i" % dfanswer
overlapping_3x3_and_row_or_col(self):
"""Block and Column / Row Interactions (name
from Simon Armstrong)
://www.simes.clara.co.uk/programs/sudokutechnique3.htm
known as 'slicing and dicing'
"""
#For a given 3x3, and a given digit, want to see if
#all the remaining candidates are in a single row or column..
#Want to see if x only occurs once in this row/col/3x3...check_list
in TxT_ITER :x in range(1,9+1) : #1 to 9 inclusive
#print "Checking %i in 3x3" % x, check_list_for_x =
[]_for_x = [](row,col) in check_list :x in self.squares[row][col] :
#print "Found possible %i at (%i,%i)" % (x, row, col)row
not in rows_for_x : rows_for_x.append(row)col not in cols_for_x :
cols_for_x.append(col)
#Are they all in the same row?len(rows_for_x)==1 and
len(cols_for_x) > 1 :
#print "%i must be in row %i using cols %s"
% (x, rows_for_x[0]+1, ",".join(map(lambda i : str(i+1),cols_for_x)))
#print self
#This means, we can remove X from all the rest of the row...=
rows_for_x[0]col in range(0,9) :col not in cols_for_x :.cell_exclude(row,col,x)
#We can also remove x from all the rest of this
3x3...(row,col) in check_list :col not in cols_for_x :row not in rows_for_x
:.cell_exclude(row,col,x)
#Are they all in the same col?len(cols_for_x)==1 and
len(rows_for_x) > 1 :
#print "%i must be in col %i using rows %s"
% (x, cols_for_x[0]+1, ",".join(map(lambda i : str(i+1),rows_for_x)))
#print self
#This means, we can remove X from all the rest of the row...=
cols_for_x[0]row in range(0,9) :row not in rows_for_x :.cell_exclude(row,col,x)
#We can also remove x from all the rest of this
3x3...(row,col) in check_list :col not in cols_for_x :row not in rows_for_x
:.cell_exclude(row,col,x)
one_level_supposition(self):
"""Probably what is known as 'Nishio',
try a number and see if it leads to a dead end.
all the ambigous squares, try each possible each entry
and seeits OK, or if it leads to a contradiction. In the case of a
contradictioncan remove it as a possibility...
level suppositions (two guess) may be required for extreme
puzzles..."""=Trueprogress :=False
#print "Doing one level supposition..."row in
range(0,9) :col in range(0,9):len(self.squares[row][col]) > 1 :_x = []x in
self.squares[row][col] :
#print "/-- Trying setting (%i,%i) to %i" % (row,col,x)_copy
= self.copy():_copy.set_cell(row,col,x)_copy.check(level=1)AssertionError, e :
#Leads to an error :)
#This means that this square cannot be x
#print e
#print "%s cannot be %i" % (str(self.squares[row][col]),
x)_x.append(x)sudoku_copy
#print "\-- End of exp"len(bad_x) == 0 :len(bad_x)
< len(self.squares[row][col]) :x in bad_x :.cell_exclude(row,col,x).check()
=True:False, "Bugger! All possible values for square (%i,%i) fail" \
% (row,col)
#print "One level supposition done"
two_level_supposition(self) :=Trueprogress :=False
#print "Doing two level supposition..."row in
range(0,9) :col in range(0,9):len(self.squares[row][col]) > 1 :_x = []x in
self.squares[row][col] :
#print "/-- Trying setting (%i,%i) to %i" % (row,col,x)_copy
= self.copy():_copy.set_cell(row,col,x)
#sudoku_copy.check()
#sudoku_copy.one_level_supposition()_copy.check(level=2)AssertionError,
e :_x.append(x)sudoku_copy
#print "\-- End of exp"len(bad_x) == 0
:len(bad_x) < len(self.squares[row][col]) :x in bad_x
:.cell_exclude(row,col,x).check() =True:False, "Bugger! All possible
values for square (%i,%i) fail" \
% (row,col)
Генератор судоку методом открытий
# sudoku.py
# Robert Wohleb
# 20051115
random
board:= []= []
generate(self, numFilled=(9*9)):= []= []
.seed()
# setup board= [0,0,0,0,0,0,0,0,0]i in range(0, 9):.boardlist.append(row[:])
j in range(0, 9):i in range(0, 9):.append((i,j))
.search(slots, 0)
len(slots) > 0:= random.randint(0,
len(slots)-1).append(slots[i])slots[i]
# setup boardi in range(0,
9):.partialboardlist.append(row[:])
i in range(0, numFilled):=
fillOrder[i].partialboardlist[j[0]][j[1]] = self.boardlist[j[0]][j[1]]
search(self, slots, index):= []= []
len(slots) == index:self.check()
i in range(1, 10):.append(i)
len(nums) > 0:= random.randint(0,
len(nums)-1).append(nums[i])nums[i]
i in fillOrder:= slots[index][0]=
slots[index][1].boardlist[x][y] = i
#print
#print x, y, i
#self.printBoard()(self.check()):self.search(slots,
index+1):True.boardlist[x][y] = 0False
check(self):i in range(0, 9):(not self.checkRow(i)) or (not
self.checkCol(i)) or (not self.checkSquare(i)):FalseTrue
checkRow(self, row):= []i in range(0, 9):not
self.boardlist[i][row] == 0:self.boardlist[i][row] in found:
#print 'checkRow', i, row,
self.boardlist[i][row]False.append(self.boardlist[i][row])True
checkCol(self, col):= []j in range(0, 9):not
self.boardlist[col][j] == 0:self.boardlist[col][j] in found:
#print 'checkCol', j, col, self.boardlist[col][j]False.append(self.boardlist[col][j])True
checkSquare(self, square):= []= (3*(square % 3))= int(square
/ 3) * 3
#print 'checkSquare -- ', i, j, self.boardlist[xoffset+i][yoffset+j]False.append(self.boardlist[xoffset+i][yoffset+j])True
getList(self): # setup board= [0,0,0,0,0,0,0,0,0]i in
range(0, 9):.boardlist.append(row[:])self.boardlist
printBoard(self):j in range(0, 9):i in range(0,
9):self.boardlist[i][j] == 0:'.',:self.boardlist[i][j],
printPartialBoard(self):j in range(0, 9):i in range(0,
9):self.partialboardlist[i][j] == 0:'.',:self.partialboardlist[i][j],
getBoard(self):= []j in range(0, 9):.append([])i in range(0,
9):[j].append(self.boardlist[i][j])data
getPartialBoard(self):= []j in range(0, 9):.append([])i in
range(0, 9):[j].append(self.partialboardlist[i][j])data