Программа для решения системы обыкновенных дифференциальных уравнений

Программа для решения системы обыкновенных дифференциальных уравнений

Министерство образования и науки РФ

Федеральное бюджетное государственное образовательное учреждение

высшего профессионального образования

«Тульский государственный университет»

Институт высокоточных систем им. В.П. Грязева

Факультет «Системы автоматического управления»

Кафедра «Системы автоматического управления»

Реферат по дисциплине

" Программирование и основы алгоритмизации"

Разработал студент гр.130101

Алясов А. А.

Консультировал: Илюхин А. С.

Тула 2011 г.

Содержание

Задание на курсовую работу

Система, приведенная к виду Коши

Исходные данные

Описание метода

Описание алгоритма

Описание исходных данных программы

Текст программы. Текст файла с исходными данными

Результат работы программы

График зависимости x(t)

Список использованной литературы

Задание на курсовую работу

На основе базовой программы для решения системы обыкновенных дифференциальных уравнений разработать программу для решения системы уравнений:

=

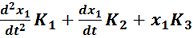
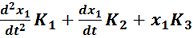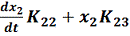
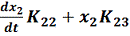=F

Разработать программу в системе программирования Паскаль АВС, выполняющую следующие действия.

.        Чтение исходных данных из внешнего файла.

.        Вывод исходных данных и результатов на дисплей и во внешний файл.

Программа должна состоять из главной программы, Главная программа должна выполнять обращение к процедурам вычисления функций «правых частей» и процедуры, реализующей метод Ейлера.

Система, приведенная к виду Коши

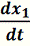
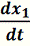=x₃

=

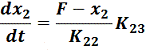
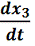
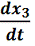Исходные данные

Начальные условия - нулевые.

K₁ =K₂=K₃=K₂₂=K₂₃=F=1.0

t_k=5.

Описание метода

Уравнения, содержащие производные от функции, возникают при решении многих научно-технических задач, причем существует большое разнообразие классов подобных уравнений. Для решения некоторых из них могут быть использованы аналитические методы, рассматриваемые в курсах математики, однако в большинстве случаев приходится применять численные методы.

Сначала рассмотрим один из простейших классов дифференциальных уравнений, на примере которого будут показаны особенности использования численных методов.

Пусть задано дифференциальное уравнение первого порядка с начальным условием (задача Коши)

dy/dx=F(x,y),(1)

У(х₀) = Уо(2)

где F(x,y) - заданная функция двух переменных х и у, х₀, у₀ - известные числа. Требуется определить функцию у→у(х) при x→х₀. Уравнение (1) можно рассматривать как задание кривой через ее производную в координатной плоскости x, у, поскольку известно как вычислить производную в каждой точке этой кривой через ее координаты. В общем случае уравнению (1) удовлетворяет целое семейство кривых; начальное условие (2) позволяет выбрать из этого семейства одну определенную кривую, которая проходит через заданную точку х₀, y₀.

Для численного решения (1), (2) заменим область непрерывного изменения аргумента x дискретным множеством точек, т.е. введем сетку. Положим, что величина х изменяется от значения х=х₀ до значения х=Ь. Тогда, рассматривая равномерную сетку, получаем узловые точки x₀, x₁,... x_k,...b, находящиеся на расстоянии h друг от друга, т.е.

x_k+1-x_k=h, k=0,1...,(3)

где h - шаг сетки. Соответствующие значения функции будем обозначать y_k, т.е.

y_k=y*(x_k)

Здесь у* (х) - функция, которая является приближенным решением (1), (2). Для получения численного решения, дифференциальное уравнение (1) заменяется уравнениями относительно значений функций у*(х) в узловых точках. Эти уравнения называются разностными. Простейшее разностное уравнение для (1) имеет вид

(y_k+1-y_k)/h=F(x_k, y_k) k=0,1,..., (4)

Уравнение (4) следует из (I), если производную dy/dx приближенно представить через значения функции у(х) в соседних узлах.

Соотношения (2. 12.4) можно записать в виде

y_k+1=y_k+h*F(x_k, y_k) (5)

Тогда, учитывая (2), с помощью формулы (5) можно последовательно определить значения y₁, y₂,..... Этот метод приближенного решения (1), (2) называется методом Эйлера. Геометрическая интерпретация этой схемы дана на. рис.1, где изображено поле интегральных кривых. Использование только первого члена формулы Тейлора означает движение не по интегральной кривой, а по касательной к ней. На каждом шаге мы заново находим касательную; следовательно, траектория движения будет ломаной линией. Из-за этого метод Эйлера иногда называют методом ломаных.

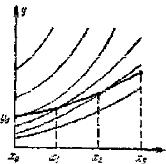Рис.1

Доказывается, что если шаг сетки h стремится к нулю, то приближенное решение, определяемое (5), стремится к точному решению (1), (2), т.е. имеется факт сходимости приближенного решения к точному при h→0. Однако в условиях реальных вычислений на компьютере при конечном шаге целесообразно знать насколько полученное приближенное решение близко к точному.

программирование паскаль файл язык

3. Описание исходных данных программы

Текст программы

program kursach;jm=3;mas=array[1..3]of real;k1,k2,k3,k22,k23,fs:real;,t,tk,h:real;,n:integer;,x0,x:mas;:text;:string;rp(t:real;var x0,f:mas);

{процедура вычисления правых частей}

begin[1]:= x[3];[2]:= (fs-k23*x[2])/k22;[3]:= (x[2]-x[3]*k2-x[1]*k3)/k1;;eu(var t,t0,h:real;var x0:mas;var x:mas);

{процедура, выполняющая действия по методу Ейлера}

var j:integer;(t,x0,f);j:=1 to 3 do[j]:=x0[j]+h*f[j];:=t0+h;

end;

begin

writeln('введите путь к файлу с исходными данными');

readln(l);(d,l);(d);(d,k1,k2,k3,k22,k23,fs);(d) ;

writeln('введите путь к файлу вывода');

readln(l);(d,l);(d);:=0.0; tk:=5.0;:=0.01;

{k1:=1.0; k2:=1.0; k3:=1.0; k22:=1.0; k23:=1.0; fs:=1.0; }:=0;[1]:=0.0; x0[2]:=0.0; x0[3]:=0.0;:=t0;('t=',t:2:2,'; x1=',x0[1]:5:6,'; x2=',x0[3]:5:6,'; x3=',x0[2]:5:6,';');(d,'t=',t:2:2,'; x1=',x0[1]:5:6,'; x2=',x0[3]:5:6,'; x3=',x0[2]:5:6,';');t<=tk do(t,t0,h,x0,x);:=n+1;n=10 then(d,'t=',t:2:2,'; x1=',x[1]:5:6,'; x2=',x[3]:5:6,'; x3=',x[2]:5:6,';');('t=',t:2:2,'; x1=',x[1]:5:6,'; x2=',x[3]:5:6,'; x3=',x[2]:5:6,';');:=0;;j:=1 to 3 do0[j]:=x[j];

t0:=t;

end;

close(d);

end.

Файл с исходными данными

Результат работы программы

График зависимости x(t)

Список использованной литературы

1. А.М. Епанешников, В.А. Епанешников. Программирование в среде TURBO PASCAL 7.0. - 3-е изд.,стер. - М.: «ДИАЛОГ-МИФИ», 2004 - 367с.

. Вирт Н. Алгоритмы и структуры данных с примерами на Паскале.- 2-е изд. - СПб. : Невский диалект, 2007 .- 352с.

. Марченко А.И. Программирование в среде Turbo Pascal 7.0 / А.И. Марченко,Л.А. Марченко .- 8-е изд. - Киев : Корона Принт, 2004 .- 464с.

. Фаронов, В.В. Turbo Pascal : учеб. пособие для вузов / В.В. Фаронов .- М.[и др.] : Питер, 2007 .- 367с

. Шафрин Ю. А. Информационные технологии: В 2 ч. - М.: Лаборатория Базовых Знаний, 2001.