Организация эксперимента в химической промышленности
1. АНАЛИЗ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
1.1 Оценка надежности аналитической методики
Таблица 1 - Исходные данные для оценки
аналитической методики
|
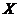 
|
|
|
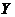 9,59,29,610,29,39,49,79,69,89,5 9,59,29,610,29,39,49,79,69,89,5
|
|
|
|
|
|
|
|
|
|
|
Определим среднее значение выходного параметра:
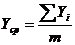 ,
,
где  - число параллельных определений;
- число параллельных определений;
 .
.
Определим выборочную дисперсию,
которая характеризует меру отклонения (рассеивания) результатов параллельных
определений от их среднего значения:
 ,
,
где 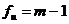 - число степеней свободы выборочной
дисперсии.
- число степеней свободы выборочной
дисперсии.
В данном случае
 ;
;

Определим среднюю квадратичную
погрешность отдельного или единичного результата:
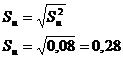
Проверим результаты на анормальность
(на наличие промахов).
Анормальный результат - это резко
отклоняющийся результат из серии параллельных определений, полученный в
результате грубой ошибки со стороны исследователя.
Обнаружение анормальных результатов
проводится двумя способами:
а) с помощью критерия промаха 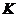 (грубый
способ):
(грубый
способ):

Вывод: анормальных результатов не
обнаружено, так как все результаты параллельных определений попадают в данный
интервал;
б) с помощью критерия
анормальности 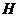 (самый
точный способ):
(самый
точный способ):
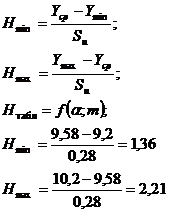
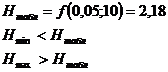
Вывод: поскольку расчетное значение
критерия анормальности для максимального результата превышает табличное, то
исключаем этот результат и расчет начинаем сначала:
Определим среднее значение выходного
параметра:
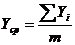 ,
,
где  - число параллельных определений;
- число параллельных определений;
 .
.
Определим выборочную дисперсию,
которая характеризует меру отклонения (рассеивания) результатов параллельных
определений от их среднего значения:
 ,
,
где 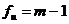 - число степеней свободы выборочной
дисперсии.
- число степеней свободы выборочной
дисперсии.
В данном случае
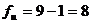 ;
;
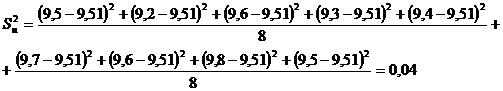
Определим среднюю квадратичную
погрешность отдельного или единичного результата:
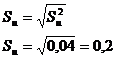
Проверим результаты на анормальность
(на наличие промахов).
Обнаружение анормальных результатов
проводится двумя способами:
а) с помощью критерия промаха 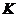 (грубый
способ):
(грубый
способ):
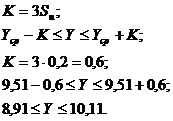
Вывод: анормальных результатов не
обнаружено, так как все результаты параллельных определений попадают в данный
интервал;
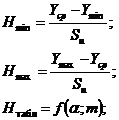
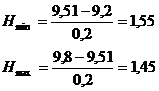

Вывод: так как оба расчетных
значения критерия анормальности (для минимального и максимального результатов)
не превышают табличного, то анормальных результатов среди параллельных
определений нет.
Определим среднюю квадратичную
погрешность среднего арифметического результата:
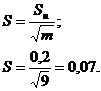
Определим табличное значение
критерия Стьюдента, которое представляет собой нормированную погрешность:
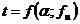 ,
,
где 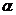 - уровень значимости, показывающий
допустимую долю (или процент) ошибок; в расчетах чаще всего принимают значение
- уровень значимости, показывающий
допустимую долю (или процент) ошибок; в расчетах чаще всего принимают значение  (или 5 %);
(или 5 %);
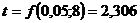 .
.
Определим абсолютную максимальную
погрешность опыта:
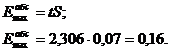
Определим относительную максимальную
погрешность опыта (в процентах):
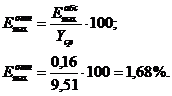
Главный вывод: так как относительная
максимальная погрешность опыта не превышает 5 %, то аналитическую методику
можно считать надежной, и она может быть использована для определения параметра
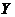 в
последующем эксперименте.
в
последующем эксперименте.
Установим доверительный интервал,
т.е. интервал, в котором находится истинное значение параметра 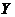 с
вероятностью
с
вероятностью 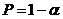 :
:
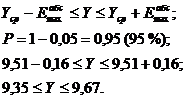
Установим стабильность параметра 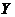 по
коэффициенту вариации (в процентах):
по
коэффициенту вариации (в процентах):

Вывод: так как коэффициент вариации
не превышает 5 %, то параметр 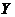 является стабильным, т.е. не
изменяется во времени.
является стабильным, т.е. не
изменяется во времени.
Установим необходимое число
параллельных определений для получения результатов с погрешностью, не
превышающей 5 %:

Вывод: в каждом опыте требуется
производить не менее трех параллельных определений.
1.2 Дисперсионный анализ результатов опытов
Таблица 2 - Исходные данные для дисперсионного
анализа результатов опытов
|
Опыт
|
|
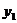   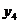 
|
|
|
|
|
|
1
|
11,5
|
10,3
|
11,7
|
11,0
|
10,5
|
|
2
|
16,8
|
16,0
|
15,2
|
16,3
|
15,7
|
|
3
|
20,3
|
19,4
|
21,0
|
19,8
|
20,7
|
Определим среднее значение параметра в каждом
опыте:
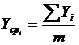 ,
,
где  - число параллельных определений в
- число параллельных определений в 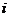 -ом опыте;
-ом опыте;

Определим выборочную (построчную)
дисперсию для каждого опыта - меру отклонений результатов параллельных
определений в каждом из опытов от соответствующей им величины:
 ,
,
где 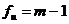 - число степеней свободы выборочной
дисперсии;
- число степеней свободы выборочной
дисперсии;
 ;
;
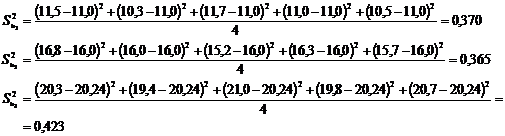
Проверим однородность дисперсий и
воспроизводимость опытов по критерию Кохрена:
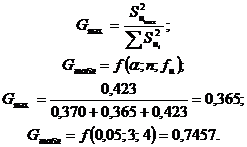
Вывод: 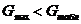 ,
следовательно, дисперсии однородны, а опыты воспроизводимы.
,
следовательно, дисперсии однородны, а опыты воспроизводимы.
Определим внутригрупповую дисперсию
- среднюю меру отклонения всей совокупности результатов параллельных
определений от соответствующих значений 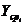 в каждом из опытов:
в каждом из опытов:
 ,
,
где 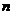 - число опытов;
- число опытов;
 .
.
Число степеней свободы
внутригрупповой дисперсии:
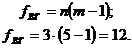
Определим среднее значение параметра
во всем эксперименте:

Определим межгрупповую дисперсию -
меру отклонения средних значений параметра в опытах от среднего значения этого
параметра во всем эксперименте:
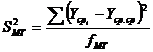 ;
;
где  - число степеней свободы
межгрупповой дисперсии,
- число степеней свободы
межгрупповой дисперсии, 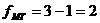 ;
;
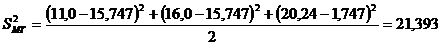 .
.
Определим критерий Фишера:
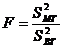 ;
;
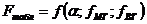 ;
;
где 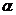 - уровень значимости;
- уровень значимости;
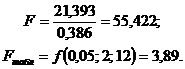
Главный вывод: так как 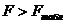 , то фактор
, то фактор 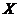 существенно
влияет на систему.
существенно
влияет на систему.
1.3 Аппроксимация результатов эксперимента
Таблица 3 - Исходные данные для аппроксимации
результатов эксперимента
|
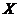 0,511,522,53 0,511,522,53
|
|
|
|
|
|
|
|
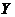 502515842 502515842
|
|
|
|
|
|
|
Результаты эксперимента описываются уравнением
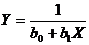 .
.
Построим график по опытным данным
(Рисунок 1):

Рисунок 1 - Зависимость 
Уравнение связи имеет вид 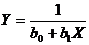 (по условию
задачи).
(по условию
задачи).
Определим коэффициенты данного
уравнения. Так как уравнение нелинейное, проведем его линеаризацию путем
нахождения обратной дроби:
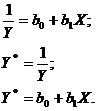
В результате получаем данные для
определения коэффициентов уравнения:
Таблица 4 - Данные для аппроксимации
после линеаризации уравнения
|
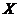 0,511,522,53 0,511,522,53
|
|
|
|
|
|
|
|
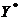 0,020,040,070,130,250,50 0,020,040,070,130,250,50
|
|
|
|
|
|
|
. Метод средних
Используем все пары значений 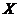 и
и 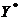 , составляем
систему уравнений:
, составляем
систему уравнений:

Полученную систему уравнений делим
на две части (с первого по третье и с четвертого по шестое уравнения,
соответственно), в каждой уравнения почленно складываем:
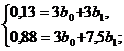
Получим уравнение
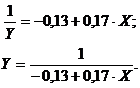
2. Графический метод
Строим график зависимости 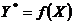 (Рисунок
2).
(Рисунок
2).
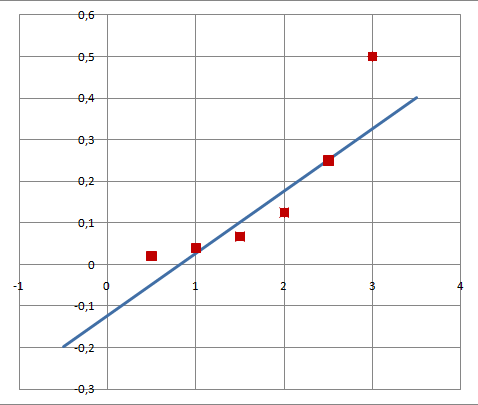
Рисунок 2 - Зависимость 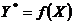
По графику определяем:
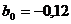 (отрезок, отсекаемый прямой по оси
ординат);
(отрезок, отсекаемый прямой по оси
ординат);
 .
.
Получаем уравнение
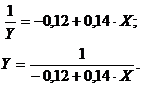 .
.
3. Метод избранных точек
Выберем вторую и пятую опытные
точки, соответствующие им пары значений 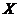 и
и 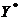 подставим в уравнение
подставим в уравнение 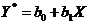 :
:

Получаем уравнение
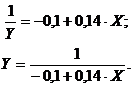 .
.
4. Метод наименьших квадратов
Расчетная система уравнений в данном случае
имеет вид:
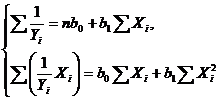
Или
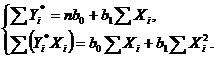
Найдем каждую сумму:
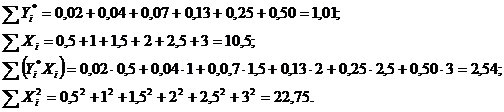
Полученные значения подставляем в
исходную систему и решаем ее:

Получаем уравнение
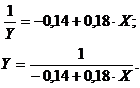 .
.
Оценим надежность уравнения,
полученного методом наименьших квадратов (самое точное уравнение).
1. Способ 1 не используем, так как в опытах
параллельные определения не проводились.
. Способ 2.
Определим среднее значение параметра в
эксперименте:
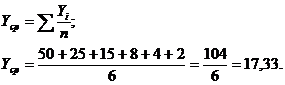
Определим дисперсию относительного
среднего:
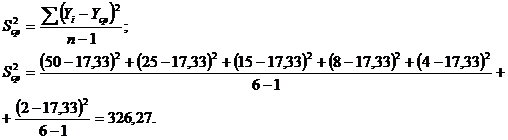
Число степеней свободы  .
.
Определим расчетное значение
параметра 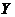 :
:
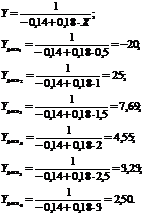
Определим остаточную дисперсию:

Число степеней свободы 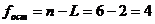 .
.
Определим значение критерия Фишера:
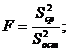

Так как 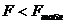 , то
уравнение
, то
уравнение 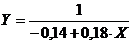 статистически
не значимо и не имеет смысла по сравнению со средней величиной выходного
параметра.
статистически
не значимо и не имеет смысла по сравнению со средней величиной выходного
параметра.
3. Способ 3.
Определим среднее значение параметра в
эксперименте:
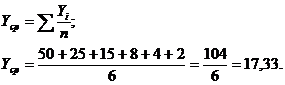
Определим  (числитель
дисперсии относительного среднего):
(числитель
дисперсии относительного среднего):
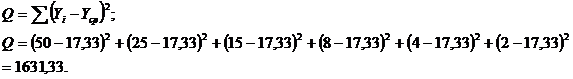
Определим расчетные значения
параметра 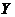 :
:

Определим 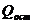 (числитель
остаточной дисперсии):
(числитель
остаточной дисперсии):
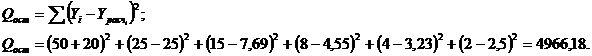
Определим 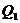 :
:
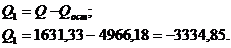
Определим значение критерия Фишера:

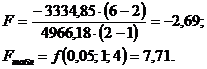
Так как 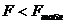 , то
уравнение
, то
уравнение 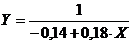 статистически
не значимо.
статистически
не значимо.
4. Способ 4.
Определим средние значения
параметров (с учетом замены переменной 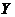 ):
):

Определим средние квадратические
отклонения параметров:
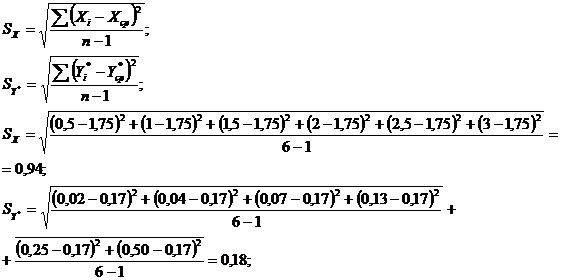
Определим выборочный коэффициент
корреляции:
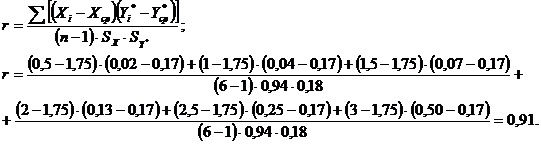
Так как  , необходимо
оценить значимость коэффициента корреляции по критерию Стьюдента:
, необходимо
оценить значимость коэффициента корреляции по критерию Стьюдента:
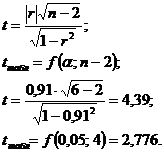
Так как 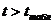 , то
коэффициент корреляции значим, следовательно, предполагаемая зависимость,
описываемая уравнением
, то
коэффициент корреляции значим, следовательно, предполагаемая зависимость,
описываемая уравнением 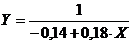 , между
переменными существует, причем при увеличении одного параметра второй
уменьшается и наоборот.
, между
переменными существует, причем при увеличении одного параметра второй
уменьшается и наоборот.
2.
ОПИСАНИЕ МНОГОФАКТОРНОЙ СИСТЕМЫ
Таблица 5 - Исходные данные для расчета
линейного уравнения связи
Подставляя данные в уравнение 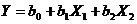 , получим
следующую систему:
, получим
следующую систему:
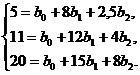
Решаем систему линейных уравнений
методом Крамера. Вычислим определитель матрицы системы:
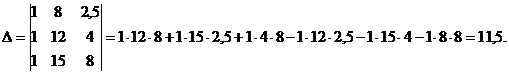
Вычисляем побочные определители:
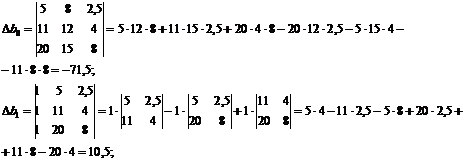
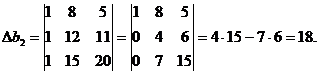
Определяем значения коэффициентов:

Линейное уравнение связи имеет вид
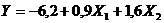 .
.
Данное уравнение справедливо для
области исследования факторов:
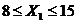 ,
, 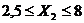 .
.
Построим линии равного отклика 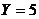 и
и  (Рисунок
3).
(Рисунок
3).
Расчет линий равного отклика:

Рисунок 3 - Линии равного отклика
.2 Расчет полного квадратного уравнения
Таблица 6 - Исходные данные для расчета полного
квадратного уравнения
|
 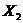 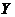
|
|
|
|
4,0
|
6
|
1,2
|
|
5,6
|
8
|
3,4
|
|
8,2
|
5
|
5,4
|
|
9,4
|
4
|
8,6
|
|
10,2
|
2
|
12,2
|
|
12,0
|
1
|
15,0
|
Подставляем исходные данные в полином второй
степени и получаем следующую систему:
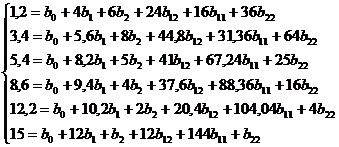
Решаем данную систему методом
Гаусса:


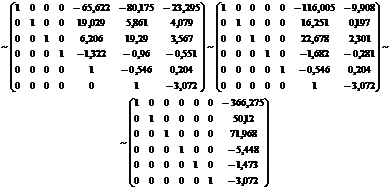
Таким образом, полное квадратное
уравнение (полином II степени) имеет вид:
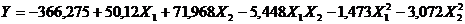
3.
РАСЧЕТ ТЕХНОЛОГИЧЕСКОГО АППАРАТА
3.1 Определение типа химического реактора
Таблица 7 - Исходные данные для определения типа
химического реактора
|
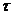 ,
мин0123456 ,
мин0123456
|
|
|
|
|
|
|
|
|
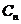 ,
г/л00,21,831,80,20 ,
г/л00,21,831,80,20
|
|
|
|
|
|
|
|
Среднее время пребывания индикатора в системе:
 (мин).
(мин).
Уравнение для расчета безразмерного
времени:
Условная концентрация индикатора на
входе:
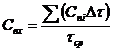 ,
,
где 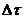 - интервал отбора проб.
- интервал отбора проб.
Так как по условию задачи  , то
, то
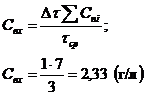
Уравнение для расчета безразмерной
концентрации:
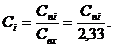
В результате получаем безразмерные
величины для построения 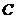 -выходной
кривой (таблица 8).
-выходной
кривой (таблица 8).
Таблица 8 - Безразмерные величины
для построения 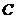 -выходной
кривой
-выходной
кривой
|
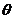 00,330,6711,331,672 00,330,6711,331,672
|
|
|
|
|
|
|
|
|
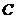 00,090,771,290,770,090 00,090,771,290,770,090
|
|
|
|
|
|
|
|
Используя данные таблицы 8, строим 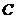 -выходную
кривую
-выходную
кривую 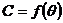 (Рисунок
4):
(Рисунок
4):

Рисунок 4 - Отклик реактора
Согласно визуальной оценке,  -выходной
кривой аппарат следует ячеечной модели.
-выходной
кривой аппарат следует ячеечной модели.
Для окончательного вывода о типе
реактора проведем статистическую оценку  -выходной кривой.
-выходной кривой.
Определим размерную дисперсию:
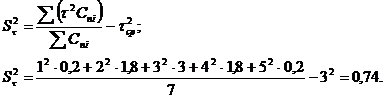
Определим безразмерную дисперсию:
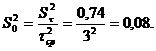
Определим обратную величину
диффузионного критерия Пекле:

Так как 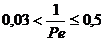 , то реактор
следует ячеечной модели и называется каскадом реакторов.
, то реактор
следует ячеечной модели и называется каскадом реакторов.
3.2 Определение объема химического реактора
В реакторе протекает реакция  при
начальной концентрации реагента
при
начальной концентрации реагента  :
: 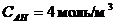 , конечных концентрациях
, конечных концентрациях 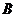 :
: 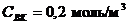 и
и 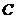 :
:  . Степень
превращения реагента
. Степень
превращения реагента 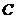 равна 90 %.
Производительность реактора
равна 90 %.
Производительность реактора  . Константа скорости химической
реакции
. Константа скорости химической
реакции 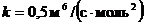 . Определить
объемы всех типов реакторов.
. Определить
объемы всех типов реакторов.
Найдем начальную концентрацию
реагента 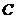 :
:
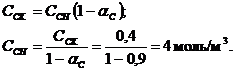
Найдем конечную концентрацию
реагента  и начальную
концентрацию реагента
и начальную
концентрацию реагента 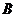 через связь
реагентов. Для данного уравнения расход всех реагентов одинаков:
через связь
реагентов. Для данного уравнения расход всех реагентов одинаков:  .
.
Расход реагента 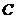
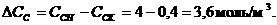
Тогда расход реагентов  и
и 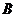
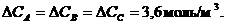
Отсюда
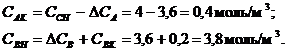
Определим степени превращения
реагентов  и
и 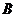 :
:

Найдем размерность константы
скорости химической реакции, используя уравнение скорости реакции по закону
действующих масс:
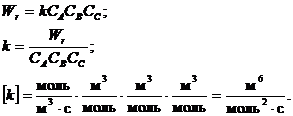
Рассчитаем реактор смешения:
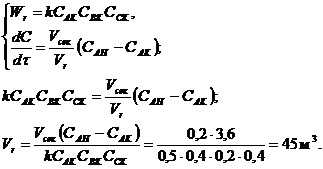
Выбираем стандартный аппарат объемом
 .
.
Перед расчетом реактора вытеснения и
каскада реакторов установим связь между концентрациями реагентов. Для этого
используем связь расходов:
 .
.
В произвольный момент времени:

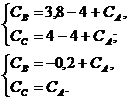
Установленная зависимость
справедлива для любого момента времени, в том числе и для начала и конца
процесса:

Рассчитаем реактор вытеснения:
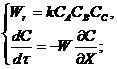
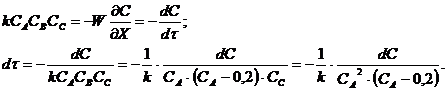
Разложим полученную дробь на сумму
простейших дробей:
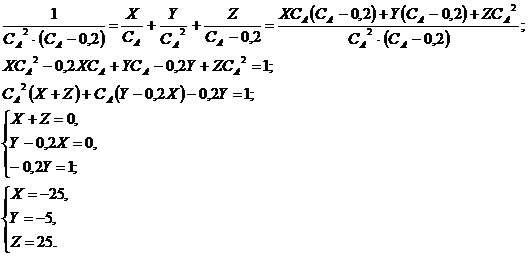
Тогда
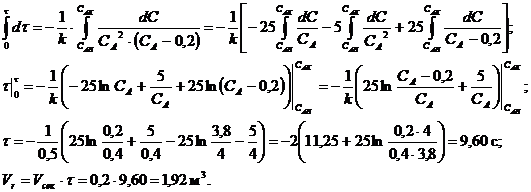
Выбираем стандартный аппарат объемом
 .
.
Рассчитаем каскад из двух реакторов:
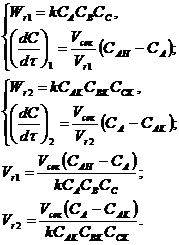
Исходя из условия  , получаем:
, получаем:
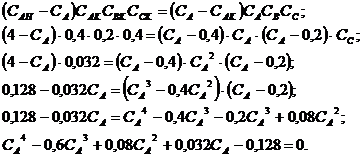
Решая данное уравнение в системе MathCAD, получаем:
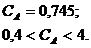
Тогда
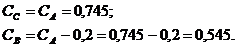
Рассчитаем объемы:
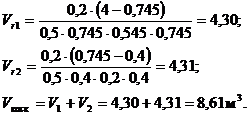
надежность эксперимент
дисперсионная химический аппарат
Выбираем стандартный аппарат объемом
 .
.