Прохождение и отражение звука на слоистой среде

Прохождение и отражение звука на слоистой среде

Задание

На бесконечную плоскую границу раздела двух сред 1 и 2, под углом θ, отсчитываемым от нормали к границе раздела, из среды 1 падает плоская гармоническая волна.

1.      Найти аналитическое выражение для коэффициентов отражения и прохождения по давлению и по энергии.

2.      Определить критический угол.

.        Получить аналитическое выражение для неоднородной волны.

.        Провести численный анализ модулей и фаз коэффициентов отражения и прохождения по давлению и по энергии в диапазоне углов падения от 0^о до 90^о.

Результаты численного анализа представить в графической форме. Номера вариантов и физические параметры рассматриваемых сред приведены в таблицах 1 и 2.

Таблица 1

Таблица 2

Нахождение аналитического выражения для коэффициентов отражения и прохождения по давлению и по энергии.

         Z

I         Ɵ₁  Ɵ₁

      p₁,            с_{1 0    X}

          p₂,      с₂

II              Ɵ₂

Для описание волн воспользуемся частным решением волнового уравнения в прямоугольной системе координат:

Теперь запишем это уравнение в проекциях на оси для каждой волны:

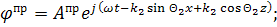
Для нахождения неизвестных амплитуд отраженной и преломленной волн воспользуемся граничными условиями:

непрерывностью нормальной компоненты вектора колебательной скорости и непрерывностью давления.

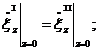
Учитывая, что :;

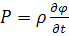
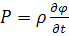
Получим

Теперьподставив сюда уравнения из системы 1, получим:

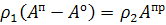
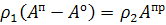(3)

Теперь систему (2) разделим на  и учитывая, что

 ; получим:

Решим эту систему относительно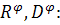

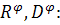
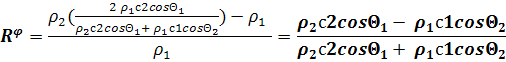
Коэффициенты по давлению выразим через полученные коэффициенты по потенциалу, для этого выразим давление через потенциал колебательной скорости:

-комплексная амплитуда давления. Коэффициент отражения по давлению тогда будет:

Коэффициенты отражения и прохождения по плотности потока энергии

В акустических расчетах чаще всего используются комплексные формы записи величин. Однако при вычислениях энергетических характеристик используются только вещественные части комплексных величин, входящих в расчетные соотношения. Мгновенные значения вектора плотности потока энергии можно вычислить как:

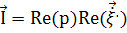
Представляет интерес среднее за период колебаний значение вектора плотности потока энергии:

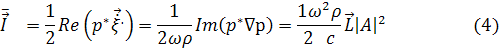
Где черта означает усреднение за период, а звездочка - комплексное сопряжение.

А - амплитуда потенциала колебательной скорости.

Коэффициенты отражения и прохождения определим для проекции среднего за период вектора плотности потока энергии на направление распространение волны

Коэффициенты отражения и прохождения по потоку энергии

Поток энергии - это количество энергии, проходящее в единицу времени через плоскую площадку площадью S.

Среднее за период значение потока энергии можно представить как::

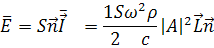
Где 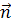 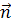- единичная нормаль к площадке площадью S.

Если волна распространяется перпендикулярно площадке, то и можно записать:

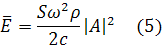
Для получения коэффициентов отражения и прохождения рассмотрим энергетические трубки падающей, отраженной и преломленной волн с площадями сечений соответственно  эти сечения будем считать прямоугольными, причем ширина всех сечений в направлении оси у будет одинакова, так как все энергетические трубки параллельны плоскости падения xz. Представим площади сечений следующим образом:

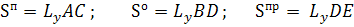
Выразив AC, BD, DEчерез длину общей области взаимодействия трубок AD, учитывая, что  получим:

Тогда с учетом (5) коэффициенты отражения и прохождения будут иметь вид:

На основании закона сохранения энергии полученные коэффициенты связаны соотношением:

Отметим, что полученную формулу можно использовать только в случае, если в процессе отражения- преломления отсутствует явление полного внутреннего отражения, когда преломленная волна является неоднородной.

Определение критических углов

Из закона Снеллиуса следует, что если , то 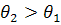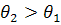. Это говорит о том, что при увеличении угла падения  угол преломления 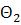 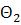достигнет значения  раньше, чем угол падения. При этом преломленная волна начнет «скользить» вдоль границы раздела сред. Угол падения при котором преломленная волна «скользит» вдоль границы раздела сред и , называется критическим углом.

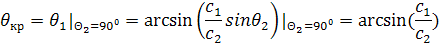
Аналитическое выражение для неоднородной волны

При углах падения являются действительными величинами. При критическом угле , . При коэффициенты отражения и преломления становятся комплексными величинами. Причем 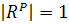 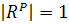и имеет место явление полного внутреннего отражения. Покажем это.

Так как при

т.е. является мнимой величиной, то

Где

Из (6) видим, что после критического угла 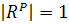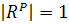, т.е. отражение полное. Отраженная волна давления приобретает на границе раздела z=0 сдвиг фазы 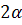 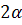относительно фазы падающей волны, причем этот сдвиг монотонно зависит от угла падения:

В то же самое время, как показывает (6), модуль коэффициента прохождения:

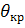
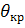При изменении от  до  уменьшается от двух до нуля. Сдвиг фазы преломленной волны относительно падающей при z=0 составляет половину от сдвига фазы при отражении и равен 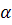 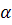. Представляет интерес анализ поля преломленной волны в нижней среде (II). Из (1) и (2) следует:

Учитывая, что , , получим

Видно, что поле в нижней среде при полном внутреннем отражении представляет собой неоднородную плоскую волну, распространяющуюся вдоль оси х, т.е. вдоль границы раздела сред. Амплитуда волны экспоненциально изменяется вдоль оси z, т.е. вдоль фронта волны. На основе принципа предельного поглощения амплитуда волны при удалении от границы раздела должна уменьшаться, а не увеличиваться. Поэтому для области двойные знаки в выражении (8) и во всех ему предшествующих необходимо заменить одним знаком - нижним. Преломленная волна имеет вид:

Введем обозначения 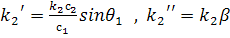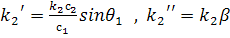. Учитывая, что

 , легко получить

Из (8) следует: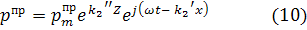

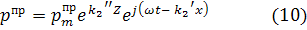
Фазовую скорость волны можно представить как:

Можно сделать вывод о том, что фазовая скорость неоднородной плоской волны меньше скорости однородной плоской волны в той же среде. Представим (10) в векторной форме:

Где 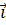 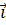и  - орты вдоль осей ох и oz; знак «-» в показателе первой экспоненты означает противоположное направление векторов  и . Ранее было показано, что, причем . Представляет интерес движение материальных частиц в неоднородной волне. Для его рассмотрения воспользуемся линеаризованным уравнением движения частиц в преломленной волне:

Учитывая, что для гармонического процесса:

Из уравнения движения получим выражение для вектора смещения частиц:

Так согласно (10) неоднородная волна не имеет зависимости от координаты y, то для компонент вектора смещения имеем:

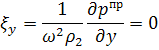
Видно, что частицы движутся в вертикальной плоскости xoz, т.е. в плоскости падения. Для физической интерпретации процесса перейдем от комплексной формы записи величин к вещественной:

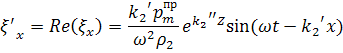
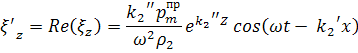
Если выразим из полученных соотношений синус и косинус, возведем каждый из них в квадрат и сложим, то, следуя известной тригонометрической формуле, получим:

Это каноническое уравнение эллипса. Таким образом, частицы в неоднородной волне движутся по эллиптическим траекториям с полуосями, описанными выражениями в скобках знаменателей, и центрами в местах невозмущенного положения частиц. Так как то большая ось лежит в направлении распространения волны; малая ось - в направлении перпендикуляра к границе раздела. Анализируя энергетический процесс при полно внутреннем отражении, целесообразно воспользоваться энергетическим коэффициентом прозрачности границы

Получим среднее за период колебаний значение нормальной к границе раздела компоненты вектора плотности потока энергии в преломленной волне 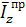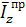, воспользовавшись (3*):

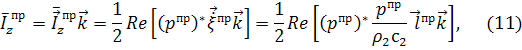
Подставив (12), (13) в (11), получим:

Т.к. в квадратных скобках оказалось чисто мнимая величина, т.о. и граница при полном внутреннем отражении является энергетически непрозрачной. Однако , и это значит, что вектор плотности потока энергии параллелен оси x, т.е. границе раздела. Эта энергия сразу же уходит в верхнюю среду. Т.о. , энергия, приносимая падающей волной к границе раздела, полностью возвращается в верхнюю среду в отраженной волне.