Описание реологических свойств наполненных систем
Министерство
образования республики Беларусь
Учреждение
образования
Брестский
государственный университет имени А.С.Пушкина
Физический
факультет
Кафедра
теоретической физики и астрономии
Курсовая
работа
по
специализации: Теоретическая физика
тема:
Описание реологических свойств наполненных систем
Брест
2011
Введение
Реология (от греч. ρέος,
«течение,
поток» и -логия) - раздел физики, изучающий деформации и текучесть вещества.
Композиционные материалы (далее композиты) -
материалы, образованные объемным сочетанием химически разнородных компонентов с
четкой границей раздела между ними. Характеризуются свойствами, которыми не
обладает ни один из компонентов, взятый в отдельности. По прочности, жесткости
и другим свойствам превосходят обычные конструкционные материалы.
Комбинируя объемное содержание компонентов,
можно, в зависимости от назначения, получать материалы с требуемыми значениями
прочности, жаропрочности, модуля упругости, абразивной стойкости, а также
создавать композиции с необходимыми магнитными, диэлектрическими,
радиопоглощающими и другими специальными свойствами. Однако, необходимо
помнить, что комбинирование материалов, которое улучшает отдельные свойства,
часто сопровождается ухудшением других свойств. Таким образом, следует
рассматривать все определяющие характеристики композита и часто приходится
принимать компромиссные решения.
Среди многих разделов механики деформируемых
сред линейная теория упругости дала, вероятно, наиболее широкий спектр
приложений. Огромные успехи линейной теории упругости можно объяснить
несколькими факторами. Во-первых, что наиболее важно, линейная теория упругости
реалистично описывает поведение широкого класса материалов. Во-вторых,
многочисленные разделы этого предмета высокоразвиты. К настоящему времени
имеется обширный набор непосредственно применимых готовых методов и
результатов. В-третьих, во многих практических задачах окончательные результаты
представлены в простом, но в то же время в достаточно общем виде, удобном для
расчетов.
По этим причинам изложим предмет о механическом
поведении гетерогенных сред с точки зрения линейной теории упругости.
. Элементы механики сплошных сред
1.1 Краевая задача
Наиболее общая форма линейно-упругих соотношений
напряжение-деформация для анизотропных сред (закон Гука) имеет вид:
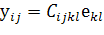 ,
, 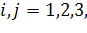 (1.1.1)
(1.1.1)
где 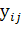 и
и
 -
тензоры линейных напряжений и деформации соответственно, а
-
тензоры линейных напряжений и деформации соответственно, а  -
тензор упругих модулей четвертого ранга, тензор жесткостей. Используем
прямоугольную декартову систему координат с обычными декартовыми обозначениями,
включая суммирование по повторяющимся индексам. Потребуем, чтобы тензоры
напряжений и деформаций были симметричными. Тензор жесткости как тензор
четвертого ранга имеет 81 независимую компоненту. Однако симметрия тензоров
-
тензор упругих модулей четвертого ранга, тензор жесткостей. Используем
прямоугольную декартову систему координат с обычными декартовыми обозначениями,
включая суммирование по повторяющимся индексам. Потребуем, чтобы тензоры
напряжений и деформаций были симметричными. Тензор жесткости как тензор
четвертого ранга имеет 81 независимую компоненту. Однако симметрия тензоров 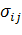 и
и
 уменьшает
число независимых компонент до 36. В данном разделе рассматривается однородная
среда, следовательно,
уменьшает
число независимых компонент до 36. В данном разделе рассматривается однородная
среда, следовательно,  не зависят от
координат.
не зависят от
координат.
Тензор малых деформаций определяется через
компоненты перемещения соотношениями Коши
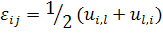 , (1.1.2)
, (1.1.2)
где запятая означает частное дифференцирование
по координате, символ которой следует за запятой. Шесть независимых компонент
деформаций выводятся из трех независимых компонент перемещений, поэтому
компоненты деформаций не могут быть независимыми. Это приводит к условиям
совместности деформаций. Уравнения совместности деформаций имеют вид
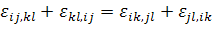 . (1.1.3)
. (1.1.3)
Конечно, большинство из 81 уравнения в (1.1.3)
не независимы. Как правило, уравнения (1.1.3) записываются в виде группы из
шести уравнений, но только три из них независимы.
Уравнения баланса импульсов имеют вид
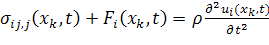 , (1.1.4)
, (1.1.4)
где 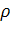 -
массовая плотность и
-
массовая плотность и  - компоненты
объемной силы.
- компоненты
объемной силы.
В совокупности с соответствующими формулировками
граничных и начальных условии соотношения (1.1.1)-(1.1.4) образуют полную
систему определяющих соотношений, решение которой даст распределение полей
переменных в частной краевой задаче.
Обратимся далее к соотношению между
напряжениями, деформациями и энергией деформирования.
1.2 Энергия
деформирования
Наиболее удобно вывести соотношения между
напряжениями, деформациями и энергией при помощи термодинамического анализа.
Напряжение выражается как производная энергии деформирования  по
деформации:
по
деформации:
 , (1.2.1)
, (1.2.1)
где
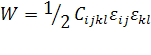 . (1.2.2)
. (1.2.2)
Соотношения напряжение-деформация (1.1.1) легко
обратить для выражения деформаций через напряжения в общем случае. Для
изотропии соотношения напряжение-деформация можно записать в виде
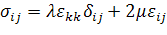 , (1.2.3)
, (1.2.3)
где  и
и
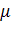 -
упругие константы Ламе, а
-
упругие константы Ламе, а 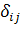 - символ
Кронекера. Кроме того, соотношения можно компактно записать через девиаторы и
шаровые части тензоров. Пусть
- символ
Кронекера. Кроме того, соотношения можно компактно записать через девиаторы и
шаровые части тензоров. Пусть 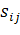 и
и  -
девиаторные компоненты напряжений и деформаций, определяемые как
-
девиаторные компоненты напряжений и деформаций, определяемые как
 . (1.2.4)
. (1.2.4)
Тогда соотношения напряжение-деформация (1.2.3)
принимают вид
 , (1.2.5)
, (1.2.5)
где, как мы теперь видим, константа 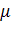 -
модуль сдвига, а константа
-
модуль сдвига, а константа  - объемный модуль.
Конечно, только две из трех характеристик
- объемный модуль.
Конечно, только две из трех характеристик  ,
,
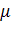 ,
,
 независимы.
Обычно, используемые модуль при одноосном нагружении (модуль Юнга)
независимы.
Обычно, используемые модуль при одноосном нагружении (модуль Юнга) 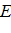 и
коэффициент Пуассона
и
коэффициент Пуассона  связаны с
связаны с 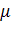 и
и
 посредством
следующих соотношений:
посредством
следующих соотношений:
 ,
,  .
(1.2.6)
.
(1.2.6)
1.3 Теоремы о минимуме
В линейной теории упругости имеются два
фундаментальных энергетических принципа или теоремы, которые полезны и
необходимы при исследовании гетерогенных сред. Эти энергетические теоремы
устанавливают, что некоторый функционал энергетического типа принимает
минимальное значение для единственных значений переменных физических полей,
которые представляют собой решение краевой задачи, в отличие от значений
функционала для других «допустимых» значений этих переменных. Теперь перейдем к
формулировке этих теорем: о минимуме потенциальной энергии и о минимуме
дополнительной энергии.
Рассмотрим статическую упругую задачу с
объемными силами 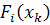 и граничными
условиями
и граничными
условиями
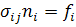 на
на 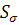 , (1.3.1)
, (1.3.1)
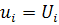 на
на 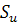 , (1.3.2)
, (1.3.2)
где 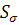 и
и
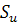 -
дополняющие друг друга части поверхности тела объема
-
дополняющие друг друга части поверхности тела объема 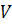 ,
а
,
а 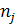 -
компоненты единичной внешней нормали к поверхности. Определим далее функционал
потенциальной энергии
-
компоненты единичной внешней нормали к поверхности. Определим далее функционал
потенциальной энергии
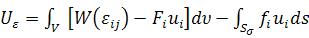 , (1.3.3)
, (1.3.3)
где 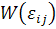 задается
уравнением (1.2.2).
задается
уравнением (1.2.2).
Определим в качестве допустимого поля
перемещений  некоторое поле
непрерывных перемещений, которое удовлетворяет граничным условиям в
перемещениях (1.3.2), но во всех других отношениях выбрано произвольно (за
исключением обычного требования регулярности производных). Теорему о минимуме
потенциальной энергии можно теперь сформулировать следующим образом:
некоторое поле
непрерывных перемещений, которое удовлетворяет граничным условиям в
перемещениях (1.3.2), но во всех других отношениях выбрано произвольно (за
исключением обычного требования регулярности производных). Теорему о минимуме
потенциальной энергии можно теперь сформулировать следующим образом:
Среди всех допустимых полей перемещений
абсолютный минимум функционала потенциальной энергии (1.3.3) обеспечивает лишь
то, которое удовлетворяет уравнениям равновесия.
Математически этот результат формулируется
следующим образом:
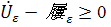 ,
,
где  -
функционал (1.3.3), вычисленный для какого-либо допустимого поля перемещений
-
функционал (1.3.3), вычисленный для какого-либо допустимого поля перемещений  .
Доказательство этой теоремы, данное во многих источниках, основано на свойстве
положительной определенности потенциальной энергии деформирования (1.2.2):
.
Доказательство этой теоремы, данное во многих источниках, основано на свойстве
положительной определенности потенциальной энергии деформирования (1.2.2):
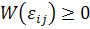 .
.
Теорема о минимуме дополнительной энергии
формулируется аналогично. Определим функционал дополнительной энергии
 ,
, 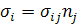 , (1.3.4)
, (1.3.4)
где энергия деформирования (1.2.2) выражена в
напряжениях
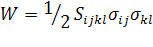 , (1.3.5)
, (1.3.5)
а  -
тензор упругих податливостей. Определим допустимые напряженные состояния
-
тензор упругих податливостей. Определим допустимые напряженные состояния 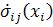 как
такие напряженные состояния, которые удовлетворяют уравнениям равновесия и
граничным условиям в напряжениях (1.3.1), но во всех других отношениях
произвольны. Будем вновь подразумевать, что непрерывности напряжений и их
производных достаточно для доказательства теоремы.
как
такие напряженные состояния, которые удовлетворяют уравнениям равновесия и
граничным условиям в напряжениях (1.3.1), но во всех других отношениях
произвольны. Будем вновь подразумевать, что непрерывности напряжений и их
производных достаточно для доказательства теоремы.
Теорему о минимуме дополнительной энергии теперь
можно сформулировать следующим образом:
Среди всех допустимых полей напряжений
абсолютный минимум функционала дополнительной энергии (1.3.4) обеспечивает лишь
то, которое удовлетворяет уравнениям совместности деформаций.
Математическую формулировку этого вывода можно
представить в виде:
 ,
,
где  -
функционал (1.3.4), вычисленный для любого допустимого поля напряжений.
Ключевой шаг в доказательстве теоремы основан на использовании свойства
положительной определенности функции W
(1.3.5).
-
функционал (1.3.4), вычисленный для любого допустимого поля напряжений.
Ключевой шаг в доказательстве теоремы основан на использовании свойства
положительной определенности функции W
(1.3.5).
2. Эффективные модули среды со
сферическими включениями
2.1 Модель среды с малой
объемной долей включений
Выведем решения для эффективного модуля сдвига
упругой среды с упругими сферическими включениями. Рассмотрим поведение
однородной среды в состоянии чистого сдвига. Компоненты перемещений в
декартовой системе координат в осях  ,
,
 ,
,
 определяются
следующим образом
определяются
следующим образом
где максимум деформации сдвига имеет значение 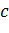 .
Перепишем выражения для перемещений, соответствующих (2.1.1), в сферической
системе координат.
.
Перепишем выражения для перемещений, соответствующих (2.1.1), в сферической
системе координат.
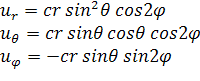 . (2.1.2)
. (2.1.2)
Руководствуясь формулами для деформации
однородной среды, запишем общее решение для неоднородной среды в виде
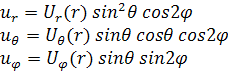 . (2.1.3)
. (2.1.3)
где 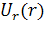 ,
,
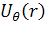 ,
,
 -
неизвестные функции
-
неизвестные функции 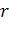 , которые подлежат
определению из уравнения равновесия. Уравнения равновесия в сферических
координатах имеют вид:
, которые подлежат
определению из уравнения равновесия. Уравнения равновесия в сферических
координатах имеют вид:
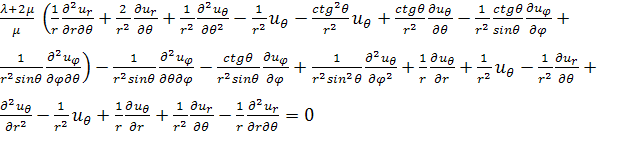 , (2.1.4)
, (2.1.4)
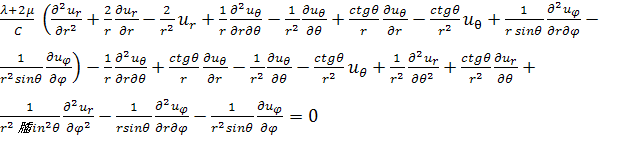 , (2.1.5)
, (2.1.5)
 . (2.1.6)
. (2.1.6)
Подставляя (2.1.3) в (2.1.4) - (2.1.6) и
приравнивая к нулю коэффициенты при 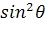 и
при членах, не зависящих от
и
при членах, не зависящих от 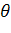 , получим три
определяющих уравнения:
, получим три
определяющих уравнения:
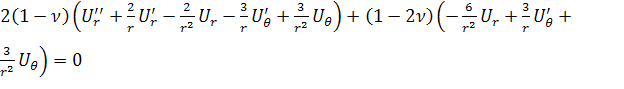 , (2.1.7)
, (2.1.7)
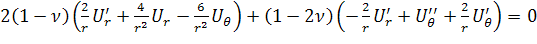 , (2.1.8)
, (2.1.8)
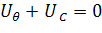 , (2.1.9)
, (2.1.9)
где штрих обозначает производную по 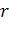 .
Решение (2.1.7)-(2.1.9) дается выражениями
.
Решение (2.1.7)-(2.1.9) дается выражениями
 , (2.1.10)
, (2.1.10)
Перепишем решения (2.1.10) отдельно для
включения и для матрицы:
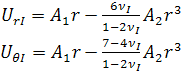 , (2.1.11)
, (2.1.11)
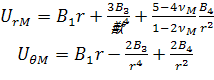 , (2.1.12)
, (2.1.12)
причем решение для 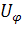 для
каждой фазы следует из (2.1.10). Отдельные слагаемые (2.1.10), отсутствующие в
(2.1.11) и (2.1.12), берутся с нулевыми коэффициентами, чтобы избежать
сингулярности или нарушения граничных условий.
для
каждой фазы следует из (2.1.10). Отдельные слагаемые (2.1.10), отсутствующие в
(2.1.11) и (2.1.12), берутся с нулевыми коэффициентами, чтобы избежать
сингулярности или нарушения граничных условий.
Коэффициент 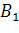 рассматривается
как заданный, поскольку он определяет состояние приложенного чистого сдвига при
рассматривается
как заданный, поскольку он определяет состояние приложенного чистого сдвига при
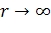 .
Таким образом, (2.1.11) и (2.1.12) содержат 4 константы, подлежащие
определению.
.
Таким образом, (2.1.11) и (2.1.12) содержат 4 константы, подлежащие
определению.
На границе фаз должны выполняться условия
непрерывности следующих величин: 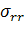 ,
,
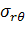 ,
,
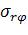 ;
;
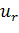 ,
,
 ,
,
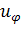 на
радиусе
на
радиусе 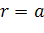 сферического
включения. Но только 4 из этих условий независимы. Окончательно условия
непрерывности на границе фаз принимают вид
сферического
включения. Но только 4 из этих условий независимы. Окончательно условия
непрерывности на границе фаз принимают вид
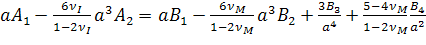 , (2.1.13)
, (2.1.13)
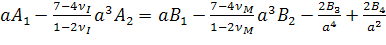 , (2.1.14)
, (2.1.14)
 , (2.1.15)
, (2.1.15)
 . (2.1.16)
. (2.1.16)
Используем формулу Эшелби и энергетический
критерий эквивалентности гомогенной и гетерогенной сред. Вначале запишем формулу
Эшелби в виде
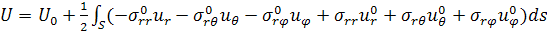 , (2.1.17)
, (2.1.17)
Перемещения определяются из (2.1.3), (2.1.10) и
(2.1.13)-(2.1.16), а напряжения - непосредственно из соотношений
напряжение-деформация линейной теории упругости. Напряжения и перемещения вычисляются
в каждой фазе на поверхности 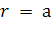 .
.
Использование условия малости объемной доли
включений 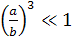 окончательно
приводит выражение к виду
окончательно
приводит выражение к виду
 , (2.1.18)
, (2.1.18)
где  -
объемная доля сферических включений.
-
объемная доля сферических включений.
Описанную выше процедуру определения
эффективного модуля сдвига можно использовать и для определения эффективного
объемного модуля  . Эта задача
значительно проще, так как поля переменных обладают сферической симметрией и,
таким образом, задача является одномерной. При условии малой объемной доли
включений эффективный объемный модуль
. Эта задача
значительно проще, так как поля переменных обладают сферической симметрией и,
таким образом, задача является одномерной. При условии малой объемной доли
включений эффективный объемный модуль  определяется
по формуле
определяется
по формуле
 . (2.1.19)
. (2.1.19)
2.2 Полидисперсная
модель
В предыдущем разделе были определены эффективные
модуль сдвига и объемный модуль упругой среды с малой объемной долей упругих
сферических включений. Перейдем теперь к описанию сред с произвольной объемной
долей включений. Логично сделать этот шаг путем введения модели гетерогенной
среды с частной геометрической характеристикой и затем решить задачу о ее
свойствах. Естественно, мы хотим, чтобы такая модель отражала основные особенности
реальных сред. Перейдем теперь к описанию модели более общего характера.
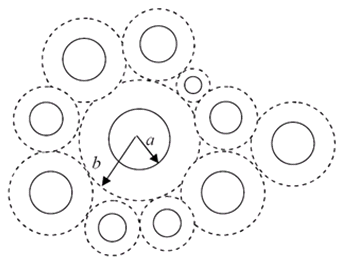
Рис. 2.2.1 Полидисперсная модель среды со
сферическими включениями.
Рассмотрим непрерывную среду со сферическими
включениями различного размера. Распределение размеров, однако, не случайное, а
скорее имеет весьма частный характер. Схематически модель изображена на рис.
2.2.1 Штриховыми линиями на рис. 2.2.1 ограничены области матрицы, связанные с
каждым отдельным включением. Отношение радиусов 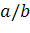 принято
постоянным для каждой такой составной частицы независимо от ее абсолютного
размера. Поэтому распределение размеров частиц должно быть таким, чтобы весь
объем был заполнен составными частицами с
принято
постоянным для каждой такой составной частицы независимо от ее абсолютного
размера. Поэтому распределение размеров частиц должно быть таким, чтобы весь
объем был заполнен составными частицами с 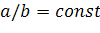 .
Очевидно, что это распределение требует, чтобы размеры частиц уменьшились до
бесконечно малых.
.
Очевидно, что это распределение требует, чтобы размеры частиц уменьшились до
бесконечно малых.
Потребовав равенства перемещений на внешней
границе составной частицы и эквивалентной гомогенной частицы получим решение
для  в
виде:
в
виде:
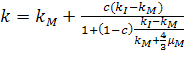 (2.2.1)
(2.2.1)
Таким образом, эффективный объемный модуль
выражается в виде
 (2.2.2)
(2.2.2)
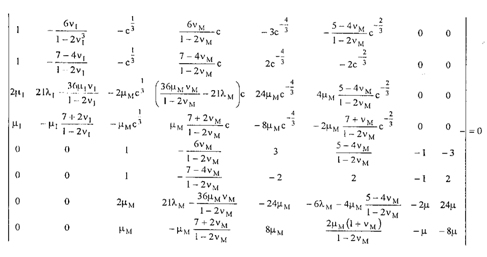
Определив эффективный объемный модуль для
рассмотренной модели составных сфер, перейдем теперь к определению эффективного
модуля сдвига для той же модели. Задача об определении 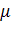 ,
как уже отмечалось, должна быть более сложной, чем задача об определении
,
как уже отмечалось, должна быть более сложной, чем задача об определении  ,
так как первая представляет собой трехмерную задачу теории упругости, в то
время как задача для
,
так как первая представляет собой трехмерную задачу теории упругости, в то
время как задача для  была одномерной.
Тем не менее, процедура нахождения
была одномерной.
Тем не менее, процедура нахождения 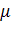 в
действительности основана на найденных в предыдущем разделе упругих решениях.
Как и в случае
в
действительности основана на найденных в предыдущем разделе упругих решениях.
Как и в случае  , для нахождения
верхней и нижней границ
, для нахождения
верхней и нижней границ 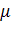 использованы
теоремы теории упругости о минимуме потенциальной и дополнительной энергии. В
противоположность ситуации с объемным модулем оценки модуля сдвига не
совпадают, за исключением случаев очень малых и очень больших долей включений.
Формула для малых объемных долей имеет следующий вид
использованы
теоремы теории упругости о минимуме потенциальной и дополнительной энергии. В
противоположность ситуации с объемным модулем оценки модуля сдвига не
совпадают, за исключением случаев очень малых и очень больших долей включений.
Формула для малых объемных долей имеет следующий вид
 , (2.2.3)
, (2.2.3)
совпадает с ранее полученным (2.1.18).
Выражение для больших объемных долей имеет вид
 . (2.2.4)
. (2.2.4)
То, что верхняя и нижняя оценки не совпадают в
задаче о модуле сдвига, малоутешительно, но не удивительно. В случае, когда на
поверхности составной сферы задаются компоненты перемещения при чистом сдвиге,
результирующие напряжения на границе не соответствуют напряженному состоянию
при чистом сдвиге. Следовательно, когда на границе задаются напряжения чистого
сдвига, результирующее деформированное состояние не соответствует чистому
сдвигу. Таким образом, результатом являются только оценки 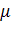 ,
и чем больше несоразмерность между
,
и чем больше несоразмерность между  и
и
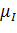 ,
тем больше расхождение между оценками. Очевидно, для получения точного решения
или даже оценки эффективного модуля сдвига для описанной выше полидисперсной
модели композита нужен другой подход.
,
тем больше расхождение между оценками. Очевидно, для получения точного решения
или даже оценки эффективного модуля сдвига для описанной выше полидисперсной
модели композита нужен другой подход.
2.3 Трехфазная
модель
Не добившись успеха в предыдущем разделе в
поисках решения для эффективного модуля сдвига в рамках полидисперсной модели,
испробуем другой подход.
Вновь обратимся к модели композита, изображенной
на рис. 2.2.1. Теперь заменим все, за исключением одной, составные сферические
частицы эквивалентной гомогенной средой, как показано на рис. 2.3.1.
Представим, что бесконечная область подвергнута однородной деформации на
большом расстоянии от начала координат. Внешний слой, будучи эквивалентной
гомогенной средой, обладает неизвестными эффективными свойствами 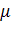 и
и
 .
Модель композита на рис. 2.3.1 эквивалентна
эффективной гомогенной среде при условии, что энергия деформирования обеих
систем одинакова при равенстве осредненных деформаций. Рассмотрим соответствие
трехфазной и полидисперсном моделей.
.
Модель композита на рис. 2.3.1 эквивалентна
эффективной гомогенной среде при условии, что энергия деформирования обеих
систем одинакова при равенстве осредненных деформаций. Рассмотрим соответствие
трехфазной и полидисперсном моделей.
У нас нет гарантий того, что решения задачи для
трехфазной модели на рис. 2.3.1 в точности описывают эффективные свойства
композита, представленного полидисперсной моделью (рис. 2.2.1). Мы можем
рассматривать это только как гипотезу и проверить ее на примере. В частности, в
случае эффективного объемного модуля  мы
знаем решение для полидисперсной модели композита.
мы
знаем решение для полидисперсной модели композита.
Оно представлено соотношением (2.2.2). Задачу
для гетерогенной среды, изображенной на рис. 2.3.1,
можно решить для объемного деформированного состояния, и тем самым определить  для
эквивалентной гомогенной среды.
для
эквивалентной гомогенной среды.
Рис. 2.3.1.
Трехфазная модель.
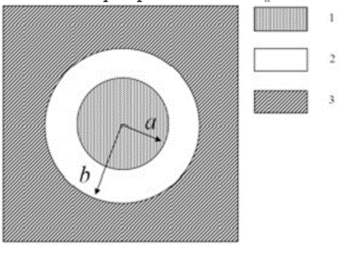
- сферическое включение;
- фаза матрицы;
- эквивалентная гомогенная среда.
Эффективные модули  для
моделей композитной среды на рис. 2.3.1 и рис. 2.2.1 идентичны, что внушает
уверенность в тождественности моделей. С этим обнадеживающим результатом и
перейдем к поиску решения для эффективного модуля сдвига модели, изображенной
на рис. 2.3.1. Необходимо, однако, подчеркнуть, что остается открытым вопрос о
том, является ли решение для
для
моделей композитной среды на рис. 2.3.1 и рис. 2.2.1 идентичны, что внушает
уверенность в тождественности моделей. С этим обнадеживающим результатом и
перейдем к поиску решения для эффективного модуля сдвига модели, изображенной
на рис. 2.3.1. Необходимо, однако, подчеркнуть, что остается открытым вопрос о
том, является ли решение для 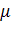 для модели на рис.
2.3.1 решением и для модели композита на рис. 2.2.1. Можно лишь сказать, что
полученные результаты точны для модели на рис. 2.3.1. Последняя представляет
интерес сама по себе независимо от того, соответствует ли ее поведение при
сдвиге поведению полидисперсной модели композита или нет.
для модели на рис.
2.3.1 решением и для модели композита на рис. 2.2.1. Можно лишь сказать, что
полученные результаты точны для модели на рис. 2.3.1. Последняя представляет
интерес сама по себе независимо от того, соответствует ли ее поведение при
сдвиге поведению полидисперсной модели композита или нет.
Метод решения задачи для модели, показанной на
рис. 2.3.1, прямо следует решению для упругих сред с малой объемной долей
сферических частиц, рассмотренному ранее. В частности, решения (2.3.1)
используются для условия деформации чистого сдвига на большом расстоянии от
начала координат. Функции 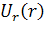 ,
, 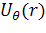 ,
,
 ,
как установлено из решения уравнений равновесия, имеют вид (2.1.10). Отдельно
следует рассматривать решения для трех областей, показанных на рис.
2.3.1.
,
как установлено из решения уравнений равновесия, имеют вид (2.1.10). Отдельно
следует рассматривать решения для трех областей, показанных на рис.
2.3.1.
В частности, получим
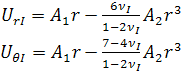 , (2.3.1)
, (2.3.1)
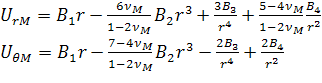 , (2.3.2)
, (2.3.2)
и в третьей фазе, образованной эквивалентной
гомогенной средой
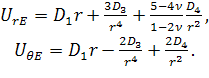 (2.3.3)
(2.3.3)
где 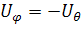 .
Коэффициент Пуассона
.
Коэффициент Пуассона  , входящий в
(2.3.3), и есть эффективное свойство нужного типа для эквивалентной гомогенной
среды. Константа
, входящий в
(2.3.3), и есть эффективное свойство нужного типа для эквивалентной гомогенной
среды. Константа 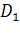 в (2.3.3),
рассматривается как заданная из условия наложения деформированного состояния
чистого сдвига на большом расстоянии от начала координат. Остается определить
восемь констант. Условия непрерывности напряжений и перемещений на двух
границах раздела фаз обеспечивают требуемые восемь соотношений. Четыре
соотношения, полученные из условий непрерывности при
в (2.3.3),
рассматривается как заданная из условия наложения деформированного состояния
чистого сдвига на большом расстоянии от начала координат. Остается определить
восемь констант. Условия непрерывности напряжений и перемещений на двух
границах раздела фаз обеспечивают требуемые восемь соотношений. Четыре
соотношения, полученные из условий непрерывности при 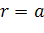 ,
уже установлены уравнениями (2.1.13) - (2.1.16). Оставшиеся четыре соотношения
получаются из условия непрерывности при
,
уже установлены уравнениями (2.1.13) - (2.1.16). Оставшиеся четыре соотношения
получаются из условия непрерывности при  ,
т. е. на поверхности раздела между матрицей и эффективной гомогенной средой.
Эти уравнения имеют вид
,
т. е. на поверхности раздела между матрицей и эффективной гомогенной средой.
Эти уравнения имеют вид
 , (2.3.4)
, (2.3.4)
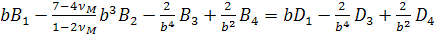 , (2.3.5)
, (2.3.5)
 , (2.3.6)
, (2.3.6)
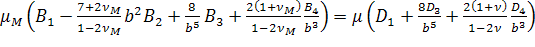 , (2.3.7)
, (2.3.7)
Следуя в точности той же процедуре, что и в
разд.
2.1,
используем соответствующие выражения для напряжений и деформаций; тогда получим
очень простой результат
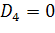 . (2.3.8)
. (2.3.8)
Задача сводится к решению системы 8-ми уравнений
(2.1.13)-(2.1.16) и (2.3.4)-(2.3.7) для  .
Полученное решение полагается равным нулю. Отсюда имеем критерий для определения
эффективного модуля сдвига
.
Полученное решение полагается равным нулю. Отсюда имеем критерий для определения
эффективного модуля сдвига 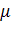 . В процессе
решения сокращаются константы
. В процессе
решения сокращаются константы  и
и  ,
остается только одно неизвестное
,
остается только одно неизвестное 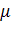 .
.
Эффективный модуль сдвига 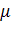 находится
из следующего квадратного уравнения:
находится
из следующего квадратного уравнения:
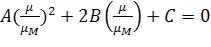 , (2.3.9)
, (2.3.9)
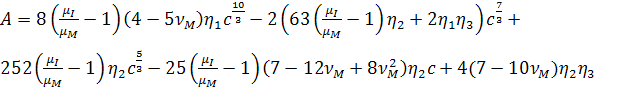 ,
,
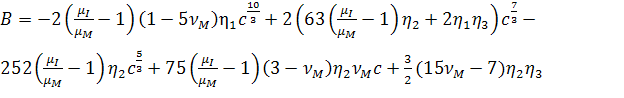 , (2.3.11)
, (2.3.11)
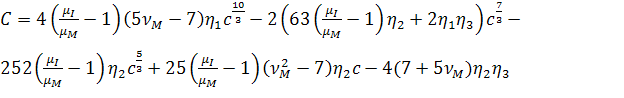 , (2.3.12)
, (2.3.12)
в свою очередь
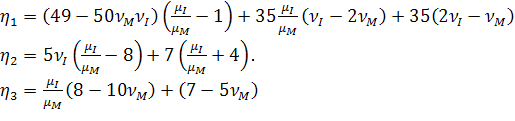 (2.3.13)
(2.3.13)
Как и ранее 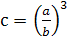 характеризует
объемную долю включений.
характеризует
объемную долю включений.
Конечное решение (2.3.9) сводится к ранее
выведенной формуле (2.1.18) для упругой среды с малой объемной долей упругих
сферических включений. Отметим, что в данной задаче было невозможно
воспользоваться простой формулой для вычисления эффективного модуля сдвига, так
как включение образовано здесь двумя фазами и поэтому однородное
деформированное состояние не реализуется. Наконец, важно отметить внутреннюю
согласованность данного вывода. Напомним, что при определении эффективного
объемного модуля  для полидисперсной
модели композита решение для
для полидисперсной
модели композита решение для  было найдено в
форме, не связанной с другим свойством, скажем
было найдено в
форме, не связанной с другим свойством, скажем  .
Полностью аналогичная ситуация возникает и в данном выводе;
.
Полностью аналогичная ситуация возникает и в данном выводе;  было
определено в форме, не связанной с
было
определено в форме, не связанной с  .
Это дает косвенную поддержку той точки зрения, что данный результат может быть
точным решением для эффективного модуля сдвига полидисперсной модели композита.
Однако в данной ситуации с определенностью можно сказать, что найдено решение
для модели, изображенной на рис. 2.3.1.
.
Это дает косвенную поддержку той точки зрения, что данный результат может быть
точным решением для эффективного модуля сдвига полидисперсной модели композита.
Однако в данной ситуации с определенностью можно сказать, что найдено решение
для модели, изображенной на рис. 2.3.1.
3. Эффективные модули среды с
включениями цилиндрической и пластинчатой формы
механика деформирование включение
полидисперсный
3.1 Полидисперсная модель среды с
цилиндрическими включениями
Займемся поиском решения задачи об эффективных
свойствах композитов, армированных волокнами. Для этого достаточно найти пять
независимых констант. Итак, наша цель состоит в представлении в аналитическом
виде пяти констант через свойства компонентов (волокон и матрицы) и их объемное
содержание.
Для выполнения этой задачи следует ввести
структурную модель композита. Наиболее часто употребляется полидисперсная
модель среды с цилиндрическими включениями, описанная Хашином и Розеном.
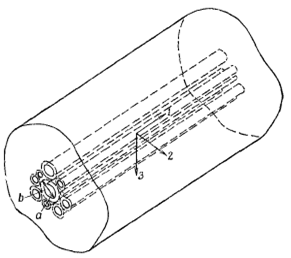
Рис. 3.1.1 Полидисперсная модель среды с
цилиндрическими включениями.
Эта модель является двумерным аналогом
трехмерной полидисперсной модели среды со сферическими включениями.
Принимается, что волокна представляют собой бесконечно длинные круговые
цилиндры, заключенные в непрерывную матрицу. Модель схематически представлена
на рис. 3.1.1. Согласно этой модели, с каждым отдельным волокном радиуса a
связана оболочка из материала матрицы радиуса b.
Каждая отдельная комбинация волокна и матрицы называется составным цилиндром.
Абсолютные значения радиусов a
и b цилиндров
различны, так что получается конфигурация, целиком заполненная этими
цилиндрами. Отношение радиусов цилиндра a/b
должно оставаться, тем не менее, постоянным. Естественно, абсолютный размер
отдельных цилиндров при этом меняется вплоть до бесконечно малого. Практичность
подобной модели объясняется тем, что для определения четырех из пяти
эффективных модулей представительного элемента объема достаточно рассматривать
отдельный составной цилиндр.
Итак, наша цель заключается вначале в
определении модуля Е11 при одноосном нагружении. Для этого примем
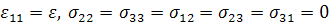 ,
,
где ось 1 в прямоугольной декартовой системе
координат совпадает с направлением оси составного цилиндра. Переходя к
цилиндрической системе координат, предположим существование следующего поля
перемещений:
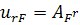 ,
, 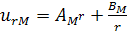 ,
, 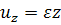 . (3.1.1)
. (3.1.1)
Легко показать, что решение в таком виде
удовлетворяет уравнению равновесия. Константа AF
относится к внутреннему цилиндру (волокну), а AM
и BM - к оболочке
(матрице). Для определения этих констант используем условия на границе
при 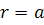 ,
, 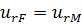 ,
,
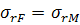 , (3.1.2)
, (3.1.2)
при 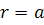 ,
,
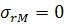 . (3.1.3)
. (3.1.3)
В контексте нашей задачи эффективный модуль E11
определяется выражением
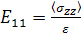 ,
,
которое можно записать в другом виде:
 , (3.1.4)
, (3.1.4)
где A
- площадь поперечного сечения (3.1.4) дает
 . (3.1.5)
. (3.1.5)
Выражение (3.1.5) определяет
эффективный модуль упругости при одноосном нагружении в направлении оси
одиночного составного цилиндра. Теперь остается показать, что полученный
результат действительно характеризует свойства представительного элемента
объема. Чтобы показать, что (3.1.5) является оценкой снизу соответствующей
характеристики представительного элемента объема, можно применить теорему о
минимуме потенциальной энергии. С другой стороны, использование теоремы о
минимуме дополнительной энергии позволяет при наложении граничных условий в
напряжениях, а не в перемещениях найти оценку E11
сверху.
Выполнив эти процедуры, установим, что значения оценок совпадают и что (3.1.5),
таким образом, есть точное решение.
Поставленная задача позволяет найти точное
решение и для эффективного значения коэффициента Пуассона 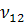 ,
если ось 1 совпадает с направлением волокон и
,
если ось 1 совпадает с направлением волокон и 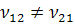 .
.
Можно показать, что
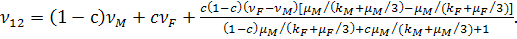 (3.1.6)
(3.1.6)
Формула (3.1.5) для E11
очень хорошо аппроксимируется правилом смесей, если пренебречь последним
членом. Формула (3.1.6) также аппроксимируется правилом смесей, однако менее
точно. Далее увидим, что значения оставшихся трех эффективных уже нельзя
описать этим правилом с достаточной точностью.
Задачи об определении еще двух констант можно
сформулировать и решить подобным же образом, получив точные решения для
объемного модуля при плоском деформированном состоянии K23
и
модуля сдвига в плоскости, параллельной волокнам  .
Можно показать, что
.
Можно показать, что
 , (3.1.7)
, (3.1.7)
 . (3.1.8)
. (3.1.8)
Задачи об определении K23
и  являются
простыми в том смысле, что поле переменных решения включает только одну
компоненту перемещения. Развернутые формулы (3.1.5) - (3.1.8) выведены Хиллом и
Хашином.
являются
простыми в том смысле, что поле переменных решения включает только одну
компоненту перемещения. Развернутые формулы (3.1.5) - (3.1.8) выведены Хиллом и
Хашином.
После того как найдены четыре из пяти констант
трансверсально изотропной среды, кажется, что поставленная задача почти решена.
К сожалению, это не совсем так. Остается определить последнюю константу, модуль
сдвига  в
плоскости изотропии, а это оказывается трудной задачей, если использовать
полидисперсную модель. Можно определить оценку для
в
плоскости изотропии, а это оказывается трудной задачей, если использовать
полидисперсную модель. Можно определить оценку для  сверху,
решая задачу в перемещениях, и оценку для
сверху,
решая задачу в перемещениях, и оценку для  снизу,
решая задачу в напряжениях. Как показал Хашин и Розен, эти оценки не совпадают,
за исключением случаев очень малой и очень высокой объемных долей включений. До
настоящего времени точное решение для
снизу,
решая задачу в напряжениях. Как показал Хашин и Розен, эти оценки не совпадают,
за исключением случаев очень малой и очень высокой объемных долей включений. До
настоящего времени точное решение для  не
получено.
не
получено.
В следующем разделе, используя другую модель, мы
выведем выражение, которое можно считать решением  и
для полидисперсной модели среды с цилиндрическими включениями.
и
для полидисперсной модели среды с цилиндрическими включениями.
3.2 Трехфазная модель среды с
цилиндрическими включениями
Дилемма, с которой мы столкнулись в предыдущем
разделе, разрешима, по-видимому, при помощи другой модели. В частности, было
доказано, что модуль сдвига в плоскости изотропии определить при помощи
полидисперсной модели нелегко. Поэтому введем модель, очень близкую к уже
рассмотренной, но позволяющую найти точное решение для модуля сдвига  .
.
Снова обратимся к рис. 3.1.1. заменим все, кроме
одного, составные цилиндры эквивалентной гомогенной средой, как показано на
рис. 3.2.1. Теперь при помощи этой модели попытаемся определить эффективный
модуль сдвига в плоскости изотропии.
Рассмотрим представительный элемент объема,
подверженный деформации сдвига. В частности, деформированное состояние
эквивалентной гомогенной среды в полярной системе координат выражается в виде:
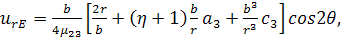 (3.2.1)
(3.2.1)
 , (3.2.2)
, (3.2.2)
Рис. 3.2.1 Трехфазная модель:
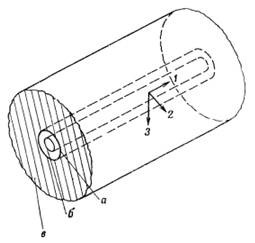
а - матрица
б - волокно
в - эквивалентная гомогенная среда
При 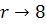 соотношение
(3.2.1), (3.2.2) описывают заданное состояние чистого сдвига. Модуль
соотношение
(3.2.1), (3.2.2) описывают заданное состояние чистого сдвига. Модуль  и
коэффициент Пуассона
и
коэффициент Пуассона  являются
неизвестными константами эквивалентной гомогенной среды. Легко показать, что
соотношения (3.2.1), (3.2.2) удовлетворяют уравнениям равновесия, так же как и
приведенные ниже выражения для перемещения в матрице:
являются
неизвестными константами эквивалентной гомогенной среды. Легко показать, что
соотношения (3.2.1), (3.2.2) удовлетворяют уравнениям равновесия, так же как и
приведенные ниже выражения для перемещения в матрице:
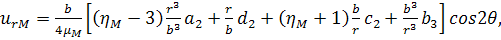 (3.2.4)
(3.2.4)
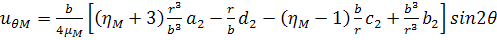 (3.2.5)
(3.2.5)
и в волокне
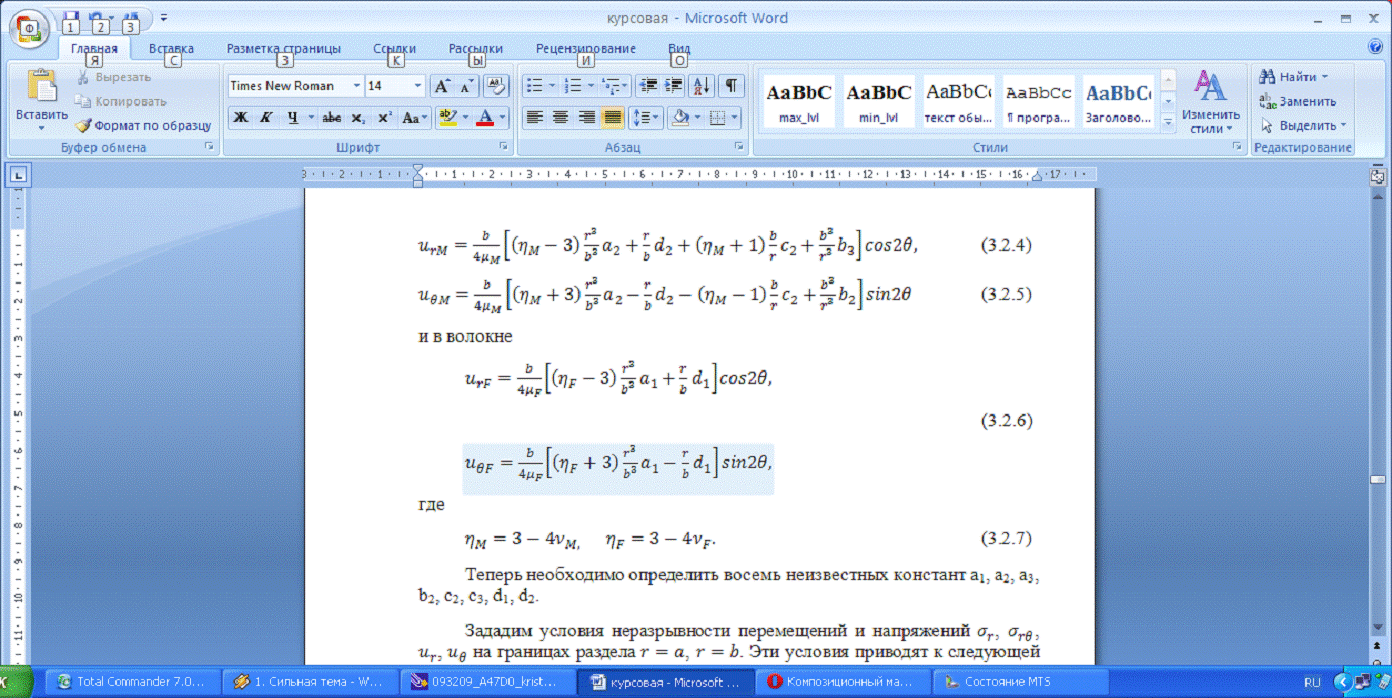
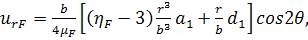

Теперь необходимо определить восемь неизвестных
констант a1,
a2,
a3,
b2,
c2,
c3,
d1,
d2.
Зададим условия неразрывности перемещений и
напряжений 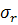 ,
,  ,
,
 ,
,
 на
границах раздела
на
границах раздела 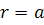 ,
, 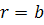 .
Эти условия приводят к следующей системе восьми независимых уравнений:
.
Эти условия приводят к следующей системе восьми независимых уравнений:
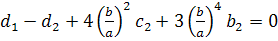 ,
,
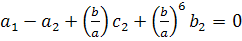 ,
,
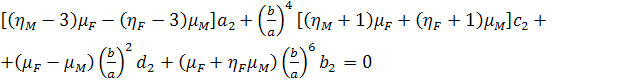 ,
,
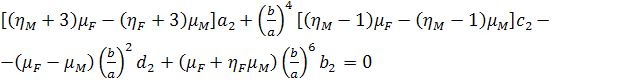 , (3.2.8)
, (3.2.8)
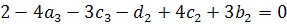 ,
,
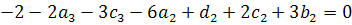 ,
,
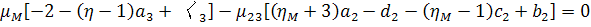
Принятый критерий определения эффективных
свойств требует равенства энергий деформирования гетерогенной среды и
эквивалентной гомогенной среды. Запишем это условие
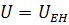 . (3.2.9)
. (3.2.9)
Теперь используем формулу Эшелби для оценки
энергии, запасаемой в гетерогенной среде
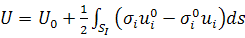 .
(3.2.10)
.
(3.2.10)
Интегрирование проводим по поверхности
составного включения (рис. 3.2.1). В формуле (3.2.10) член  относится
к энергии деформирования среды, у которой включение заменено окружающим его
материалом. Для рассматриваемой модели - это среда с эквивалентными однородными
свойствами. Таким образом,
относится
к энергии деформирования среды, у которой включение заменено окружающим его
материалом. Для рассматриваемой модели - это среда с эквивалентными однородными
свойствами. Таким образом,
 .
(3.2.11)
.
(3.2.11)
Объединяя (3.2.9) и (3.2.11) с формулой
(3.2.10), получим следующее выражение в полярных координатах:
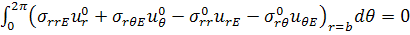 , (3.2.12)
, (3.2.12)
Входящие в (3.2.12) члены имеют вид
 ,
,
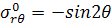 ,
,
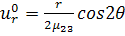 ,
(3.2.13)
,
(3.2.13)
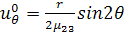 ,
,
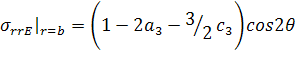 ,
,
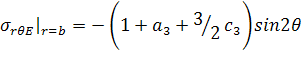 ,
,
а 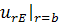 и
и
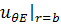 выражены
в соответствии с (3.2.1), (3.2.2). Подставив (3.2.1), (3.2.2) и (3.2.13) в
(3.2.1) и проведя интегрирование, приходим к простому результату:
выражены
в соответствии с (3.2.1), (3.2.2). Подставив (3.2.1), (3.2.2) и (3.2.13) в
(3.2.1) и проведя интегрирование, приходим к простому результату:
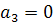 .
(3.2.14)
.
(3.2.14)
Выразив 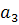 из
(3.2.8) и приравняв его нулю в соответствии с (3.2.14), получим соотношения для
определения
из
(3.2.8) и приравняв его нулю в соответствии с (3.2.14), получим соотношения для
определения  :
:
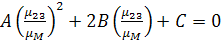 , (3.2.15)
, (3.2.15)
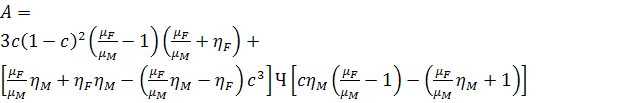 ,
,
 ,
,
 ,
,
а объемная доля волокон задается в виде 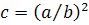 .
Можно показать, что при малых объемных долях волокон уравнение (3.2.15)
преобразуется к простому виду:
.
Можно показать, что при малых объемных долях волокон уравнение (3.2.15)
преобразуется к простому виду:
 . (3.2.15)
. (3.2.15)
Выражение (3.2.15) и есть то решение, которое мы
ищем. Это выражение позволяет найти модуль сдвига  для
модели композита, представленной на рис. 3.2.1, через характерные параметры и
объемные доли компонент.
для
модели композита, представленной на рис. 3.2.1, через характерные параметры и
объемные доли компонент.
3.3 Среда с малой объемной долей
пластинчатых включений
В предыдущем разделе показана возможность
анализа напряженного состояния среды с включениями в виде вытянутого эллипсоида
для моделирования волокнистого однонаправленного композита. Очевидно, включение
пластинчатой формы, являющееся компонентом слоистого композита, можно
представить в виде сплющенного эллипсоида.
Рассмотрим свойства среды с малой объемной долей
произвольно ориентированных тонких пластинчатых включений. Пластинчатые
включения будем моделировать сплющенными эллипсоидами.
Равновероятность всех возможных ориентаций
включений позволяет получить среду с изотропными эффективными свойствами.
Соответствующие формулы для нахождения 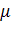 и
и
 имеют
следующий вид:
имеют
следующий вид:
 и
и 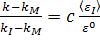 , (3.3.1)
, (3.3.1)
где 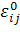 -
наложенное однородное деформированное состояние, а
-
наложенное однородное деформированное состояние, а  и
и
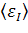 -
объемное осреднение соответственно сдвиговых и объемных деформаций по
включению. Таким образом, необходимо определить деформированное состояние
включений в среде с малой их объемной долей.
-
объемное осреднение соответственно сдвиговых и объемных деформаций по
включению. Таким образом, необходимо определить деформированное состояние
включений в среде с малой их объемной долей.
Деформацию включений можно записать в виде суммы
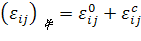 , (3.3.2)
, (3.3.2)
где 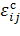 определено
в следующем виде
определено
в следующем виде
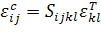 , (3.3.3)
, (3.3.3)
причем 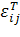 -
является решением следующего уравнения:
-
является решением следующего уравнения:
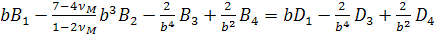 .
(3.3.4)
.
(3.3.4)
Решение уравнения (3.3.4) запишем в символической
форме:
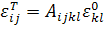 .
(3.3.5)
.
(3.3.5)
Объединяя (3.3.3) и (3.3.5), получим
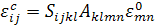 .
(3.3.6)
.
(3.3.6)
Подстановка (3.3.6) в (3.3.2) позволяет записать
последнее как
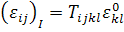 ,
(3.3.7)
,
(3.3.7)
Выражение (3.3.7) представляет собой прямое
преобразование приложенного поля однородной деформации в деформированное
состояние включения. Вспомним, что в рассматриваемых условиях деформированное
состояние включения однородно.
Рассмотрим далее заданное состояние объемной
деформации:
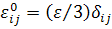 .
(3.3.9)
.
(3.3.9)
Подставляя (3.3.9) в (3.3.7), получим
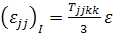 .
(3.3.10)
.
(3.3.10)
Теперь  есть
инвариант тензора
есть
инвариант тензора 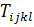 , и соотношение
(3.3.10) показывает, что изменение объема эллипсоидального включения не зависит
от его ориентации. Этот вывод необходим для решения рассматриваемой задачи. Подстановка
(3.3.10) в (3.3.1) дает
, и соотношение
(3.3.10) показывает, что изменение объема эллипсоидального включения не зависит
от его ориентации. Этот вывод необходим для решения рассматриваемой задачи. Подстановка
(3.3.10) в (3.3.1) дает
 . (3.3.11)
. (3.3.11)
Задача, таким образом, сводится к нахождению  ,
определенному в (3.3.8). Тензор
,
определенному в (3.3.8). Тензор  входит в (3.3.8) в
явном виде, а также неявно через
входит в (3.3.8) в
явном виде, а также неявно через  .
Следующий шаг состоит в поиске подходящей формы тензора
.
Следующий шаг состоит в поиске подходящей формы тензора  для
случая сплющенного эллипсоида.
для
случая сплющенного эллипсоида.
Тензор  в
необходимом частном виде определен следующим выражением:
в
необходимом частном виде определен следующим выражением:

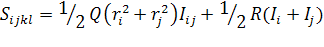 ,
,
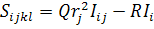
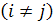 ,
,
Для подстановки в (3.3.12) следует вычислить 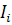 и
далее
и
далее 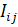 .
.
 , (3.3.13)
, (3.3.13)
где 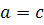 и
и
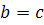 при
при
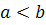 -
полуоси сплющенного эллипсоида, a
направление I соответствует оси
симметрии эллипсоида. Наибольший интерес для исследования представляют очень
тонкие эллипсоиды. Рассмотрим только предельный случай, когда
-
полуоси сплющенного эллипсоида, a
направление I соответствует оси
симметрии эллипсоида. Наибольший интерес для исследования представляют очень
тонкие эллипсоиды. Рассмотрим только предельный случай, когда 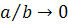 .
При этом из (3.3.13) следует
.
При этом из (3.3.13) следует
 ,
,
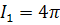 ,
, 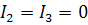 .
(3.3.14)
.
(3.3.14)
Сравним теперь (3.3.14) с соответствующими
выражениями для тонких вытянутых эллипсоидов:
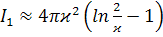 ,
,
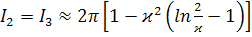 ,
,

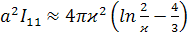 ,
,
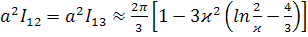 ,
,
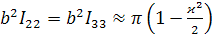 ,
,
 ,
,
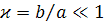 .
.
На основании (3.3.14) из формул Эшелби следуют
значения 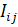 ,
,
 определяется
из (3.3.12) и, наконец,
определяется
из (3.3.12) и, наконец, 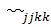 - из (3.3.8).
Подробные математические выкладки длинны, однако достаточно очевидны и подобны
уже проделанным в предыдущем разделе.
- из (3.3.8).
Подробные математические выкладки длинны, однако достаточно очевидны и подобны
уже проделанным в предыдущем разделе.
Конечный результат имеет вид
 .
(3.3.16)
.
(3.3.16)
Теперь у нас достаточно исходных данных для
решения задачи определения эффективного модуля сдвига 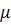 .
Для этого положим, что состояние сдвиговой деформации описывается следующим
образом:
.
Для этого положим, что состояние сдвиговой деформации описывается следующим
образом:
 ,
, 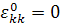 .
(3.3.17)
.
(3.3.17)
Эти условия после подстановки в (3.3.7) позволяют
определить деформации сдвига во включении:
 .
(3.3.18)
.
(3.3.18)
Далее следует найти объемное среднее 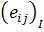 для
всех равновероятных ориентаций эллипсоидального включения.
для
всех равновероятных ориентаций эллипсоидального включения.
Обозначим среднее 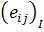 для
всех возможных ориентаций включения через
для
всех возможных ориентаций включения через  .
Эта величина быть линейной функцией инвариантов первой степени от
.
Эта величина быть линейной функцией инвариантов первой степени от 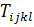 , а именно
, а именно 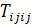 и
и
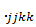 .
Для отыскания линейной функции от этих инвариантов запишем частные формы для
уравнения
.
Для отыскания линейной функции от этих инвариантов запишем частные формы для
уравнения
 ,
(3.3.19)
,
(3.3.19)
где из первоначальной формы уравнения
эффективных свойств (3.3.1) следует, что  -
константа. Для деформации сдвига в плоскости (1, 2) из (3.3.7) и (3.3.19) имеем
-
константа. Для деформации сдвига в плоскости (1, 2) из (3.3.7) и (3.3.19) имеем
 , где
, где 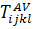 получается
интегрированием
получается
интегрированием 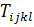 по всем возможным
ориентациям эллипсоида. Еще два уравнения подобного типа вытекают из условий
сдвигового деформирования в двух других плоскостях. Далее определяется
деформация сдвига типа
по всем возможным
ориентациям эллипсоида. Еще два уравнения подобного типа вытекают из условий
сдвигового деформирования в двух других плоскостях. Далее определяется
деформация сдвига типа  .
.
Это и есть искомый результат, так как 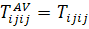 и
и
 вследствие
инвариантности свойств тензора
вследствие
инвариантности свойств тензора 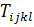 .
.
Таким образом, можно записать
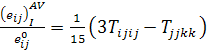 .
(3.3.20)
.
(3.3.20)
Поступая так же, как и при вычислении  ,
найдем
,
найдем 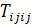 ,
,  для
предельного случая сплющенного эллипсоида и, используя (3.3.1) и (3.3.20),
получим
для
предельного случая сплющенного эллипсоида и, используя (3.3.1) и (3.3.20),
получим
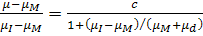 ,
(3.3.21)
,
(3.3.21)
где
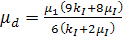 .
.
Окончательные результаты (3.3.16) и (3.3.21) и
составляют основу для оценки армирующего действия пластинчатых включений при
малой их объемной доле. Важность этих формул определяется не только тем, что
они позволяют непосредственно оценить армирующий эффект. Их можно рассматривать
и как значения максимально достижимого эффекта армирования.
Заключение
Композитные материалы изучаются уже достаточно
долго, как и используются в различных сферах жизни человека. Можно найти
большое количество областей применения композитов, начиная с военной
промышленности, машиностроения, научной деятельности, исследования космоса, и
заканчивая обычным бытом человека. Композиты во всех аспектах превосходят
обычные конструкционные материалы, это, конечно, связанно с большим интересом
человека к ним и большим количествам исследований в данной области.
В проблеме композиционных материалов,
разумеется, много сложных вопросов. Создание нового композита с заданными
свойствами - сложная и трудоемка с научной стороны задача. Зачастую, для
улучшения одних физических свойств приходится жертвовать другими. Сам процесс
изготовления композиции - сложная технологическая задача.
Оценка перспектив упрочнения металлов и
неметаллов приводит к выводам, что исследования в этом направлении приведут к
разработке целой группы новых конструкционных материалов, обладающих ценными
свойствами.
Список литературы:
1. Кристенсен, Р. Введение в
механику композитов / Р. Кристенсен. - М.
: Мир, 1982. - 436 с.
2. Ландау Л. Д. Теория упругости
/
Л.
Д. Ландау, Е. М. Лифшиц. - М. : Наука, 1965. - 204 с.
. Говорухин, В.Н., Цибулин,
В.Г. Компьютеры в математическом исследовании Maple,
MATLAB, LaTeX.
Учебный курс / В.Н. Говорухин. -
СП. : Питер, 2001, 456 с.
4. <http://ru.wikipedia.org/>
. <http://sopromat.h12.ru/content/biblio/mexan/chap1.php>