Сверточное кодирование
Введение
Подавляющее число современных систем
связи работает при передаче самого широкого спектра сообщений (от телеграфа до
телевидения) в цифровом виде. Из-за наличия помех в каналах связи сбой при
приеме любого элемента вызывает искажение цифровых данных, что может привести,
особенно в космических системах связи, к катастрофическим последствиям. В
настоящее время по каналам связи передаются цифровые данные со столь высокими
требованиями к достоверности передаваемой информации, что удовлетворить эти требования
традиционным совершенствованием антенно-фидерных трактов радиолиний,
увеличением излучаемой мощности, снижением собственного шума приемника
оказывается экономически невыгодным или просто невозможным.
Высокоэффективным средством борьбы с
помехами в цифровых системах связи является применение помехоустойчивого
кодирования, основанного на введении искусственной избыточности в передаваемое
сообщение, что приводит к расширению используемой полосы частот и уменьшению
информационной скорости передачи.
В связи с прогрессом в теории и
технике кодирования в современных системах связи используются в той или иной
степени помехоустойчивые коды. Так, в системах персонального радиовызова
(пейджинговые системы) используются блочные циклические коды, в сотовых системах
связи применяются как блочные, так и сверточные коды, в подавляющем большинстве
спутниковых систем связи, в основном, используются непрерывные сверточные коды.
Разработка программного эмулятора
системы передачи данных на основе сверточного кодирования, явиляется целью
данного дипломного проекта. Программа дает возможность поэтапно отследить
процесс сверточного кодирования и декодирования, а также имитацию передачи
данных по каналу связи.
В первом разделе данной
пояснительной записки определены задачи которые необходимо решить для
достижения цели данной работы. Также описаны требования к разработанному
программному эмулятору.
Во втором разделе раскрыта
актуальность использования сверточных кодов. Кратко раскрыт принцип передачи
данных по каналам связи. Рассмотрены возможные виды помехоустойчивых кодов и
произведена классификация сверточных кодов в общей системе помехоустойчивого
кодирования. Описаны алгоритмы сверточного кодирования и декодирования Витерби,
рассмотрены примеры.
В третьем разделе охарактеризована
структура программы. Описан алгоритм программы, осуществляющей сверточное
кодирование, декодирование и имитацию канала связи. Обоснован выбор языка
программирования и среда разработки для создания программных модулей. Также
произведено тестирование работы модулей программы и общее тестирование всего
программного эмулятора осуществляющего передачу данных методом сверточного
кодирования. Сделаны соответствующие выводы.
В четвертом разделе была проведена
экономическая оценка внедрения и разработки программного продукта. Рассчитаны
затраты на создание данного ПО и определена его цена.
В пятом разделе рассмотрены вопросы,
касающиеся охраны труда и окружающей среды, проведен анализ условий труда в
помещении, в котором разработано данное ПО.
В шестом разделе коротко рассмотрены
вопросы касающиеся гражданской обороны.
Программный эмулятор предназначен
для использования в учебном процессе. Использование данной программы позволяет
существенно ускорить и упростить процесс расчета.
сверточный кодирование
программный
1. Постановка задачи
Результатом данной работы должен
стать программный модуль, производящий сверточное кодирование/декодирование и
имитацию физического канала связи.
Для достижения цели работы
необходимо решить следующие задачи:
- Исследовать возможные виды
помехоустойчивых кодов.
- Классифицировать сверточный
код в общей системе помехоустойчивого кодирования
Ознакомиться с методом
сверточного кодирования
Ознакомиться с методом
сверточного декодирования
Разработать алгоритм
программы, осуществляющей сверточное кодирование/декодирование и имитацию
канала связи.
В соответствии со
спроектированным алгоритмом, предварительно выбрав язык программирования и
среду разработки, создать программный модуль.
Входными данными в данной работе
являются:
- Вид помехоустойчивого
кодирования: сверточный код
- Эффективная скорость
передачи кода R=1/2
Алгоритм декодирования
Витерби
Графическое отображение
решетчатой диаграммы при декодировании
Локальная версия программы,
которая устанавливается на конкретный компьютер, авторизуется и работает только
на нем
Программа предназначена для
работы в среде ОС Windows. К аппаратным средствам выдвигаются те же требования, которые
необходимы операционной системе для стабильной работы: 1Гб оперативной памяти и
более, процессор с частотой 1 ГГц, порядка 5 Мб дискового пространства,
видеокарта с памятью 32 Мб и более.
2. Предметная область
.1 Актуальность
использования сверточных кодов
Сверточные коды нашли широкое
применение в сотовых и в спутниковых системах связи [1].
Системы сотовой подвижной связи
(ССПС) впервые стали эксплуатироваться в конце 70-х - начале 80-х годов.
Сотовый принцип топологии сети с повторным использованием частот в сотах во
многом решил проблему дефицита частотного ресурса и в настоящее время является
основным в создаваемых системах подвижной связи общего пользования.
Стандартизация в области ССПС привела к тому, что на смену девяти отдельным
аналоговым стандартам сотовой связи первого поколения пришли три цифровых
стандарта второго поколения (GSM, D-AMPS, JDC), один из них - GSM признан
«глобальным». В связи с широким распространением этого стандарта во всем мире,
GSM стали расшифровывать как Global System for Mobile Communications (глобальная система для мобильной связи).
Каналы связи в стандарте GSM разделяются
на физические и логические. Физический канал образуется путем комбинирования
временного (ВРК) и частотного (ЧРК) разделения сигналов.
До формирования физического канала
сообщения данные, представленные в цифровом виде, группируются и объединяются в
логические каналы двух типов:
- канал связи - для передачи
кодированной речи и данных;
- канал управления - для
передачи сигналов управления и синхронизации.
Кодирование и перемежение являются
важными ступенями тракта обработки информационных цифровых сигналов и сигналов
управления. В цифровых ССПС осуществляется преобразование аналогового речевого
сигнала в цифровую последовательность, которая подвергается шифрованию и
кодированию, что необходимо для защиты информации от ошибок в процессе передачи
и приема. Для этого используются:
- блочное кодирование - для
быстрого обнаружения ошибок при приеме;
- сверточное кодирование -
для исправления одиночных ошибок;
перемежение - для
преобразования пакета ошибок в одиночные ошибки.
В цифровых ССПС кодируются все передаваемые
по радиоканалу сигналы. В аналоговых ССПС кодируют цифровые сигналы управления.
При кодировании преследуют различные
цели. Самый низкий уровень имеет выявление (обнаружение) ошибок в полностью
принятом сигнале. По сравнению с ним более высоким уровнем обладает обнаружение
ошибок в отдельных сегментах сигнала, которое может быть выполнено с помощью
простых блоковых кодов, например, с проверкой на четность. В современных
системах используют коды с исправлением ошибок. Это могут быть блоковые коды (каналы
сигнализации в NMT-450, DECT) и сверточные коды (GSM, системы с кодовым
разделением - CDMA). Выбор кода определяет большое число факторов:
характеристики каналов, скорость передачи, вид модуляции и т. п. Важное
значение приобретает элементно-технологическая база. Применение
быстродействующих процессорных СБИС открыло путь к использованию мощных
сверточных кодов при обработке сигналов в реальном времени. Сверточные коды
хорошо исправляют случайные одиночные ошибки, но дают плохие результаты при
пакетах ошибок. Поэтому сверточное кодирование и совмещают с перемежением
(перетасовкой) информационных символов, которое обеспечивает преобразование
пакетов ошибок в одиночные.
В ССПС основные свойства речевых
каналов и каналов управления значительно отличаются друг от друга. Для речевых
каналов необходима связь в реальном масштабе времени с короткими задержками при
сравнительно низких требованиях к вероятности ошибки в канале. Для канала
управления требуется абсолютная достоверность данных и исправление ошибок, но
допускается более длительное время передачи и задержки.
В различных логических каналах
используются различные сверточные коды, поскольку скорости передачи и
требования по защите от ошибок также различны. Для упрощения процедур
кодирования и декодирования при формировании кодов используются только
несколько полиномов. Это позволяет использовать в стандарте GSM сверточный код
с одной скоростью R = 1/2. В ряде режимов для выравнивания скорости в речевом
канале до R = 1/2 применяют прореживание, т. е. периодический пропуск
(перфорацию) кодированных символов. Поскольку сложность декодирования по
наиболее выгодному, с точки зрения реализации, алгоритму Витерби возрастает
экспоненциально с увеличением длины кодового ограничения l, то типовые значения
ДКО малы и лежат в интервале l = 3 - 10.
Сверточные коды и алгоритмы
декодирования по максимуму правдоподобия, алгоритм Витерби находят основное
применение в системах космической и спутниковой связи. Это объясняется тем, что
каналы связи в этих системах близки по своим свойствам к каналам с белым
гауссовским шумом, которые являются симметричными каналами без памяти. Для
подобных систем характерны жесткие ограничения по мощности передаваемого
сигнала, поэтому для них важно осуществить наиболее эффективное кодирование и
декодирование, позволяющее уменьшить вероятность ошибки на декодированный
информационный символ при малом энергетическом потенциале [1].
Для существенного улучшения
помехоустойчивости при использовании сверточных кодов необходимо увеличивать
скорость передачи символов, а следовательно, и ширину полосы, например, в 2
раза при относительной скорости передачи кода 1/2 или в 4/3 раза при
относительной скорости 3/4. Таким образом, применение сверточных кодов
оказывается особенно выгодным в спутниковых системах связи, энергетический
потенциал которых ограничивается мощностью бортового ретранслятора, т.е. в
каналах, где определяющим фактором является ограничение мощности, а не полосы
частот [1]. В системах с ограниченной энергетикой кодирование позволяет уменьшить
необходимое отношение сигнал - шум, оптимальным образом распределить мощность
ретранслятора между каналами и увеличить число каналов.
Большая задержка на трассах
распространения в цифровых спутниковых системах связи (ССС) не позволяет
использовать для повышения верности системы с автозапросом (с обратным
каналом), в которых коды служат для обнаружения ошибок. Поэтому в ССС и
используются, в основном, сверточные коды, решающие задачу непосредственного
исправления ошибок.
Таким образом, сверточные коды применяются
в широком спектре современных систем связи.
2.2 Передача информации
по каналам связи
Канал связи - это совокупность
средств, предназначенных для передачи сигналов (сообщений).
Для анализа информационных процессов
в канале связи можно использовать его обобщенную схему, приведенную на рис.
2.1.

Рисунок 2.1 - Обобщенная схема
канала связи
На рисунке 2.1 приняты следующие
обозначения: X, Y, Z, W - сигналы, сообщения; f - помеха; ЛС - линия связи; ИИ,
ПИ - источник и приемник информации; П - преобразователи (кодирование,
модуляция, декодирование, демодуляция).
Существуют различные типы каналов,
которые можно классифицировать по различным признакам:
1. По типу линий связи: проводные;
кабельные; оптико-волоконные;
2. линии электропередачи;
радиоканалы и т.д.
. По характеру сигналов:
непрерывные; дискретные; дискретно-непрерывные (сигналы на входе системы
дискретные, а на выходе непрерывные, и наоборот).
. По помехозащищенности:
каналы без помех; с помехами.
Каналы связи характеризуются:
1. Емкость канала определяется как
произведение времени использования канала Tк, ширины спектра частот,
пропускаемых каналом Fк и динамического диапазона Dк.,
который характеризует способность канала передавать различные уровни сигналов
Vк = Tк Fк
Dк. (1)
Условие согласования сигнала с
каналом:
c £ Vk; Tc
£ Tk; Fc
£ Fk; Vc
£ Vk; Dc
£ Dk.
2. Скорость передачи информации -
среднее количество информации, передаваемое в единицу времени.
3. Пропускная способность
канала связи - наибольшая теоретически достижимая скорость передачи информации
при условии, что погрешность не превосходит заданной величины.
. Избыточность - обеспечивает
достоверность передаваемой информации (R = 0¸1).
Скорость передачи данных в
значительной мере зависит от передающей среды в каналах связи, в качестве
которых используются различные типы линий связи.
Проводные:
1. Проводные - витая пара (что
частично подавляет электромагнитное излучение других источников). Скорость
передачи до 1 Мбит/с. Используется в телефонных сетях и для передачи данных.
2. Коаксиальный кабель.
Скорость передачи 10-100 Мбит/с - используется в локальных сетях, кабельном
телевидении и т.д.
. Оптико-волоконная. Скорость
передачи 1 Гбит/с.
4. В средах 1-3 затухание в дБ
линейно зависит от расстояния, т.е. мощность падает по экспоненте. Поэтому
через определенное расстояние необходимо ставить регенераторы (усилители).
Радиолинии:
. Радиоканал. Скорость передачи
100-400 Кбит/с. Использует радиочастоты до 1000 МГц. До 30 МГц за счет
отражения от ионосферы возможно распространение электромагнитных волн за
пределы прямой видимости. Но этот диапазон сильно зашумлен (например,
любительской радиосвязью). От 30 до 1000 МГц - ионосфера прозрачна и необходима
прямая видимость. Антенны устанавливаются на высоте (иногда устанавливаются
регенераторы). Используются в радио и телевидении.
. Микроволновые линии. Скорости
передачи до 1 Гбит/с. Используют радиочастоты выше 1000 МГц. При этом
необходима прямая видимость и остронаправленные параболические антенны.
Расстояние между регенераторами 10-200 км. Используются для телефонной связи,
телевидения и передачи данных.
. Спутниковая связь. Используются
микроволновые частоты, а спутник служит регенератором (причем для многих
станций). Характеристики те же, что у микроволновых линий.
2.3 Помехоустойчивые
коды
Обнаружение ошибок в технике связи -
действие, направленное на контроль целостности данных при
записи/воспроизведении информации или при её передаче по линиям связи.
Исправление ошибок (коррекция ошибок) - процедура восстановления информации
после чтения её из устройства хранения или канала связи.
Для уменьшения вероятности ошибок
применяют помехоустойчивое кодирование. Его сущность - введение при кодировании
дополнительной избыточности, что увеличивает возможность обнаружения и
исправления ошибок. Применяемые при этом коды называются корректирующими.
Для обнаружения ошибок используют
коды обнаружения ошибок, для исправления - корректирующие коды (коды,
исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
Помеха - белый шум с Гауссовским
законом распределения. В природе и технике «чисто» белый шум (то есть белый
шум, имеющий одинаковую спектральную мощность на всех частотах) не встречается
(ввиду того, что такой сигнал имел бы бесконечную мощность), однако под
категорию белых шумов попадают любые шумы, спектральная плотность которых
одинакова (или слабо отличается) в рассматриваемом диапазоне частот. Иногда
ошибочно предполагается, что гауссовский шум (то есть шум с гауссовским
распределением по амплитуде - нормальное распределение) обязательно является
белым шумом. Однако эти понятия неэквивалентны. Гауссовский шум предполагает
распределение значений сигнала в виде нормального распределения, тогда как
термин «белый» имеет отношение к корреляции сигнала в два различных момента
времени (эта корреляция не зависит от распределения амплитуды шума).
Нормальное распределение, также
называемое гауссовским распределением или распределением Гаусса - распределение
вероятностей, которое играет важнейшую роль во многих областях знаний.
Физическая величина подчиняется нормальному распределению, когда она подвержена
влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне
распространена, поэтому можно сказать, что из всех распределений в природе чаще
всего встречается именно нормальное распределение - отсюда и произошло одно из
его названий. Нормальное распределение зависит от двух параметров - смещения и
масштаба, то есть является с математической точки зрения не одним
распределением, а целым их семейством. Значения параметров соответствуют
значениям среднего (математического ожидания) и разброса (стандартного
отклонения).
2.3.1 Способы борьбы с
ошибками
В процессе хранения данных и
передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности
данных и исправление ошибок - важные задачи на многих уровнях работы с
информацией (в частности, физическом, канальном, транспортном уровнях модели
OSI).
В системах связи возможны несколько
стратегий борьбы с ошибками:
обнаружение ошибок в блоках данных и
автоматический запрос повторной передачи повреждённых блоков - этот подход
применяется в основном на канальном и транспортном уровнях;
обнаружение ошибок в блоках данных и
отбрасывание повреждённых блоков - такой подход иногда применяется в системах
потокового мультимедиа, где важна задержка передачи и нет времени на повторную
передачу;
исправление ошибок (forward error
correction) применяется на физическом уровне.
2.3.2 Коды обнаружения и
исправления ошибок
Корректирующие коды - коды, служащие
для обнаружения или исправления ошибок, возникающих при передаче информации под
влиянием помех, а также при её хранении.
Для этого при записи (передаче) в
полезные данные добавляют специальным образом структурированную избыточную
информацию (контрольное число), а при чтении (приёме) её используют для того,
чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое
можно исправить, ограничено и зависит от конкретного применяемого кода.
С кодами, исправляющими ошибки,
тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут
только установить факт наличия ошибки в переданных данных, но не исправить её.
В действительности, используемые
коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды,
исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть
также использован для обнаружения ошибок (при этом он будет способен обнаружить
большее число ошибок, чем был способен исправить).
По способу работы с данными коды,
исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты
постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные,
работающие с данными как с непрерывным потоком. Свёрточные коды, как правило,
порождаются дискретной линейной инвариантной во времени системой. Поэтому, в
отличие от большинства блоковых кодов, свёрточное кодирование - очень простая
операция, чего нельзя сказать о декодировании. Кодирование свёрточным кодом
производится с помощью регистра сдвига (автомат Мили), отводы от которого
суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.
Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби,
который пытается восстановить переданную последовательность согласно критерию
максимального правдоподобия. Свёрточные коды эффективно работают в канале с
белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер
ошибается, на его выходе всегда возникает пакет ошибок.
2.4 Классификация конечных абстрактных автоматов
Абстрактный автомат (в теории
алгоритмов) - математическая абстракция, модель дискретного устройства,
имеющего один вход, один выход и в каждый момент времени находящегося в одном
состоянии из множества возможных. На вход этому устройству поступают символы
одного языка, на выходе оно выдаёт символы (в общем случае) другого языка. По
способу формирования функций выходов выделяют автоматы Мили и Мура.
2.4.1 Автомат Мили
Автомат Мили (англ. Mealy machine) -
конечный автомат, выходная последовательность которого (в отличие от автомата
Мура) зависит от состояния и входной последовательности.
Математическая модель автомата
состоит из совокупность пяти объектов:

где:
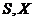 и
и  -
конечные непустые множества, а
-
конечные непустые множества, а 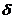 и
и 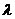 -
отображения вида:
-
отображения вида:
 и
и 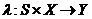
со связью элементов
множеств S, X и Y в абстрактном времени T = {0, 1, 2, …}
уравнениями:
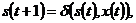
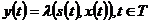
(Отображения 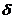 и
и
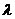 получили
названия, соответственно функции переходов и функции выходов автомата A).
получили
названия, соответственно функции переходов и функции выходов автомата A).
Особенностью автомата
Мили является то, что функция выходов является двухаргументной и символ в
выходном канале y(t) обнаруживается только при наличии символа во
входном канале x(t).
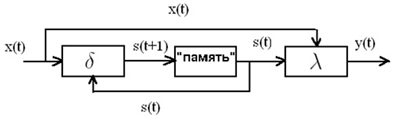
Рисунок 2.2 -
Функциональная схема автомата Мили
2.4.2 Автомат Мура
Зависимость выходного сигнала только
от состояния представлена в автоматах типа Мура (англ. Moore machine). В
автомате Мура функция выходов определяет значение выходного символа только по
одному аргументу - состоянию автомата. Эту функцию называют также функцией
меток, так как она каждому состоянию автомата ставит метку на выходе.
Конечным детерминированным автоматом
типа Мура называется совокупность пяти объектов:
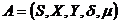
где 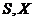 ,
,
 и
и
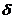 -
соответствуют определению автомата типа Мили, а
-
соответствуют определению автомата типа Мили, а 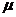 является отображением
вида:
является отображением
вида: 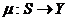 .
.
с зависимостью состояний
и выходных сигналов во времени уравнением:
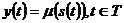
Особенностью автомата
Мура является то, что символ y(t) в выходном канале существует все
время, пока автомат находится в состоянии s(t).
Для любого автомата Мура
существует автомат Мили, реализующий туже самую функцию. И наоборот: для любого
автомата Мили существует соответствующий автомат Мура.
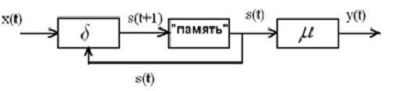
Рисунок 2.3 -
Функциональная схема автомата Мура
2.5 Сверточное
кодирование
Типичная функциональная
схема системы цифровой связи использующая сверточное кодирование/декодирование
и модуляцию/демодуляцию, показана на рисунке 2.4. Исходное сообщение на входе
обозначается последовательностью 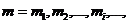 где
где 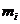 ,
- двоичный знак (бит), a i - индекс времени. Если быть точным, то
элементы m следовало бы дополнять индексом члена класса (например, для
бинарного кода, 1 или 0) и индексом времени. В дальнейшем для простоты будем
использовать только индекс, обозначающий время (или расположение элемента
внутри последовательности). Будем предполагать, что все
,
- двоичный знак (бит), a i - индекс времени. Если быть точным, то
элементы m следовало бы дополнять индексом члена класса (например, для
бинарного кода, 1 или 0) и индексом времени. В дальнейшем для простоты будем
использовать только индекс, обозначающий время (или расположение элемента
внутри последовательности). Будем предполагать, что все 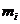 ,
равновероятно равны единице или нулю и независимы между собой. Будучи
независимой, последовательность битов нуждается в некоторой избыточности, т.е.
знание о бите
,
равновероятно равны единице или нулю и независимы между собой. Будучи
независимой, последовательность битов нуждается в некоторой избыточности, т.е.
знание о бите 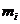 ,
не дает никакой информации о бите
,
не дает никакой информации о бите 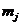 , (при
, (при 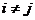 ).
Кодер преобразует каждую последовательность m в уникальную
последовательность кодовых слов
).
Кодер преобразует каждую последовательность m в уникальную
последовательность кодовых слов 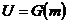 . Даже несмотря на то
что последовательность m однозначно определяет последовательность U,
ключевой особенностью сверточных кодов является то, что данный k-кортеж внутри m не однозначно определяет связанные с ним n-кортежи внутри U, поскольку кодирование каждого из k-кортежей является функцией не только k-кортежей,
но и предыдущих К-1 k-
кортежей. Последовательность U можно разделить на последовательность
кодовых слов:
. Даже несмотря на то
что последовательность m однозначно определяет последовательность U,
ключевой особенностью сверточных кодов является то, что данный k-кортеж внутри m не однозначно определяет связанные с ним n-кортежи внутри U, поскольку кодирование каждого из k-кортежей является функцией не только k-кортежей,
но и предыдущих К-1 k-
кортежей. Последовательность U можно разделить на последовательность
кодовых слов: 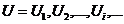 .
Каждое кодовое слово U, состоит из двоичных кодовых символов, часто
называемых канальными символами, канальными битами, или битами кода; в отличие
от битов входного сообщения, кодовые символы не являются независимыми.
.
Каждое кодовое слово U, состоит из двоичных кодовых символов, часто
называемых канальными символами, канальными битами, или битами кода; в отличие
от битов входного сообщения, кодовые символы не являются независимыми.
В типичных системах
связи последовательность кодовых слов U модулируется сигналом 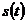 .
В ходе передачи сигнал искажается шумом, в результате чего, как показано на
рисунке 2.4, получается сигнал
.
В ходе передачи сигнал искажается шумом, в результате чего, как показано на
рисунке 2.4, получается сигнал 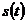 и демодулированная
последовательность
и демодулированная
последовательность 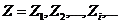 Задача
декодера состоит в получении оценки
Задача
декодера состоит в получении оценки  исходной
последовательности сообщения с помощью полученной последовательности Z и
априорных знаний о процедуре кодирования.
исходной
последовательности сообщения с помощью полученной последовательности Z и
априорных знаний о процедуре кодирования.
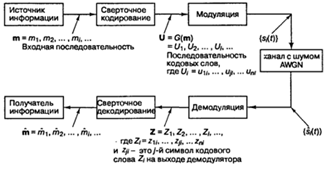
Рисунок 2.4 -
Кодирование/декодирование и модуляция/демодуляция в канале связи
Обычный сверточный
кодер, показанный на рисунке 2.5, реализуется с kK-разрядным
регистром сдвига и n
сумматорами по модулю 2, где K
- длина кодового ограничения. Длина кодового ограничения - это количество k-битовых сдвигов, после которых один информационный бит может
повлиять на выходной сигнал кодера. В каждый момент времени на место первых k разрядов регистра перемещаются k
новых бит; все биты в регистре смещаются на k
разрядов вправо, и выходные данные n
сумматоров последовательно дискретизируются, давая, в результате, биты кода.
Затем эти симво лы кода используются модулятором для формирования сигналов, которые
будут пере даны по каналу. Поскольку для каждой входной группы из к бит
сообщения имеется n
бит кода, степень кодирования равна k/n бит сообщения на бит кода, где k
< n.
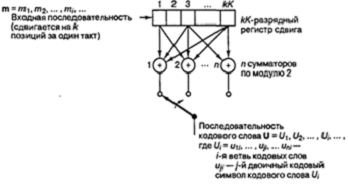
Рисунок 2.5 - Сверточный
кодер с длиной кодового ограничения K
и степенью кодирования k/n
Рассмотрим только
наиболее часто используемые двоичные сверточные кодеры, для которых k - 1, т.е. те кодирующие устройства, в которых биты сооб щения
сдвигаются по одному биту за раз, хотя обобщение на алфавиты более высоких
порядков не вызывает никаких затруднений [2]. Для кодера с k = 1, за i-й
момент времени бит сообщения 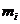 , будет перемещен на
место первого разряда регистра сдвига; все предыдущие биты в регистре будут
смещены на один разряд вправо, а выход ной сигнал n
сумматоров будет последовательно оцифрован и передан. Поскольку для каждого
бита сообщения имеется
, будет перемещен на
место первого разряда регистра сдвига; все предыдущие биты в регистре будут
смещены на один разряд вправо, а выход ной сигнал n
сумматоров будет последовательно оцифрован и передан. Поскольку для каждого
бита сообщения имеется 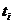 n бит кода, степень кодирования равна 1/n.
Имеющиеся в момент времени
n бит кода, степень кодирования равна 1/n.
Имеющиеся в момент времени 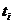 , n кодовых символов составляют i-е
кодовое слово ветви,
, n кодовых символов составляют i-е
кодовое слово ветви, 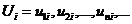 где
где
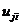 (j - 1, 2, ..., n)
- это j-й кодовый символ, принадлежащий i-му
кодовому слову ветви. Отметим, что для кодера со степенью кодирования 1/n, kK-разрядный
регистр сдвига для простоты можно называть K-разрядным
регистром, а длину кодового ограничения K,
которая выражается в единицах разрядов k-кортежей,
можно именовать длиной кодового ограничения в битах.
(j - 1, 2, ..., n)
- это j-й кодовый символ, принадлежащий i-му
кодовому слову ветви. Отметим, что для кодера со степенью кодирования 1/n, kK-разрядный
регистр сдвига для простоты можно называть K-разрядным
регистром, а длину кодового ограничения K,
которая выражается в единицах разрядов k-кортежей,
можно именовать длиной кодового ограничения в битах.
2.5.1 Представление
сверточного кодера
Чтобы иметь возможность
описывать сверточный код, необходимо определить кодирующую функцию 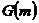 так,
чтобы по данной входной последовательности m
можно было быстро вычислить выходную последовательность U. Для реализации сверточного кодирования используется несколько
методов; наиболее распространенными из них являются графическая связь, векторы,
полиномы связи, диаграмма состояния, древовидная и решетчатая диаграммы. Все
они рассматриваются ниже.
так,
чтобы по данной входной последовательности m
можно было быстро вычислить выходную последовательность U. Для реализации сверточного кодирования используется несколько
методов; наиболее распространенными из них являются графическая связь, векторы,
полиномы связи, диаграмма состояния, древовидная и решетчатая диаграммы. Все
они рассматриваются ниже.
2.5.2 Представление
связи
При рассмотрении сверточных кодеров
в качестве модели будем использовать сверточный кодер, показанный на рисунке
2.6. На этом рисунке изображен сверточный кодер (2, 1) с длиной кодового
ограничения K = 3. В нем имеется n = 2 сумматора по модулю 2; следовательно, степень кодирования
кода k/n равна 1/2. При каждом поступлении бит помещается в крайний левый
разряд, а биты регистра смещаются на одну позицию вправо. Затем коммутатор на
выходе дискретизирует выходы всех сумматоров по модулю 2 (т.е. сначала верхний
сумматор, затем нижний), в результате чего формируются пары кодовых символов,
образующих кодовое слово, связанное с только что поступившим битом. Это
выполняется для каждого входного бита. Выбор связи между сумматорами и
разрядами регистра влияет на характеристики кода. Всякое изменение в выборе
связей приводит в результате к различным кодам.
В отличие от блочных кодов, имеющих
фиксированную длину слова n, в сверточных кодах нет определенного размера блока. Однако с
помощью периодического отбрасывания сверточным кодам часто принудительно
придают блочную структуру. Это требует некоторого количества нулевых разрядов,
присоединенных к концу входной последовательности данных, которые служат для
очистки (или «промывки») регистра сдвига от бит данных. Поскольку добавленные
нули не несут дополнительной информации, эффективная степень кодирования будет
ниже k/n. Чтобы степень кодирования оставалась близкой к k/n, период отбрасывания
чаще всего делают настолько большим, насколько это возможно.
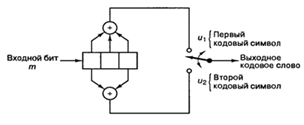
Рисунок 2.6 - Сверточный кодер
(степень кодирования 1/2, K - 3)
Один из способов
реализации кодера заключается в определении n
векторов связи, по одному на каждый из n
сумматоров по модулю 2. Каждый вектор имеет размерность K и описывает связь регистра сдвига кодера с соответствующим
сумматором по модулю 2. Единица на i-Й
позиции вектора указывает на то, что соответствующий разряд в регистре сдвига
связан с сумматором по модулю 2, а нуль в данной позиции указывает, что связи
между разрядом и сумматором по модулю 2 не существует. Для кодера на рисунке
2.6 можно записать вектор связи 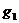 для верхних связей, a
для верхних связей, a 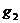 -
для нижних.
-
для нижних.
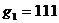

Предположим теперь, что
вектор сообщения m = 1 0 1 закодирован
с использованием сверточного кода и кодера, показанного на рисунке 2.6. Введены
три бита сообщения, по одному в момент времени  ,
, 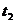 и
и
 ,
как показано на рисунке 2.7. Затем для очистки регистра в моменты времени t4 и t5
введены (К - 1) = 2 нуля, что в результате приводит к смещению конечного
участка на всю длину регистра. Последовательность на выходе выглядит следующим
образом: 1 1 1 0 0 0 1 0 1 1, где крайний левый символ представляет первую
передачу. Для декодирования сообщения нужна полная последовательность на выходе
(включающая кодовые символы). Для удаления со общения из кодера требуется на
единицу меньше нулей, чем имеется разрядов в регистре, или К - 1 очищенных бит.
В момент времени t6
показан нулевой выход, это должно дать читателю возможность убедиться в том,
что в момент времени t5
регистр устанавливается в исходное состояние. Таким образом, в
момент времени t6 уже
можно передавать новое сообщение.
,
как показано на рисунке 2.7. Затем для очистки регистра в моменты времени t4 и t5
введены (К - 1) = 2 нуля, что в результате приводит к смещению конечного
участка на всю длину регистра. Последовательность на выходе выглядит следующим
образом: 1 1 1 0 0 0 1 0 1 1, где крайний левый символ представляет первую
передачу. Для декодирования сообщения нужна полная последовательность на выходе
(включающая кодовые символы). Для удаления со общения из кодера требуется на
единицу меньше нулей, чем имеется разрядов в регистре, или К - 1 очищенных бит.
В момент времени t6
показан нулевой выход, это должно дать читателю возможность убедиться в том,
что в момент времени t5
регистр устанавливается в исходное состояние. Таким образом, в
момент времени t6 уже
можно передавать новое сообщение.
2.5.3 Реакция кодера на
импульсное возмущение
Мы можем описать кодер через его
импульсную характеристику, т.е. в виде отклика кодера на единичный проходящий
бит. Рассмотрим содержимое регистра (рисунок 2.6) при прохождении через него
двоичной единицы.
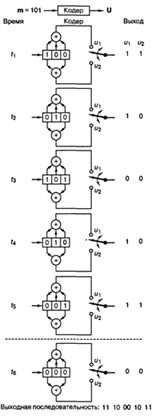
Рисунок 2.7 - Сверточное кодирование
последовательности сообщения со степенью кодирования 1/2 кодером с К = 3.

Рис.
Последовательность на выходе при
единице на входе называется откликом кодера на импульсное возмущение, или его
импульсной характеристикой. Для входной последовательности m = 1 0 1 данные на выходе могут быть
найдены путем суперпозиции или линейного сложения смещенных во времени входных
"импульсов".
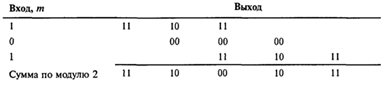
Рис.
Следует отметить, что эти данные на
выходе такие же, как и на рис. 2.7, что указывает на линейность сверточных
кодов - точно так же как и в блочных кодах. Название сверточный кодер (convolutional encoder) возникло именно
вследствие этого свойства генерации данных на выходе с помощью линейного
сложения (или свертки) смещенных во времени импульсов последовательности на
входе с импульс ной характеристикой кодера. Такие устройства часто описываются
с помощью матричного генератора бесконечного порядка [2].
Отметим, что в рассмотренном выше
примере входной последовательности из 3 бит и последовательности на выходе из
10 бит эффективная степень кодирования составляет k/n = 3/10, что значительно меньше
величины 1/2, которую можно было бы ожидать, зная, что каждый бит данных на
входе порождает пару канальных битов на выходе. Причина этого заключается в
том, что финальные биты данных нужно про вести через кодер. Все канальные биты
на выходе требуются в процессе декодирования. Если бы сообщение было длиннее,
скажем 300 бит, последовательность кодовых слов на выходе содержала бы 640 бит
и значение для степени кодирования кода 300/640 было бы значительно ближе к
1/2.
2.5.4 Полиномиальное
представление
Иногда связи кодера
описываются с помощью полиномиального генератора для описания реализации
обратной связи регистра сдвига циклических кодов. Сверточный кодер можно
представить в виде набора из n
полиномиальных генераторов, по одному для каждого из n
сумматоров по модулю 2. Каждый полином имеет порядок K
- 1 или меньше и описывает связь кодирующего регистра сдвига с соответствующим
сумматором по модулю 2, почти так же как и вектор связи. Коэффициенты возле
каждого слагаемого поли нома порядка (К - 1) равны либо 1, либо 0, в
зависимости от того, имеется ли связь между регистром сдвига и сумматором по
модулю 2. Для кодера на рис 2.6 можно записать полиномиальный генератор 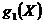 для
верхних связей и
для
верхних связей и 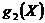 -
для нижних.
-
для нижних.
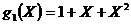
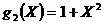
Здесь слагаемое самого
нижнего порядка в полиноме соответствует входному разряду регистра. Выходная
последовательность находится следующим образом:
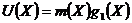 чередуется с
чередуется с 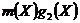
Прежде всего, выразим
вектор сообщения m = 1 0 1 в виде
полинома, т.е. 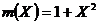 .
Для очистки регистра мы снова будем предполагать использование нулей, следующих
за битами сообщения. Тогда выходящий полином U(X), или выходящая последовательность U
кодера (рис. 2.6) для входного сообщения m
может быть найдена следующим образом:
.
Для очистки регистра мы снова будем предполагать использование нулей, следующих
за битами сообщения. Тогда выходящий полином U(X), или выходящая последовательность U
кодера (рис. 2.6) для входного сообщения m
может быть найдена следующим образом:
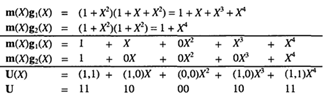
Рис.
В этом примере мы начали
обсуждение с того, что сверточный кодер можно трактовать как набор регистров
сдвига циклического кода. Мы представили кодер в виде полиномиальных генераторов,
с помощью которых описываются циклические коды. Однако мы пришли к той же
последовательности на выходе, что и на рис. 2.7, и к той же, что и в предыдущем
разделе, полученной при описании реакции на импульсное возмущение.
2.5.5 Представление
состояния и диаграмма состояний
Сверточный кодер
принадлежит классу устройств, известных как конечный авто мат. Для сверточного
кода со степенью кодирования 1/n
состояние представлено содержимым K
- 1 крайних правых разрядов (рис. 2.7). Знание состояния плюс знание следующих
данных на входе является необходимым и достаточным условием для определения
данных на выходе. Итак, пусть состояние кодера в момент времени 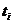 ,
определяется как
,
определяется как 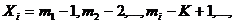 .
i-я ветвь кодовых слов U,
полностью определяется состоянием X, и введенными в настоящее время
битами
.
i-я ветвь кодовых слов U,
полностью определяется состоянием X, и введенными в настоящее время
битами 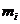 ;
таким образом, состояние X, описывает предысторию кодера для определения
данных на его выходе. Состояния кодера считаются Марковскими в том смысле, что
вероятность
;
таким образом, состояние X, описывает предысторию кодера для определения
данных на его выходе. Состояния кодера считаются Марковскими в том смысле, что
вероятность 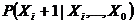 нахождения
в состоянии
нахождения
в состоянии  ,
определяемая всеми предыдущими состояниями, зависит только от самого последнего
состояния
,
определяемая всеми предыдущими состояниями, зависит только от самого последнего
состояния 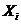 ,
т.е. она равна
,
т.е. она равна 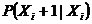 .
.
Одним из способов
представления простых кодирующих устройств является диаграмма состояния (state diagram);
такое представление кодера, изображенного на рис. 2.6, показано на рис. 2.8.
Состояния, показанные в рамках диаграммы, представляют собой возможное
содержимое К - 1 крайних правых разрядов регистра, а пути между состояниями -
кодовые слова ветвей на выходе, являющиеся результатом переходов между такими
состояниями. Состояния регистра выбраны следующими: а = 00, b = 10, с = 01 и d
= 11; диаграмма, показанная на рис. 2.8, иллюстрирует все возможные смены
состояний для кодера, показанного на рис. 2.6. Существует всего два исходящих
из каждого состояния перехода, соответствующие двум возможным входным битам.
Далее для каждого пути между со стояниями записано кодовое слово на выходе,
связанное с переходами между со стояниями. При изображении путей, сплошной
линией принято обозначать путь, связанный с нулевым входным битом, а пунктирной
линией - путь, связанный с единичным входным битом. Отметим, что за один
переход невозможно перейти из данного состояния в любое произвольное. Так как
за единицу времени перемещается только один бит, существует только два
возможных перехода между состояниями, в которые регистр может переходить за
время прохождения каждого бита.

Рисунок 2.8 - Диаграмма
состояний кодера (степень кодирования 1/2, К= 3)
2.5.6 Древовидные
диаграммы
Несмотря на то, что диаграммы
состояний полностью описывают кодер, по сути, их нельзя использовать для легкого
отслеживания переходов кодера в зависимости от времени, поскольку диаграмма не
представляет динамики изменений. Древовидная диаграмма (tree diagram) прибавляет к диаграмме
состояния временное измерение.
Древовидная диаграмма сверточного
кодера, показанного на рис. 2.6, изображена на рис. 2.9. В каждый последующий
момент прохождения входного бита процедура кодирования может быть описана с
помощью перемещения по диаграмме слева направо, причем каждая ветвь дерева
описывает кодовое слово на выходе. Правило ветвления для нахождения
последовательности кодовых слов следующее: если входным битом является нуль, то
он связывается со словом, которое находится путем перемещения в следующую (по
направлению вверх) правую ветвь; если входной бит - это единица, то кодовое
слово находится путем перемещения в следующую (по направлению вниз) правую
ветвь.
Предполагается, что первоначально
кодер содержал одни нули. Диаграмма показывает, что если первым входным битом
был нуль, то кодовым словом ветви на выходе будет 00, а если первым входным
битом была единица, то кодовым словом на выходе будет 11. Аналогично, если
первым входным битом была единица, а вторым - нуль, на выходе вторым словом
ветви будет 10. Если первым входным битом была единица и вторым входным битом
была единица, вторым кодовым словом на выходе будет 01. Следуя этой процедуре,
видим, что входная последовательность 110 11 представляется жирной линией,
нарисованной на древовидной диаграмме (рис. 2.9). Этот путь соответствует
выходной последовательности кодовых слов 1 1 0 1 0 1 0 0 0 1.
Добавленное измерение времени в
древовидной диаграмме (по сравнению с диаграммой состояния) допускает
динамическое описание кодера как функции конкретной входной последовательности.
Однако при попытке описания с помощью древовидной диаграммы последовательности
произвольной длины возникает проблема: число ответвлений растет как 2L, где L - это количество кодовых слов
ветвей в последовательности.
2.5.7 Решетчатая
диаграмма
Исследование древовидной диаграммы
на рис. 2.9 показывает, что в этом приме ре после третьего ветвления в момент
времени t4 структура повторяется
(в общем случае древовидная структура повторяется после К ответвлений, где К -
длина кодового ограничения). Пометим каждый узел в дереве (рис. 2.9), ставя в
соответствие четыре возможных состояния в регистре сдвига: а = 00, b = 10, с = 01 и d = 11. Пер вое ветвление древовидной
структуры в момент времени дает пару узлов, помеченных как а и b. При каждом последующем ветвлении
количество узлов удваивается. Второе ветвление в момент времени t2 дает в результате четыре узла, помеченных как а, b, с и d. После третьего ветвления всего
имеется восемь узлов: два - а, два - b, два - с и два - d.
Из рисунка 2.9 можно видеть, что все
ветви выходят из двух узлов одного и того же состояния, образуя идентичные
ветви последовательностей кодовых слов. В этот момент дерево делится на
идентичные верхнюю и нижнюю части. Смысл этого становится яснее после
рассмотрения кодера, изображенного на рис. 2.6. Когда четвертый входной бит
входит в кодер слева, первый входной бит справа выбрасывается и больше не
влияет на кодовые слова на выходе.
Следовательно, входные
последовательности 1 0 0 х у... и 0 0 0 х у..., где крайний левый бит является
самым ранним, после (К = 3)-го ветвления генерируют одинаковые кодовые слова
ветвей.
Это означает, что любые
состояния, имеющие одинаковую метку в один и тот же момент 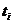 можно
соединить, поскольку все последующие пути будут неразличимы. Если мы проделаем
это для древовидной структуры, показанной на рис. 2.9, получим иную диаграмму,
называемую решетчатой.
можно
соединить, поскольку все последующие пути будут неразличимы. Если мы проделаем
это для древовидной структуры, показанной на рис. 2.9, получим иную диаграмму,
называемую решетчатой.
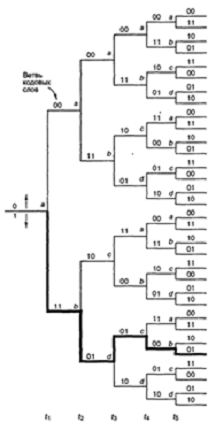
Рисунок 2.9 - Древовидное
представление кодера (степень кодирования 1/2, К= 3)
Решетчатая диаграмма, которая использует
повторяющуюся структуру, дает более удобное описание кодера, по сравнению с
древовидной диаграммой. Решетчатая диаграмма для сверточного кодера,
изображенного на рис. 2.6, показана на рис. 2.10.
При изображении решетчатой диаграммы
(рисунок 2.10) мы воспользовались теми же условными обозначениями, что и для
диаграммы состояния: сплошная линия обозначает выходные данные, генерируемые
входным нулевым битом, а пунктирная - выходные данные, генерируемые входным
единичным битом.

Рисунок 2.10 - Решетчатая диаграмма
кодера (степень кодирования 1/2, К= 3)
Узлы решетки представляют состояния
кодера; первый ряд узлов соответствует состоянию a = 00, второй и последующие -
состояниям b = 10, с = 01 и d - 11. В каждый момент времени для представления 2К-1
возможных со стояний кодера решетка требует 2К-1 узлов. В нашем
примере после достижения глубины решетки, равной трем (в момент времени t4), замечаем, что решетка имеет фиксированную периодическую структуру.
В общем случае фиксированная структура реализуется после достижения глубины К.
Следовательно, с этого момента в каждое состояние можно войти из любого из двух
предыдущих состояний. Также из каждого состояния можно перейти в одно из двух
состояний. Из двух исходящих ветвей одна соответствует нулевому входному биту,
а другая - единичному входному биту. На рис. 2.10 кодовые слова на выходе
соответствуют переходам между состояниями, показанными как метки на ветвях
решетки.
Один столбец временного интервала
сформировавшейся решетчатой структуры кодирования полностью определяет код.
Несколько столбцов показаны исключительно для визуализации последовательности
кодовых символов как функции времени. Со стояние сверточного кодера
представлено содержанием крайних правых K - 1 разрядов в регистре кодера.
Некоторые авторы описывают состояние с помощью крайних левых K -1 разрядов. Какое описание
правильно? Они оба верны. Каждый переход имеет начальное и конечное состояние.
Крайние правые K - 1 разрядов описывают начальное состояние для текущих входных
данных, которые находятся в крайнем левом разряде (степень кодирования
предполагается равной 1/n). Крайние левые К - 1 разрядов являются конечным состоянием для
такого перехода. Последовательность кодовых символов характеризуется N
ветвями (что представляет N бит данных), занимающими N интервалов
времени. Она связана с конкретным состоянием в каждый из N +1 интервалов
времени (от начала до конца). Таким образом, мы запускаем биты в моменты
времени t1, t2, ..., tN и интересуемся метрикой состояния в моменты времени t1, t2, ..., tN+1. Здесь использовано следующее условие: текущий бит располагается
в крайнем левом разряде, а крайние правые K - 1 разрядов стартуют из состояния
со всеми нулями. Этот момент времени обозначим как начальное время, t1. Время завершения последнего перехода обозначим как время
прекращения работы, tN+1.
2.6 Декодирование по
методу максимального правдоподобия
Если все входные
последовательности сообщений равновероятны, минимальная вероятность ошибки получается
при использовании декодера, который сравнивает условные вероятности и выбирает
максимальную. Условные вероятности также называют функциями правдоподобия 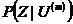 ,
где Z - это принятая последовательность, a
,
где Z - это принятая последовательность, a  -
одна из возможных переданных последовательностей. Декодер выбирает
-
одна из возможных переданных последовательностей. Декодер выбирает  ,
если
,
если
 (2.1)
(2.1)
по всем  .
.
Принцип максимального
правдоподобия, определяемый уравнением (2.1), является фундаментальным
достижением теории принятия решений [1]; это формализация способа принятия
решений, основанного на "здравом смысле", когда имеются
статистические данные о вероятностях. При рассмотрении двоичной демодуляции
предполагается передача только двух равновероятных сигналов 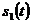 и
и
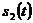 .
Следовательно, принятие двоичного решения на основе принципа максимального
правдоподобия, касающееся данного полученного сигнала, означает, что в качестве
переданного сигнала выбирается
.
Следовательно, принятие двоичного решения на основе принципа максимального
правдоподобия, касающееся данного полученного сигнала, означает, что в качестве
переданного сигнала выбирается 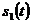 , если
, если

В противном случае
считается, что передан был сигнал 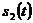 . Параметр z представляет со бой величину z(T), значение принятого сигнала до детектирования в конце каждого
периода передачи символа t=T. Однако при использовании принципа максимального правдоподобия в
задаче сверточного декодирования, в сверточном коде обнаруживается наличие
памяти (полученная последовательность является суперпозицией текущих и
предыдущих двоичных разрядов). Таким образом, применение принципа максимального
правдоподобия при декодировании бит данных, закодированных сверточным кодом,
осуществляется в контексте выбора наиболее вероятной последовательности, как
показано в уравнении (2.1). Обычно имеется множество возможных переданных
последовательностей кодовых слов. Что касается двоичного кода, то последовательность
из L кодовых слов является членом набора из 2L возможных последовательностей. Следователь но, в контексте
максимального правдоподобия можно сказать, что в качестве переданной
последовательности декодер выбирает
. Параметр z представляет со бой величину z(T), значение принятого сигнала до детектирования в конце каждого
периода передачи символа t=T. Однако при использовании принципа максимального правдоподобия в
задаче сверточного декодирования, в сверточном коде обнаруживается наличие
памяти (полученная последовательность является суперпозицией текущих и
предыдущих двоичных разрядов). Таким образом, применение принципа максимального
правдоподобия при декодировании бит данных, закодированных сверточным кодом,
осуществляется в контексте выбора наиболее вероятной последовательности, как
показано в уравнении (2.1). Обычно имеется множество возможных переданных
последовательностей кодовых слов. Что касается двоичного кода, то последовательность
из L кодовых слов является членом набора из 2L возможных последовательностей. Следователь но, в контексте
максимального правдоподобия можно сказать, что в качестве переданной
последовательности декодер выбирает 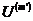 , если правдоподобие
, если правдоподобие 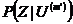 больше
правдоподобия всех остальных возможно переданных последовательностей. Такой
оптимальный декодер, минимизирующий вероятность ошибки (когда все переданные
последовательности равновероятны), известен как декодер, работающий по принципу
максимального правдоподобия (maximum likelihood detector). Функция
правдоподобия за дается или вычисляется, исходя из спецификации канала.
Предположим, что мы имеем дело с аддитивным белым гауссовым шумом с нулевым
средним, следовательно, каналом без памяти, т.е. шум влияет на каждый символ
кода независимо от остальных символов. При степени кодирования сверточного
кода, равной 1/n, правдоподобие можно
выразить следующим образом:
больше
правдоподобия всех остальных возможно переданных последовательностей. Такой
оптимальный декодер, минимизирующий вероятность ошибки (когда все переданные
последовательности равновероятны), известен как декодер, работающий по принципу
максимального правдоподобия (maximum likelihood detector). Функция
правдоподобия за дается или вычисляется, исходя из спецификации канала.
Предположим, что мы имеем дело с аддитивным белым гауссовым шумом с нулевым
средним, следовательно, каналом без памяти, т.е. шум влияет на каждый символ
кода независимо от остальных символов. При степени кодирования сверточного
кода, равной 1/n, правдоподобие можно
выразить следующим образом:
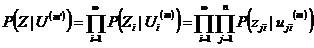 (2.2)
(2.2)
где  -
i-я ветвь принятой последовательности Z
-
i-я ветвь принятой последовательности Z
 - это ветвь отдельной
последовательности кодовых слов
- это ветвь отдельной
последовательности кодовых слов 
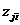 - это j-й кодовый символ
- это j-й кодовый символ 
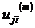 - это j-й кодовый символ
- это j-й кодовый символ  , а каждая ветвь состоит
из n кодовых символов.
, а каждая ветвь состоит
из n кодовых символов.
Задача декодирования
заключается в выборе пути сквозь решетку, показанную на рис. 2.10 (каждый
возможный путь определяет последовательность кодовых слов), таким образом,
чтобы произведение
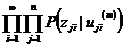 было максимальным.(2.3)
было максимальным.(2.3)
Как правило, при вычислениях удобнее
пользоваться логарифмом функции правдоподобия, поскольку это позволяет
произведение заменить суммированием. Мы можем воспользоваться таким
преобразованием, поскольку логарифм является монотонно возрастающей функцией и,
следовательно, не внесет изменений в выбор окончательного кодового слова.
Логарифмическую функцию правдоподобия можно определить следующим образом:
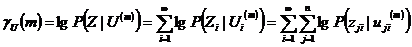 (2.4)
(2.4)
Теперь задача
декодирования заключается в выборе пути вдоль дерева на рис. 2.9 или решетки на
рис. 2.10 таким образом, чтобы 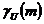 было максимальным. При
де кодировании сверточных кодов можно использовать как древовидную, так и
решетчатую структуру. При древовидном представлении кода игнорируется то, что
пути снова объединяются. Для двоичного кода количество возможных
последовательностей, состоящих из L кодовых слов, равно 2L. Поэтому декодирование полученных последовательностей, основанное
на принципе максимального правдоподобия с использованием древовидной диаграммы,
требует метода "грубой силы" или исчерпывающего сопоставления 2L накопленных логарифмических метрик правдоподобия, описывающих все
варианты возможных последовательностей кодовых слов.
было максимальным. При
де кодировании сверточных кодов можно использовать как древовидную, так и
решетчатую структуру. При древовидном представлении кода игнорируется то, что
пути снова объединяются. Для двоичного кода количество возможных
последовательностей, состоящих из L кодовых слов, равно 2L. Поэтому декодирование полученных последовательностей, основанное
на принципе максимального правдоподобия с использованием древовидной диаграммы,
требует метода "грубой силы" или исчерпывающего сопоставления 2L накопленных логарифмических метрик правдоподобия, описывающих все
варианты возможных последовательностей кодовых слов.
Поэтому рассматривать
декодирование на основе принципа максимального правдоподобия с помощью
древовидной структуры практически невозможно. В предыдущем разделе было
показано, что при решетчатом представлении кода декодер можно по строить так,
чтобы можно было отказываться от путей, которые не могут быть кандидатами на
роль максимально правдоподобной последовательности. Путь декодирования выбирается
из некоего сокращенного набора выживших путей. Такой декодер тем не менее
является оптимальным; в том смысле, что путь декодирования та кой же, как и
путь, полученный с помощью декодера критерия максимального правдоподобия,
действующего "грубой силой", однако предварительный отказ от
неудачных путей снижает сложность декодирования.
Существует несколько
алгоритмов, которые дают приблизительные решения задачи декодирования на основе
критерия максимального правдоподобия, включая последовательный и пороговый [2].
Каждый из этих алгоритмов является подходящим для узкоспециальных задач; однако
все они близки к оптимальному. Алгоритм декодирования Витерби, напротив,
осуществляет декодирование на основе критерия максимального правдоподобия шире,
следовательно, является оптимальным. Это не означает, что алгоритм Витерби в
любой реализации является наилучшим; при его использовании существуют жесткие
условия, налагаемые на аппаратное обеспечение. Алгоритм Витерби будет описан в
последующих разделах.
2.6.1 Алгоритм сверточного
декодирования Витерби
В 1967 году Витерби разработал и
проанализировал алгоритм [3], в котором, по сути, реализуется декодирование,
основанное на принципе максимального правдоподобия; однако в нем уменьшается
вычислительная нагрузка за счет использования особенностей структуры конкретной
решетки кода. Преимущество декодирования Витерби, по сравнению с декодированием
по методу "грубой силы", заключается в том, что сложность декодера
Витерби не является функцией количества символов в последовательности кодовых
слов. Алгоритм включает в себя вычисление меры подобия (или расстояния), между
сигналом, полученным в момент времени ti, и всеми путями
решетки, входящими в каждое состояние в момент времени ti. В
алгоритме Витерби не рассматриваются те пути решетки, которые, согласно
принципу максимального правдоподобия, заведомо не могут быть оптимальными. Если
в одно и то же состояние входят два пути, выбирается тот, который имеет лучшую
метрику; такой путь называется выживающим. Отбор выживающих путей выполняется
для каждого состояния. Таким образом, декодер углубляется в решетку, принимая
решения путем исключения менее вероятных путей. Предварительный отказ от
маловероятных путей упрощает процесс декодирования. В 1969 году Омура (Omura)
показал, что основу алгоритма Витерби составляет оценка максимума правдоподобия
[2]. Следует отметить, что задачу отбора оптимальных путей можно выразить как
выбор кодового слова с максимальной метрикой правдоподобия или минимальной
метрикой расстояния.
2.6.2 Пример сверточного
декодирования Витерби
Для простоты предположим, что мы
имеем дело с каналом BSC; в таком случае приемлемой мерой расстояния будет
расстояние Хэмминга. Кодер для этого приме ра показан на рис. 2.6, а решетчатая
диаграмма - на рис. 2.10. Для представления декодера, как показано на рис.
2.11, можно воспользоваться подобной решеткой. Мы начинаем в момент времени t1, в состоянии 00 (вследствие очистки кодера между сообщениями
декодер находится в начальном состоянии). Поскольку в этом примере возможны
только два перехода, разрешающих другое состояние, для начала не нужно
показывать все ветви. Полная решетчатая структура образуется после момента
времени t3. Принцип работы
происходящего после процедуры декодирования можно понять, изучив решетку кодера
на рис. 2.10 и решетку декодера, показанную на рис. 2.11. Для решетки декодера
каждую ветвь за каждый временной интервал удобно пометить расстоянием Хэмминга
между полученным кодовым символом и кодовым словом, соответствующим той же
ветви из решетки кодера.
На рис. 2.11 показана
последовательность сообщений m, соответствующая последовательности кодовых слов U, и искаженная
шумом последовательность Z = 11 01 01 10 01 ... . Как показано на рис. 2.6,
кодер характеризуется кодовыми словами, находящимися на ветвях решетки кодера и
заведомо известными как кодеру, так и декодеру. Эти слова являются кодовыми
символами, которые можно было бы ожидать на выходе кодера в результате каждого
перехода между состояниями. Пометки на ветвях решетки декодера накапливаются
декодером в процессе. Другими словами, когда получен кодовый символ, каждая
ветвь решетки декодера помечается метрикой подобия (расстоянием Хэмминга) между
полученным кодовым символом и каждым словом ветви за этот временной интервал.
Из полученной последовательности Z, показан ной на рис. 2.11, можно видеть, что
кодовые символы, полученные в (следующий) момент времени t1 - это 11. Чтобы пометить ветви декодера подходящей метрикой
расстояния Хэмминга в (прошедший) момент времени t1 рассмотрим решетку ко дера на рис. 2.10. Видим, что переход между
состояниями 00 -> 00 порождает на вы ходе ветви слово 00. Однако получено
11. Следовательно, на решетке декодера помечаем переход между состояниями 00
-> 00 расстоянием Хэмминга между ними, а именно 2. Глядя вновь на решетку
кодера, видим, что переход между состояниями 00 -> 10 порождает на выходе
кодовое слово 11, точно соответствующее полученному в момент г, кодовому
символу. Следовательно, переход на решетке декодера между состояниями 00 -з>
10 помечаем расстоянием Хэмминга 0. В итоге, метрика входящих в решетку
декодера ветвей описывает разницу (расстояние) между тем, что было получено, и
тем, что "могло бы быть" получено, имея кодовые слова, связанные с
теми ветвями, с которых они были переданы. По сути, эти метрики описывают величину,
подобную корреляциям между полученным кодовым словом и каждым из кандидатов на
роль кодового слова. Таким же образом продолжаем помечать ветви решетки
декодера по мере получения символов в каждый момент времени t1. В алгоритме декодирования эти метрики расстояния Хэмминга
используются для нахождения наиболее вероятного (с минимальным расстоянием)
пути через решетку. Смысл декодирования Витерби заключается в следующем. Если
любые два пути сливаются в одном состоянии, то при поиске оптимального пути
один из них всегда можно исключить. Например, на рис. 2.12 показано два пути,
сливающихся в момент времени t5 в состоянии 00.
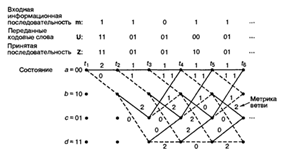
Рисунок 2.11 - Решетчатая диаграмма
декодера (степень кодирования i/2, К = 3)
Определим суммарную метрику пути по
Хэммингу для данного пути в момент времени t1, как сумму метрик расстояний Хэмминга ветвей, по которым про
ходит путь до момента t1. На рис. 2.12 верхний
путь имеет метрику 4, нижний - метрику 1. Верхний путь нельзя выделить как оптимальный,
поскольку нижний путь, входящий в то же состояние, имеет меньшую метрику. Это
наблюдение поддерживается Марковской природой состояний кодера. Настоящее
состояние завершает историю кодера в том смысле, что предыдущие состояния не
могут по влиять на будущие состояния или будущие ветви на выходе.
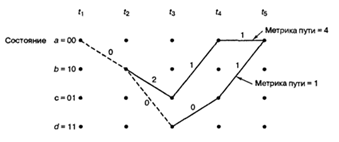
Рисунок 2.12 - Метрики пути для
сливающихся путей
В каждый момент времени ti, в решетке
существует 2K-1 состояний, где K - это длина кодового ограничения, и
в каждое состояние может войти два пути. Декодирование Витерби состоит в
вычислении метрики двух путей, входящих в каждое состояние, и исключении одного
из них. Такие вычисления проводятся для каждого из 2K-1 состояний или узлов в момент времени ti; затем декодер переходит
к моменту времени ti+1 и процесс повторяется.
В данный момент времени метрика выжившего пути для каждого состояния
обозначается как метрика для этого состояния в этот момент времени. Первые
несколько шагов в примере декодирования будут следующими (рис. 2.13).
Предположим, что последовательность входных данных m, кодовое слово U и полученная
последовательность Z аналогичны показанным на рис. 2.11. Допустим, что декодер
знает верное исходное состояние решетки. (Это предположение не является
необходимым, одна ко упрощает объяснения.) В момент времени t1, получены кодовые символы 11. Из состояния 00 можно перейти
только в состояние 00 или 10, как показано на рис. 2.13, а. Переход между
состояниями 00 -> 10 имеет метрику ветви 0; переход между состояниями 00 -»
00 - метрику ветви 2. В момент времени t2 из каждого состояния также может выходить только две ветви, как
показано на рис. 3.13, б.
Суммарная метрика этих ветвей
обозначена как метрика состояний Гa, Гb, Гc и Гd, соответствующих
конечным состояниям. В момент времени t3 на рис. 2.13, в опять
есть две ветви, выходящие из каждого состояния. В результате имеется два пути,
входящих в каждое состояние, в момент времени t4. Один из путей,
входящих в каждое состояние, может быть исключен, а точнее - это путь, имеющий
большую суммарную метрику пути. Если бы метрики двух входящих путей имели
одинаковое значение, то путь, который будет исключаться, выбирался бы
произвольно.
Выживший путь в каждом состоянии
показан на рис. 2.13, г. В этой точке процесса декодирования имеется только
один выживший путь, который называется полной ветвью, между моментами времени t1
и t2. Следовательно, декодер теперь может решить, что между
моментами t1 и t2 произошел переход 00 -»
10. Поскольку переход вызывается единичным входным битом, на выходе декодера
первым битом будет единица.
Здесь легко можно проследить процесс
декодирования выживших ветвей, поскольку ветви решетки показаны пунктирными
линиями для входных нулей и сплошной линией для входных единиц. Заметим, что
первый бит не декодируется, пока вычисление метрики пути не пройдет далее
вглубь решетки. Для обычного декодера такая задержка декодирования может
оказаться раз в пять больше длины кодового ограничения в битах.
На каждом следующем шаге процесса
декодирования всегда будет два пути для каждого состояния; после сравнения
метрик путей один из них будет исключен. Этот шаг в процессе декодирования
показан на рис. 2.13, д. В момент t5 снова имеется по два входных
пути для каждого состояния, и один путь из каждой пары подлежит исключению.
Выжившие пути на момент f5 показаны на рис. 2.13, е. Заметим, что в нашем
примере мы еще не можем принять решения относительно второго входного
информационного бита, поскольку еще остается два пути, исходящих в момент t2
из состояния в узле 10. В момент времени t6 на рис. 2.13, ж снова
можем видеть структуру сливающихся путей, а на рис. 2.13, з - выжившие пути на
момент t6. Здесь же, на рис.
2.13, з, на выходе декодера в качестве второго декодированного бита показана
единица как итог единственного оставшегося пути между точками t2 и t3. Аналогичным образом
декодер продолжает углубляться в решетку и принимать решения, касающиеся
информационных битов, устраняя все пути, кроме одного.
Отсекание (сходящихся путей) в
решетке гарантирует, что у нас никогда не будет путей больше, чем состояний. В
этом примере можно проверить, что после каждого отсекания (рис. 2.13, б- д)
остается только 4 пути. Если сравнить это с попыткой приме нить "грубую
силу" (без привлечения алгоритма Витерби) при использовании для получения
последовательности принципа максимального правдоподобия, то в этом случае число
возможных путей (соответствующее возможным вариантам последовательности)
является степенной функцией длины последовательности. Для двоичной
последовательности кодовых слов с длиной кодовых слов L имеется 2L возможные
последовательности.
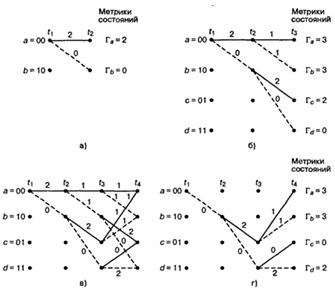
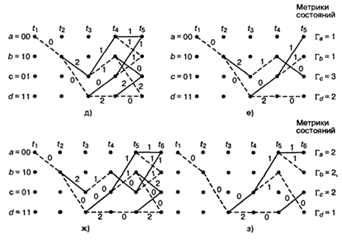
Рисунок 2.13 - Выбор выживших путей:
а) выжившие на момент t2; б) выжившие на момент
t3; в) сравнение метрик в момент t4; г) выжившие на момент t5; д) сравнение метрик в
момент t5; е) выжившие на момент t5; ж) сравнение метрик
в момент t6; з) выжившие на момент t6
2.6.3 Реализация
декодера
В контексте решетчатой
диаграммы, показанной на рис. 2.11, переходы за один промежуток времени можно
сгруппировать в 2v-1
непересекающиеся ячейки; каждая ячейка будет изображать четыре возможных
перехода, причем 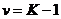 называется
памятью кодера (encoder memory). Если К = 3, то v = 2, и, следовательно, мы
имеем 2v-1=2 ячейки. Эти ячейки показаны на рис. 3.14, где буквы а, b, с и d обозначают состояния в момент ti а а’, b’, с’ и d’ - состояния в
момент времени ti+1.
Для каждого перехода изображена метрика ветви
называется
памятью кодера (encoder memory). Если К = 3, то v = 2, и, следовательно, мы
имеем 2v-1=2 ячейки. Эти ячейки показаны на рис. 3.14, где буквы а, b, с и d обозначают состояния в момент ti а а’, b’, с’ и d’ - состояния в
момент времени ti+1.
Для каждого перехода изображена метрика ветви 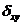 , индексы которой
означают переход из состояния х в состояние у. Эти ячейки и соответствующие
логические элементы, которые корректируют метрики со стояний {Гx}, где х означает конкретное расстояние состояния, представляют
основные составляющие элементы декодера.
, индексы которой
означают переход из состояния х в состояние у. Эти ячейки и соответствующие
логические элементы, которые корректируют метрики со стояний {Гx}, где х означает конкретное расстояние состояния, представляют
основные составляющие элементы декодера.

Рисунок 2.14 - Примеры
ячеек декодера
Процедура сложения,
сравнения и выбора
Вернемся к примеру двух
ячеек с К = 3. На рис. 2.15 показан логический блок, со ответствующий ячейке 1.
Логическая схема осуществляет специальную операцию, которая называется
сложение, сравнение и выбор (add-compare-select - ACS). Метрика состояния Гa’ вычисляется путем прибавления метрики предыдущего состояния а, Гa к метрике ветви  - и метрики предыдущего
состояния c, Гc
к метрике ветви
- и метрики предыдущего
состояния c, Гc
к метрике ветви  .
Это даст в результате две метрики путей в качестве кандидатов для новой метрики
состояния Гa’.
.
Это даст в результате две метрики путей в качестве кандидатов для новой метрики
состояния Гa’.
Оба кандидата
сравниваются в логическом блоке, показанном на рис. 2.15. Наиболее
правдоподобная из двух метрик путей (с наименьшим расстоянием) запоминается как
новая метрика состояния Гa’
- для состояния а’. Также сохраняется новая история путей 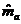 для
состояния a, где
для
состояния a, где 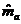 -
история пути информации для данного состояния, дополненная сведениями о
выжившем пути.
-
история пути информации для данного состояния, дополненная сведениями о
выжившем пути.
На рис. 2.15 также
показана логическая схема ACS для ячейки 1, которая дает новую метрику
состояния Гb’
новую историю состояния 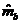 .
Операция ACS аналогичным образом осуществляется и для путей в других ячейках.
Выход декодера составляют последние биты на путях с наименьшими метриками
состояний.
.
Операция ACS аналогичным образом осуществляется и для путей в других ячейках.
Выход декодера составляют последние биты на путях с наименьшими метриками
состояний.
Вид процедуры сложения,
сравнения и выбора на решетке
Рассмотрим тот же пример
для описания декодирования на основе алгоритма Витерби. Пусть
последовательность сообщений имеет вид m = 1 1 0 1 1, последовательность
кодовых слов - U = 11 01 01 00 01, а принятая последовательность - Z = 11 01 01
10 01.
Рисунок 2.15 -
Логический блок, предназначенный -для осуществления операций сложения,
сравнения и выбора
Решетчатая диаграмма
декодирования, аналогичная показанной на рис. 2.11, изображена на рис. 2.16.
Метрика ветви, которая описывает каждую ветвь, - это расстояние Хэмминга между
принятым кодовым символом и соответствующим кодовым словом из решетки кодера.
Еще на решетке (рис.
3.16) показаны значения каждого состояния х в каждый момент t2-t6,
метрика состояния которых обозначена Гx.
Операция ACS выполняется после появления двух переходов, входящих в состояние,
т.е. для момента t4
и более поздних.
Например, в момент
времени t4 значение метрики состояния для состояния а вычисляется
суммированием метрики состояния Гa
= 3 в момент t3 и метрики ветви  -= 1, что в итоге дает
значение 4. В то же время к метрике состояния Гc
= 2 в момент времени t3
прибавляется метрика ветви
-= 1, что в итоге дает
значение 4. В то же время к метрике состояния Гc
= 2 в момент времени t3
прибавляется метрика ветви  = 1, что дает значение
3. В ходе процедуры ACS происходит отбор наиболее правдоподобной метрики (с
минимальным расстоянием), т.е. новой метрики состояния; поэтому для состояния a в момент t4
но вой метрикой состояния будет Га’ = 3. Отобранный путь изображен
жирной линией, а путь, который был отброшен, показан светлой линией.
= 1, что дает значение
3. В ходе процедуры ACS происходит отбор наиболее правдоподобной метрики (с
минимальным расстоянием), т.е. новой метрики состояния; поэтому для состояния a в момент t4
но вой метрикой состояния будет Га’ = 3. Отобранный путь изображен
жирной линией, а путь, который был отброшен, показан светлой линией.
На рис. 2.16 на решетке
слева направо показаны все метрики состояний. Убедимся, что в любой момент
времени значение каждой метрики состояния получается суммированием метрики
состояния, соединенного с предыдущим состоянием вдоль отобранного пути (жирная
линия), и метрики ветви, соединяющей эти состояния.
Через некоторое время на
выход декодера будут поданы выжившие ветви, прослеженные до самых ранних битов.
Чтобы показать это, посмотрим на рис. 2.16 в момент t6.
Видим, что значение метрики со стояния, соответствующей минимальному
расстоянию, равно 1. Отобранный путь можно проследить из состояния d обратно, к
моменту t1 и убедиться, что декодированное сообщение совпадает с
исходным. Отметим, что пунктирные и сплошные линии соответствуют двоичным
единице и нулю.
2.6.4 Память путей и
синхронизация
Требования к памяти декодера,
работающего согласно алгоритму Витерби, растут с увеличением длины кодового
ограничения как степенная функция. Для кода со степенью кодирования 1/n после каждого шага декодирования
декодер держит в памяти набор из 2К-1 путей.

Рисунок 2.16. Операция сложения,
сравнения и выбора при декодировании по алгоритму Витерби
С высокой степенью вероятности можно
утверждать, что при значительном превышении существующей на данный момент
глубины декодирования эти пути не будут взаимно непересекающимися [2]. Все 2К-1
пути ведут к полной ветви, которая в конце концов разветвляется на разные
состояния. Поэтому, если декодер сохраняет историю 2К-1 путей, самые
первые биты на всех путях будут одинаковы. Следовательно, простой декодер имеет
фиксированный объем истории путей и выдает самые ранние биты произвольного пути
каждый раз, когда продвигается на один уровень вглубь решетки. Требуемый объем
сохраняемых путей будет равен следующему [2]:
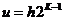
Здесь h - длина истории
пути информационного бита на состояние. При уточнении, которое проводится для
минимизации h, вместо самых ранних битов произвольных путей на выходе декодера
используются самые ранние биты наиболее вероятных путей. Было показано [2], что
значения h, равного 4 или 5 длинам кодового ограничения, достаточно, чтобы
характеристики декодера были близки к оптимальным. Необходимый объем памяти и
является основным ограничением при разработке декодеров, работающих согласно
алгоритму Витерби. В серийно выпускаемых декодерах длина кодового ограничения
равна величине порядка К = 10. Попытка повысить эффективность кодирования за
счет увеличения длины кодового ограничения вызывает экспоненциальный рост требований
к памяти (и сложности).
Синхронизация кодовых
слов ветвей - это процесс определения начала слова ветви в принятой
последовательности. Такую синхронизацию можно осуществить, не прибавляя новую
информацию к потоку передаваемых символов, поскольку можно видеть, что, пока
принятые данные не синхронизированы, у них непомерно высокая частота появления
ошибок. Следовательно, синхронизацию можно осуществить просто: нужно проводить
сопутствующее наблюдение за уровнем частоты появления ошибок, т.е. нас должна
интересовать частота, при которой увеличиваются метрики состояний, или частота,
при которой сливаются выжившие пути на решетке. Пара метр, за которым следят,
сравнивается с пороговым значением, после чего соответствующим образом
осуществляется синхронизация.
3.
Разработка программного обеспечения системы кодирования сверточным кодом
сверточный кодирование
програамный
3.1 Описание программы
Разрабатываемая программа
представляет собой реализацию метода сверточного кодирования. Основные
требования, предъявляемые к программе, сводятся к следующим:
1) Наглядность и понятность
интерфейса, т.к. разрабатываемое ПО ориентировано на обычного пользователя ЭВМ;
2) Надёжность, т.е. полнота,
точность, достоверность и своевременность получаемой результирующей информации.
Т.о. основной упор при разработке ПО
был сделан на проектирование наглядного интерфейса, а, следовательно, все
основные функции программы привязаны к элементам формы.
В качестве среды разработки было
выбрано выпущенное компанией Borland средство быстрой разработки приложений, позволяющее создавать
приложения на языке object pascal - Delphi 6. Обоснование такого выбора приведено в последующем пункте.
В ходе создания данного дипломного
проекта был написан кодер и декодер. Описание алгоритмов их функционирования
приведено ниже.
3.2 Описание блок схем
алгоритмов программы
На рисунке 3.1 представлены этапы
преобразования данных в разработанной программе.

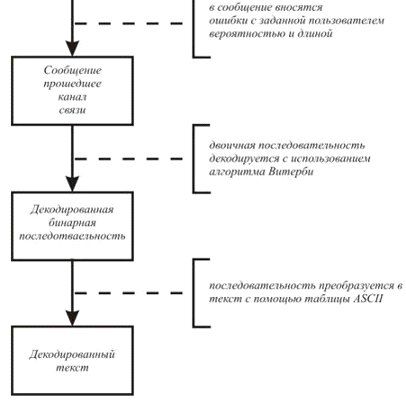
Рисунок 3.1 - Этапы преобразования
исходных данных в программе
Ниже представлены блок схемы
алгоритмов каждого этапа.
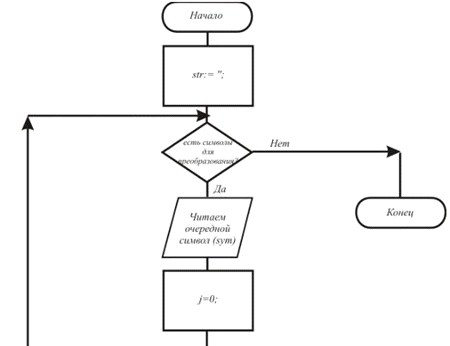
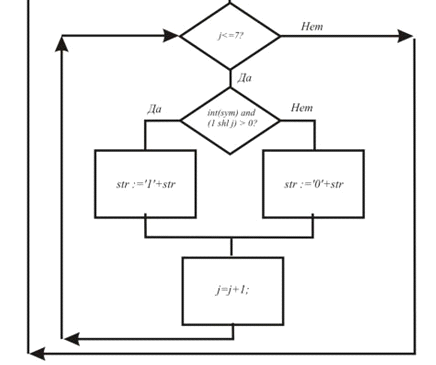
Рисунок 3.2 - Блок схема для
алгоритма преобразования текстового сообщения в двоичный код
Как видно из рисунка 3.2 исходное
текстовое сообщение преобразуется в набор бит посимвольно. Каждый символ имеет
свое двоичное представление (ASCII код (См. Приложение Б)). На очередной итерации применяя операцию
побитового маскирования (1 shl j > 0) алгоритм определяет является ли текущий бит символом 1
или 0 и конкатенирует результат в итоговую строку str. Стандартный набор
символов ASCII состоит из 128 десятичных чисел в пределах от 0 до 127,
назначенных буквам, цифрам, знакам препинания и самым употребляемым специальным
символам. Расширенный набор символов ASCII дополнительно содержит 128 десятичных чисел в пределах от 128 до
255, представляющих дополнительные специальные, математические, графические и
иностранные символы. На рисунке 3.3 приведена блок схема для алгоритма
функционирования сверточного кодера.
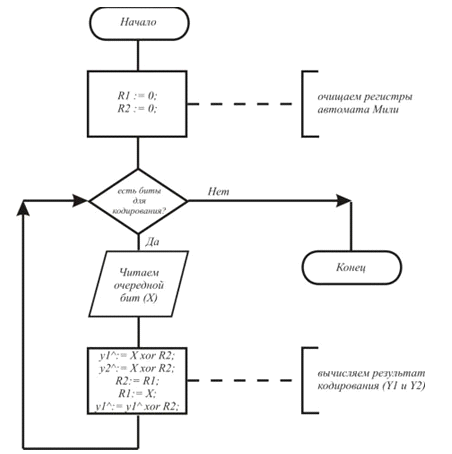
Рисунок 3.3 - Блок схема для
алгоритма функционирования сверточного кодера
На очередном этапе преобразования
сообщения вызывается функция coding класса MealyAutomaton, которая осуществляет преобразование согласно формуле приведенной
на рисунке 3.3
На рисунке 3.4 приведена блок схема
алгоритма имитации передачи через канал связи.
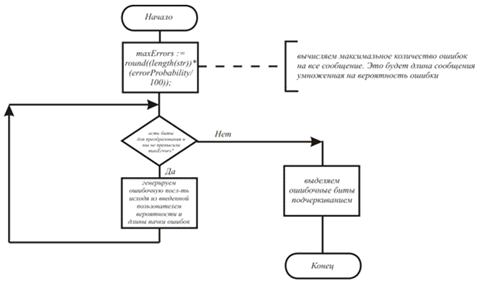
Рисунок 3.4 - Блок схема для
алгоритма имитации передачи через канал связи
Как видно из приведенного выше
алгоритма максимальное количество генерируемых ошибок вычисляется по формуле:
Max = Nсообщ * Pош / 100 (3.1)
где Мax - максимальное
количество ошибок
Nсообщ - длина сообщения
Рош - вероятность ошибки (%)
Т.е. если длина сообщения равна 100
бит, а вероятность ошибки - 10 % то генератор сгенерирует от 0 до 10 ошибок.
Схема генерации ошибок такова: функция на очередной итерации генерирует
случайную величину X, используя стандартную функцию rand следующим образом:(99)
+ 1
затем данное если данное значение меньше
вероятности ошибки:(random(99) + 1 <= errorProbability)
то происходит генерации ошибочных
бит (нули заменяются на единицы и наоборот) в зависимости от параметра «длина
пачки ошибок» начиная с позиции i (переменная цикла обработки). Затем происходит инкремент
переменной цикла i и все повторяется сначала до тех пор, пока не закончится
сообщение или число сгенерированных ошибок не превысит число допустимых ошибок.
На рисунках ниже приведена
статистика по тестированию генератора ошибок при длине тестового сообщения 100
бит.
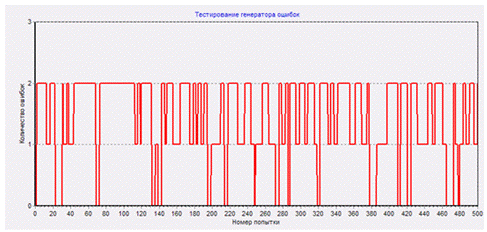
Рисунок 3.5 - Тестирование
генератора ошибок:
Длина тестового сообщения - 100 бит;
Вероятность ошибок: 0,02; Длина пачки ошибок: 1

Рисунок 3.6 - Тестирование
генератора ошибок:
Длина тестового сообщения - 100 бит;
Вероятность ошибок: 0,1; Длина пачки ошибок: 1
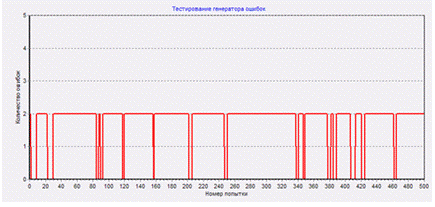
Рисунок 3.7 - Тестирование
генератора ошибок:
Длина тестового сообщения - 100 бит;
Вероятность ошибок: 0,02; Длина пачки ошибок: 2
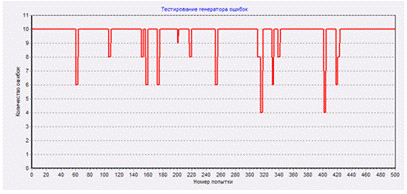
Рисунок 3.8 - Тестирование
генератора ошибок:
Длина тестового сообщения - 100 бит;
Вероятность ошибок: 0,1; Длина пачки ошибок: 2
На рисунке 3.9 приведена блок схема
алгоритма функционирования декодера.
На каждой итерации декодер (TTreeHandler) вызывает процедуру createLevel которая исходя из
входящего кода (2 декодируемых бита) строит очередной уровень сети (который
может иметь 1, 2 или 4 узла) и рассчитывает метрики путей. Согласно структуре TListElemPtr все уровни сети связаны
указателями pnext и pprev. После полного построения сети декодер выбирает узел
на последнем уровне с минимальной метрикой пути, а затем, возвращаясь по
указателям pprev, строит декодируемый путь (процедура decode). После чего отображает
построенную сеть (функции printTree);
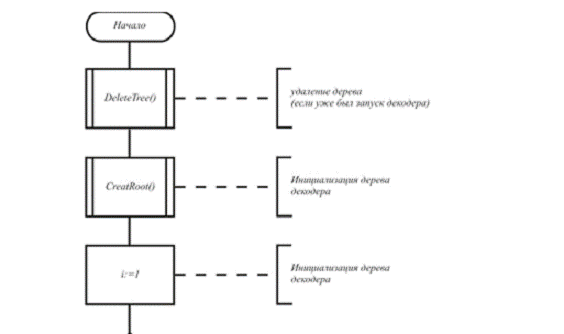

Рисунок 3.9 - Блок схема для
алгоритма функционирования декодера

Рисунок 3.10 - Блок схема для
алгоритма преобразования из двоичного кода в текстовое сообщение
Как видно из рисунка 3.10 исходный
набор бит преобразуется в текстовое сообщение поблочно (по 8 бит - 1символ в ASCII представлении). На
очередной итерации преобразования переменная sym (это будущий текстовый
символ) сдвигается на 1 бит вправо (sym shr j), после чего к ней прибавляется очередной бит X. После того как в переменную sym попало 8 бит,
результирующая строка конкатенируется с переменной sym.
На рисунках ниже приведена
статистика по тестированию декодера при длине тестового сообщения 100 бит.

Рисунок 3.11 - Тестирование
сверточного декодера:
Длина тестового сообщения - 100 бит;
Вероятность ошибок: 0,05; Длина пачки ошибок: 1
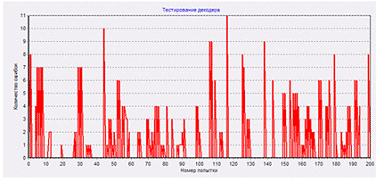
Рисунок 3.12 - Тестирование
сверточного декодера:
Длина тестового сообщения - 100 бит;
Вероятность ошибок: 0,1; Длина пачки ошибок: 1
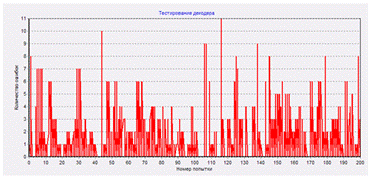
Рисунок 3.13 - Тестирование
сверточного декодера:
Длина тестового сообщения - 100 бит;
Вероятность ошибок: 0,05; Длина пачки ошибок: 2

Рисунок 3.14 - Тестирование
сверточного декодера:
Длина тестового сообщения - 100 бит;
Вероятность ошибок: 0,1; Длина пачки ошибок: 2
3.3 Обоснование выбора
языка программирования
Современное визуальное
программирование позволило свести проектирование пользовательского интерфейса к
простым и наглядным процедурам, которые дают возможность за минуты или часы
сделать то, на что ранее уходили месяцы работы. То есть программирование
сводится, фактически, к размещению компонентов на форме, заданию некоторых их
свойств и написанию при необходимости обработчиков событий.
Данный программный продукт был
написан в среде разработки Borland Delphi на языке Object Pascal. Borland Delphi 6.0 - это современный программный продукт, позволяющий создавать
широкий спектр приложений для среды Microsoft Windows. Обоснованность данного выбора заключается в следующем:
- Позволяет быстро создавать
(даже начинающим программистам) оконный интерфейс, имеющий профессиональный
вид, для любых приложений, написанных на любом языке;
- Объектная
ориентированность. Основным назначением применения в Delphi модели компонентов
является обеспечение возможности многократного использования компонентов и
создания новых.
Динамическая идентификация
типа данных или интроспекция (возможность определить тип и структуру объекта во
время выполнения программы).
Поддержка визуального проектирования
Поддержка методологии
событийного программирования
Исходя из всего вышесказанного,
выбранная среда разработки и язык программирования полностью удовлетворяют
современным требованиям и являются удобным средством для программирования под
ОС Windows.
3.4 Тестирование
программы
В качестве примера закодируем
сообщение «ау» (см. рисунок 4.15)

Рисунок 3.15 - Тестирование
программы (кодирование)
В двоичном коде оно будет иметь вид:
А после кодирования сверточным
кодером станет таким:
Так как вероятность ошибки была
равная нулю (рисунок 3.7) то сообщение миновало канал без изменений и было
декодировано верно.
Теперь попробуем внести в принятое
сообщение одиночные ошибки канала (см. рисунок 3.16)
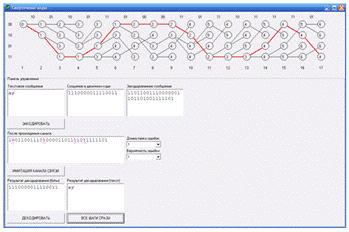
Рисунок 3.16 - Тестирование
программы (имитация канала связи)
Как видно из рисунка 3.16 ошибки
изменили веса вершин, но итоговый путь, построенный декодером (отмечен жирной
линией) не изменился.
Теперь попробуем внести в сообщение
двойные ошибки (рисунок 3.17)
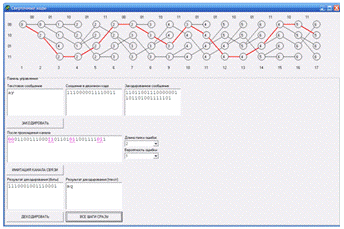
Рисунок 3.17 - Тестирование
программы (декодирование)
Как видно из рисунка 3.17 декодер не
смог исправить двойные ошибки, вследствие чего результирующее сообщение было
искажено.
3.5 Быстродействие
программы
На рисунке 3.18 изображен график
зависимости скорости работы кодера в зависимости от длины входной
последовательности

Рисунок 3.18 - Тестирование
быстродействия кодера
На рисунке 3.19 изображен график
зависимости скорости работы декодера в зависимости от длины декодируемой
последовательности

Рисунок 3.19 - Тестирование
быстродействия декодера
Как видно из графиков 3.18 и 3.19
графики зависимости быстродействия кодера и декодера имеют линейный характер.
Исходя из графиков получается, что средняя скорость кодирования 0,016 мс/бит, а
скорость декодирования составляет 0,0053 мс/бит. Что является довольно не
плохим показателем для поточного кодера/декодера.
Заключение
Перед тем как, началась разработка
алгоритма программы, было проведено изучение алгоритма сверточного кодирования,
в соответствии с которым была разработана блок схема алгоритма программы.
После разработки блок схемы
алгоритма программы был написан программный модуль, реализующий указанную выше
функциональность.
В разделе технико-экономического
обоснования были рассчитаны затраты на создание данного ПО и определена его
цена - 6723 грн. Капитальные затраты для разработчика составили 3630 грн.
Рентабельность данного программного продукта составляет 28%. Анализ
экономической эффективности подтвердил целесообразность создания данного
программного продукта.
В разделе «Охрана труда и окружающей
среды» проведён анализ условий труда в помещении, в котором производится
разработка данного ПО.
В разделе «Гражданская оборона»
оценена обстановка и предусмотрены мероприятия по защите студентов и работников
университета в зоне радиоактивного загрязнения после аварии на АЭС.
Библиографический список
.Никитин Г. И. Сверточные коды: Учебное пособие.. - С-П.: Сов.
радио, 2001. - 78 с
.Бернард Скляр Цифровая связь. Теоретические основы и практическое
применение.
.Витерби А.Д., Омура Дж.К. Принципы цифровой связи и кодирования
/Пер. с англ. под ред. К.Ш. Зигангирова. - М.: Радио и связь, 1982. - 536 с.
.Чернега В., Платтнер Б. Компьютерные сети: Учебник для вузов/ В.
Чернега, Б. Платтнер - Севастополь: Изд-во СевНТУ, 2006. - 500 с.
.Культин Н.Б. Delphi 6. Программирование на Object pascal.
БХВ-Петербург, 2001 г. 528с.
Приложение А
Текст
программыViterbi_Unit;,
Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,, StdCtrls,
ComCtrls, Grids;
{**
* сокращенные названия для типов
*}
pint = ^integer;
int = integer;
{**
* узел сети используемый при
декодировании
*}= ^TNodeData;= record:
string;// содержимое вершины: int;// метрика длины пути
minWayBelong: bool;// принадлежит минимальному пути
parent: TNodeDataPtr;// указатель на родителя
end;
{**
* уровень сети используемой при
декодировании
*}
TListElemPtr
=^TListElem;= record: array [0..3] of TNodeDataPtr;// узлы текущего уровня: string;// декодируемый код
pnext: TListElemPtr;// указатель на следующий уровень
pprev: TListElemPtr;// указатель на предыдущий уровень
end;
{**
* форма
*}= class(TForm)Btn:
TButton;Btn: TButton;Btn: TButton;: TButton;: TGroupBox;: TRichEdit;Data:
TRichEdit;Data: TRichEdit;Data: TRichEdit;Data: TRichEdit;Data: TRichEdit;:
TLabel;Label: TLabel;: TLabel;: TLabel;Label: TLabel;: TLabel;Label: TLabel;:
TLabel;: TComboBox;: TComboBox;: TScrollBar;step1BtnClick(Sender:
TObject);step2BtnClick(Sender: TObject);step3BtnClick(Sender:
TObject);allStepsBtnClick(Sender: TObject);FormCreate(Sender:
TObject);FormPaint(Sender: TObject);leftTreePaintPositionChange(Sender:
TObject);printTree(t:TListElemPtr; levelNum
:int);step0();step1();step2();step3();step4();: TBitmap;
{ Public declarations };
{**
* автомат Мили (кодер)
*}= class:int;//
регистры сдвига:int;
// конструкторinit;
// побитовый
кодерcoding(X:int; Y1:pint; Y2:pint);;
{**
* декодер работающий по алгоритму
Витерби
*}
TTreeHandler = class
public
pleft: TListElemPtr;// указатель на корневой узел сети
// вычисляет сумму по модулю 2 для
двух строк
function
xorStrings(val_1: string; val_2: string) : string;
// конструктор
constructor init;
// вычисление пути до узла
function
calcWayToNode(parent: TNodeDataPtr; nodeVal:string; inputCode: string):int;
// создание корня
procedure creatRoot;
// создание узла сети
function
createNode(parent1: TNodeDataPtr; parent2: TNodeDataPtr; nodeVal:string;
inputCode: string):TNodeDataPtr;
// вес
вершиныweightCalc(val: string) : int;
// Создание очередного
уровня сетиcreateLevel(temp:TListElemPtr; code:string);
// Удаление всех узлов
сетиdeleteTree(pleft:TListElemPtr);
// декодирование
function decode() : string;
// инвертирование строки
function
rotateString(val: string): string;;: TmyForm;// форма: MealyAutomaton;// кодер:
TTreeHandler;// декодер
{$R *.dfm}
// автомат Мили - НАЧАЛО
{**
* конструктор
*}MealyAutomaton.init;:=0;:=0;;
{**
* побитовый кодер
*}MealyAutomaton.coding(X:int;
Y1:pint; Y2:pint);^:= X xor R2;^:= X xor R2;:= R1;:= X;1^:= y1^ xor R2;
end;
// автомат Мили - КОНЕЦ
// декодер - НАЧАЛО
{**
* вычисляет сумму по модулю 2 для двух строк
*}TTreeHandler.xorStrings(val_1:
string; val_2: string) : string;: string;: int;(length(val_1) <>
length(val_2)) then:= '';i:=1 to length(val_1) do(val_1[i] = val_2[i])
then:=res+'0':=res+'1';;:= res;;
{**
* конструктор
*}TTreeHandler.init;:=
NIL;;
{**
* вычисление пути до узла
*}
function
TTreeHandler.calcWayToNode(parent: TNodeDataPtr; nodeVal:string; inputCode:
string):int;: int;:= 0;
// Вершина
"00"(parent^.val = '00') then
// левый потомок(nodeVal
= '10') then:= parent^.way + WeightCalc(xorStrings('11', inputCode));
// правый потомок:=
parent^.way + WeightCalc(xorStrings('00', inputCode));
// Вершина
"10"if(parent^.val = '10') then
// левый потомок(nodeVal
= '11') then:= parent^.way + WeightCalc(xorStrings('01', inputCode));
// правый потомок:=
parent^.way + WeightCalc(xorStrings('10', inputCode));
// Вершина
"11"if(parent.val = '11') then
// левый потомок(nodeVal
= '11') then:= parent^.way + WeightCalc(xorStrings('10', inputCode));
// правый потомок:=
parent^.way + WeightCalc(xorStrings('01', inputCode));
// Вершина
"01"if(parent^.val = '01') then
// левый потомок(nodeVal
= '10') then:= parent^.way + WeightCalc(xorStrings('00', inputCode));
// правый потомок:=
parent^.way + WeightCalc(xorStrings('11', inputCode));;:= resultWay;;
{**
* создание корня
*}TTreeHandler.creatRoot;(pleft);^.pnext:=
NIL;^.pprev:= NIL;(pleft^.nodes[0]);^.nodes[0]^.val:= '00';^.nodes[0]^.way:=
0;^.nodes[0]^.minWayBelong := true;^.nodes[0]^.parent:= NIL;^.nodes[1]:=
NIL;^.nodes[2]:= NIL;^.nodes[3]:= NIL;;
{**
* создание узла сети
*}TTreeHandler.createNode(:
TNodeDataPtr;: TNodeDataPtr;:string;: string
):TNodeDataPtr;:
TNodeDataPtr;: TNodeDataPtr;: int;: int;: int;((parent1 = NIL) AND (parent2 =
NIL)) then:= NIL;(parent1 = NIL) then:= parent2;if (parent2 = NIL) then:=
parent1;:= calcWayToNode(parent1, nodeVal, inputCode);:= calcWayToNode(parent2,
nodeVal, inputCode);(way2 > way1) then nodeParent := parent1nodeParent:=
parent2;;:= calcWayToNode(nodeParent, nodeVal, inputCode);(resultNode);^.val :=
nodeVal;^.way := resWay;^.minWayBelong := false;^.parent := nodeParent;;:=
resultNode;;
{**
* вес вершины
*}TTreeHandler.weightCalc(val:
string) : int;: int;: int;:= 0;i:=1 to length(val) do(val[i] = '1') then:= res
+ 1;;
:= res;
end;
{**
* Создание очередного уровня
*}TTreeHandler.createLevel(temp:TListElemPtr;
code:string);: TListElemPtr;((temp^.pnext <> NIL)) then(temp.pnext,
code);(newLevel);^.pnext := newLevel;^.code:= code;^.pnext:= NIL;^.pprev:=
temp;^.nodes[0]:= createNode(temp^.nodes[0], temp^.nodes[2], '00',
code);^.nodes[1]:= createNode(temp^.nodes[0], temp^.nodes[2], '10',
code);^.nodes[2]:= createNode(temp^.nodes[1], temp^.nodes[3], '01',
code);^.nodes[3]:= createNode(temp^.nodes[1], temp^.nodes[3], '11', code);
end;
{**
* Удаление всех узлов дерева
*}TTreeHandler.deleteTree(pleft:TListElemPtr);(pleft
<> NIL) then(pleft.pnext);(pleft);;:= NIL;;
{**
* декодирование
*}TTreeHandler.decode()
: string;: TListElemPtr;: string;: TNodeDataPtr;: int;:= pleft;(temp^.pnext
<> NIL) do:= temp^.pnext;;:= NIL;i:=0 to 3 do(temp^.nodes[i] = NIL)
then;;((minWayNode = NIL) OR (minWayNode^.way > temp^.nodes[i]^.way)) then:=
temp^.nodes[i];;;(minWayNode^.parent <> NIL) do:= resultStr + minWayNode^.val[1];^.minWayBelong
:= true;:= minWayNode^.parent;;:= rotateString(resultStr);;
{**
* инвертирование строки
*}TTreeHandler.rotateString(val:
string): string;: string;: int;: int;:= '';:= length(val);:= strLen;(i >= 1)
do:= res + val[i];:= i-1;;:= res;;
// декодер - КОНЕЦ
// методы формы - НАЧАЛО
{**
* Создание формы
*}TmyForm.FormCreate(Sender:
TObject);
// инициализируем
автомат мили:= MealyAutomaton.init();
// инициализируем
декодер:= TTreeHandler.init();.DoubleBuffered := true;:=
TBitmap.Create;();.Clear();.Text := 'тест1.';;
{**
* перерисовка формы
*}TmyForm.FormPaint(Sender:
TObject);(treeHandler.pleft, 0);;
{**
* Отображение дерева
*}TmyForm.printTree(t:TListElemPtr;
levelNum :int);: int;: TNodeDataPtr;: TNodeDataPtr;: int;: int;: int;: int;:
int;: int;: int;: int;: int;: int;:= 60 - leftTreePaintPosition.Position;:=
40{+myForm.GroupBox2.Height};:=35;:=60;:=12;:= 0;:= 0;
// очищаем канву.Width
:= myForm.Width;.Height := myForm.Height;.Canvas.Brush.Color:=
{clWhite}clBtnFace;.Canvas.Pen.Style:= psSolid;.Canvas.Pen.Color:=
clBlack;.Canvas.FillRect(Rect(0,0,myForm.Width,myForm.Height));
// Рекурсивное прохождение
заканчивается на пустом поддереве
while (t <> NIL)
do:= leftPos + levelWidth*levelNum;i:=0 to 3 do(t^.nodes[i] <> NIL)then:=
topPos + levelHeight*i; := t^.nodes[i];
// рисуем связь с родителем
nodeParent :=
node^.parent;(nodeParent <> NIL) then(nodeParent.val = '00') then
parentNodeY :=0if(nodeParent.val = '10') then parentNodeY :=1if(nodeParent.val
= '01') then parentNodeY :=2parentNodeY :=3;:= topPos + levelHeight*parentNodeY;:=
levelX-levelWidth;
// выделяем минимальный
путь(node^.minWayBelong) then.Canvas.Pen.Color:= clRed;.Canvas.Pen.Width
:=2;.Canvas.Pen.Color:= clBlack;.Canvas.Pen.Width :=1;;.Canvas.MoveTo(levelX,
levelY);.Canvas.LineTo(parentNodeX, parentNodeY);;.Canvas.Pen.Color:=
clBlack;.Canvas.Pen.Width :=1;
// рисуем текущий
узел.Canvas.Ellipse(levelX-ellipse, levelY-ellipse, levelX+ellipse,
levelY+ellipse);.Canvas.TextOut(levelX-7, levelY-6, IntToStr(node^.way));
// перерисовывам
родителя(nodeParent <> NIL) then.Canvas.Ellipse(parentNodeX-ellipse,
parentNodeY-ellipse, parentNodeX+ellipse,
parentNodeY+ellipse);.Canvas.TextOut(parentNodeX-7, parentNodeY-6,
IntToStr(nodeParent^.way));;;
// номер
уровня.Canvas.TextOut(levelX-7, topPos-6 + levelHeight*4,
IntToStr(levelNum+1));
// декодируемый
код.Canvas.TextOut(levelX-7+ trunc(levelWidth/2), 10, t^.code);;
// рисуем следующий уровень
t := t^.pnext;
levelNum :=
levelNum+1;;(treeHandler.pleft <> NIL)
then.Canvas.FillRect(Rect(0,0,40,myForm.Height));.Canvas.TextOut(10, topPos-6,
'00');.Canvas.TextOut(10, topPos-6 + levelHeight, '10');.Canvas.TextOut(10,
topPos-6 + levelHeight*2, '01');.Canvas.TextOut(10, topPos-6 + levelHeight*3,
'11');.Canvas.Draw(0,0,bitmap);:= levelNum * levelWidth - myForm.Width + 40;(max
> 0) then.Visible := true;.Max := max;.Visible := false;.Visible := false;;;
{**
* преобразование строки в двоичный
код
*}TmyForm.step0();:
char;: int;: int;: string;Data.Text := '';i := 1 to length(inputData.Text) do:=
inputData.Text[i];:= '';j:=0 to 7 do(int(sym) and (1 shl j) > 0) then str
:='1'+strstr :='0'+str;;Data.Text := step0Data.Text + str;;Label.Caption :=
'Соощение в двоичном коде ('+IntToStr(length(step0Data.Text))+' бит)';;
{**
* кодирование строки с помощью
автомата мили
*}
procedure TmyForm.step1();
var
y1: int;// Выходы автомата Мили
y2: int;
res: string;// Результат кодирования
i: int;: int;:=
'';.init();i := 1 to length(step0Data.Text) do((step0Data.Text[i] = '0') OR
(step0Data.Text[i] = '1')) then:= int(step0Data.Text[i])-int('0');.Coding(sym,
@y1, @y2);:= res + IntToStr(y1)+IntToStr(y2);;;Data.Text := res;Label.Caption
:= 'Закодированное сообщение ('+IntToStr(length(step1Data.Text))+' бит)';;
{**
* имитация канала связи
*}TmyForm.step2();:
int;: int;: int;: int;: int;// промежуток, в котором возможно появление пачки
ошибок: int;//
местоположение ошибки: string; : int;// максимальное
количество ошибок
errorCount : int;// счетчик количества ошибок
begin:= 1;:=
StrToInt(errorMultiplicityBox.Text);:= trunc(StrToFloat(errorProbabilityBox.Text)
* 100);
// очищаем
стилиData.SelStart:= 1;Data.SelLength :=
length(step2Data.Text);Data.SelAttributes.Color:=
clBlack;Data.SelAttributes.Style:= [];Data.Lines.Clear();:=
step1Data.Text;();:= round(length(str) * (errorProbability/100));:= 0;:=1;((i
<= length(str)) AND (maxErrors > 0)) do(errorCount >= maxErrors)
then;;(random(99) + 1 <= errorProbability) then
errorPosition := 0;
// меняем 1 на 0 и 0 на 1 (т.е.
генерируем ошибку)
for j:=i+errorPosition
to i+errorPosition+errorMultiplicity - 1 do(j > length(str)) then;;(str[j] =
'0') then[j] := '1'[j] := '0';;:= errorCount + 1;:= i + 1;; := i - 1;
// стараемся сделать так, чтобы
ошибки не "слепливались"
if ((errorProbability
<> 100) AND (random(99) + 1 > errorProbability)) then:= i + 1;;;:= i +
errorInterval;;Data.Text := str;Label.Caption := 'После прохождения канала
('+IntToStr(length(step2Data.Text))+' бит)';
// выделяем ошибочные
символыi:=1 to length(str) do(str[i] <>
step1Data.Text[i])thenData.SelStart:= i-1;Data.SelLength:=
1;Data.SelAttributes.Color:= clFuchsia;Data.SelAttributes.Style:= [fsUnderline,
fsBold];;
end
end;
{**
* декодирование в двоичный код
*}TmyForm.step3();:
string;: int;: int;:= step2Data.Text;:= length(code);(codeLen > 0) then
// удаление дерева (если уже был
запуск декодера)
treeHandler.DeleteTree(treeHandler.pleft);
// Инициализация дерева
treeHandler.CreatRoot();
// строим дерево декодера
i := 1;
while (i < codeLen)
do.createLevel(treeHandler.pleft, copy(code, i, 2)); := i+2;
end;
// выводим результат декодирования
step3Data.Text := treeHandler.decode();
// рисуем дерево декодера
printTree(treeHandler.pleft,
0);;;
{**
* перевод из двоичного кода в строку
*}TmyForm.step4();:
string;: int;: int;: int;:= '';:= 1;(i < length(step3Data.Text)) do
{str := str +
copy(step3Data.Text, i, 8);}:= 0;j:=0 to 7 do:= (sym shl 1) +
(byte(step3Data.Text[i+j]) and 1) ;
{sym +
integer(step3Data.Text[i+j])-integer('0');:= sym shr 1;};
//sym := 176;:= str +
char(sym);:= i+8;;Data.Text := str;;
{**
* кнопка "закодировать"
*}TmyForm.step1BtnClick(Sender:
TObject);();();;
{**
* кнопка "канал
связи"
*}TmyForm.step2BtnClick(Sender:
TObject);();;
{**
* кнопка
"декодировать"
*}TmyForm.step3BtnClick(Sender:
TObject);();();;
{**
* кнопка "все шаги
сразу"
*}TmyForm.allStepsBtnClick(Sender:
TObject);();();();();4();
end;
{**
* прокрутка отображения дерева
*}
procedure
TmyForm.leftTreePaintPositionChange(Sender: TObject);(treeHandler.pleft, 0);;
// методы формы - КОНЕЦ
end.
Приложение Б
Таблица ASCII кодов ASCII Таблица символов 0 - 127.
|
dec
|
hex
|
симв
|
пояснение
|
dec
|
hex
|
симв
|
dec
|
hex
|
симв
|
dec
|
hex
|
симв
|
|
0
|
0
|
NUL
|
Пустой символ
|
32
|
20
|
пробел
|
64
|
40
|
@
|
96
|
60
|
`
|
|
1
|
1
|
SOH
|
Начало заголовка
|
33
|
21
|
!
|
65
|
41
|
A
|
97
|
61
|
a
|
|
2
|
2
|
STX
|
Начало текста
|
34
|
22
|
"
|
66
|
42
|
B
|
98
|
62
|
b
|
|
3
|
3
|
ETX
|
Конец текста
|
35
|
23
|
#
|
67
|
43
|
C
|
99
|
63
|
c
|
|
4
|
4
|
EOT
|
Конец передачи
|
36
|
24
|
$
|
68
|
44
|
D
|
100
|
64
|
d
|
|
5
|
5
|
ENQ
|
Запрос
|
37
|
25
|
%
|
69
|
45
|
E
|
101
|
65
|
e
|
|
6
|
6
|
ACK
|
Подтвержд. получения
|
38
|
26
|
&
|
70
|
46
|
F
|
102
|
66
|
f
|
|
7
|
7
|
BEL
|
Звуковой сигнал
|
39
|
27
|
'
|
71
|
47
|
G
|
103
|
67
|
g
|
|
8
|
8
|
BS**
|
Обратный ход каретки
|
40
|
28
|
(
|
72
|
48
|
H
|
104
|
68
|
h
|
|
9
|
9
|
TAB**
|
Горизонт. табуляция
|
41
|
)
|
73
|
49
|
I
|
105
|
69
|
i
|
|
10
|
A
|
LF**
|
Начало строки
|
42
|
2A
|
*
|
74
|
4A
|
J
|
106
|
6A
|
j
|
|
11
|
B
|
VT
|
Вертикальная табуляция
|
43
|
2B
|
+
|
75
|
4B
|
K
|
107
|
6B
|
k
|
|
12
|
C
|
FF
|
Начало формы
|
44
|
2C
|
,
|
76
|
4C
|
L
|
108
|
6C
|
l
|
|
13
|
D
|
CR**
|
Возврат каретки
|
45
|
2D
|
-
|
77
|
4D
|
M
|
109
|
6D
|
m
|
|
14
|
E
|
SO
|
Передача
|
46
|
2E
|
.
|
78
|
4E
|
N
|
110
|
6E
|
n
|
|
15
|
F
|
SI
|
Прием
|
47
|
2F
|
/
|
79
|
4F
|
O
|
111
|
6F
|
o
|
|
16
|
10
|
DLE
|
Закр. канала связи
|
48
|
30
|
0
|
80
|
50
|
P
|
112
|
70
|
p
|
|
17
|
11
|
DC1
|
Упр. устройством 1
|
49
|
31
|
1
|
81
|
51
|
Q
|
113
|
71
|
q
|
|
18
|
12
|
DC2
|
Упр. устройством 2
|
50
|
32
|
2
|
82
|
52
|
R
|
114
|
72
|
r
|
|
19
|
13
|
DC3
|
Упр. устройством 3
|
51
|
33
|
3
|
83
|
53
|
S
|
115
|
73
|
s
|
|
20
|
14
|
DC4
|
Упр. устройством 4
|
52
|
34
|
4
|
84
|
54
|
T
|
116
|
74
|
t
|
|
21
|
15
|
NAK
|
Отрицание получения
|
53
|
35
|
5
|
85
|
55
|
U
|
117
|
75
|
u
|
|
22
|
16
|
SYN
|
Синхронизация
|
54
|
36
|
6
|
86
|
56
|
V
|
118
|
76
|
v
|
|
23
|
17
|
ETB
|
Конец пакета
|
55
|
37
|
7
|
87
|
57
|
W
|
119
|
77
|
w
|
|
24
|
18
|
CAN
|
Отмена
|
56
|
38
|
8
|
88
|
58
|
X
|
120
|
78
|
x
|
|
25
|
19
|
EM
|
Закрытие среды
|
57
|
39
|
9
|
89
|
59
|
Y
|
121
|
79
|
y
|
|
26
|
1A
|
SUB
|
Замена
|
58
|
3A
|
:
|
90
|
5A
|
Z
|
122
|
7A
|
z
|
|
27
|
1B
|
ESC
|
Завершение
|
59
|
3B
|
;
|
91
|
5B
|
[
|
123
|
7B
|
{
|
|
28
|
1C
|
FS
|
Разделитель файлов
|
60
|
3C
|
<
|
92
|
5C
|
\
|
124
|
7C
|
|
|
|
29
|
1D
|
GS
|
Разделитель групп
|
61
|
3D
|
=
|
93
|
5D
|
]
|
125
|
7D
|
}
|
|
30
|
1E
|
RS
|
Разделитель записей
|
62
|
3E
|
>
|
94
|
5E
|
^
|
126
|
7E
|
~
|
|
31
|
1F
|
US
|
Разделитель модулей
|
63
|
3F
|
?
|
95
|
5F
|
_
|
127
|
7F
|
|
Значениями 0-32 и 127 закодированы
непечатаемые символы. Они не имеют графического представления, но в зависимости
от приложения, могут влиять на отображение текста.
Таблица символов 128 - 255.
|
dec
|
hex
|
симв
|
dec
|
hex
|
симв
|
dec
|
hex
|
симв
|
dec
|
hex
|
симв
|
|
128
|
80
|
€
|
160
|
A0
|
пробел
|
192
|
C0
|
А
|
224
|
E0
|
а
|
|
129
|
81
|
�
|
161
|
A1
|
¡
|
193
|
C1
|
Б
|
225
|
E1
|
б
|
|
130
|
82
|
‚
|
162
|
A2
|
¢
|
194
|
C2
|
В
|
226
|
E2
|
в
|
|
131
|
83
|
ƒ
|
163
|
A3
|
£
|
195
|
Г
|
227
|
E3
|
г
|
|
132
|
84
|
„
|
164
|
A4
|
¤
|
196
|
C4
|
Д
|
228
|
E4
|
д
|
|
133
|
85
|
…
|
165
|
A5
|
¥
|
197
|
C5
|
Е
|
229
|
E5
|
е
|
|
134
|
86
|
†
|
166
|
A6
|
¦
|
198
|
C6
|
Ж
|
230
|
E6
|
ж
|
|
135
|
87
|
‡
|
167
|
A7
|
§
|
199
|
C7
|
З
|
231
|
E7
|
з
|
|
136
|
88
|
ˆ
|
168
|
A8
|
¨
|
200
|
C8
|
И
|
232
|
E8
|
и
|
|
137
|
89
|
‰
|
169
|
A9
|
©
|
201
|
C9
|
Й
|
233
|
E9
|
й
|
|
138
|
8A
|
Š
|
170
|
AA
|
ª
|
202
|
CA
|
К
|
234
|
EA
|
к
|
|
139
|
8B
|
‹
|
171
|
AB
|
«
|
203
|
CB
|
Л
|
235
|
EB
|
л
|
|
140
|
8C
|
Œ
|
172
|
AC
|
¬
|
204
|
CC
|
М
|
236
|
EC
|
м
|
|
141
|
8D
|
�
|
173
|
AD
|
|
205
|
CD
|
Н
|
237
|
ED
|
н
|
|
142
|
8E
|
Ž
|
174
|
AE
|
®
|
206
|
CE
|
О
|
238
|
EE
|
о
|
|
143
|
8F
|
�
|
175
|
AF
|
¯
|
207
|
CF
|
П
|
239
|
EF
|
п
|
|
144
|
90
|
�
|
176
|
B0
|
°
|
208
|
D0
|
Р
|
240
|
F0
|
р
|
|
145
|
91
|
‘
|
177
|
B1
|
±
|
209
|
D1
|
C
|
241
|
F1
|
с
|
|
146
|
92
|
’
|
178
|
B2
|
²
|
210
|
D2
|
Т
|
242
|
F2
|
т
|
|
147
|
93
|
«
|
179
|
B3
|
³
|
211
|
D3
|
У
|
243
|
F3
|
у
|
|
148
|
94
|
«
|
180
|
B4
|
´
|
212
|
D4
|
Ф
|
244
|
F4
|
ф
|
|
149
|
95
|
•
|
181
|
B5
|
µ
|
213
|
D5
|
Х
|
245
|
F5
|
х
|
|
150
|
96
|
-
|
182
|
B6
|
¶
|
214
|
D6
|
Ц
|
246
|
F6
|
ц
|
|
151
|
97
|
-
|
183
|
B7
|
·
|
215
|
D7
|
Ч
|
247
|
F7
|
ч
|
|
152
|
98
|
˜
|
184
|
B8
|
¸
|
216
|
D8
|
Ш
|
248
|
F8
|
ш
|
|
153
|
99
|
™
|
185
|
B9
|
¹
|
217
|
D9
|
Щ
|
249
|
F9
|
щ
|
|
154
|
9A
|
š
|
186
|
BA
|
º
|
218
|
DA
|
Ъ
|
250
|
FA
|
ъ
|
|
155
|
9B
|
›
|
187
|
BB
|
«
|
219
|
DB
|
Ы
|
251
|
FB
|
ы
|
|
156
|
9C
|
œ
|
188
|
BC
|
¼
|
220
|
DC
|
Ь
|
252
|
FC
|
ь
|
|
157
|
9D
|
�
|
189
|
BD
|
½
|
221
|
DD
|
Э
|
253
|
FD
|
э
|
|
158
|
9E
|
ž
|
190
|
BE
|
¾
|
222
|
DE
|
Ю
|
254
|
FE
|
ю
|
|
159
|
9F
|
Ÿ
|
191
|
BF
|
¿
|
223
|
DF
|
Я
|
255
|
FF
|
я
|
Приложение В
Руководство пользователя
Министерство образования и науки
Украины
Севастопольский национальный
технический университет
Кафедра Информационных систем
Программа, осуществляющая
кодирование/декодирование сверточным кодом и имитирующая канал связи
РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ
Выполнила:
Мартынова С. В.
НАЗНАЧЕНИЕ ПРОГРАММЫ
Программа предназначена для
кодирования/декодирования текстовых сообщений сверхточным кодом и имитацию
канала связи.
В связи с тем, что программа была
написана для работы в среде OC Windows, можно утверждать, что для нормальной работы программы к
аппаратным средствам выдвигаются те же требования, которые выдвигает операционная
система для своей стабильной работы:
1) 1 Гб оперативной памяти или
лучше.
2) Процессор с частотой 1 ГГц
или лучше.
) Порядка 5 Мб дискового
пространства или больше.
) Видеокарта с памятью 32 Мб
или лучше.
3
Выполнение программы
С точки зрения пользователя
программа представляет собой исполняемый EXE-файл. Для запуска программы
необходимо два раза кликнуть на файле Viterbi.EXE. При запуске программы на экран выводится окно главного меню
(рисунок 1).

Рисунок 1 - Главное окно программы
Данная форма разделена на две
области:
1) Панель управления
2) Область для вывода дерева
декодера (верхняя пустая часть формы)
Назначение кнопок, находящихся в
области управления:
Кнопка «Закодировать» - осуществляет
перевод введенного текстового сообщения в двоичный код и кодирование полученной
двоичной последовательности сверточным кодом.
Кнопка «Имитация канала связи» -
осуществляет генерацию случайным образом в двоичной последеовательности ошибок,
с заданной длиной и вероятность.
Кнопка «Декодировать» -производит
декодирование двоичной последовательности с использованием алгоритма Витерби и
последующий перевод результата в текстовую строку.
Кнопка «Все шаги сразу» - имитирует
последовательное нажатие на все вышеуказанные кнопки.
Пример результатов работы программы
приведен на рисунке 2.
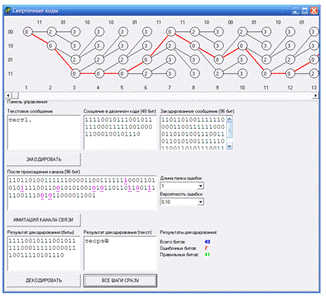
Рисунок 2 - Пример работы программы