|
№ лекции
|
Примерное
содержание лекции
|
Количество
часов на изучение данной темы
|
Всего часов
|
|
1
|
Задача об
объеме цилиндрического бруса. Понятие двойного интеграла. Необходимое условие
интегрируемости функции двух переменных. Суммы Дарбу. Свойства сумм Дарбу.
Необходимое и достаточное условие функции двух переменных. Интегрируемость
непрерывной функции. Основные свойства двойного интеграла.
|
2
|
6
|
|
2
|
Теорема о
среднем. Вычисление двойного интеграла повторным интегрированием в случае
прямоугольной области. Вычисление двойного интеграла повторным
интегрированием в случае криволинейной области.
|
2
|
|
|
3
|
Преобразование
областей при регулярных отображениях. Криволинейная система координат.
Полярная система координат. Замена переменных в двойном интеграле.
|
2
|
|
В качестве основных требований к чтению лекции выдвигают:
- высокий, научный уровень излагаемой информации,
имеющий, как правило, мировоззренческое значение;
- большой объем четко и плотно систематизированной и
методически переработанной современной научной информации;
доказательность и аргументированность высказанных
суждений;
достаточное количество приводимых убедительных
фактов, примеров, текстов и документов;
ясность изложения мыслей и активизация мышления
слушателей, постановка вопросов для самостоятельной работы по обсуждаемым
проблемам;
анализ разных точек зрения на решение поставленных
проблем;
выведение главных мыслей и положений, формулировка
выводов;
разъяснение вводимых терминов и названий;
предоставление студентам возможности слушать, осмысливать и кратко записывать
информацию;
умение устанавливать педагогический контакт с
аудиторией, использование дидактических материалов и технических средств;
применение основных материалов текста, конспекта,
блок - схем, чертежей, таблиц, графиков [5].
Лекция должна быть органически связана с другими видами
учебных занятий: семинарами, лабораторными работами, учебной и производственной
практикой, самостоятельной работой студентов» [5].
«Учебная лекция должна отражать актуальные проблемы
современного производства, науки, культуры и перспективы их развития.
Необходимо соблюдать логическую последовательность в изучении тем и разделов,
обеспечить эффективную взаимосвязь с другими видами учебных занятий и особенно
с самостоятельной работой студентов [23].
Лекционный курс, составляющий 6 часов, позволяет изложить
материал, входящий в содержание курса, и создает теоретическую основу для всех
видов учебной деятельности по математическому анализу. При чтении лекций
рекомендуется использовать новейшие информационные технологии (подробный
обзорный материал о подготовке и проведении таких лекций изложен в следующих разделах).
Можно указать следующие методические рекомендации к использованию
информационных технологий в процессе изучения раздела математического анализа
«Двойной интеграл»:
) В соответствии с учебной программой можно организовать
изучение отдельных вопросов на практических занятиях в компьютерных классах:
а) изучение теоретических вопросов;
б) изучение практического содержания темы;
в) комплексное изучение предлагаемых тем.
) Можно проводить контрольные мероприятия по отдельным
разделам темы. Проводится контроль:
а) усвоения теоретического содержания темы;
б) уровня сформированности умений и навыков по решению
базовых задач, включенных в обязательные результаты обучения.
) На первом занятии преподавателем даются указания к работе с
обучающими программами. После чего студентам предлагается самостоятельно
изучить темы во внеаудиторное время. Контрольные мероприятия преподаватель
может проводить либо с использованием тестовых систем, либо с использованием
других форм (устные и письменные опросы, фронтальные проверки).
Для контроля усвоения студентами части лекционного материала
рекомендуется провести коллоквиум [18].
Резкое сокращение аудиторного времени на изучение курса
«Математический анализ» ставит задачу усиления самостоятельной работы студентов
по проработке важнейших разделов курса. На лекции преподаватель может успеть
лишь в тезисной форме изложить основные вопросы курса. Все остальное изучение
материала ложится на плечи студентов в виде их самостоятельной работы [18].
В процессе изучения раздела «Двойной интеграл»
предусматриваются следующие виды самостоятельной работы студентов над изучаемым
материалом:
- проработка и осмысление лекционного материала;
- работа с учебниками и учебными пособиями по
лекционному материалу;
самостоятельная проработка тем и вопросов,
предусмотренных программой, но нераскрытых полностью на лекции (доказательство
свойств сумм Дарбу, теоремы о необходимом и достаточном условии интегрируемости
функции двух переменных);
подготовка к коллоквиумам по учебникам, учебным
пособиям и лекционному материалу [18].
Планирование самостоятельной работы студентов необходимо
проводить в соответствии с уровнем подготовки студентов к изучаемому курсу.
Студент может получить разъяснения по непонятным вопросам у преподавателя на
индивидуальных консультациях в соответствии с графиком консультаций [18].
Студент может также обратиться к рекомендуемым преподавателем
учебникам и учебным пособиям, в которых теоретические вопросы изложены более
широко и подробно, чем на лекциях и с достаточным обоснованием [18].
Средством итогового контроля по теме «Двойной интеграл»
является экзамен на втором курсе в 4 семестре.
Использование
информационных технологий в образовании
Современное общество начала третьего тысячелетия
характеризуется рядом особенностей, к которым прежде всего следует отнести
возросшую значимость интеллектуального труда, ориентированного на использование
информационного ресурса глобального масштаба; усилившуюся миграцию населения,
обусловленную как политическими, так и социокультурными причинами; потребность
в осуществлении оперативной коммуникации между отдельными личностями, группами
или сообществами людей; стремление к взаимному приятию и уважению культур
разных народов; необходимость решения глобальных экологических проблем
совместными усилиями специалистов различных стран или общественных организаций.
Эти особенности современного социума влекут за собой необходимость постоянного
повышения профессионального уровня как отдельного человека, так и групп
специалистов или целых коллективов в области владения информационными и
коммуникационными технологиями [24].
Развитость и совершенство методов и средств современных
информационных технологий создает реальные возможности для их использования в
системе образования с целью развития творческих способностей человека в
процессе его образования. Именно с новыми информационными технологиями сегодня
связаны реальные возможности построения открытой образовательной системы,
позволяющей каждому человеку выбирать свою собственную траекторию обучения;
коренного изменения технологии получения нового знания посредством более
эффективной организации познавательной деятельности обучаемых в ходе учебного
процесса на основе такого важнейшего дидактического свойства компьютера, как
индивидуализация учебного процесса при сохранении его целостности за счет
программируемости и динамической адаптированности учебных программ [24].
Совершенно новые возможности для преподавателей и студентов
открывают Интернет и телекоммуникационные сети и интеллектуальные компьютерные
системы. Объединение таких систем и сетей уже сегодня составляет основу новой
инфраструктуры планеты - инфосферы [24].
Использование компьютерных технологий создает принципиально
новые возможности не только в получении человеком новых знаний, но и в
совершенствовании его чувственных ощущений [24].
Современный уровень развития информационных и
коммуникационных технологий дает основание сегодня говорить о реальной
возможности создания глобальной системы дистанционного образования, позволяющей
на основе новых информационных технологий обеспечивать эффект непосредственного
общения между преподавателем и обучаемым, что всегда было преимуществом и
отличительной чертой очного обучения, независимо от того, на каком физическом
расстоянии они находятся друг от друга. Становление и последующее развитие
системы дистанционного образования должно в будущем привести к созданию так
называемых электронных библиотек и университетов распределенного типа, которые
заложат реальную основу формирования единого образовательного пространства для всего
мирового сообщества, в том числе для тех его членов, которые по тем или иным
причинам лишены свободного доступа к образованию [24].
Последнее утверждение в первую очередь следует отнести к
людям, нуждающимся в специальном образовании. В этом видится высокая
гуманистическая роль новых информационных технологий в образовании, посредством
которых «искусственная природа» восполняет для этих людей то, что не додала им
естественная природа, что отняли у них войны, межнациональные конфликты,
человеческая жестокость и природные катастрофы. При этом важно осознавать, что
создаваемая с помощью информационных технологий коммуникационная среда общения
«людей со специальными потребностями» и так называемых «обычных людей» ведет к
их взаимному обогащению, расширяет новые возможности интеллектуального,
физического и духовного развития человека, закладывает реальные основы
осуществления провозглашенного ЮНЕСКО девиза: «Образование без границ» [24].
Для того, чтобы эффективно использовать возможности
информационных технологий, такие новые области, как компьютерная психология,
компьютерная дидактика и компьютерная этика должны быть лучше изучены и
использованы преподавателями. Уже на этой стадии разработчики новых и будущих
информационных и коммуникационных технологий должны ориентироваться на их
практическое применение, учитывая не только технические возможности этих
технологий, но также и более широкие культурные, образовательные и этические
цели [24].
Становление информационного общества повлечет за собой
радикальные изменения в сфере производства и деловой активности людей, а также
и во всей социальной сфере. Будущим поколениям предстоит решать проблему
адаптации к условиям жизни в этом обществе, где решающую роль будут играть не
вещество и энергия, а информация и научные знания - факторы, которые станут
определять как общий стратегический потенциал общества, так и перспективы его
дальнейшего развития [24].
В связи с актуальностью рассматриваемой проблемы возникла
необходимость в разработке и применении в обучении новых компьютерных
технологий, ориентированных на обучение новому материалу и контроль знаний
учащихся. Широкое распространение получают электронные учебники и системы
тестового контроля. В рамках данного исследования была разработана
обучающе-контролирующая программа, в которую входят материал фондовых лекций и
решенные практические задания (обучающая часть) и тест (контролирующая часть).
Использование
ТСО при проведении лекционных занятий
В вузе функционируют разнообразные организационные формы
обучения: лекции, практические занятия в их разновидности - семинары,
лабораторные работы, практикум, НИРС, самостоятельная работа студентов под
контролем преподавателя, производственная практика. В дидактике эти формы
трактуются как способы управления познавательной деятельностью для решения
определенных дидактических задач. В то же время лекция, семинар, практическое
занятие, самостоятельная работа выступают как организационные формы обучения,
так как являются способами осуществления взаимодействия студентов и преподавателей,
в рамках которых реализуются содержание и методы обучения. Процесс обучения
сопровождается и завершается различными формами контроля [5].
На протяжении всей истории высшей школы с момента зарождения
до наших дней ведущей организационной формой и методом обучения является
лекция. С нее начинается первое знакомство студента с учебной дисциплиной,
именно лекция закладывает основу научных знаний [5].
Развитие отечественной образовательной системы, ее
гуманизация, тенденция к ориентации на отдельного человека, на реализацию его
творческих способностей обусловили разработку и появление новых лекционных
форм. Одной из них является лекция - визуализация [5].
Лекция - визуализация возникла как результат поиска новых
возможностей реализации принципа наглядности. Психолого-педагогические
исследования показывают, что наглядность не только способствует более успешному
восприятию и запоминанию учебного материала, но и позволяет проникнуть глубже в
существо познаваемых явлений [5].
Визуализированная лекция представляет собой устную
информацию, преобразованную в визуальную форму. Видеоряд, будучи воспринятым и
осознанным, сможет служить опорой адекватных мыслей и практических действий.
Преподаватель должен выполнить такие демонстрационные материалы, такие формы
наглядности, которые не только дополняют словесную информацию, но сами
выступают носителями содержательной информации. Подготовка такой лекции состоит
в реконструировании, перекодировании содержания лекции или ее части в
визуальную форму для предъявления студентам через ТСО. Чтение такой лекции
сводится к сводному, развернутому комментарию подготовленных визуальных
материалов, которые должны:
- обеспечить систематизацию имеющихся знаний;
- обеспечить усвоение новой информации;
обеспечить создание и разрешение проблемных
ситуаций;
демонстрировать различные способы визуализации [5].
В визуализированной лекции важны: определенная визуальная
логика и ритм подачи материала, его дозировка, мастерство и стиль общения
преподавателя с аудиторией. Основные трудности такой лекции - в разработке
визуальных средств и режиссуре процесса чтения лекции. Необходимо учитывать:
- уровень подготовленности и образованности аудитории;
- профессиональную направленность;
особенности конкретной темы [5].
Отбор технических средств обучения, наглядных пособий и
способ их применения зависит от содержания учебного материала, методов
обучения, дидактических целей занятия. Наиболее полной реализации дидактических
целей обучения, повышению эффективности труда преподавателя способствует
комплексное использование наглядных пособий и ТСО. Рассмотрим наиболее часто
применяющиеся виды ТСО.
Диапроектор служит для проектирования на экран
диапозитивов 24х36 мм, вмонтированных в рамку 50х50 мм и диапозитивов 18х24 мм.
Осветительно-проекционная система состоит из источника света (лампа мощностью
100 Вт), зеркального контротражателя, конденсора и объектива с просветленной
оптикой. При работе аппарат нагревается, что необходимо учитывать.
Эпипроектор - оптический прибор, предназначенный для
проектирования на экран изображений, нанесенных на непрозрачную основу и
непрозрачных плоских объектов через кадровое окно 19х19 мм в хорошо затемненном
помещении. В устройство эпипроектора входит мощная лампа, вентилятор,
предметный столик, лампа подсветки, микровыключатель, который автоматически
включает проекционную лампу при подъеме предметного столика. Во избежание
перегрева аппарата рекомендуется после 10 минут непрерывной работы выключать
проекционную лампу минимум на 5 минут.
Графопроектор (кодоскоп) предназначен для проецирования
на экран записей, сделанных на прозрачной пленке. Он имеет световой поток 2000
люмен, что позволяет использовать его без затемнения. Графопроектор работает по
принципу диаскопической проекции, когда графический материал, находящийся на
поверхности крышки прибора, проецируется на экран. Изображение при этом
получается прямым. Графическое изображение может наноситься на прозрачную
пленку в рулоне, которая подается с катушки на катушку перемоточного
устройства. Светофильтровая нить лампы очень чувствительна к перегрузкам,
поэтому включение лампы сразу на полный накал, минуя пониженное напряжение,
может вывести ее из строя. Нельзя работать при неисправном вентиляторе. Кроме
описанных выше аппаратов статичной проекции, процессе обучения применяется аудио-
и видеоаппаратура. К ней относятся такие приборы, как электрофон, магнитофон,
видеомагнитофон, кинопроектор, телевизор.
Тенденция к сокращению объема лекционных занятий ставит
задачу существенного повышения информативности и эффективности каждого часа
лекции. Техническим средством решения этой задачи и новой формой подготовки и
чтения лекций становятся компьютерные мультимедийные технологии.
Прежде всего, следует обратить внимание на дидактические
возможности использования в учебном процессе электронного конспекта лекций. В
электронном конспекте лекций (ЭКЛ), в отличие от электронного учебника
(пособия), не предоставлена большая свобода выбора темпа и порядка изучения
учебного материала пользователем. ЭКЛ предназначен для лектора и используется
лектором с учетом его индивидуальной манеры чтения лекции, специфики
дисциплины, уровня подготовленности аудитории и т.д.
ЭКЛ совмещает технические возможности компьютерной и
мультимедийной техники с живым общением лектора с аудиторией. Его практическое
использование предполагает наличие TV-выхода в лекционном компьютере (или внешнего TV-кодера), видеопроектора
или телевизоров с большой длиной диагонали экранов [36].
При подготовке ЭКЛ преподавателю необходимо увеличить шрифт
текста лекции до 36-38 размера. При подключении телевизора к компьютеру
появляется возможность отображения текста, хранящегося на гибком магнитном
диске, на экран телевизора. Текст озвучивается лектором, а студенты, глядя на
экран, записывают сложные формулы, изображают рисунки.
Основной единицей ЭКЛ является слайд, или кадр представления
учебной информации, учитывающий эргономические требования визуального
восприятия информации. Требования касаются разборчивости шрифтов обозначений и
надписей, отсутствия агрессивных полей и неприятных ощущений при динамическом
воспроизведении графических материалов, правильного расположения информации в
поле восприятия, отсутствия цветового дискомфорта, оптимизации яркости графиков
по отношению к фону [36].
Социологический опрос студентов вузов России показал, что при
использовании информационных технологий восприятие учебного материала
повысилось. Более 70% студентов считают необходимым использование время от
времени лекций-визуализаций. Около 75% студентов отметили улучшение
эмоционального состояния на лекции и повышение интереса к изучаемому предмету.
При этом всегда успевали конспектировать лекцию около 78% слушателей,
постоянные трудности с конспектированием отметили примерно 6% студентов. Ни
один из респондентов не хотел бы вернуться к традиционной форме лекции [36].
Применение информационных технологий подготовки ЭКЛ требует
новых подходов к эстетике лекционного процесса. Оформление не должно заметно
отставать от уровня дизайна web-страниц Интернета. В таких условиях повышаются
профессиональные требования к преподавателям в плане владения современными
программными средствами и (или) организации совместной работы над курсом лекций
предметников и компьютерных дизайнеров. Достигаемое с помощью новых средств
повышение информативности и обзорности лекций, увеличение динамизма и
выразительности излагаемого материала (фактически привносятся элементы шоу в
достаточно консервативную область) желательно сочетать с увеличение объема
раздаточных материалов для самостоятельной работы как в традиционном формате
внутривузовских изданий, так и в электронном варианте (практикум студенты могут
скопировать на дискету и выполнять самостоятельно) [36].
2.
Теоретические основы изучения раздела математического анализа «двойной
интеграл»
2.1
Определение и простейшие свойства двойного интеграла
Задача
об объеме цилиндрического тела
Наподобие того, как задача о площади криволинейной трапеции
приводит к понятию простого определенного интеграла, аналогичная задача об
объеме цилиндрического бруса приводит к новому понятию - двойного (определенного)
интеграла.
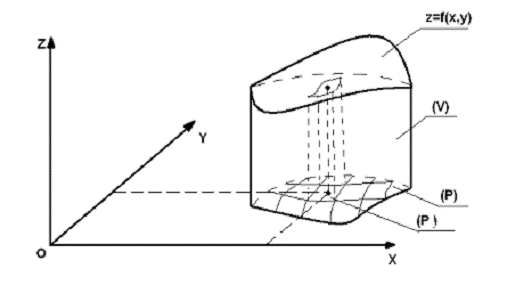
Рассмотрим тело  , которое сверху ограничено поверхностью
, которое сверху ограничено поверхностью 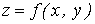 , с боков - цилиндрической поверхностью с
образующими, параллельными оси
, с боков - цилиндрической поверхностью с
образующими, параллельными оси  , наконец, снизу - плоской фигурой
, наконец, снизу - плоской фигурой  на плоскости
на плоскости  (рис. 14). Требуется найти объем
(рис. 14). Требуется найти объем 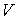 тела [1].
тела [1].
Для решения этой задачи прибегнем к обычному в интегральном
исчислении приему, состоящему в разложении искомой величины на элементарные
части, приближенному подсчету каждой части, суммированию и последующему предельному
переходу. С этой целью разложим область  сетью кривых на части
сетью кривых на части  и рассмотрим ряд цилиндрических столбиков, которые имеют своими
основаниями эти частичные области и в совокупности составляют данное тело.
и рассмотрим ряд цилиндрических столбиков, которые имеют своими
основаниями эти частичные области и в совокупности составляют данное тело.
Для подсчета объема отдельных столбиков возьмем произвольно в
каждой фигуре  по точке:
по точке:  . Если приближенно принять каждый столбик за настоящий цилиндр с
высотой, равной аппликате
. Если приближенно принять каждый столбик за настоящий цилиндр с
высотой, равной аппликате 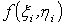 , то объем отдельного столбика оказывается
приближенно равным
, то объем отдельного столбика оказывается
приближенно равным
 ,
,
где  означает площадь плоской фигуры
означает площадь плоской фигуры  [1]. В таком случае приближенное
выражение объема всего тела будет
[1]. В таком случае приближенное
выражение объема всего тела будет

Для повышения точности этого равенства будем уменьшать размеры
площадок  , увеличивая их число. В пределе, при
стремлении к нулю l (наибольшего
из диаметров всех областей
, увеличивая их число. В пределе, при
стремлении к нулю l (наибольшего
из диаметров всех областей  ) это равенство делается точным, так что
) это равенство делается точным, так что
 ,
,
и задача решена.
Предел этого вида и есть двойной интеграл от функции  по области
по области  ; он обозначается символом
; он обозначается символом
 ,
,
так что формула для объема принимает вид
 .
.
Таким образом, двойной интеграл является прямым обобщением
понятия простого определенного интеграла на случай функции двух переменных. Он
играет важную роль также при определении различных геометрических и физических
величин [1].
Понятие
двойного интеграла
Введем понятие интегральной суммы для функции двух переменных  , заданной в ограниченной области
, заданной в ограниченной области  . При этом данную функцию будем иногда
называть функцией точки области
. При этом данную функцию будем иногда
называть функцией точки области  , отождествляя совокупность значений аргументов с той точкой, для
которой эти значения служат координатами. Например, будем иногда писать
, отождествляя совокупность значений аргументов с той точкой, для
которой эти значения служат координатами. Например, будем иногда писать  вместо
вместо  , если
, если 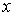 ,
, 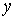 - координаты точки
- координаты точки  [6].
[6].
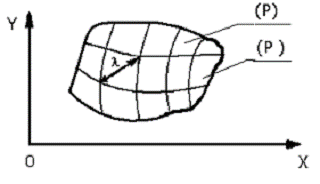
Для дальнейшего потребуется понятие диаметра области.
Определение 1. Диаметром замкнутой области  называется наибольшее расстояние между
двумя точками контура этой области или просто наибольшая хорда области
называется наибольшее расстояние между
двумя точками контура этой области или просто наибольшая хорда области  (рис. 15) [6].
(рис. 15) [6].

Например, диаметром прямоугольника будет длина его диагонали;
диаметром параллелограмма является длина его большей диагонали; диаметром
эллипса служит длина его большой оси.
Пусть в квадратируемой области  определена некоторая функция
определена некоторая функция  . Разобьем область
. Разобьем область  произвольным образом сетью кривых на конечное число частей
произвольным образом сетью кривых на конечное число частей  , площади которых соответственно обозначим
через
, площади которых соответственно обозначим
через  (рис. 16).
(рис. 16).
В каждой из частичных областей  (
( ) возьмем произвольную точку
) возьмем произвольную точку  и составим сумму
и составим сумму
 ,
,
которую будем называть интегральной суммой для функции  в области
в области  .
.
Обозначим через λ наибольший из диаметров частичных областей  . Эту величину, характеризующую, насколько
мелко разбита область
. Эту величину, характеризующую, насколько
мелко разбита область  , иногда называют рангом произведенного
разбиения [5].
, иногда называют рангом произведенного
разбиения [5].
Определение 2.
Если интегральная сумма 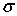 при
при  имеет определенный конечный предел
имеет определенный конечный предел  :
:
 ,
,
не зависящий ни от способа разбиения области  , ни от выбора точек
, ни от выбора точек  в частичных областях, то этот предел
называется двойным интегралом функции
в частичных областях, то этот предел
называется двойным интегралом функции  по области
по области  и обозначается символом
и обозначается символом
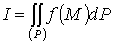 или
или  ,
,
функция же  в этом случае называется интегрируемой в
области
в этом случае называется интегрируемой в
области  .
.
Символ  называют элементом площади. Иногда,
говоря об элементе площади в прямоугольных координатах,
называют элементом площади. Иногда,
говоря об элементе площади в прямоугольных координатах,  . Такое представление
. Такое представление  напоминает выражение площади частичной
области, если разбиение фигуры
напоминает выражение площади частичной
области, если разбиение фигуры  осуществить прямыми, параллельными координатным осям, и записать
площадь «маленького» прямоугольника в виде произведения
осуществить прямыми, параллельными координатным осям, и записать
площадь «маленького» прямоугольника в виде произведения  [5].
[5].
Определение 3.
Интегральная сумма σ стремится
к пределу I:
 ,
,
если каждому  отвечает такое
отвечает такое  , что для любого разбиения области (P) на конечное число частей (Pi) лишь бы
, что для любого разбиения области (P) на конечное число частей (Pi) лишь бы
 и при любом выборе точек
и при любом выборе точек  имеет место неравенство
имеет место неравенство  [5].
[5].
Замечание. Если положить  всюду в области
всюду в области  , то получим выражение площади области
, то получим выражение площади области  в виде двойного интеграла:
в виде двойного интеграла:
 .
.
Действительно, непосредственно из определения интеграла следует,
что
 .
.
Необходимое
условие интегрируемости функции двух переменных
Теорема. Если
функция  интегрируема в области
интегрируема в области  , то она ограничена в
, то она ограничена в  [5].
[5].
Доказательство. Если бы  была не ограничена в области
была не ограничена в области  , то при любом разбиении области
, то при любом разбиении области  на части она была бы неограниченна хотя
бы в одной из ее частей.
на части она была бы неограниченна хотя
бы в одной из ее частей.
Тогда за счет произвольного выбора точки  в этой части
в этой части  можно сделать значение функции
можно сделать значение функции 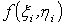 , а с ним и интегральную сумму
, а с ним и интегральную сумму 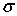 по абсолютной величине сколь угодно
большой.
по абсолютной величине сколь угодно
большой.
В этом случае интегральная сумма 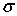 , очевидно, не будет иметь конечного предела и, следовательно,
функция
, очевидно, не будет иметь конечного предела и, следовательно,
функция  не будет интегрируема.
не будет интегрируема.
Замечание. 1. Обратное утверждение неверно, т.е. не всякая
ограниченная функция интегрируема.
2. Это лишь необходимое, но не достаточное условие.
3. В дальнейшем будем всегда считать  ограниченной в
ограниченной в  , т.е.
, т.е.
 [5].
[5].
Суммы
Дарбу
Как и в одномерном случае при изучении двойных интегралов
существенную роль играют так называемые верхняя и нижняя суммы Дарбу

где через 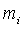 ,
, обозначены соответственно точная нижняя и верхняя границы функции
обозначены соответственно точная нижняя и верхняя границы функции
 в i-й области
в i-й области  .
.
Легко видеть, что суммы Дарбу являются более простыми суммами по
сравнению с интегральными суммами, они однозначно определяются выбранным
разбиением области на части; этого нельзя сказать об интегральных суммах. Для
непрерывной функции, как легко заметить, суммы Дарбу при заданном способе
разбиения области  являются просто наименьшей и наибольшей
из интегральных сумм
являются просто наименьшей и наибольшей
из интегральных сумм 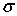 [5].
[5].
Для данного способа разбиения области на части независимо от выбора точек
на части независимо от выбора точек  будем иметь двойное неравенство:
будем иметь двойное неравенство: , которое сразу вытекает из очевидных
неравенств
, которое сразу вытекает из очевидных
неравенств 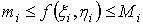 , если члены обоих этих неравенств
умножить на
, если члены обоих этих неравенств
умножить на  и просуммировать по i [5].
и просуммировать по i [5].
Свойства
сумм Дарбу
10. При дальнейшем дроблении частей области
области с добавлением к старым линиям деления новых нижняя сумма Дарбу не
убывает, верхняя не возрастает [1].
с добавлением к старым линиям деления новых нижняя сумма Дарбу не
убывает, верхняя не возрастает [1].
Доказательство. Для доказательства этого свойства достаточно ограничиться
присоединением к уже имеющимся линиям деления еще одной линии деления.
Пусть эта линия разбивает частичную область  на части
на части 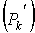 и
и 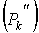 .
.
Если через  обозначить новую верхнюю сумму, то от
прежней
обозначить новую верхнюю сумму, то от
прежней  она будет отличаться только тем, что в
сумме
она будет отличаться только тем, что в
сумме  частичной области
частичной области  отвечало слагаемое
отвечало слагаемое  а в новой сумме
а в новой сумме  этой частичной области отвечает сумма
двух слагаемых
этой частичной области отвечает сумма
двух слагаемых
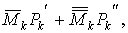
где  и
и  суть точные верхние границы функции f (x, y) в областях
суть точные верхние границы функции f (x, y) в областях 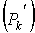 и
и 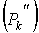 . Так как эти частичные области являются частями области
. Так как эти частичные области являются частями области  , то
, то

так что

Складывая эти неравенства почленно, получим:  Отсюда и следует, что
Отсюда и следует, что  Для нижней суммы Дарбу доказательство
проводится аналогично.
Для нижней суммы Дарбу доказательство
проводится аналогично.
0.
Каждая нижняя сумма Дарбу не превосходит каждой верхней суммы Дарбу, даже если
они соответствуют разным разбиениям области  . [1].
. [1].
Доказательство. Разобьем область  произвольным образом на части и составим для этого разбиения
суммы Дарбу
произвольным образом на части и составим для этого разбиения
суммы Дарбу  и
и  .
.
Рассмотрим теперь некоторое другое, никак не связанное с первым,
разбиение области  на частичные области. Ему также будут
отвечать его суммы Дарбу
на частичные области. Ему также будут
отвечать его суммы Дарбу  и
и  .
.
Требуется доказать, что  . С этой целью объединим те и другие точки деления; тогда получим
некоторое третье, вспомогательное, разбиение, которому будут отвечать суммы
. С этой целью объединим те и другие точки деления; тогда получим
некоторое третье, вспомогательное, разбиение, которому будут отвечать суммы  и
и  .
.
Третье
разбиение получено из первого добавление новых линий деления; поэтому, на
основании доказанного первого свойства сумм Дарбу, имеем 
Сопоставив
теперь второе и третье разбиения, точно так же заключаем, что  .
.
Но  , так что из только что полученных
неравенств вытекает
, так что из только что полученных
неравенств вытекает  , ч. т.д.
, ч. т.д.
Остается справедливым для функции двух переменных следующее
неравенство:
 , где
, где  [1].
[1].
Необходимое
и достаточное условие интегрируемости функции двух переменных
Теорема. Для
существования двойного интеграла необходимо и достаточно, чтобы было  или в других обозначениях
или в других обозначениях  , где
, где  есть колебание
есть колебание  функции
функции  в частичной области
в частичной области  [5].
[5].
Доказательство необходимости. Предположим, что существует двойной интеграл от функции f (x, y). Тогда по любому заданному  найдется такое
найдется такое  , что лишь только все диаметры частичных областей
, что лишь только все диаметры частичных областей 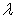 станут меньше
станут меньше  , тотчас будет выполняться
, тотчас будет выполняться
 или
или 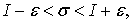
при любом разбиении области  на частичные подобласти и произвольном выборе точек
на частичные подобласти и произвольном выборе точек  в частичных областях
в частичных областях  . Но суммы s и S при заданном разбиении области
. Но суммы s и S при заданном разбиении области  , являются, как было установлено ранее,
для интегральных сумм, соответственно, точными нижней и верхней гранями;
поэтому для них будут иметь место неравенства
, являются, как было установлено ранее,
для интегральных сумм, соответственно, точными нижней и верхней гранями;
поэтому для них будут иметь место неравенства

так что

откуда и следует, что  [5].
[5].
Доказательство достаточности. Предположим, что выполняется условие  Тогда из неравенства
Тогда из неравенства  сразу ясно, что
сразу ясно, что  и, если обозначить их общее значение
через I, то выполняется неравенство
и, если обозначить их общее значение
через I, то выполняется неравенство 
Пусть теперь 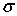 - одно из значений интегральной суммы,
отвечающей тому же разбиению области (P), что и
суммы s и S, тогда, как известно,
- одно из значений интегральной суммы,
отвечающей тому же разбиению области (P), что и
суммы s и S, тогда, как известно, 
Согласно условию  , если предположить все
, если предположить все  достаточно малыми, суммы s и S разнятся меньше, чем на произвольно
взятое
достаточно малыми, суммы s и S разнятся меньше, чем на произвольно
взятое  . Но в таком случае это справедливо и
относительно заключенных между ними чисел
. Но в таком случае это справедливо и
относительно заключенных между ними чисел 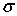 и
и  :
:  , так что
, так что  является пределом для
является пределом для 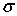 , т.е. двойным интегралом [1]. ч. т.д.
, т.е. двойным интегралом [1]. ч. т.д.
Интегрируемость
непрерывной функции
Теорема. Всякая
непрерывная в области  функция
функция  интегрируема [1].
интегрируема [1].
Доказательство. Действительно, если функция  непрерывна в (замкнутой) области
непрерывна в (замкнутой) области  , то по свойству равномерной непрерывности каждому
, то по свойству равномерной непрерывности каждому 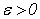 отвечает такое
отвечает такое  , что в любой части области
, что в любой части области  с диаметром, меньшим чем
с диаметром, меньшим чем  , колебание функции будет меньше чем
, колебание функции будет меньше чем  . Пусть теперь область
. Пусть теперь область  разложена на части
разложена на части  , диаметры которых все меньше
, диаметры которых все меньше  . Тогда все колебания
. Тогда все колебания  и
и
 ,
,
откуда и следует выполнение необходимого и достаточного
условия интегрируемости функции двух переменных. Этим интегрируемость функции
доказана [1].
Основные
свойства двойного интеграла
10. Если область  , в которой задана непрерывная функция
, в которой задана непрерывная функция  , непрерывной кривой разложена на две
области
, непрерывной кривой разложена на две
области  и
и 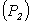 , то из интегрируемости функции
, то из интегрируемости функции  во всей области
во всей области  следует ее интегрируемость в частичных областях
следует ее интегрируемость в частичных областях  и
и 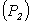 , и обратно - из интегрируемости функции в обеих областях
, и обратно - из интегрируемости функции в обеих областях  и
и 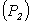 вытекает интегрируемость в области
вытекает интегрируемость в области  . При этом
. При этом
Доказательство. Разобьем области  и
и 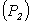 на части. Это разбиение порождает
разложение всей области
на части. Это разбиение порождает
разложение всей области  на части, причем
на части, причем
 (1*)
(1*)
Так как  непрерывна на
непрерывна на  , то она интегрируема на
, то она интегрируема на  ,
,  и
и 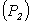 следовательно, существует предел от левой
части выражения (1*), следовательно, будут существовать и пределы
каждой части справа.
следовательно, существует предел от левой
части выражения (1*), следовательно, будут существовать и пределы
каждой части справа.
Перейдем к пределу при  в выражении (1*) и получим формулу (1) [1].
в выражении (1*) и получим формулу (1) [1].
0.
Если умножить интегрируемую в области  функцию
функцию на постоянную
на постоянную  , то полученная функция
, то полученная функция  также будет интегрируема в (Р), и при этом
также будет интегрируема в (Р), и при этом

Доказательство. Если перейти к пределу при  в верном равенстве
в верном равенстве
 , то получим нужную формулу [1].
, то получим нужную формулу [1].
0.
Если в области  интегрируемы функции
интегрируемы функции  и
и 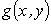 , то интегрируема и функция
, то интегрируема и функция  , причем
, причем
 .
.
Доказательство. Свойство доказывается при предельном переходе при  в верном равенстве
в верном равенстве
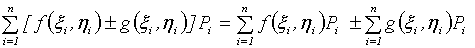 [1].
[1].
40. Если для интегрируемых в области  функций
функций  и
и 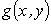 выполняется неравенство
выполняется неравенство  , то
, то

Доказательство. Доказательство основано на предельном переходе при  в верном неравенстве
в верном неравенстве  [1].
[1].
0.
В случае интегрируемости функции  в области (Р) интегрируема и функция
в области (Р) интегрируема и функция 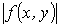 , и имеет место неравенство
, и имеет место неравенство
 .
.
Доказательство. Пусть S' и s' верхняя и нижняя суммы Дарбу на области (Р) для
функции |f (x, y)|, а S и s - верхняя и нижняя суммы Дарбу
для функции f (x, y).
Составим разность S'-s' для функции |f (x, y)|:
 ,
,
так как  .
.
При λ→0
разность S-s стремится к нулю, так как функция f (x, y) интегрируема на (Р) по условию, а, значит, и S'-s' стремится к
нулю при λ→0
подавно.
Так как S'-s' стремится к нулю при λ→0, то функция |f (x, y)| интегрируема на (Р).
При λ→0 в
очевидном неравенстве  переходим к пределу и получаем формулу
свойства [1].
переходим к пределу и получаем формулу
свойства [1].
Теорема
о среднем значении
Теорема 1.
Если функция  интегрируема в замкнутой области (P) и
выполняется неравенство
интегрируема в замкнутой области (P) и
выполняется неравенство  , то:
, то:
. Справедливо неравенство  , где m, M - наименьшее и наибольшее значения функции в области
(P), а P площадь области (P).
, где m, M - наименьшее и наибольшее значения функции в области
(P), а P площадь области (P).
. Существует такая точка с из отрезка 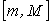 , что выполняется:
, что выполняется:

Доказательство. 1. Первое утверждение теоремы получается при предельном переходе в
двойном неравенстве

2. Пусть некоторая точка с имеет значение  .
.
3. Разделим двойное неравенство пункта 1 на Р. Получим

4. С учетом пункта 2 из того, что 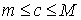 следует, что
следует, что  и
и
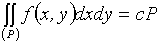 [1].
[1].
Теорема 2.
Если функция двух переменных  непрерывна на замкнутой области (P), то существует такая точка
непрерывна на замкнутой области (P), то существует такая точка  , что будет выполняться:
, что будет выполняться:

Доказательство. Так как область (P) замкнута, то по теореме Вейерштрасса
существуют наибольшее и наименьшее значения функции 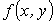 в области (P).
в области (P).
Пусть М - наибольшее значение функции  , m - наименьшее значение функции в
области (P).
, m - наименьшее значение функции в
области (P).
Из теоремы 1 следует, что 
Тогда по теореме Больцано-Коши непрерывная функция  проходит через все промежуточные
значения.
проходит через все промежуточные
значения.
Значит, в области (P) существует точка  такая, что
такая, что  .
.
Поэтому в соответствии с теоремой 1 получаем:
 [1].
[1].
2.2
Вычисление двойного интеграла
Вычисление
двойного интеграла повторным интегрированием в случае прямоугольной области
Сначала рассмотрим двойной интеграл по некоторому
прямоугольнику со сторонами, параллельными осям координат [1].
Теорема. Если
для функции  , определенной в прямоугольнике
, определенной в прямоугольнике 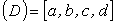 , существует двойной интеграл
, существует двойной интеграл

и при каждом постоянном значении  из
из  существует определенный интеграл
существует определенный интеграл
 ,
,
то существует также повторный интеграл
 ,
,
и выполняется равенство
 .
.
Доказательство. Изобразим область  (рис. 17).
(рис. 17).
Разобьем отрезки  и
и  соответственно на
соответственно на  и
и  частичных отрезков
частичных отрезков
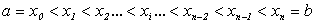 ,
,
 .
.

Тогда область  разобьется на nk частичных прямоугольников.
разобьется на nk частичных прямоугольников.
Частичный прямоугольник  определяется так:
определяется так:
 .
.
Пусть 
Обозначим через 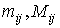 точную нижнюю и точную верхнюю грани функции
точную нижнюю и точную верхнюю грани функции  в частичном прямоугольнике
в частичном прямоугольнике  .
.
Тогда в каждом частичном прямоугольнике будет выполняться
неравенство:
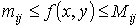 .
.
Выберем произвольно точку  .
.
Проинтегрируем по y на частичном отрезке 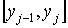 неравенство
неравенство
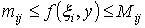 .
.
Получим:  , что равносильно
, что равносильно
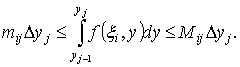
Суммируя последнее неравенство по всем  , получим:
, получим:
 .
.
Так как по условию теоремы существует определенный интеграл
 , то
, то  (2)
(2)
Пусть λ→0
(где λ-наибольший
диаметр частичного прямоугольника  ), тогда
), тогда  .
.
Крайние члены двойного неравенства (2) представляют собой верхнюю
и нижнюю суммы Дарбу, а значит, они стремятся к двойному интегралу .
.
Таким образом, должен существовать предел от средней части
двойного неравенства и он равен следующему двойному интегралу:
 или
или  .
.
Но по условию теоремы
 [1].
[1].
Замечание. Если переменную х поменять на у в рассмотренной
теореме, то будет доказано существование повторного интеграла

и справедливость формулы  [1].
[1].
Вычисление
двойного интеграла повторным интегрированием в случае криволинейной области
Теорема.
Если для функции  , определенной в области
, определенной в области  , ограниченной снизу и сверху двумя
непрерывными кривыми:
, ограниченной снизу и сверху двумя
непрерывными кривыми:
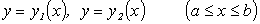 ,
,
а с боков - двумя ординатами:  и
и  , существует двойной интеграл
, существует двойной интеграл 
и при каждом постоянном значении  из
из  существует определенный интеграл
существует определенный интеграл
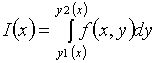 ,
,
то существует также повторный интеграл

и выполняется равенство
 [1].
[1].
Доказательство. Изобразим область  (рис. 18).
(рис. 18).

Пусть  .
.
Заключим область  в прямоугольник
в прямоугольник  , где
, где
 .
.
Введем вспомогательную функцию 
Функция  удовлетворяет всем условиям предыдущей
теоремы:
удовлетворяет всем условиям предыдущей
теоремы:
) интегрируема в области  , так как
, так как 
) интегрируема в области  , так как
, так как  =0.
=0.
На основании одного из свойств двойного интеграла: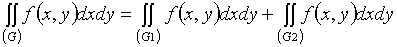 , и условия, что функция
, и условия, что функция  интегрируема на области
интегрируема на области  , получаем:
, получаем:
 .
.
По условию теоремы для всех  существует определенный интеграл
существует определенный интеграл 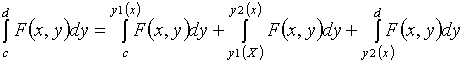 , так как существует каждый из трех определенных интегралов
справа.
, так как существует каждый из трех определенных интегралов
справа.
Действительно, на отрезках  и
и  областей вне области
областей вне области  значение функции равно нулю.
значение функции равно нулю.
Следовательно, первый и третий интегралы существуют и равны нулю,
а второй интеграл существует по условию теоремы, так как  в области
в области  . Следовательно,
. Следовательно,  .
.
Таким образом, для функции  выполняются все условия предыдущей теоремы.
выполняются все условия предыдущей теоремы.
Значит, и двойной интеграл от функции  -
- может быть сведен к повторному:
может быть сведен к повторному:  .
.
Замечание. Если в данной теореме поменять ролями переменные х и у,
то теорема будет утверждать существование следующего повторного интеграла:
 [1].
[1].
2.3
Замена переменных в двойном интеграле
Преобразование
областей при регулярных отображениях
Этот раздел посвящен задаче преобразования двойного интеграла

с помощью замены переменных вида 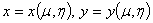 .
.
Окажется, что 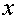 и
и  удобно рассматривать как компоненты
отображения некоторого открытого подмножества плоскости с координатами
удобно рассматривать как компоненты
отображения некоторого открытого подмножества плоскости с координатами  в координатную плоскость с координатами
в координатную плоскость с координатами 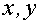 [33].
[33].
Если 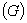 - некоторая замкнутая область, то будем
обозначать
- некоторая замкнутая область, то будем
обозначать  - ее границу,
- ее границу, 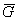 - область вместе с границей, то есть
- область вместе с границей, то есть  .
.
Рассмотрим две плоскости 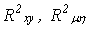 и в них исследуем две замкнутые области
и в них исследуем две замкнутые области 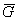 и
и  . Каждая из этих областей может быть и неограниченной, в частности
может охватывать и всю плоскость. Контур или границу области (если область не
охватывает всей области) будем предполагать кусочно-гладкой кривой.
. Каждая из этих областей может быть и неограниченной, в частности
может охватывать и всю плоскость. Контур или границу области (если область не
охватывает всей области) будем предполагать кусочно-гладкой кривой.
Пусть  и
и  соответственно - границы указанных областей.
соответственно - границы указанных областей.
Допустим, что в области  дана система непрерывных функций:
дана система непрерывных функций:
 (3)
(3)
которая каждой точке  области
области  относит одну определенную точку
относит одну определенную точку 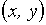 области
области 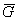 , причем ни одна точка
, причем ни одна точка 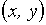 из
из 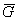 не будет пропущена, так что каждая такая
точка отнесена хоть одной точке
не будет пропущена, так что каждая такая
точка отнесена хоть одной точке  из
из  . Если различным точкам
. Если различным точкам  отвечают различные же точки
отвечают различные же точки 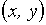 , так что каждая точка
, так что каждая точка 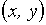 отнесена лишь одной точке
отнесена лишь одной точке  , то формулы (3) однозначно разрешимы
относительно
, то формулы (3) однозначно разрешимы
относительно  . Переменные
. Переменные  в свою очередь являются однозначными
функциями от
в свою очередь являются однозначными
функциями от 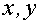 в области
в области 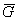 :
:
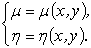 (4)
(4)
Таким образом, между областями 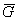 и
и  устанавливается взаимно-однозначное
соответствие. Говорят также, что формулы (3) осуществляют преобразование
устанавливается взаимно-однозначное
соответствие. Говорят также, что формулы (3) осуществляют преобразование области
области  в область
в область 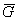 , а формулы (4) дают преобразование
, а формулы (4) дают преобразование  области
области 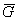 в область
в область  .
.
Если названные области заполняют соответствующие плоскости,
то имеем дело с преобразованием одной плоскости в другую.

Будем предполагать, что функции 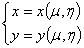 и
и  не только непрерывны в соответствующих
областях, но и имеют непрерывные частные производные (первого порядка)
не только непрерывны в соответствующих
областях, но и имеют непрерывные частные производные (первого порядка)  , что частные производные второго порядка
(смешанные)
, что частные производные второго порядка
(смешанные)  непрерывны на области
непрерывны на области 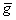 , что функциональный определитель (равный
якобиану поля Т)
, что функциональный определитель (равный
якобиану поля Т)  отличен от нуля всюду на области
отличен от нуля всюду на области  .
.
Значит, определитель  - непрерывен на области
- непрерывен на области  , так как состоит из непрерывных функций и сохраняет постоянный
знак [1].
, так как состоит из непрерывных функций и сохраняет постоянный
знак [1].
Если взять в области  простую кусочно-гладкую кривую
простую кусочно-гладкую кривую  , то с помощью преобразования
, то с помощью преобразования 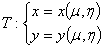 она перейдет в подобную же кривую
она перейдет в подобную же кривую  в области
в области  [1].
[1].
Теорема.
Пусть Т - преобразование области  в область
в область  . Тогда кусочно-гладкая кривая,
принадлежащая области
. Тогда кусочно-гладкая кривая,
принадлежащая области  , перейдет в кусочно-гладкую кривую,
принадлежащую области
, перейдет в кусочно-гладкую кривую,
принадлежащую области  [1].
[1].
Доказательство. Ограничимся гладким куском кривой, так как для кусочно-гладкой
кривой доказательство будет аналогичным.
Пусть уравнения кривой  будут:
будут:
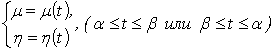 ,
,
причем так как кривая  гладкая, можно функции
гладкая, можно функции  считать имеющими непрерывные производные на отрезке
считать имеющими непрерывные производные на отрезке  , не обращающиеся одновременно в ноль.
, не обращающиеся одновременно в ноль.
Подставляя эти функции в формулы преобразования (3), получим
параметрические уравнения соответствующей кривой  :
:
 .
.
Легко видеть, что эти функции также имеют непрерывные производные: , (так как
, (так как 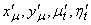 непрерывны на
непрерывны на  ), которые к тому же не могут одновременно обратиться в ноль.
Следовательно, кривая
), которые к тому же не могут одновременно обратиться в ноль.
Следовательно, кривая  - гладкая кривая [1].
- гладкая кривая [1].
Криволинейная
система координат
Преобразования областей для удобства трактуют как переход от
прямоугольной декартовой системы координат к криволинейной системе координат
[42].
Пусть поле  преобразует область
преобразует область  плоскости
плоскости  в область
в область  плоскости
плоскости  .
.

Координатная сетка в плоскости  наводит координатную сеть в области
наводит координатную сеть в области  :
:  . Координатные линии параллельны осям
. Координатные линии параллельны осям  и
и  .
.
При преобразовании  эти прямые (частный случай гладкой кривой) переходят в гладкие
кривые в области
эти прямые (частный случай гладкой кривой) переходят в гладкие
кривые в области  (в соответствии с доказанной в предыдущем
пункте теоремой).
(в соответствии с доказанной в предыдущем
пункте теоремой).
Они образуют сеть гладких кривых в области  и называются криволинейными координатными
линиями (координатные прямые области
и называются криволинейными координатными
линиями (координатные прямые области  порождают координатные кривые области
порождают координатные кривые области  ) [42].
) [42].
Так как поле  взаимно однозначно, то через каждую точку
взаимно однозначно, то через каждую точку
 проходят только две координатные
криволинейные линии, которые являются образами линий
проходят только две координатные
криволинейные линии, которые являются образами линий  .
.
Эти координатные кривые линии сопоставляют точке с координатами  два числа
два числа  , которые называются криволинейными координатами точки
, которые называются криволинейными координатами точки  . Криволинейные координаты
. Криволинейные координаты  точки
точки  связаны с прямоугольной декартовой системой координат прямыми
уравнениями
связаны с прямоугольной декартовой системой координат прямыми
уравнениями 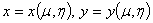 и обратными уравнениями
и обратными уравнениями  [42].
[42].
Полагая в (4) 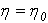 , получим параметрическое представление координатной линии:
, получим параметрическое представление координатной линии:

(роль параметра здесь играет 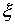 ). Неявное уравнение той же линии получим, полагая
). Неявное уравнение той же линии получим, полагая 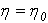 во втором из уравнений (4).
во втором из уравнений (4).
Аналогично при  , получим следующее параметрическое представление координатной
линии:
, получим следующее параметрическое представление координатной
линии:

Имея криволинейные координаты  , можно трактовать преобразование
, можно трактовать преобразование  областей как переход в
областей как переход в  от криволинейных координат
от криволинейных координат  к прямоугольной декартовой системе координат
к прямоугольной декартовой системе координат  [42].
[42].
А преобразование 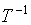 области
области  в
в  - как переход от прямоугольной декартовой системы координат
- как переход от прямоугольной декартовой системы координат  к криволинейной системе координат
к криволинейной системе координат  с помощью систем уравнений
с помощью систем уравнений  , где каждая точка
, где каждая точка  .
.
Значит, любая точка области  имеет две пары координат: прямоугольные декартовы и криволинейные
[42].
имеет две пары координат: прямоугольные декартовы и криволинейные
[42].
Полярная
система координат
Простейшим и важнейшим примером криволинейных координат являются
полярные координаты  . Они имеют наглядное геометрическое
истолкование, как полярный радиус-вектор и полярный угол, но могут быть введены
и формально, с помощью известных соотношений:
. Они имеют наглядное геометрическое
истолкование, как полярный радиус-вектор и полярный угол, но могут быть введены
и формально, с помощью известных соотношений:

где  . Если значения
. Если значения  и
и 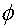 откладывать по двум взаимно перпендикулярным осям, считая,
например,
откладывать по двум взаимно перпендикулярным осям, считая,
например,  - абсциссой, а
- абсциссой, а 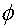 - ординатой (при правой ориентации осей),
то каждой точке полуплоскости
- ординатой (при правой ориентации осей),
то каждой точке полуплоскости  по указанным формулам отвечает одна определенная точка на
плоскости
по указанным формулам отвечает одна определенная точка на
плоскости  [1].
[1].
В этом случае координатные линии имеют вид: прямым  , отвечают круги радиуса
, отвечают круги радиуса  с центром в начале координат, а прямым
с центром в начале координат, а прямым  отвечают лучи, исходящие из начала
координат под углом
отвечают лучи, исходящие из начала
координат под углом 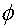 к оси
к оси  .
.
Однако в данном случае формулы преобразования, вообще, не будут
однозначно разрешимы: изменение величины угла 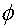 на
на  (где
(где 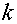 - целое) не отразится на значениях
- целое) не отразится на значениях 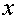 и
и  . Для того, чтобы получить все точки
плоскости
. Для того, чтобы получить все точки
плоскости  , достаточно ограничиться значениями
, достаточно ограничиться значениями  ,
,  [1].
[1].
Каждой точке  , отличной от начала, отвечает одно
значение
, отличной от начала, отвечает одно
значение  и одно значение
и одно значение 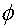 в указанных пределах. Но неустранимое
нарушение однозначности соответствия связано с началом координат: точке
в указанных пределах. Но неустранимое
нарушение однозначности соответствия связано с началом координат: точке 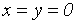 отвечает на плоскости
отвечает на плоскости 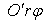 вся ось
вся ось  (или ее отрезок от
(или ее отрезок от  до
до  ).
).
Рассмотрим на плоскости 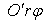 замкнутый прямоугольник
замкнутый прямоугольник 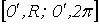 или
или 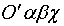 (рис. 22); легко видеть, что на плоскости
(рис. 22); легко видеть, что на плоскости
 ему отвечает замкнутый круг, описанный
вокруг начала 0 радиусом R=OA. Но весь контур этого круга отвечает
одной лишь стороне
ему отвечает замкнутый круг, описанный
вокруг начала 0 радиусом R=OA. Но весь контур этого круга отвечает
одной лишь стороне  упомянутого прямоугольника; сторонам
упомянутого прямоугольника; сторонам  и
и 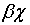 (обеим!) отвечает один и тот же радиус ОА круга; наконец, всей
стороне
(обеим!) отвечает один и тот же радиус ОА круга; наконец, всей
стороне  отвечает лишь точка О. Здесь явно не
соблюдены указанные в предыдущем пункте условия. (радиуса
отвечает лишь точка О. Здесь явно не
соблюдены указанные в предыдущем пункте условия. (радиуса  ) и отрезок ОА
) и отрезок ОА
Однако если сдвинуть сторону  на малую величину
на малую величину  , а сторону
, а сторону  на
на  , то новому прямоугольнику
, то новому прямоугольнику  будет отвечать на плоскости
будет отвечать на плоскости  фигура
фигура  , полученная из круга удалением малого
круга радиусом
, полученная из круга удалением малого
круга радиусом  и сектора с центральным углом
и сектора с центральным углом  , с соблюдением уже всех требований. При
перемещении точки на плоскости
, с соблюдением уже всех требований. При
перемещении точки на плоскости 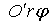 по отрезкам
по отрезкам  соответствующая точка на плоскости Oxy опишет по порядку неполную окружность C’O (радиуса r) и отрезок ОА.
соответствующая точка на плоскости Oxy опишет по порядку неполную окружность C’O (радиуса r) и отрезок ОА.

Найдем первые частные производные функций  :
:
 .
.
Найдем якобиан:  , т.е. Якобиан сохраняет положительный знак [1].
, т.е. Якобиан сохраняет положительный знак [1].
Прямые уравнения, связывающие прямоугольную декартову систему
координат с полярной системой координат, имеют вид: 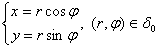 .
.
Обратные уравнения, связывающие полярную систему координат с
прямоугольной декартовой системой координат, имеют вид:
 [1].
[1].
Замена
переменных в двойном интеграле
1. Пусть функция  непрерывна в замкнутой
области
непрерывна в замкнутой
области 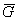 с кусочно-гладкой
границей.
с кусочно-гладкой
границей.
. Пусть поле  осуществляет преобразование области
осуществляет преобразование области  в область
в область  ,
, 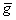 имеет кусочно-гладкую
границу.
имеет кусочно-гладкую
границу.
. Пусть области 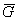 и
и 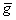 являются ограниченными.
являются ограниченными.
4. Так как 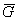 и
и 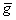 имеют непрерывные
границы, то они измеримы, а, следовательно, имеют площадь, т.е. квадратируемы.
имеют непрерывные
границы, то они измеримы, а, следовательно, имеют площадь, т.е. квадратируемы.
5. Пусть поле 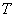 задано двумя функциями:
задано двумя функциями:  . Смешанные производные
. Смешанные производные 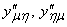 непрерывны в
непрерывны в 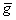 , т.е. на
, т.е. на 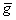 выполняется равенство
выполняется равенство 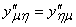 . При всех указанных
условиях справедлива следующая формула:
. При всех указанных
условиях справедлива следующая формула:
 . (5)
. (5)
Доказательство. Изобразим области 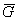 и
и 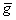 (рис. 23).
(рис. 23).

Разобьем область 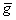 сетью кусочно-гладких
кривых на частичные области
сетью кусочно-гладких
кривых на частичные области  ,
,  , причем каждая область
, причем каждая область  имеет кусочно-гладкую
границу [25].
имеет кусочно-гладкую
границу [25].
Преобразование 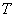 порождает разбиение
области
порождает разбиение
области 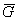 на частичные подобласти
на частичные подобласти 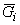 с помощью конечного
числа кусочно-гладких кривых
с помощью конечного
числа кусочно-гладких кривых  [25].
[25].
Между областями  и
и 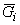 существует простая
связь:
существует простая
связь:
а) они имеют кусочно-гладкие границы, следовательно, границы
непрерывны и области измеримы;
б) частичные области имеют площади, т.е. они квадратируемы и
 [25].
[25].
Это равенство будет получено при рассмотрении криволинейного
интеграла и доказано. Площадь криволинейного частичного прямоугольника равна
площади прямоугольника, умноженной на якобиан.
При исследовании определенного интеграла составляли
интегральную сумму. Составим и в данном случае сумму вида
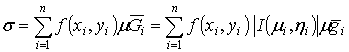 . (6)
. (6)
Так как точка  выбрана произвольно в области
выбрана произвольно в области 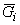 , то можно принять, что
, то можно принять, что  .
.
При таком условии правая часть интегральной суммы примет вид:
 .
.
Если меру площади  устремить к 0, то в
пределе получим двойной интеграл по области
устремить к 0, то в
пределе получим двойной интеграл по области 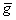 :
: . Переходя к пределу в
левой части выражения (6) при
. Переходя к пределу в
левой части выражения (6) при  , получим двойной интеграл
, получим двойной интеграл  [25].
[25].
Значит, справедливость формулы (5) доказана. Существует
предел от левой и правой частей интегральной суммы, так как функция  непрерывна по области
непрерывна по области 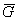 и непрерывным является
каждый из сомножителей
и непрерывным является
каждый из сомножителей 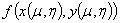 и
и 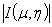 в
в 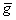 .
.
Замечание. Устремление меры площади к 0 приводит к устремлению к 0
наибольшего диаметра частичных областей, т.е.  ,
,  - наибольший диаметр частичной области
- наибольший диаметр частичной области  и
и  ,
,  -наибольший диаметр частичной области
-наибольший диаметр частичной области 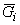 [25].
[25].
Заключение
Результатом выпускной квалификационной работы являются
разработанные методические рекомендации к проведению лекционных и практических
занятий по теме «Двойной интеграл», конспект фондовых лекций,
обучающе-контролирующая программа.
При разработке лекционных и практических занятий соблюдались
основные принципы дидактики: принцип наглядности, принцип научности, принцип
систематичности и последовательности, принцип доступности, принцип связи теории
с практикой.
Разработанные методики были апробированы на втором курсе
факультета математики и информатики СГПИ в феврале - марте 2003-2004 учебного
года. Также с целью выявления направленности учебной мотивации было проведено
анкетирование, результаты которого учитывались при апробации. Результаты
апробации показали, что новые образовательные технологии (в данном случае,
педагогика сотрудничества и информационные технологии) целесообразно применять
на занятиях по математическому анализу.
При разработке практических занятий и создании компьютерной
программы учитывались психологические особенности студенческого возраста.
Материалы выпускной квалификационной работы будут полезны
студентам второго курса математического факультета педагогического вуза,
желающим расширить и систематизировать свои знания по теме «Двойной интеграл»,
а также при самостоятельном изучении темы. В разработанных практических
занятиях подробно рассматриваются методы решения всех основных типов задач на
вычисление двойного интеграла, что позволит студентам лучше разобраться в сложных
для них вопросах.
Кроме того, результаты исследования будут полезны
преподавателям при подготовке и проведении лекционных занятий, поскольку
содержат рекомендации к применению новейших информационных технологий; и
практических занятий, так как включают в себя практические рекомендации по
использованию метода сотрудничества на занятиях по математическому анализу.
Литература
1. Фихтенгольц
Г.М. Курс дифференциального и интегрального исчисления. В 3-х томах. - СПб:
издательство «Лань», 1997.
2. Баас
Р., Фервай М. Delphi 4: полное руководство. - Киев: BHV, 1999 - 850 с.
3. Басова
Н.В. Педагогика и практическая психология. - Ростов н/Д: издательство «Феникс»,
1999 - 346 с.
. Бермант
Г.Н. Сборник задач по курсу математического анализа. - М.: Наука, 1969. - 378
с.
. Бордовская
Н.В., Реан А.А. Педагогика: учебник для вузов. - СПб: издательство «Питер»,
2001 -275 с.
. Бохан
Н.А. и др. Курс математического анализа. В 2-х томах-М.: Просвещение, 1965. -
562 с.
. Бугров
Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное
исчисление: учебник для вузов. - 4-е изд., переработка и дополнение. - Ростов
н/Д: издательство «Феникс», 1997. - 512 с.
. Бугров
А.С., Никольский С.М. Дифференциальное и интегральное исчисление. - Ростов н/Д:
Феникс, 1997. - 438 с.
. Задачник
по курсу математического анализа. Ч. 2. / Под ред. Н.Я. Виленкина. - М.:
Просвещение, 1971.-432 с.
. Власов
В.Г. Конспект лекций по высшей математике. - М.: Айрис, 1996.-533 с.
. Гусак
А.А. Высшая математика. Т. 2. - Минск: БГУ, 1976. - 326 с.
. Давыдов
Н.А., Коровкин П.П., Никольский В.Н. Сборник задач по математическому анализу.
- М.: Просвещение, 1973. - 376 с.
. Данко
П.Е. и др. Высшая математика в упражнениях и задачах. Т. 1. - М.: высшая школа,
1980.-328 с.
. Сборник
задач и упражнений по матанализу / Под ред. Б.П. Демидовича. - М.: Наука, 1990.
- 376 с.
. Дубовицкая
Т.Д. Методика диагностики направленности учебной мотивации. // Психологическая
наука и образование // , №2 - 2002 г. - 42-45 с.
. Зимняя
И.А. Педагогическая психология. - М.: Логос, 2001. - 362 с.
. Зиновьева
Л.А. Сборник задач по математическому анализу для студентов второго курса
факультета математики-информатики. Ч. 4. - Славянск-на-Кубани: СФАГПИ, 1998. -
48 с.
. Зиновьева
Л.А., Мурашко С.А. Учебная программа курса «Математический анализ» факультет
математики и информатики курсы I-II семестры 1 - 4. - Славянск-на-Кубани, 2000.
- 22 с.
. Зиновьева
Л.А., Чернышев А.Н. Математический анализ: методические рекомендации к
практическим занятиям и самостоятельной работе для студентов педагогических
вузов (2 курс, 4 семестр). - Славянск - на - Кубани, 2000 - 12 с.
. Зорич
В.А. Математический анализ. Т.2. - М.: Наука, 1981. - 364 с.
. Зорич
В.А. Математический анализ, Ч. 2, - М.: Наука, Главная редакция
физико-математической литературы, 1981. - 544 с.
. Игошин
В.И. Логика и интуиция в математическом образовании. // Педагогика // , №9 -
2002 г. - 40-46 с.
. Инструктивное
письмо №5 МВ и ССО СССР от 3.04.1981 «О повышении уровня лекций, усилении их
значения в подготовке специалистов».
. Кинелев
В.Г. Контуры системы образования XXI в. // Информатика и образование // , №5 -
2000 г. - 5-8 с.
. Коровкин
П.П. Математический анализ. Ч. 2. - М.: Просвещение, 1974. - 452 с.
. Кудрявцев
Л.Д. Курс математического анализа Т.2. - М.: Высшая школа, 1998. - 342 с.
. Кудрявцев
В.А., Демидович Б.П. Краткий курс высшей математики. - М.: Наука, 1989. 97 -
104 с.
. Монахов
А.И. И др. Учебный курс «Математический анализ» в педагогическом университете.
- М.: издательский центр МГОПУ, 1999. - 160 с.
. Натансон
И.П. Краткий курс высшей математики. - Ч. 2. СПб.: Лань, 1997. - 328 с.
. Никольский
С.М. Курс математического анализа. Т.1. - М.: Наука, 1973. - 352 с.
. Полат
Е.С. Новые педагогические и информационные технологии в системе образования:
учебное пособие для студентов педагогических вузов и системы повышения
квалификации педагогических кадров.-М.: Академия, 2001. - 272 с.
. Поршнев
А.В. Психологические принципы разработки компьютерных программ для обучения
студентов французскому языку. // Психологическая наука и образование // , №2 -
2001 г. - 81-85 с.
. Райков
Д.А. Многомерный математический анализ. - М.: Высшая школа, 1989. - 432 с.
. Самыгин
С.И. Педагогика и психология высшей школы: учебное пособие. - Ростов н/Д:
издательство «Феникс», 1998. - 517 с.
. Смирнов
С.Д. Педагогика и психология высшего образования: от деятельности к личности:
учебное пособие для слушателей факультетов и институтов повышения квалификации
преподавателей вузов и аспирантов - М.: АспектПресс, 1995. - 271 с.
. Стародубцев
В.А. Использование информационных технологий на лекциях по естественнонаучным
дисциплинам. // Информатика и образование // , №1 - 2003 г. - 14-19 с.