Расчет щелевых импедансных нагрузок
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. КРАТКИЙ ОБЗОР ЛИТЕРАТУРЫ
2. ПОСТАНОВКА ЗАДАЧИ
3. РЕШЕНИЕ ЗАДАЧИ
3.1 Вывод
интегрального уравнения
3.2 Расчет
поверхностного импеданса конструкции
.3 Решение
вспомогательной задачи
3.3.1 Решение
задачи возбуждения идеально проводящей поверхности нитью магнитного тока
3.3.2 Решение
задачи возбуждения полости треугольного поперечного сечения нитью магнитного
тока
4. АЛГОРИТМИЗАЦИЯ
ЗАДАЧИ
4.1 Метод
Крылова-Боголюбова
4.2 Выражения
для коэффициентов системы линейных алгебраических уравнений
5. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО ЭКСПЕРИМЕНТА
СПИСОК
ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
Как известно рассеивающими свойствами проводящих тел можно управлять с
помощью непрерывно распределенного импеданса или с помощью дискретных нагрузок
[1]. Наиболее известным способом реализации распределенного импеданса является
ребристая структура, в которой управление импедансом осуществляется только за
счет изменения глубины канавки, то есть данная импедансная структура имеет одну
степень свободы управления импедансом, что является существенным недостатком
так как приводит к значительному увеличению толщины, а следовательно и массы
импедансной структуры [1].
Поэтому возникает интерес к импедансным нагрузкам с несколькими степенями
свободы, подобными приведенным в [1]. В данной работе рассматривается щелевая
импедансная нагрузка на основе полости с поперечным сечением в виде
равностороннего треугольника.
1. КРАТКИЙ ОБЗОР ЛИТЕРАТУРЫ
В
течение уже нескольких десятилетий широко проводится изучение электромагнитной
связи двух объемов через отверстия. Проблема возникла с появлением простейших
дифракционных антенн в виде круглого отверстия или прямоугольной щели на
поверхности эндовибратора (полого резонатора), исследованных экспериментально
[5]. Теория таких антенн разработана без учета влияния полости, расположенной
за щелью [5-11]. В работах [12-13] вариационным методом решены задачи о
нахождении входного импеданса щелей с полостями простой геометрической формы
(круглой и прямоугольной), однако высшие моды в полости не учитывались. В
работе [14] приведено решение методом частичных областей задачи о возбуждении
радиального резонатора с кольцевой щелью, но рассмотрена только узкая щель ( , где
, где  - ширина
щели,
- ширина
щели, 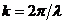 ,
, 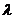 - длина
волны).
- длина
волны).
Таким
образом, имеются решения задачи о возбуждении щелей с полостями определенных
геометрических форм заданными возбуждающими источниками. Данная работа
посвящена решению задачи рассеяния электромагнитных волн на щели с полостью в
виде равностороннего треугольника.
2.
ПОСТАНОВКА ЗАДАЧИ
В
бесконечно тонком, идеально проводящем экране прорезана щель площадью  . Неограниченное пространство делится экраном на две
области: область
. Неограниченное пространство делится экраном на две
области: область  с параметрами
с параметрами  ,
, 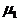 и возбуждающими источниками
и возбуждающими источниками 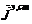 ,
, 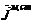 ,
расположенными в объеме
,
расположенными в объеме  , и область
, и область 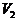 с
параметрами
с
параметрами  ,
,  без
возбуждающих источников. Область
без
возбуждающих источников. Область  занимает
все верхнее полупространство, область
занимает
все верхнее полупространство, область 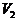 совпадает
с внутренним объемом треугольной полости.
совпадает
с внутренним объемом треугольной полости.
Характеристики
возбуждающих источников и параметры конструкции будем считать независимыми от
координаты 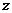 (двумерная задача), внутренние стенки треугольной
области, как и экран, - идеально проводящими. Необходимо определить входной
импеданс устройства, который должен зависеть как от геометрических размеров
полости (ширины щели), так и от диэлектрической
(двумерная задача), внутренние стенки треугольной
области, как и экран, - идеально проводящими. Необходимо определить входной
импеданс устройства, который должен зависеть как от геометрических размеров
полости (ширины щели), так и от диэлектрической  и
магнитной
и
магнитной  проницаемостей.
проницаемостей.
К постановке задачи
Рис.1
3.РЕШЕНИЕ ЗАДАЧИ
.1 Вывод интегрального уравнения
Решение
задачи будем проводить методом интегральных уравнений с наложением условий
непрерывности на касательные составляющие векторов поля в пределах щели. Для
составления интегрального уравнения воспользуемся леммой Лоренца в интегральной
форме. Запишем лемму Лоренца для областей  и
и 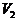 :
:
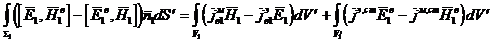 , (3.1)
, (3.1)
 ; (3.2)
; (3.2)
где
 ,
, 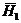 и
и 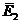 ,
, 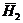 - искомые
электрические и магнитные поля соответственно в объемах
- искомые
электрические и магнитные поля соответственно в объемах  и
и 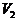 ;
; 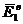 ,
, 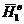 и
и 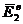 ,
, 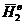 -
электрические и магнитные поля вспомогательных источников в объемах
-
электрические и магнитные поля вспомогательных источников в объемах  и
и 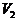 ;
; 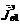 ,
, 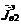 и
и 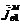 ,
, 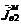 - токи
вспомогательных электрического и магнитного источников в объемах
- токи
вспомогательных электрического и магнитного источников в объемах  и
и 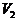 ;
; 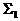 - поверхность, включающая
- поверхность, включающая  ,
,  и
поверхность бесконечной полусферы в области
и
поверхность бесконечной полусферы в области  ;
;  - поверхность, включающая
- поверхность, включающая  ,
, 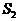 ,
,  ,
, 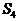 ;
символом
;
символом  для сокращения записи обозначены внешние нормали к
поверхностям полости
для сокращения записи обозначены внешние нормали к
поверхностям полости 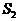 ,
,  ,
, 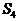 .
.
Для
упрощения решения задачи наложим на касательные составляющие вспомогательного
электрического поля 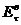 граничные условия вида
граничные условия вида
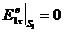 ;
; 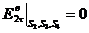 . (3.3)
. (3.3)
Для
касательных составляющих векторов электрического поля должно выполняться
условие
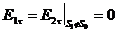 . (3.4)
. (3.4)
В
соответствии с условиями излучения интеграл по бесконечной полусфере в области  равен нулю, поэтому, учитывая (3.3) и (3.4), из (3.1)
и (3.2) получим
равен нулю, поэтому, учитывая (3.3) и (3.4), из (3.1)
и (3.2) получим
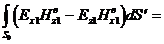
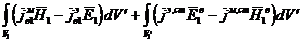 ; (3.5)
; (3.5)
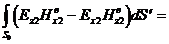
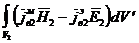 . (3.6)
. (3.6)
Выберем
в качестве вспомогательного и возбуждающего источников нити магнитного тока, то
есть:
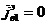 ,
, 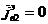 ;
; 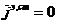 ;
; 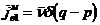 ,
, 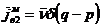 ;
;  ;(37)
;(37)
где
 - амплитуда возбуждающего тока. Устремляя точку
наблюдения
- амплитуда возбуждающего тока. Устремляя точку
наблюдения 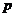 к
к  ,
учитывая (3.3), (3.7) и двумерность задачи, из (3.5) и (3.6) получим
,
учитывая (3.3), (3.7) и двумерность задачи, из (3.5) и (3.6) получим
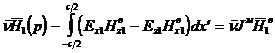 ; (3.8)
; (3.8)
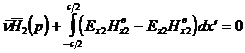 . (3.9)
. (3.9)
Рассмотрим
случай H - поляризации, т. е.  , тогда
из (3.8), (3.9) получим
, тогда
из (3.8), (3.9) получим
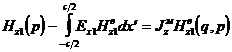 ; (3.10)
; (3.10)
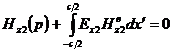 . (3.11)
. (3.11)
Для
определения касательных составляющих поля используем граничные условия в
раскрыве щели, т. е. 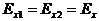 ,
, 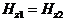 при
при 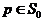 , в результате чего из (3.10) и (3.11) получим
, в результате чего из (3.10) и (3.11) получим
 . (3.12)
. (3.12)
Таким
образом получено интегральное уравнение относительно неизвестной касательной
составляющей электрического поля в раскрыве щели.
Вспомогательные
поля 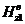 и
и  можно
найти из решения соответствующих граничных задач: возбуждение синфазными нитями
магнитного тока плоской, идеально проводящей поверхности и треугольной полости.
можно
найти из решения соответствующих граничных задач: возбуждение синфазными нитями
магнитного тока плоской, идеально проводящей поверхности и треугольной полости.
3.2 Расчет поверхностного импеданса конструкции
В
результате решения интегрального уравнения (3.12) определяется касательная
составляющая электрического поля в раскрыве щели 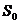 .
Магнитное поле можно найти из формулы (3.10). Однако, на практике результаты в
виде распределений касательных составляющих полей не всегда являются удобными,
и часто их описывают с помощью интегральной характеристики - эквивалентного
поверхностного импеданса. Понятие эквивалентного поверхностного импеданса
.
Магнитное поле можно найти из формулы (3.10). Однако, на практике результаты в
виде распределений касательных составляющих полей не всегда являются удобными,
и часто их описывают с помощью интегральной характеристики - эквивалентного
поверхностного импеданса. Понятие эквивалентного поверхностного импеданса 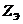 вводится, исходя из энергетических соотношений,
следующим образом: выбирается некоторое постоянное число
вводится, исходя из энергетических соотношений,
следующим образом: выбирается некоторое постоянное число 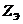 , такое чтобы выполнялось равенство
, такое чтобы выполнялось равенство
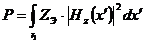 , (3.13)
, (3.13)
где
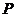 -погонная комплексная мощность в раскрыве щели,
-погонная комплексная мощность в раскрыве щели,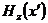 - комплексная амплитуда вектора
- комплексная амплитуда вектора 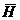 в раскрыве щели, определяемая по формуле (3.10).
Кроме того, точное значение комплексной мощности в раскрыве щели
в раскрыве щели, определяемая по формуле (3.10).
Кроме того, точное значение комплексной мощности в раскрыве щели 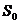 можно найти по формуле
можно найти по формуле
 , (3.14)
, (3.14)
где
 - комплексная амплитуда вектора
- комплексная амплитуда вектора  в раскрыве щели, определяемая из решения
интегрального уравнения (3.12).
в раскрыве щели, определяемая из решения
интегрального уравнения (3.12).
Приравнивая
соотношения (3.13) и (3.14), получим:
 , (3.15)
, (3.15)
где
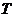 - интервал усреднения импеданса.
- интервал усреднения импеданса.
Таким
образом видно, что вычисление всех интересующих нас характеристик не вызывает затруднений,
если определены касательные составляющие электрического и магнитного полей в
раскрыве щели, которые определяются, в свою очередь, из решения интегрального
уравнения (3.12), поэтому в дальнейшем уделим основное внимание вопросам,
связанным с решением интегрального уравнения.
3.3 Решение вспомогательной задачи
.3.1 Решение задачи возбуждения идеально проводящей поверхности нитью
магнитного тока
Вспомогательное
поле 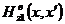 находится из решения задачи возбуждения нитью
магнитного тока плоской, идеально проводящей поверхности.
находится из решения задачи возбуждения нитью
магнитного тока плоской, идеально проводящей поверхности.
Решение
этой задачи приведено в [1]. Выражение для вспомогательного поля 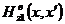 при
при 
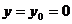 имеет
вид
имеет
вид
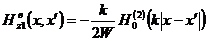 , (3.16)
, (3.16)
где
 - функция Ханкеля второго рода нулевого порядка,
- функция Ханкеля второго рода нулевого порядка, 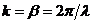 ,
, 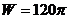 .
.
В
силу того, что поле возбуждается плоской волной, можно считать, что
возбуждающий источник находится на бесконечности и, следовательно, можно
воспользоваться асимптотикой функции Ханкеля при больших значениях аргумента
[1]
 (3.17)
(3.17)
При
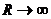 можно принять
можно принять 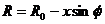 ,
подставляя теперь (3.17) в (3.16) получим выражение для правой части уравнения
(3.12)
,
подставляя теперь (3.17) в (3.16) получим выражение для правой части уравнения
(3.12)
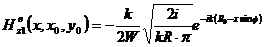 (3.18)
(3.18)
Для
простоты примем амплитуду источника равной единице, т. е. положим, что
выполняется условие
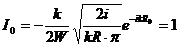 (3.19)
(3.19)
С
учетом (3.19) из (3.18) окончательно получим
 (3.20)
(3.20)
3.3.2 Решение задачи возбуждения полости треугольного поперечного сечения
нитью магнитного тока
Для решения этой задачи необходимо получить функцию Грина для полости с
поперечным сечением в виде равностороннего треугольника. В [3] приведена
функция Грина для треугольной полости следующей геометрии:
где
 ,
, 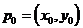 , а
, а 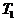 и
и  определяются
следующим образом:
определяются
следующим образом:
 (3.22)
(3.22)
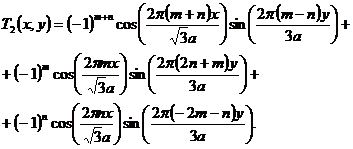 (3.23)
(3.23)
Необходимо
перейти к геометрии решаемой задачи (рис. 3.2). Для этого заменим в выражении
для 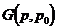
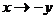 , а
, а 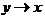 . Таким
образом получим
. Таким
образом получим
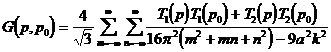 , (3.24)
, (3.24)
где
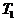 и
и 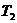 имеют
вид: (3.25), (3.26).
имеют
вид: (3.25), (3.26).
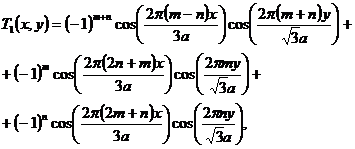 (3.25)
(3.25)
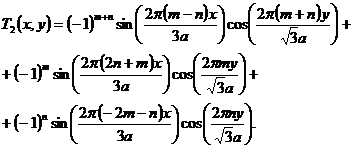 (3.26)
(3.26)
Рис. 3.2
Найдем
теперь, используя полученную функцию Грина, векторный потенциал 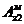 .
.
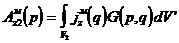 , (3.27)
, (3.27)
где
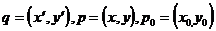 , а
, а  .
Подставим в (3.27) выражение для функции Грина (3.24)
.
Подставим в (3.27) выражение для функции Грина (3.24)
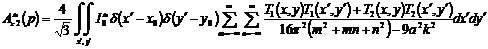 . (3.28)
. (3.28)
Изменим
в (3.28) порядок интегрирования и суммирования
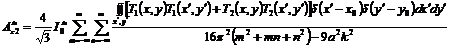 . (3.29)
. (3.29)
Теперь, используя основное свойство дельта-функции, получим
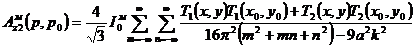 . (3.30)
. (3.30)
Используем
теперь формулу связи полей и потенциалов [1]
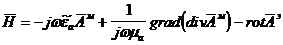 . (3.31)
. (3.31)
В
нашем случае 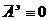 , так как отсутствует электрический ток. Заметим
также, что
, так как отсутствует электрический ток. Заметим
также, что 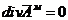 , так как
, так как 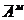 не
зависит от
не
зависит от 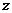 . Получим упрощенное выражение, связывающее
вспомогательное магнитное поле и найденный векторный потенциал
. Получим упрощенное выражение, связывающее
вспомогательное магнитное поле и найденный векторный потенциал
 . (3.32)
. (3.32)
Подставим
найденный векторный потенциал (3.30) в (3.32)
 . (3.33)
. (3.33)
Положим
для простоты, что 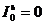 , а
, а 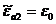 . Тогда
выражение (3.33) примет вид
. Тогда
выражение (3.33) примет вид
 . (3.34)
. (3.34)
Запишем
окончательно выражения для вспомогательных полей при 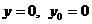 :
:
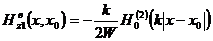 , (3.35)
, (3.35)
 . (3.36)
. (3.36)
4.
АЛГОРИТМИЗАЦИЯ ЗАДАЧИ
Известно, что интегральные уравнения электродинамики редко имеют
аналитическое решение. Большинство же таких задач решаются численными методами.
Существует несколько различных методов решения интегральных уравнений. Однако в
электродинамике наиболее часто применяется метод моментов, суть которого
заключается в следующем:
·
для разложения
неизвестной функции выбирается система базисных функций;
·
берется скалярное
произведение каждой пробной функции с левой и правой частями интегрального
уравнения, в результате получается система линейных алгебраических уравнений;
·
в результате
решения полученной системы уравнений определяются коэффициенты разложения
неизвестной функции.
Следует отметить, что наиболее распространены два частных случая метода
моментов:
1. Метод Крылова-Боголюбова. Базисные
функции при этом выбираются кусочно-постоянными, а пробные - дельта-функции;
2. Метод Галеркина. Базисные функции и
пробные функции выбираются одинаковыми [4].
Для численного решения интегрального уравнения (3.12) применялся метод
Крылова-Боголюбова. Рассмотрим его подробнее.
Метод Крылова-Боголюбова
Имеем исходное интегральное уравнение 1-го рода
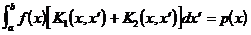 , (4.1)
, (4.1)
где
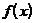 - неизвестная функция,
- неизвестная функция, 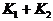 - ядро
интегрального уравнения,
- ядро
интегрального уравнения,  - известная правая часть.
- известная правая часть.
Разобьем
интервал  на
на  равных
участков, в центре каждого участка выделим точку
равных
участков, в центре каждого участка выделим точку  ,
где
,
где  . Будем считать значение функции
. Будем считать значение функции 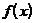 , внутри каждого участка, неизменным. То есть
фактически заменим непрерывную функцию
, внутри каждого участка, неизменным. То есть
фактически заменим непрерывную функцию 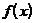 -
кусочно-линейной
-
кусочно-линейной
 , (4.2)
, (4.2)
где
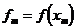 ,
, 
Теперь
интегральное уравнение принимает вид
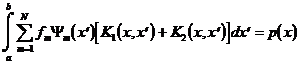 . (4.3)
. (4.3)
Вводим
систему пробных функций 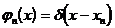 и образуем скалярное произведение каждой функции с
левой и правой частями интегрального уравнения.
и образуем скалярное произведение каждой функции с
левой и правой частями интегрального уравнения.
 (4.4)
(4.4)
для
 .
.
Пользуясь
основным свойством  -функции преобразуем полученное выражение.
-функции преобразуем полученное выражение.
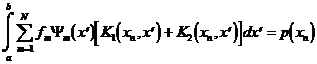 , (4.5)
, (4.5)
для
 .
.
Далее
вынесем сумму за знак интеграла.
 , (4.6)
, (4.6)
для
 .
.
Функция
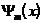 на интервале
на интервале  не равна
нулю лишь на участке
не равна
нулю лишь на участке 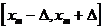 , а внутри этого участка она равна единице, поэтому
получим окончательное выражение
, а внутри этого участка она равна единице, поэтому
получим окончательное выражение
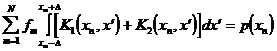 , (4.7)
, (4.7)
для
 .
.
Таким
образом исходное интегральное уравнение сведено к системе линейных
алгебраических уравнений вида
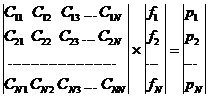 , (4.8)
, (4.8)
решение
которой при помощи среды программирования MathCad 7.0 не
представляет труда.
4.1
Выражения для коэффициентов системы линейных алгебраических уравнений
Запишем выражения для коэффициентов системы (4.8):
 , (4.9)
, (4.9)
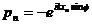 . (4.10)
. (4.10)
С
точки зрения програмной реализации в среде MathCad 7.0
первый интеграл выражения (4.9) не представляется сложным, так как пакет MathCad
7.0 имеет встроенную процедуру численного интегрирования, а функция Ханкеля
второго рода нулевого порядка, входящая в выражение для 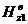 выражается через функции Бесселя, также имеющиеся в
пакете MathCad 7.0, следующим образом:
выражается через функции Бесселя, также имеющиеся в
пакете MathCad 7.0, следующим образом:
 . (4.11)
. (4.11)
Второй
же интеграл выражения (4.9) наиболее трудоемок в процессе вычисления
коэффициентов, так как он берется от функции  , которая
сама по себе представляет собой двойную сумму. С целью сокращения машинного
времени, требующегося для просчета коэффициентов (4.11), упростим выражение для
, которая
сама по себе представляет собой двойную сумму. С целью сокращения машинного
времени, требующегося для просчета коэффициентов (4.11), упростим выражение для
 .
.
Запишем
исходное выражение для вспомогательного магнитного поля  (3.36)
(3.36)
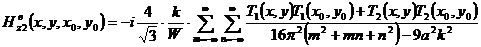 .(4.12)
.(4.12)
Двойную
сумму в этом выражении можно разложить следующим образом:
где
 , (4.14)
, (4.14)
а
коэффициенты с отрицательными индексами образуются из соответсвующих
коэффициентов с положительными индексами путем изменения знака индекса
(домножением на 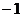 ) в выражении (4.14).
) в выражении (4.14).
Найдем
теперь коэффициенты разложения (4.13).
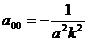 (4.15)
(4.15)
Далее
при 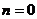 найдем значения коэффициентов первой суммы разложения
(4.13). Для этого подставим
найдем значения коэффициентов первой суммы разложения
(4.13). Для этого подставим 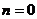 в
выражения для функций
в
выражения для функций 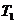 (3.25) и
(3.25) и 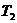 (3.26).
(3.26).
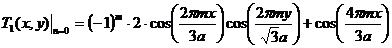 , (4.16)
, (4.16)
обозначим
полученное выражение через 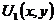 , то есть
, то есть
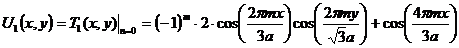 . (4.17)
. (4.17)
Далее
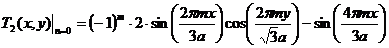 , (4.18)
, (4.18)
это
выражение обозначим через 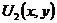 , то есть
, то есть
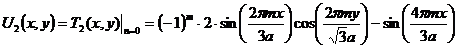 . (4.19)
. (4.19)
Запишем
окончательно выражения для коэффициентов  и
и 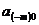 :
:
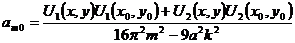 ; (4.20)
; (4.20)
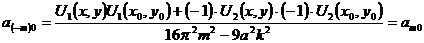 . (4.21)
. (4.21)
Найдем
теперь выражения для коэффициентов второй суммы разложения (4.13). Проделав
аналогичные выкладки можно показать, что эти коэффициенты также равны между собой
и к тому же идентичны коэффициентам (4.20), (4.21). Это значит первую и вторую
сумму разложения (4.13) можно объединить в одну следующим образом:
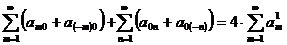 , (4.22)
, (4.22)
где
 . (4.23)
. (4.23)
Для
нахождения коэффициентов третьей суммы разложения (4.13) заметим, что функция 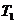 содержит только четные функции, а именно - косинусы,
а значит она является четной относительно обоих индексов
содержит только четные функции, а именно - косинусы,
а значит она является четной относительно обоих индексов  и
и 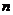 . Функция
же
. Функция
же 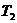 - напротив нечетна. Поэтому получаем равенство
коэффициентов
- напротив нечетна. Поэтому получаем равенство
коэффициентов  и
и 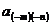 .
Коэффициенты же
.
Коэффициенты же  и
и 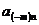 также
равны, но отличаются от коэффициентов
также
равны, но отличаются от коэффициентов  и
и 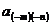 знаком индекса
знаком индекса 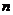 .
.
Запишем
окончательно:
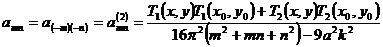 , (4.24)
, (4.24)
 . (4.25)
. (4.25)
С
учетом (4.22), (4.24) и (4.25) разложение (4.13) приобретает вид:
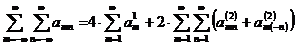 . (4.26)
. (4.26)
Это
выражение и будем использовать в дальнейшем при составлении программы.
5. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО ЭКСПЕРИМЕНТА
Используя все, сказанное выше, была разработана в среде программирования MathCad 7.0 универсальная программа,
позволяющая, используя численное решение интегрального уравнения, рассчитывать
зависимости эквивалентного поверхностного импеданса от геометрических размеров
конструкции, частоты падающего поля, а также от угла падения волны.
Ниже приведены некоторые зависимости, найденные с помощью этой программы.
Рис.
5.1. Распределение модуля касательной составляющей 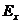
Рис.
5.2. Распределение действительной части касательной составляющей 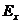
Рис.
5.3. Распределение мнимой части касательной составляющей 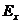
Рис.
5.4. Зависимость нормированного значения мнимой части эквивалентного
поверхностного импеданса от размеров щели 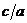 , при
, при  ,
, 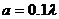
Рис.
5.5. Зависимость нормированного значения мнимой части эквивалентного
поверхностного импеданса от размеров щели 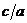 , при
, при  ,
, 
Рис.
5.6. Зависимость нормированного значения мнимой части эквивалентного
поверхностного импеданса от размеров щели 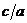 , при
, при  ,
, 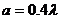
Рис.
5.7. Зависимость нормированного значения мнимой части эквивалентного
поверхностного импеданса от размеров щели 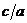 , при
, при  ,
, 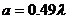
Рис.
5.8. Зависимость нормированного значения мнимой части эквивалентного
поверхностного импеданса от размеров щели 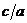 , при
, при  ,
, 
Рис.
5.9. Зависимость нормированного значения мнимой части эквивалентного
поверхностного импеданса от размеров щели 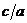 , при
, при  ,
, 
Рис.
5.10. Зависимость нормированного значения мнимой части эквивалентного
поверхностного импеданса от частоты, при 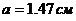 ,
, 
Рис.
5.11. Зависимость нормированного значения мнимой части эквивалентного
поверхностного импеданса от угла падения волны, при 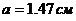 ,
, 
СПИСОК
ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
щелевая импедансная нагрузка поверхностная
1. Марков Г.Т., Петров Б.М., Грудинская
Г.П. Электродинамика и распространение радиоволн. - М.: Советское радио, 1979.
2. Юханов Ю.В., Кошкидько В.Г.,
Рассеяние электромагнитных волн на микрополосковой импедансной нагрузке. - В
кн.: Рассеяние электромагнитных волн: Междуведомственный тематический научный
сборник, вып. 5. - Таганрог: ТРТИ, 1985, с. 17-22.
3. Гупта К., Гардж Р., Чадха Р. Машинное
проектирование СВЧ устройств. - М.: Радио и связь, 1987.
4. Канторович Л.В., Крылов В.И.
Приближенные методы высшего анализа. - Л.: Физмат, 1962.
5. Пистолькорс А.А. Общая теория
дифракционных антенн. - ЖТФ, 1944, т. 14, № 12, с. 693-702.
6. Пистолькорс А.А. Теория кольцевой
дифракционной антенны. - ЖТФ, 1944, т. 14, № 12, с. 681-692.
7. Lewine H., Papas C.H.
Theory of the circular diffraction antenna. - J. Appl. Phys., 1951, vol. 22, № 1, p. 29-43.
8. Фельд Я.Н. Основы теории щелевых
антенн. - М.: Советское радио, 1948.
9.
Lewine
H., Schwinger J. On the theory of difraction by aperture n an infinite screen
plane. - Phys. Rew., 1948, vol. 74, № 8, p. 958-974.
10.Wait J.R. A low-frequency annular-slot antenna. - J. Res.
NBS, 1958, vol. 60, Jap., p. 59-64.
11.Meixner
J., Klopfer W. Theory der ebenen Ring-spalt-antenne. - Z. angew. Phys., 1951,
B. 3, № 5, s. 171-178.
12.Galejs
S., Thompson T.W. Adwittance of a cavity-backed annular slot antenna. - IRE
Trans. Antennas and Propagat., 1962, vol. 10, № 6, p. 671-678.
13.Попереченко
Б.А. Розбуждение радиального резонатора с кольцевой щелью. - Сб.: Антенны /Под.
ред. Пистолькорса А.А., вып. 11, с. 3-14.
14.Bahr
A.J. Using electromagnatic scattering for estimate the depth of a rectangular slot.
- IEEE Trans. Antennas and Propagat., 1979, vol. 27, № 6, p. 738-746.