Разработка формы учебных текстов для шестого класса на примере темы 'Делимость'

Разработка формы учебных текстов для шестого класса

на примере темы ”Делимость”

(Дипломная работа)

Содержание

 

Введение

Глава 1. Обзор существующих форм учебной литературы

§1. Назначения и характеристики учебных текстов разного типа

§2. Анализ литературы, описывающей процесс математического исследования

Глава 2. Учебно-исследовательская деятельность шестиклассников на уроках “Начала алгебры”

§1. Учебно-исследовательская деятельность шестиклассников

§2. Характеристика программы “Начала алгебры” для 6-го класса

§3. Вывод

Глава 3. Апробация разработанных текстов

§1. Апробация текстов “описания исследования”

§2. Апробация текстов “помощники”

Заключение

Список литературы

Приложение

Введение

В традиционной программе алгебра представлена преимущественно в виде набора процедур и алгоритмов [34]. А развивающее обучение (РО) направлено на то, что учащиеся в начальной школе сами открывают способы действия [15], во второй ступени школы осваивают способы учебного исследования и оформляют эти исследования [3], [11].

Любое обучение должно быть обеспечено методическими материалами. Традиционное обучение обеспечено учебниками, где приводятся образцы решения и задания, дидактическими материалами, где содержатся варианты контрольных работ, карточки. Заметим, что развивающее обучение по математике в гораздо меньшей степени обеспечено методическими материалами. Так, например, в программе развивающего обучения разработанной С.Ф. Горбовым есть только учебник-тетрадь, где содержатся задания и оставлено место для выполнения этих заданий. В дополнении к этому учебнику-тетради приходится дополнительно использовать учебники для традиционного обучения. Программа курса “Начала алгебры” для шестого класса авторов О.В. Знаменской и Ю.Г. Юдиной, также разработанного в логике развивающего обучения, обеспечена задачником и рабочей тетрадью по теме “Признаки делимости в системе счисления по основанию р”. При апробации этого курса обнаружилась необходимость в текстах, описывающих ход математического исследования. Тексты такого рода необходимы, чтобы учащиеся учились различать некоторые виды рассуждений, и также для того, чтобы задать нормы оформления математического исследования.

Так же при апробации курса “Начала алгебры” обнаружен дефицит текстов, направленных на освоение алгоритмов действия. Такого рода тексты, нужны для того, чтобы учащийся мог отработать решение задач индивидуально. Аналоги таких текстов “помощников” существуют, например, карточки для коррекции знаний [22], справочная литература, подобного рода карточки, разработанные учителем, но большинство существующих текстов такого рода содержит только пошаговый алгоритм решения, и как показывает опыт, не являются реальными “помощниками” для слабых учащихся. Для тем “Сравнение, сложение и вычитание обыкновенных дробей” и “Сложение и вычитание отрицательных и положительных дробей” указанного курса тексты такого рода не были разработаны.

Таким образом, возникает разработческая задача: создать недостающее учебное обеспечение для 6-го класса развивающего обучения.

Цель дипломной работы - разработка учебных материалов к курсу “Начала алгебры” для учащихся шестых классов, а именно, текстов направленных на освоение типов рассуждений и текстов, необходимых для освоения алгоритмов действия.

Таким образом, мной разрабатывались два типа учебных текстов:

1)   Тексты, которые были условно мной названы “Описание хода исследования”, необходимые для освоения типов описания исследования на материале темы “Признаки делимости в системе счисления по основанию р”;

2)   Тексты - “помощники”, для освоения алгоритмов действия с действительными числами (обыкновенные дроби и отрицательные числа).

При достижении этой цели решались следующие задачи:

1. Анализ образцов учебной литературы с целью выделения назначений и соответствующих им характеристик текстов.

2.      Анализ литературы, в которой описывается процесс математического исследования, и выделение структуры таких текстов.

.        Изучение содержания программы курса “Начала алгебры” для шестого класса с целью выделения требования, которым должны удовлетворять учебные тексты для шестого класса.

.        Разработка формы учебных текстов и методики их применения.

Объектом разработки является учебные тексты.

Предметом разработки является форма и содержание учебных текстов.

Дипломная работа состоит из введения, трех глав, заключения, приложения и списка литературы (из 39 наименований).

В первой главе описываются назначения и характеристики учебных текстов разного типа. Анализируются тексты вузовских и школьных учебников, задачников, справочной литературы и выделяются следующие назначения текстов: передать знания, научить способам решения задач, помочь в подготовке к экзаменам, предоставить информацию, развить мышление.

Так же в этой главе приводится анализ текстов (в которых описывается математическое исследование) следующих авторов: Адамара Ж., Вагутена В.Н., Лакатоса И., Носова Н.Н., Пойа Д. Были выделены следующие характеристики, по которым сравниваются тексты, посвященные описанию исследования:

1. Стиль изложения

«Авторитарный» (квази-общение с читателем; обычно употребление глаголов в 1-м лице мн. числа) ( “Вы наталкиваетесь…”, “вам приходит в голову…”).

· рассуждение

- от лица автора (от 1-го лица) (“Я стал думать…”, “я сложил…”, “я принимаю…”).

- безличное (“Не трудно обнаружить…”)

2. Форма изложения

·  диалог

- автора с читателем (“Случайно вы наталкиваетесь…и замечаете… Вам приходит в голову…”)

вымышленных героев

(Сигма. …если у вас есть доказательство, то, пожалуйста, дайте его.

Учитель. Действительно, я его имею…

Дельта. Вы должны назвать это теперь теоремой…”).

·  монолог (“Я хотел представить… мной руководила… Я спрашивал себя… мне без труда удалось…”).

3. Наличие верных и неверных ходов

Мной выделено три вида описания исследования:

1) “ход мыслей” (описывается от лица автора, в нем присутствуют как верные, так и неверные ходы) (Лакатос И, Носов Н.Н.);

2)      “нормативное” описанием (описание безличное или “авторитарное”, наличие только верных ходов) (Вагутен В.Н., Пойа Д.);

)        событийно (описание от лица автора, описываются события, при которых происходило исследование) (Адамар Ж.).

4. Наличие ключевых слов

Таких как: я стал думать, я подметил, вы наталкиваетесь, выпишем и т.п. По ключевым словам, можно определить, кто проводит исследование либо автор (Адамар Ж.), либо вымышленный герой (Лакатос И., Носов Н.Н.), либо математик (Пойа Д.), либо читатель вслед за автором (Пойа Д.).

5. Присутствие или отсутствие метаязыка, описывающего исследование

Есть ли в тексте такие слова как: определение, контрпример, теорема, доказательство, гипотеза, открытие, результат, исследование. Я заметила, что метаязык используется теми героями, которые компетентны в исследовании. Например, у Лакатоса метаязык присутствует у учителя, а у учеников он отсутствует. Чем больше компетентность в вопросе исследования, тем больше метаслов используется.

6. Наличие вопросов

Задаются ли в тексте вопросы, на которые затем даются ответы или которые остаются без ответа (на которые должен ответить читатель).

Вторая и третья главы посвящены описанию учебно-исследовательской деятельности шестиклассников и анализу программы курса “Начала алгебры” для 6-го класса, а также апробации разработанных мною учебных текстов и анализу этой апробации.

Остановимся подробнее на текстах “описывающих исследование”, поскольку аналогов таких текстов нет в традиционном обучении, и их также не удалось обнаружить в занимательной литературе для шестиклассников.

В 6-ом классе учащимися осваивается новое предметное действие - учебное исследование.

Материал темы “Признаки делимости в системе счисления по основанию р” идеален для постановки и решения учащимися учебно-исследовательской задачи, а также для пропедевтики понятия доказательства. Продолжается работа по выводу, записи и обоснованию общих утверждений о делимости (учащиеся должны “сконструировать” математически грамотную запись признаков делимости). По теме “Признаки делимости в системе счисления по основанию р” существует следующее математическое обеспечение: объяснительная записка, методические рекомендации, задачник и рабочая тетрадь. Однако для успешного прохождения этой темы и получения желаемых результатов необходимы учебные тексты в виде образцов рассуждений.

Разработанный мной текст, описывающий ход исследования имеет следующую структуру. Он состоят из четырех частей: первая - это постановка задачи, а три - это три независимых друг от друга рассуждения, каждое из которых излагается от лица одного из школьников.

Рассуждение младшего школьника (полный перебор), имеет следующую структуру: перебор всех двузначных чисел (7-ичная система счисления), выбор из них удовлетворяющих условию делимости на 7, вывод (в 7-ичной системе счисления), аналогичный выбор однозначных и двузначных чисел удовлетворяющих делимости на 7 (14-ичная система счисления), вывод (в 14-ичной системе счисления), общий вывод.

Рассуждение ровесника (эмпирическое обобщение), имеет следующую структуру: произвольно выписываются трехзначные числа, из них выбираются делящиеся на 7 (переводом), выделяется не верная закономерность, выделенная закономерность проверяется и опровергается, поиск новой закономерности, проверка и подтверждение этой закономерности, вывод.

Рассуждение старшеклассника (содержательный анализ), имеет следующую структуру: выделение знания, на которое можно опираться (свойство делимости суммы), представление трехзначного числа в позиционной записи, выделение признака с помощью свойства делимости суммы и общего вида записи, вывод о признаке делимости в виде утверждения 1, анализ проделанного решения и обобщение по количеству знаков и виду системы счисления, результат в виде утверждения 2, описание результатов исследования в виде теоремы и доказательства.

Мной разработана форма учебных текстов. Рассуждение ведется от лица школьника, который рассказывает о своем решение, сформулированной в самом начале задачи. Каждое рассуждение построено как монолог, чтобы в чистом виде выделить сам способ рассуждения. В заключение рассказа каждого школьника приведены вопросы на понимание его рассуждения, для того, чтобы читающий рассуждение ученик мог выделить их логику и особенности.

Следует подчеркнуть, что употребление метаязыка свидетельствует о компетентности выполняющего исследование. Я вводила в рассуждение старшеклассника термины: утверждение, предположение, теорема, доказательство. У ровесника метаязык присутствует в меньшей мере, у него встречаются такие термины как предположение и контрпример, В рассуждение младшего школьника метаязык отсутствует.

Нормативное описание, как исследования, так и его результатов предлагается в четвертой части текста. Реальное описание в рассуждение ровесника, для него характерно наличие верных и неверных предположений.

По результатам первой апробации была скорректирована структура текста ровесника и старшего школьника. Вторая апробация выделила необходимость вопросов в конце рассказа каждого школьника о своем решении, которые помогли бы учащимся понять задачи текста.

Последний вариант текста приведен в приложение 4.

Совместно с учителями Анишиной Н.Н. и Ольшевской Н.А. была разработана методика работы с текстом, специфика которой заключается в том, что учащимся предоставлялась возможность ответить на вопросы класса, приняв позицию автора. Эта методика позволила обнаружить особенности понимания школьниками данных текстов. Практически все шестиклассники легко смогли занять позицию автора первого рассуждения, второй смогли понять в коллективно-распределенной форме, используя помощь учителя, не смотря на то, что это типичный способ рассуждения, который шестиклассники демонстрируют при решении подобных задач.

Наибольшую трудность представлял последний текст, даже с помощью учителя учащимся с трудом удалось выделить логику, и некоторые моменты так и остались непонятны.

В результате апробации на Школе молодого ученого, замечено, что семиклассники и восьмиклассники из развивающего обучения вполне способны понять последний текст и легко удерживают позицию автора, а дети из традиционной школы не понимают последнее рассуждение.

Таким образом, можно предположить, что именно в шестом классе развивающего обучения одновременная работа с текстами, описывающими все способы рассуждений, может задать “вектор” движения учащихся по освоению ими изложения решения учебно-исследовательской задачи.

Таким образом, можно сделать вывод, что способ - содержательный анализ для шестиклассников лежит в “зоне ближайшего развития”, а некоторыми семиклассниками и восьмиклассниками, присутствующими на Школе молодого ученого, этот способ освоен, т.к. они могут самостоятельно понять последний текст, и могут построить свои рассуждения способом - содержательный анализ.

Что касается текстов “помощников”, основное нововведение состоит в том, что эти “помощники” содержат не только алгоритм решения, но и пустые ячейки, которые ученик должен заполнить самостоятельно по аналогии с образцом и образцы оформления результата (что писать в тетради). Данная форма текстов, как показывает апробация, облегчает понимание алгоритмов действия и делает работу школьника более интересной.

В приложении приводятся образцы экспериментальных и итоговых вариантов учебных текстов разных типов.

Приложение 1 - 4. Тексты описывающие “ход исследования”.

Приложение 5 - 6. Тексты - “помощники”.

В заключение хочу выразить большую благодарность учителям Анишиной Наталье Николаевне (учитель гимназии №1 “Универс”) и Ольшевской Надежде Анатольевне (учитель лицея №1) за оказанную помощь в апробации разработанных учебных текстов.

алгебра учебный урок апробация

Глава 1. Обзор существующих форм учебной литературы

§1. Назначения и характеристики учебных текстов разного типа

 

Я выделила следующие цели учебных текстов: передачу знаний, научить способам решения задач, помощь в подготовке к экзаменам, предоставление информации, развитие мышления. Остановимся подробнее на выделенных нами особенностях текста, соответствующих каждому назначению.

Цель передать знания: овладеть основами (или тонкостями) определенной области науки, ее понятиями и методами [2], [8], [13], [19], [30], [38] ставят учебники и учебные пособия (курсы лекций и т.п.).

В вузовских учебниках почти всегда логическое описание строения, схемы курса, связь с другими областями науки, указываются общие объекты и методы [13].

В школьных учебниках логическое строение текста задано не явно. Иногда показывается связь с другими науками.

Как в вузовских, так и в школьных учебниках, теоретическая часть начинается с введения понятий (возможно на примерах показать разрывы в имеющихся знаниях и необходимость введения новых понятий), редко встречается подход к утверждениям и формулам с помощью рассуждений, часто встречается просто доказательство. Часто в тексте встречаются примеры и упражнения, иллюстрирующие доказательство.

Научить способам решения задач по некоторой тематике, признаны сборники задач и упражнений [10], [17], [35]. Они представляют уже известные способы и множество задач для упражнения и выработке навыков решения.

Чаще всего вузовские задачники представлены отдельной от учебника книгой. В вузовских задачниках иногда встречаются тексты, направленные на то, чтобы научить решать задачи, содержащие общие указания и рекомендации по решению задач, по поиску этих решений [37]. Часто вначале каждого параграфа приведены необходимые определения и краткие (предполагается, что читатель уже знаком с материалом) теоретические сведения. Теоретическая часть состоит из определений и теорем (критериев, формул, принципов и т.п.); доказательства или рассуждения, результатом которого является теорема, не приводятся, за исключением случаев, когда в них содержится описание метода. Теоретический материал иллюстрирует большим количеством примеров, существует образец применения способа в подробном разборе решения некоторой типичной задачи. Однако иногда теоретической части не существует. Типы задач и методы их решения систематизированы. Значительную часть параграфа составляют задания, которые нацелены на усвоение понятий и отработку методов решения задач. Количество заданий (различной степени трудности) превышает необходимый минимум, для усвоения основного материала обеспечивая достаточно богатый выбор. Оговариваются условия и границы применения изложенных методов, их практическое применение.

Школьные задачники чаще всего входят в учебник и поэтому теоретическая часть, для этих задачников, содержится в учебнике. Но некоторые задачники существуют вне учебника, в них теоретическая часть отсутствует.

С ними схожи пособия, ставящие своей целью помощь в подготовке к экзаменам [14], [21], [31].

После кратких теоретических сведений дается набор наиболее распространенных задач из вариантов экзаменов. Для каждой задачи приводится неправильное и правильное решение, либо типичные ошибки указываются после описания метода.

Предоставление информации (справочники [4], [9], [12], [24], [36], справочные пособия таблицы и др.). Основное назначение справочника то, что в нем можно навести “моментальную” справку. Кроме того, он может служить для повторения ранее изученного материала. Справочники имеют целью собрать в одном издании сведения (из одной или разных областей науки) рассредоточенные по многим источникам.

Структура таких текстов топическая, каждая глава автономна, есть ссылки на те параграфы, где разъяснены упоминаемые термины.

Во всех справочниках справка наводится с помощью алфавитного указателя или подробного оглавления.

Определения, правила, формулы и теоремы сопровождаются примерами. Ведущая роль играет фактический материал (доказательства и рассуждения приводится только в особых случаях). В таких текстах нет постановки проблем. Исторические сведения иногда представлены в определенных параграфах (обычно в начале главы по данной теме).

Книгу, авторы которой заявляли бы своей прямой целью развитие мышления, мне найти не удалось, хотя некоторые авторы заявляют близкие к этому цели: «Побудить читателя к самостоятельному творческому мышлению, к дальнейшему совершенствованию своих математических знаний» [27]. Обычно такие книги представляют собой сборники занимательных задач или любопытных фактов. Например, у Кордемского Б.А. [20] дается последовательность задач, через которые накапливается опыт мышления.

К этой цели близки книги описывающие ход математического исследования [7], [23], [28]. Их цель научить способам, позволяющим лучше разбираться в трудных математических вопросах, открывать математические теоремы, решать задачи.

Стиль изложения либо рассуждение от лица автора, либо безличное, либо квази-общение с читатилем.

Часто в тексте встречаются смысловые разрывы, использованные автором для показа необходимости построения новых понятий, для постановки проблемы, для демонстрации способа рассуждения.

В конце главы или в самой главе часто встречаются примеры и задачи позволяющие отработать предлагаемые способы рассуждений и приводящие к результату.

§2. Анализ литературы описывающей процесс математического исследования

Результаты научных исследований по математике излагаются в виде научных статей [4], [16], [18] и обзоров. За века математической науки установилась стандартная форма статей. До утверждений и теорем обязательно нужно привести все необходимые определения и леммы с доказательствами. После формулировки теоремы строгое доказательство и следствия с доказательствами.

Часто отмечается новизна полученных результатов и описание проблемы, которая была решена (или возникла, если проблема и есть результат исследования). Стиль изложения - “отстраненный”, изложение ведется от первого лица.

Заметим, что процесс исследования остается за рамками изложения, как было проведено математическое исследование, не обсуждается.

Однако некоторые авторы обращают внимание на процесс получения результатов (исследования). В этом параграфе я приведу анализ таких описаний некоторыми авторами:

1) Лакатос И. “Доказательства и опровержения”[23];

2) Носов Н.Н. “Витя Малеев в школе и дома”[25];

3)      Вагутин В.Н. статья “Близкие дроби” из журнала “Квант”[7];

)        Пойа Д. “Математика и правдоподобные рассуждения”[28];

)        Адамар Ж. “Исследование психологии процесса изобретения в области математики”[1].

1). “Доказательства и опровержения”

Автор пытается показать, что теоремы не появляются из неоткуда, что они появляются через непрерывное улучшение догадок при помощи размышления и критики, при помощи логики доказательств и опровержений. Для этого берется стереометрическая теорема, касающаяся соотношения между числами сторон, вершин и граней многогранника, и разбираются ее возможные доказательства.

Изложение ведется в двух планах: один из них - это рассказ об исследовании связи между сторонами, вершинами и гранями многогранника в форме диалога между учителем и учениками. В процессе диалога рассматривается связь с обсуждением правильности рассматриваемых доказательств.

Таким образом, текст излагается в диалогической форме. Диалог ведется между учителем и 15 учениками (названными буквами греческого алфавита).

“… Альфа. Вообразите твердое тело, заключающееся между двумя всаженными друг в друга кубами, т. е. парой кубов, из которых один находится внутри другого, но не касается его. Этот полный куб делает не верной вашу первую лемму, так как после отнятия грани у внутреннего куба многогранник уже нельзя будет растянуть на плоскости. Не поможет отнятие грани и от внешнего куба. Кроме того, для куба V - E + F = 2, так что для полного куба V - E + F = 4.

Учитель. Очень хорошо. Назовем его контрапримером номер 1. Ну и что же?

Гамма. Сэр, ваше спокойствие удивляет меня. Один отвергает догадку так же эффективно, как и десять. Ваша догадка и ее доказательство полностью взорваны. Руки вверх! Вам нужно сдаться. Сотрите ложное предположение, забудьте о нем и попробуйте найти радикально новый подход.

Учитель. Согласен с вами, что контрапример Альфы - серьезная критика этого предположения. Но нельзя сказать, что доказательство “полностью взорвано”… Мое доказательство действительно доказало предположение Эйлера в первом смысле, но не обязательно во втором… Я интересуюсь доказательствами, даже если они не выполняют их первоначального назначения. Колумб не достиг Индии, но он открыл нечто очень интересное”.

Другой план в книге составляют подстрочные примечания, дающие действительную историю доказательств и вскрывающие ошибки, которые делались при этом математиками 19 века. Диалоги учеников - это по существу и есть наглядное отражение этой истории.

Структура текста линейная, если ты не прочитал предыдущий параграф, то тебе будет не совсем понятно, то, что говорится в последующих параграфах.

Текст построен в следующем порядке:

.   Учителем ставится задача;

2.      Учителем дается доказательство;

Далее текст построен в виде цикла состоящего из следующих этапов:

.   Ученики пытаются опровергнуть доказательство. Высказываются догадки, пытаются опровергнуть догадки, испытывают разными способами. Результат подкрепляет догадку и наводит на мысль, что она может быть доказана.

4.      Ученики пытаются доказать.

“Учитель. На нашем последнем уроке мы пришли к догадке относительно многогранников, а именно: что для всех многогранников V-E+F=2, где V - число вершин, E - число ребер и F - число граней. Мы испытали ее разными способами. Но мы пока не доказали ее. Может быть, кто-нибудь нашел доказательство?

Сигма. …пока не придумал строгого доказательства этой теоремы… Но если у вас есть доказательство, то, пожалуйста, дайте его.

Учитель. Действительно, я его имею. Оно состоит в следующем мысленном эксперименте…

Дельта. Вы должны назвать это теперь теоремой. Теперь здесь уже нет ничего из области догадок”.

В тексте используются метаязык: лемма, доказательство, контрпример, теорема, определение. Метаязык вводит учитель, т.к. он самый компетентный в вопросе исследовании.

У каждого персонажа в этом тексте своя роль. Я рассмотрю роли пяти персонажей, на мой взгляд, самых главных: учителя, ученика Альфа, ученика Бета, ученика Гамма, ученика Дельта.

1.Учитель

Учитель предлагает содержательные ходы, например, дает доказательство, которое далее пытаются опровергнуть. Также он направляет урок в нужном направлении. Например, он говорит: “Давайте прервем вашу дискуссию и вернемся к нашему рассуждению”.

Учитель вводит термины при помощи, которых можно описать исследование.

“…давайте введем такую терминологию. Локальным контрпримером я буду называть пример, который отвергает лемму (не отвергая необходимо основную догадку)…”.

Также он выделяет в высказываниях учеников определения и контрпримеры, и нумерует их. Учитель вводит метаязык, т. к. он более опытен в вопросе исследования.

Если ученики опровергают лемму, доказательство, предположение или определение, предложенное учителем, то учитель заменяет это на другое похожее, но более точное или слегка измененное.

“Я легко могу переработать, улучшить доказательство, заменив неверную лемму слегка исправленной, которую ваш контрпример не сможет опровергнуть…”

Также учитель уточняет высказывания учеников.

“Каппа. Охотно соглашусь, что соответствующая такой операции лемма будет истинной: конечно, если мы вынимаем треугольники один за другим, так, чтобы V-E+F не изменилось, то V-E+F не будет изменяться.

Учитель. Нет. Лемма заключается в том, что треугольники в нашей сети могут быть перенумерованы так, что при вынимании их в правильной последовательности V-E+F не будет изменяться, пока мы не достигнем последнего треугольника ”.

2. Ученик Альфа.

Он усомневается.

“…Я вижу, что этот эксперимент можно выполнить с кубом и с тетраэдром, но как я могу знать, что его можно произвести с любым многогранником. Кстати, уверены ли вы, сэр, что всякий многогранник после устранения одной грани, может быть, развернут плоско на доске? У меня есть сомнения относительно вашего первого шага”.

Приводит контрпримеры, опровергает. Опровержение и контрпример Альфы приведены в процитированном куске текста, который показывает, что у Лакатоса изложение ведется в диалогической форме. В контрпримерах он “изобретает” почти все рассматриваемые многогранники, которые Дельта называет “монстрами”.

Мне кажется, что Альфа самый умный ученик.

. Ученик Бета.

Является серединой между Альфой и Дельтой. Тем, что он относит многогранники Альфы в отдельный случай и говорит, что они являются исключением, он как бы поддерживает Альфу. А тем, что он предлагает устранить этих “монстров” для правильности первоначальной догадки, он поддерживает Дельту.

Бета дает определения, выделяет формулы и старается “сделать их совершенными”. Выделяет свой метод - “методом устранения исключений”, и использует его для точного определения области, в которой является правильной догадка Эйлера.

Он легко принимает критику и быстро изменяет свои утверждения относительно критике.

“Бета. Для всех многогранников, не имеющих полостей (вроде пары куб в кубе) и туннелей (как рама картины), V-E+F=2.

Учитель. Вы уверены?

Бета. Да, вполне.

Учитель. А как быть с тетраэдрами-близнецами?

Бета. Извините. Для всех многогранников, которые не имеют полостей, туннелей и “кратной структуры””.

4. Ученик Гамма.

Задает вопросы.

“Уверены ли вы, что когда вы будете откидывать треугольники один за другим, то получите только две альтернативы - исчезновения одного ребра или одной вершины? Уверены ли вы также, что в конце процесса, останется только с одним треугольником? У меня есть сомнения относительно вашего третьего шага”.

Гамма задает вопросы и этим старается добиваться точности.

“Учитель. Подозрение - это еще не критика.

Гамма. А контрпример будет критикой?”

“Гамма. Значит, догадка может быть верной, но ваше доказательство ее не доказывает?”

5. Ученик Дельта.

Дельта старается все определить.

“…Я ищу порядка и гармонии в математике…”

“…Многогранник может быть поверхностью: он имеет грани, ребра, вершины, он может быть деформирован, растянут на доске, и ему нет никакого дела до понятия о “твердом теле”. Многогранник есть поверхность, состоящая из системы многоугольников”.

Дельта - это консерватор. Говорит, что многогранники можно определить так, что они будут удовлетворять теореме Эйлера. Насчет таких отношений Дельты Альфа позже делает такое высказывание: “Дельта я поражен. Я думал, что на свете не существует гипотез, которые вы смогли бы спасти от уничтожения при помощи, подходящей лингвистической хитрости”.

“Дельта. Но зачем же принимать контрапример? Вы доказали вашу догадку - теперь она стала теоремой. Я принимаю, что она несогласна с этим так называемым контрапримером. Кто-то из них должен уйти. Но почему же должна уходить теорема, если она была доказана. Нужно отступить “критике”. Это поддельная критика. Пара всаженных кубов совсем не будет многогранником. Это монстр, патологический случай, а не контрапример”.

Мне кажется, что роль Дельты такова, что он своим консерватизмом, своим “отрицанием” побуждает других, доказывая ему обратное придумывать контрпримеры, формулировать определения, делать новые догадки и доказывать их.

2). Витя Малеев в школе и дома

Пример рассуждения встречается, когда Витя пытается решить задачу заданную на дом.

“… я стал думать, как решить задачу. Сначала я думал, что если 12 топоров и 3 пилы стоят 84 рубля, то надо сложить все топоры и пилы вместе и 84 поделить на то, что получилось. Я сложил 12 топоров и 3 пилы, получилось 15,. Тогда я стал делить 84 на 15, но у меня не поделилось, потому что остался остаток. Я понял, что произошла какая-то ошибка, и стал искать другой выход. Другой выход нашелся такой: я сложил 12 топоров и 5 пил, получилось 17, и тогда я стал делить 100 на 17, но у меня опять получился остаток. Тогда я сложил все 24 топора между собой и стал делить рубли на топоры с пилами, но деление все равно не вышло. Тогда я стал отнимать пилы от топоров, а деньги делить на то, что получилось, но все равно у меня не получилось. Потом я еще пробовал складывать между собой пилы и топоры по отдельности, а потом отнимать топоры от денег, и то, что осталось, делить на пилы, и чего я только не делал, никакого толку не входило. Тогда я взял задачу и пошел к Ване Пахомову.

Слушай, - говорю, - Ваня, 12 топоров и 3 пилы вместе стоят 84 рубля, а 12 топоров и 5 пил стоят 100 рублей. Сколько стоит один топор и одна пила? Как, по-твоему, надо сделать задачу?

А как ты думаешь? - спросил он.

Я думаю, нужно сложить 12 топоров и 3 пилы и 84 поделить на15.

Постой! Зачем тебе складывать пилы и топоры?

Ну, я знаю, сколько было всего, потом 84 разделю, на сколько всего и узнаю, сколько стоила одна.

Что - одна? Одна пила или один топор?

Пила, - говорю, - или топор.

тогда получится, что они стоили одинаково.

А они разве не одинаково?

Конечно, не одинаково. Ведь в задаче не говорится, что они стоили поровну. Наоборот, спрашивается, сколько стоит топор и сколько пила отдельно. Значит, мы не имеем права их складывать.

Да их, - говорю, - хоть складывай, хоть не складывай, все равно ничего не выходит,

Вот поэтому и не выходит.

Что же делать? - спрашиваю я.

А ты подумай.

Да я уже два часа думал!

Ну, присмотрись к задаче, - говорит Ваня. - Что ты видишь?

Вижу, - говорю, - что 12 топоров и 3 пилы стоят 84 рубля, а 12 топоров и 5 пил стоят 100 рублей.

Ну, ты замечаешь, что в первый раз и во второй топоров куплено одинаковое количество, а пил на две больше?

Замечаю, - говорю я.

А замечаешь, что во второй раз уплатили на 16 рублей дороже?

Тоже замечаю. В первый раз уплатили 84 рубля, а во второй раз - 100 рублей, 100 минус 84, будет 16.

А как ты думаешь, почему во второй раз уплатили на 16 рублей больше?

Это каждому ясно, - ответил я, - купили две пилы, вот и пришлось уплатить лишних 16 рублей.

Значит, 16 рублей заплатили за две пилы?

Да, - говорю, - за две.

Сколько же стоит одна пила?

Раз две 16, то одна, - говорю, - 8.

Вот ты и узнал, сколько стоит одна пила.

Тьфу! - говорю. - Совсем простая задача! Как это я сам не догадался?!

Постой, тебе еще надо узнать, сколько стоит топор.

Ну, это уж пустяк, - говорю я. - 12 топоров и 3 пилы стоят 84 рубля. 3 пилы стоят 24 рубля. 84 минус 24, будет 60. Значит, 12 топоров стоят 60 рублей, а один топор - 60 поделить на 12, будет 5 рублей.

Я пошел домой, и очень мне было досадно, что я не сделал эту задачу сам…”

Сначала рассуждение ведется в виде монолога Вити, затем в виде диалога Вити и Вани. В рассуждении встречаются ключевые слова: я стал думать, которые показывают, что рассуждение ведется от первого лица.

Рассуждение Вити - это рассуждение ребенка, так может рассуждать реальный ребенок. Витя перебирает способы решения, которые только может придумать, поэтому рассуждение Вити не нормативное, в нем не заданы нормы того, как надо решать задачу. Правильное решение приводится тогда, когда идет диалог Вити с Ваней. В отличие от рассуждения Лакатоса И. в этом рассуждении метаязык отсутствует, т.к. в этом рассуждении не присутствует персонажа, который был бы компетентен в исследовании. В рассуждение есть вопросы, так как ведется диалог между персонажами.

3).Статья “Близкие дроби” из журнала “Квант”

“Выпишем все правильные дроби, у которых знаменатель не больше 7;

_{1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5/6, 1/6,1/7, 2/7, 3/7, 4/7, 5/7, 6/7}.

(мы пропустили сократимые дроби: 2/4, 2/6, 3/6, 4/6 - из дробей, представляющих одно то же число, мы выбираем одну дробь, а именно ту, у которой числитель и знаменатель наименьшие). Теперь запишем те же дроби в порядке возрастания:

_{1/7, 1/6, 1/5, 1/4, 2/7, 1/3/ 2/5, 3/7, 1/2, 4/7, 3/5, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7}. (1)

… При этом соблюдается интересная закономерность: числитель разности двух соседних дробей всегда получается равным единице, точнее,

А. Для любых двух соседних дробей a/b, c/d (где a/b< c/d) выполняется равенство bc-ad=1.

Какие еще закономерности присущи ряду дробей (1)? Не трудно обнаружить, что сумма двух дробей симметрично стоящих в этом ряду, равна 1. Интересно, заметил ли читатель, что

Б. Каждая дробь получается из соседних с ней двух дробей следующим образом: надо сложить их числители и разделить полученное число на сумму знаменателей…

Дадим два определения, связанными с нашими наблюдениями.

Определение 1. Назовем две дроби a/b, c/d,близкими, если bc-ad равно 1 или -1.

Упражнение 4. Выберите из дробей (1) все пары близких дробей”.

Схема, по которой описывает свое исследование В.Н. Вагутен: сначала он подбирает материал для исследования, затем ставит себе более узкую задачу и описывает, выделенную им закономерность, формулирует и обосновывает гипотезу и оформляет результат в виде определений и упражнений.

Это нормативное рассуждение, т. к. никаких рассуждений, которые нам не понадобятся, в тексте не встречается, показываются только те ходы, которые нам нужны для того, чтобы заметить закономерности.

Стиль изложения в этом рассуждении - это не явный диалог автора с читателем, об этом нам говорит фраза: “Интересно, заметил ли читатель, что…” Этим он как бы разговаривает с читателем, как бы спрашивает: “А вы заметили, что…”

В тексте используется метаязык: закономерность, определение, упражнение…

4).” Математика и правдоподобные рассуждения”

Автор ставил перед собой задачу указать начинающему математику пути к математическому творчеству, научить его способам, позволяющим лучше разбираться в трудных математических вопросах, открывать математические теоремы, решать задачи.

“…Случайно вы наталкиваетесь на соотношения

+ 7=10,

+17=20,

+17=30

и замечаете между ними некоторое сходство. Вам приходит в голову, что числа 3, 7, 13, и 17 являются нечетными простыми числами. Сумма двух нечетных простых чисел есть обязательно четное число; действительно, числа 10, 20, и 30-четные. А что можно сказать о других четных числах? Ведут ли они себя подобным же образом? Первое четное число, является суммой двух нечетных простых чисел, если, конечно,

=3+3.

Двигаясь дальше, находим, что

=3+5,

=3+7=5+5,

=5+7,

=3+11=7+7,

=3+13=5+11.

Всегда ли так будет продолжаться? Как бы то ни было, частные случаи, которые мы наблюдали, наводят на мысль об общем утверждении; любое четное число, большее чем 4, представимо в виде суммы двух нечетных простых чисел. Поразмыслив об исключительных случаях-числах 2 и 4, которые не могут быть расщеплены в сумму двух нечетных простых чисел, мы можем предпочесть следующее менее непосредственное утверждение: любое четное число, не являющееся ни простым числом, ни квадратом простого числа, представимо в виде суммы двух нечетных простых чисел.

Итак, нам удалось сформулировать предположение. Мы нашли это предположение с помощью индукции. Иными словами, оно возникло у нас в результате наблюдения, было указано отдельными частными примерами”.

Сначала, автор как бы рассказывает, что делает читатель, случайно натолкнувшись на некоторое соотношение, для этого он использует такие ключевые слова как: ”Вы наталкиваетесь…”, “вам приходит в голову…” Потом незаметно, он переходит на совместные действия с читателем, для того, чтобы это показать, он использует следующие ключевые слова: “…Двигаясь дальше, находим…”, “…мы наблюдали…”, “…мы можем предпочесть…”

После рассуждения в тексте выделяются шаги.

“Взглянем теперь назад и попытаемся уловить в предыдущем рассуждении такие шаги, которые могли бы быть типичными для процесса индукции.

Сначала мы подметим некоторое сходство. Мы осознали, что 3, 7, 13 и 17 - простые, а 10, 20 и 30 - четные числа и что три соотношения 3+7=10, 3+17=20, 13+17=30 аналогичны между собой.

Следующим шагом было обобщение. От четырех чисел 3, 7, 13 и 17 мы перешли ко всем нечетным простым числам; от 10, 20 и 30 - ко всем четным числам, а затем - к возможному общему соотношению

четное число = простому числу + простое число.

Мы пришли, таким образом, к отчетливо сформулированному общему утверждению, которое, однако, является только предположением, только пробным утверждением. Это значит, что утверждение не в коей степени не является доказанным, никак не может претендовать на истинность, оно является только попыткой подойти к истине”.

Рассуждение является нормативным, т. к. в нем встречаются только верные рассуждения, а неверных нет. Так же об этом нам говорят используемые слова, такие как “поразмыслив”.

В рассуждении используется метаязык: предположение, индукция, обобщение, утверждение.

Рассуждение в основном построено на рассмотрении частных случаев, из которых делается предположение.

В рассуждении очень много вопросов: “Всегда ли так будет продолжаться?”

”А что можно сказать о других четных числах?”

За каждой главой следуют упражнения. Некоторые из упражнений дают читателю возможность заново рассмотреть детали, только намеченные в тексте. Однако большая часть упражнений дает возможность читателю вывести свои собственные правдоподобные заключения.

5).”Исследование психологии процесса изобретения в области математики”

Рассуждение ведется от первого лица.

“Действительно, в течение одной бессонной ночи и при обстоятельствах, к которым мы еще вернемся, он построил первый класс автоморфных функций. Затем он пожелал найти для них выражение: «Я хотел представить эти функции в виде отношения двух рядов: эта идея была совершенно сознательной и обдуманной; мной руководила аналогия с эллиптическими функциями. Я спрашивал себя, какими свойствами должны обладать эти ряды, если они существуют, и мне без труда удалось построить эти ряды, которые я назвал тета-автоморфными. В этот момент я покинул Кан, где я тогда жил, чтобы принять участие в геологической экскурсии, организованной Горной школой. Перипетии этого путешествия заставили меня забыть о моей работе. Прибыв в Кутанс, мы сели в омнибус для какой-то прогулки; в момент, когда я встал на подножку, мне пришла в голову идея безо всяких, казалось бы, предшествовавших раздумий с моей стороны, -идея о том, что преобразования, которые я использовал, чтобы определить автоморфные функции, были тождественны преобразованиям неевклидовой геометрии. Из-за отсутствия времени я ничего не проверил и, едва сев в омнибус, продолжал начатый разговор, но я уже был вполне уверен, в правильности сделанного открытия для очистки совести проверил найденный результат.

В то время я занялся изучением некоторых вопросов теории чисел, не получая при этом никаких существенных результатов и не подозревая, что это может иметь малейшее отношение к прежним исследованиям. Разочарованный своими неудачами, я поехал провести несколько дней на берегу моря и думал совсем о другом предмете. Однажды, когда я прогуливался на взморье, мне так же внезапно, быстро и с той же мгновенной уверенностью пришла идея, что арифметические преобразования тройничных неопределенных квадратичных форм тождественны преобразованиям неевклидовой геометрии»”.

В этом рассуждение не описывается само исследование, а описываются события, при которых происходило это исследование, т. к. зто важно для психологов. Для них важно выделить те явления, при которых происходит исследование, чтобы потом выделить этапы, которые обязательно проходит исследование. Например, Пуанкаре А. в своей работе “Математическое творчество” говорит, что творчество проходит несколько необходимых этапов.

“То, что вас удивит прежде всего, это видимость внутреннего озарения, являющаяся результатом длительной неосознанной работы; роль этой бессознательной работы в математическом изобретении мне кажется несомненной и ее следы можно найти и в других случаях, когда это менее очевидно. Часто, когда работают над трудным вопросом, с первого раза не удается ничего хорошего, затем наступает более или менее длительный период отдыха и потом снова принимаются за дело. В течение первого получаса дело вновь не двигается, а затем вдруг нужная идея приходит в голову. Можно было бы сказать, что сознательная работа стала более плодотворной, так как была прервана, и отдых вернул уму его силу и свежесть. Но более вероятно предположить, что этот отдых был заполнен бессознательной работой и что результат этой работы внезапно явился математику точно так, как это было в случае, который я рассказал; только озарение вместо того, чтобы произойти во время прогулки или путешествия происходит во время сознательной работы, но совершенно независимо от этой работы, которая, самое большее, играет роль связующего механизма, переводя результаты, полученные во время отдыха, но оставшиеся неосознанными, в осознанную форму”.

События, при которых происходило исследование, происходили в следующем порядке.

Сначала во время бессонной ночи построил класс автоморфных функций.

Затем он задал себе вопрос.

Потом путешествие заставило его забыть о работе.

Следующим шагом было то, что когда он вставал на подножку омнибуса, ему пришла идея, которую он сразу не проверил.

Затем, когда он прогуливался на взморье, ему внезапно пришла новая идея.

В рассуждении используются следующие слова для описания процесса исследования: идея, открытие, результат, исследование.

Анализируя все эти источники можно выделить следующие характеристики:

1. Стиль изложения · «Авторитарный» (квази-общение с читателем; обычно употребление глаголов в 1-м лице мн. числа); · рассуждение - от лица автора (от 1-го лица) - безличное; 2. Форма изложения · диалог - автора с читателем   - вымышленных героев;    · монолог.

“Вы наталкиваетесь…”, “вам приходит в голову…”.   “Я стал думать…”, “я сложил…”, “я принимаю…”. “Не трудно обнаружить…”  “Случайно вы наталкиваетесь… и замечаете... Вам приходит в голову…”  Сигма. …если у вас есть доказательство, то, пожалуйста, дайте его. Учитель. Действительно, я его имею… Дельта. Вы должны назвать это теперь теоремой…”. “Я хотел представить… мной руководила… Я спрашивал себя… мне без труда удалось…”

 

3. Наличие верных и неверных ходов

Мной выделено три вида описания исследования:

a. “ход мыслей” (описывается от лица автора, в нем присутствуют как верные, так и неверные ходы) (Лакатос И, Носов Н.Н.);

b.      “нормативное” описанием (описание безличное или “авторитарное”, наличие только верных ходов) (Вагутен В.Н., Пойа Д.);.      событийно (описание от лица автора, описываются события, при которых происходило исследование) (Адамар Ж.).

4. Наличие ключевых слов

Таких как: я стал думать, я подметил, вы наталкиваетесь, выпишем и т.п. По ключевым словам, можно определить, кто проводит исследование либо автор (Адамар Ж.), либо вымышленный герой (Лакатос И., Носов Н.Н.), либо математик (Пойа Д.), либо читатель вслед за автором (Пойа Д.).

5. Присутствие или отсутствие метаязыка, описывающего исследование

Есть ли в тексте такие слова как: определение, контрпример, теорема, доказательство, гипотеза, открытие, результат, исследование. Я заметила, что метаязык используется теми героями, которые компетентны в исследовании. Например, у Лакатоса метаязык присутствует у учителя, а у учеников он отсутствует. Чем больше компетентность в вопросе исследования, тем больше метаслов используется.

6. Наличие вопросов

Задаются ли в тексте вопросы, на которые затем даются ответы или которые остаются без ответа (на которые должен ответить читатель).

Глава 2. Учебно-исследовательская деятельность шестиклассников на уроках “Начала анализа”

§1. Учебно-исследовательская деятельность шестиклассников

Существенное отличие развивающего обучения на материале математики как обучение математике от традиционного изучения этого предмета в школе авторы экспериментальных программ видят, прежде всего, в том, что [3]:

·  особый способ организации материала и деятельности по его усвоению позволяют формировать у детей содержательные (научно-теоретические) понятия;

·        на уроках математики дети могут осуществлять деятельность, являющуюся, в каком-то смысле, аналогом математической деятельности.

По мнению авторов программ развивающего обучения в начальной школе ребенок осваивает предметное действие - изобретение, порождающее малорасчлененную предметную единицу (формирование научно-теоретического понятия числа занимает большой промежуток времени, поэтому число не представлено учащимся как предметное действие). Появление в шестом классе сложно структурированных математических объектов и операций с ними требует освоения учащимися нового предметного действия - учебного-исследования, позволяющего удерживать и преобразовывать целостную расчлененную предметную единицу.

Появление сложно структурированных математических объектов и новых предметных действий, с самого начала шестого класса предъявляет новые требования к учащимся. Им приходится заново выстраивать отношение к изменившемуся предмету и к самой урочной форме.

Психологи отмечают [3], [33], что для детей 1-5 классов учебная деятельность является ведущей. Однако учебная деятельность для подростков перестает быть ведущей, на первый план выходит деятельность социального экспериментирования, проб собственных сил и возможностей. Поэтому, чтобы обучение было успешным, нужно выстраивать такие формы учебной жизни, которые адекватны подросткам. Необходимо задать пространство предмета как пространство проб и экспериментирования с собственным действием и материалом, воссоздание значения собственного действия по отношению к предмету, перевод “пробности" в предметном содержании из зоны ближайшего развития в актуальную зону. Предполагается, что такая деятельность ребенка на уроке адекватна как возрасту; так и содержанию изучаемого предмета и реальной деятельности математика.

Белоконь О.В. и Знаменская О.В. считаю, что существенными составляющими развивающего обучения математике в среднем и старшем звене школы являются развитие учебной деятельности школьниками и воспроизводство математической культуры. Акцент делается на научности, культурности открываемых понятий и способов работы с ними.

В традиционном обучении знания, как правило, сообщаются “в готовом виде”. “…В учебных предметах по основам наук… предъявление нового учебного материала происходит в основном путем изложения системы знаний (в сочетание со средствами наглядности)”, которые требуется “усвоить” и научиться применять [34]. Такой способ изучения не требует обращения к личному мнению ученика, оставляя его не востребованным. Присвоение культурных значений в традиционном обучении можно охарактеризовать как не учитывающее индивидуальное (личное) мнение учащихся.

В статье Белоконь О.И. [6] говорится, что в развивающем обучении изложение (построение нового понятия, способа) происходит через оформление и столкновение версий учеников, что зачастую, в ходе урока, при попытке описать другим собственное понимание, открытый в группе способ ученики, испытываю затруднение в средствах выражения своих мыслей, связанные с дефицитом специальных слов, терминов. И учащиеся придумывают свой “рабочий” язык, но т.к. в развивающем обучение акцент делается на научности, культурности открываемых понятий и способов работы с ними, то необходимо обеспечение “перевода” полученных учащимися на уроках результатов и описаний на культурный язык теории и язык деятельности (решения исследовательской задачи).

§2. Характеристика программы “Начала алгебры” для 6-го класса

Основным результатом обучения в среднем звене должна являться математическая грамотность учащихся как общекультурное умение, в которое входит [39]:

·  владение основными понятиями и методами изучения математических объектов (такими как обобщение, спецификация, аналогия, распространение, систематизация и др.);

·        умение эффективно использовать математические способы вычислений, преобразований и др.;

·        владение языком изложения математических знаний (письменная математическая речь);

·        владение терминологией, связанной с исследованием (гипотеза, утверждение, доказательство).

В книге “Учебно-образовательное пространство в педагогике развития: математическое образование” [3] говорится, что основы математической грамотности закладываются на пятом году обучения (6-ой класс). К концу этого года обучения учащиеся должны иметь навыки работы с записью (построение и преобразование формы записи), умение формулировать утверждение и проверять их на правдоподобность, различать способы проверки утверждения для произвольного и для конкретного случая, понимать разницу между утверждениями, теоремой, гипотезой, оценивать эффективность применения способа.

Так же авторы проекта РО считают, что единицей обучения в курсе “Начала алгебры” является учебный цикл, состоящий из шести этапов[3]:

- оформление существующих знаний;

-        постановка, проблемы (задачи);

         открытие нового понятия (может использоваться рабочий язык);

         систематизация новых знаний;

         анализ текстов учебников (переход на культурный язык);

         выделение класса типовых задач (на навык);

         контроль и оценка.

Программа для шестого класса направлена на овладение учащимися учебно-исследовательской деятельности.

Курс “Начала алгебры” шестого класса РО состоит из следующих разделов:

Раздел 1. Теория делимости натуральных чисел;

Раздел 2. Положительное рациональное число;

Раздел 3. Рациональное число;

Раздел 4. Система координат. Графики.

Материал темы: “Признаки делимости в системе счисления по основанию р” из раздела ”Теория делимости натуральных чисел ” выходит за рамки традиционной школьной программы для 6-го класса, однако он органично вписывается в программу РО. Также материал данной темы идеален для постановки и решения учащимися учебно-исследовательской задачи, а также для пропедевтики понятия доказательства.

При изучении данной темы у учащихся формируется представление о признаках делимости как об одном из способов определения истинности/ложности утверждений о делимости, вырабатывается умение использовать свойства отношения делимости как средство обоснования рассуждений и доказательства общих утверждений, умение применять признаки делимости в системах счисления по основанию р при решении задач на делимость.

Продолжается работа по выводу, записи и обоснованию общих утверждений о делимости (учащиеся должны “сконструировать” математически грамотную запись признаков делимости).

По этой теме существует задачник и рабочая тетрадь. Однако для успешного прохождения этой темы и получения желаемых результатов необходимы учебные тексты в виде образцов рассуждений.

§3. Вывод

Появление в шестом классе сложно структурированных математических объектов и операций с ними требует освоения учащимися нового предметного действия - учебного-исследования, позволяющего удерживать и преобразовывать целостную расчлененную предметную единицу.

Так как в РО изложение (построение нового понятия, способа) происходит через оформление и столкновение версий учеников, что зачастую, в ходе урока, при попытке описать другим собственное понимание, открытый в группе способ ученики, испытываю затруднение в средствах выражения своих мыслей, связанные с дефицитом специальных слов, терминов, то учащиеся придумывают свой “рабочий” язык. Но так как в развивающем обучение акцент делается на научности, культурности открываемых понятий и способов работы с ними, то необходимо обеспечение “перевода” полученных учащимися на уроках результатов и описаний на культурный язык теории и язык деятельности (решения учебно-исследовательской задачи). Поэтому существует необходимость образцов текстов, которые бы помогали учащимся осваивать этот культурный язык.

Как уже говорилось ранее, материал темы: “Признаки делимости в системе счисления по основанию р” из раздела ”Теория делимости натуральных чисел ” выходит за рамки традиционной школьной программы для 6-го класса, однако он органично вписывается в программу РО. Также материал данной темы идеален для постановки и решения учащимися учебно-исследовательской задачи, а также для пропедевтики понятия доказательства.

По этой теме существует задачник и рабочая тетрадь. Однако для успешного прохождения этой темы и получения желаемых результатов необходимы учебные тексты в виде образцов рассуждений.

Образцов таких текстов практически не существует. Существующие образцы текстов описывающих исследование не ориентированны на детей, только один способ исследования и отсутствует метаязык.

Глава 3. Апробация разработанных текстов

§1. Апробация текстов “описывающих ход исследования”

Краткая характеристика разработанных текстов “описывающих ход исследования” и методика применения этих текстов.

Сначала эти тексты состояли просто из рассуждений. В результате обсуждения с научным руководителем и учителями решили, что текст будет лучше восприниматься, если рассуждения в нем будут излагаться от лица младшего школьника, ровесника и старшеклассника. Поэтому тексты изменились. Разработанные мной тексты, описывающие ход исследования состоят из трех независимых друг от друга рассуждений, каждое из которых является рассуждением одного из школьников.

-ое младшего школьника - способ полный перебор,

-ое ровесника - эмпирическое исследование,

-е старшеклассник - содержательный анализ.

В этих рассуждениях присутствуют как верные так и не верные ходы. У младшего школьника метаязык отсутствует, у ровесника появляется метаязык, а у старшеклассника присутствует, т.к. рассуждение старшеклассника - это уже рассуждение человека имеющего опыт в исследование.

За счет разработанной методики работы с текстами форма текста в виде рассуждения трех школьников стала необходимой. Разработанная методика работы с текстами такого типа следующая. Учащимся даются тексты, затем дается задание прочитать первое рассуждение и написать к нему вопросы. Затем учитель спрашивает: “Кому понятно?” И один или два человека из тех, кому полностью понятно рассуждение становятся экспертами (принимают позицию автора) и отвечают на вопросы остальной части класса. Тоже самое проделывается и с остальными рассуждениями.

Апробация на уроке в 6-ом класс

Проект урока

Тема: ”Признаки делимости в системах счисления по основанию р”

Вид урока: учебно-ролевая игра

Цель:1) Отработать пройденный материал;

) Освоение культурных образцов рассуждения;

) Возможность соотнесения учащимися своего опыта и образцов.

Методическая цель: Создать методическое обеспечение для освоения учащимися способов описания исследования.

План урока:

1. Приветствие

2.      Работа с учебными текстами

.        Завершение занятия

Виды работы: 1. Самостоятельная работа с текстами;

. Общее обсуждение.

Средства: Учебные тексты (приложение 1).

Ход урока

1. Приветствие

2.      Учитель дает задание 1. Прочитать задачу 1 и 2. Чем отличается задача 2 от задачи 1?

Ответы учеников:

Виталя. Задача 1 общая, а в задаче 2 говорится про конкретную систему счисления.

Максим. Задачу 1 нельзя решить, потому что нет системы счисления.

Учитель. Как понять набор признаков в разных системах счисления?

Ника. Например, признак делимости на 7 в 10-чной системе счисления один, в 7-чной - другой, в 14-чной третий, а в какой-нибудь 8-чной может быть совсем не существует такого признака.

Учитель. А как вы думаете, существует ли признак делимости на 7 в 7-чной и в 14-чной системах счисления?

Ответ: Наверное, существует.

Вера. Если в задаче написано вывести, значит, этот признак существует.

Учитель. Далее в этом тексте вам предлагается решение этой задачи тремя учениками: младшим школьником, ровесником и старшеклассником.

Задание 2. Прочтите рассуждение младшего школьника и составьте вопросы к этому тексту.

Дается время.

Затем учитель спрашивает: Кому это рассуждение полностью понятно.

Руки подняли 10 человек из 22-х присутствующих на уроке.

Учитель. Кто хотел бы и мог выступить в роли младшего школьника и ответить на вопросы одноклассников?

Руки подняли 5 человек. Учитель предложил им отвечать на вопросы одноклассников по очереди.

Вопросы:

.Зачем надо было выписывать столько чисел?

.Как ты понял, что 10₇,20₇ и так далее делятся на 7?

.Зачем выписывать все двузначные числа в 14-чной системе счисления?

.Почему ты взял именно двузначные числа? А не однозначные или трехзначные?

.Почему ты считаешь, что можно сделать такой вывод?

Ответы:

. Чтобы заметить закономерность.

. Перевел в десятичную систему счисления и посчитал.

. а) Чтобы убедиться, что нет дольше таких чисел, которые бы делились на 7.

б) Чтобы не пропустить ни одного числа.

4. Потому что среди однозначных чисел нет делящихся на 7, а трехзначные слишком долго перебирать.

. Потому что я перебрал все двузначные числа.

Задание 3. Прочитайте рассуждение ровесника.

Дается время.

Учитель. Все ли вам понятно в этом рассуждении? Задайте вопросы.

Это рассуждение стало понятным: 6-м ученикам, причем, в роли ровесника согласились выступить только двое из них. На вопросы они отвечали вмести, дополняя друг друга.

Вопросы:

. Почему ты выбрал именно эти числа?

. Почему ты взял только трехзначные числа?

. Причем тут признак делимости на 9? Почему бы ни взять признак делимости на 2 или 5?

. Зачем ты стал переставлять цифры, если предположение уже есть и на многих числах они действуют?

. Почему ты взял число в 14-чной системе счисления? Зачем брал числа в 14-чной системе счисления?

. Почему именно так переставил цифры?

. Почему ты сделал вывод, что твое предположение неверно, может быть это просто исключение?

. Почему ты взял именно 7-чную и 14-чную систему счисления?

. На основании чего ты сделал предположение, что второе предположение верно для любых чисел?

Ответы:

1. Я выбрал их наугад.

2. Так легче считать. Захотелось мне так. Так нагляднее.

3. Первый попавшийся признак делимости.

4. Мне попалось число, которое не делится на 7, хотя его сумма цифр на 7 делилась. Я подумал исключение это или закономерность? Попробовал переставить цифры в одном из моих чисел.

5. В задаче говорится, что сформулировать признаки делимости в 7-чной и 14-чной системах счисления?

6. Можно переставить по другому, но смысл от этого не изменится.

7. Это не исключение, а контрпример, а если есть контрпример, значит предположение не верно.

8. В условии задачи так требуется.

9. У нас есть два типа признаков делимости: по сумме цифр и по последней цифре, если не подходит один признак делимости, мы пробуем другой.

- А может быть, там совсем никакого признака нет?

Если бы не было признаков, то и не было бы задачи.

Задание 4. Прочитайте рассуждение старшеклассника и задайте вопросы.

Это рассуждение не было полностью понятно ни кому. Когда учитель спросил: Кому понятно рассуждение? Робко поднял руку один мальчик. Учитель попросил его выступить в роли старшеклассника, но он согласился отвечать только с помощью учителя.

Вопросы:

1. Почему ты решил взять позиционную запись?

2. Что такое а₀ а₁а₂?

3. Зачем здесь нужны буквы а₀ а₁а₂? Нельзя ли обойтись без них?

Почему можно сделать вывод, что 14 делится на 7 следовательно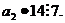

1. Разве можно 0 делить на 7?

2. Откуда появились утверждения?

3. Что такое теорема? Зачем ее доказывать?

4. Что такое 14ⁿ?

5. Не понятно, почему эти буковки доказывают теорему?

Ответы:

1. Мы изучали позиционную запись числа и свойства делимости, и знаем, что число можно разложить в позиционную запись.

2.      Этими буквами мы заменяем цифры в числе, а цифры возле букв показывают разряд цифры в числе.

.        Теперь у нас число стало любым и мы можем формулировать утверждение в общем виде.

.        Мы изучали свойство, что если один из множителей произведения делится на данное число, то и все произведение делится на это число. И тогда нам не важно какое значение имеет а₂.

5.      Ноль делится на любое число, и все равно получается ноль. Ноль на конце числа не играет роли, т.к. ноль показывает, что нет разряда единиц, а есть только десятки. Например, 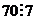 не смотря на то, что оно оканчивается на ноль, оно делится на 7.

.        Заметили закономерность и сформулировали утверждение.

.        Теорема - это доказанное утверждение. Поэтому ее надо доказывать.

.        Значит, что число 14 можно возвести в любую степень.

.        Теорему доказывают не буковки, а логические утверждения.

3. Учитель дает домашнее задание и завершает урок.

Апробация в Школе молодого ученого (ШМУ)

Занятие 1 в ШМУ

Проект занятия

Тема: “Признаки делимости”

Вид урока: учебно-ролевая игра

Цель: 1) Освоение культурных образцов рассуждения;

2) Приобретение учащимися опыта рассуждений, для использования этого опыта при написании творческих работ.

Методическая цель: Создать методическое обеспечение для освоения учащимися способов описания исследования.

План занятия:

1. Сообщение необходимых знаний.

Что такое:

системы счисления;

позиционная запись числа.

Вспомнить признаки делимости в 10-чной системе счисления.

2. Работа с текстами.

Виды работы: 1. Самостоятельная работа с текстами;

. Общее обсуждение.

Средства: Учебные тексты (приложение 2).

Ход занятия

Часть1

Начинается занятие, все садятся и успокаиваются.

Ведущий занятия приветствует всех.

Ведущий (В). Тема нашего сегодняшнего занятия: Признаки делимости. Для работы нам понадобятся некоторые дополнительные знания. Мы с вами какими цифрами записываем числа?

Дети (Д). 1,2,3,4,5,6,7,8,9,0.

Записывают на доске:

,1,2,3,4,5,6,7,8,9.

В. А дальше?

Записывают на доске дальше:

,1,2,3,4,5,6,7,8,9,10,11,12,13,14

В. А давайте представим, что мы с вами инопланетяне, и, что мы считаем пятерками. Какие цифры у нас будут?

Д. 1,2,3,4,0

Записывают на доске:

,1,2,3,4

В. А дальше?

Записывают:

,1,2,3,4,10,11,12,13,14,20,21

В. А как отличить десятки?

Учителя помогают: Надо написать индекс в кружочке.

Подписали индекс.

В. называет системы, и дети отвечают, сколько в ней будет цифр.

В. Если надо число 31₅, какое ему будет равно число в десятичной системе счисления?

Мальчик. 16₁₀.

В. Как ты нашел?

Мальчик. 31₅ =3·5+1

Проверили, дописав ряды чисел.

В. Как называется запись 3·5+1

Д. Разложение на разряды.

В. помогает: позиционная запись.

В. записывает позиционную запись числа.

₁₀ =3·10² +5·10¹+1·10⁰

В. записывает на доске числа

₁₀, 42₁₀, 152₆.

В. Запишите позиционную запись этих чисел.

Дети записывают в тетрадях.

Затем ведущий просит записать на доске то, что написали в тетрадях.

Все боятся.

Затем вышел мальчик и записал:

₁₀=1·10² +2·10¹+3·10⁰;

₆=1·6² +5·6¹+2·6⁰.

В. А теперь посчитайте в десятичной системе счисления.

Продолжают запись

₆=1·6² +5·6¹+2·6⁰=36+30+2=68.

В. вспомните признаки делимости в десятичной системе счисления. Какие вы знаете?

Д. На 3,9,5,10,2.

В. Запишем на 3 и 9.

Дети произносят признак. Ведущий записывает на доске:

на 3 и 9

по сумме цифр

В. А на 5,2,10?

Записывают: на 5,2,10

по последней цифре

В. Все признаки делимости вспомнили?

Д. Да.

В. Теперь задание. Надо написать, верны или нет утверждения

Определили легко, истинны или ложны утверждения, кроме последнего утверждения.

В. Как проверить?

Д. Перевести.

Проверяют последнее выражение переводом.

В. Какую задачу можем поставить?

Д. Вывести признаки делимости в других системах счисления.

Часть 2. Чтение текстов

Детям раздаются тексты.

Дается задание прочитать рассуждение 1 и написать к рассуждению вопросы. Давалось 20 минут. В. Кому все понятно почти все подняли руки.

Почти все подняли руки.

В. А кто бы мог выступить в роли экспертов и ответить на вопросы аудитории?

Никто не поднял руки. Предложили выйти двум мальчикам, они, чуть-чуть поколебавшись, согласились.

Вопросы и ответы:

1. По какому признаку вы выбирали числа?

Ответ. Выписали все двузначные числа в 7-чной и 14-чной системах счисления.

2. Почему взяли 14-чную систему счисления? Как записать числа в 14-чной системе счисления?

Ответ. Дано по условию задачи. Числа записываются 78₁₄.

3. А как, например, записать число 11 десятков и 13 единиц?

Ответ. (Учителя помогают) Можно писать в кружочке, а можно числа 10,11,12,13 заменить буквами:

Чаще используют вторую запись bd₁₄.

4. Как перебрали все числа в 14-чной системе счисления?

Ответ. Выписали все однозначные и двузначные числа, а затем проверяли, делятся они или нет переводом.

5. Почему среди всех двузначных чисел нет чисел с a, b, g,d?

Ответ. (Мальчики замялись. Учитель ответил за них) Это не доработка разработчика.

6. Почему в 7-чной системе счисления не берутся однозначные, а в 14-чной берутся и однозначные и двузначные числа?

Ответ. Потому что в 7-чной системе счисления нет однозначных чисел делящихся на 7, а в 14-чной системе счисления есть однозначное число, делящееся на 7 и это число 7.

7. Какую закономерность школьник увидел в записи чисел?

Ответ. Что на 7 в 7-чной системе счисления делятся двузначные числа, оканчивающиеся на 0. А на 7 в 14-чной системе счисления делятся однозначные и двузначные числа, оканчивающиеся на 0 и 7.

8. Задача формулируется общая, а рассуждения были для однозначных и двузначных чисел. Решил ли школьник задачу?

Ответ. Решил для двузначных чисел, но поставленную задачу не решил.

Затем мальчики сели. Ведущий дал задание прочитать рассуждение 2 и составить вопросы (времени было дано мало, т.к. мы не укладывались в рамки занятия).

В. Все ли всем понятно в данном рассуждении.

Все было понятно студентам, учителям и двум ученикам, которые до этого были экспертами. Поэтому в роли экспертов предложили выйти двум студентам.

Вопросы и ответы:

1. Почему появилась аналогия с признаком делимости на 9?

Ответ. Так как в десятичной системе счисления мы знаем признаки по сумме цифр числа и по последней цифре, то просто решили попробовать воспользоваться признаком делимости по сумме цифр.

2. Если сумма цифр 21, будет ли число делиться на 7?

Ответ. Не обязательно, т.к. по сумме мы не можем определить делится ли число на7 в 7-чной и 14-чной системах счисления.

3. Почему взяли трехзначные числа?

Ответ. Потому что их большее количество.

4. Уверены, что ваш признак верный?

Ответ. Нам не удалось найти контрпример, поэтому мы можем предположить, что он верен, но нам так же и не удалось его доказать, поэтому мы не можем утверждать, что он верен.

5. Решил ли ровесник задачу?

Ответ. Да, мы вывели признак, которым будем пользоваться.

По рассуждав, аудитория ответила, что нет, рассмотрели только для трехзначных.

Девочки сели.

Было дано задание прочитать третье рассуждение и написать вопросы.

Время вышло (было дано 10 минут).

В. Кому понятно третье рассуждение.

Оно было понятно все тем же двум мальчикам, студентам и учителям.

В роли эксперта мы попросили выступить Валентину Захаровну (учитель), но даже она взяла себе в помощники Оксану Ивановну (учитель).

Вопросы и ответы:

. Что означает a₂a₁a_{0 14,} a_n…a_{0 р}?

Ответ. a₂a₁a_{0 14} обозначает произвольное трехзначное число в 14-чной системе счисления, а a_n…a_{0 р} произвольное число в системе счисления по основанию р.

.Почему делается обобщение на произвольную систему счисления, основание которой делится на 7?

Ответ. Это получается из позиционной записи числа.

.Почему так мало примеров вы рассмотрели?

Ответ. Опирались на доказанные свойства, а не на конкретные примеры?

.Можно ли взять 3-чную, 6-чную и 12-чную будет ли аналогичной теория (признак делимости на 7)?

Ответ. Нет.

.Это правда, что вы теперь можете больше, чем там написали?

Ответ. Мы решили более общую задачу, чем задача, которую мы решали.

6.Говорилось про 28-чную систему счисления, будет ли этот признак работать?

Ответ. Да.

В. А теперь как вы думаете, кому принадлежит 1-ое рассуждение, кому 2-ое, а кому 3-е?

Ответ. 1-ое - младший школьник, 2-ое - ровесник, 3-е - старшеклассник.

В. А как по вашему старшеклассник - это сколько лет?

Ответ. От десятого класса и до 21 года.

В. А для чего вам может пригодится это рассуждение?

Ответ. Для того, чтобы выводить признаки делимости. Для проведения аналогичных рассуждений. Для оформления своих творческих работ.

В. Домашнее задание: Решите аналогичную задачу и опишите ее по аналогии с одним из рассуждений.

На этом занятие закончили.

Занятие 2 в ШМУ

Проект занятия

Тема: “Признаки делимости”

Вид урока: Отработка полученных способов исследования

Цель: Попробовать, по полученному образцу исследования, провести свое исследование.

План занятия:

1. Повторение

2.      Работа в группах

.        Сообщение полученных результатов

Виды работы: 1. Работа по группам;

. Доклад полученных результатов.

Средства: Учебные тексты (приложение 2);

Карточки с заданиями (приложение 3).

Ход урока

Раздали листочки с заданиями.

В. Тема сегодняшнего занятия: Признаки делимости. На этом занятие я предлагаю сделать свое исследование. Давайте повторим. Как будем переводить 45₅?

Записывают .

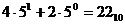В. А если у нас 111₂?

Записывают .

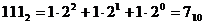В. Вспомнили?

Д. Да.

В. Давайте вспомним признаки делимости в 10-чной системе счисления.

Д. По сумме цифр числа - признаки на 3 и 9,

По последней цифре - признаки на 2, 5, 10.

В. Теперь давайте приступим к выполнению заданий из карточек. Я засекаю время и вам надо за 10 минут сделать как можно больше примеров.

Трем мальчикам дается индивидуальное задание (решить и обобщить как можно больше примеров).

Все решают переводом, только один мальчик натолкнулся на мысль о признаке.

В. Время вышло. Кто сколько решил?

Одна девочка 7 примеров, один мальчик 5 примеров, остальные 4 и меньше.

В. Как решали?

Д. Переводили и смотрели.

В. Но это не очень действенный способ. Как можно быстрее научиться решать такие примеры?

Валентина Захаровна (учитель). Я думаю можно с помощью рассуждения два (ровесника) в конце.

В. Т.е. Валентина Захаровна предлагает использовать признак. Ускорило бы это решение примеров?

Д. Да.

В. Как вы думаете, сильно ли признаки делимости в других системах счисления отличаются от признаков в 10-чной системе счисления?

Д. Нет.

В. Я предлагаю попробовать вывести несколько признаков делимости, а затем доложить и обсудить их. Дома вы попробуете описать выведенные признаки.

группа в 12-чной системе счисления на 6,

группа в 6-чной системе счисления на 2,

группа в 6-чной системе счисления на 3,

группа в 12-чной системе счисления на 2.

Кому нужна помощь, могут обращаться. Вам раздали рассуждения, можете ими пользоваться.

Дети работают в группах. Выдвигают свои предположения.

Затем дается время на то, чтобы обсудить, что будут докладывать, и кто будет докладывать.

В. Задание для всех, определить к какому рассуждению относится рассказываемое рассуждение.

Докладывают.

Гр.4.

Вывод: Если число четное, то делится на 2. В любой четной системе счисления на 2 делятся те числа, которые оканчиваются на 0 или четное число.

Наше рассуждение аналогично рассуждениям 1 и 2.

Гр.2. Мы рассмотрели некоторые числа

и вывели предположение: Если число оканчивается на 0, 2, 4 в 6-чной системе счисления, то оно будет делиться на 2.

Наше рассуждение относится ко второму, потому что сделали предположение, но не удалось доказать.

Гр.3.

Мы выписывали, переводили, и получили, что делятся только те, которые оканчиваются на 3 и 0. Количество цифр в числе не имеет значения.

Сделали формулу

+3=12

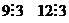
Формула: Если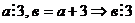

Рассуждение относится к концу второго началу третьего.

Гр.1.

Выписывали цифры в этой системе счисления: 0,1,2,3,4,5,6,7,8,9,10,11.

Мы вывели закономерность, что каждое число делится на 6, если начинается с делимого делящегося на 6. Т.е. в 12-чной системе счисления будут делиться числа оканчивающиеся на 0 и 6.

Мы брали числа и раскладывали в позиционную запись (переводом) и проверяли.

Рассуждение относится ко второму, потому что на частных примерах, но доказать не удалось.

Домашнее задание: Получили отношение к исследованиям. Попробуйте описать свои рассуждения с учетом замечаний и возможно продолжением.

Мальчики, которые выполняли отдельно задания, решили три задачи.

Анализ апробации текстов описывающих исследование

Одновременная работа с текстами, описывающими все способы рассуждений, может задать “вектор” движения учащихся по освоению ими изложения решения учебно-исследовательской задачи. Так как обнаружены особенности понимания школьниками данных текстов: первый способ рассуждения понимают и могут осознанно использовать практически все учащиеся шестых классов, второй текст учащиеся могли понять лишь в коллективно-распределенной форме используя помощь учителя, наибольшую трудность представлял последний текст, даже с помощью учителя учащимся с трудом удалось выделить логику и некоторые моменты так и остались непонятны.

Однако некоторые семиклассники и восьмиклассники присутствующие на ШМУ могут самостоятельно понять последний текст и могут построить свои рассуждения способом содержательный анализ. То, что некоторые учащиеся понимают и могут самостоятельно построить аналогичные рассуждения, говорит о том, что ими этот способ освоен.

Как показало данное исследование эти тексты пригодны для уроков, но не пригодны для других форм работы с ними, например, для ШМУ. Но может быть результат апробации не совсем удачный из-за того, что рассчитывали, что занятие будет проходить 2 часа, а оно проходило 1,5 часа. И поэтому вторая часть занятия получилась “скомканной”, давалось мало времени на чтение и понимание текста. Еще учащиеся апробации в 6-ом классе соотносили описанные рассуждения со своими рассуждениями, а у учащихся ШМУ не было своего опыта. Однако второе занятие в ШМУ показало, что способ полный перебор освоен всеми участниками, способ эмпирического исследования многими, а способ содержательного анализа лишь несколькими участниками.

После апробации и еще более подробного изучения текстов, тексты были слегка изменены, и получился итоговый образец текстов, описывающих ход исследования (приложение 4). В этом варианте текста уточнены фразы учеников, учтена недоработка, которая обнаружена в результате апробации (в 14-ичной системе счисления вставлены числа α0, α7, β0, β7,γ0, γ7,δ0, δ7). Вставлены вопросы, отвечая на которые, учащийся может отследить основные ходы.

§2. Апробация текстов “помощники”

Проект занятия 1 с помощниками

Тема: “Сравнение и сложение дробей с разными знаменателями”.

Вид урока: Отработка навыков.

Цель:1)Отработать сравнение и сложение дробей с разными знаменателями.

)Проверить уяснили ли дети материал по данной теме.

Методическая цель: Создать методическое обеспечение для самостоятельной работы учащихся по отработке навыков, Детям, не усвоившим материал предложить тексты предназначенные для заполнения пробелов в знаниях по данной теме. Пронаблюдать, как дети используют тексты, помогают ли они им в усвоении материала.

План урока:

1. Организационный момент, 2 минуты.

2. Повторение пройденного материала, 5 минут.

3. Самостоятельное выполнение заданий с использованием “помощников”, 30 минут.

4. Сдача тетрадей и карточек, и получение домашнего задания.

Виды работы:

1. Фронтальный опрос;

. Самостоятельная работа по карточкам.

Средства:

Карточки пяти видов:

1. На сравнение дробей;

2.      На сложение дробей;

.        На вычитание дробей;

.        Два действия в одном примере и сложение и вычитание;

5. Повышенной сложности.

Помощники (приложение 5)

Ход урока:

1. Организационный момент

Дети очень долго успокаивались, и поэтому на организационную часть ушло больше планируемого времени (примерно 5 минут).

2. Повторение пройденного материала

Учитель: На прошлом уроке мы проходили с вами сравнение и сложение дробей. Как сравнить две дроби?

Учащиеся: Надо привести дроби к наименьшему общему знаменателю (НОЗ).

Учитель: Правильно. А какие два способа нахождения наименьшего общего знаменателя вы знаете?

Учащиеся: Первый - это разложением на множители. Второй- это выписывание класса равных дробей.

Учитель: Правильно. Расскажите, в чем заключается способ разложения на множители.

Учащиеся рассказывают способ.

Затем учитель просит рассказать второй способ. Учащиеся рассказывают.

Учитель: Нашли наименьший общий знаменатель, теперь что будем делать?

Учащиеся: Разделим наименьший общий знаменатель на знаменатели данных дробей, т.е. найдем дополнительные множители для дробей. Умножим числитель каждой дроби на ее дополнительный множитель и полученные дроби сравним.

Учитель: А как сложить дроби?

Учащиеся: Найдем наименьший общий делитель. Разделим наименьший общий знаменатель на знаменатели данных дробей, т.е. найдем для каждой дроби дополнительные множители. Умножим числитель каждой дроби на ее дополнительный множитель. Полученные дроби сложим.

3. Работа по карточкам

Первую карточку надо выполнить всем. Пятая дается сильным ученикам. Остальным ученикам надо сделать на выбор либо вторую и третью карточки, либо четвертую. Учащиеся берут карточки на выбор. Когда учащиеся начали решать сразу же послышались фразы типа: ”А я не знаю, как решать”, “Я не умею”.

Учителю не приходилось объяснять, как это делать, он просто давал учащимся помощники и наблюдал, как дети с ними работают.

4. Сдача тетрадей и карточек, и получение домашнего задания

Анализ работы с помощниками

Вверху “помощника” было написано при выполнении. которого задание этот “помощника” может помочь. Далее шло конкретное задание, которое затем решалось. Задание было хорошо выделено и сформулировано. Решение и описание решения (общий алгоритм решения) были разбиты на две колонки, мы думали, что так “помощник” будет лучше читаться. Но оказалось, что учащиеся не соотносят записи в двух разных колонках. Одна девочка позвала меня и сказала: ”А я не знаю, как находить дополнительные множители?” Я ей показала на то место, где в описании написано, как находить дополнительные множители, но она ответила, что она не знает, как это записать, и я ей указала на колонку с решением, где и было написано, как это записать. И такой случай был не единственный.

Замечен еще один недостаток “помощника”, учащимся не понятно, что и как должно быть записано в тетради.

Чаще всего учащиеся обращались к помощнику на приведение дробей к НОЗ, т.к. задание было сравнить, сложить или вычислить дроби, а для того, что бы это сделать, надо привести дроби к НОЗ. А в “помощниках” на сравнение и сложение этого не было. И поэтому учащимся приходилось обращаться к “помощнику” на приведение дробей к НОЗ.

Проектирование новых “помощников”

Проанализировав недостатки “помощников” сделали новые. Они были в виде таблиц двух видов. Первый “помощник” был на сложение отрицательных чисел. Вверху было название ”Как сложить отрицательные числа”. Далее “помощник” был разделен на две части: в одной был решен и описан пример (образец), а в другой был пример для самостоятельного решения с указанием того, что надо делать (сделай сам). В части “сделай сам” были пустые ячейки, в которые по аналогии с образцом надо было записать решение примера. В низу таблицы с левой стороны было “Что писать в тетради”, а с правой стороны “Запиши” и надо было записать решенный пример, так как бы его записали в тетради. Второй “помощник” “Как сложить отрицательные и положительные числа” был тоже в виде таблицы, но в этом “помощнике” не было места для решения примера, здесь был только разобранный образец решения. В левых ячейках был общий алгоритм решения. А в правых, решение конкретного примера. Внизу было “Что писать в тетради” и записано, что и как должны писать в тетрадь. Был еще и третий “помощник”, на нем было название “Сложение чисел равных по модулю, противоположных по знаку” состоял из задания и решения в виде правила.

Проект урока 2

Тема: “Сложение и вычитание отрицательных и положительных чисел”.

Вид урока: Отработка навыков.

Цель:1)Отработать сложение и вычитание отрицательных и положительных чисел.

)Проверить уяснили ли дети материал по данной теме.

Методическая цель: Создать методическое обеспечение для самостоятельной работы учащихся по отработке навыков: карточки с заданиями и “помощников”, Раздать детям карточки и “помощники”, понаблюдать работают ли дети с ними, есть ли недостатки у “помощников” и какой из предлагаемых “помощников” лучше.

План урока:

1. Организационный момент, 2 минуты.

.        Самостоятельное выполнение заданий с использованием “помощников”, 28 минут.

.        Ответы на вопросы, 3 минуты,

.        Сдача тетрадей и карточек, и получение домашнего задания.

Виды работы:

1. Фронтальный опрос;

. Самостоятельная работа по карточкам.

Средства:

Карточки с заданиями.

Помощники (приложение 6).

Ход урока 2

1. Организационный момент

Учащиеся успокоились быстро, т.к. на уроке, присутствовало всего пол класса, и им было интересно, что же мы сегодня будем делать.

2. Повторение пройденного материала

Повторили правило вычитания чисел, правило сложения отрицательного и положительного чисел, правило сложения отрицательных чисел, правило сложения равных по модулю, но противоположных по знаку чисел.

3. Самостоятельное выполнение заданий с использованием “помощников”.

Каждому учащемуся раздали по карточке с заданием и три разных “помощника”. Учитель объяснил, как надо использовать “помощники”, рассказал, что в них есть, и попросил сделать задание в таблице 1. Вопросов почти не было. Только некоторые спрашивали: ”А как это делать?” и мне приходилось спрашивать, какие они числа складывают, и показывать им на название “помощников”. Учащиеся успели все вовремя сделать.

4. Ответы на вопросы

На доске было написано два вопроса:

1. Пользовались ли вы “помощниками”?

2.      Какой таблицей легче пользоваться?

Учитель попросил учащихся ответить на эти вопросы в тетради.

Ответили на вопросы.

5. Сдали тетради и карточки, и получили домашнее задание.

Анализ урока 2 с “помощниками”

Дисциплина на уроке была хорошая, быстро успокоились и стали выполнять задания. Почти все учащиеся заполнили таблицу 1.

Только один мальчик напротив, того “Как решать” стал писать решение примера, который ему надо решить. А еще один мальчик в этой же ячейке решил пример, который ему надо было решить, а в ячейках, где надо было решать пример, записал решение придуманного примера. Поэтому в этом “помощнике” не должно существовать пустых ячеек.

Еще я думаю, что надо четче разделить “образец” и ”сделай сам”, т.к. некоторые дети сначала не могли разделить эти две части и не понимали, что где.

Анализ ответов на вопросы показывает, что если дети ответили, что они пользовались “помощниками”, то почти все считают, что легче пользоваться таблицей 1. Даже мальчик, который обычно ничего не делает на уроке, стал пытаться заполнить таблицу. Я это заметила, подошла к нему, и мы с ним вместе заполнили таблицу.

Заключение

Удалось разработать новую форму учебных текстов по теме: “Признаки делимости в системах счисления по основанию р” описывающих ход исследования. Раньше такая форма текстов не использовалась, но по программе для шестого класса разработанной Знаменской О.В. тексты такого типа необходимы.

За счет разработанной методики работы с текстами форма текстов в виде независимых рассуждений трех школьников стала необходимой, но осталось не решенной проблема, а что было бы, если тексты были бы в форме диалога. Разработана следующая методика работы с текстами такого типа. Учащимся даются тексты, затем дается задание прочитать первое рассуждение и написать к нему вопросы. Затем учитель спрашивает: “Кому понятно?” И один или два человека из тех, кому полностью понятно рассуждение становятся экспертами (принимают позицию автора) и отвечают на вопросы остальной части класса. Тоже самое проделывается и с остальными рассуждениями.

Также, осталось не решенной проблема, правильно ли выделены основания, для написания учебных текстов вида рассуждения, может быть, должны были быть выделены другие характеристики сравнения текстов описывающих исследование, и в результате этого может быть, могла быть другая форма текстов.

Осталась не решенной проблема того, что должно измениться в самих последующих текстах или в работе с ними, т.к. новизна пропадает.

Также я внесла изменения в учебные тексты типа “помощники”. Тексты стали в виде таблиц, одна половина которых пустая, и учащиеся заполняют ее по аналогии с образцом. Такая форма “помощников", как показала апробация, более эффективна, т.к. даже учащиеся которые обычно ничего не делают, пытались заполнить эти помощники.

Необходима дальнейшая работа по данной теме, т.к. осталось еще очень много не сделанного и не исследованного по данной теме.

Список литературы

1. Адамар Ж. Исследование психологии процесса изобретения в области математики. Франция. 1959. Пер. с франц. “Издательство советское радио”, Москва, 1970.

2. Алгебра: Учебник для 7-го кл. сред. шк./[Ю.Н. Макарычев и др.] - М.: Просвещение, 1991.

3. Аронов А. М., Ермаков С. В., Знаменская О. В. Учебно-образовательное пространство в педагогике развития: математическое образование: Монография/ Краснояр. гос. ун-т. Красноярск, 2001.

4. Баврин И.И. Математика: Краткий справочник школьника.5 - 11 кл. - М.: Дрофа,1997.

5. Безнощенко Н.Я. К обратной задаче математического потенциала//Сибирский математический журнал; том XV №1, 1974.

6. Белоконь О.И., О «культурном» и «рабочем» языках на уроках математики РО в 6 - 9 классах. www. Experiment. lv./ rus/ biblio/ obraz.21 veva/ utu. Образование 21 век: достижения и перспективы. Международный сборник теории, методических и практических работ по проблемам образования.

7. Вагутин В.Н. Близкие дроби//Квант, №8, 1996.

8. Виленкин Н.Я. и др. Математика: учебник для 5 класса средней школы. - СПб.: Свет, 1995.

9. Воднев В.Т. и др. Основные математические формулы: Справочник. - Минск: Вышейшая школа, 1995.

10.Волковыский Л. М., Сборник задач по теории функций комплексного переменного, - М.: Наука, 1975.

11.Воронцов А.Б. География. 6 - 8 класс. Программа. (Система Д.Б. Эльконина - В.В. Давыдова.) - М.:ЦПРО «Развитие личности»,1998.

12.Выгодский М. Я., Справочник по элементарной математике, М.: Наука, 1976.

13.Геометрия: учеб. Пособие для 9-го класса средней школы/ Клопский В. М., Скопец З. А., Ягодовский М. И., М., Просвещение, 1975.

14.Григорьев Т. В., Дураков Б. К., Математика в помощь абитуриенту, «Горница», Красноярск, 1994.

15.Давыдов В.В. Теория развивающего обучения. - М.:ИНТОР, 1996.

16.Дектярев И.М., Вопросы распределения значения в размерностях, больших единицы.//Успехи математических наук. Том XXV выпуск 6(156), 1970.

17.Задачи по математике. Начала анализа: Справ. Пособие/ Вавилов В. В. и др. - М.: Наука, 1990.

18.Кожухов С.Ф. Регулярно полные абелевы группы.//Известия Вузов. Математика. №12, 1980.

19.Колмогоров А. Н., фомин С. В., Элементы теории функций и функционального анализа, - М.: Наука, 1989.

20.Кордемский Б. А., Математическая смекалка, - М., Юнисам, МДС, 1994.

21.Кузьмин Ю.Н., Математика: Пособие для поступающих в вузы, «Специальная литература», С.-Пб., 1995.

22.Лавитас Г.Г. Карточки для коррекции знаний по математике для 5 - 6 классов. - М.: Илекса, 2000.

23.Лакатос И. Доказательства и опровержения (Как доказывается теорема) пер. с англ. И.Н. Веселовского. М.: Наука, 1967.

24.Математика: Справочник абитуриента/ сост. О.А. Смирнова. - М.: “Слово”, “Ключ - С”, АСТ, 1997.

25.Носов Н.Н. Витя Малеев в школе и дома//Собрание сочинений в трех томах, Т.1., М.:”ОНИКС”, 1998.

26.Остер Г.Б. Задачник: Ненаглядное пособие по математике. - М.: РОСМЭН, 1998.

27.Перельман Я. И., Занимательная алгебра, «Триада-литература», М., 1994.

28.Пойа Д. Математика и правдоподобные рассуждения, 1975.

29.Рожков В.И. Сборник задач математических олимпиад. - М.,1987.

30.Совайленко В.К. Лебедева О.В. Математика 6 класс: Учебник для учащихся средней школы - Ростов н/Д: Феникс, 1995.

31.Самусенко А. В., Казаченок В. В., Математика: типичные ошибки абитуриентов, «Вышейшая школа», Минск, 1995.

32.Сидоров Ю. В.., Федорюк М. В., Шабунин М. И., Лекции по теории функций комплексного переменного, - М.: Наука, 1989.

33.Соколова Г.И., Принципы и способы организации учебного исследования на уроках, - Самара. 2001.

34.Теоретические основы процесса обучения в советской школе. Под. Ред. Краевского В.В., Лернева И.Я. - М,: Педагогика,1989.

35.Трегонин В. А. И др., Задачи и упражнения по функциональному анализу, - М.: Наука, 1984.

36.Фильчаков П. Ф., Справочник по высшей математике, «Науковыдумка», Киев, 1973.

37.Фридман Л. М., Турецкий Е. Н., Как научиться решать задачи, - М., Просвещение, 1984.

38.Цих А. К., Введение в специальность «математика»: учебное пособие, Красноярск, 1997.

39.Яковлева О. В. О курсе алгебры в развивающем обучении // Педагогика развития: Проблемы современного детства и задачи школы: Материалы III науч.-практ. конф. Ч.2. Красноярск, 1996.

Приложение 1

 

Тексты описывающие “ход исследования”, опробованные в 6-ом классе

 

Признак делимости на 7

Задача1. Вывести признак делимости на 7.

Так как задача общая, уточним систему счисления, в которой будем решать задачу. Например, возьмем системы счисления по основанию 7 и 14.

Задача 2. Вывести признак делимости на 7 в 7-ной и 14-ной системах счисления.

Задачу решали три ученика: младший школьник, ваш ровесник и старшеклассник.

 

Рассуждение младшего школьника

Выпишу все двузначные числа в 7-ной системе счисления. Это числа:10₇, 11₇, 12₇, 13₇, 14₇, 15₇, 16₇, 20₇, 21₇, 22₇, 23₇, 24₇, 25₇, 26₇, 30₇, 31₇, 32₇, 33₇, 34₇, 35₇, 36₇, 40₇, 41₇, 42₇, 43₇, 44₇, 45₇, 46₇, 50₇, 51₇, 52₇, 53₇, 54₇, 55₇, 56₇, 60₇, 61₇, 62₇, 63₇, 64₇, 65₇, 66₇.

Возьму и выпишу из них все двузначные числа, делящиеся на 7. Это числа:10₇, 20₇, 30₇, 40₇, 50₇, 60₇.

Вижу, что на 7 в 7-ной системе счисления делятся двузначные числа, оканчивающиеся на 0.

Так же возьму и выпишу все однозначные и двузначные числа в 14-ной системе счисления делящиеся на 7.

₁₄, 10₁₄, 17₁₄, 20₁₄, 27₁₄, 30₁₄, 37₁₄, 40₁₄, 47₁₄, 50₁₄, 57₁₄, 60₁₄, 67₁₄, 70₁₄, 77₁₄, 80₁₄, 87₁₄, 90₁₄, 97₁₄.

Вижу, что на 7 в 14-ной системе счисления делятся двузначные числа, оканчивающиеся на 0 и 7.

Я перебрал все числа, поэтому делаю вывод, что:

) На 7 в 7-ной системе счисления делятся двузначные числа, оканчивающиеся на 0.

) на 7 в 14-ной системе счисления делятся двузначные числа, оканчивающиеся на 0 и 7.

Рассуждение ровесника

Требуется найти признак делимости на 7 в 7-ичной и 14-ной системе счисления.

Может мне удастся подметить закономерность в записи чисел делящихся на 7 в 7-ной и 14-ной системах счисления.

Выберу произвольно несколько чисел из этих систем счисления. Например, числа: 365₇; 250₇; 160₇; 520₇; 437₁₄; 793₁₄; 340₁₄; 347₁₄; 874₁₄.

Переведя числа в десятичную систему счисления и поделив на 7, я обнаружил, что на 7 делятся следующие числа:

₇ ; 160₇; 520₇; 437₁₄ ; 340₁₄; 347₁₄.

Как увидеть закономерность? На что смотреть?

В случае признака делимости на 9 в десятичной системе счисления смотрели, например, на сумму цифр числа. Посмотрю и здесь.

250₇             2+5+0=7:7

₇                   1+6+0=7:7

₇             5+2+0=7:7

₁₄                4+3+7=14:7

₁₄            3+4+0=7:7

₁₄                3+4+7=14:7

Вижу, что сумма цифр числа всегда делится на 7.

Мне кажется верным предположение: на 7 в 7-ной и 14-ной системах счисления делятся те числа, сумма цифр, в записи которых делится на 7. Для чисел 250₇; 160₇; 520₇; 437₁₄; 340₁₄; 347₁₄ мое предположение верно. Но верно ли оно для любого числа?

Переставлю цифры в числе 437₁₄ (от этого сумма цифр не изменится) и получу число 743_14.. Сумма цифр этого числа делится на 7, но само число не делится на 7. Это можно проверить переводом числа из 14-ной системы счисления в 10-ную и делением на 7.

Следовательно, мое предположение для любого числа неверно и нужно искать другую закономерность.

Еще в случае признаков делимости на 2 и 5 в 10-ной системе счисления смотрели на последнюю цифру числа. Посмотрю и здесь.

Вижу, что на 7 в 7-ной и 14-ной системах счисления делятся числа оканчивающиеся на 0 или 7.

Сделаю предположение: на 7 в 7-ной и 14-ной системах счисления делятся числа, оканчивающиеся на 0 или 7.

Предположение опровергнуть мне не удалось, поэтому я думаю, что оно верно для любых чисел в 7-ной и 14-ной системах счисления.

 

Рассуждение старшеклассника

Рассмотрю два числа: 43714 и 74314. Представлю эти числа как сумму трех слагаемых при помощи позиционной записи числа: 43714=4.142+3.14+7 74314=7.142+4.14+3. Замечу, что любое трехзначное число в 14-ной системе счисления можно записать в виде:  a2a1a0 14 =a2. 142+a1.14+a0. Мне известно свойство делимости суммы: Если каждое слагаемое суммы делится на 7, то сумма делится на 7. Из того, что 14 делится на 7, следует, что сумма первых двух слагаемых всегда будет делиться на 7. Для того, чтобы вся сумма делилась на 7 необходимо, чтобы последнее слагаемое этой суммы делилось на 7.  А последнее слагаемое в сумме a2. 142+a1.14+a0 - это последняя цифра в записи числа a2a1a0 14.     Использовали  Свойство делимости суммы: Дано G+C+D/ GK; CK; DK

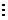(G+C+D)K

Определение отношения делимости

Вывод: Число a₂a₁a_{0 14} в 14-ной системе счисления кратно 7, если последняя цифра в его записи 7 или 0.

Тогда 437₁₄ -кратно, а 743₁₄ -не кратно.

Утверждение 1.

Любое трехзначное число в 14-ичной системе счисления делится на 7 в том и только в том случае, когда последняя цифра этого числа делится на 7.

Замечание 1. Если для делимости необходимо, чтобы последняя цифра (разряд единиц) делилась на 7, то не важно, сколько разрядов будет иметь число. Их может быть n.

Замечание 2. Число a_n^. 14ⁿ+…+a₁^.14+a₀

делится на 7, т.к. 14 делится на 7. Если в утверждении 1 вместо 14 взять основание 7 или 28, или другие числа, делящиеся на 7, то получится также справедливое утверждение:

Утверждение 2.

Пусть число А записано в системе счисления, основание которой делится на 7. Тогда число А делится на 7 в том и только в том случае, когда его последняя цифра делится на 7.

Результат моего исследования можно представить в виде теоремы.

Теорема: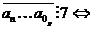

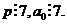
Доказательство.

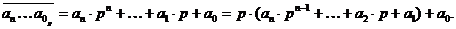
Последняя сумма делится на 7р7,а₀7. Теорема доказана.

Приложение 2

Тексты описывающие “ход исследования”, опробованные в Школе молодого ученого.

Признак делимости на 7

Задача1. Вывести признак делимости на 7.

Так как задача общая, уточним систему счисления, в которой будем решать задачу. Например, возьмем системы счисления по основанию 7 и 14.

Задача 2. Вывести признак делимости на 7 в 7-ной и 14-ной системах счисления.

Задачу решали три ученика: младший школьник, ваш ровесник и старшеклассник.

Рассуждение 1

Выпишу все двузначные числа в 7-ной системе счисления. Это числа:10₇, 11₇, 12₇, 13₇, 14₇, 15₇, 16₇, 20₇, 21₇, 22₇, 23₇, 24₇, 25₇, 26₇, 30₇, 31₇, 32₇, 33₇, 34₇, 35₇, 36₇, 40₇, 41₇, 42₇, 43₇, 44₇, 45₇, 46₇, 50₇, 51₇, 52₇, 53₇, 54₇, 55₇, 56₇, 60₇, 61₇, 62₇, 63₇, 64₇, 65₇, 66₇.

Возьму и выпишу из них все двузначные числа, делящиеся на 7. Это числа:10₇, 20₇, 30₇, 40₇, 50₇, 60₇.

Вижу, что на 7 в 7-ной системе счисления делятся двузначные числа, оканчивающиеся на 0.

Так же возьму и выпишу все однозначные и двузначные числа в 14-ной системе счисления делящиеся на 7.

₁₄, 10₁₄, 17₁₄, 20₁₄, 27₁₄, 30₁₄, 37₁₄, 40₁₄, 47₁₄, 50₁₄, 57₁₄, 60₁₄, 67₁₄, 70₁₄, 77₁₄, 80₁₄, 87₁₄, 90₁₄, 97₁₄.

Вижу, что на 7 в 14-ной системе счисления делятся двузначные числа, оканчивающиеся на 0 и 7.

Я перебрал все числа, поэтому делаю вывод, что:

) На 7 в 7-ной системе счисления делятся двузначные числа, оканчивающиеся на 0.

) на 7 в 14-ной системе счисления делятся двузначные числа, оканчивающиеся на 0 и 7.

Рассуждение 2

Требуется найти признак делимости на 7 в 7-ичной и 14-ной системе счисления. Может мне удастся подметить закономерность в записи чисел делящихся на 7 в 7-ной и 14-ной системах счисления.

Выберу произвольно несколько чисел из этих систем счисления. Например, числа: 365₇; 250₇; 160₇; 520₇; 437₁₄; 793₁₄; 340₁₄; 347₁₄; 874₁₄. Переведя числа в десятичную систему счисления и поделив на 7, я обнаружил, что на 7 делятся следующие числа:

₇; 160₇; 520₇; 437₁₄; 340₁₄; 347₁₄.

Как увидеть закономерность? На что смотреть? В случае признака делимости на 9 в десятичной системе счисления смотрели, например, на сумму цифр числа. Посмотрю и здесь.

₇            2+5+0=7:7

₇            1+6+0=7:7

₇            5+2+0=7:7

₁₄                4+3+7=14:7

₁₄           3+4+0=7:7

₁₄               3+4+7=14:7

Вижу, что сумма цифр числа всегда делится на 7.

Мне кажется верным предположение: на 7 в 7-ной и 14-ной системах счисления делятся те числа, сумма цифр, в записи которых делится на 7. Для чисел 250₇; 160₇; 520₇; 437₁₄; 340₁₄; 347₁₄ мое предположение верно. Но верно ли оно для любого числа?

Переставлю цифры в числе 43714 (от этого сумма цифр не изменится) и получу число 74314.. Сумма цифр этого числа делится на 7, но само число не делится на 7. Это можно проверить переводом числа из 14-ной системы счисления в 10-ную и делением на 7.

Контрпример- это пример, опровергающий утверждение.

Следовательно, мое предположение для любого числа неверно и нужно искать другую закономерность.

Еще в случае признаков делимости на 2 и 5 в 10-ной системе счисления смотрели на последнюю цифру числа. Посмотрю и здесь. Вижу, что на 7 в 7-ной и 14-ной системах счисления делятся числа оканчивающиеся на 0 или 7.

Сделаю предположение: на 7 в 7-ной и 14-ной системах счисления делятся числа, оканчивающиеся на 0 или 7.

Предположение опровергнуть мне не удалось, поэтому я думаю, что оно верно для любых чисел в 7-ной и 14-ной системах счисления.

Рассуждение 3

Мне известно свойство делимости суммы: если каждое слагаемое суммы делится на 7, то сумма делится на 7. Попробую применить это свойство для вывода признака делимости на 7.

Рассмотрю два числа: 437₁₄ и 743₁₄. Представлю эти числа как сумму трех слагаемых при помощи позиционной записи числа:

437₁₄=4^.14²+3^.14+7

₁₄=7^.14²+4^.14+3.

Замечу, что любое трехзначное число a₂a₁a_{0 14} в 14-ной системе счисления можно записать в виде суммы трех слагаемых

a₂a₁a_{0 14} =a_2. 14²+a₁^.14+a₀

Из того, что 14 делится на 7, следует, что a_2. 14²+a₁^.14 всегда будет делиться на 7. Для того, чтобы вся сумма делилась на 7 нужно, чтобы последнее слагаемое этой суммы также делилось на 7. А последнее слагаемое в сумме a_2. 14²+a₁^.14+a₀ - это последняя цифра в записи числа a₂a₁a_{0 14.}

Можно сделать вывод, что число a₂a₁a_{0 14} в 14-ной системе счисления кратно 7, если последняя цифра в его записи 7 или 0.

Видно, что 437₁₄ -кратно, а 743₁₄ -не кратно семи.

Теперь я могу сформулировать верное утверждение:

Утверждение 1.Любое трехзначное число в 14-ичной системе счисления делится на 7 в том и только в том случае, когда последняя цифра этого числа делится на 7.

Просматривая еще раз свое решение, я заметил две вещи:

) если для делимости необходимо, чтобы последняя цифра (разряд единиц) делилась на 7, то не важно, сколько разрядов будет иметь число. Их может быть n;.

2) число a_n…a_{0 14} =a_n^. 14ⁿ+…+a₁^.14+a₀ делится на 7, т.к. 14 делится на 7. Вместо 14 взять числа 7 или 28, или другие числа, делящиеся на 7, и мой признак делимости остается справедливым.

Теперь я могу сформулировать верное утверждение:

Утверждение 2.

Пусть число А записано в системе счисления, основание которой делится на 7. Тогда число А делится на 7 в том и только в том случае, когда его последняя цифра делится на 7.

Я могу представить результат своего исследования в виде теоремы.

Теорема: Число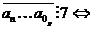

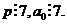
Доказательство. Верны равенства

 

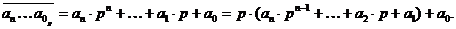
Из свойства делимости суммы следует, что последняя сумма делится на 7 тогда и только тогда, когда р Знак делится на 7 и 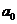 делится на 7.Теорема доказана.

Приложение 3

Карточки с заданиями для занятия 2 в Школе молодого ученого. Определить, истинны ли утверждения:

 

Приложение 4

Итоговый вариант текстов описывающих “ход исследования”.

Признак делимости на 7

При изучении признаков делимости возникает такой интересный вопрос: как выглядит признак делимости на 7 в разных системах счисления? Три ученика- младший школьник, ваш ровесник и старшеклассник изучали этот вопрос для чисел, записанных в системах счисления по основаниям 7 и 14.

Они решали такую задачу: Вывести признак делимости на 7 в 7-ной и 14-ной системах счисления.

 

! Прочитайте и изучите рассуждения этих учеников и ответьте на вопросы 1-24.

 

Рассуждение младшего школьника

Выпишу все двузначные числа в 7-ной системе счисления. Это числа:10₇, 11₇, 12₇, 13₇, 14₇, 15₇, 16₇, 20₇, 21₇, 22₇, 23₇, 24₇, 25₇, 26₇, 30₇, 31₇, 32₇, 33₇, 34₇, 35₇, 36₇, 40₇, 41₇, 42₇, 43₇, 44₇, 45₇, 46₇, 50₇, 51₇, 52₇, 53₇, 54₇, 55₇, 56₇, 60₇, 61₇, 62₇, 63₇, 64₇, 65₇, 66₇.

Возьму и выпишу из них все двузначные числа, делящиеся на 7. Это числа:10₇, 20₇, 30₇, 40₇, 50₇, 60₇.

Вижу, что на 7 в 7-ной системе счисления делятся двузначные числа, оканчивающиеся на 0.

Так же возьму и выпишу все однозначные и двузначные числа в 14-ной системе счисления, делящиеся на 7: 7₁₄, 10₁₄, 17₁₄, 20₁₄, 27₁₄, 30₁₄, 37₁₄, 40₁₄, 47₁₄, 50₁₄, 57₁₄, 60₁₄, 67₁₄, 70₁₄, 77₁₄, 80₁₄, 87₁₄, 90₁₄, 97₁₄. Чтобы разобрать остальные двузначные числа, я возьму и обозначу 10 буквой α, 11 буквой β, 12 буквой γ, 13 буквой δ. Тогда остальные числа запишутся: α0₁₄, α7₁₄, β0₁₄, β7₁₄, γ0₁₄, γ7₁₄, δ0₁₄, δ7₁₄.

Вижу, что на 7 в 14-ной системе счисления делятся двузначные числа, оканчивающиеся на 0 и 7.

Я перебрал все числа, поэтому делаю вывод, что:

) На 7 в 7-ной системе счисления делятся двузначные числа, оканчивающиеся на 0.

) на 7 в 14-ной системе счисления делятся двузначные числа, оканчивающиеся на 0 и 7.

1.Сколько двузначных чисел рассматривал школьник?

.Какую закономерность школьник увидел в записи чисел?

.Что позволило младшему школьнику сделать правильный вывод?

.Решил ли младший школьник задачу?

Рассуждение ровесника

Требуется найти признак делимости на 7 в 7-ичной и 14-ной системе счисления. Может мне удастся подметить закономерность в записи чисел делящихся на 7 в 7-ной и 14-ной системах счисления.

Выберу произвольно несколько чисел из этих систем счисления. Например, числа: 365₇ ; 250₇; 160₇; 520₇; 437₁₄; 793₁₄; 340₁₄; 347₁₄; 874₁₄. Переведя числа в десятичную систему счисления и поделив на 7, я обнаружил, что на 7 делятся следующие числа:

₇ ; 160₇; 520₇; 437₁₄ ; 340₁₄; 347₁₄.

Как увидеть закономерность? На что смотреть? В случае признака делимости на 9 в десятичной системе счисления смотрели, например, на сумму цифр числа. Посмотрю и здесь.

₇            2+5+0=7:7

₇                 1+6+0=7:7

₇            5+2+0=7:7

₁₄                4+3+7=14:7

₁₄           3+4+0=7:7

₁₄               3+4+7=14:7

Вижу, что сумма цифр числа всегда делится на 7.

Мне кажется верным предположение 1: на 7 в 7-ной и 14-ной системах счисления делятся те числа, сумма цифр, в записи которых делится на 7. Для чисел 250₇; 160₇; 520₇; 437₁₄; 340₁₄; 347₁₄ мое предположение верно. Но верно ли оно для любого числа?

Переставлю цифры в числе 43714 (от этого сумма цифр не изменится) и получу число 74314.. Сумма цифр этого числа делится на 7, но само число не делится на 7. Это можно проверить переводом числа из 14-ной системы счисления в 10-ную и делением на 7.

Контрпример- это пример, опровергающий утверждение.

Следовательно, мое предположение для любого числа неверно и нужно искать другую закономерность.

Еще в случае признаков делимости на 2 и 5 в 10-ной системе счисления смотрели на последнюю цифру числа. Посмотрю и здесь. Вижу, что на 7 в 7-ной и 14-ной системах счисления делятся числа оканчивающиеся на 0 или 7.

Сделаю предположение: на 7 в 7-ной и 14-ной системах счисления делятся числа, оканчивающиеся на 0 или 7.

Предположение опровергнуть мне не удалось, поэтому я думаю, что оно верно для любых чисел в 7-ной и 14-ной системах счисления.

5.Какие числа рассматривал ровесник?

.Почему из этих чисел он выбрал числа: 250₇; 160₇; 248₁₄; 520₇; 437₁₄; 340₁₄; 347₁₄ ?

.Какая закономерность была подмечена в записи чисел?

.Как проверялось, верна ли выделенная закономерность?

.Какие знания привлекались в рассуждении?

.Какое неверное предположение сделал ровесник? Как вы думаете, из-за чего это предположение оказалось неверным?

..Мог ли способ, используемый в рассуждении, привести к верному выводу? В каком случае?

.Какое верное утверждение сформулировал ровесник?

.Как вы думаете, сомневается ли ровесник в том, что его утверждение верно?

.Решил ли ровесник задачу?

Рассуждение старшеклассника

Мне известно свойство делимости суммы: если каждое слагаемое суммы делится на 7, то сумма делится на 7. Попробую применить это свойство для вывода признака делимости на 7.

Рассмотрю два числа: 437₁₄ и 743₁₄. Представлю эти числа как сумму трех слагаемых при помощи позиционной записи числа:

437₁₄=4^.14²+3^.14+7

₁₄=7^.14²+4^.14+3.

Замечу, что любое трехзначное число a₂a₁a_{0 14} в 14-ной системе счисления можно записать в виде суммы трех слагаемых

a₂a₁a_{0 14} =a_2. 14²+a₁^.14+a₀

Из того, что 14 делится на 7, следует, что a_2. 14²+a₁^.14 всегда будет делиться на 7. Для того, чтобы вся сумма делилась на 7 нужно, чтобы последнее слагаемое этой суммы также делилось на 7. А последнее слагаемое в суммеa_2. 14²+a₁^.14+a₀ - это последняя цифра в записи числа a₂a₁a_{0 14.}

Можно сделать вывод, что число a₂a₁a_{0 14} в 14-ной системе счисления кратно 7, если последняя цифра в его записи 7 или 0.

Видно, что 437₁₄ -кратно, а 743₁₄ -не кратно семи.

Теперь я могу сформулировать верное утверждение:

Утверждение 1. Любое трехзначное число в 14-ичной системе счисления делится на 7 в том и только в том случае, когда последняя цифра этого числа делится на 7.

Просматривая еще раз свое решение, я заметил две вещи:

) если для делимости необходимо, чтобы последняя цифра (разряд единиц) делилась на 7, то не важно, сколько разрядов будет иметь число. Их может быть n;.

2) число a_n…a_{0 14} =a_n^. 14ⁿ+…+a₁^.14+a₀ делится на 7, если , т.к. 14 делится на 7. Вместо 14 взять числа 7 или 28, или другие числа, делящиеся на 7, и мой признак делимости остается справедливым.

Теперь я могу сформулировать верное утверждение:

Утверждение 2.

Пусть число А записано в системе счисления, основание которой делится на 7. Тогда число А делится на 7 в том и только в том случае, когда его последняя цифра делится на 7.

Я могу представить результат своего исследования в виде теоремы.

Теорема: Число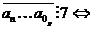

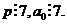
Доказательство. Верны равенства

 -

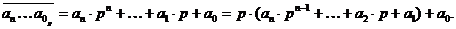Из свойства делимости суммы следует, что последняя сумма делится на 7 тогда и только тогда, когда р делится на 7 и  делится на 7.Теорема доказана. Знак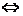заменяет слова “тогда и только тогда, когда”.

15.Что в этом рассуждении вам понятно, а что трудно понять?

. Каким свойством решил воспользоваться старшеклассник, чтобы вывести признак делимости на 7?

.Почему, оказалось, достаточно рассмотреть всего 2 числа?

. Что старшеклассник сделал с числами 437₁₄ и 743₁₄?

.Какая закономерность была подмечена старшеклассником в записи трехзначных чисел в 14-ной системе счисления?

. Как вы думаете, зачем старшекласснику понадобилось просматривать еще раз свое решение? Что при этом выяснилось?

. Мог ли способ рассуждения старшеклассника привести к неверному выводу? Почему?

. Какие верные утверждения сформулировал старшеклассник?

. Как вы думаете, сомневается ли старшеклассник в том, что его теорема верна?

. Решил ли старшеклассник задачу?

. Какие задачи решили младший школьник, старшеклассник, ровесник? Сформулируйте их.

. Решите аналогичную задачу, опишите свои рассуждения и сравните с рассуждениями школьников, которые вы изучили. Что вы обнаружили?

Приложение 5

Первоначальный вариант текстов “помощники”.

Приведение дробей к наименьшему общему знаменателю

Задание: Привести к наименьшему общему знаменателю дроби

Решение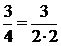

 

 

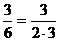
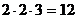
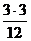
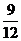 и 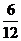Описание

Разложим знаменатели данных дробей на простые множители.

Найдем наименьший общий знаменатель. Общим множителем в знаменателях дробей является 2.

Наименьший общий знаменатель будет равен произведению общего множителя и остальных сомножителей знаменателей данных дробей.

Наименьший общий знаменатель дробей и будет равен 12.

Разделим наименьший общий знаменатель на знаменатели данных дробей, т.е. найдем для каждой дроби дополнительный множитель.

Умножим числитель каждой дроби на ее дополнительный множитель.

Получили дроби с одинаковыми знаменателями.

Сравнение дробей

Задание: Сравните дроби

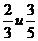
  Решение

НОЗ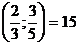

 

 

 

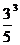
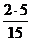
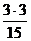
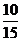
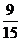
Описание

Приведем данные дроби к наименьшему общему знаменателю.

НОЗ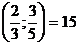

Разделим наименьший общий знаменатель на знаменатели данных дробей, т.е. найдем для каждой дроби дополнительный множитель.

Умножим числитель каждой дроби на ее дополнительный множитель.

Получим дроби

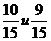
Теперь сравним полученные дроби.

Сложение дробей

Задание: Вычислить:

Решение 

НОЗ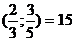

 

 

 

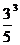
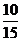
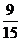
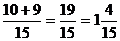Описание

Приведем данные дроби к наименьшему общему знаменателю

Разделим наименьший общий знаменатель на знаменатели данных дробей, т.е. найдем для каждой дроби дополнительные множители.

Умножим числитель каждой дроби на ее дополнительный множитель.

Получим дроби

Теперь сложим полученные дроби.

Приложение 6

Второй вариант текстов “помощники”

Таблица 1.

Как сложить отрицательные числа
Задание. Вычислить: -3+(-2)		Задание. Вычислить: 25+(-14)
Как решать:
Образец:		Сделай сам:
1.Найдем модули  данных чисел	|-3|=3 и |-2|=2	1.Найди модули  данных чисел	и
2.Сложим эти модули	|-3|+|-2|=3+2=5	2.Сложи эти модули
3.Перед полученным числом поставим  знак “минус”	-5	3.Перед полученным числом поставь знак “минус”
Что писать в тетради: -3+(-2)=(+)= - (3+2)= - 5Запиши:

Таблица 2

Как сложить отрицательное и положительное числа
Задание. Вычислить: 3+(-4)
Как решать:
1. Найдем модули данных чисел	|3|=3 и |-4|=4
2. Найдем больший модуль	|-4|=4 больше, чем |3|=3
3. Вычтем из большего модуля меньший	|-4|-|3|=4-3=1
4. Поставим перед суммой знак большего по модулю числа	-4 по модулю больше 3, значит, ставим знак “минус”.
Что писать в тетради: 3+(-4)=-(|-4|-|3|)= - (4+3)= - 1

 

Сложение чисел равных по модулю, противоположных по значению

Задание. Вычислить:

5+(-5)

Решение: При сложении равных по модулю чисел с разными знаками всегда получается ноль.