Использование современной компьютерной техники и программного обеспечения для решения прикладной задачи из инженерно-буровой практики
Министерство
образования и науки Российской Федерации
Федеральное
государственное бюджетное образовательное учреждение
высшего
профессионального образования
Санкт-Петербургский
государственный горный университет
КУРСОВАЯ
РАБОТА
По дисциплине
Математические методы в бурении
ПОЯСНИТЕЛЬНАЯ
ЗАПИСКА
Тема:
Использование современной компьютерной техники и программного обеспечения для
решения прикладной задачи из инженерно-буровой практики
Санкт-Петербург
2011
Аннотация
В разведочном бурении, при проведении опытов, всегда возникают
погрешности и дважды получить одинаковые результаты очень трудно. Для того,
чтобы учесть такие изменения при дальнейших расчетах, необходимо использовать
статистические методы.
Методы, которые используются в курсовой работе, позволяют отыскать
эффективное технологическое решение и обеспечивают достоверность и надежность
результатов исследования.
Цель данной работы изучить применение математических и статистических
методов в процессе бурения.
Оглавление
1. Определение основных
статистических оценок выборки
.1 Исходные данные
.2 Среднее арифметическое
выборки
.3 Дисперсия
.4 Среднеквадратическое
отклонение
.5 Коэффициент вариации V
.6 Отбраковка по критерию
Шовене
.7 Правило «трёх сигм»
.8 Интервальная оценка параметров
выборки
.9 Необходимое и достаточное
количество экспериментов
.11 Группировка данных
. Оценка значимости различий
двух выборок
.1 Исходные данные
.2 Основные статистические
параметры выборки
.3 Критерий Стьюдента
.4 Критерий Фишера
. Парный регрессионный анализ
.1 Исходные данные
.2 Аналитическое решение
задачи
.3 Начальные значения
. Множественный регрессионный
анализ
.1 Исходные данные
.2 Вычисление переменных
.3 Проверка зависимости
. Оценка влияния двух
реагентов на предельное напряжение сдвига бурового раствора
.1 Исходные данные
.2 Полный факторный
эксперимент и обработка его результатов
.3 Составление уравнения
регрессии
5.4 Оценка качества
эксперимента и уравнения регрессии
Вывод
Список литературы
1.
Определение основных статистических оценок выборки
1.1 Исходные данные
|
49,13
|
46,55
|
49,07
|
|
57,92
|
57,55
|
48,57
|
|
51,28
|
50,2
|
46,41
|
|
49,78
|
53,49
|
47,58
|
|
48,38
|
41,42
|
50,36
|
|
53,04
|
54,4
|
57,36
|
|
50,57
|
47,03
|
51,97
|
|
50,49
|
50,68
|
45,2
|
|
53,13
|
47,41
|
|
|
44,31
|
51,77
|
|
|
48,28
|
48,63
|
|
|
56,06
|
53,89
|
|
|
47,99
|
46,29
|
|
|
49,38
|
54,42
|
|
|
49,7
|
50,83
|
|
|
49,61
|
51,74
|
|
|
54,73
|
58,27
|
|
|
42,48
|
52,63
|
|
|
53,53
|
48,77
|
|
|
53,13
|
42,89
|
|
1.2 Среднее арифметическое выборки
Среднее значение - это среднеарифметическое из всех измеренных значений:
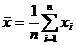 ,
,
где
 - значение случайной величины, n - количество
случайной величины;
- значение случайной величины, n - количество
случайной величины;

1.3 Дисперсия
Мерой отклонения случайной величины от средних значений служит дисперсия
и среднеквадратическое отклонение. Дисперсия - это число, равное среднему
квадрату отклонений значений случайной величины от её среднего значения:
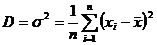 ,
,
где D - дисперсия.

.4 Среднеквадратическое отклонение
Среднеквадратическое отклонение - это число, равное квадратному корню из
дисперсии:
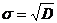

1.5 Коэффициент вариации V
На практике широко применяют также характеристику рассеяния, называемую
коэффициентом вариации V, который представляет собой отношение среднего
квадратичного отклонения к среднему значению. Коэффициент вариации показывает
насколько велико рассеяние по сравнению со средним значением случайной
величины. Коэффициент вариации выражается в долях единицы или в процентах.
Вычисление коэффициента вариации имеет смысл для положительных случайных
величин:


.6 Отбраковка по критерию Шовене
При проведение опытов при одинаковых условиях часто наблюдаются значения,
резко отличающиеся от остальных. Отбраковка таких значений производится с
помощью специальных методов. В работе мы использовали критерий Шовене.
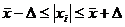 ,
,
где
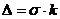 , k - коэффициент Шовене, для n=48 он равен 2,49.
, k - коэффициент Шовене, для n=48 он равен 2,49.
 , все
элементы выборки вошли в интервал.
, все
элементы выборки вошли в интервал.
1.7
Правило «трёх сигм»
Правило
«трёх сигм» основано на том, что случайная величина при нормальном законе
распределения практически полностью (на 99,7%) заключена в пределах от 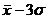 до
до 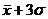 . Если
значение случайной величины отличается от среднего значения
. Если
значение случайной величины отличается от среднего значения 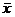 больше чем на 3
больше чем на 3 , то оно
является аномальным.
, то оно
является аномальным.
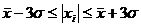
 , все
элементы выборки вошли в интервал.
, все
элементы выборки вошли в интервал.
.8 Интервальная оценка параметров выборки
Интервальная
оценка с принятой вероятностью p или уровнем значимости 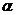 определяет диапазон, в котором будет находиться
истинное значение средней величины
определяет диапазон, в котором будет находиться
истинное значение средней величины
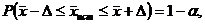
где
Р - это доверительная вероятность, α - уровень значимости
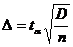 ,
,

=n-1,
где
k - степень свободы, 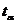 - критерий Стьюдента, для 48 равен 2,01 с α=0,05.
- критерий Стьюдента, для 48 равен 2,01 с α=0,05.
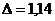
.9 Необходимое и достаточное количество экспериментов
Зависит от точности, которую нам нужно получить.


где
n - это количество экспериментов, которое у нас было.  =0,57
=0,57
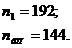
.10 Проверка закона распределения
Плотность вероятности:

Нормальный
закон распределения выполняется в том случае, если соблюдается два условия:
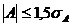
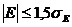
где
A - показатель ассиметрии (характеризует симметричность левой и правой ветвей
кривой), равный
 .
.
А=
-0,038
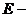 показатель
эксцесса (характеризует форму вершины кривой),
показатель
эксцесса (характеризует форму вершины кривой),
 ,
,
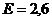
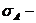 среднеквадратическое
отклонение ассиметрии нормального закона.
среднеквадратическое
отклонение ассиметрии нормального закона.
 ,
,
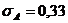
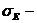 среднеквадратическое
отклонение эксцесса нормального распределения
среднеквадратическое
отклонение эксцесса нормального распределения
 ,
,
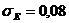
Оба
условия выполнены, следовательно, выборка подчиняется нормальному закону
распределения.
.11 Группировка данных
Весь диапазон данных разбивают на классы.

где
 - количество классов.
- количество классов. 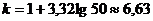 .
Результат округляем до целого. Размер каждого класса находим по формуле:
.
Результат округляем до целого. Размер каждого класса находим по формуле:

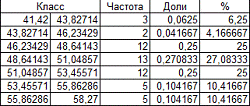

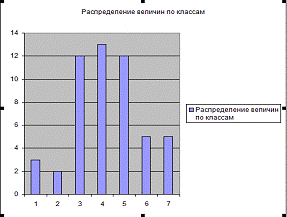
2. Оценка значимости различий двух выборок
.1 Исходные данные
|
21,42
|
14,52
|
|
24,39
|
15,56
|
|
19,27
|
17,84
|
|
18,14
|
14,81
|
|
20,66
|
16,69
|
|
20,98
|
14,83
|
|
23,09
|
18,96
|
|
21,87
|
17,80
|
|
25,25
|
14,35
|
|
21,01
|
15,28
|
|
19,90
|
14,57
|
|
21,72
|
10,20
|
|
23,84
|
20,56
|
|
22,11
|
17,84
|
|
26,65
|
15,02
|
|
22,76
|
18,38
|
|
20,31
|
16,14
|
|
22,02
|
17,00
|
|
23,51
|
17,53
|
|
19,95
|
12,50
|
|
20,09
|
17,77
|
|
22,91
|
15,21
|
|
24,62
|
16,21
|
|
24,65
|
17,48
|
|
21,24
|
13,38
|
|
24,98
|
14,54
|
|
25,75
|
15,24
|
|
19,60
|
19,04
|
|
20,36
|
16,48
|
|
19,93
|
15,05
|
|
18,41
|
11,93
|
|
22,64
|
17,46
|
|
24,48
|
15,86
|
|
18,68
|
14,33
|
|
23,33
|
14,38
|
|
20,09
|
12,75
|
|
27,35
|
16,03
|
|
24,41
|
18,34
|
|
14,75
|
13,48
|
|
24,43
|
15,62
|
|
18,38
|
19,71
|
|
25,35
|
17,87
|
|
18,65
|
17,77
|
|
22,17
|
17,22
|
.2 Основные статистические параметры выборки
1. Математическое ожидание
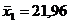

. Дисперсия
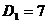
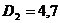
2. Среднеквадратическое отклонение
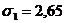

.3 Критерий Стьюдента
бурение математический статистический дисперсия
Для расчета абсолютной ошибки при малом количестве измерений вводится
специальный коэффициент, зависящий от надежности и числа измерений, называемый
коэффициентом Стьюдента tα.
Вычисляем экспериментальный коэффициент Стьюдента:
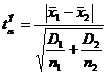 ,
,
где
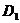 и
и  -
дисперсии выборок,
-
дисперсии выборок, 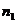 и
и 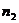 -
количество испытаний,
-
количество испытаний,  и
и 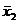 - среднее
значения выборок.
- среднее
значения выборок.
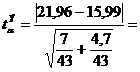 11,44,
11,44,
 ,
, .
.
Определяем
табличное значение коэффициента Стьюдента при 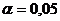 и
и  .
. 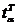 = 1,99.
= 1,99.
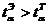 ;
11,44>1,99,
;
11,44>1,99,
Различие
коэффициентов существенно, следовательно, выборки не относится к одной
генеральной совокупности. Требуется дополнительное исследование с помощью
критерия Фишера.
.4 Критерий Фишера
Критерий Фишера применяется для проверки равенства дисперсий двух
выборок. Его относят к критериям рассеяния. Он основан на дополнительных
предположениях о независимости и нормальности выборок данных.
Вычисляем расчетное значение критерия Фишера:
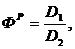
где
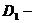 большее значение дисперсии.
большее значение дисперсии.
 ,
,
Для
определения табличного значения коэффициента Фишера рассчитываем число степеней
свободы:
 ;
;
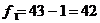 ;
;
 ;
;
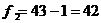 .
.
Табличное
значение для критерия Фишера при 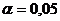 равно
1,6.
равно
1,6.
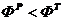 , 1,48,6.
Расчетное значение меньше табличного, следовательно, расхождение D
несущественно различны.
, 1,48,6.
Расчетное значение меньше табличного, следовательно, расхождение D
несущественно различны.
3.
Парный регрессионный анализ
3.1 Исходные данные
|
№
|
xi
|
yi
|
|
1
|
1
|
3
|
|
2
|
2
|
7
|
|
3
|
3
|
20,4
|
|
4
|
4
|
51,6
|
|
5
|
5
|
102,1
|
|
6
|
6
|
183,8
|
|
7
|
7
|
296,2
|
По исходным данным, методом линейной регрессии, определим вид
приближающей линии:
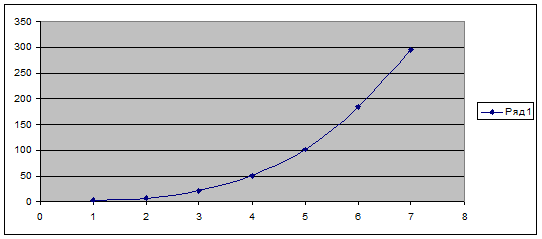
Полиномиальная линия тренда лучше остальных описывает зависимость
значений.
.2 Аналитическое решение задачи
График выражает нелинейную зависимость, следовательно, для обработки
данных будем использовать метод наименьших квадратов.
Необходимо найти формулу, выражающую таблично заданные значения. Для
этого составим и решим систему уравнений:
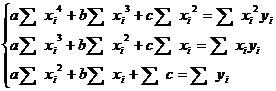
3.3 Начальные значения
|
№
|
x4i
|
x3i
|
x2i
|
xi
|
x2iyi
|
xiyi
|
yi
|
|
1
|
1,00
|
1,00
|
1,00
|
1,00
|
3
|
3
|
3
|
|
2
|
16,00
|
8,00
|
4,00
|
2,00
|
28
|
14
|
7
|
|
3
|
81,00
|
27,00
|
9,00
|
3,00
|
183,6
|
61,2
|
20,4
|
|
4
|
256,00
|
64,00
|
16,00
|
4,00
|
825,6
|
206,4
|
51,6
|
|
5
|
625,00
|
125,00
|
25,00
|
5,00
|
2552,6
|
510,5
|
102,1
|
1296,00
|
216,00
|
36,00
|
6,00
|
6616,8
|
1102,8
|
183,8
|
|
7
|
2401,00
|
343,00
|
49,00
|
7,00
|
14513,8
|
2073,4
|
296,2
|
|
сумма
|
4676,00
|
784,00
|
140,00
|
28,00
|
24723,3
|
3971,3
|
664,1
|
На основе табличных данных получим систему уравнений:
a+784b+140c = 24723
a+140b+28c = 3971
a+28b+7c = 664
Решив данную систему, получим=10.97=-40,8=38,7
Отсюда уравнение кривой будет иметь вид:= 10.97х2-40.8х+38.7
Сравнение фактических yi и теоретических yт
значений, рассчитанных по уравнению параболы, свидетельствует об
удовлетворительном их совпадении.
Для проверки построим линию тренда для исходного графика.

Можно сделать вывод, что найденное теоретически уравнение соответствует
набору исходных данных. Корреляционное отклонение близко к единице,
следовательно, параболическая зависимость хорошо аппроксимирует эмпирические данные.
4. Множественный регрессионный анализ
4.1 Исходные данные

4.2 Вычисление переменных
Процедуру вычисления коэффициентов множественной регрессии рассмотрим на
примере регрессии с двумя переменными:
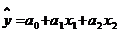 ,
,
Для
того, чтобы найти коэффициенты а0, а1 и а2 найдем
некоторые произведения.

Используя
данные таблицы можно вычислить коэффициенты а1 и а2 по
формулам:
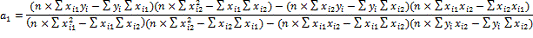
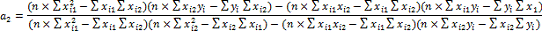
Подставив
известные значения в формулы и получим:
|
A1=
|
0,002192308
|
|
A2=
|
-0,002174958
|
Зная коэффициенты а1 и а2 а также средних значений
x1i , x2i и yi найдем значение коэффициента а0
по формуле:
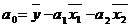 ,
,
.3 Проверка зависимости
Зная
значения коэффициентов а0, а1 и а2 можно найти
значений y` по формуле, в нашем случае 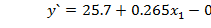 .
. 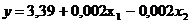

Различие
между экспериментальными и теоретическими данными невелико. Полученные данные
позволяет нам найти зависимость 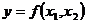 ,
,
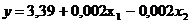
5. Оценка влияния двух реагентов на предельное напряжение
сдвига бурового раствора
5.1 Исходные данные
Факторный эксперимент связан с варьированием одновременно всех факторов с
проверкой достоверности результатов математико-статистическими методами. В этом
разделе производится оценка влияния концентраций двух химических реагентов CaCl2
и КССБ на величину предельного напряжения сдвига бурового раствора.
Пределы изменения концентраций реагентов:
. CaCl2: 0 - 2 %;
. КССБ: 1 - 3 %.
Проведено четыре эксперимента (N=4) по три опыта в каждом (n=3).
|
N
|
n
|
|
Y1
|
Y2
|
Y3
|
|
1
|
20
|
18
|
20
|
|
2
|
9
|
11
|
10
|
|
3
|
28
|
26
|
27
|
|
4
|
12
|
14
|
13
|
.2 Полный факторный эксперимент и обработка его результатов
Концентрации реагентов вычисляется по формулам:
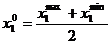
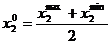 ,
,
где
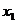 - концентрация хлорида кальция и
- концентрация хлорида кальция и  - концентрация КССБ.
- концентрация КССБ.
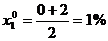

Интервал
варьирования факторов определяется по формулам:

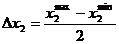

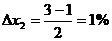
Матрица планирования с учетом взаимодействия факторов между собой
выглядит следующим образом:
Стандартная матрица планирования с учетом взаимодействия факторов
|
№
|
 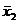 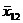 Y1Y2Y3 Y1Y2Y3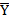 Si2 Si2
|
|
|
|
|
|
|
|
|
1
|
-1
|
-1
|
1
|
Y11
|
Y12
|
Y13
|
Y1
|
S12
|
|
2
|
-1
|
1
|
-1
|
Y21
|
Y22
|
Y23
|
Y2
|
S22
|
|
3
|
1
|
-1
|
-1
|
Y31
|
Y32
|
Y33
|
Y3
|
S32
|
|
4
|
1
|
1
|
1
|
Y41
|
Y42
|
Y43
|
Y4
|
S42
|
Si2- стандарт.
.3 Составление уравнения регрессии
Предположим, что под воздействием изменения концентраций химических
реагентов величина предельного напряжения сдвига изменяется прямо
пропорционально.
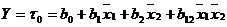 ,
,
Определим средние значения функции отклика по каждому из четырех
экспериментов, используя формулу:
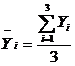 ;
;
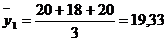
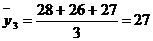

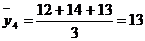
Расчет
коэффициентов уравнения регрессии выполняется по следующим формулам:
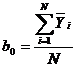 и
и 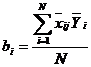 ;
;
где
b0 - свободный член уравнения;-количество экспериментов (N = 4).
Выполнив
вычисления по формуле, получаем:
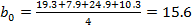


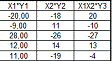

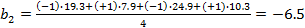
Уравнение
регрессии: 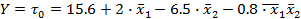
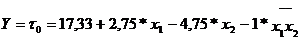
5.4 Оценка качества эксперимента и уравнения регрессии
Оценим значимость коэффициентов уравнения регрессии. Для этого определяем
дисперсию экспериментов по формуле:
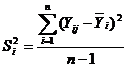 ;
;
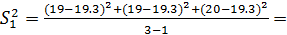
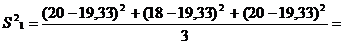 0,89
0,89

 0.67
0.67
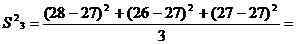
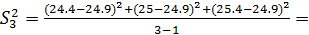 0.67
0.67
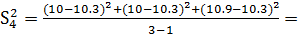
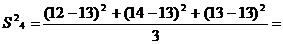 0.67
0.67
Средняя дисперсия:
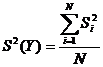
 ;
;
Далее оценивается адекватность уравнения регрессии в целом по критерию
Фишера:
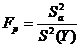 ,
,
где
 - остаточная дисперсия, оценивающая разброс расчетных
и опытных данных:
- остаточная дисперсия, оценивающая разброс расчетных
и опытных данных:
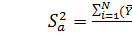
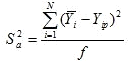 ,
,
-количество
факторов.
|
N
|
n
|
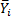
|
Yip
|
|
Y1
|
Y2
|
Y3
|
|
|
|
1
|
20
|
18
|
20
|
19,33
|
18,33333
|
|
2
|
9
|
11
|
10
|
10
|
9,83333
|
|
3
|
28
|
26
|
27
|
27
|
24,83333
|
|
4
|
12
|
14
|
13
|
13
|
15,33333
|
|
|
|
|
|
|
|
|
|
|
Находим =5,58. Расчетный критерий Фишера =5,15384
=5,58. Расчетный критерий Фишера =5,15384
Сравним
значение критерия Фишера с табличным, которое находится при двух степенях
свободы  =4,46.
=4,46.
Расчетное значение критерия Фишера меньше табличного, значит уравнение
регрессии адекватно.
Вывод
Для успешного решения ряда математических задач необходимо использование
вычислительной техники. Это позволяет повысить качество расчетов и намного ускорить
процесс работы.
В разведочном бурении, при проведении опытов, всегда возникают
погрешности и дважды получить одинаковые результаты очень трудно. Для того,
чтобы учесть такие изменения при дальнейших расчетах, необходимо использовать
статистические методы.
В работе были закреплены знания о статистическом анализе эксперимента:
нахождение среднеарифметического выборки, среднеквадратического отклонения,
дисперсии, коэффициента корреляции.
Проанализировав результаты статистическими методами, получили достоверную
оценку данных.
Список литературы
1. Ганджумян
Р.А. Математическая статистика в разведочном бурении. Справочное пособие.- М.:
Недра, 1990.- 218 с.
. Власов Г.П.
«Методы научных исследований и организации экспериментов». СПб. 2000-122с.