Математические вопросы теории надежности

Математические вопросы теории надежности

Министерство образования и науки РФ

Федеральное Агентство по образованию

ГОУ ПВО «Таганрогский государственный педагогический институт»

Курсовая работа

на тему:

Математические вопросы теории надежности

Выполнила: студентка ФМФ 43 гр.

Сыпко Галина Александровна.

Научный руководитель:

старший преподаватель,

кандидат технических наук

Драгныш Н.В.

Таганрог. 2010 г.

СОДЕРЖАНИЕ

Введение

. Количественная оценка надежности. Надежность элемента и надежность системы

. Потоки отказов, внезапные отказы. Возможности использования предельных теорем

. Наиболее распространенные потоки случайных событий и их характеристики

. Выбор закона распределения отказов при расчетах надежности

. Расчет надежности, основанный на составлении графа переходов изделия в различные состояния работоспособности

Заключение

Литература

ВВЕДЕНИЕ

Внимание к теории надежности непрерывно возрастает во всем мире. Проблема надежности является ключевой проблемой в развитии техники на протяжении многих лет. Вопросами повышения надежности продукции начинают интересоваться не только отдельные инженеры и ученые, но и государственные деятели, организаторы пауки, а также специалисты многих областей знания-врачи, астрономы, физики и биологи. И этот интерес не случаен, так как он вызван к жизни всем устремлением современной науки и техники, в силу которого для управления различного рода процессами и для научного исследования все шире используются механизмы и электронные устройства.

Ответственность функций, поручаемых аппаратуре, возрастает, а вместе с этим возрастает и сложность этих устройств. Выработка критериев экономической эффективности продукции и разыскание оптимальных путей организации производства могут и должны стать центральными задачами теории надежности. При возрастающей важности функций, выполняемых электронными приборами и автоматическими системами, остро встает проблема обеспечения их надежности- Недопустимо, чтобы в устройствах, насчитывающих многие тысячи электронных и механических элементов, выход из строя одного или даже нескольких элементов вызвал нарушение процесса работы. Это ставит серьезные задачи по повышению надежности элементов. Но еще более важно создать такие методы построения сложных комплексов, которые обеспечивали бы надежную работу даже при выходе из строя отдельных элементов, подобно тому как отдельные повреждения в живом организме не нарушают его нормальной деятельности. B этих направлениях уже предложен ряд принципов, но стоит задача создания теоретических основ обеспечения надежности. Одной из таких задач является расчет надежности системы.

Расчет надежности систем производится несколькими способами:

) расчет надежности, основанный на использовании параллельно- последовательных систем;

) расчет, основанный на непосредственном использовании логических уравнений;

) расчет надежности, основанный на составлении графа переходов изделия в различные состояния работоспособности;

) расчет надежности, основанный на использовании производящих функций;

) расчет функциональной надежности.

Все эти способы имеют свои преимущества, но и имеются какие-либо минусы. Например, первый способ хорош, для вычисления надежности системы элементы, которой соединены последовательно и параллельно, данный метод сводится к расчету надежности каждого элемента, и дальнейшее суммирование и дает нам надежность всей системы, и этот способ является наипростейшим. Но в данном методе не учитывается то, что при параллельном соединении если один элемент не работает, то другие продолжают свою работу. Второй способ дает нам возможность преобразовать любую структуру надежности к параллельно- последовательной системе. Метод, основанный на составлении графа переходов, можно применять при различных вариантах расчета. С помощью этого метода производится расчет системы с учетом противодействующих процессов (отказ, восстановление). Метод, основанный на использовании производящих функций удобен в использовании в разных случаях, но он не учитывает противодействующие силы.

Из перечисленных выше методов расчета логико-вероятностный метод- наиболее универсальный для расчетов аппаратурной надежности. Отдавать предпочтение какому-либо из методов расчета можно только после внимательного изучения поставленной задачи.

1.КОЛИЧЕСТВЕННАЯ ОЦЕНКА НАДЕЖНОСТИ. НАДЕЖНОСТЬ ЭЛЕМЕНТА И НАДЕЖНОСТЬ СИСТЕМЫ

Основным исходным понятием теории надежности является надежность системы (элемента и др.). Под надежностью системы (элемента и т. п.) обычно понимают способность этой системы выполнять поставленную перед ней задачу при заданных требованиях на качество работы. Это чисто качественное понятие должно измеряться различными количественными показателями.

Под надежностью системы (как количественной характеристикой) принято понимать вероятность безотказной ее работы в течение заданного интервала времени. Такой узкий подход к понятию надежности в ряде случаев недостаточен. Поэтому в некоторых работах, например, предлагаются «более общие» термины: эффективность и др. [2]

Заметим, что при том многообразии требований, с которым приходится сталкиваться на практике, нередко нужно характеризовать надежность изделий посредством то одного, то другого показателя. Так, в одних случаях может потребоваться, чтобы возможно большей была долговечность изделия, в других - максимальная вероятность безотказной работы в течение заданного промежутка T, а в-третьих, чтобы средняя длительность безотказной работы была максимально большой. Может возникнуть необходимость достижения максимальной величины сразу нескольких характеристик. Иногда эти требования могут оказаться и взаимно противоречивыми. Тогда следует добиться оптимального в каком-то определенном смысле решения. Выбор понятия оптимальности при этом всецело определяется назначением того устройства, которое подвергается исследованию.

Рассмотрим общий путь построения математической модели изучения надежности некоторой системы C. Каждое состояние системы С мы считаем элементом x множества возможных ее состояний.

Разным, с точки зрения надежности, состояниям системы соответствуют различные точки x. Совокупность всех состояний x образует фазовое пространство состояний системы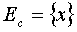  

С течением времени некоторые элементы, составляющие систему, либо выходят из строя, либо меняются параметры, определяющие их работу, поэтому в разные моменты времени состояние системы описывается точками фазового пространства .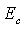

Если обозначить через x(t) состояние системы в момент t, то последовательное изменение состояний x(t) с течением времени t является, вообще говоря, случайным процессом, развивающимся в фазовом пространстве 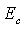. Случайный характер его объясняется случайным изменением параметров, определяющих работу элементов, и случайным характером отказов этих элементов. Самой элементарной иллюстрацией сказанного может служить следующий пример: пусть система может находиться только в конечном числе состояний, различающихся с точки зрения надежности 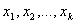 , которые и составляют фазовое пространство. Если предположить, что законы распределения длительности безотказной работы элементов и длительности их замены - показательны, то время пребывания в состоянии  до перехода в 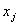, также имеет показательное распределение со средним временем пребывания . Случайный процесс x(t) в этом случае является цепью Маркова.

Итак, каждой физической системе С мы сопоставляем некоторое фазовое пространство 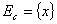 и описываем эволюцию системы во времени случайным процессом x(t). Различные количественные характеристики надежности строятся как математические ожидания от функционалов, заданных на траекториях процесса. Таким образом, если x(t) -траектория и 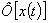 есть некоторый функционал. При надлежащем выборе функционала 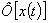 можно получить все известные числовые характеристики надежности. Так, например, если система отказывает (состояние x(t) входит в некоторое критическое подмножество К, являющееся частью фазового пространства 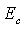), то рассматривая функцию

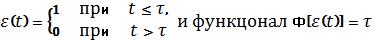
(τ-время первого попадания в подмножество К), получим, что вероятность безотказной работы в течение времени t равна:

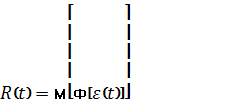
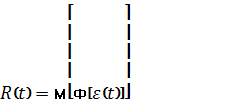(2)

Аналогичным образом можно получить и другие характеристики надежности. В ряде работ предлагается вводить в качестве показателя надежности функцию эффективности. Если каждое состояние х из фазового пространства 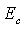 мы оцениваем некоторым числом f(x), то получающаяся при этом функция y = f(x) называется функцией эффективности.

Очень часто предполагают, что функция эффективности принимает только два значения 0 и 1. Средняя эффективность системы в момент t

 (3).

Заметим, что для различных систем или для одних и тех же систем, но находящихся в разных условиях использования, в качестве основных численных показателей надежности надо выбирать различные характеристики. В одних случаях, например в системах управления, особую роль играет вероятность безотказной их работы в течение заданного времени, в других случаях (линии связи без особо срочных сообщений) особую роль играет так называемый коэффициент готовности, равный средней доле времени, в течение которого система исправна.

В заключение этого параграфа необходимо отметить, что для систем характерно деление на блоки, которые в свою очередь состоят либо из более мелких блоков, либо из элементов (сопротивлений, конденсаторов и т. п.). Одной из основных задач теории надежности является такое конструирование систем, чтобы их надежность была не ниже, а даже выше надежностей отдельных составляющих ее блоков и элементов.

. ПОТОКИ ОТКАЗОВ, ВНЕЗАПНЫЕ ОТКАЗЫ. ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ПРЕДЕЛЬНЫХ ТЕОРЕМ

Предположим, что система может находиться только в двух состояниях: исправном и неисправном. Моменты 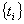 появления отказов аппаратуры являются, вообще говоря, случайными величинами. Случайную последовательность точек 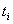 на прямой называют случайным потоком. Многие задачи теории надежности являются по существу задачами, связанными с изучением случайных потоков отказов. Например, вероятность безотказной работы в интервале (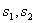) равна вероятности того, что на этот интервал не попадает ни одна точка 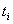. Следует заметить, что в теории вероятностей уже сравнительно давно занимаются изучением случайных потоков. Более полно о случайных потоках изложено в приложении.

Рассмотрим теперь схему процесса восстановления, представляющую значительный интерес для теории надежности. Предположим, что в начальный момент t=0 используется элемент, который работает безотказно до момента 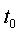, в момент 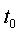 он мгновенно заменяется новым, который безотказно работает до момента 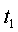 и т. д.

Моменты отказов 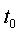,,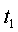 ,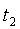... образуют случайную последовательность точек. При этом предполагается, что сроки службы отдельных элементов, т. е. 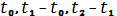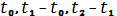,… являются взаимно независимыми случайными величинами, 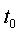имеет функцию распределения 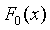, а все остальные разности  одинаково распределены с функцией распределения F(x). Эта, казалось бы, весьма частная схема находит себе многочисленные применения, в том числе и в теории надежности.

В теории надежности естественное приложение находят предельные теоремы типа суммирования взаимно независимых случайных величин.

Система, как правило, состоит из большого числа N элементов. Если моменты отказов i -гo элемента,(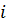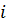=1,N) образуют случайный поток  то поток отказов всей аппаратуры будет представлять собой объединение потоков отказов отдельных элементов.

Еще в телефонии было давно замечено, что поток вызовов, поступающих на телефонную станцию, является близким к пуассоновскому. Первая попытка нестрогого обоснования была дана Пальмом, затем строгое доказательство этого факта при весьма широких условиях было получено А. Я. Хинчиными [1].

В указанной выше предельной теореме Пальма-Хинчина-Ососкова рассматривается лишь стационарный случай. Однако ее можно обобщить и на нестационарный случай. Особый интерес здесь представляет выяснение степени приближения к пуассоновскому потоку при росте числа элементов системы.

Итак, в системах, состоящих из большого числа относительно надежных элементов, поток отказов с большой степенью приближения можно считать пуассоновским.

Само понятие отказа не является простым. Не всегда ясно, отказала система или еще продолжает исправно работать. Дело в том, что работа системы определяется значениями параметров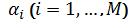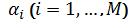, которые могут меняться различным образом.

В случае так называемых внезапных отказов один из параметров меняется скачком за допустимые пределы (замыкание или обрыв). В случае постепенных отказов параметр медленно «плывет» за допустимые границы. Оказывается, что момент наступления постепенного отказа имеет в ряде случаев распределение, близкое к нормальному.

В некоторых работах исследуется модель отказов, основанная на анализе прочности и усилия. Предположим, что изделие характеризуется прочностью ξ а усилие, прилагаемое к нему при использовании равно . Обе величины ξ и 𝜂 случайны. Под надежностью естественно понимать 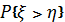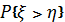. В такой ситуации оценка надежности сводится к оценке параметров распределений ξ и 𝜂.Случайный вектор (ξ,𝜂) обладает нормальным распределением.

Наконец, естественно еще выделить так называемые сбои, или перемежающиеся отказы. Сбой - это такой отказ, который возникает и исчезает случайным образом без всякого внешнего воздействия. Сбои являются одним из самых характерных типов отказов, возникающих в электронных вычислительных машинах.

. НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ ПОТОКИ СЛУЧАЙНЫХ СОБЫТИЙ И ИХ ХАРАКТЕРИСТИКИ

В теории надежности и практике ее исследования наибольшее распространение имеют следующие потоки случайных событий: а) простейший (стационарный пуассоновский поток); б) Эрланга κ-го порядка.[3]

Простейший поток.

Простейший поток событий - поток, обладающий свойствами ординарности, стационарности и отсутствием последствия.

Ординарный поток имеет место, если вероятность двух и более событий на элементарном отрезке времени пренебрежимо мала по сравнению с вероятностью одного события (события редки).

Если интервалы являются неслучайными, то поток называется регулярным или детерминированным и полностью характеризуется законом изменения длины интервалов в потоке. В противном случае поток называется случайным и характеризуется совместным законом распределения системы случайных величин (, ,, ..., ,).

На практике наиболее часто приходится иметь дело с потоками, в которых интервалы времени между двумя соседними событиями ,(i=1,…,n) - непрерывные случайные величины. Такой случайный поток характеризуется многомерной плотностью вероятности

Отсутствие последствия означает, что события возникают независимо друг от друга. Число событий, попадающих на некоторый участок времени, не зависит от того, сколько таких событий произошло на других участках времени.

Простейший поток называется также стационарным пуассоновским потоком. Если параметр потока λ не постоянен, а меняется по некоторому закону 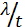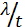, то поток называется нестационарным пуассоновским потоком.

Простейший поток широко распространен в теории надежности по следующим причинам: а) отказы в современных устройствах, даже достаточно сложных- события редкие и потому поток их может быть отнесен к разряду ординарных; б) плотность отказов сложного устройства в нормальном режиме эксплуатации постоянна (в этом режиме не возникают еще, как правило, износовые отказы с нарастанием интенсивности); в) отказы устройства представляют собой суммирование воздействий отказов элементов устройства, которые, как правило, независимы, многочисленны и примерно одинаковы по степени влияния на надежность устройства. При этих условиях возникает стационарный результирующий поток отказов устройства, обладающий свойством отсутствия последействия.

Для простейшего потока отказов справедливы следующие свойства:

)вероятность того, что за время τ произойдет m событий, определяется равенством

,

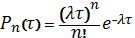
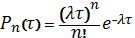где λ-интенсивность случайного события (закон Пуассона).

)время между двумя событиями, подчиняется показательному закону распределения;

)среднее число событий за время τ равно α=λτ;

4) вероятность того, что за время τ не произойдет ни одного события,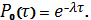

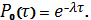
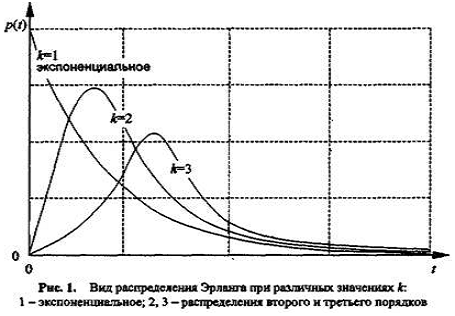
Потоки Эрланга.

Нарушение условий стационарности, или наличие последствия, приводит к тому, что поток становится непростейшим. К непростейшим потокам относятся, например, потоки Эрланга различного порядка, которые возникают при ‹‹просеивании›› простейшего потока отказов. Поток Эрланга го порядка- поток получающийся в результате сохранения каждого κ-го события в простейшем потоке. При κ=1 поток Эрланга простейший. С увеличением κ возрастает последействие. При κ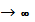 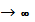поток приближается к регулярному потоку с постоянным интервалом между событиями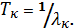

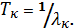
Дифференциальный закон распределения потока Эрланга следующий:

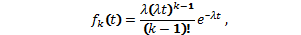
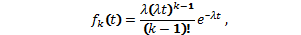(1)

где λ-интенсивность простейшего исходного потока.

Интенсивность отказов потока Эрланга

Математическое ожидание времени между событиями

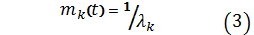
Дисперсия времени между событиями

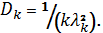
Уравнения (2) и (3) позволяют заменять любые производительные функции распределения на эквивалентные им функции распределения Эрланга, если известны средние значения и дисперсия времени между событиями для произвольных функций распределения.

Пример. Определить характер потока отказов и вид функции распределения времени работы до отказа, если среднее время между отказами 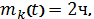 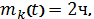дисперсия

Решение

.

.

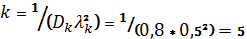
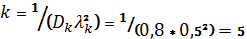
Поток эквивалентен потоку Эрланга 5-го порядка. Его функция распределения

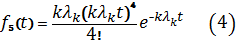
4. ВЫБОР ЗАКОНА РАСПРЕДЕЛЕНИЯ ОТКАЗОВ ПРИ РАСЧЕТАХ НАДЕЖНОСТИ

Определение закона распределения отказов имеет большое значение при исследованиях и оценках надежности. Определение P(t) по одной и той же исходной информации о T, но при различных предложениях о законе распределения может привести к существенно отличающимся результатам.

Закон распределения отказов можно определить по экспериментальным данным, но для этого необходимо проведение большого числа опытов в идентичных условиях. Практически эти условия, как правило, трудно обеспечить. Кроме того, такое решение содержит черты пассивной регистрации событий.

Более рационально - изучение условий, при которых возникает то или другое распределение. При этом составляются модели возникновения отказов и соответствующие им законы распределения времени до появления отказа, что позволяет делать обоснованные предположения о законе распределения.

Рассмотрим наиболее распространенные законы распределения.

).Биноминальный закон распределения числа k появления распределения А в n независимых опытах.[4] Если вероятность появления события А в одном испытании равна p, вероятность не появления события А равна q=1-p; число независимых испытаний равно m, то вероятность появления n событий в испытаниях будет

Свойства распределения:

.        Число событий k- целое положительное число;

.        Математическое ожидание числа событий равно np;

.        Дисперсия равна npq;

.        Среднеквадратичное отклонение числа событий

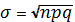
2).Закон Пуассона - распределения чисел 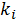 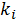случайного события за время τ. [5] Вероятность возникновения случайного события k раз за время τ

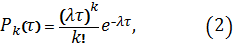
Свойства распределения следующие:

1.       Математическое ожидание числа событий за время τ равно λτ:

2.       Среднеквадратичное отклонение числа событий

.

Характерный признак распределения Пуассона - равенство математического ожидания и дисперсии. Закон Пуассона используется тогда, когда необходимо определить вероятность того, что в изделии за данное время произойдет один, два, три и т.д. отказов.

) Нормальное распределение случайной величины. Нормальное распределение случайной величины Х возникает всякий раз, когда Х зависит от большого числа однородных по своему влиянию случайных факторов, причем влияние каждого из этих факторов по сравнению с совокупностью всех остальных незначительно. Это условие характерно для времени возникновения отказа, вызванного износами, старением. Плотность отказа этого распределения

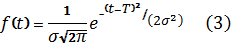
Вероятность отказа за время t

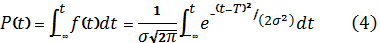
Значение функции распределения определяется формулой

Вероятность отсутствие отказа за время t

P(t)=1-Q(t)=0,5-Ф

. РАСЧЕТ НАДЕЖНОСТИ, ОСНОВАННЫЙ НА СОСТАВЛЕНИИ ГРАФА ПЕРЕХОДОВ ИЗДЕЛИЯ В РАЗЛИЧНЫЕ СОСТОЯНИЯ РАБОТОСПОСОБНОСТИ

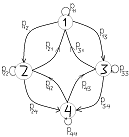
Рис.2. Граф переходов изделия в возможные его состояния

В практике исследования надежности имеют место случайные процессы, т.е. процессы перехода изделия из одного состояния в другое. Поток событий- совокупность переходов. Наиболее подходящий способ представления переходов в различные состояния - граф переходов. [3] В качестве примера на рис 2 представлен граф переходов для следующих условий.

Система, состоящая из двух подсистем, может находиться в следующих состояниях:

) все части системы исправны;

2) подсистема 1 отказала и поставлена на ремонт (вероятность ее отказа равна 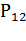, вероятность восстановления равна
);

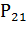) подсистема 2 отказала и поставлена на ремонт (вероятность ее отказа равна 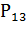, вероятность восстановления равна);

) отказ подсистем 1 и 2, т.е. отказ системы.

Вероятность перехода из второго состояния в четвертое ; вероятность перехода из третьего состояния в четвертое 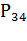; Вероятность перехода системы из четвертого состояния в третье 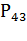, а из четвертого во второе . Вероятность того, что система остается в некотором i-м состоянии, обозначаются .

Граф переходов может быть представлен либо матрицей переходов, либо системой уравнений.

Матрица перехода для графа, изображенного на рисунке 2, имеет следующий вид:

Первое уравнение системы читается следующим образом: вероятность того, что система за время (t+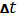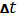) не выйдет из первого состояния, равна произведению вероятности того, что система находилась в момент времени t в первом состоянии и не перейдет из него за время ∆t во второе и третье состояния, плюс вероятности того, что система находилась во втором или третьем состоянии и перейдет из них в первое состояние.

Если вероятности отказов и вероятности восстановления заданы в виде функций интенсивностей, тогда с достаточной для практических целей точностью можно принять

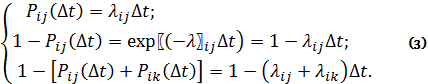
Если в каждом из этих уравнений 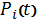 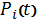перенести в левую часть уравнения и учесть, что

то (4) перепишется следующим образом:

Решение (5) можно осуществить, использовав преобразование Лапласа, позволяющее преобразовать систему дифференциальных уравнений.

Существует следующее правило, позволяющее записывать уравнения непосредственно по графу состояния: в левой части уравнения записать 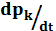 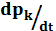(где -вероятность k-го состояния) и в правой части столько членов, сколько стрелок связано с данным состоянием. Если стрелка направлена в данное состояние, то ставится плюс, если из данного состояния- минус. Каждый член равен плотности вероятности потока событий λ, переводящего систему по данной стрелке, умноженной на вероятность того состояния, из которого исходит стрелка.

Пример. Требуется рассчитать надежность устройства, схема которого изображена на рис. 3.

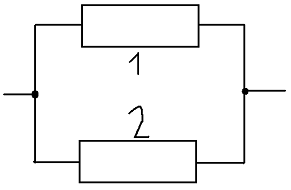
Вероятность безотказного состояния каждого из элементов за t=100ч равна 0,9.Определить вероятность безотказного состояния устройства за t=100ч.

Решение

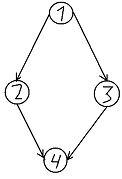
1. Составляем перечень возможных событий: состояние первое - элементы 1 и 2 исправны; состояние второе - элемент 1 отказал, элемент 2 работает, состояние третье- элемент 2 отказал, элемент 1 работает, состояние четвертое- отказали элементы 1 и 2.

. Определяем интенсивности переходов:

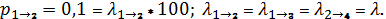
. Составляем граф переходов (рис. 4)

. Составляем систему дифференциальных уравнений для работоспособных состояний:

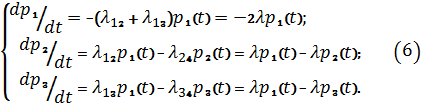
. Решаем систему (6) операторным методом:

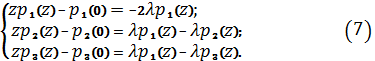
Учитывая, что 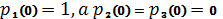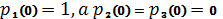, из (7) получим:

Решение системы (8) будет следующим:

Перейдем от 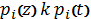 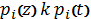в соответствии с уравнениями перехода

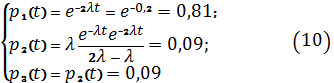
Вероятность безотказного состояния устройства

Р=0,81+0,09+0,09=0,99.

Этот результат можно было получить по формуле для параллельной структуры:

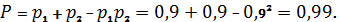
Метод, основанный на составлении графа переходов, можно применять при различных вариантах расчета. Его преимущества заметны тогда когда производится расчет системы с учетом противодействующих процессов (отказ и восстановление). При этом он становится практически единственно возможным методом.

ЗАКЛЮЧЕНИЕ

надежность теорема граф поток случайный

В данной работе был рассмотрен только один метод расчета надежности системы. Этого недостаточно для решения некоторых задач, т.к. существуют и более простые методы расчетов, знание их намного упрощает решение задач связанных с теорией надежности. В дальнейшей работе будет рассмотрено большее количество методов для расчета надежности систем. И показано на примерах их применение.

ЛИТЕРАТУРА

. Хинчин А.Я., Математические методы теории массового обслуживания. Тр. Матем. ин-та АН СССР, 1955, 49, 122 (РЖМат, 1957, 5032)

. Гнеденко Б.В., Беляев Ю.К., Соловьев А.Д., Математические методы в теории надежности, М. „Наука", 1965.

3. Голинкевич Т.А. Прикладная теория надежности. Учебник для вузов. М., «Высшая школа», 1977г.

. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов/ В.Е. Гмурман- 8е изд., стер. - М.: Высш. Шк., 2003.

. Вентцель Е.С. Теория вероятностей, М.: Наука, 1969.

.Надежность и диагностика технологических систем КГТУ им АН Туполева г. Казань Для студентов заочной формы обучения. Методическое пособие.

7.<http://www.obzh.ru/nad/4.html>-«Надежность технических систем и техногенный риск.»