|
Время
контактирования,с
|
Выход
аммиака,%
|
|
1,8
|
2
|
|
2,0
|
3
|
|
2,5
|
3,7
|
|
4
|
6
|
|
4,5
|
6,7
|
|
5
|
7,3
|
|
6
|
8,4
|
|
7,5
|
9,5
|
|
8
|
10
|
|
10
|
10,7
|
2. Численное моделирование на ЭВМ
.1 выбор численного метода решения
задачи на ЭВМ
В тех случаях, когда информации о
рассматриваемом процессе недостаточно или процесс настолько сложен, что
невозможно составить его детерминированную модель, прибегают к
экспериментально-статистическим методам. Процесс при этом рассматривают как
«чёрный ящик». Различают пассивный и активный эксперимент.
Пассивный эксперимент является традиционным
методом, когда ставится большая серия опытов с поочерёдным варьированием каждой
из переменных. К пассивному эксперименту относится также сбор исходного
статистического материала в режиме нормальной эксплуатации на промышленном
объекте. Обработка опытных данных в этом случае для получения математической
модели проводится методами классического регрессионного и корреляционного
анализа.
Активный эксперимент ставится по заранее
составленному плану, при этом предусматривается одновременное изменение всех
параметров, влияющих на процесс, что позволяет сразу установить силу
взаимодействия параметров и поэтому сократить общее число опытов.
Используя при обработке опытных данных принципы
регрессионного и корреляционного анализа, удаётся найти зависимость между
переменными и условиями оптимума. В обоих случаях математической моделью
является функция отклика, связывающая параметр оптимизации, характеризующий
результаты эксперимента, с переменными параметрами, которыми экспериментатор
варьирует при проведении опытов:
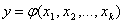 (2.1)
(2.1)
При использовании статистических
методов математическая модель представляется в виде полинома - отрезка ряда
Тейлора, в который разлагается неизвестная зависимость 2.1:
 , (2.2)
, (2.2)
где 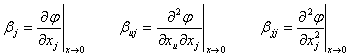 .
.
В связи с тем, что в реальном
процессе всегда существуют неуправляемые и неконтролируемые переменные,
изменение величины носит случайный характер.
Поэтому при обработке
экспериментальных данных получаются так называемые выборочные коэффициенты
регрессии  являющиеся
оценками теоретических коэффициентов
являющиеся
оценками теоретических коэффициентов  Уравнение регрессии, полученное на
основании опыта, запишется следующим образом:
Уравнение регрессии, полученное на
основании опыта, запишется следующим образом:
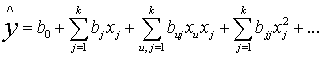 (2.3)
(2.3)
Коэффициент  называется
свободным членом уравнения регрессии; коэффициенты
называется
свободным членом уравнения регрессии; коэффициенты 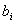 - линейными
эффектами; коэффициенты
- линейными
эффектами; коэффициенты  -
квадратичными эффектами;
-
квадратичными эффектами; 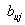 - эффектами
взаимодействия. Коэффициенты уравнения 2.3 определяются методом наименьших
квадратов из условия:
- эффектами
взаимодействия. Коэффициенты уравнения 2.3 определяются методом наименьших
квадратов из условия:
 (2.4)
(2.4)
Здесь N - объём
выборки из всей совокупности значений исследуемых параметров. Разность между
объёмом выборки N и числом связей, наложенных на эту
выборку l, называется
числом степеней свободы выборки f:
 (2.5)
(2.5)
При малых объемах выборки N
увеличение порядка полинома может привести к росту остаточной дисперсии. Для
того чтобы уменьшить число неопределенных коэффициентов, используют
трансцендентную регрессию. Вычисление коэффициентов трансцендентной регрессии
может оказаться весьма трудоемким вследствие необходимости решать систему
нелинейных уравнений. Вычисление упрощается, если провести замену переменных.
Например, зависимости показательного и дробно-степенного типа
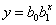
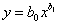
линеаризуются путем
логарифмирования:
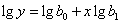
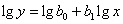
Положив
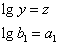

получим линейные уравнения
относительно новых переменных:
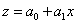
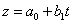
Коэффициенты 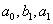 определяются
по методу наименьших квадратов. По полученным
определяются
по методу наименьших квадратов. По полученным 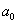 и
и  определяются коэффициенты
определяются коэффициенты 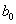 и
и 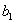 .Следует,
однако, иметь в виду, что полученные таким образом коэффициенты регрессии
являются смещенными оценками для соответствующих генеральных коэффициентов.
.Следует,
однако, иметь в виду, что полученные таким образом коэффициенты регрессии
являются смещенными оценками для соответствующих генеральных коэффициентов.
2.2 Разработка алгоритма блок-схемы
задачи
При изучении зависимости от одного
переменного параметра полезно для определения вида уравнения регрессии
построить эмпирическую линию регрессии. Для этого весь диапазон изменения 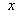 на поле
корреляции разбивается на равные интервалы
на поле
корреляции разбивается на равные интервалы 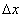 . Все точки попавшие в данный
интервал
. Все точки попавшие в данный
интервал  , относятся
к его середине
, относятся
к его середине  . Для этого
подсчитывают частные средние
. Для этого
подсчитывают частные средние 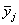 для каждого интервала:
для каждого интервала:
 (2.6)
(2.6)
Здесь 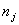 - число точек в интервале
- число точек в интервале  .
.
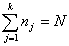 (2.7)
(2.7)
где 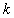 - число интервалов разбиения;
- число интервалов разбиения;  - объём
выборки.
- объём
выборки.
Затем последовательно соединяют
точки  отрезками
прямой. Полученная ломаная называется эмпирическим уравнением регрессии
отрезками
прямой. Полученная ломаная называется эмпирическим уравнением регрессии  по
по 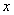 . По виду
эмпирической линии регрессии можно подобрать уравнение регрессии
. По виду
эмпирической линии регрессии можно подобрать уравнение регрессии  .
.
Задача определения параметров
уравнения регрессии сводится практически к определению минимума функции многих
переменных. Если
 (2.8)
(2.8)
есть функция дифференцируемая и
требуется 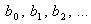 выбрать
так, чтобы
выбрать
так, чтобы
 (2.9)
(2.9)
необходимым условием минимума 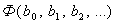 является
выполнения равенства
является
выполнения равенства
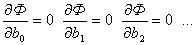 (2.10)
(2.10)
или
 (2.11)
(2.11)
После преобразований получим:
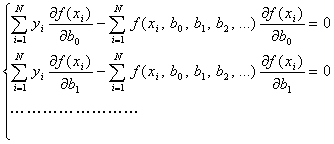 (2.12)
(2.12)
Система уравнений 2.12 содержит
столько же уравнений сколько неизвестных коэффициентов 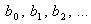 входит в
уравнение регрессии и называется в математической статике системой нормальных
уравнений.
входит в
уравнение регрессии и называется в математической статике системой нормальных
уравнений.
Величина 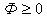 при любых
при любых 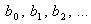 ;
следовательно, у неё обязательно должен существовать хотя бы один минимум.
Поэтому, если система нормальных уравнений имеет единственное решение, то оно и
является минимумом для величины
;
следовательно, у неё обязательно должен существовать хотя бы один минимум.
Поэтому, если система нормальных уравнений имеет единственное решение, то оно и
является минимумом для величины  . Решать систему в общем виде
нельзя. Для этого надо задаться конкретным видом функции f.
. Решать систему в общем виде
нельзя. Для этого надо задаться конкретным видом функции f.
Если уравнение регрессии
представляет собой полином некоторой степени, то при применении метода
наименьших квадратов коэффициенты этого полинома находят решением системы
линейных уравнений. Например, требуется определить по методу наименьших
квадратов коэффициенты квадратичной функции - параболы второго порядка:
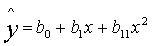 (2.13)
(2.13)
В этом случае
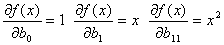 (2.14)
(2.14)
и система нормальных уравнений имеет
вид:
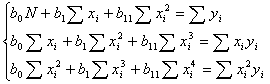 (2.15)
(2.15)
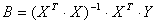 (2.16)
(2.16)
Решив данную систему уравнений,
которая решается в матричной форме по уравнению 2.16, мы получим значения
коэффициентов 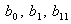 . Далее
необходимо провести проверку на значимость данных коэффициентов по неравенству:
. Далее
необходимо провести проверку на значимость данных коэффициентов по неравенству:
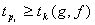 (2.17)
(2.17)
где 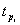 - расчётное значение коэффициента
Стьюдента;
- расчётное значение коэффициента
Стьюдента; 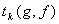 -
критическое значение коэффициента Стьюдента.
-
критическое значение коэффициента Стьюдента.
Если данное неравенство выполняется,
то коэффициент считается значимым и включается в уравнение 2.13. Если
неравенство не выполняется, то коэффициент считается незначимым.
Далее осуществляется проверка
адекватности математической модели по критерию Фишера. В нашем случае нет
параллельных опытов, поэтому расчёт критерия Фишера производим по следующей
формуле:
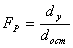 (2.18)
(2.18)
где 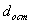 - остаточная дисперсия.
- остаточная дисперсия.
Далее критерий Фишера сравнивается с
табличным. Если он больше табличного, то модель адекватна.
Описание блок-схемы:
) весь диапазон изменения 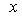 на поле
корреляции разбивается на равные интервалы
на поле
корреляции разбивается на равные интервалы  ;
;
) подсчитываем частные
средние  для каждого
интервала по формуле 2.6;
для каждого
интервала по формуле 2.6;
) подбираем уравнение
регрессии 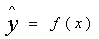 ;
;
) определяем значения
коэффициентов 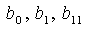 по формуле
2.16;
по формуле
2.16;
) проводим проверку на значимость
данных коэффициентов по неравенству 2.17;
) осуществляем проверку
адекватности математической модели по критерию Фишера
Блок-схема алгоритма представлена на рисунке 2.1

Рисунок 2.1- Блок-схема алгоритма
2.3 Составление программы и анализ
результатов моделирования
Вид математической модели определяем при помощи
регрессионного анализа. Сначала определяем коэффициенты регрессионной модели,
затем проверяем значимость коэффициентов и адекватность регрессионной модели.
Данный метод реализуем в пакете Mat
Lab.
2.3.1 Вид зависимости выхода аммиака
от температуры
%Зависимость выхода аммиака от температуры
clc, clear
P=[723 748 773 873 973 1020]';=[35.5
31.0 26.2 12.84 7.28 4.89]';=length(P);=corrcoef(P, w);=[ones(n,1) P P.^2
];=(X'*X)^(-1)*X'*w=700:1:1020;=A(1)+A(2)*x+A(3)*x.^2(P,w,'*',x,f,'g');=n-1;=0.95;=tinv(p,l)=cov(w);=diag((X'*X)^(-1));=length(A);i=1:k(i)=abs(A(i))/sqrt(dw*c(i));=n-1;=n-k;=finv(p,f1,f2)=X*A;=((Y-w)'*(Y-w))/f2;=dw/dost
%Модель
адекватна,
т.к.
Fr>Fk!
Результаты расчётов:=1.0e+003
.6165
.0136= 2.0150=0.0493 0.0549 0.0586=
230.1619=4.3577e+003
Графически зависимость отображена на рисунке
2.2.
Математическая модель выхода аммиака от
температуры имеет следующий окончательный вид:
W=1,0e+003-2.6165x+0.0136x2
(2.19)
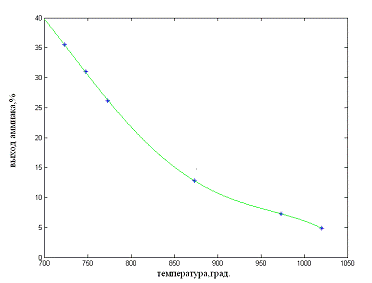
Рисунок. 2.2 - Выход аммиак от температуры
2.3.2 Вид зависимости выхода аммиака
от давления
%Зависимость выхода аммиака от давления.
clc, clear=[25 25.6 26.26 27.57
28.06 29.55 30.8]';=[14 13.9 13.79 13.65 13.6 13.61
13.6]';=length(P);=corrcoef(P, w);=[ones(n,1) P
P.^2];=(X'*X)^(-1)*X'*w=24:0.1:31;=A(1)+A(2)*x+A(3)*x.^2;(P,w,'*',x,f,'g');
%Проверка значимости по критерию Стьюдента.
l=n-1;=0.135=tinv(p,l)=cov(w);=diag((X'*X)^(-1));=length(A);i=1:k(i)=abs(A(i))/sqrt(dw*c(i));
end
%Проверка адекватности по критерию
Фишера.=n-1;=n-k;
Fk=finv(p,f1,f2)=X*A;=((Y-w)'*(Y-w))/f2;=dw/dost
%Модель
адекватна,
т.к.
Fr>Fk!
Результаты расчётов:
A =31.9385
.2462
.0211
p = 0.1350
tk = -1.2150
tr =2.1861
1.1836 1.1193
Fk =0.3730
Fr = 61.7702
Графически зависимость отображена на рисунке
2.3.

Рисунок 2.3 - Выход аммиака в зависимости от
давления
Математическая модель выхода аммиака от давления
имеет следующий вид:
W=31.9385-1.2462x+0.0211x2
(2.20)
2.3.3 Вид зависимости выхода аммиака
от соотношения реагирующих компонентов
%Зависимость выхода аммиака от соотношения
реагирующих компонентов
T=[3.3 3.2 3.1 3.0 2.9 2.8
2.7]';=[14.5 14 13.6 13.4 13.26 13.18 13.12]';=length(T);=corrcoef(T,
w);=[ones(n,1) T T.^2];=(X'*X)^(-1)*X'*w=2.7:0.01:3.3=A(1)+A(2)*x+A(3)*x.^2;(T,w,'*',x,f,'g');
%Проверка значимости по критерию Стьюдента.
l=n-1;=0,135;=tinv(p,l)=cov(w);=diag((X'*X)^(-1));=length(A);i=1:k(i)=abs(A(i))/sqrt(dw*c(i));
tr
%Проверка адекватности по критерию Фишера.
f1=n-1;
f2=n-k;
Fk=finv(p,f1,f2)=X*A;=((Y-w)'*(Y-w))/f2;=dw/dost
%Модель
адекватна,
т.к.
Fr>Fk!
Результаты расчётов:
A =48.8362
.8143
.6667
p =0
tk = -Inf
tr =0.9877
0.7806 0.8471
Fk =0
Fr =113.1839
Графически зависимость отображена на рисунке
2.4.
Математическая модель выхода аммиака от
соотношения имеет следующий окончательный вид:
W=48.8362-23.8143x+4.6667x2
(2.21)
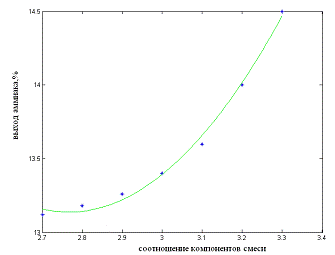
Рисунок. 2.4 - Выход аммиака от соотношения
2.3.4 Вид зависимости выхода аммиака
от времени контактирования
%Зависимость выхода аммиака от времени.
T=[1.8 2.0 2.5 4 4.5 5 6 7.5 8
10]';=[2 3 3.7 6 6.7 7.3 8.4 9.5 10 10.7]';=length(T);=corrcoef(T,
w);=[ones(n,1) T
T.^2];=(X'*X)^(-1)*X'*w=1:0.01:10.7=A(1)+A(2)*x+A(3)*x.^2;(T,w,'*',x,f,'g');
%Проверка значимости по критерию Стьюдента.
l=n-1;=0,135;=tinv(p,l)=cov(w);=diag((X'*X)^(-1));=length(A);i=1:k(i)=abs(A(i))/sqrt(dw*c(i));
tr
%Проверка адекватности по критерию Фишера.
f1=n-1;
f2=n-k;
Fk=finv(p,f1,f2)=X*A;=((Y-w)'*(Y-w))/f2;=dw/dost
%Модель
адекватна,
т.к.
Fr>Fk!
Результаты расчётов:
A =-1.4006
.2739
.1068
p =0
tk = -Inf
tr =0.3289
1.3135 0.7089
Fk =0
Fr = 279.6078
Графически зависимость отображена на рисунке
2.5.

Рисунок 2.5 - Выход аммиака в зависимости от
времени контактирования
Математическая модель выхода оксида азота от
времени контактирования имеет следующий окончательный вид:
W=-1.4006+2.2739x-0.1068x2
(2.22)
На основании полученных данных можно сделать
вывод что все полученные модели адекватны, а коэффициенты значимы.
3.Задача оптимизации
технологического процесса
.1 Выбор критерия оптимизации
Оптимизация заключается в нахождении оптимума
рассматриваемой функции и соответственно оптимальных условий проведения данного
процесса. Для оптимизации ХТП необходимо выразить критерий оптимизации в
зависимости от конкретных условий протекания ХТП. В качестве критерия
оптимизации может быть выбран технологический параметр, например максимальная
производительность процесса при заданном качестве продукции, или экономический
параметр, например минимальная себестоимость при заданных тратах на
производство. На основании выбранного критерия составляется функция выгоды -
целевая функция. Она представляет собой зависимость критерия оптимизации от
параметров, влияющих на его значение. Задача оптимизации заключается в
нахождении экстремума целевой функции при заданных начальных и граничных условиях.
Проблема оптимизации возникает в тех случаях, когда необходимо решать дачу
преимущественного улучшения двух и более количественных характеристик,
различным образом влияющих на переменные показатели процесса, балансируя один
против другого.
Любой ХТП, исходя из внешних признаков, можно
представить в виде следующей схемы:
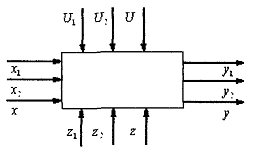
Рисунок 3.1 - Схема реального ХТП
Можно выделить 4 группы параметров, влияющих на
состояние процесса: входные контролируемые параметры х1, х2,...,хn
(они определяют качество сырья); управляющие параметры, которые можно изменять
в процессе управления U1,
U2,...,Un
(количество сырья, температура, давление и т.д.);
неконтролируемые возмущающие параметры,
изменяющиеся случайным образом, неизвестна их природа и место приложения z1,
z2, …, zn
(примеси, износ оборудования, старение катализатора и т. д.);
выходные параметры у1, у2,..., уn.
Исходя из этого, математическую модель процесса
можно представить как
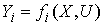 (3.1)
(3.1)
где У, X, V - векторная
форма записи параметров.
Критерий оптимизации R в общем
виде зависит от векторов входных, управляющих, выходных параметров процесса:
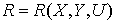 (3.2)
(3.2)
Решение задачи оптимизации в этом
случае представляется в виде зависимости управляющих параметров V от выходных
параметров X, времени Г,
пространственной координаты %:
 (3.3)
(3.3)
В нашем случае в качестве критериев
оптимизации выступает напряжённость температура N , давление Р, соотношение К и время
контактирования t.
3.2 Обоснование выбора метода
оптимизации
В настоящее время для решения задачи оптимизации
применяются аналитические и численные методы. Первые являются классическими
методами определения экстремального значения функции. Они применяются когда
оптимизируемые функции заданы аналитически и число независимых переменных
невелико. При большом числе переменных возникает так называемый барьер
многомерности, и применение аналитических методов становится затруднительным.
К аналитическим методам оптимизации относят
следующие:
) Метод исследования функций классического
анализ.
Исследования функций
классического анализа представляют собой наиболее известные методы решения/
несложных оптимальных задач, с которыми инженер знакомится при изучении курса
математического анализа. Обычной областью использования данных методов являются
задачи с известным аналитическим выражением критерия оптимальности, что
позволяет найти не очень сложное, также аналитическое выражение для
производных. Полученные приравниванием нулю производных уравнения, определяющие
экстремальные решения оптимальной задачи, крайне редко удается решить
аналитическим путем, поэтому, как правило, применяют вычислительные машины. При
этом надо решить систему конечных уравнений, чаще всего нелинейных, для чего
приходится использовать численные методы, аналогичные методам нелинейного
программирования.
Дополнительные трудности при
решений оптимальной задачи методами исследования функций классического анализа
возникают вследствие того, что система уравнений, получаемая в результате их
применения, обеспечивает лишь необходимые условия оптимальности. Поэтому все
решения данной системы (а их может быть и несколько) должны быть проверены на
достаточность. В результате такой проверки сначала отбрасывают решения, которые
не определяют экстремальные значения критерия оптимальности, а затем среди
остающихся экстремальных решений выбирают решение, удовлетворяющее условиям
оптимальной задачи, т. е. наибольшему или наименьшему значению критерия
оптимальности в зависимости от постановки задачи.
Методы исследования при наличии
ограничений на область изменения независимых переменных можно использовать
только для отыскания экстремальных значений внутри указанной области, В
особенности это относится к задачам с большим числом независимых переменных
(практически больше двух), в которых анализ значений критерия оптимальности на
границе допустимой области изменения переменных становится весьма сложным.
Метод исследования функции
классического анализа в основном применяют в тех случаях, когда известен
аналитический вид зависимости оптимизируемой функции 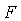 от
независимых переменных
от
независимых переменных 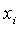 . Это
позволяет найти также в аналитическом виде производную оптимальной функции,
используя которые и формулируют необходимые и достаточные условия существования
экстремума.
. Это
позволяет найти также в аналитическом виде производную оптимальной функции,
используя которые и формулируют необходимые и достаточные условия существования
экстремума.
Суть метода заключается в нахождении
производной 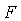 по
определяемому параметру и приравнивание её к нулю. Вид экстремума (максимум или
минимум) определяется по производной целевой функции высшего порядка.
по
определяемому параметру и приравнивание её к нулю. Вид экстремума (максимум или
минимум) определяется по производной целевой функции высшего порядка.
Недостатком является трудность
применения метода с увеличением числа переменных в целевой функции. Данный
метод обладает одним существенным преимуществом - простотой.
)Метод неопределённых множителей
Лагранжа.
Метод множителей Лагранжа
применяют для решения задач такого же класса сложности, как и при использовании
обычных методов исследования функций, но при наличии ограничений типа равенств
на независимые переменные. К требованию возможности получения аналитических выражений
для производных от критерия оптимальности при этом добавляется аналогичное
требование относительно аналитического вида уравнений ограничения.
В основном при использовании
метода множителей Лагранжа приходится решать те же задачи, что и без
ограничений. Некоторое усложнение в данном случае возникает лишь от введения
дополнительных неопределенных множителей, вследствие чего порядок системы
уравнений, решаемой для нахождения экстремумов Критерия оптимальности,
соответственно повышается на число ограничений. В остальном процедура поиска
решений и проверки их на оптимальность отвечает процедуре решения задач без
ограничений.
Множители Лагранжа можно
применять для решения задач оптимизации объектов с распределенными параметрами
и задач динамической оптимизации . При этом вместо решения системы конечных
уравнений для отыскания оптимума необходимо интегрировать систему
дифференциальных уравнений.
Следует отметить, что множители
Лагранжа используют также в качестве вспомогательного средства и при решении
специальными методами задач других классов с ограничениями типа равенств,
например, в вариационном исчислении и динамическом программировании. Особенно
эффективно применение множителей лагранжа в методе динамического
программирования
Метод обычно используется, когда на переменные
накладывается ограничения типа равенства. Суть метода сводится к нахождению
дополнительной функции, включающей множители Лагранжа, и её решению. При этом
множители носят вспомогательный характер.
) Метод линейного программирования.
Для решения большого круга
задач линейного программирования имеется практически универсальный алгоритм -
симплексный метод, позволяющий за конечное число итераций находить оптимальное
решение подавляющего большинства задач. Тип используемых ограничений (равенства
или неравенства) не сказывается на возможности применения указанного алгоритма.
Дополнительной проверки на оптимальность для получаемых решений не требуется.
Как правило, практические задачи линейного программирования отличаются весьма
значительным числом независимых переменных. Поэтому для их решения обычно
используют вычислительные машины, необходимая мощность которых определяется
размерностью решаемой задачи.
Данный метод применяется для нахождения
экстремума целевой функции линейного вида и при наличии ограничительных условий
типа неравенства. Достоинством метода является то, что при наличии многих
переменных он легко реализуется не ЭВМ.
Следует отметить, что значение линейного
программирования не исчерпывается решением задач только указанных типов. В методах
решения задач так называемого выпуклого программирования существенным образом
используется вычислительный аппарат линейного программирования. Кроме того,
иногда при рассмотрении сложного нелинейного объекта удаётся представить его
математическое описание в некоторых локальных областях изменения независимых
переменных приближёнными линейными соотношениями. Это позволяет свести исходную
задачу оптимизации к задаче линейного программирования. Тем самым становиться
возможным применять его математический аппарат, который в настоящее время
разработан достаточно подробно и при наличии цифровой вычислительной машины
обеспечивает решение оптимальных задач весьма высокой размерности.
) Методы вариационного исчисления
Методы вариационного исчисления
обычно используют для решения задач, в которых критерии оптимальности
представляются в виде функционалов и решениями которых служат неизвестные
функции. Такие задачи возникают обычно при статической оптимизации процессов, с
распределенными параметрами или в задачах динамической оптимизации.
Вариационные методы позволяют в
этом случае свести решение оптимальной задачи к интегрированию системы
дифференциальных уравнений Эйлера, каждое из которых является нелинейным
дифференциальным уравнением второго порядка с граничными условиями, заданными
на обоих концах интервала интегрирования. Число уравнений указанной системы при
этом равно числу неизвестных функций, определяемых при решении оптимальной
задачи. Каждую функцию находят в результате интегрирования получаемой системы.
Уравнения Эйлера выводятся как
необходимые условия экстремума функционала. Поэтому полученные интегрированием
системы дифференциальных уравнений функции должны быть проверены на экстремум
функционала
5) Методы геометрического программирования
Геометрическое программирование
есть метод решения одного специального класса задач нелинейного
программирования, в которых критерий оптимальности и ограничения задаются в
виде позиномов - выражений, представляющих собой сумму произведений степенных
функций от независимых переменных. С подобными задачами иногда приходится
сталкиваться в проектировании. Кроме того, некоторые задачи нелинейного
программирования иногда можно свести к указанному представлению, используя
аппроксимационное представление для целевых функций и ограничений.
Специфической особенностью
методов решения оптимальных чадач (за исключением методов нелинейного
программирования) является то, что до некоторого этапа оптимальную задачу
решают аналитически, т. е. находят определенные аналитические выражения,
например, системы конечных или дифференциальных уравнений, откуда уже
отыскивают оптимальное решение. В отличие от указанных методов при
использовании методов нелинейного программирования, которые, как уже отмечалось
выше, могут быть названы прямыми, применяют информацию, получаемую при
вычислении критерия оптимальности, изменение которого служит оценкой
эффективности того или иного действия.
Важной характеристикой любой
оптимальной задачи является ее размерность п, равная числу переменных, задание
значений которых необходимо для однозначного определения состояния
оптимизируемого объекта. Как правило, решение задач высокой размерности связано
с необходимостью выполнения большого объема вычислений. Ряд методов (например,
динамическое программирование и дискретный принцип максимума) специально
предназначен для решения задач оптимизации процессов высокой размерности,
которые могут быть представлены как многостадийные процессы с относительно
невысокой размерностью каждой стадии.
6)Методы динамического программирования.
Динамическое программирование
служит эффективным методом решения задач оптимизации дискретных многостадийных
процессов, для которых критерий оптимальности задается как аддитивная функция
критериев оптимальности отдельных стадий. Без особых затруднений указанный
метод можно распространить и на случай, когда критерий оптимальности задан в
другой форме, однако при этом обычно увеличивается размерность отдельных
стадий.
По существу метод динамического
программирования представляет собой алгоритм определения оптимальной стратегии
управления на всех стадиях процесса. При этом закон управления на каждой стадии
находят путем решения частных задач оптимизации последовательно для всех стадий
процесса с помощью методов исследования функций классического анализа или
методов нелинейного программирования. Результаты решения обычно не могут быть
выражены в аналитической форме, а получаются в виде таблиц.
Ограничения на переменные
задачи не оказывают влияния на общий алгоритм решения, а учитываются при
решении частных задач оптимизации на каждой стадии процесса. При наличии
ограничений типа равенств иногда даже удается снизить размерность этих частных
задач за счет использования множителей Лагранжа. Применение метода
динамического программирования для оптимизации процессов с распределенными
параметрами или в задачах динамической оптимизации приводит к решению
дифференциальных уравнений в частных производных. Вместо решения таких
уравнений зачастую значительно проще представить непрерывный процесс как
дискретный с достаточно большим числом стадий. Подобный прием оправдан особенно
в тех случаях, когда имеются ограничения на переменные задачи и прямое решение
дифференциальных уравнений осложняется необходимостью учета указанных
ограничений. При решении задач методом динамического программирования, как
правило, используют цифровые вычислительные машины, обладающие достаточным
объемом памяти для хранения промежуточных результатов решения, которые обычно
получаются в табличной форме.
7)Методы нелинейного программирования.
Методы нелинейного
программирования применяют для решения оптимальных задач с нелинейными
функциями цели. На независимые переменные могут быть наложены ограничения также
в виде нелинейных соотношений, имеющих вид равенств или неравенств. По существу
методы нелинейного программирования используют, если ни один из перечисленных
выше методов не позволяет сколько-нибудь продвинуться в решении оптимальной
задачи. Поэтому указанные методы иногда называют также прямыми методами решения
оптимальных задач.
Для получения численных
результатов важное место отводится нелинейному программированию и в решении
оптимальных задач такими мето- дами, как динамическое программирование, принцип
максимума и т. п. на опре деленных этапах их применения.
Названием «методы нелинейного программирования»
объединяется большая группа численных методов, многие из которых приспособлены
для решения оптимальных задач соответствующего класса. Выбор того или иного
метода обусловлен сложностью вычисления критерия оптимальности и сложностью
ограничивающих условий, необходимой точностью решения, мощностью имеющейся
вычислительной машины и т.д. Ряд методов нелинейного программирования
практически постоянно используется в сочетании с другими методами оптимизации,
как, например, метод сканирования в динамическом программировании. Кроме того,
эти методы служат основой построения систем автоматической оптимизации -
оптимизаторов, непосредственно применяющихся для управления производственными
процессами.
Этих методов множество, но наиболее эффективные
градиентные (метод наискорейшего спуска при поиске минимума целевой функции и
метод крутого восхождения при поиске максимума нелинейной целевой функции).
Преимуществом метода является простота реализации на ЭВМ.
Задача поиска оптимума (максимума)
численным методом сводится к локализации области наибольших значений функции
близких к экстремальным ( от
от  до
до 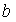 ) и
уточнение значения функции в точке экстремума. При нахождении минимума
необходимо исходную функцию рассматривать как отрицательную.
) и
уточнение значения функции в точке экстремума. При нахождении минимума
необходимо исходную функцию рассматривать как отрицательную.
Численные методы можно
классифицировать:
.метод локализации экстремума
функции одной переменной
.метод поиска с использованием чисел
Фибоначчи
.метод поочередного изменения
переменных
.метод сканирования
.метод равномерного поиска;
.метод поразрядного приближения;
.метод дихотомии;
.метод золотого сечения;
.метод квадратичной интерполяции.
1) Метод локализации экстремума
функции одной переменной
Предположим, что задача состоит
в определении положения экстремума функции одной переменной на интервале [а, b].
Для решения этой задачи разобьем весь интервал на N равных частей. На рисунке
показано такое разбиение для N = 4. На границах всех подынтервалов, включая
конечные точки интервала [а, b],
вычисляются значения функции R(x).
Среди полученных значений R(x)
находится то, которое соответствует типу отыскиваемого экстремума. Например,
при отыскании минимума функции R(х)
(рис. IX-16)
наименьшее значение R(x)
среди вычисленных значений R(x)
(к = 0, ..., 4)
Далее выбирается новый
интервал, включающий два подынтервала с наименьшим вычисленным значением
функции на их общей границе. Таким интервалом является [х(2) , x(4)]
Очевидно, что поскольку на границах нового интервала значение функции R(x)
больше, чем в его середине, минимум расположен в интервале . Тем самым искомый
минимум локализован в интервале, размеры которого меньше исходного
Применяя к новому интервалу тот
же прием разбиения и вычисляя значение R(х) на границах полученных
подынтервалом. можно еще более сузить интервал, где находится искомый минимум.
Нетрудно показать, что
наилучшие результаты поиска могут быть достигнуты в том случае, если используется
разбиение на четыре подынтервала (N= 4). При этом для каждого разбиения нужно
вычислять значения целевой функции только в двух новых точках, так как ее
значения на концах нового интервала и в его середине известны. Ошибка в
нахождении положения экстремума с увеличением числа точек, в которых
вычисляется значение целевой функции, определяется выражением
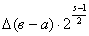 (3.4)
(3.4)
причем s - число расчетов значений
целевой функции, которое в используемом методе может быть только нечетным. Так,
при s = 21
относительная ошибка в нахождении положения экстремума составляет:

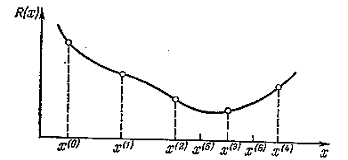
Рисунок 3.2 Одномерный поиск
методом локализации экстремума
'
2) Метод поиска с
использованием чисел Фибоначчи
Показано, что свойства
последовательности чисел Фибоначчи, описываемой рекуррентным соотношением
F(k)=F(k-1)+F(k-2)(3.6)
можно использовать для
организации оптимального поиска экстремума функции одной переменной.
Доказывается , что если
требуется найти положение экстремума функции, определенной на интервале [а, b]
с абсолютной ошибкой, не превышающей
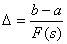 (3.7)
(3.7)
где F(s) - s-ое число
Фибоначчи, то для отыскания положения экстремума достаточно вычислить не более
5 значений функции R(х). Так, например, при выполнении s = 21
расчетов точность определения экстремума составит:
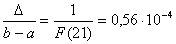 (3.8)
(3.8)
т. е. оказывается более
высокой, чем в приведенных ниже методах поиска делением интервала на равные
части и «золотого сечения».
Рассмотрим теперь алгоритм
поиска, использующий числа Фибоначчи. Порядок его выполнения при поиске
минимума складывается из следующих этапов:
1.По заданной точности  , с которой
необходимо найти положение экстремума функции R(х) в
интервале [а, b],
рассчитывается число N
, с которой
необходимо найти положение экстремума функции R(х) в
интервале [а, b],
рассчитывается число N


. Для получения значения
N находится такое число Фибоначчи F(s),
чтобы выполнялось неравенство:
F(s-1)
< N < F(s)(3.10)
.Определяется минимальный шаг
поиска по формуле:
 (3.11)
(3.11)
. Рассчитывается значение
функции R(х) в начале
интервала, т. е. R (а).
5. Следующая точка, в
которой вычисляется значение R(х),
находится по формуле:
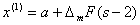 (3.12)
(3.12)
6. Если этот шаг оказался
удачным, т. е. R(x1)<R(a)
то следующая точка определяется как
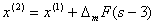 (3.13)
(3.13)
При R(x1)>R(a)
(шаг неудачный)

7. Последующие шаги
выполняются с уменьшающейся величи ной шага, которая для i-го шага будет равна
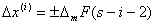 (3.15)
(3.15)
в соответствии со следующим
правилом. Если при выполнении шага  значение функции в точке
значение функции в точке
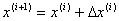 (3.16)
(3.16)
оказывается меньше, т. е. R(x(i+1))>R(x(i)) (шаг
удачный), то следующий (i+ 1)-й шаг выполняется из точки
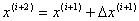 (3.17)
(3.17)
Указанный процесс продолжается
до тех пор, пока не будут исчерпаны все числа Фибоначчи в убывающей
последовательности
На рисунке 3.3 процедура такого
поиска при N = 21 (s = 7), что
отвечает точности поиска порядка 5%. На рисунке цифрами отмечена
последовательность вычисления значений функции R(х).
Видно, что в процессе поиска третий и пятый шаги оказываются неудачными, что
вызывает изменение направления последующих шагов.
Можно показать, что алгоритм
поиска с использованием чисел Фибоначчи в пределе с высокой точностью,
совпадает с методом «золотого сечения».
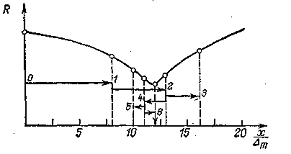
Рисунок 3.3- Одномерный поиск с
использованием чисел Фибоначчи
3) Метод поочередного изменения переменных
Метод поочередного изменения
переменных, называемый также методом Гаусса-Зейделя, по существу аналогичен
рассмотренному выше методу релаксации. Отличие заключается лишь в том, что в
этом методе не определяется осевое направление, вдоль которого значение целевой
функции изменяется наиболее сильно, а поочередно изменяются все независимые
переменные так, чтобы по каждой из них достигалось наименьшее (наибольшее)
значение целевой функции. Очередность варьирования независимых переменных при
этом устанавливается произвольно и обычно не меняется в процессе поиска.
Заметим, что для двух независимых переменных оба метода поиска, т. е. метод
релаксации и метод поочередного изменения переменных, совпадают.
Как и в методе релаксации,
каждая уточняемая переменная варьируется до тех пор, пока в данном осевом
направлении не будет найден минимум, после чего начинается процесс шагового
поиска по следующему осевому направлению. Стратегия поиска минимума по каждой
переменной при этом может быть также
любая. В частности, можно
использовать один из описанных выше методов поиска экстремума функции одной
переменной.
Очевидно, что поскольку варьирование независимых
переменных происходит в установленном порядке, метод их поочередного изменения
приводит к оптимуму более длинным путем. Однако общий объем вычислений по
сравнению с методом релаксации в данном случае может оказаться меньше, так как
при переходе, к уточнению следующей переменной производные целевой функции не
вычисляются. Естественно, что недостатки метода релаксации, к которому
относятся трудности поиска при наличии ограничений или особенностей целевой
функции (овраги), целиком присущи и методу поочередного изменения переменных.
Вместе с тем, простота метода и сравнительно небольшой объем вычислений,
необходимых для его реализации, обусловили его распространение в системах
автоматического отыскания экстремума.
) Метод сканирования.
Метод сканирования заключается
в последовательном просмотре значений критерия оптимальности в ряде точек,
принадлежащих области изменения независимых переменных, и нахождении среди этих
точек такой, в которой критерий оптимальности имеет минимальное (максимальное)
значение. Точность метода, естественно, определяется тем, насколько «густо»
располагаются выбранные точки в допустимой области изменения независимых
переменных.
Основным достоинством метода
сканирования является то, что при его использовании с достаточно «густым»
расположением исследуемых точек всегда гарантируется отыскание глобального
оптимума, так как анализируется вся область изменения независимых переменных.
Другое достоинство - независимость поиска от вида оптимизируемой функции.
К недостаткам метода относится,
в первую очередь, необходимость вычисления значений целевой функции для
большего числа точек. Это должно гарантировать, что оптимум не будет пропущен
при применении данного метода поиска.
Общий недостаток градиентных
методов в оптимизации, за исключением, может быть, метода «тяжелого шарика»,
состоит в том, что все они «застревают» в ближайшем локальном оптимуме, 1 в
область «притяжения» которого попадает выбранная начальная точка спуска. В
отличие от этих методов метод сканирования ни-1 как не связан с наличием
локальных оптимумов целевой функции. Поэтому его можно использовать иногда для
предварительного грубого установления границ областей «притяжения» указанных
оптимумов, после чего могут уже применяться градиентные методы спуска для
измерения точной «глубины» каждого локального оптимума.
Наиболее простой алгоритм
поиска оптимума методом сканирования, называемый еще иногда поиском на сетке
переменных, заключается в том, что по каждой независимой переменной даются
приращения в соответствующем порядке, обеспечивающем заполнение всей области
изменения этих переменных равномерной и достаточно густой сеткой. В простейшем
случае двух переменных x1 и x2 сканирование сводится к просмотру значений
критерия оптимальности при заданном значении одной переменной х2 для ряда
значений другой х1, которые определяются как отстоящие друг от друга на
величину шага по переменной x1 После того как весь диапазон изменения
переменной хх при заданном значении x2
исследован и для него найдено минимальное значение критерия оптимальности,
изменяется значение переменной x2
также на величину некоторого шага по этой переменной и т. д.
Для произвольного числа
независимых переменных шаг по каждой следующей переменной производится после
того, как полностью завершен цикл по предыдущей.
Дополнительные ограничения на
независимые переменные по существу не усложняют процедуры использования метода
сканирования, так как в этом случае точки, которые не удовлетворяют заданным
условиям, просто исключаются из рассмотрения и значения критерия оптимальности
в них не вычисляются. Наличие дополнительных ограничений на независимые
переменные даже ускоряет решение задачи, если, конечно, эти ограничения не
заданы в виде трудновычислимых соотношений, поскольку возможный диапазон
изменения при этом сужается и значения критерия оптимальности рассчитываются с
меньшим числом точек.
Особенно просто обстоит дело,
если ограничения заданы в виде неравенств, когда приемлемость точки решается
простой проверкой этих условий. Однако метод сканирования можно применить также
и в случае, если ограничения имеют вид равенств. Наиболее простой путь при этом
состоит в замене ограничений типа
 (3.18)
(3.18)
Ограничением
определяющим некоторую е-окрестность
гиперповерхности, описываемой уравнением (3.18), где и используется метод
сканирования.
Другой прием, который может быть
применен когда ограничение (3.19) представляется в виде
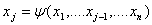 (3.20)
(3.20)
При этом сканирование ведется по п -
1 переменным, а соответствующее значение переменной x рассчитывается из
выражения (3.20). Разумеется, что находимое значение х} также проверяется
допустимый диапазон изменения, который для нормализованных переменных,
например, равен [0, 1].
Нетрудно получить оценку
вычислительных затрат при применении метода сканирования. Так, в случае поиска
оптимума целевой функции при условии, что точность определения положения этого
оптимума равна  , т. е.
искомые значения нормализованных переменных не должны отличаться от истинного
положения оптимума на величину, большую, чем
, т. е.
искомые значения нормализованных переменных не должны отличаться от истинного
положения оптимума на величину, большую, чем  , число рассчитываемых значений
целевой функции составит:
, число рассчитываемых значений
целевой функции составит:
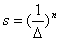 (3.21)
(3.21)
где п - число независимых
переменных решаемой задачи (размерность задачи).
Таким образом, число вычислений
критерия оптимальности при определении положения оптимума методом сканирования
возрастает в показательной зависимости от размерности решаемой задачи. Поэтому
эффективное применение данного метода в основном ограничивается задачами
невысокой размерности п = 2 - 3, если используется простейший алгоритм поиска,
рассмотренный выше, для отыскания оптимума с невысокой точностью.
Существуют различные
модификации метода сканирования, применяемые в основном для сокращения объема
вычислений. Одна из таких модификаций заключается в том, что используется
алгоритм с переменным шагом сканирования. Вначале величина шага выбирается
достаточно большой, по возможности значительно превышающей требуемую точность
определения положения оптимума, и выполняется грубый поиск, который локализует
область нахождения глобального оптимума. После того как область определена,
производится поиск с меньшим шагом только в пределах указанной области.
Практически можно организовать целый ряд таких процедур последовательного
уточнения оптимума. Необходимый объем вычислений значений целевой функции при
этом существенно сокращается и может быть подсчитан по формуле
 (3.22)
(3.22)
в которой п - размерность задачи;  - точность
определения оптимума; r - число этапов уточнения поиска, на которых шаг поиска
уменьшается в к раз. Начальный шаг сетки переменных в данном случае
определяется формулой:
- точность
определения оптимума; r - число этапов уточнения поиска, на которых шаг поиска
уменьшается в к раз. Начальный шаг сетки переменных в данном случае
определяется формулой:
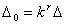 (3.23)
(3.23)
Например, при поиске оптимума
функции двух переменных (n = 2) с точностью  = 0,001,
используя два этапа уточнения величины шага (r = 2) в к =
10 раз, т. е. с начальным шагом
= 0,001,
используя два этапа уточнения величины шага (r = 2) в к =
10 раз, т. е. с начальным шагом  0 = 0,1, необходимый объем
вычислений составит,
0 = 0,1, необходимый объем
вычислений составит,
S=
104(103)2 + 2-(20)2 = 900(3.24)
что более чем в 1000 раз сокращает объем
вычислений при сканировании с постоянным шагом
На рисунке 3.4 показан поиск с
переменным шагом для функции двух переменных. Кружком обозначено истинное
положение оптимума, а крестом - приближение, найденное в результате грубого
поиска.
Важнейшим моментом при использовании
метода сканирования с переменным шагом является выбор начального грубого шага
поиска. Если начальная величина шага  выбрана слишком большой, может
возникнуть опасность пропуска глобального оптимума. Если же начальный шаг
выбран слишком малым, может быть велик необходимый для поиска объем вычислений.
При выборе величины начального шага существенную помощь может оказать
информация о поведении целевой функции, наличии локальных экстремумов.
выбрана слишком большой, может
возникнуть опасность пропуска глобального оптимума. Если же начальный шаг
выбран слишком малым, может быть велик необходимый для поиска объем вычислений.
При выборе величины начального шага существенную помощь может оказать
информация о поведении целевой функции, наличии локальных экстремумов.

Рисунок 3.4 - Поиск методом сканирования с
переменным шагом
) Метод равномерного поиска
Для поиска экстремума функции  на отрезке
на отрезке  в данном
методе реализуется следующий алгоритм. Переменной
в данном
методе реализуется следующий алгоритм. Переменной  присваивается
значение
присваивается
значение 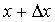 , где
, где 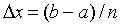 - шаг
поиска,
- шаг
поиска, 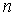 - число разбиений.
На каждом шаге вычисляется значение
- число разбиений.
На каждом шаге вычисляется значение  и проверяется условие
и проверяется условие 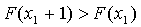 , где l - номер
шага. Если данное условие выполняется, переменной
, где l - номер
шага. Если данное условие выполняется, переменной  даётся
новое приращение и процесс повторяется. Если на выполняется, то величина
даётся
новое приращение и процесс повторяется. Если на выполняется, то величина  -
экстремальное значение, а
-
экстремальное значение, а  принимаем
равным
принимаем
равным  , при этом
счёт заканчивается. Точность вычисления экстремума зависит от величины шага.
, при этом
счёт заканчивается. Точность вычисления экстремума зависит от величины шага.
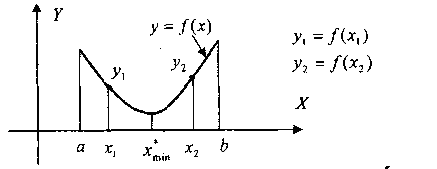
Рисунок 3.5-Метод равномерного
поиска
) Метод поразрядного приближения
Данный метод является разновидностью
метода равномерного поиска. Он реализуется следующим алгоритмом:
) задают  ,
, 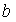 и принимают
и принимают
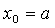 , находят
, находят 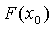 ;
;
) задают начальный шаг поиска
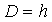 ,
, 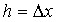 ;
;
) полагаем что 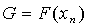 и
и  ;
;
) задаём  и вычисляем
и вычисляем
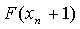 ;
;
) если 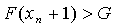 , то
возвращаемся к пункту 1, если условие не выполняется, то переходим к пункту 6;
, то
возвращаемся к пункту 1, если условие не выполняется, то переходим к пункту 6;
) 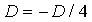 и проверяем
условие
и проверяем
условие 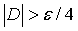 , где
, где  - заданная
погрешность вычисления, если это выполняется, то возвращаемся к пункту 3, если
нет, то заканчиваем счёт и принимаем за
- заданная
погрешность вычисления, если это выполняется, то возвращаемся к пункту 3, если
нет, то заканчиваем счёт и принимаем за 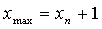 . Точность метода зависит от
величины шага поиска и погрешности вычисления.
. Точность метода зависит от
величины шага поиска и погрешности вычисления.
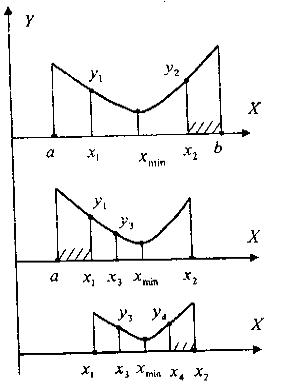
Рисунок 3.6- Применение метода поразрядного
приближения
) Метод дихотомии
Данный метод заключается в делении отрезка на
котором ведётся поиск экстремума на две равные части. Он реализуется следующим
алгоритмом:
1) проверяем условие 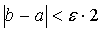 , если
условие выполняется, то переходим к пункту 5, если нет, то к пункту 2;
, если
условие выполняется, то переходим к пункту 5, если нет, то к пункту 2;
2) делим отрезок пополам и
вычисляем  ,
, 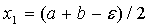 ,
, 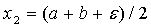 ;
;
3) находим 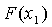 и
и 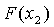 ;
;
4) проверяем условие  >
>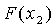 , если оно
выполняется, то
, если оно
выполняется, то 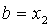 и
возвращаемся к пункту 1, если нет, то
и
возвращаемся к пункту 1, если нет, то 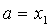 и возвращаемся к пункту 1;
и возвращаемся к пункту 1;
5) вычисляем 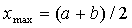 и
и 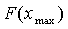 .
.
Точность расчётов зависит от величины заданной
погрешности вычисления.
7) Метод золотого сечения

Рисунок 3.7 - Одномерный поиск методом «золотого
сечения»
Данный метод основан на делении отрезка на
котором находят экстремум напополам. Он позволяет сузить данный отрезок и
количество вычислений в два раза по сравнению с методом дихотомии. Алгоритм
расчёта следующий:
1) находим коэффициент деления  ;
;
) находим 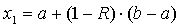 и
и 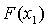 ;
;
) находим 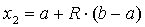 и
и 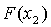 ;
;
) проверяем условие  , если оно
выполняется, то находим
, если оно
выполняется, то находим  и
и  , счёт
прекращаем, если нет, то переходим к пункту 5;
, счёт
прекращаем, если нет, то переходим к пункту 5;
) проверяем условие 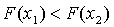 , если оно
выполняется, то полагаем
, если оно
выполняется, то полагаем 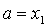 и переходим
к пунктам 3 и 4, если нет, то
и переходим
к пунктам 3 и 4, если нет, то 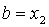 и переходим к пункту 2 и 4
и переходим к пункту 2 и 4
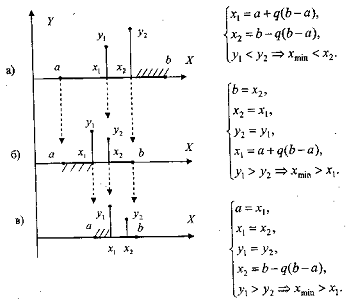
Рисунок 3.8 Поиск и условия применения метода
«золотое сечение»
) Метод квадратичной интерполяции.
Данный метод заключается в замене исходной
функции 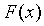 на
интервале от
на
интервале от  до
до  (где
(где  -
первоначальное значение,
-
первоначальное значение, 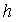 -
полуинтервал поиска) вблизи к экстремуму на квадратичную параболу:
-
полуинтервал поиска) вблизи к экстремуму на квадратичную параболу:
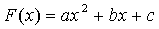 (3.25)
(3.25)
После нахождения приближённого
значения экстремума замененной функции, сужают рассматриваемый интервал и вновь
производят замену исходной функции. Процесс осуществляют до тех пор, пока
экстремум на будет найден с определённой заданной погрешностью. Если поиск
экстремума проводят в пределах интервала, то это интерполяция, если вне, то -
экстраполяция.
Алгоритм метода следующий:
) задаём начальное
приближение  на
интервале от
на
интервале от  до
до 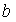 ;
;
) вычисляем 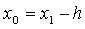 и
и 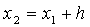 , где
, где 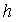 -
полуинтервал поиска;
-
полуинтервал поиска;
) вычисляем 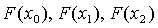 ;
;
) находим коэффициенты 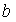 и
и 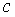 для
параболы
для
параболы 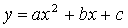 :
:
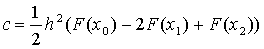 (3.26)
(3.26)
 (3.27)
(3.27)
5) находим 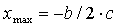 ;
;
) проверяем условие 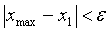 , если оно
выполняется, то
, если оно
выполняется, то 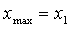 и
возвращаемся к пункту 1, если нет, то
и
возвращаемся к пункту 1, если нет, то 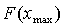 и заканчиваем счёт.
и заканчиваем счёт.
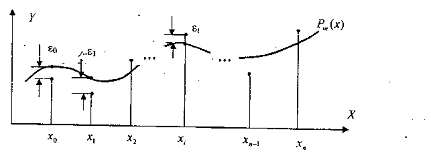
Рисунок 3.9 - Применение метода квадратичная
интерполяция
Преимуществами данного метода является то, что
он без всякой замены исходной функции позволяет найти как максимум, так и
минимум, причём даже за пределами заданного интервала. Данный метод
сравнительно легко реализуется на ЭВМ. Для большинства гладких функций данный
метод даёт значительный выигрыш во времени.
Для оптимизации математической модели процесса
получения серной кислоты будем использовать метод дихотомии.
Существует довольно очевидная теорема:
"Если непрерывная функция на концах некоторого интервала имеет значения
разных знаков, то внутри этого интервала у нее есть корень (как минимум, один,
но может быть и несколько)". Вот на базе этой теоремы и построено
численное нахождение приближенного значения корня функции. Обобщенно этот метод
называется "дихотомией", т.е. "делением отрезка на две
части". Метод дихотомии заключается в следующем: выяснив, сколько всего
элементов в отсортированном массиве, мы сравниваем число "X" со
средним элементом массива. Если средний элемент массива больше, чем
"X" - значит все элементы массива стоящие после среднего элемента
массива тоже больше чем число "X", ведь мы работаем с отсортированным
массивом. Следовательно, нам следует продолжить поиск в оставшейся части
массива, расположенной до среднего элемента. Выяснив, сколько элементов в
оставшейся части массива, мы опять выбираем средний элемент и сравниваем с ним
число "X". Итак, для поиска нужного элемента остаётся только четверть
массива. Затем границы поиска сужаются ещё больше - до восьмой части массива и
так далее, до тех пор, пока не найдётся элемент массива равный числу
"X" или пока не останутся два элемента массива, один больше числа
"X", а другой меньше.
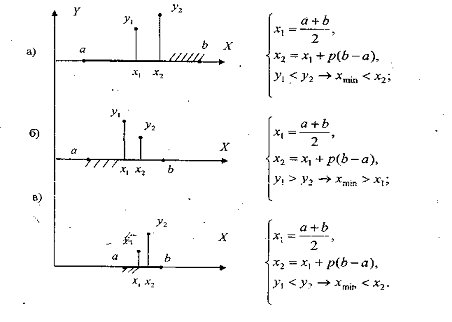
Рисунок 3.10-Условия и поиск экстремумов с
помощью метода дихотомии
3.3 Описание численного метода
оптимизации
Один из методов нахождения минимума функции f(x)
состоит в многократном вычислении функции и поиске локального минимума. Для
уменьшения количества вычислений функции важно иметь хорошую стратегию, чтобы
определить, где вычислять функцию f(x).
Одним из наиболее эффективных методов является поиск методом золотого сечения,
который так назван из-за отношения, используемого при выборе точек.
Пусть [0; 1] - начальный интервал. Если 0,5 <
r < 1, то 0 <
1 - r < 0,5 и
интервал делится на три подынтервала: [0,1 - r],
[1 - r; r]
и [r; 1] В процессе
решения используется либо сжатие вправо и получение нового интервала [0;r],
либо сжатие влево и получение интервала [1 - r,
1] Затем эти новые подинтервалы делятся на три подинтервала в таком же
соотношении, как и интервал [0; 1].
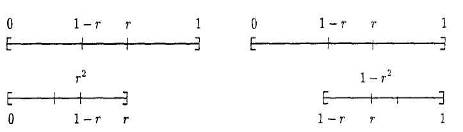
Рисунок 3.11- Интервалы, которые используются
при поиске методом золотого сечения
Требуется так выбрать r, чтобы одна
из старых точек была в правильном положении относительно нового интервала, как
показано на рис 4.1. Из этого следует, что отношение (1 -r):r такое же,
как и r: 1
Следовательно, r удовлетворяет уравнению 1 - r = r2, которое
можно записать в виде квадратного уравнения r2 + r - 1 = 0
Решение r,
удовлетворяющее неравенству 0,5 < r < 1,
равно г = (
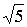 - 1) /2.
- 1) /2.
Функция f(x) должна
удовлетворять особым условиям, которые гарантируют существование истинного
минимума на интервале, чтобы можно было использовать поиск минимума функции f(х) методом
золотого сечения
Функция f(x) является
унимодальной на интервале I = [a, b], если
существует такое единственное число p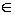 I, что
I, что
f(х) убывает
на [а,р]
f(x) возрастает
на [р,b].
Если известно, что функция f(x)
унимодальна на интервале [а,b], то можно заменить интервал
подинтервалом, на котором функция f(x) принимает
минимальное значение Для поиска методом золотого сечения требуется, чтобы
использовались две внутренние точки, с = а + (1 - r)(b - а) и d = а + r(b - а), где r является
золотым сечением, о котором упоминалось выше Эти точки удовлетворяют
неравенству а < с < d < b. Условие,
что функция f(x)
унимодальна, гарантирует, что значения функции f(с) и f(d) меньше,
чем mах{f(а),f(b)}
Рассмотрим два случая.
Если f(с) < f(d), то
минимум должен находиться на подинтервале [a; d] Заменяем b на d и
продолжаем поиск на новом подинтервале. Если f(d) < f(с), то
минимум должен находиться на подинтервале [с; b]. Заменяем
а на с и продолжаем поиск. В следующем примере метод нахождения корня
сравнивается с поиском методом золотого сечения. Сравниваем на каждом шаге
значения функции f(с) и f(d) и
принимаем решение продолжать поиск на интервале [a;d] или [с;b].
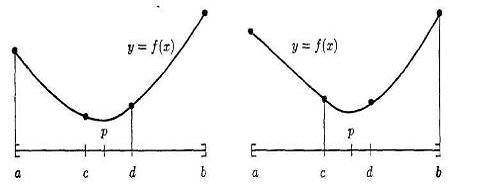
Рис. 3.12 - Процесс решения для
поиска методом золотого сечения
4. Решение задачи оптимизации на
основе моделирования на ЭВМ
.1 Разработка алгоритма
и блок-схемы задачи
В качестве метода оптимизации используем метод
золотого сечения. Данный метод основан на делении отрезка на котором находят
экстремум пополам. Он позволяет сузить данный отрезок и количество вычислений в
два раза по сравнению с методом дихотомии. Алгоритм расчета следующий:
1) определяется коэффициент деления отрезка
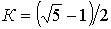 (4.1)
(4.1)
2) вычисляются величины аргумента
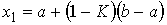 (4.2)
(4.2)
 (4.3)
(4.3)
3) вычисляются соответствующие значения
функций F(x1),
F(x2);
4) проверяется условие: x2-x1<έ,
если выполняется, то вычисляется xm=(x1+x2)/2
и F(xm),
если не выполняется, то переходим к пункту 5;
) проверяется условие: F(x1)<F(x2),
если выполняется, то принимается a=x1
и переходим к пункту 2, если не выполняется, принимаем b=x2
и переходим к пункту 2.
Блок-схема метода золотого сечения представлена
на рисунке 4.1.
4.2 Разработка
программы и анализ результатов моделирования
4.2.1 Оптимизация
выхода аммиака от температуры
В качестве критерия оптимизации
выбираем оптимизацию выхода аммиака от температуры., clear=(sqrt(5)-1)/2 %
вычисление коэффициента деления отрезка
a=723;=1020;=0.1;=1.0e+003;=
-2.6165;=
0.0136;=a+(1-r)*(b-a)=A1+A2*x1+A3*x1.^2=a+r*(b-a)=A1+A2*x2+A3*x2.^2x1-x2<s=(x1+x2)/2=A1+A2*xm+A3*xm.^2if
F1<F2=x1=x2=a+r*(b-a);=A1+A2*x2+A3*x2.^2
%Результаты
расчетов:=0.6180=
836.4439= 8.3265e+003= 906.5561=9.8051e+003 = 871.5000 %
оптимальное значение температуры
Fm
=9.0491e+003 % оптимальное
значение выхода аммиака
Оптимальное значение
температуры 871оС
4.2.2 Оптимизация
выхода аммиака от давления
В качестве критерия оптимизации
выбираем оптимизацию выхода аммиака от давления.
clc,
clear
r=(sqrt(5)-1)/2
% вычисление коэффициента деления отрезка
a=25;=30.8;=0.01;=31.9385;=
-1.2462;=
0.0211;=a+(1-r)*(b-a)=A1+A2*x1+A3*x1.^2=a+r*(b-a)=A1+A2*x2+A3*x2.^2x1-x2<s=(x1+x2)/2=A1+A2*xm+A3*xm.^2if
F1<F2=x1=x2=a+(1-r)*(b-a);=A1+A2*x1+A3*x1.^2=a+r*(b-a);2=A1+A2*x2+A3*x2.^2
end
%Результаты расчетов:
r
=0.6180
x1
= 27.2154
F1
=13.6510
x2
=28.5846
F2
=13.5567
xm
= 27.9000 % оптимальное значение давления;
Fm
= 13.5940 % оптимальное значение выхода аммиака .
Отимальное значение давления
27.9 МПа
4.2.3 Оптимизация
выхода аммиака от соотношения реагирующих компонентов
В качестве критерия оптимизации
выбираем оптимизацию выхода аммиака от соотношения реагирующих компонентов.
clc,
clear
r=(sqrt(5)-1)/2
% вычисление коэффициента деления отрезка
a=2.7;=3.3;=0.01;=48.8362;=-25.8143;=
4.6667;=a+(1-r)*(b-a)=A1+A2*x1+A3*x1.^2=a+r*(b-a)=A1+A2*x2+A3*x2.^2x1-x2<s=(x1+x2)/2=A1+A2*xm+A3*xm.^2if
F1<F2=x1=x2=a+(1-r)*(b-a);=A1+A2*x1+A3*x1.^2=a+r*(b-a);
F2=A1+A2*x2+A3*x2.^2
%Результаты расчетов:
r
=0.6180
x1
=2.9292
F1
=13.2622
x2
=3.0708
F2
= 13.5718
xm
=3 % оптимальное значение соотношения реагирующих веществ;
Fm
=13.3936 % оптимальное значение выхода аммиака.
Оптимальное значение
соотношения реагирующих веществ 3
4.2.4 Оптимизация
выхода аммиака от времени контактирования
В качестве критерия оптимизации
выбираем оптимизацию выхода аммиака от времени контактирования.
clc,
clear
r=(sqrt(5)-1)/2
% вычисление коэффициента деления отрезка
a=1.8;=10;=0.01;=-1.4006;=2.2739;=
-0.1068;=a+(1-r)*(b-a)=A1+A2*x1+A3*x1.^2=a+r*(b-a)=A1+A2*x2+A3*x2.^2x1-x2<s=(x1+x2)/2=A1+A2*xm+A3*xm.^2if
F1<F2=x1=x2=a+(1-r)*(b-a);=A1+A2*x1+A3*x1.^2=a+r*(b-a);
F2=A1+A2*x2+A3*x2.^2
%Результаты расчетов:
r
=0.6180
x1
= 4.9321
F1
=7.2166
x2
=6.8679
F2
=9.1788
xm
=5.9000 % оптимальное значение времени контактирования;
Fm
= 8.2977 % оптимальное значение выхода аммиака.
Оптимальное значение времени
контактирования 6секунд
Заключение
В данной курсовой работе рассмотрен
технологический процесс промышленного синтеза аммиака на установке 600 т/сутки.
Были построены и проанализированы зависимости выхода аммиака от температуры,
давления, соотношения реагирующих веществ и времени контактирования газовой
смеси.
На основе данных зависимостей была проведена
оптимизация химико-технологического процесса синтеза аммиака. Были получены
следующие оптимальные значения технологических параметров:
оптимальное значение температуры 850 град., при
выходе аммиака 9,05%
оптимальное значение давления 27,9 МПа, при
выходе аммиака 13,6%
оптимальное значение соотношения реагирующих
веществ 3, при выходе аммиака 13,9%
оптимальное значение времени контактирования 5,9
секунд, при выходе аммиака 8,3%
Список
использованных источников
1.
Салтанова В.П. Технология связанного азота. - М.: Высшая школа,1981. - 205с.
.
Атрощенко В.И. и др. Методы расчётов по технологии связанного азота. 2-е изд. -
К.: Вища школа, 1978. - 312 с.
.
Олевский В.М. Производство азотной кислоты в агрегатах большой единичной
мощности. - М.: Химия, 1985. - 400 с.
.
Атрощенко В.И., Каргин С.И. Технология азотной кислоты. - М.: Химия, 1970. -
496 с.
5.
Атрощенко В.И. и др. Технология связанного азота. - К.: Вища школа, 1985. - 327
с.
6.
Вэйлас С. Химическая кинетика и расчёты промышленных реакторов. - М.: Химия,
1967. - 416 с.
.
Бояринов А.И., Кафаров В.В. Методы оптимизации в химической технологии. - М.:
Химия, 1975. - 576 с.
.
Закгейм А.Ю. Введение в моделирование химико-технологических процесс -сов. -
М.: Химия, 1973. - 224 с.
.
Кафаров В.В. Методы кибернетики в химии и химической технологии. - М.: Химия,
1976. - 464 с.