Внеклассная работа по математике в 7-9 классах

Министерство образования и науки Республики Казахстан

Павлодарский государственный педагогический институт

Кафедра: Алгебры, геометрии и МПМ

ВНЕКЛАССНАЯ РАБОТА ПО МАТЕМАТИКЕ В 7-9 КЛАССАХ

САДЫМОВА КУЛЬШАТ МАУЛЕНОВНА

Научный руководитель А.Б. Найманова

Павлодар, 2005

Содержание

Введение

Глава І. Цели проведения внеклассной работы по математике в 7-9 классах

1.1 Общая характеристика внеклассной работы по математике

.2 Классификация внеклассной работы

Глава ІІ. Роль внеклассной работы по математике

2.1 Внеклассная работа учащихся по математике и методика её проведения

.2 Роль внеклассной работы в подготовке учащихся, отстающих от других в изучении программного материала

.3 Роль внеклассной работы в подготовке учащихся, проявляющих к изучению математики повышенный интерес и способности

.4 Работа учащихся с дополнительной литературой при обучении математике

Глава ІІІ. Виды внеклассной работы по математике

3.1 Факультативные занятия по математике и методика их проведения

.2 Кружковые занятия по математике и методика их проведения

.3 Общая характеристика школьных математических олимпиад. Примеры задач математических олимпиад для 8-9 классов

.4 Математический бой. Схема проведения

.5 Игровые формы занятия

Заключение

Список использованной литературы

ПриложениЯ

ВВЕДЕНИЕ

Одно из главных направлений реформы общеобразовательной и профессиональной школы - повысить качество образования и воспитания учащихся. Наряду с уроком основной формой учебного процесса в школах все большее значение приобретает внеклассная работа по математике. Способствуя глубокому и прочному овладению изучаемым материалом, повышения математической культуры, привитию навыков самостоятельной работы, внеклассная работа развивает интерес к изучению математики и творческие способности школьников.

Внеклассная работа по математике формирует и развивает способности и личность ребёнка. Управлять этим процессом - значит не только развивать и совершенствовать заложенное в человеке природой, но формировать у него потребность в постоянном саморазвитии и самореализации, так как каждый человек воспитывает себя, прежде всего сам, здесь добытое лично - добыто на всю жизнь.

Цели обучения математике обусловлены структурой личности, общими целями образования, концепцией предмета математики, её статусом и ролью в науке, культуре и жизнедеятельности общества, ценностями математического образования, новыми образовательными идеями, среди которых важное место занимает развивающее обучение.

Под внеклассной работой понимается не обязательные, систематические занятия с учащимися во внеурочное время. Математические школы, факультативные занятия и кружки призваны углублять математические знания школьников, уже определивших основной круг своих учебных интересов. Учитывая, что потребность в специалистах- математиках сейчас очень велика, необходимо формировать соответствующий интерес еще в школе.

На уроках математики имеется немало возможностей заинтересовать школьников содержанием этой науки. Вместе с тем основная цель занятий всё же состоит в обучении определённому комплексу процедур математического характера, занимательность изложения подчинена этой цели, развитие способностей учащихся происходит в рамках изучения обязательного материала.

Нередко участие во внеклассной работе по математике может явиться первым этапом углубленного изучения математики и привести к выбору факультатива по математики, к поступлению в математическую школу, к самостоятельному изучению заинтересовавшего материала и т.п.

Данная тема на сегодняшний день актуальна, так как внеклассная работа помогает учителю не только формировать знания, умения, навыки по математике, но и развивать логическое мышление, память, повышает интерес к предмету. Также внеклассная работа помогает проверять свои силы, математические способности и осознавать роль и значимость данного предмета и глубже его познавать.

ГИПОТЕЗА - развитие способности и интереса к математике будет более высоким и эффективным если будут различные виды внеклассной работы.

ГЛАВА І. ЦЕЛИ ПРОВЕДЕНИЯ ВНЕКЛАССНОЙ РАБОТЫ ПО МАТЕМАТИКЕ В 7-9 КЛАССАХ

.1 Общая характеристика внеклассной работы по математике

Одной из важнейших целей проведения внеклассной работы по математике является развитие интереса учащихся к математике, привлечение учащихся к занятиям в факультативах. У учащихся имеется большое желание проверить свои силы, математические способности, умение решать нестандартные задачи. Их привлекает возможность добровольного участия.

Проведение внеклассной работы по математике является прекрасным средством повышения квалификации учителей. Одной из целей является расширение изучаемого материала курса математики, иногда такое расширение выходит за рамки обязательной программы. Рассмотрение на дополнительных занятиях таких вопросов неизбежно приводит учителя к необходимости основательного знакомства с этим материалом и с методикой его изложения учащимся.

Так же это помогает выявить учащихся, имеющих интерес и склонности к занятиям математикой, что весьма важно для решения вопроса о подготовке большого числа новых математических и научно-методических кадров. Современная школа должна управлять воспитательным процессом.

Управлять воспитательным процессом - значит не только развивать и совершенствовать заложенное в человеке природой, корректировать намечающиеся нежелательные социальные отклонения в его поведении и сознании, но информировать у него потребность в постоянном саморазвитии, самореализации физических и духовных сил, так как каждый человек воспитывает себя, прежде всего сам.

Основные цели проведения внеклассной работе по математике следующие:

. Определить степень заинтересованности учеников и учителей во внеклассной работе по математике.

. Определить степень совпадения интересов педагога и учеников.

. Определить место внеклассной работы по математике средних и старших классов в школьной жизни.

. Определить направленность этой внеклассной работы.

.2 Классификация внеклассной работы

математика обучение занятие игровой

Существуют различные виды классификации внеклассной работы по математике, они весьма подробно освещены в многочисленной педагогической и методической литературе. Ю.М.Колягин различает два вида внеклассной работы по математике.

1. Работа с учащимися, отстающими от других в изучении программного материала, т.е. дополнительные занятия по математике.

2. Работа с учащимися проявляющими интерес к математике.

Но можно выделить ещё и третий вид работы.

.        Работа с учащимися по развитию интереса в изучении математики.

Основной целью первого вида внеклассной работы является ликвидация пробелов и предупреждение неуспеваемости. Бытует мнение, что если такая дополнительная работа ведётся. То это говорит, что недостаточно организована работа на уроке. В любом случае эта работа должна носить ярко выраженный индивидуальный характер и требует от учителя особого такта и характера.

Цели второго вида внеклассной работы по математике могут быть очень разнообразны и зависят от того, что интересно и что хотят узнать нового о математике ученики так, например:

. Развитие и углубление знаний по программному материалу.

. Привитие им навыков исследовательской работы.

. Воспитание культуры математического мышления.

. Развитие представлений о практическом применении математики и т.п.

Третий вид внеклассной работы может носить подобные цели, но главный упор делается на развитие интересов математики в соответствии с возможностями этой группы учащихся.

Существуют следующие формы внеклассной работы:

1. Математический кружок.

2. Факультатив.

3. Олимпиады конкурсы, викторины.

4. Математические олимпиады.

5. Математические дискуссии.

6. Неделя математики.

7. Школьная и классная математическая печать.

8. Изготовление математических моделей.

9. Математические экскурсии.

Указанные формы часто пересекаются и поэтому трудно провести между ними резкие границы. Более того, элементы многих форм могут быть использованы при организации работы по какой либо одной из них. Например, при проведении математического вечера можно использовать соревнования, конкурсы, доклады и т. д.

ГЛАВА ІІ. РОЛЬ ВНЕКЛАССНОЙ РАБОТЫ ПО МАТЕМАТИКЕ

.1 Внеклассная работа учащихся по математике и методика её проведения

Требования, предъявляемые программой по математике, школьными учебниками и сложившейся методикой обучения, рассчитаны на так называемого "среднего" ученика. Однако уже с первых классов начинается резкое расслоение коллектива учащихся: на тех, кто легко и с интересом усваивают программный материал по математике, на тех, кто добивается при изучении математики лишь удовлетворительных результатов, и тех, кому успешное изучение математики дается с большим трудом.

Все это приводит к необходимости индивидуализации обучения математике, одной из форм которой является внеклассная работа.

Под внеклассной работой по математике понимаются необязательные систематические занятия учащихся с преподавателем во внеурочное время.

Следует различать два вида внеклассной работы по математике: работа с учащимися, отстающими от других в изучении программного материала (дополнительные внеклассные занятия);

работа с учащимися, проявляющими к изучению математики повышенный, по сравнению с другими, интерес и способности (собственно внеклассная работа в традиционном понимании смысла этого термина).

Говоря о первом направлении внеклассной работы, следует отметить, что этот вид внеклассной работы с учащимися по математике в настоящее время имеет место в каждой школе. Вместе с тем повышение эффективности обучения математике с необходимостью должно привести к снижению значения дополнительной учебной работы с отстающими. В идеальном случае первый вид внеклассной работы должен иметь ярко выраженный индивидуальный характер и проявляться лишь в исключительных случаях (например, в случае продолжительной болезни учащегося, перехода из школы другого типа т. п.). Однако в настоящее время эта работа требует еще значительного внимания со стороны учителя математики.

.2 Роль внеклассной работы в подготовке учащихся, отстающих от других в изучении программного материала

Основной целью ее является своевременная ликвидация (и предупреждение) имеющихся у учащихся пробелов в знаниях и умениях по курсу математики.

Передовой опыт работы учителей математики свидетельствует об эффективности следующих положений, связанных с организацией и проведением внеклассной работы с отстающими.

. Дополнительные (внеклассные) занятия по математике целесообразно проводить с небольшими группами отстающих (по 3-4 человека в каждой); эти группы учащихся должны быть достаточно однородны как с точки зрения имеющихся у школьников пробелов в знаниях, так и с точки зрения способностей к обучаемости.

. Следует максимально индивидуализировать эти занятия (например, предлагая каждому из таких учащихся заранее подготовленное индивидуальное задание и оказывая в процессе его выполнения конкретную помощь каждому).

. Занятия с отстающими в школе целесообразно проводить не чаще одного раза в неделю, сочетая эту форму занятий с домашней работой учащихся по индивидуальному плану.

. После повторного изучения того или иного раздела математики на дополнительных занятиях необходимо провести итоговый контроль с выставлением оценки по теме.

. Дополнительные занятия по математике, как правило, должны иметь обучающий характер; при проведении занятий полезно использовать соответствующие варианты самостоятельных или контрольных работ из "Дидактических материалов", а также учебные пособия (и задания) программированного типа.

. Учителю математики необходимо постоянно анализировать причины отставания отдельных учащихся при изучении ими математики, изучать типичные ошибки, допускаемые учащимися при изучении той или иной темы. Это делает дополнительные занятия по математике более эффективными.

.3 Роль внеклассной работы в подготовке учащихся, проявляющих к изучению математики повышенный интерес и способности

Второе из указанных выше направлений внеклассной работы по математике - занятия с учащимися, проявляющими к ее изучению повышенный интерес, отвечает следующим основным целям:

. Пробуждение и развитие устойчивого интереса учащихся к математике и ее приложениям.

. Расширение и углубление знаний учащихся по программному материалу.

. Оптимальное развитие математических способностей у учащихся и привитие учащимся определенных навыков научно-исследовательского характера.

. Воспитание высокой культуры математического мышления.

. Развитие у учащихся умения самостоятельно и творчески работать с учебной и научно-популярной литературой.

. Расширение и углубление представлений учащихся о практическом значении математики в технике и практике социалистического строительства.

. Расширение и углубление представлений учащихся о культурно-исторической ценности математики.

. Воспитание учащихся чувства коллективизма и умения сочетать индивидуальную работу с коллективной.

. Установление более тесных деловых контактов между учителем математики и учащимися и на этой основе более глубокое изучение познавательных интересов и запросов школьников.

. Создание актива, способного оказать учителю математики помощь в организации эффективного обучения математике всего коллектива данного класса (помощь в изготовлении наглядных пособий, занятиях с отстающими, в пропаганде математических знаний среди других учащихся).

Предполагается, что реализация этих целей частично осуществляется на уроках. Однако в процессе классных занятий, ограниченных рамками учебного времени и программы, это не удается сделать с достаточной полнотой. Поэтому окончательная и полная реализация этих целей переносится на внеклассные занятия по математике этого вида.

2.4 Работа учащихся с дополнительной литературой при обучении математике

Общая характеристика работы учащихся с дополнительной литературой по математике. Психологические основы эффективной работы школьников с математической литературой. Обучение школьников общим приемам работы с дополнительной литературой по математике

Перед школой стоят задачи повышения общего уровня развития учащихся, подготовки школьников к дальнейшему образованию и самообразованию и к практической творческой деятельности по любой специальности. Для решения этих задач учителю математики необходимо не только обеспечить определенный запас знаний у школьников, но и выработать умение добывать эти знания, развить в учениках стремление и способности к самостоятельному приобретению новых знаний.

Среди различных источников новых знаний по математике одно из первых мест занимает книга. Всю литературу, знакомящую школьников с основами математики и с их применением, можно разделить на учебную (стабильные учебники, дидактические материалы, сборники задач, справочники) и дополнительную (научно-популярные книги и статьи, сборники задач олимпиадного характера).

В процессе обучения математике учащиеся весьма широко используют основную учебную литературу; однако дополнительную литературу по математике все еще читают весьма немногие, причем это чтение не носит организованного характера. Между тем обучающее значение работы учащихся с дополнительной литературой по математике весьма велико, так как именно эта работа способствует не только повышению качества знаний учащихся, но и развитию у них устойчивого интереса к математике.

Немалое обучающее и развивающее значение имеют также умения и навыки работы с математической литературой.

Опыт, приобретаемый школьниками в процессе работы с учебной литературой, оказывается недостаточным для успешной работы с дополнительной литературой. Поэтому умения и навыки работы школьников с математической литературой необходимо целенаправленно развивать, причем развивать систематически. Этому, в частности, способствует:

) возможно более полное соответствие изучаемой литературы направлениям познавательных интересов школьников;

) систематическое использование учителем и учащимися дополнительной литературы в процессе обучения математике (на классных занятиях и в домашней работе учащихся);

) целенаправленная деятельность учителя по обучению учащихся общим приемам работы с математической литературой;

) постановка специальных заданий школьникам, требующих привлечения дополнительной литературы по математике и контроль за их выполнением;

) постоянное использование дополнительной математической литературы на факультативных занятиях и т. д.

Эффективность самостоятельной работы учащихся с учебной или дополнительной литературой вообще (и математической в частности) зависит и от некоторых психологических факторов (установка, вдохновение, интерес, волевое усилие, самостоятельность, трудолюбие и т.п.).

Одним из важнейших условий успешной работы с книгой является наличие особого состояния умственной деятельности, называемого установкой.

Под установкой понимается готовность к действию в определенном направлении, т. е. своеобразное состояние психики, возникающее при единстве мотива деятельности (потребности в ней) и ситуации, которая ему соответствует.

Экспериментальные исследования, проведенные психологом Д. Н. Узнадзе и другими, показали, что наличие четкой установки к деятельности значительно повышает ее эффективность.

Применительно к работе с книгой такая установка способствует активизации внимания и памяти, способствует точности восприятия содержания, помогает выделять в тексте главную мысль, развивает способность творчески воспринимать получаемую информацию и т. д., т. е. способствует выработке умений и навыков самостоятельного приобретения новых знаний в процессе работы над литературой.

"Процесс формирования всякого навыка есть выработка и фиксация у субъекта установки на осуществление определенного действия.

Учение - определенная форма поведения, управление которым достигается установкой индивида. Установку следует считать опорой нормального функционирования механизма обратных связей в организме у каждого учащегося".

Поэтому целенаправленность работы учащихся с дополнительной (и учебной) литературой, наличие сильной мотивации (соответствия познавательных интересов и деятельности) во многом определяют эффективность этого важного вида учебной деятельности.

К числу основных компонентов, определяющих выработку умений и навыков эффективной самостоятельной работы учащихся с научной (математической) литературой, относятся:

) умение логически (структурно) осмыслить текст;

) умение читать с пониманием;

) умение выделить и запомнить главное;

) умение акцентировать свое внимание на той или иной основной мысли, выраженной в тексте;

) умение творчески перерабатывать информацию (в том числе "читать между строк");

) умение составить план, конспект на тему, сделать из него выписки;

) самостоятельность и критичность восприятия;

) усилие воли, чтобы заставить себя работать и в случае возникновения трудностей и неясностей (что особенно характерно для работы с математическим текстом);

) настойчивость в преодолении трудностей.

В связи с последними из этих компонентов уместно привести следующее высказывание В. И. Ленина: "...сразу кое-кого, может быть, и отпугнет трудность изложения, - надо опять предупредить, что этим не следует смущаться, что непонятное на первый раз при чтении будет понятно при повторном чтении, или когда вы подойдете к вопросу впоследствии с, несколько иной стороны... "

В перечне этих условий заложена своеобразная программа обучающей деятельности учителя математики при организации самостоятельной работы учащихся с книгой.

Для формирования и развития рассмотренных выше умений и навыков полезно применять определенную систему специальных учебных заданий.

. Задания, формулирующие и развивающие умение выборочного чтения дополнительной литературы по математике. Такие задания обычно выражены в форме вопросов, ответы на которые явно или скрыто содержатся в данной для изучения дополнительной литературе. Таковы, например, задания по наведению справок исторического характера, задания типа "Установить, какая фигура называется ромбоидом", "Найти в данной книге одно-два предложения, эквивалентных аксиоме параллельности Евклида" и т. д.

. Задания, формулирующие способность сопоставления новых знаний, полученных при чтении дополнительной литературы, с уже усвоенными знаниями.

Так, например, после самостоятельного изучения учащимися преобразования инверсии по дополнительной литературе учащимся предлагаются задания: "Сравнить свойства инверсии со свойствами гомотетии" и т. п.

. Задания, формирующие способность применения новых знаний, полученных при чтении дополнительной литературы. Так, например, при изучении какого-либо нового метода решения задач учащимся предлагается применить этот метод к решению уже известной задачи или самим подобрать (составить) задачи, решаемые этим методом.

. Задания, формирующие умение свести прочитанное в определенную целостную систему. Таковы, например, задания:

а) подготовить доклад по прочитанному;

б) прореферировать данную книгу (главу книги);

в) составить какую-либо таблицу (диаграмму, схему) по прочитанному и т. д.

ГЛАВА ІІІ. ВИДЫ ВНЕКЛАССНОЙ РАБОТЫ ПО МАТЕМАТИКЕ

.1 Факультативные занятия по математике и методика их проведения

Факультативные занятия по математике ведутся в школе с 7 класса со следующим числом недельных часов: 7 класс - 1 час, 8 класс -1 час, 9 - 2 часа.

Главной целью факультативных занятий по математике является углубление и расширение знаний, развитие интереса учащихся к предмету, развитие их математических способностей, привитие школьникам интереса и вкуса к самостоятельным занятиям математикой, воспитание и развитие их инициативы и творчества.

Программа основного курса математики вместе с программой факультативных занятий по математике для средней школы составляют программу повышенного уровня по данному предмету для учащихся данного класса.

Программа факультативных занятий по математике составлена так, что все вопросы ее могут изучаться синхронно с изучением основного курса математики в школе. В тех случаях, когда в данном классе основной курс математики ведет один учитель, а факультативный - другой, изучение тем факультатива может проводиться независимо от основного курса программы (в этом случае изучение тем можно проводить с некоторым запозданием по отношению к основному курсу программы).

Для того чтобы факультативные занятия по математике были эффективными, необходимо их организовать там, где есть:

) высококвалифицированные учителя или другие специалисты, способные вести занятия на высоком научно-методическом уровне;

) не менее 15 учащихся, желающих изучать данный факультативный курс.

Если школа имеет классы с небольшой наполняемостью (что особенно характерно для некоторых сельских школ), то группы учащихся для факультативных занятий можно комплектовать по параллелям или из учащихся смежных классов (7-9 классы).

Запись учащихся на факультативные занятия производится на добровольных началах в соответствии с их интересами. Не следует принуждать учащихся обязательно изучать факультативные предметы. Особенно внимательно следует относиться к тем учащимся, которые встречают трудности в изучении математики или совмещают обучение в школе с другими видами занятий (спорт, музыка и т. д.). По окончании факультативного курса учащиеся сдают зачет (с оценкой), о чем делается отметка в аттестате. Учитель математики несет полную ответственность за качество факультативных занятий; факультативные занятия вносятся в расписание и оплачиваются учителю.

Проведение факультативных занятий по математике не означает отказа от других форм внеклассной работы (математические кружки, вечера, олимпиады и т. д.). Они должны дополнять эти формы работы с учащимися, которые интересуются математикой.

Возможность 1-2 часа в неделю дополнительно работать со школьниками, проявляющими повышенный интерес и способности к математике, представляет собой одно из проявлений новой формы обучения математике - дифференцированного обучения.

По существу факультативные занятия являются наиболее динамичной разновидностью дифференциации обучения.

В какой бы форме и какими бы методами не проводились факультативные занятия по математике, они должны строиться так, чтобы быть для учащихся интересными, увлекательными, а подчас и занимательными. Необходимо использовать естественную любознательность школьника для формирования устойчивого интереса к своему предмету. Известный французский физик Луи де Бройль писал, что современная наука - "дочь удивления и любопытства, которые всегда являются ее скрытыми движущими силами, обеспечивающими ее непрерывное развитие".

Основными формами проведения факультативных занятий по математике являются в настоящее время изложение узловых вопросов данного факультативного курса учителем (лекционным методом), семинары, собеседования (дискуссии), решение задач, рефераты учащихся (как по теоретическим вопросам, так и по решению цикла задач), математические сочинения, доклады учащихся и т. д.

Однако учителю не следует отдавать предпочтение какой-либо одной форме или методу изложения. Вместе с тем, памятуя о том, что на факультативных занятиях по математике самостоятельная работа учащихся должна занять ведущее положение, следует все же чаще применять решение задач, рефераты, доклады, семинары-дискуссии, чтение учебной и научно-популярной литературы и т. п.

Одной из возможных форм ведения факультативных занятий по математике является разделение каждого занятия на две части. Первая часть посвящается изучению нового материала и самостоятельной работе учащихся по заданиям теоретического и практического характера. По окончании этой части занятия учащимся предлагается домашнее задание по изучению теории и ее приложений. Вторая часть каждого занятия посвящена решению задач повышенной трудности и обсуждению решений особенно трудных или интересных задач. Эта форма проведения факультативных занятий может способствовать успешному переходу от форм и методов обучения в школе к формам и методам обучения в высших учебных заведениях.

Естественно также при проведении факультативных занятий в основном использовать методы изучения (а не обучения) математики, а также проблемную форму обучения.

В частности, ее можно осуществить, если представить изучаемый факультативный курс в виде серии последовательно расположенных задач. "Решая последовательно все задачи самостоятельно или при незначительной помощи преподавателя, школьники постепенно изучают курс при большом личном участии, проявляя активность и самостоятельность, овладевая техникой математического мышления. Теоремы имеют вид задач. Если теорема, которую учащиеся должны доказать, является большой или трудной, то она разбивается на несколько задач так, что решение предыдущей помогает решить последующую. Определения либо включаются преподавателем в текст задачи, либо сообщаются особо. В необходимых случаях преподаватель проводит предварительную беседу или делает обобщения. Листочки с заданиями, размноженные на машинке, на каждое занятие выдаются всем ученикам"

Полезно также широко использовать задачи проблемного характера

В настоящее время факультативные занятия по математике проводятся по двум основным направлениям:

а) изучение курсов по программе "Дополнительные главы и вопросы курса математики";

б) изучение специальных математических курсов. Содержание программы "Дополнительные главы и вопросы" систематического курса математики позволяет решить и углубить изучение программного материала, ознакомить учащихся с некоторыми общими современными математическими идеями, раскрыть приложение математики в практике, готовит учителя к работе по новой программе".

В качестве конкретного примера постановки факультативного курса рассмотрим объединенную тему "Множества и операции над ними. Бесконечные множества".

Содержание программы по этой факультативной теме явно ориентирует на то, чтобы общие понятия о множествах, элементах множества и операциях над множествами возникали из рассмотрения конкретных примеров множеств решений уравнений, неравенств и их систем.

Такая постановка вопроса не соответствует той роли, которую играет понятие множества вне рамок учения об уравнениях и неравенствах как в математике, так и за пределами этой науки. Поэтому не исключено, что после изучения этой темы учащиеся не заметят первоначального объективного источника возникновения понятия о множестве и не поймут фундаментального значения этого понятия для всей математики. Для того чтобы указанная тема наиболее полно способствовала углублению математических знаний учащихся, у них должно быть сформировано представление о понятии множества как о первоначальном понятии математики, из которого развивается наука-математика. Здесь не идет речь о строгом логическом обосновании математики. Достаточно показать на конкретных примерах, как проявляются понятия множества, отношения между множествами и операции над множествами в различных разделах математики - арифметике, алгебре, геометрии, в учениях о функциях, уравнениях и неравенствах. Вот эта линия и должна последовательно проводиться на факультативных занятиях.

Объем материала по теории множеств, изучаемого на факультативных занятиях в девятых классах, зависит от того, изучались или не изучались элементы теории множеств на факультативных занятиях в восьмых классах.

Если эта тема изучалась в 9 классе, то некоторые из входящих в нее вопросов рассматриваются лишь в порядке повторения (полезнее - при решении соответствующих задач); если же эта тема не ставилась ранее, то в целях сокращения материала некоторые из более элементарных задач или упражнений следует опустить. Рассмотрение универсального множества имеет важное значение в развитии функционального мышления учащихся. Раскрытию содержания этого понятия, его относительного характера должно быть уделено большое внимание. В 9 классе для обоснования свойств отношений между множествами и операций над множествами вполне достаточно применение кругов Эйлера. В 10 классе кругами Эйлера целесообразно иллюстрировать результаты аналитических обоснований.

Если учитель дополнит алгебру множеств сведениями из математической логики (логические функции, область истинности предиката), то это без сомнения будет способствовать более углубленному и осознанному усвоению учащимися многих вопросов школьного курса математики, в частности вопросов теории уравнений, неравенств и их систем.

При изучении вопроса о бесконечных множествах даже на факультативных занятиях нет возможности основательно ознакомить учащихся с арифметикой трансфинитных чисел. Да в этом, на наш взгляд, и нет необходимости. Важно лишь, чтобы учащиеся осознали главные особенности конечных и бесконечных множеств, проявляющиеся в специфике арифметики натуральных и трансфинитных чисел.

Уже после первого занятия учащиеся систематически получают задания для самостоятельного изучения соответствующего материала.

На самих занятиях качество усвоения теории проверяется в процессе решения задач и примеров. Здесь совершенно недопустимы такие формы работы, которые сковывали бы инициативу учащихся. Занятие начинается с постановки упражнения для всех учащихся. За время, которое отводится на выполнение задачи или примера, учитель успевает проследить, кто и как справляется с заданием. Не следует торопить учащихся. Обычно, если не все, то некоторые из них выполняют задание в запланированное учителем время, а затем начинается разбор и теоретическое обоснование решений. Инициатива в оценке способов решения, в исправлении ошибок, в постановке вопросов представляется самим учащимся. В процессе этой работы достигается логическая точность в формулировках определений понятия или их свойств. В заключительном слове учитель дает мотивированную оценку знаний учащихся. Помимо указанной формы контроля знаний, целесообразно проводить кратковременные 15-20-минутные проверочные работы. Занятия по курсу 9 класса полезно завершить часовой контрольной работой.

Для особого факультативного изучения полезно отнести:

а) решение нестандартных математических задач;

б) элементы программирования и принцип работы электронно-вычислительных машин;

в) творческие индивидуальные работы учащихся над избранными ими самими вопросами элементарной математики.

Приведем пример факультативного занятия по математике для учеников 7-х классов отстающих от школьной программы. Для того, чтобы выяснить уровень ученика, по теме: сложение и вычитание дробей с разными знаменателями. Зададим ученикам несколько теоретических и практических заданий. Во время опроса ученики не должны пользоваться учебниками, тетрадями и другой литературой.

Теоретические вопросы.

.        Сформулируйте правило сложения дробей с одинаковыми знаменателями.

.        Сформулируйте правило вычитания дробей с одинаковыми знаменателями.

.        Как выполняют сложение и вычитание дробей с разными знаменателями.

Теоретические вопросы у всех должны быть одинаковые. Зачастую ученики не могут ответить на теоретические вопросы, именно поэтому возникают проблемы с практическим заданием. Важно на факультативных занятиях более подробно рассматривать нужные правила. Ученик не должен стесняться задавать вопросы.

Далее подробно решить задание. Например: сложим дроби 1/6а+1/3в=2.

Знаменатели дробей представляют собой одночлены. Наиболее простым общим знаменателями являются одночлен 12ав. Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей дробей, а каждая переменная взята с наибольшим показателем, с которым она входит в знаменатели дробей. Дополнительные множители к числителям и знаменателям этих дробей равны 3в и 2а.

На основании этого примера дать ученикам попробовать еще раз справиться с заданием. Желающие могут выйти к доске.

На факультативных занятиях для отстающих учеников, главное дать понять ученику, что он сможет решить предложенные задания. Даже если поначалу ученику помогают, то впоследствии ему будет важно добиться самостоятельных успехов.

3.2 Кружковые занятия по математике и методика её проведения

Математический кружок - одна из наиболее действенных и эффективных форм внеклассных занятий. В основе кружковой работы лежит принцип строгой добровольности. Обычно кружковые занятия организуются для хорошо успевающих учащихся. Однако следует иметь в виду, что иногда и слабо успевающие учащиеся изъявляют желание участвовать в работе математического кружка и нередко весьма успешно занимаются там; учителю математики не следует этому препятствовать. Необходимо лишь более внимательно отнестись к таким учащимся, постараться укрепить имеющиеся у них ростки интереса к математике, проследить за тем, чтобы работа в математическом кружке оказалась для них посильной. Конечно, наличие слабо успевающих учащихся среди членов математического кружка затрудняет работу учителя, однако путем индивидуализации заданий, предлагаемых учителем кружковцам, можно в некоторой степени ослабить эти трудности. Главное - сохранить массовый характер кружковых занятий по математике, являющийся следствием доступности посещения кружковых занятий всеми желающими.

Уже при организации математического кружка необходимо заинтересовать учащихся, показать им, что работа в кружке не является дублированием классных занятии, четко сформулировать цели и раскрыть характер предстоящей работы (для этого целесообразно выделить часть времени на одном из уроков математики с тем, чтобы обратиться с сообщением об организации кружка ко всему классу).

На первом занятии кружка надо наметить основное содержание работы, выбрать старосту кружка, договориться с учащимися о правах и обязанностях члена кружка, составить план работы и распределить поручения за те или иные мероприятия (выпуск математической стенной газеты, ведение документации работы кружка и т. п.).

Занятия кружка целесообразно проводить один раз в неделю, выделяя на каждое занятие по одному часу. К организации работы математического кружка целесообразно привлекать самих учащихся (поручать им подготовку небольших сообщений по изучаемой теме, подбор задач и упражнений по конкретной теме, подготовку справок исторического характера, изготовление моделей и рисунков к данному занятию и т. д.). На занятиях математического кружка учитель должен создать "атмосферу" свободного обмена мнениями и активной дискуссии. Тематика кружковых занятий по математике в современной школе весьма разнообразна. В тематике кружковых занятий для 5-11 классов находят место вопросы, связанные с историей математики, жизнью и деятельностью российских и зарубежных известных математиков.

.3 Общая характеристика школьных математических олимпиад. Примеры задач математических олимпиад для 7-9 классов

Школьные математические олимпиады представляют собой более массовые соревнования, поскольку они охватывают учеников не одного, а всех параллельных классов школы.

Олимпиады в школе проводятся несколько раз в год с целью повышения интереса учеников к математике, расширения их мировоззрения, выявления наиболее способных учеников, подведения итогов работы математических кружков или клуба юных математиков, повышение общего уровня преподавания математики в средних и старших классах.

Примеры олимпиадных задач 1998 года, решения и комментарии к этим задачам.

класс

. Турист листая дневник путешествия, заметил, что на позапрлошлой неделе он прошел на 5 км больше, чем на прошлой, а на прошлой неделе - на 60 км меньше, чем на этой и позапрошлой неделях вместе. Сколько километров он прошел на этой неделе?

. Существуют ли 2003 натуральных числа, сумма которых равна их произведению? Если да, то приведите пример, если нет, то обоснуйте ответ.

класс

.На острове Чунга-Чанга 80% мужчин женаты, а 40% женщин -замужем. Какая доля населения этого острова состоит в браке?

.Можно ли треугольник с тремя различными сторонами разрезать на два равных треугольника?

.В таблице 3*3 расставлены положительные числа. Произведение чисел в каждой строке и в каждом столбце равно 1, а произведение чисел в любом квадрате 2*2 равно 4. Какое число стоит в центре квадрата?

.Доказать, что число 2001*2003³ - 2002*2002³ является кубом натурального числа.

.В пробирке находится 2001 красная амёба, 2002 синие амёбы и 2003 зелёные амёбы. Две амёбы двух разных цветов могут сливаться в одну амёбу третьего цвета (красная и зелёная - в синюю, красная и синяя - в зелёную, зелёная и синяя - в красную). После нескольких таких слияний в пробирке осталась ровно одна амёба. Каков её цвет?

класс

1. Бизнесмен Вася купил 2 автомобиля, заплатив в сумме 36000$, и перепродал их, получив 25% прибыли. При перепродаже первого автомобиля прибыль составила 50%, а при перепродаже второго - 12,5%. Но о второй сделке Вася не сообщил в налоговую инспекцию, и в конце года с него взяли штраф, равный половине первоначальной стоимости второго автомобиля. Сколько долларов потерял Вася в результате данной сделки?

2. В таблице расставлены числа. В каждой строке и в каждом столбце произведение чисел равно 1. В каждом квадрате произведение чисел равно 2. Найти произведение чисел, стоящих в двух верхних клетках третьего столбца.

3. Докажите, что число 5¹⁶ + 2¹⁴ - составное число.

4. Дана окружность с центром в точке О₁. Окружность с центром О₂ проходит через точку О₁. А и В - точки пересечения этих окружностей. Касательная к окружности с центром О₂, проходящая через точку В пересекает первую окружность в точке С. Докажите, что AB=BC.

5. По кругу сидят 2002 хамелеона, которые могут менять цвет в следующем порядке: синий, оранжевый, фиолетовый, зелёный. Если прикоснуться к одному из них, то он меняет цвет на следующий по порядку, и одновременно с ним меняют свой цвет трое следующих за ним по часовой стрелке. В начальный момент времени все хамелеоны - синие. Можно ли добиться того, чтобы все хамелеоны стали зелёными?

РЕШЕНИЯ

класс

. Обозначим через х, у ,z количество километров, которые прошел турист на этой, прошлой и позапрошлой неделях соответственно. Тогда z=y+5 x+z=y+60

Откуда  z-y=5 и z-y=60-х.

=60-хх=55 км.

. Например, можно взять числа 2003, 2 и еще 2001, 1. Тогда их произведение будет равно их сумме.

*2*1=2003+2+2001*1=4006

КЛАСС.

1. Количество мужчин и женщин, состоящих в браке, - одно и то же. Обозначим его . Тогда мужчин на острове - , женщин - . Общее число жителей - .

Состоящих в браке - . Тогда искомая величина: .

. Пусть

 разрезан на два равных треугольника (см. рис). Тогда в должен быть равен одному из углов . Но  не может равняться  или , так как внешний угол треугольника всегда больше внутреннего угла, не смежного с ним. Если же , то , значит  является высотой. Так как в равных треугольниках против равных углов лежат равные стороны, то , что противоречит тому, что  - разносторонний. Следовательно, разносторонний треугольник нельзя разрезать на два равных треугольника.

3. (ABDE)(BCEF)=(ABC)(DEF)(BE).

Учитывая, что ABDE=BCEF=4, ABC=DEF=1, получаем равенство: 16=BE. Аналогично получим, что EH=16. Перемножаем полученные равенства: (BE)(EH)=(BEH)E. 1616=E.

Ответ: E=256.

4. Обозначим 2001=. Тогда данное нам числовое выражение запишется в виде:

Тогда .

5. Пусть N_k, N_s и N_z - количество красных, синих и зелёных амёб, соответственно. В начальный момент времени , - нечётны, - чётно. Нетрудно проверить, что при любом слиянии эти чётности сохраняются. Поэтому в конце концов , . Ответ: последняя амёба - синяя.

9 КЛАСС

1. Пусть x$ - стоимость первого автомобиля, y$ - стоимость второго автомобиля. При продаже Вася получил 9000$ чистой прибыли. Составляем систему уравнений:

 .

Решив систему, найдём . Тогда сумма штрафа составляет 12000$. 12000 - 9000=3000.

Таким образом, Вася потерял 3000$.

2. (A₁A₂A₃B₁B₂B₃C₁C₂C₃) (A₃A₄A₅B₃B₄B₅C₃C₄C₅) (A₆A₇A₈B₆B₇B₈C₆C₇C₈)=(A₁A₂A₃A₄A₅A₆A₇A₈) (B₁B₂B₃B₄B₅B₆B₇B₈) (C₁C₂C₃C₄C₅C₆C₇C₈)(A₃B₃C₃).

Т.е. A₃B₃C₃=8. Аналогично - C₁C₂C₃=8.

Произведение чисел в квадрате 66, стоящем на пересечении 3-8 столбцов и 3-8 строк равно 16, так как этот квадрат разбивается на 4 квадрата 33. В оставшемся уголке (на рисунке он заштрихован) произведение чисел равно 1/16, так как во всей таблице произведение равно 1. Но произведение чисел в закрашенном уголке можно также получить, перемножив числа первой и второй строк, первого и второго столбца и разделив всё это на A₁A₂B₁B₂. Отсюда A₁A₂B₁B₂=16.

(A₁A₂B₁B₂)( A₃B₃C₃)( C₁C₂C₃)=(A₁A₂A₃B₁B₂B₃C₁C₂C₃)C₃.

88=2С₃. Откуда С₃=512, A₃B₃=8/512=1/64.

Ответ: 1/64.

.        .

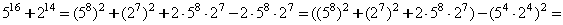
.Пусть вписанный в первую окружность . Соответствующий ему центральный угол . Но  вписан во вторую окружность, поэтому .  - это угол между касательной BC и секущей AB, поэтому .

Тогда по теореме о сумме углов треугольника,

. Значит,  - равнобедренный. AB=BC, что и требовалось доказать.

5. Каждому цвету поставим в соответствие один из остатков по модулю 4. Синий - 0, оранжевый - 1, фиолетовый - 2, зелёный - 3. Вместо хамелеонов будем рассматривать 2002 целых числа, стоящие по кругу. Операция смены цвета в новой трактовке будет равносильна прибавлению 1 к четырём последовательно стоящим числам. (При этом, если будет получаться число, большее 3, то оно заменяется на остаток от деления на 4.) В начальный момент времени по кругу стоят нули и нам требуется узнать, можно ли путём указанной операции сделать все числа, равные трём.

В начальный момент времени сумма равна 0 и на каждом шаге она может изменяться лишь на величину, кратную четырём, т.е. сумма всех чисел на каждом шаге будет делиться на 4. Поэтому 2002 тройки (которые в сумме дают 6006=41501+2) получить нельзя.

.4       Математический бой. Схема проведения

Схема матбоя.

Математический бой - это соревнование двух команд в решении нестандартных задач, подобранных жюри, в умении рассказывать решение у доски и в умении проверять чужие решения.

Команды получают одинаковые задачи и решают их в разных помещениях в течении заданного времени. Таким образом, матбой состоит из двух частей: решение задач и собственно боя.

Чтобы определить, в каком порядке команды будут рассказывать решения задач, команды делают вызовы: одна называет номер задачи, решение которой она желает услышать, другая сообщает, принят ли вызов. Обычно команды вызывают друг друга по очереди.

Если вызванная команда хочет отвечать, то она выставляет докладчика, а другая команда - оппонента для проверки решения. Командам могут даваться минутные перерывы для помощи докладчику или оппоненту.

Если вызванная команда отказалась, то она вызвавшая команда должна сама рассказать решение задачи. При этом если оппонент докажет, что у докладчика нет решения, то вызов считают некорректным. Тогда вызвавшая команда должна повторить вызов.

Команда может отказаться делать очередной вызов (если у нее не осталось решенных задач и не хочет делать некорректный вызов). Тогда другая команда получает право рассказывать решения любых задач, оставшихся не разобранными.

После каждого выступления жюри дает командам очки как за доклад, так и за оппонирования.

.Предельное число выходов к доске одного человека (обычно два).

.Число минутных перерывов (обычно три).

.Примерное время на доклад (обычно пятнадцать мин.), после которого жюри решает, дать еще время или передать слово оппоненту.

.Можно ли оппоненту дополнять докладчика, если он не нашел пробелов в решении (обычно «нет»).

.Какую разницу очков считать ничейной (обычно не больше трех).

.Какой круг фактов и методов можно использовать без доказательства.

.Можно ли пользоваться литературой и калькуляторами во время решения задач (обычно «да»).

.Можно ли выходить к доске с записанным решением (обычно «да»).

НАЧАЛО БОЯ.

Когда время на решение задач истекло команда и жюри собираются вместе.

Целесообразно создать обстановку (расставить столы) для удобного общения членов команд и жюри (рис. 1).

Команда 1

Капитаны сообщают названия команд. На доске изображается таблица результатов.

Существуют ограничения на общение участников, которые показаны на схеме (Рисунок 2: например, оппонент может общаться только с докладчиком и жюри, а капитан - только со своей командой и с жюри).

Примеры задач и игр для конкурса капитанов

1. Сколько существует трехзначных чисел?

2. На столе лежат 20 спичек, двое по очереди берут 1 или 2 спички. Побеждает тот, кто берет последнюю спичку.

3. Газету разорвали на 3 части, потом 1 из частей разорвали еще на 3 части, и так делали 40 раз. Сколько получилось частей?

4. Полный бидон молока весит 30 кг., а наполненный наполовину 15,5 кг. Сколько весит бидон?

5. Разрежьте квадрат на 5 прямоугольников, чтобы у соседних прямоугольников стороны не совпадали.

6. Найдите хотя бы 1 решение неравенства 0,01<x<0,011.

7. Сколько диагоналей в правильном семиугольнике?

8. В строке написано несколько минусов. Двое по очереди переправляют один или два соседних минуса на плюс. Выигрывает тот , кто переправит последний минус.

9. Замените звёздочки числами так , чтобы сумма любых трёх соседних чисел равнялась 20.

7, *, *, *, *, *, *, 9

. Известно, что дробь

В*А*Р*Е*Н*Ь*Е

К*А*Р*Л*С*О*Н

Равно целому числу, где разные буквы обозначают разные цифры, а между цифрами стоит знак умножения. Чему равна дробь?

. Три охотника варили кашу. Один положил 2 кружки крупы, второй - 1 кружку, а у третьего крупы не было. Они съели кашу поровну. Третий охотник и говорит: «Спасибо за кашу! У меня осталось 5 патронов, - и вот вам задача: как поделить патроны в соответствии с вашим вкладом?»

. На озере росли лилии. Каждый день их число удваивалось, и на 20 день заросло всё озеро. На какой день заросла половина озера?

. Есть 2 сковородки на каждой помещается 1 блин. Надо пожарить 3 блина с двух сторон. Каждая сторона блина жариться 1 минуту за какое наименьшее время можно это сделать?

. Два мальчика хотели купить книгу. Одному из них не хватало 27 копеек, а второму - 1 копейки. Они сложили свои деньги, но денег всё равно не хватило. Сколько стоит книга?

. Одна кастрюля вдвое выше другой, зато вторая вдвое шире первой. В какой из них больше войдет воды?

. Шоколадка стоит рубль и еще пол шоколадки. Сколько стоит шоколадка?

Образцы задач математического боя для восьмых классов

. Какое наименьшее число выстрелов всегда достаточно, чтобы попасть в четырех клеточный корабль при игре в морской бой?

. Известно, что доля блондинов среди голубоглазых больше, чем доля блондинов среди всех людей. Что больше: доля голубоглазых среди блондинов или доля голубоглазых среди всех людей?

. На сторонах произвольного многоугольника произвольным образом расставлены стрелки. Докажите, что число вершин, в которое входят 2 стрелки, равно числу вершин, из которых выходят 2 стрелки.

. Докажите, что среднее арифметическое двух последовательных простых чисел не является простым числом.

. На прямой отмечено 45 точек, лежащих вне отрезка АБ. Докажите, что сумма расстояния от этих точек до точки А не равна сумме расстояний от этих точек до точки Б.

. Дано 100 положительных чисел. Известно, что произведение любых 7 из них больше 1. Докажите, что произведение всех чисел больше 1.

. Путешественник отправился из родного города А в саамы удаленный от него город страны В, затем из В - в самый удаленный от него город С и т.д. Докажите, что если С не совпадает с А, то путешественник никогда не попадет домой. (Расстояние между городами различно).

. В углах шахматной доски 3х3 стоят 4 коня: два белых (в соседних углах) и два черных. Можно ли за несколько ходов (конь ходит буквой «Г») поставить коней так, чтобы во всех соседних углах стояли кони разного цвета.

. На стороне угла дана точка А. Постройте на этой же стороне точку М, которая одинаково удалена от точки А и от другой стороны угла.

. По кругу расставлены 10 точек. Двое по очереди соединяют их отрезками. Начало 1 отрезка - в любой точке, а каждый следующий отрезок начинается из конца предыдущего. Проигрывает тот, кто не может провести новый отрезок (дважды проводить отрезок нельзя, а пересекать - можно). Предположим, что игроки не делают ошибок. Кто из них победит?

Ответы к задачам конкурса капитанов

1. 900. 2. Первый каждым ходом берет столько спичек, чтобы остаток делился на 3. 3. 81. 4. 1 кг. 5. см. рисунок 3. 6. х=0,0105. 7. 14. 8. Первый ходит в центр, а затем ходит симметрично второму. 9. 7, 9, 4, 7, 9, 4, 7, 9. 10. 0. 11. Все патроны надо дать первому охотнику. 12. За 19 дней. 13. За 3 минуты. 14. 27 копеек. 15. В широкую войдет вдвое больше. 16. 2 руб.

Краткие решения задач математического боя

. Будем располагать выстрелы по параллельным диагоналям с интервалом 3 клетки, начиная с диагонали А4 - Г1. Понятно, что четырех клеточному (крейсер) кораблю укрыться будет негде. Получаем, что 24 выстрела всегда достаточно. Покажем, что 24 выстрела необходимо. Для этого разместим на доске 24 крейсера без наложений. Кстати, мы заодно доказали, что на доске 10х10 нельзя разместить 25 крейсеров без наложений (иначе не хватило бы 24 выстрелов).

. Обозначим ЧБ - число блондинов, ЧГ - число голубоглазых, ЧБГ - число голубоглазых блондинов, а ЧВ - число всех людей. Тогда по условию:

(ЧБГ/ЧГ) > (ЧБ/ЧВ), следовательно (ЧБГ/ЧБ) > (ЧГ/ЧВ)

Итак, доля голубоглазых среди блондинов больше, чем доля голубоглазых среди всех людей.

. Задача кажется простой, поскольку по определению последовательных простых чисел между ними нет простых чисел, но вот неожиданный вопрос: «Почему среднее арифметическое двух чисел лежит между ними?». Нагляднее всего это можно доказать так: пусть А < В, тогда

А = (А+А)/2 <= (А+В)/2 <= (В+В)/2 = В

. Заметим, что расстояние от любой точки до А и до Б отличается на длину отрезка АБ. При переходе от точки А к точке Б все расстояния от «левых» точек увеличиваются, а от «правых» уменьшаются на длину отрезка АБ. Но число точек слева не равно числу точек справа, следовательно, сумма расстояний до точки Б будет отличаться от суммы расстояний до точки А по крайней мере на величину отрезка АБ.

. Заметим, что количество чисел, меньших 1 не больше 6, а все остальные больше 1. Перемножим все числа, меньшие 1 и еще несколько чисел, чтобы всего было 7 чисел. Их произведение больше 1, а все остальные числа больше 1, значит произведение всех чисел больше 1.

. Если путник из В не вернулся в А, то расстояние ВС строго больше АВ, а каждое следующие расстояние не меньше предыдущего. (Почему нельзя сказать: больше предыдущего, ведь расстояния различны?) Если бы путник потом вернулся в город А, то последнее расстояние было бы больше АВ, а это противоречит тому, что В - самый дальний город для А.

.Построим схему движений коней по клеткам. Для этого занумеруем клетки и впишем их номера в том порядке в котором конь может их обойти. Тогда видно, что кони как бы бегают по кругу, т.е. любой ход коня не меняет порядка следования их цветов на схеме, а значит, нельзя изменить чередования их цветов в углах доски.

.Пусть М - искомая точка. Опустим из неё перпендикуляр на другую сторону угла и получим точку С. Можно выразить углы треугольника АМС через величину исходного угла, а тогда легко построить точки С и М. Но суть задачи заключается в том, что у неё есть два решения, одно из которых обычно теряют: точку М можно отложить по разные стороны от точки А.

.Выигрывает начинающий: первым ходом он соединяет любые точки А и В, а затем проводит отрезок либо к точке А, либо к точке В. Это всегда возможно, поскольку второй игрок вынужден каждый раз ходить в новую точку, которая еще не была соединена с точками А и В. При такой стратегии начинающий не может проиграть, ничья невозможна, поскольку число отрезков конечно.

3.5 Игровые формы занятий

Внеклассная работа по математике является неотъемлемой частью всей учебно-воспитательной работы в школе. Она углубляет знания учащихся, способствует развитию их дарований, расширяет кругозор.

Формы проведения внеклассных занятий и приемы, используемые на этих занятиях, должны удовлетворять ряду требований. Они должны быть разнообразными, выбираться с учетом возрастных особенностей учащихся, должны быть рассчитаны на различные категории учащихся: на интересующихся математикой и одаренных учащихся и на учащихся, не проявляющих еще интерес к предмету. Они должны во многом отличаться от форм проведения уроков и других обязательных мероприятий. Последнее необходимо не только потому, что внеклассная работа строится на добровольных началах, но еще и потому, что она, как правило, проводится после уроков или в вечернее время после выполнения домашних заданий, после шестичасового, и иногда и восьмичасового умственного труда. При организации внеклассных занятий важно не только серьезно задуматься над их содержанием, но обязательно над методикой их проведения, формой. Надо использовать такие приемы, которые отвечали бы потребностям всех учащихся.

К формам, широкое использование которых является целесообразным во внеклассной работе по математике (особенно в 5-8-х классах), относятся игровые формы занятий - занятия с элементами игры, соревнования, содержащие игровые ситуации.

Игры и игровые формы должны включаться не для того, чтобы развлечь учащихся, а чтобы возбудить у них стремление к преодолению трудностей. Цель их введения состоит в том, чтобы удачно соединить игровые и учебные мотивы и постепенно сделать переход от игровых мотивов к учебным, познавательным. Для этого нужно так разрабатывать методику игровых занятий, чтобы деятельность учащихся была игровой по форме, т. е. вызывала бы те же эмоции, переживания, что и игра, и в то же время давала возможность активно приобретать нужные сведения, восполнять пробелы в знаниях, способствовала бы воспитанию познавательных интересов.

Дидактическая игра, игровые занятия должны разрабатываться таким образом, чтобы к участникам были предъявлены определенные требования в отношении знаний.

Чтобы играть, нужно знать - вот первое требование, которое придает игре (занятию) познавательный характер и оправдывает наличие игровых моментов, игровых ситуаций.

Правила игр, игровые ситуации должны быть действенными, т. е. такими, чтобы у учащихся появилось желание участвовать в игре. Поэтому игровые занятия должны составляться с учетом вида игр, интересов, знаний учащихся данного возраста. Так, для младших школьников можно составлять дидактические игры с включением ролей, сюжетов, привлекающих учеников (расшифровка таинственных записей, путешествия и др.). Кроме того, полезно в дидактические игры включать элементы соревнования.

Правила и организация дидактических игр должны составляться и разрабатываться с учетом индивидуальных особенностей учащихся, т. е. с учетом различных групп (слабых и сильных, активных и пассивных и т. д.). Они по возможности должны быть такими, чтобы для каждой категории учеников были созданы условия для проявления самостоятельности, настойчивости, смекалки, возможности проявления чувства удовлетворенности, успеха.

Дидактические игры и игровые занятия должны быть разнообразными и разрабатываться с учетом особенностей предмета и его материала. Все многообразие игр должно составлять продуманную систему. Это может повысить эффективность внеклассной работы, послужит дополнительным источником систематических и прочных знаний.

Игра-соревнование «Математический турнир»

Математический турнир является одной из форм командных соревнований. Основным содержанием турнира является решение разнообразных задач.

Описанная игра-соревнование может найти широкое применение в учебной работе по математике в 5-7-х классах (по усмотрению организатора могут быть внесены изменения: заменены некоторые задачи, изменены оценки-баллы и т. д.).

За шесть недель учащиеся были поставлены в известность о предстоящем турнире, проведено краткое знакомство с его «сценарием». Учащимся было предложено собрать и аккуратно оформить (в виде альбома, раскладушки, плаката) пословицы, поговорки, строфы из стихотворений и куплеты из песен, в которых упоминаются числа. За две недели до начала турнира был проведен более детальный инструктаж, было предложено каждому из участвующих в игре классов (6А и 6Б) создать команду из шести человек, выбрать капитанов команд и капитанов болельщиков, изготовить эмблемы, подобрать название команды и соответствующий девиз.

В назначенное время участники турнира под звуки музыки входят в зал и занимают места в правой и левой его частях (по классам). Ведущий учитель (или старшеклассник) объявляет о начале турнира, знакомит с составом жюри (учащиеся 8-9-х классов и учитель математики), объясняет правила проведения турнира (особое требование - соблюдение дисциплины, порядка). После соответствующего указания ведущего капитаны команд (по очереди) выводят свою команду на сцену.

Оборудование: магнитофон, две настольные лампы, часы с секундной стрелкой, доска с металлическим покрытием, магниты, указка, калькулятор (для жюри), удлинители, тройники, высказывания о математике.

Ведущий.

Сейчас вам будет предложено 10 задач. Каждую задачу я буду читать дважды: первый раз в быстром темпе, а второй - в медленном. Перед чтением условия задачи буду указывать время, выделяемое команде и ее болельщикам для решения задачи и оценку - количество баллов. Над решением задачи работают члены команды и болельщики. Если у команды готов ответ, капитан включает лампу на столе. После второго чтения я буду говорить слово «время». Раньше, чем услышите это слово, капитан не должен включать лампу, если даже у команды уже есть решение. Услышав слово «время», один из членов жюри начинает вести учет времени. Если ни одна из команд не нашла правильный ответ за отведенное время, жюри объявляет «время истекло» и право ответа предоставляется болельщикам.

Желаю удачи!

Начали! (Звучит легкая музыка.)

Задача 1. (Время на решение - 1 мин; оценка 3 или 5 баллов.)

Самолет пролетает расстояние от Москвы до Хабаровска за 9 ч. Скорый поезд преодолевает это расстояние за 9 суток.

Во сколько раз быстрее можно добраться от Москвы до Хабаровска на самолете, чем на скором поезде?

Решение.

-й способ (3 балла)

. 24•9 = 216 (ч) - время, за которое можно добраться от Москвы до Хабаровска на поезде.

-й способ (5 баллов)

Так как количество часов и суток одинаково, то на самолете можно добраться во столько раз быстрее, сколько часов в одних сутках, т. е. 24 раза.

Задача 2. (Время на решение - 1 мин; оценка - 3 балла.)

Ты должен уплатить за купленную вещь 19 р. У тебя - одни трехрублевки, а у кассира - только пятирублевки. Можешь ли ты расплатиться и как именно?

Решение. Да. Я даю 13 трехрублевок, т. е. 3•13 = 39 (р.), а кассир дает сдачу четырьмя пятирублевками, т. е.

•4 = 20 (р.). 39 - 20 = 19 (р.)

Задача 3. (Время на обдумывание - 0,5 мин; оценка - 2 балла.)

Из Киева в Одессу вышел автобус и шел со скоростью 80 км/ч. Другой автобус вышел ему навстречу из Одессы в Киев и шел со скоростью 90 км/ч. На каком расстоянии автобусы будут друг от друга за 1 ч до их встречи?

Решение. 80 + 90 = 170 (км).

Задача 4. (Время для решения - 2 мин; оценка - 4 балла.)

Имеется 16 кг муки и несколько одинаковых по весу пустых мешков. Имеются чашечные весы, но гирь нет. Как, не имея гирь, взвесить 12 кг муки?

Решение. Пересыпанием из полного мешка в пустой получим 8 кг муки. Полученные 8 кг в одном из мешков разделить пополам, т. е. по 4 кг и высыпать эти 4 кг в мешок, в котором 8 кг.

+ 4 = 12 (кг).

Задача 5. (Время для решения - 1,5 мин; оценка - 4 балла.)

Коля и Петя живут в одном доме: Коля - на шестом этаже, а Петя - на третьем. Возвращаясь из школы домой, Коля проходит 60 ступенек. Сколько ступенек проходит Петя, поднимаясь по лестнице на свой этаж? (На первом этаже ступенек нет.)

Решение. На шестой этаж ведут 5 пролетов со ступеньками, значит, между этажами 12 ступенек. На третий этаж ведут 2 пролета, поэтому Петя проходит 12•2 = 24 ступеньки.

После решения пятой задачи ведущий предлагает болельщику каждой команды приступить к изучению таблицы чисел от 1 до 90.

Задача 6. (Время для решения - 0,5 мин; оценка - 2 балла.)

Портной имеет кусок сукна в 16 м, от которого он отрезает ежедневно по 2 м. По истечении скольких дней он отрежет последний кусок?

Решение. Отрезав предпоследний, седьмой кусок, он тем самым отрежет и последний, восьмой кусок. Ответ. 7 дней.

Задача 7. (Время для решения - 2 мин; оценка - 4 балла.)

На поверхности пруда растут кувшинки. Площадь, которую они занимают, с каждый днем удваивается. Весь пруд зарос кувшинками через 20 дней. Через сколько дней заросла половина пруда?

Ответ. Через 19 дней.

Задача 8. (Время для решения - 2 мин; оценка - 3 балла.)

Сколько ударов в сутки делают часы с боем?

Решение: (1 + 2 + 3 + ... + 12)•2 = 78•2 = 156.

Ответ: 156 ударов.

Задача 9. (Время для решения - 1 мин; оценка - 4 балла)

Два лесоруба работали в лесу. Решили на обед сварить кашу. Первый лесоруб высыпал в кастрюлю 2 стакана крупы, а второй - 1 стакан. Как только каша была готова, к ним подошел проголодавшийся охотник. Разделили они кашу поровну, и каждый съел свою долю. Охотник после обеда нашел в своем кармане 6 р. и сказал: «Не обессудьте, братцы, больше при себе ничего нет. Поделитесь по справедливости». Как должны разделить деньги лесорубы?

Ответ: 1-й лесоруб - 6 р., 2-й лесоруб - 0 р.

Задача 10. (Время для решения - 0,5 мин; оценка - 1 балл)

За столом сидят два отца и два сына. Между ними три яблока. Как разделить яблоки так, чтобы каждому досталось целое яблоко?

Ответ: за столом сидит три человека - дедушка, отец и сын.

После решения первых десяти задач членам команд предоставляется возможность отдохнуть (они присоединяются к своим болельщикам). Жюри объявляет результаты первого этапа турнира.

Ведущий.

Объявляется конкурс «Борьба за число».

На доске вывешивается таблица с числами от 1 до 24, расположенными в «беспорядке».

К доске приглашаются капитаны болельщиков. Они становятся спиной к доске и слушают инструктаж ведущего. Капитаны по очереди (второй не следит за работой первого) должны показать указкой и назвать подряд все числа от 1 до 24. Жюри учитывает время, затраченное каждым игроком, и следит за правильностью ответа. Побеждает (2 балла) тот, кто потратит на это задание меньше времени. Если победитель выполнит задание быстрее, чем за 1 мин, то он принесет команде 4 балла.

Ведущий объявляет о начале конкурса «Верный глаз». На доске вывешивается увеличенная до размеров двойного стандартного листа копия таблицы чисел от 1 до 90 (копия той таблицы, которая была выдана раньше одному из болельщиков каждого класса). К доске приглашаются по одному болельщику (те, которые получили таблицы раньше для ознакомления). Им предоставляется возможность на протяжении 3 мин каждому по очереди (второй не следит за работой первого) показать указкой и назвать как можно больше чисел по порядку, начиная с 1. Побеждает тот, кто за 3 мин (жюри следит за временем и верностью ответа) назовет больше чисел. Конкурс «Верный глаз» оценивается в 3 балла.

Жюри объявляет результат первой части турнира. Представители болельщиков от каждого класса зачитывают по 10 поговорок и пословиц, содержащих числа (члены жюри следят за тем, чтобы не было повторов).

Ведущий объявляет десятиминутный перерыв. Звучит «танцевальная» музыка, желающие могут потанцевать.

После перерыва команды занимают свои места за столами. В составы команд могут быть внесены изменения. (Капитаны команд должны во время перерыва предупредить об этом ведущего и жюри.)

Ведущий объявляет о начале второй части турнира.

Задача 11. (Время для решения - 1 мин; оценка - 1 балл.)

У Коли и Саши было поровну тетрадей. Коля дал Саше 26 тетрадей. На сколько больше тетрадей стало у Саши, чем у Коли?

Ответ: на 52 тетради.

Задача 12. (Время для решения - 1 мин; оценка - 2 балла.) Если число 12 345 679 умножить на 9, то получится 111 111 111. На какое число нужно умножить 12 345 678, чтобы получилось число, записанное с помощью шести пятерок?

Ответ: 45.

Задача 13. (Время для решения - 2 мин; оценка - 2 балла.)

Запишите в строчку через одну клеточку подряд цифры 2, 3, 4, 5 и 6. Не меняя порядка цифр, вставьте между ними знаки действий так, чтобы в результате получилась единица.

Ответ: 2•3 - 4 + 5 - 6 = 1.

Задача 14. (Время для решения - 2 мин; оценка - 2 балла.)

В ящике лежат 70 шаров: 20 красных, 20 синих, 20 желтых, остальные - черные и белые. Какое наибольшее число шаров надо взять, не видя их, чтобы среди них было не меньше 10 шаров одного цвета?

Ответ: 38 шаров.

Задача 15. (Время для решения - 1 мин; оценка - 1 балл.)

Отцу - 30 лет, а его сыну - 5 лет. Через сколько лет отец будет старше сына на 27 лет?

Ответ: никогда.

Задача 16. (Время для решения - 1,5 мин; оценка - 2 балла.)

Рабочий за смену вставил замки в двери шести квартир нового дома, но при этом забыл прикрепить к ключам бирки с номерами квартир. Какое число проб он должен сделать в худшем случае, чтобы подобрать ключи ко всем квартирам?

Ответ: 15 проб.

Задача 17. (Время для решения - 1 мин; оценка - 2 балла.)

В клубе 28 рядов кресел по 32 кресла в каждом ряду. Все места пронумерованы, начиная с первого ряда. В каком ряду находится № 375?

Ответ: в 12-м ряду.

Задача 18. (Время для решения - 1,5 мин; оценка - 2 балла.)

Турист проехал на лошади расстояние между двумя городами за 20 ч. За сколько часов мотоциклист проедет в 7 раз большее расстояние, если скорость его будет в 4 раза больше скорости лошади?

Ответ: 35 ч.

Задача 19. (Время для решения - 2 мин; оценка - 4 балла.)

Часы спешат на 2 мин в сутки. Сейчас они показывают точное время. Через какое время они снова покажут точное время?

Ответ: 360 суток.

Задача 20. (Время для решения - 1 мин; оценка - 2 балла.)

Одного человека спросили, сколько у него детей. Он ответил замысловато: «У меня сыновей столько, сколько дочерей, а у каждого сына по три сестры». Сколько детей в этой семье? Ответ: 6 детей.

Ведущий объявляет о завершении турнира команд. Члены команд занимают свои места в зале. Жюри подводит итоги прошедшей части турнира.

Болельщикам и членам команд предлагается по очереди продекламировать по 1-2 строфы из стихотворений, в которых упоминаются числа, зачитать 10 пословиц. После этого жюри объявляет результаты прошедшей части турнира.

Ведущий. Турнир продолжается. Объявляю начало конкурса «Попробуй, сосчитай»! Умеете ли вы считать до тысячи? А до миллиона? Если умеете, то попробуйте сосчитать до тридцати. (На доске вывешивается таблица с изображением геометрических фигур.) Представители команд (по три человека от каждой) должны сосчитать фигуры подряд, начиная с верхней строки, но только по особому правилу: «Первый треугольник, первый угол, первый круг, второй угол, первый отрезок, второй круг, второй отрезок» и т. д. Считать будут смельчаки по очереди, кто собьется - выбывает.

Капитанам болельщиков предлагается выделить по три человека для участия в конкурсе. Они становятся спиной к таблице. Потом по очереди поворачиваются лицом к таблице и, показывая фигуры указкой, считают по указанной схеме.

Жюри внимательно следит за результатами счета. Чтобы не пропустить ошибки и быть объективным при оценке, каждому члену жюри выдается запись правильного счета.

Один из членов жюри ведет учет времени, на протяжении которого правильно считал каждый участник конкурса. Числа в скобках указывают номер изображенной фигуры (это нужно жюри для объективного подведения итогов).

Жюри может вести учет в форме (члены жюри должны быть детально проинструктированы перед началом турнира и обеспечены всеми необходимыми формами и таблицами).

Из приведенного примера видно, что победителями оказались игроки 6А класса, и класс получает дополнительно 4 балла.

Пока жюри подводит итоги этого конкурса, участники турнира от каждого класса зачитывают (лучше - пропевают) куплеты из песен, в которых упоминаются числа.

Жюри объявляет результаты конкурса «Попробуй, сосчитай» и называют общее число баллов, полученных каждым классом.

Ведущий. Следующий конкурс «Не собьюсь!». В конкурсе принимают участие по 5 человек от каждого класса (можно предложить участвовать в конкурсе по одному родителю каждого из классов). Суть конкурса заключается в следующем. Каждый участник конкурса должен внимательно считать, начиная с 1. При этом будет указана цифра, которую при счете нельзя называть, причем не только ее, а и такие числа, которые на нее делятся и в которые она входит. Например, выбрана цифра 4. Первый игрок начинает считать. Вместо числа 4, любого числа, кратного 4, или в запись которого входит цифра 4 он говорит слово «гоп». Тот, кто собьется, выбывает из игры. Игрок из другой команды начинает счет сначала. Начало счета: 1 - 2 - 3 - гоп! - 5 - 6 - 7 - гоп! - 9 - 10 - 11 - гоп! - 13 - гоп! - 15 - гоп! - 17 - 18 - 19 - гоп! - 21 - 22 - 23 - гоп! - 25 и т. д.

Считать нужно в быстром темпе, так как учитывается время, затраченное на счет.

Жюри внимательно следит за правильностью счета и ведет учет времени, затраченного на счет каждым участником конкурса.

При данном раскладе победила команда 6А класса. Можно предложить жюри определить самого внимательного счетчика в команде и среди участников конкурса.

Ведущий. Итак, я объявляю цифру 6. Конкурс оценивается в 3 балла. У каждого члена жюри карточка контроля за результатом счета (сделать ксерокопию приложения 4).

После окончания конкурса «Не собьюсь!» жюри подводит итоги, а командам предлагается (по очереди) зачитать по 10 поговорок и пословиц и назвать количество всех собранных пословиц, строф из стихотворений и куплетов из песен. Жюри объявляет результаты конкурса «Не собьюсь!».

Капитаны болельщиков сдают членам жюри свои сборники пословиц, стихотворений, песен. Жюри оценивает количество (от 3 до 6 баллов) и качество оформления (2-4 балла). После этого объявляется общий итог турнира.

Ведущий благодарит всех участников, капитанов команд и болельщиков, членов жюри за активное участие в турнире, поздравляет победителей. Желательно вручить каждому классу специально испеченный в школьной столовой пирог, а классу-победителю еще и дополнительный приз. Капитаны команд и болельщиков называют фамилии самых результативных участников турнира (желательно вручить каждому из них приз).

Ответы к конкурсу «Не собьюсь!»

- 2 - 3 - 4 - 5 - гоп! - 7 - 8 - 9 - 10 - 11 - гоп! - 13 - 14 - 15 - гоп! - 17- гоп! - 19 - 20 - 21 - 22 - 23 - гоп! - 25 - гоп! - 27 - 28 - 29 - гоп! - 31 - 32 - 33 - 34 - 35 - гоп! - 37 - 38 - 39 - 40 - 41 - гоп! - 43 - 44 - 45 - гоп! - 47 - гоп! - 49 - 50 - 51 - 52 - 53 - гоп! - 55 - гоп! - 57 - 58 - 59 - гоп! - гоп! - гоп! - гоп! - гоп! - гоп! - гоп! - гоп! - гоп! - гоп! - 70 - 71 - гоп! - 73 - 74 - 75 - гоп! - 77 - гоп! - 79 - 80 - 81 - 82 - 83 - гоп! - 85 - гоп! - 87…

ЗАКЛЮЧЕНИЕ

В данной дипломной работе рассматривалась тема «Внеклассная работа по математике в 7-9 классах».

Внеурочная работа по математике предоставляет школьникам дополнительные возможности для развития способностей, прививает интерес к математике. Главное назначение внеклассной работы - не только расширение и углубление теоретического материала, изученного на уроках, но и развитию умений применять полученные на уроках знания к решению нестандартных задач, воспитанию у учеников определенной культуры работы над задачей.

Список использованной литературы

1.       Епишева О.Б. Общая методика преподавания математики в средней школе / Тобольск, Изд-во ТГПИ им. Д.И. Менделеева, 1997

.        Ермолаева Н.А. Маслова Г. Г. Новое в курсе математики средней школы / М:, Просвещение, 1978.

.        Журнал "Математика в школе ", № 5, 1999; № 14, 2001

.        Колягин Ю.М., Луканкин Г.Л., Мокрушин Е.Л. и другие. Методика преподавания математики в средней школе. Частные методики / М., Просвещение, 1977.

.        Методика преподавания математики в средней школе : Общая методика; Учебное пособие для студентов физико-математического факультета педагогических институтов / В.А. Оганесян, Ю.М. Колягин, Г.Л. Луканкин, В.Я. Саннинский, -2-е издание переработано и дополнено / М., Просвещение ,1980.

.        Методические рекомендации по изучению курса методики преподавания математики / Сост. Петрова Е.С., Саратов, Изд-во "Полиграфист", 1983

.        Пичурин Л.Ф., Репьев В.В. Вопросы Общей методики преподавания математики / Москва Изд-во "Просвещение", 1979

.        Перельман Я.И. Живая математика / М, 1978

.        Черкасов Р.С., Столяр А.А. Методика преподавания математики в средней школе / Москва, Изд-во "Просвещение", 1985

.        Первое сентября «Математика», № 46, 2004; № 45, 2004

ПриложениЯ

Приложение 1

МАТЕМАТИЧЕСКИЙ КВН «ТУРНИР СМЕКАЛИСТЫХ»

Цели проведения игры:

.        Развивать интуицию, догадку, эрудицию и владение методами математики;

.        Пробудить математическую любознательность и инициативу;

.        Воспитывать культуру математического мышления;

.        Прививать навыки самостоятельного решения задач, учить детей делать выводы.

Почему торжественность вокруг?

Слышите, как быстро смолкла речь?

Явился гость - царица всех наук,

И не забыть нам радость этих встреч.

Есть о математике молва,

Что она в порядок ум приводит,

Потому хорошие слова

Часто говорят о ней в народе.

Ты нам, математика, даешь

Для победы трудностей закалку.

Учится с тобою молодежь

Развивать и волю, и смекалку.

И за то, что в творческом труде

Выручаешь в трудные моменты,

Мы сегодня искренне тебе

Посылаем гром аплодисментов!

В зал входят обе команды «Синус» и « Косинус».

Ведущие представляют их.

Приветствие команды «Синус»(Поют на мотив «Коробейников»):

Эх, полным-полно болельщиков, негде яблоку упасть.

Помогите нам, пожалуйста, место первое занять.

Вы похлопайте в ладоши, напишите лозунг нам,

И тогда команда наша благодарна будет вам.

Приветствие команды «Косинус» (Поют на мотив «Мы так давно не отдыхали»)

Давно, давно мы с вами не соревновались,

И, наконец, настал, друзья, сраженья час.

И, даже если вы сильнее оказались,

То все равно мы очень рады видеть вас.

Еще немного сказать хотим -

Мы с математикою дружим.

Мы твердо верим, что победим,

Болельщик, ты нам очень нужен!

Разминка.

Ведущие задают поочередно вопросы обеим командам.

Ответы даются сразу.

         Какой математический термин вы встречали на уроках литературы? Объясните его смысл. (Гипербола)

         Назовите самую большую хорду в круге. (Диаметр)

         Сколько раз к наибольшему однозначному числу нужно прибавить наибольшее двузначное, чтобы получить наибольшее трехзначное число? (9+99.10=999. То есть 10 раз).

         Из трехзначного числа вычли двузначное и в результате получили однозначное. Назовите эти числа. (100-99=1)

         К однозначному числу приписали такое же число. Во сколько раз увеличилось число? (в 11 раз)

         Если в 12 часов ночи идет дождь, то можно ли ожидать, что через 72 часа будет солнечная погода? (Нет, так как будет опять ночь).

Ведущие:

         Каждая команда приготовила по одному вопросу в стихах. Итак, о чем идет речь в стихотворении?

. Гордый Рим трубил победу

Над твердыней Сиракуз,

Но трудами Архимеда

Много больше я горжусь.

Надо нынче нам заняться,

Оказать такую честь.

Чтобы нам не ошибаться,

Чтоб окружность верно счесть.

Надо только постараться

И запомнить все, как есть:

Три - четырнадцать - пятнадцать -

Девяносто два и шесть. (Число пи)

Ведущий:

         Куда бы мы не обратили свой взор, везде мы видим трудолюбивое число пи: и в самом простом колесе, и в самом сложном механизме. Вычисления точного значения числа пи увлекали сотни математиков, затративших бесценные годы своей жизни в надежде решить эту задачу, не поддававшуюся усилиям предшественников, и снискать себе бессмертие.

         Автором обозначения числа пи был математик, который, кстати, впервые применил двоеточие для обозначения действия деления. Его фамилия Джонс.

         Слово второй команде.

Опять ужасная, Опять в журнале будет двойка.

Слеза стекает на тетрадь,

Нет сил держаться стойко.

Несчастный класс сидит в тоске,

От горя чуть не плачет.

А на доске, а на доске - Ужасные задачи!

Как час расплаты настает, Такая вот работа.

Холодный прошибает пот,

В глазах круги без счета.

А за столом, пугая всех,

Грозя кнутом и ссылкой,

Сидит ужасный человек

С язвительной ухмылкой

Суров, неумолим и тих,

Внушая страх и трепет,

Он соберет работы их

И всем по двойке влепит!

И греет лишь одно сердца учеников несчастных:

Что две минуты до конца

Мучений их ужасных.

Что прозвенит звонок опять - Луч света в царстве школьном

И, можно вновь спокойно спать, забыв о дне ужасном.

(Контрольная работа)

Конкурс поэтов «Буриме»

Ведущий: Командам предлагается написать стихотворение, в котором бы присутствовала рифма: «двойка - головомойка» и «пять - посчитать».

Пока команды готовятся, проведем Конкурс болельщиков.

Ø  Один говорит, двое глядят, двое слушают.(Язык, глаза, уши)

Ø  Семь братьев, годами равные, именами разные.(Дни недели)

Ø  У двух матерей по пяти сыновей, все на одно имя.(Пальцы на руках)

Ø  Пять чуланов, одна дверь.(Перчатка)

Ø  Две головы, две руки, шесть ног.(Всадник на лошади)

Ø  Экипаж, запряженный тройкой лошадей, за 1 час проехал 15 км.

С какой скоростью ехала каждая лошадь?(15 км/ч)

Конкурс поэтов.

Представители команд читают стихи.

Жюри считает поставленные баллы.

Конкурс художников.

Ведущий приглашает по одному художнику от каждой команды. Им предлагается нарисовать одновременно одной рукой 3 треугольника, а другой - 3 окружности.

Конкурс капитанов. Ведущие поют:

Капитаны, капитаны, постарайтесь

В форме быть от зари до зари.

Капитаны, капитаны, улыбайтесь,

Лишь веселым покоряется жюри.

Задания капитанам:

Ø  Без чего не могут обойтись математики, барабанщики, охотники?(Дробь)

Ø  Где пересекаются высоты у прямоугольного треугольника?

(В вершине прямого угла)

Ø  Пойманная рыба весит 1 кг и еще столько, сколько весит половина рыбы. Сколько весит рыба?(2 кг)

Ø  Два туриста одновременно подошли к реке. У берега была привязана лодка, в которой мог переправиться только один человек. Путешественники не умели плавать, но каждому из них удалось переправиться через реку и пойти своей дорогой. Как они это сделали?

(Они подошли к реке с разных сторон)

Ведущий: Капитаны подготовили вопросы соперникам об известных математиках. Ваша цель - угадать, о ком идет речь.

капитан:

Труды этого математика являются почти единственным руководством по одному из разделов геометрии в школе. Он никогда не допускал неискренности. Однажды царь спросил его, нет ли более краткого пути для познания его трудов для царя.

На это математик ответил, что «в математике нет царской дороги». Его книга «Начала» неоднократно переиздавалась во многих странах мира. Кто этот математик?(Евклид)

капитан:

Греческий ученый, родоначальник философии и астрономии. Платон, греческий философ 4 века, рассказывал, что этот ученый, наблюдая звезды, упал в колодец, а стоящая рядом женщина, рассмеявшись, сказала: «Хочет знать, что делается в небе, а что у него под ногами - не видит…»Ему приписывают следующие открытия: того, что диаметр делит круг пополам, о равенстве вертикальных углов, о равенстве углов при основании равнобедренного треугольника и т.д.

Он установил время равноденствий и солнцестояний, определил продолжительность года. Он доказал теорему, которая названа его именем и знакома всем школьникам. Кто он? (Фалес)

Конкурс «Домашнее задание»

Ведущий: Команды получили задание придумать новую геометрическую фигуру, дать ей название и описать ее свойства. Давайте посмотрим, что у них получилось.

Подведение итогов игры.

Выступление председателя жюри. Объявление победителя.

Ведущий:

Порой задача не решается,

Но это, в общем, не беда.

Ведь солнце все же улыбается,

Не унывая никогда.

Друзья всегда тебе помогут,

Они с тобой, ты не один.

Поверь в себя -И ты все сможешь, Иди вперед -

И победишь!

Приложение 2

Как стать миллионером

для учащихся 8 классов

Цель игры:

         обобщение и систематизация знаний по теме «Четырехугольники»;

         развитие сообразительности, логического мышления и математической эрудиции учащихся;

         воспитание познавательного интереса у учащихся, раскованности и уверенности в общении.

Правила игры:

. Игроком становится тот, кто верно ответит на вопросы отборочного тура.

. Игрок отвечает на вопросы и за каждый верный ответ получает некоторую сумму (суммы 1 и 5 - не сгораемые); в случае неверного ответа игрок выбывает из игры.

. Игра ведется до 1000 тенге.

. Игрок имеет право взять три подсказки: «спрошу друга», «помощь зала», «50/50».

Вопросы отборочных туров:

. В какой последовательности изучаются четырехугольники в школе?

. Расположите множества действительных, натуральных, рациональных и целых чисел в том порядке, в котором изучают в школе.

. Для каждого учебника укажите его автора: математика 5-6 класс, алгебра 7-9 класс, геометрия, алгебра и начала анализа?

Вопросы 1-го тура:

. Сколько лет рыбачил старик из сказки «О рыбаке и рыбке» А.С. Пушкина?

а. 30 лет и 3 года

б. 33 года

. Как называется утверждение, истинность которого доказывается?

а. аксиома в. теорема

б. высказывание г. произведение

. Параллелограмм с равными сторонами - это…

а. ромб в. квадрат

б. четырехугольник г. прямоугольник

. Какой ученый создал руководство по математике под названием «Начало»?

а. Пифагор в. Архимед

б. Евклид г. Фалес

. Как называются углы, у которых одна сторона общая, а две другие являются дополнительными полупрямыми?

а. вертикальные в. смежные

б. прямые г. острые

. Четырехугольник, у которого две стороны параллельны, а другие две - нет.

а. треугольник в. трапеция

б. прямоугольник г. ромб

. Параллелограмм, диагонали которого перпендикулярны.

а. квадрат в. прямоугольник

б. ромб г. параллелограмм

. Параллелограмм с равными диагоналями.

а. ромб в. прямоугольник

б. квадрат г. трапеция

. Отрезок, соединяющий середины боковых сторон трапеции называется…

а. лучом в. средней линией

б. биссектрисой г. медианой

. В известной сказке «Поди туда - не знаю куда, принеси то - не знаю что» царь послал стрельца Андрея за тридевять земель. Тридевять земель - это сколько?

а. 39 в. 12

б. 27 г. 10

Вопросы 2-го тура:

1. 1.Луч, делящий угол пополам:

а. биссектриса в. средняя линия

б. медиана г. высота

. Сумма смежных углов:

а. 90⁰в. 360⁰

б. 180⁰г. 270⁰

3. Вычислите :

а. -12в. -14

б. 14г. 12

. Вычислите :

а. -9в. 81

б. 9г. такого значения не существует

. Прямоугольник с равными сторонами:

а. квадрат в. четырехугольник

б. прямоугольник г. ромб

. С какого числа начинается ряд натуральных чисел?

а. 1в. -1

б. 0г. 9

. Две дочери, две матери, да бабушка с внучкой. Сколько всех?

а. 3в. 2

б. 4г. 5

. Как называют график функции ?

а. парабола в. гипербола

б. прямая г. окружность

. Сократите дробь :

а. х-1 в. 1

б. х г. х+1

. Чему равно число Пи с точностью до тысячных?

б. 3,143 г. 3,144

Вопросы 3-го тура:

. Сколько минут варится яйцо, сваренное вкрутую?

а. 5 мин в. 0 мин

б. 10 мин г. 12 мин

. Вычислите :

а. в.

б. г.

. Найдите значения выражения :

а. 81в. 5

б. 9г. 0,2

. При царе Иване IV были выпущены монеты, на которых изображен всадник с копьем в руке. Как назывались эти монеты?

а. рубль в. алтын

б. гривна г. копейка

. Диагонали равны и перпендикулярны у …

а. прямоугольника в. квадрата

б. ромба г. параллелограмма

. Если перевернуть цифру, то уменьшиться на 3.

а. 3 в. 6

б. 9 г. 12

7. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

а. медиана в. биссектриса

б. высота г. средняя линия

. Горели 7 свечей, 2 погасло. Сколько осталось свечей?

а. 5 в. 2

б. 7 г. 6

. Напишите 100 пятью 1, используя знаки математического действия.

а. 111-10 в. 110-11

б. 111-11 г.

. Откуда был родом Пифагор?

а. остров Самос в. остров Лесбос

б. остров Крит г. остров Итака