Исследование режимов и выбор основных параметров системы электропередачи
Содержание
Введение
. Исходные данные
. Выбор конструкций и типов проводов
. Сопоставление сопротивлений и
проводимостей, вычисленных по формулам и определенных с помощью
нормативно-справочной литературы
. Расчет волновых параметров ЛЭП по
точным и приближенным формулам с учетом и без учета потерь
. Определение обобщенных постоянных
А, В, С, D c учетом и без учета потерь в линии
. Расчет критериальных параметров
ЛЭП и их зависимостей
. Расчет режимов ЛЭП в режиме
максимальных и минимальных нагрузок с учетом и без учета потерь
. Построение зависимости стоимости
передачи электроэнергии от КПД ЛЭП
. Повышение пропускной способности
электропередачи
. Технико-экономические показатели
электропередачи
Заключение
Литература
Введение
Целью данной курсовой работы является анализ
режимов системы передачи и выбор основных ее параметров. Проводятся расчеты
режимных параметров с учетом и без учета потерь, сопоставление удельных
сопротивлений и проводимостей, вычисленных по формулам и определенных по
справочной литературе. Также необходимо провести расчеты волновых параметров
ЛЭП по точным и приближенным формулам с учетом и без учета потерь, обобщенных
постоянных четырехполюсника А, В, С, D
с учетом и без учета потерь в линии. Далее проводятся расчеты критериальных
параметров ЛЭП и их зависимостей с построением соответствующих графических
зависимостей. Необходимо также провести расчет одного из мероприятий по
повышению пропускной способности ЛЭП.
1. Исходные данные
Основная исходная информация содержится в
задании по курсовой работе. Рассчитаем данные необходимые для выполнения
проекта:
o Номинальное напряжение линии
электропередачи (ЛЭП) 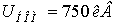 ;
;
o Протяженность ЛЭП 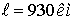 ;
;
o Передаваемая мощность в максимальном
режиме принимаем
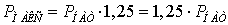 ,
,
где  -
натуральная мощность ЛЭП, МВт.
-
натуральная мощность ЛЭП, МВт.
Для напряжения 750 кВ 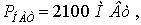 тогда
тогда
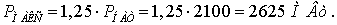
o Передаваемая мощность в минимальном
режиме, принимаем

o Число часов использования
максимальной нагрузки 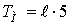 , где
, где 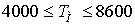
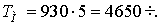
o Нагрузка  где
где 
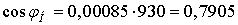
Расчетное значение 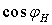 не
удовлетворяет условию
не
удовлетворяет условию  , поэтому
принимаем минимальное значение для дальнейших расчетов
, поэтому
принимаем минимальное значение для дальнейших расчетов 
o Стоимость передачи 1 кВт×ч
электроэнергии по ЛЭП 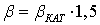
b=0,03 руб./кВт×ч,
что сильно занижено, поэтому стоимость передачи необходимо увеличить в 1,5
раза.
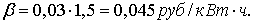
o Для каждого рассматриваемого сечения
выбираем наибольший допустимый рабочий ток проводника, обусловленный его
нагреванием 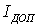 , для ВЛ с
расщепленными проводами значение увеличивается в соответствии с количеством
проводов в фазе.
, для ВЛ с
расщепленными проводами значение увеличивается в соответствии с количеством
проводов в фазе.
o Стоимость проводникового материала,
принимаем согласно [1, табл. 9.8 стр. 329], для
железобетонных опор, II район по гололеду.
. Выбор конструкций и типов проводов
На напряжение 750 кВ наиболее часто применяют
сталеалюминевые провода со следующими сечениями: 5х240/56, 5х300/66, 5х400/51,
4х400/93, 4х500/64. Но в литературе [1,c
329] нет необходимых для расчета данных о сечениях 4х400/93 и 4х500/64. Поэтому
в данном расчете не применяем эти сечения.
Проверим их по длительно допустимому току
нагрева, т.е. расчетный ток должен быть меньше наибольшего допустимого рабочего
тока проводника, обусловленного его нагреванием
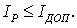 (2.1)
(2.1)
где 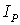 -
расчетная токовая нагрузка линии для проверки проводов по нагреву;
-
расчетная токовая нагрузка линии для проверки проводов по нагреву;
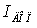 - допустимый рабочий ток проводника,
по [1, таблица 7.12].
- допустимый рабочий ток проводника,
по [1, таблица 7.12].
Проверим провода по соотношению
(2.1).
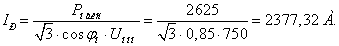 (2.2)
(2.2)
Для сечения 5×240/56 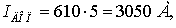 что
удовлетворяет условию (2.1). Выбранное сечение, при заданной передаваемой
мощности по линии, можно применять.
что
удовлетворяет условию (2.1). Выбранное сечение, при заданной передаваемой
мощности по линии, можно применять.
Оставшиеся проводники рассчитываем
аналогично, результаты расчетов представим в виде таблицы 2.1.
Таблица 2.1 - Результаты проверки
проводников по длительно допустимому току нагрева
|
Сечение
проводника, мм2
|
Допустимый
ток для одного провода, А
|
Допустимый
ток для трех фазных проводников, кА
|
Расчетный
ток, кА
|
Вывод
|
|
5×240/56
|
610
|
3050
|
2377,3
|
Удовлетворяет
|
|
5×300/66
|
680
|
3400
|
2377,3
|
Удовлетворяет
|
|
5×400/51
|
825
|
4125
|
2377,3
|
Удовлетворяет
|
Проведем проверку сечений по условию короны:
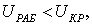 (2.3)
(2.3)
где  -
рабочее напряжение, принимаем равным номинальному, кВ;
-
рабочее напряжение, принимаем равным номинальному, кВ;
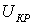 -
критическое напряжение возникновения короны, кВ.
-
критическое напряжение возникновения короны, кВ.
Критическое (линейное) напряжение
возникновения короны можно найти по выражению:
 (2.4)
(2.4)
где 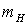 -
коэффициент, по которому учитывается состояние поверхности провода,
-
коэффициент, по которому учитывается состояние поверхности провода, 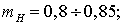
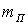 -
коэффициент, учитывающий состояние погоды, при сухой и ясной погоде
-
коэффициент, учитывающий состояние погоды, при сухой и ясной погоде 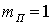 , при
тумане, дожде, инее, мокром снеге и гололеде
, при
тумане, дожде, инее, мокром снеге и гололеде 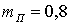 ;
;  -
коэффициент относительной плотности воздуха, при давлении 760 мм рт. ст. и
температуре воздуха 25°С
-
коэффициент относительной плотности воздуха, при давлении 760 мм рт. ст. и
температуре воздуха 25°С 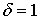 ;
;
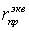 -
эквивалентный радиус расщепленной конструкцией фазы, см;
-
эквивалентный радиус расщепленной конструкцией фазы, см;
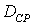 -
среднегеометрическое расстояние между фазными проводами, см.
-
среднегеометрическое расстояние между фазными проводами, см.
Проверим, удовлетворяют ли выбранные
сечения условию (2.3). Значения  ,
, 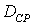 примем из пункта 3 курсовой работы.
примем из пункта 3 курсовой работы.
Сечение 5×240/56: 
Сечение 5×300/66: 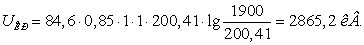
Сечение 5×400/51: 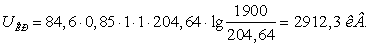
Условие (2.3) для рассматриваемых
сечений выполняется.
. Сопоставление сопротивлений и
проводимостей, вычисленных по формулам и определенных с помощью
нормативно-справочной литературы
Удельное активное сопротивление
линии исходя из [3, стр. 56, 2.4 ]
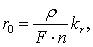 (3.1)
(3.1)
где 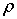 -
расчетное удельное активное сопротивление материала проводника, принимаем [3,
стр. 56] 31,5 Ом×мм2/км;
-
расчетное удельное активное сопротивление материала проводника, принимаем [3,
стр. 56] 31,5 Ом×мм2/км;
F - сечение проводника, мм2;
 -
число проводников в фазе.
-
число проводников в фазе.
Индуктивное сопротивление линии с
расщепленными фазами определяется из соотношения
 (3.2)
(3.2)
где 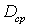 -
среднегеометрическое расстояние между фазными проводами, м, определяется по
справочной литературе [3, стр. 684]
-
среднегеометрическое расстояние между фазными проводами, м, определяется по
справочной литературе [3, стр. 684]
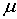 -
магнитная проницаемость материала провода, при частоте 50 Гц для провода из
цветных металлов
-
магнитная проницаемость материала провода, при частоте 50 Гц для провода из
цветных металлов 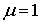 ;
;
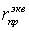 -
эквивалентный радиус расщепленной конструкции фазы, м;
-
эквивалентный радиус расщепленной конструкции фазы, м;
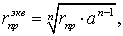 (3.3)
(3.3)
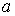 -
расстояние между проводами в фазе, равное 40-60 см;
-
расстояние между проводами в фазе, равное 40-60 см;
 -
число проводов в фазе;
-
число проводов в фазе;
 -
радиус многопроволочного провода, определяется по справочной литературе. При
отсутствии данных фактический радиус
-
радиус многопроволочного провода, определяется по справочной литературе. При
отсутствии данных фактический радиус  можно определить по суммарной
площади сечения токоведущей части F и стальной
части провода FСТ, увеличив
его с учетом скручивания на 15-20%,
можно определить по суммарной
площади сечения токоведущей части F и стальной
части провода FСТ, увеличив
его с учетом скручивания на 15-20%,
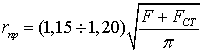 (3.4)
(3.4)
Емкостная проводимость протяженной
ЛЭП :
 (3.5)
(3.5)
Активная проводимость протяженной
ЛЭП по :
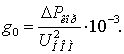 (3.6)
(3.6)
где  -
потери на корону, кВт/км, которые зависят от погоды и в зависимости от
характера задач принимаются максимальными или среднегодовыми. Согласно [3, стр.
684], для ВЛ 750 кВ выберем для каждого сечения удельные потери на корону
-
потери на корону, кВт/км, которые зависят от погоды и в зависимости от
характера задач принимаются максимальными или среднегодовыми. Согласно [3, стр.
684], для ВЛ 750 кВ выберем для каждого сечения удельные потери на корону  .
.
С учетом [2, стр. 35], коэффициенты  определим
на основе соотношений
определим
на основе соотношений
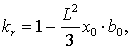 (3.7)
(3.7)
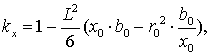 (3.8)
(3.8)
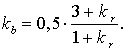 (3.9)
(3.9)
Рассчитаем удельные
сопротивления и проводимости для сечения 5×240/56.
Удельное активное сопротивление
линии
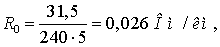
Индуктивное сопротивление линии
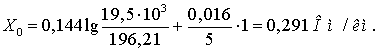
где rпр и rпрэкв определены
по (3.3) и (3.4) соответственно
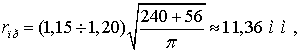

Емкостная проводимость линии
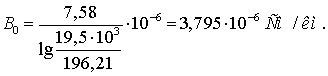
Активная проводимость линии

Уточним значения  ,
, 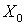 ,
, 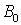 с учетом
поправочных коэффициентов (3.7-3.9).
с учетом
поправочных коэффициентов (3.7-3.9).
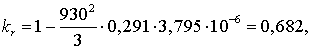

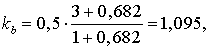
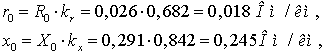
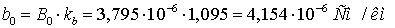 .
.
Рассчитаем удельные
сопротивления и проводимости для сечения 5×300/66.
Удельное активное сопротивление
линии

Индуктивное сопротивление линии
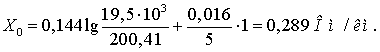
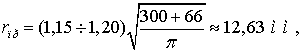
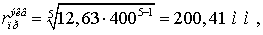
Емкостная проводимость линии
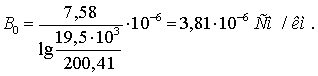
Активная проводимость линии
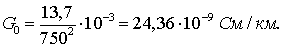
Уточним значения  ,
, 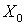 ,
, 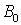 с учетом
поправочных коэффициентов (3.7-3.9).
с учетом
поправочных коэффициентов (3.7-3.9).
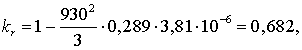
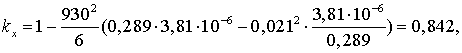
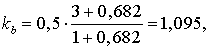

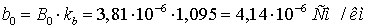
Рассчитаем удельные
сопротивления и проводимости для сечения 5×400/51.
Удельное активное сопротивление
линии
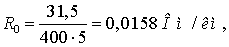
Индуктивное сопротивление линии
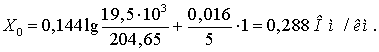

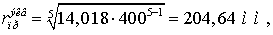
Емкостная проводимость линии
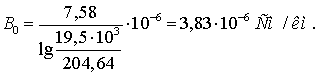
Активная проводимость линии
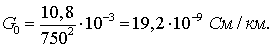
Уточним значения  ,
, 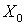 ,
, 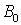 с учетом
поправочных коэффициентов (3.7-3.9).
с учетом
поправочных коэффициентов (3.7-3.9).
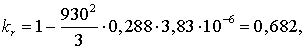
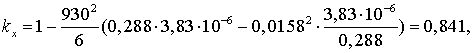

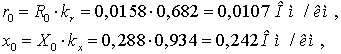
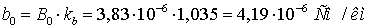
Таблица 3.1 - Рассчитанные и
определенные по справочной литературе характеристики ВЛ 750 кВ для
рассматриваемых сечений
|
Номинальное
сечение провода
|
Удельные
параметры ЛЭП 750 кВ
|
|
Расчетные
данные
|
Справочные
данные
|
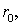
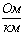
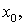
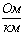
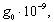
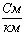

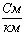
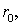
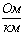
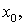
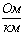
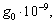
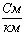
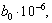
|
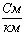
|
|
|
|
|
|
|
|
|
|
5×240/56
|
0,0178
|
0,245
|
28,44
|
4,15
|
0,024
|
0,308
|
28,44
|
3,76
|
|
5×300/66
|
0,0143
|
0,243
|
24,36
|
4,17
|
0,021
|
0,288
|
24,36
|
4,11
|
|
5×400/51
|
0,0107
|
0,242
|
19,2
|
4,19
|
0,015
|
0,286
|
19,2
|
4,13
|
4. Расчет волновых параметров ЛЭП по
точным и приближенным формулам с учетом и без учета потерь
К волновым параметрам ЛЭП относятся
- волновое сопротивление 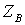 , постоянная
распространения волны
, постоянная
распространения волны 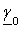 , натуральная
мощность линии
, натуральная
мощность линии  и волновая
длина
и волновая
длина 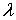 .
.
Волновое сопротивление определяется
согласно [2, стр. 25, 1.7], постоянная распространения волны по [2, стр. 25,
1.10]
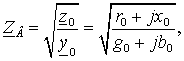 (4.1)
(4.1)
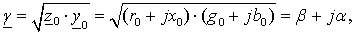 (4.2)
(4.2)
где 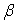 - коэффициент затухания амплитуды
волны на единицу длины;
- коэффициент затухания амплитуды
волны на единицу длины; 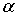 -
коэффициент изменения фазы волны на единицу длины.
-
коэффициент изменения фазы волны на единицу длины.
Значения 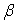 ,
, 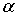 ,
, 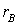 ,
,  можно
определить по выражениям [2, стр. 25, 1.19-1.22]
можно
определить по выражениям [2, стр. 25, 1.19-1.22]
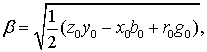 (4.3)
(4.3)
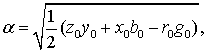 (4.4)
(4.4)
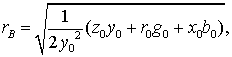 (4.5)
(4.5)
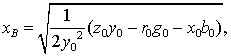 (4.6)
(4.6)
Натуральная мощность равна [2, стр.
28, 1.35]
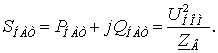 (4.7)
(4.7)
Волновая длина линии по [2, стр. 27]
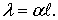 (4.8)
(4.8)
Сечение 5×240/56.
Проведем расчет волновых параметров
ЛЭП с учетом потерь.
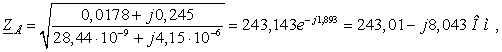

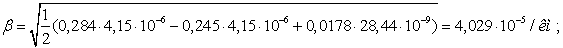
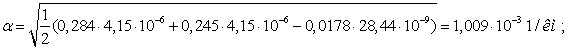
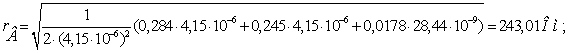
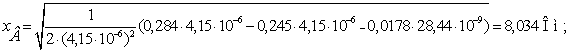
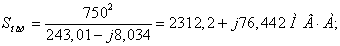
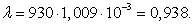
Проведем расчет волновых параметров
ЛЭП без учета потерь.

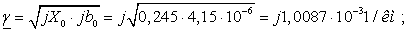
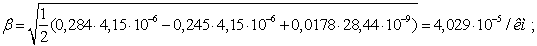
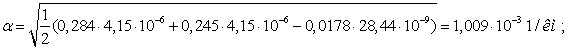

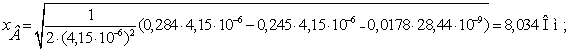
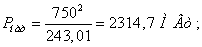
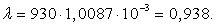
Определим погрешность расчета  на основе
каталожных данных и расчетов.
на основе
каталожных данных и расчетов.
С учетом потерь
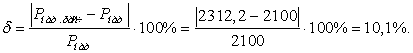
Без учета потерь
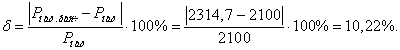
Расхождение расчетных и каталожных
параметров можно объяснить тем, что в справочной литературе даны значения,
которые не учитывают длину линии. Погрешность расчета натуральной мощности с
учетом потерь составила 10,1%, без учета потерь - 10,22%.
Выполним аналогичные расчеты для
оставшихся сечений.
Результаты расчетов сведем в таблицу
4.1.
Таблица 4.1 - Волновые параметры ЛЭП
750 кВ
|
Параметр
ЛЭП
|
Сечение
провода марки АС
|
|
5×300/66
|
5×400/51
|
|
Результаты
расчета с учетом потерь
|
|
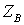 , Ом241,75-j6,39240,56-j4,77 , Ом241,75-j6,39240,56-j4,77
|
|
|
|
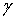 , 1/км(0,326+j10,088)∙10-4(0,246+j10,084)∙10-4 , 1/км(0,326+j10,088)∙10-4(0,246+j10,084)∙10-4
|
|
|
|
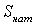 , МВ·А2325,2+j61,4652337,4+j46,376 , МВ·А2325,2+j61,4652337,4+j46,376
|
|
|
|
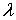 0,9370,937 0,9370,937
|
|
|
|
Результаты
расчета без учета потерь
|
|
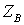 , Ом241,63240,49 , Ом241,63240,49
|
|
|
|
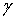 , 1/кмj 10,084∙10-4j 10,082∙10-4 , 1/кмj 10,084∙10-4j 10,082∙10-4
|
|
|
|
 , МВт2326,82338,3 , МВт2326,82338,3
|
|
|
|
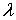 0,9370,937 0,9370,937
|
|
|
5. Определение обобщенных постоянных
А, В, С, D
c
учетом и без учета потерь в линии
Линия является некоторым передаточным звеном в
общей электрической системе и может представляться симметричным четырехполюсником
с обобщенными постоянными согласно [2, стр. 32, 1.43]
А=сhγl; В= zвshγl; D=сhγl; C=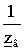 shγl. (5.1)
shγl. (5.1)
Вычисление гиперболических функций
комплексного аргумента произведем при помощи сочетаний :
сhγl= сhβlcosαl+j shβlsinαl; (5.2)
shγl= shβlcosαl+j chβlsinαl,
где по (4.2) γ=β+jα, γ - постоянная
распространения волны.
Для линии без потерь r0=0 и g0=0. Тогда
получим
сhγl= сhjαl=cosαl; shγl= shjαl=jsinαl. (5.3)
Выражения для определения обобщенных
постоянных примут вид
А= cosαl; В= jzвsinαl; D= cosαl; C=j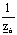 sinαl. (5.4)
sinαl. (5.4)
С учетом (5.1), (5.2)
определим обобщенные постоянные для сечения 5×240/56 с учетом
потерь в линии.
сhγl=сh(0,4028∙10-4∙930)cos(10,09∙10-4∙930)+
+jsh(0,4028∙104∙930)sin(10,09∙10-4∙930)=0,592+j0,03;
shγl=sh(0,4028∙10-4∙930)cos(10,09∙10-4∙930)+
+jch(0,4028∙104∙930)sin(10,09∙10-4∙930)=0,022+j0,807;
А=0,592+j0,03; В=(243,007-j8,034)∙(0,022+j0,807)=11,867+195,968;
D=0,592+j0,03; C=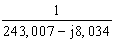 ∙(0,022+j0,807)=-1,865∙10-5+j3,321∙10-3.
∙(0,022+j0,807)=-1,865∙10-5+j3,321∙10-3.
С учетом (5.3), (5.4)
определим обобщенные постоянные для сечения 5×240/56 без учета
потерь в линии.
сhγl= cos(10,09∙10-4∙930)=0,591;
shγl= jsin(10,09∙10-4∙930)=j0,806;
А=0,591; В=242,82∙j0,806=j195,71;
D=0,591; C=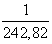 ∙j0,806=j3,319∙10-3.
∙j0,806=j3,319∙10-3.
Для сечений 5х300/66 и 5х400/51
проводим аналогичные расчеты, и результаты сводим в таблицу:
Таблица 5.1
|
Параметр
ЛЭП
|
Сечение
проводника марки АС
|
|
5×300/66
|
5×400/51
|
|
С
учетом потерь
|
|
А
|
0,591+j0,024
|
0,592+j0,018
|
|
В
|
9,49+j194,97
|
7,106+j193,888
|
|
C
|
-1,409∙10-5+j3,338∙10-3
|
-1,02∙10-5+j3,351∙10-3
|
|
D
|
0,591+j0,024
|
0,592+j0,018
|
|
Без
учета потерь
|
|
А
|
0,591
|
0,592
|
|
В
|
j194,898
|
j193,846
|
|
C
|
j3,338∙10-3
|
j3,352∙10-3
|
|
D
|
0,591
|
0,592
|
6. Расчет критериальных параметров ЛЭП
и их зависимостей
Для каждого стандартного сечения линии данного
типа и напряжения построим зависимости приведенных затрат от мощности З=f(Р).
Это выражение представляет собой согласно [3, стр. 557, 12.48] параболу вида
З=А+ВI2нб,
где Iнб=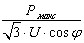 . По [3,
стр. 557, 12.49]
. По [3,
стр. 557, 12.49]
З=(Е+ра)К+Иэ+3∙Iнб2 τβн+∆РкL∙8760∙βх, (6.1)
τβн+∆РкL∙8760∙βх, (6.1)
где Е - нормативный коэффициент
эффективности капитальных затрат, равный 0,12;
ра - норма в долях от
капитальных затрат на амортизацию, согласно [3, стр. 535, таблица 12.3]
принимаем 0,024;
Иэ - эксплуатационные
расходы, по [3, стр. 534, 12.9] Иэ= рэК,
рэ - норма в долях от
капитальных затрат на текущий ремонт и обслуживание, согласно [3, стр. 535,
таблица 12.3] принимаем 0,004;
βн, βх - расчетная
стоимость 1 кВт∙ч нагрузочных потерь и потерь холостого хода, значения,
даваемые [1, стр. 317, рис. 8.1], как показал проф. П.Г. Грудинский, занижены и
их следует увеличить в 1,5 раза, поэтому βх=0,0167∙1,5=0,025
руб./кВт∙ч, βн=0,026∙1,5=0,039
руб./кВт∙ч; ∆Рк - потери электроэнергии на корону на 1
км линии.
По [3, стр. 557, 12.50]
В=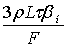 . (6.2)
. (6.2)
Задаваясь различными значениями
мощностей, найдем приведенные затраты для каждой марки провода. Зависимости
приведенных затрат от мощности показаны на рисунке 6.1.
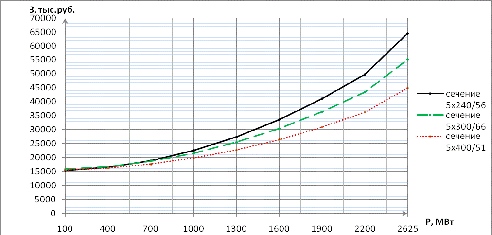
Рисунок 6.1 - Экономические
интервалы мощности
Выбираем марку провода АС-5×400/51, так как для
этого сечения при интересующих нас мощностях получаем наименьшие приведенные
затраты.
Согласно [2, стр. 174, 3.15]
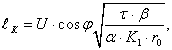 (6.3)
(6.3)
где 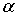 - ежегодные расходы на амортизацию
- ежегодные расходы на амортизацию 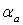 , расходы на
эксплуатацию
, расходы на
эксплуатацию 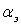 и
отчисления по нормативному коэффициенту эффективности капиталовложений
и
отчисления по нормативному коэффициенту эффективности капиталовложений 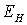 , согласно
[1, стр. 255, таблица 8.2],
, согласно
[1, стр. 255, таблица 8.2], 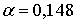 ;
;
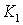 - стоимость сооружения 1 км линии,
для 5×240/56
- стоимость сооружения 1 км линии,
для 5×240/56
 для 5×300/66
для 5×300/66 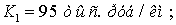 для 5×400/51
для 5×400/51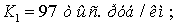
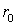 - активное сопротивление провода,
Ом/км;
- активное сопротивление провода,
Ом/км;  - время
наибольших потерь, ч. По [3, стр. 390, 9.31]
- время
наибольших потерь, ч. По [3, стр. 390, 9.31]
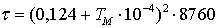 (6.4)
(6.4)
Экономический КПД линии определяется
по формуле [2, стр. 174, 3.14]
 (6.5)
(6.5)
Экономическая мощность согласно [2,
стр. 187]
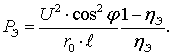 (6.6)
(6.6)
Экономическая плотность тока по [2,
стр. 186, 3.24]
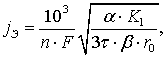 (6.7)
(6.7)
Минимальная стоимость передачи
электроэнергии по ЛЭП по [2, стр. 175, 3.17]
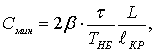 (6.8)
(6.8)
Рассчитаем критериальные параметры
для ЛЭП сечением 5×400/51.
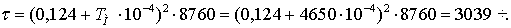
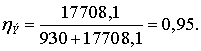
Экономическая мощность

Экономическая плотность тока

Минимальная стоимость передачи
электроэнергии по ЛЭП
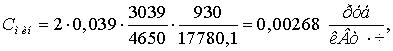
Рассчитаем критериальные параметры
для оставшихся сечений, результаты расчетов сведем в таблицу 6.1.
Таблица 6.1 - Критериальные
параметры ЛЭП 750 кВ
|
Параметр
ЛЭП
|
Сечение
провода марки АС
|
|
5×240/56
|
5×300/66
|
|
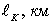 14414,415478,15 14414,415478,15
|
|
|
|
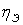 0,9390,943 0,9390,943
|
|
|
|
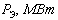 15841836,1 15841836,1
|
|
|
|
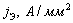 1,1951,109 1,1951,109
|
|
|
|
 0,003290,00306 0,003290,00306
|
|
|
По таблице 6.1 видно, что увеличение
сечения приводит к снижению стоимости передачи электроэнергии по ЛЭП, а также к
увеличению значения экономического КПД 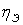 .
.
Построим графики зависимостей
критериальных параметров ЛЭП.
Таблица 6.2 - Данные к построению
зависимости 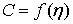
|
η
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
0,99
|
|
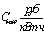 0,2290,1020,0590,0380,0260,0170,0110,00670,00360,0072 0,2290,1020,0590,0380,0260,0170,0110,00670,00360,0072
|
|
|
|
|
|
|
|
|
|
|
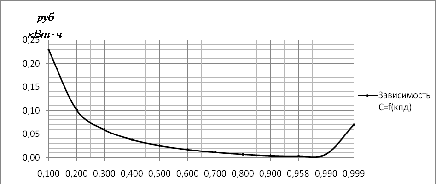
Рис. 6.2 - График функции 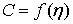
Таблица 6.3 - Данные к построению
зависимости 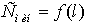
|
 050010001500200025003000350040004500 050010001500200025003000350040004500
|
|
|
|
|
|
|
|
|
|
|
|
 00,00140,00290,00430,00580,00720,00860,01010,01150,013 00,00140,00290,00430,00580,00720,00860,01010,01150,013
|
|
|
|
|
|
|
|
|
|
|
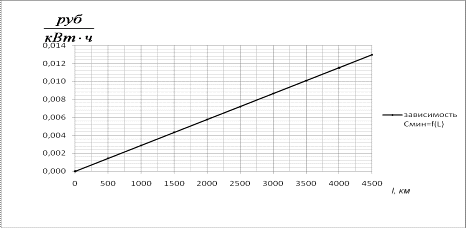
Рис. 6.3 - График функции 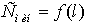
Таблица 6.4 - Данные к построению
зависимости 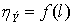
|
 0500 0500
|
1000
|
1500
|
2000
|
2500
|
3000
|
3500
|
4000
|
4500
|
5000
|
5500
|
|
|
|
 10,973 10,973
|
0,947
|
0,922
|
0,899
|
0,876
|
0,855
|
0,835
|
0,816
|
0,797
|
0,78
|
0,763
|
|
|
|
 6000650070007500 6000650070007500
|
|
|
|
|
|
|
 0,747 0,747
|
0,731
|
0,717
|
0,702
|
|
|
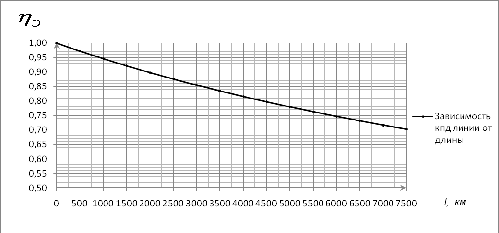
Рис. 6.4 - График функции 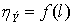
Таблица 6.5 - Данные к построению
зависимости 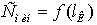
|
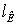 5000 5000
|
7500
|
1000
|
12500
|
15000
|
17500
|
20000
|
22500
|
25000
|
27500
|
|
|
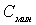 0,243 0,243
|
0,162
|
0,122
|
0,097
|
0,081
|
0,069
|
0,061
|
0,054
|
0,049
|
0,044
|
|
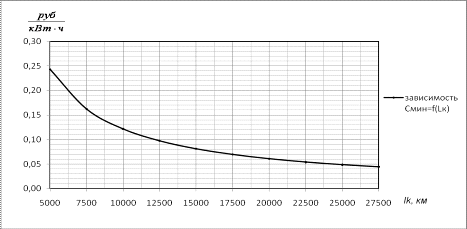
Рис. 6.5 - График функции 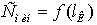
Таблица 6.6 - Данные к построению
зависимости 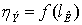
|
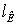 0 0
|
2500
|
5000
|
7500
|
1000
|
12500
|
15000
|
17500
|
20000
|
22500
|
25000
|
27500
|
30000
|
|
|
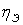 0 0
|
0,729
|
0,843
|
0,89
|
0,915
|
0,931
|
0,942
|
0,95
|
0,956
|
0,96
|
0,964
|
0,967
|
0,97
|
|
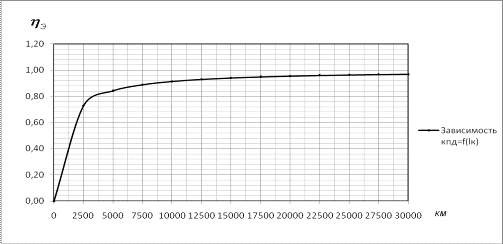
Рис. 6.6 - График функции 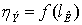
Таблица 6.7 - Данные к построению
зависимости 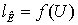
|
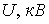 110220330400500600750 110220330400500600750
|
|
|
|
|
|
|
|
|
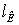 2597,175194,347791,519444,2611805,3314166,3917708,1 2597,175194,347791,519444,2611805,3314166,3917708,1
|
|
|
|
|
|
|
|
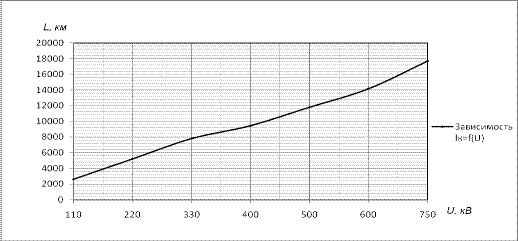
Рис. 6.7 - График функции 
Таблица 6.8 - Данные к построению
зависимости 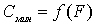
|
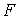 , мм21200 , мм21200
|
1500
|
2000
|
|
|
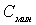 0,00329 0,00329
|
0,00306
|
0,00268
|
|
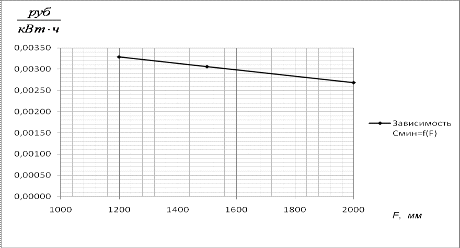
Рис. 6.8 - График функции 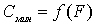
Таблица 6.9 - Данные к построению
зависимости 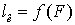
|
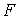 ,
мм2120015002000 ,
мм2120015002000
|
|
|
|
|
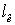 , км14414,4 , км14414,4
|
15478,15
|
17708,1
|
|
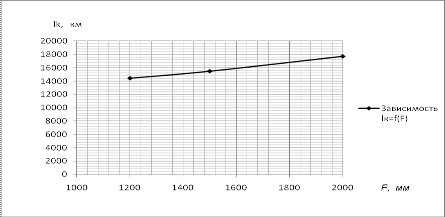
Рис. 6.9 - График функции 
7. Расчет режимов ЛЭП в режиме
максимальных и минимальных нагрузок с учетом и без учета потерь
линия электропередача
провод нагрузка
Рассчитать режим ЛЭП с учетом потерь
можно с помощью системы уравнений
 (7.1)
(7.1)
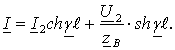 (7.2)
(7.2)
Без учета потерь рассчитать режим
ЛЭП позволяет система уравнений
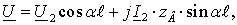 (7.3)
(7.3)
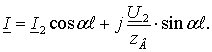 (7.4)
(7.4)
Рассчитаем режим
электропередачи, учитывая потери в ЛЭП.
В режиме наибольших нагрузок в конце
линии протекает ток 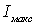 и
напряжение равно номинальному. Примем, что напряжение в конце линии совпадает
по модулю с номинальным, а его фаза равна нулю. По заданию вектор тока отстает
на угол равный
и
напряжение равно номинальному. Примем, что напряжение в конце линии совпадает
по модулю с номинальным, а его фаза равна нулю. По заданию вектор тока отстает
на угол равный 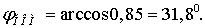 от
напряжения в конце линии.
от
напряжения в конце линии.
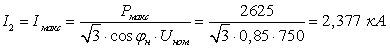
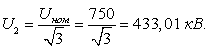
Определим ток и напряжение в начале
линии для сечения 5×400/51.
Режим максимальных нагрузок:
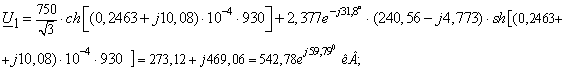
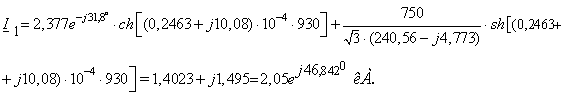
Режим минимальных нагрузок.
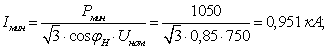
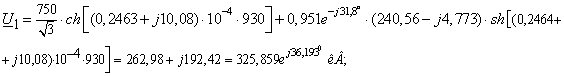

Рассчитаем режим
электропередачи, не учитывая потери в ЛЭП.
Режим максимальных нагрузок.
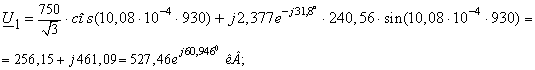
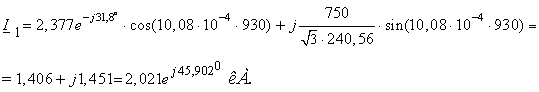
Режим минимальных нагрузок.
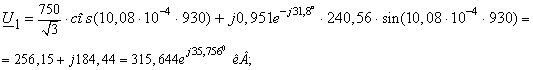

. Построение зависимости стоимости
передачи электроэнергии от КПД ЛЭП
Зависимость стоимости передачи электроэнергии от
КПД ЛЭП:

Для построения зависимости составим таблицу 8.1.
Таблица 8.1 - Данные к построению
зависимости стоимости передачи электроэнергии от КПД С=f(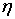 )
)
|
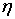 0,10,20,30,40,50,60,70,80,90,9520,99 0,10,20,30,40,50,60,70,80,90,9520,99
|
|
|
|
|
|
|
|
|
|
|
|
|
С,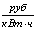 0,2290,1020,0590,0380,0260,0170,01110,00670,003 0,2290,1020,0590,0380,0260,0170,01110,00670,003
|
0,00268
|
0,0072
|
|
|
|
|
|
|
|
|
|
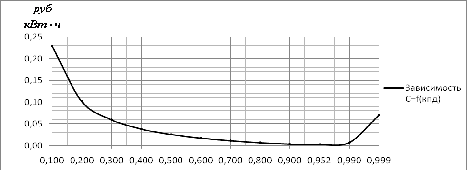
Рис. 8.1 - Зависимость стоимости передачи
электроэнергии от КПД для ЛЭП сечением 5×400/51 мм2
Из зависимости видно, что
минимальная стоимость передачи электроэнергии для сечения 5×400/51 достигается
при 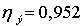 и равна
и равна 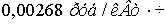 .
.
Отклонения от экономического КПД
приводят к увеличению стоимости передачи электроэнергии.
. Повышение пропускной способности
электропередачи
Под пропускной способностью
электропередачи понимается максимальная мощность, которая может быть передана
по ней с учетом всех возможных ограничений. К таким ограничениям относятся
допустимые значения напряжения в узлах электропередачи, коэффициенты запаса по
статической и динамической устойчивости, нагрев проводов свыше допустимого в
данных климатических условиях, пропускная способность оборудования подстанций.
Рассмотрим выбор реактора в качестве средства
повышения пропускной способности ЛЭП.
Реактор представляет собой катушку индуктивности
с малым активным сопротивлением, намотанную на магнитопровод. Они могут только
потреблять из сети реактивную мощность.
Проводимость шунтирующего реактора в
относительных единицах (Рбаз=Рнат) руководствуясь [2,
стр. 117, 2.21] может быть представлена в виде
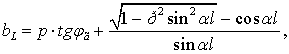 (9.1)
(9.1)
где р - удельная нагрузка линии при
передаче мощности Рмакс =2625 МВт. Определяется по [2, стр. 31,
1.41]
р=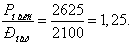
Тогда 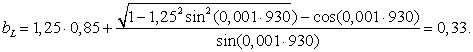
 =2100∙0.33=693 Мвар.
=2100∙0.33=693 Мвар.
Передаваемая мощность в долях от
натуральной мощности по [2, стр. 115, 2.18]
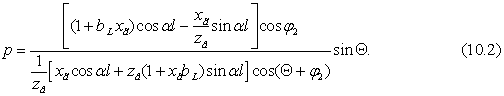
р =
=
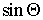 .
.
Тогда
 =arcsin(р
=arcsin(р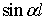 ∙
∙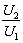 )= arcsin(
)= arcsin(
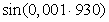 ∙
∙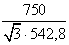 )=0,935 рад.
)=0,935 рад.
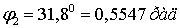
Тогда
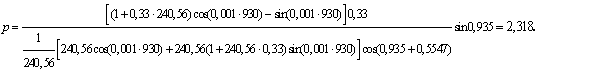
P=2100∙2,318=4867,8
МВт.
Таким образом, установка реактора рассчитанной
мощности позволит увеличить пропускную способность ЛЭП до P=2100∙2,318=4867,8
МВт.
10. Технико-экономические показатели
электропередачи
Приведенные затраты З согласно [2, стр. 476,
8.51]
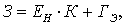 (10.1)
(10.1)
где 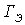 - годовые эксплуатационные расходы
- годовые эксплуатационные расходы
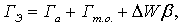 (10.2)
(10.2)
состоящие из расходов на амортизацию
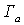 , текущий
ремонт и обслуживание
, текущий
ремонт и обслуживание  и стоимости
потерянной энергии
и стоимости
потерянной энергии 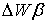 .
.
Здесь 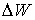 -
потерянная энергия за год в электропередаче;
-
потерянная энергия за год в электропередаче; 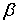 -
стоимость 1 кВт×ч потерянной
электроэнергии.
-
стоимость 1 кВт×ч потерянной
электроэнергии.
Количество энергии, пропущенной
через электропередачу
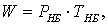 (10.3)
(10.3)
 -
наибольшая мощность и число часов использования наибольшей мощности
электропередачи.
-
наибольшая мощность и число часов использования наибольшей мощности
электропередачи.
Стоимость передачи электроэнергии СП
 (10.4)
(10.4)
Себестоимость передачи
электроэнергии
 (10.5)
(10.5)
Коэффициент полезного действия при
наибольшей нагрузке
 (10.6)
(10.6)
где  -
активная мощность конца участка электропередачи и потери активной мощности на
этом участке.
-
активная мощность конца участка электропередачи и потери активной мощности на
этом участке.
Экономический КПД, соответствующий
минимальной расчетной стоимости передачи электроэнергии по ЛЭП, находится по
выражению
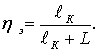 (10.7)
(10.7)
Рассчитаем технико-экономические показатели ЛЭП
сечением 5×400/51.
Капитальные затраты в ЛЭП
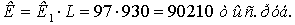
Потери мощности и электроэнергии в ЛЭП
- нагрузочные
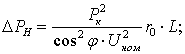


- холостого хода (потери на корону)
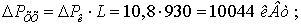

- суммарные потери мощности и
электроэнергии в ЛЭП

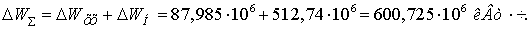
Годовые эксплуатационные расходы
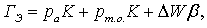

Приведенные затраты З
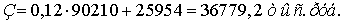
Электроэнергия отпущенная потребителям
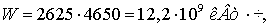
Стоимость передачи электроэнергии СП
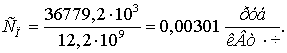
Себестоимость передачи
электроэнергии
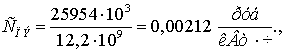
Коэффициент полезного действия при
наибольшей нагрузке
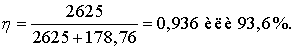
Экономический КПД, соответствующий
минимальной расчетной стоимости передачи электроэнергии по ЛЭП
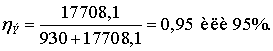
Заключение
В расчетах, проведенных в данной курсовой
работе, были определены удельные сопротивления и проводимости ЛЭП. Сравнивая
полученные значения и взятые из справочной литературы делаем вывод, что они
отличаются вследствие несовершенства формул для их расчета. На эти параметры
оказывают влияние множество факторов, которые не отражены в формулах.
Критериальные параметры ЛЭП с учетом и без учета
потерь отличаются несущественно, поэтому можно говорить о приемлемой точности
расчета без учета потерь по приближенным формулам.
При увеличении длины ЛЭП стоимость передачи
электроэнергии увеличивается, а при увеличении критериальной длины уменьшается.
При увеличении площади сечения провода стоимость передачи электроэнергии
снижается. Чем больше эквивалентная длина, тем меньше себестоимость передачи и
выше кпд.
Минимум себестоимости наблюдается в области
экономического кпд. При сдвиге кпд в ту или другую сторону себестоимость
возрастает. По построенным зависимостям затрат от мощности можно сделать вывод
что наименьшие затраты соответствуют наибольшему из рассматриваемых сечений.
Литература
1.
С.С. Рокотян и И.М. Шапиро. Справочник по проектированию электроэнергетических
систем. - 3-е изд., перераб. и доп. - М.: Энергоатомиздат, 1985.
.
Г.Е. Поспелов, В. Т. Федин. Передача энергии и электропередачи: Учеб. пособие
для студентов энерг. специальностей вузов.- Мн.: Адукацыя i
выхаванне, 2003. - 544 с.: ил.
.
А.А. Герасименко, В.Т. Федин. Передача и распределение электрической энергии.
Учебное пособие. - М.: Ростов-на-Дону Феникс, 2006.
.
Г.Е. Поспелов, В.Т. Федин. Проектирование электрических систем и сетей. - Мн.
Выш. школа., 1988. - 308 с.: ил.