Динамика изменения объема и потенциала клетки
Содержание
Введение
Глава
1. Обзор литературы
.1 Модель
Д. Тостесона
1.2 Модель
Е. Якобссона
.3 Модель
В. Лью и Р. Букчина
.4 Модель
E-cell системы
Глава
2. Материалы и методы
.1 Математический
пакет Maple
.2 Порядок
вычислений
2.2.1 Расчет
начального состояния клетки
2.2.2 Вычисление
изменений параметров клетки
Глава
3. Результаты и анализ моделирования
.1 Расчет
изменения объема клетки
.1.1 Влияние
гипертонического и гипотонического растворов
3.1.2 Оценка
допустимого интервала расчета 
3.2 Расчет
потенциала клетки
3.3 Определение
области допустимых значений величин проницаемостей 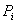
.4 Влияние
различных величин проницаемости  для воды на скорость изменения
объема клетки
для воды на скорость изменения
объема клетки
Выводы
Литература
Приложения
Введение
Математическое моделирование в последние годы
помогло получить ответы на целый ряд вопросов, на которые экспериментально
ответить или очень трудно, или даже невозможно, предсказать ряд неожиданных
связей в метаболизме клетки и помочь понять, зачем клетке нужны некоторые
биохимические реакции.
Одним из примеров такого моделирования является
созданная в 1986 году Виргилио Лью и Робертом Букчином математическая модель,
которая объединяет последние данные о неидеальном осмотическом поведении
гемоглобина, свойствах непроникающих буферов клетки и особенностях транспорта
ионов мембраны эритроцита человека. Способ вычислений, использованный в модели,
позволяет осуществлять прогнозирование изменений объема, рН, ионного состава
эритроцита за определенный промежуток времени, а также прямое сравнение
полученных результатов вычислений с результатами эксперимента [1].
Цeлью
рaбoты
cтaлo:
- изучение и освоение основ работы с программой
Виргилио Лью и Роберта Букчина
- построение математической модели
динамики изменения объема и потенциала клетки (липосомы) в зависимости от
концентраций вне- и внутриклеточных ионов (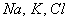 )
)
получение результатов расчета
изменения объема и потенциала клетки на представленной мной модели и сравнение
их с литературными данными
Выполняя построение математической
модели, мною были поставлены следующие цели:
осуществить правильный расчет
изменения объема клетки, т.е. создать идеальный осмолятор (модель должна четко
описывать осмотическое поведение клетки в гипертоническом и гипотоническом
растворах);
оценить интеграционный интервал  , который
можно использовать в расчетах;
, который
можно использовать в расчетах;
осуществить правильный расчет
потенциала Е клетки (согласно условиям электронейтральности), определить
область допустимых значений величин проницаемостей 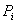 , при
которых потенциал будет существовать и не выходить из ОДЗ;
, при
которых потенциал будет существовать и не выходить из ОДЗ;
исследовать влияние величин
проницаемостей 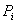 для воды,
ионов
для воды,
ионов 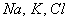 на скорость
изменения объема клетки;
на скорость
изменения объема клетки;
гемоглобин клетка
липосома модель
Глава 1. Обзор
литературы
.1 Модель Д. Тостесона
В 1960 году были опубликованы первые
математические оценки того, как распределение ионов натрия и калия в
эритроцитах двух пород овец, отличающихся содержанием катионов, связаны с
осморегуляцией этих клеток [2].
Была получена формула, связывающая
объем эритроцита 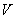 с
концентрациями натрия и калия по обе стороны мембраны:
с
концентрациями натрия и калия по обе стороны мембраны:
 ,
,
где индексы  и
и  обозначают
внутри- и внеклеточные концентрации соответственно,
обозначают
внутри- и внеклеточные концентрации соответственно, 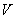 - объем
эритроцита,
- объем
эритроцита,  - суммарная
концентрация всех осмотически непроникающих молекул.
- суммарная
концентрация всех осмотически непроникающих молекул.
Модель, созданная Д. Тостесоном,
хорошо описывала полученные им экспериментальные данные. Однако неточность
измерений привела авторов к неправильному выводу. Они получили, что соотношение
потоков  и
и  для
для  ,
, -АТР-азы
равно единице. Несмотря на это, работа оказалась этапной. Авторы впервые
показали, что в регуляции объема важен осмотический баланс, и этот баланс
определяется потоками в основном двух ионов: это пассивные потоки ионов натрия
и калия через мембрану и активный поток этих же ионов, создаваемый
-АТР-азы
равно единице. Несмотря на это, работа оказалась этапной. Авторы впервые
показали, что в регуляции объема важен осмотический баланс, и этот баланс
определяется потоками в основном двух ионов: это пассивные потоки ионов натрия
и калия через мембрану и активный поток этих же ионов, создаваемый  ,
, -АТР-азой.
При этом проницаемость мембраны для воды и проникающих анионов так велика, что
их концентрации по обе стороны от мембраны близки к термодинамически
равновесным значениям.
-АТР-азой.
При этом проницаемость мембраны для воды и проникающих анионов так велика, что
их концентрации по обе стороны от мембраны близки к термодинамически
равновесным значениям.
1.2 Модель Е. Якобсона
Несмотря на то, что работы Д.
Тостесона и его группы появились в начале 60-х годов прошлого века, только в
1980 году Е. Якобссон опубликовал математическую модель [3], рассматривающую
гомеостаз  и
и  в
эритроцитах и его связь с объемом в относительно современном виде. Основными
переменными в модели были внутриклеточные концентрации катионов
в
эритроцитах и его связь с объемом в относительно современном виде. Основными
переменными в модели были внутриклеточные концентрации катионов  и
и  , основных
анионов - хлора и
, основных
анионов - хлора и  , объем
клетки и трансмембранная разность потенциалов. Изменения концентраций ионов
определяются изменениями объема и балансом пассивных потоков через мембрану и
активных потоков, создаваемых ионными насосами.
, объем
клетки и трансмембранная разность потенциалов. Изменения концентраций ионов
определяются изменениями объема и балансом пассивных потоков через мембрану и
активных потоков, создаваемых ионными насосами.
Как показано в работе Е. Якобссона,
пассивные потоки ионов в эритроцитах хорошо описываются уравнением Гольдмана
[4]
Для  и
и  имеем:
имеем:


Потоки определяют изменения
содержания ионов в клетке.
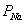 и
и  - пассивная проницаемость мембраны
для
- пассивная проницаемость мембраны
для  и
и  ,
соответственно;
,
соответственно;
 и
и  - пассивные потоки
- пассивные потоки  и
и  через
мембрану эритроцита;
через
мембрану эритроцита;
 - константа Фарадея;
- константа Фарадея;
 - универсальная газовая постоянная;
- универсальная газовая постоянная;
 - абсолютная температура;
- абсолютная температура;
 - трансмембранная разность
потенциалов;
- трансмембранная разность
потенциалов;
Индексы  и
и  обозначают
внутри- и внеклеточные концентрации соответственно.
обозначают
внутри- и внеклеточные концентрации соответственно.
Распределение анионов определяется
только пассивными потоками этих ионов через мембрану. Известно, что мембрана
эритроцитов высоко проницаема для анионов - по данным [1], проницаемость
мембраны для анионов составляет примерно 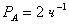 или
или  , в то время как проницаемости для
одновалентных катионов
, в то время как проницаемости для
одновалентных катионов  и
и  на два
порядка ниже:
на два
порядка ниже:
 ,
, 
или
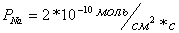 ,
,  .
.
Высокая проницаемость мембраны для
анионов позволяет считать, что концентрации анионов квазиравновесны:
 ,
,
где  - сумма концентраций проникающих
анионов. Из этого уравнения следует, что анионы между внутри- и внеклеточным
пространством распределены в соответствии с трансмембранным потенциалом.
- сумма концентраций проникающих
анионов. Из этого уравнения следует, что анионы между внутри- и внеклеточным
пространством распределены в соответствии с трансмембранным потенциалом.
Модель Е. Якобссона также учитывает
уравнения, описывающие электронейтральность внутри- и внеклеточного
содержимого, а также осмотический баланс между клеткой и окружающим
пространством:


В этих уравнениях учтено, что в
клетке есть белки, в первую очередь, гемоглобин, и низкомолекулярные компоненты
метаболизма, которые вносят свой вклад как в электронейтральность, так и в
осмос. Для простоты в этих уравнениях предположили, что суммарная концентрация
всех осмотически непроникающих молекул  , и все эти молекулы имеют один и
тот же средний заряд
, и все эти молекулы имеют один и
тот же средний заряд 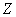 .
.
Проведенные расчеты показали, что
модель предсказывает правильные стационарные концентрации всех ионов и объема
клетки (таблица 2). Это привело Якобсона к выводам, что регуляция объема клетки
возможна лишь при значении мембранного потенциала ниже определенного уровня, а
внутренние непроникающие ионы должны нести отрицательный заряд. Главный вывод,
сделанный Якобсоном и принципиально важный для дальнейшего развития этого
направления заключался в том, что соотношение пассивного и активного транспорта
является определяющим для объема клетки и потенциала на ее мембране.
Таблица 1.1. Стационарные значения внутриклеточных
концентраций ионов и объема для нормальных физиологических значений параметров
модели
|
Переменная
|
Эксперимент
|
Единицы
измерения
|
|
 1016.6±1.6 1016.6±1.6 клеточной
воды клеточной
воды
|
|
|
|
|
 130135±5.0 130135±5.0 клеточной
воды клеточной
воды
|
|
|
|
|
 110103±107 110103±107 клеточной
воды клеточной
воды
|
|
|
|
|
Объем
|
76
|
84-107
|

|
1.3 Модель В. Лью и Р. Букина
Однако в качестве образца для написания
математической модели мной была выбрана модель, созданная в 1986 году Лью и
Букином. Она объединяет последние данные о неидеальном осмотическом поведении
гемоглобина, свойствах непроникающих буферов клетки и особенностях транспорта
ионов через мембраны эритроцита человека.
В разработке данной модели Лью и Букчин
объединили точность и достоверность в выборе начальных параметров, математическую
простоту в выборе уравнений и максимальную гибкость вычислительной стратегии.
Таким образом, модель представляет собой
возможно самое простое интегральное представление регуляторных функций
транспорта, рН и объема эритроцита.
Основными переменными и
определениями, используемыми в модели Лью и Букина, являются:
 - количество раствора
- количество раствора  в 1 л
клеточной воды (ммоль/л)
в 1 л
клеточной воды (ммоль/л)
 ,
, 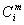 - концентрация раствора
- концентрация раствора  во внутри- (
во внутри- ( ) и
внеклеточном (
) и
внеклеточном ( )
пространстве
)
пространстве
Индекс  -
обозначает количество
-
обозначает количество 
 - ионы
- ионы 
 - гемоглобин
- гемоглобин
 - проникающий анион
- проникающий анион
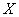 - непроникающий внутриклеточный
анион
- непроникающий внутриклеточный
анион
 - непроникающий внеклеточный
моновалентный анион
- непроникающий внеклеточный
моновалентный анион
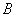 - непроникающий внутриклеточный
Н-буфер
- непроникающий внутриклеточный
Н-буфер
 - протонизированная форма
внеклеточного Н-буфера
- протонизированная форма
внеклеточного Н-буфера
 - заряд
- заряд 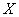 и
и  (
( )
)
 - рН клетки и среды
- рН клетки и среды
 - изоэлектрический рН гемоглобина
- изоэлектрический рН гемоглобина
 - объем клеточной воды,
приходящейся на 1 л стандартной клетки
- объем клеточной воды,
приходящейся на 1 л стандартной клетки
 - концентрация гемоглобина (
- концентрация гемоглобина (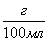 )
)
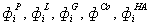 - потоки через натриевый насос
- потоки через натриевый насос  , за счет
диффузии
, за счет
диффузии 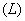 , за счет
электродиффузии
, за счет
электродиффузии  ,
электронейтральный котранспорт
,
электронейтральный котранспорт 
 , электронейтральный котранспорт
, электронейтральный котранспорт 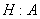
 (цикл
Якобса-Стюарта) (ммоль/л)
(цикл
Якобса-Стюарта) (ммоль/л)
 - константы проницаемости для
раствора
- константы проницаемости для
раствора  в случае
диффузионного
в случае
диффузионного 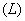 и
электродиффузионного
и
электродиффузионного  потоков
потоков
 - константы уровня оборота для
- константы уровня оборота для 
 котранспорта
и для
котранспорта
и для 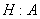
 контранспорта
контранспорта
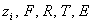 - валентность иона
- валентность иона  , постоянная
Фарадея, газовая постоянная, абсолютная температура, мембранный потенциал (
, постоянная
Фарадея, газовая постоянная, абсолютная температура, мембранный потенциал ( )
)
 - гематокрит/100
- гематокрит/100
 - интеграционный интервал (
- интеграционный интервал (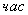 )
)
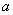 - отрицательный заряд гемоглобина,
когда
- отрицательный заряд гемоглобина,
когда  (
( )
)
 - осмотический коэффициент
гемоглобина
- осмотический коэффициент
гемоглобина
 - изменение внутриклеточного
количества раствора
- изменение внутриклеточного
количества раствора  на единицу
объема клетки в течении одного интеграционного интервала (
на единицу
объема клетки в течении одного интеграционного интервала ( )
)
Основные уравнения для эритроцита,
используемые в расчетах
4 Изотоничность

5 Начальная электронейтральность
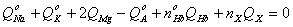
6
Неидеальное осмотическое поведение гемоглобина
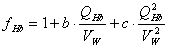
. 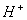 - буфер поведение гемоглобина
- буфер поведение гемоглобина

5. Уравнения потоков




6. Постоянство электронейтральности
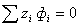
7. Вычисление переходов

8. Перераспределение проникающих растворов
между клетками и внеклеточной средой

1.4 Модель E-cell системы
Данная модель написана на
объектно-ориентированном языке программирования C++.
Основными направлениями исследования являются такие клеточные процессы, как
экспрессия генов, сигнальные процессы, процессы метаболизма, а также
виртуальное моделирование “txperiments in silico”. Состоит
из трех списков, загружаемых в процессе работы программы. Первый список
определяет все объекты, находящиеся в клетке и межклеточном пространстве.
Правила данного списка определяют все реакции, проходящие в клетке. Состояние
клетки в каждый последующий период времени представляется как список значений
концентраций объектов, находящихся в клетке, а также клеточного объема, рН и
температуры. Графические интерфейсы программы позволяют наглядно представить
результаты моделирования (графический список).
Все значения параметров клетки,
вычисленные за один период, добавляются к текущим значениям параметров, затем
происходит обновление списка значений текущих параметров клетки с целью
формирования нового состояния клетки.
Модель E-cell позволяет
пользователю определять самому численный интеграционный алгоритм и временные
интервалы для каждого объекта модели клетки.
Кинетика переходов включает в себя
такие уравнения:

где  - концентрация
- концентрация 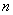 - го
объекта
- го
объекта
 - стехиометрический коэффициент для
данного объекта
- стехиометрический коэффициент для
данного объекта
Скорость каждой реакции может быть
представлена как функция  и
и  .
.
Белковые реакции выражаются с
помощью уравнения Михаэлиса-Ментен

где  - концентрация
- концентрация
 - константа Михаэлиса-Ментен
- константа Михаэлиса-Ментен
Данная модель имеет определенные
стимулы к доработке:
расчеты производятся в предположении
благоприятных окружающих условий;
все аминокислоты и нуклеотиды должны
существовать;
уровни рН и осмолярности должны быть
неизменными в течении эксперимента.
ГЛАВА 2. МАТЕРИАЛЫ И МЕТОДЫ
Для построения математической модели
расчета изменения объема и потенциала клетки я использовала математический
пакет Maple, обладающий
возможностью построения сложных условных циклов, вывода результатов расчета
после каждой последующей итерации, либо после завершения цикла, включающее
заданное оператором количество итераций, построения графиков изменения
интересующих нас параметров клетки (концентрации ионов 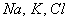 , объема,
потенциала, содержания внутри- и внеклеточной воды и т.д.).
, объема,
потенциала, содержания внутри- и внеклеточной воды и т.д.).
2.1 Мат модель
оэжлдфоаэжфдоэждваэждв
Модель описывается системой из 43
уравнений.
. 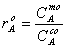 (2.1)
(2.1)
.  (2.2)
(2.2)
. 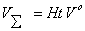
. 
. 
. 
. 
. 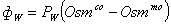
. 
. 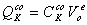
. 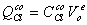
. 
. 
. 
. 
. 
. 
. 
. 
. 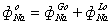
. 
. 
. 
. 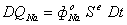
. 
. 
. 
. 
. 
. 
. 
. 
. 
. 
. 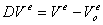
. 
. 
. 
. 
. 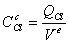
. 
. 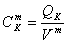
. 
В представленных уравнениях
используются следующие символы и определения:
 - количество раствора
- количество раствора  в 1 л
клеточной воды,
в 1 л
клеточной воды, 
 ,
, 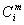 - концентрация раствора
- концентрация раствора  во внутри- (
во внутри- ( ) и
внеклеточном (
) и
внеклеточном ( )
пространстве
)
пространстве 
Индекс  -
обозначает количество
-
обозначает количество 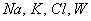
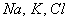 - ионы
- ионы 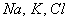
 - вода
- вода
 - исходный объем клетки,
- исходный объем клетки, 
 - изменение объема клетки за один
цикл (приращение
- изменение объема клетки за один
цикл (приращение  за
за  )
)
 - площадь поверхности клетки,
- площадь поверхности клетки, 
 - объем исследуемого образца,
- объем исследуемого образца, 
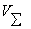 - суммарный объем всех клеток в
исследуемом образце,
- суммарный объем всех клеток в
исследуемом образце, 
 - гематокрит
- гематокрит
 и
и 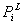 - константы проницаемости клеточной
мембраны за счет электродиффузионных (
- константы проницаемости клеточной
мембраны за счет электродиффузионных ( ) и диффузионных (
) и диффузионных ( ) потоков,
) потоков, 
 и
и  - потоки компонент
- потоки компонент  за счет
электродиффузии (
за счет
электродиффузии ( ) и диффузии
(
) и диффузии
( ),
), 
 - величина отношения внутри- и
внеклеточных концентраций проникающих анионов (
- величина отношения внутри- и
внеклеточных концентраций проникающих анионов ( )
)
 - величина межмембранного потенциала,
- величина межмембранного потенциала,

 - количество клеток в исследуемом
образце
- количество клеток в исследуемом
образце
 ,
,  - величины осмолярности во внутри-
(
- величины осмолярности во внутри-
( ) и
внеклеточном (
) и
внеклеточном ( )
пространстве
)
пространстве
 - время эксперимента
- время эксперимента
 - изменение количества раствора
- изменение количества раствора  в 1 л
клеточной воды за время прохождения одного цикла (приращение
в 1 л
клеточной воды за время прохождения одного цикла (приращение  за
за  )
)
 - заряд иона
- заряд иона
 - константа Фарадея,
- константа Фарадея, 
 - универсальная газовая постоянная,
- универсальная газовая постоянная,

 - абсолютная температура,
- абсолютная температура, 
Основные уравнения для клетки
1. Изотоничность

2. Начальная электронейтральность

3. Уравнения потоков



4. Постоянство электронейтральности
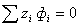
5. Вычисление переходов

6. Перераспределение проникающих растворов
между клетками и внеклеточной средой

Определения
(D1) 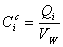
(D2) 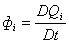
(D3) 
(D4) 
(D5) 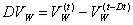
(D6) 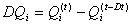
(D7) 
2.2 Процедура симуляции
На первом этапе работы программы
производится ввод начальных данных о состоянии клетки для осуществления расчета
ее исходного состояния (reference state). Все
расчеты осуществляются в единицах СГС.
Когда определены параметры исходного
состояния клетки, необходимо ввести время эксперимента и интервал между
вычислением каждой последующей итерации.
Когда данная операция произведена,
мы имеем возможность запустить цикл, условия которого были заданы выше. Maple позволяет
осуществлять расчет цикла как с выведением данных расчета и текущих графиков
(определение потенциала из условий электронейтральности) после каждой итерации,
так и без него с последующим построением результирующих графиков изменения
интересующих нас параметров клетки.
Уравнения (1) и (2) используются для
расчета начального потенциала клетки  согласно уравнению Нернста.
согласно уравнению Нернста.
Уравнение (3) осуществляет расчет
суммарного объема эритроцитов 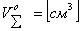 согласно заданным ранее сведениям о
начальном объеме эритроцита
согласно заданным ранее сведениям о
начальном объеме эритроцита  и значению гематоктира
и значению гематоктира  (отношение
объема эритроцитов крови к объему плазмы).
(отношение
объема эритроцитов крови к объему плазмы).
Уравнение (4) вычисляет объем
внеклеточной жидкости  в заданном
объеме образца
в заданном
объеме образца  согласно,
вычисленному ранее суммарному объему эритроцитов в данном образце.
согласно,
вычисленному ранее суммарному объему эритроцитов в данном образце.
Уравнение (5) помогает определить
количество эритроцитов  в заданном
объеме образца. В последующих расчетах данная величина принимается за
константу.
в заданном
объеме образца. В последующих расчетах данная величина принимается за
константу.
Уравнения (6) и (7) рассчитывают
осмолярность внутри- и внеклеточной среды  и
и  .
.
Уравнение (8) позволяет рассчитать
начальную величину потока воды  через мембрану эритроцита.
через мембрану эритроцита.
Уравнения (9-11) и (12-14) описывают
количество вещества  (
(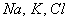 ) во внутри-
и внеклеточной среде
) во внутри-
и внеклеточной среде  и
и  .
.
Уравнения (15-17) определяют
начальные величины электродиффузионных потоков ионов  (
(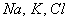 ) через
мембрану эритроцита
) через
мембрану эритроцита 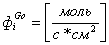 .
.
Уравнения (18-19) рассчитывают
начальные величины диффузионных потоков ионов  (
(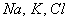 ) через мембрану эритроцита
) через мембрану эритроцита  .
.
Уравнения (20-22) являются суммами
величин электродиффузионных и диффузионных потоков ионов  (
(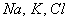 ) через
мембрану эритроцита
) через
мембрану эритроцита 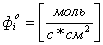 .
.
Уравнение (23) рассчитывает
количество циклов вычислений в течении данного эксперимента  .
.
Уравнения (24-26) позволяют
определить приращение количества вещества  (
(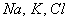 ) во внутри- и внеклеточной среде
) во внутри- и внеклеточной среде  за одну
итерацию.
за одну
итерацию.
Уравнение (27) определяет приращение
количества воды  во внутри-
и внеклеточной среде за одну итерацию.
во внутри-
и внеклеточной среде за одну итерацию.
Уравнения (28-30) и (31-33)
производят расчет нового количества вещества  (
(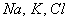 ) во внутри- и внеклеточной среде
) во внутри- и внеклеточной среде  и
и 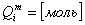 после
завершения одного цикла.
после
завершения одного цикла.
Уравнение (34) рассчитывает новый
объем эритроцита  после
завершения одного цикла.
после
завершения одного цикла.
Уравнение (35) позволяет рассчитать
приращение объема эритроцита  после завершения одного цикла.
после завершения одного цикла.
Уравнение (36) производит расчет
нового суммарного объема эритроцитов  после завершения одного цикла.
после завершения одного цикла.
Уравнение (37) определяет новый
объем внеклеточной жидкости  в заданном объеме образца
в заданном объеме образца  согласно
вычисленному ранее суммарному объему эритроцитов в данном образце после
завершения одного цикла.
согласно
вычисленному ранее суммарному объему эритроцитов в данном образце после
завершения одного цикла.
Уравнения (38-40) и (41-43)
рассчитывают новые значения концентраций ионов  (
(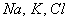 ) во внутри- и внеклеточной среде
) во внутри- и внеклеточной среде  и
и  за одну
итерацию.
за одну
итерацию.
2.2.1 Расчет начального состояния
клетки
1. Задание начальных параметров
2. Вычисляем  из
из
 (1)
(1)
. Вычисляем  согласно
согласно  (2)
(2)
. Определяем суммарный объем
внутриклеточного раствора 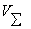
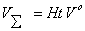 (3)
(3)
5.
Зная 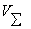 , вычисляем
объем внеклеточной жидкости в исследуемом образце
, вычисляем
объем внеклеточной жидкости в исследуемом образце 
 (4)
(4)
6. Используя заданные значения внутри- и
внеклеточных концентраций ионов, определяем осмолярность внутри- и внеклеточной
среды
 (5)
(5)
 (6)
(6)
. Определяем количество ионов
в исследуемом образце 
 (7)
(7)
8. Используя решения уравнений (7) и (8),
находим величину потока воду через клеточную
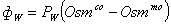 (8)
(8)
. Определяем внутри- и
внеклеточное количество вещества 
. Вычисляем потоки компонент
 за счет
электродиффузии (
за счет
электродиффузии ( ) и диффузии
(
) и диффузии
( )
)
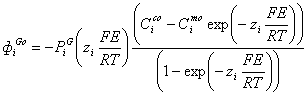 (15)-(17)
(15)-(17)
 (18)-(19)
(18)-(19)
. Находим общий поток
проникающего раствора 
 (20)-(22)
(20)-(22)
2.2.2 Вычисление изменений
параметров клетки
После того, как начальное состояние
клетки вычислено с помощью приведенных выше 43 уравнений, дальнейшие расчеты
осуществляются с помощью цикла.
Данный цикл осуществляет пересчет
всех параметров клетки указанное количество раз. По завершению каждого цикла
осуществляется построение графиков, наглядно демонстрирующих выбор нового значения
потенциала клетки программой, а также вывод всех новых значений параметров
клетки, которые на каждой последующей итерации принимаются как начальные
параметры. Потенциал клетки в каждом цикле определяется из условий
электронейтральности (равенства нулю суммы всех потоков через мембрану клетки) 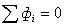 . В связи с
этим для лучшей наглядности правильности определения нового значения потенциала
(помимо решения неравенства
. В связи с
этим для лучшей наглядности правильности определения нового значения потенциала
(помимо решения неравенства 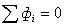 относительно потенциала Е) строится
график зависимости
относительно потенциала Е) строится
график зависимости  .
.
1. Требуемые изменения значений параметров
или концентраций, определение количества итераций
 (23)
(23)
. Определяем приращение  за
за 
 (24)-(27)
(24)-(27)
. Согласно вычисленным
значениям  находим
новые количества внутри- и внеклеточного вещества
находим
новые количества внутри- и внеклеточного вещества
 (28)-(30)
(28)-(30)
 (31)-(33)
(31)-(33)
. Вычисляем новый объем
клетки 
 (34)
(34)
. Определяем приращение  за
за 
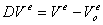 (35)
(35)
. Находим суммарный объем
клеток в исследуемом образце 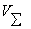
 (36)
(36)
. Вычисляем объем
внеклеточной жидкости  , определив
, определив 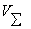 из уравнения
(36)
из уравнения
(36)
 (37)
(37)
. Теперь можно вычислить
новые внутри- и внеклеточные концентрации ионов  в конце интервала
в конце интервала  , -
, - 
 (38)-(40)
(38)-(40)
 (41)-(43)
(41)-(43)
. Когда известно значение  , становится
возможным вычислить
, становится
возможным вычислить  ,
, 
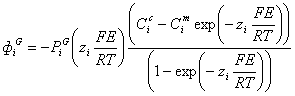

. Находим новое значение
общего потока проникающего раствора 

11. Вычисление нового значения мембранного
потенциала из условия постоянства электронейтральности
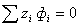 [4]
[4]
12. Новые значения осмолярности находим
согласно уравнениям
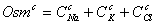

. Теперь возможно определить
новое значение потока воды через мембрану клетки за время 

Далее, вычислив все необходимые
значения параметров и концентраций за один  цикл, программа возвращается к
уравнению (24) и повторяет расчеты цикла согласно заданной продолжительности
эксперимента.
цикл, программа возвращается к
уравнению (24) и повторяет расчеты цикла согласно заданной продолжительности
эксперимента.
ГЛАВА 3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
Выполняя построение математической
модели, мною были поставлены следующие цели:
осуществить правильный расчет
изменения объема клетки, т.е. создать идеальный осмолятор (модель должна четко
описывать осмотическое поведение клетки в гипертоническом и гипотоническом
растворах);
оценить интеграционный интервал  , который
можно использовать в расчетах;
, который
можно использовать в расчетах;
осуществить правильный расчет
потенциала Е клетки (согласно условиям электронейтральности), определить
область допустимых значений величин проницаемостей 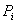 , при
которых потенциал будет существовать и не выходить из ОДЗ;
, при
которых потенциал будет существовать и не выходить из ОДЗ;
исследовать влияние величин
проницаемостей 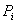 для воды,
ионов
для воды,
ионов 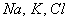 на скорость
изменения объема клетки;
на скорость
изменения объема клетки;
6.1 Расчет
изменения объема клетки
6.1.1 Влияние гипертонического и
гипотонического растворов
Согласно литературным данным [1] для расчетов
мной были выбраны в качестве начальных следующие параметры клетки:
 - концентрация ионов
- концентрация ионов  внутри
клетки
внутри
клетки
 - концентрация ионов
- концентрация ионов  внутри
клетки
внутри
клетки
 - концентрация ионов
- концентрация ионов  внутри
клетки
внутри
клетки
 - начальный объем клетки
- начальный объем клетки
 - площадь поверхности клетки
- площадь поверхности клетки
 - объем исследуемого образца
- объем исследуемого образца
 - уровень гематокрита
- уровень гематокрита
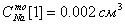 - концентрация ионов
- концентрация ионов  во
внеклеточной среде
во
внеклеточной среде
 - концентрация ионов
- концентрация ионов  во
внеклеточной среде
во
внеклеточной среде
 - концентрация ионов
- концентрация ионов  во
внеклеточной среде
во
внеклеточной среде
 - газовая постоянная
- газовая постоянная
 - постоянная Фарадея
- постоянная Фарадея
 - температура
- температура
Таким образом, исследованное
количество клеток было помещено в раствор с двойной гипертонией. Результаты
расчетов (график 1) показали, что по прошествии 200 мс (0.2 с) объем клеток
уменьшился ровно в два раза и зафиксировался, приняв в два раза меньшее
значение. Проанализировав изменения других параметров клетки, я выяснила, что
за данный период времени произошло полное выравнивание осмолярности во вне- и
внутриклеточной среде, выравнивание концентраций ионов 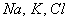 , что
привело к установлению нового фиксированного значения потенциала,
соответствующего новому состоянию равновесия клетки. Согласно графику, исходный
объем клетки составлял 90 мкм3, конечный объем - 45 мкм3 .
, что
привело к установлению нового фиксированного значения потенциала,
соответствующего новому состоянию равновесия клетки. Согласно графику, исходный
объем клетки составлял 90 мкм3, конечный объем - 45 мкм3 .
Аналогичный эксперимент был проведен
и для раствора с двойной гипотонией (график 2). В результате расчетов было
видно, что объем клеток увеличился вдвое за тот же самый период времени (0.2 с)
и зафиксировался, приняв значение в 180 мкм3 .
Сравнив результаты с литературными
данными [5], я убедилась в правильности текущих расчетов изменения объема
клеток.
|

|

|
|
График
1. Влияние гипертонического раствора на объем клетки
|
График
2. Влияние гипотонического раствора на объем клетки
|
6.1.2 Оценка допустимого интервала
расчета 
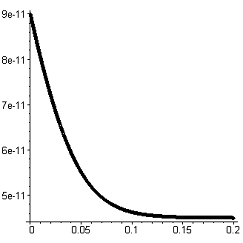
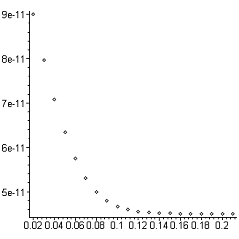
Видно (графики 3,4,5,6,7,8,9), что
если  превышает
0,01 с график функции начинает осциллировать, что указывает, на слишком большой
разброс в значениях параметров клетки на каждой итерации. Согласно данному
эксперименту мной был выбран интервал
превышает
0,01 с график функции начинает осциллировать, что указывает, на слишком большой
разброс в значениях параметров клетки на каждой итерации. Согласно данному
эксперименту мной был выбран интервал  =0,001 с для проведения дальнейшего
моделирования, т.к. он дает наиболее точные и быстрые данные расчетов.
=0,001 с для проведения дальнейшего
моделирования, т.к. он дает наиболее точные и быстрые данные расчетов.
|
|

|
|
График
3. Оценка допустимого интервала расчета  = 0,0001 сГрафик 4. Оценка
допустимого интервала расчета = 0,0001 сГрафик 4. Оценка
допустимого интервала расчета  = 0,001 с = 0,001 с
|
|
|
|

|
|
График
5. Оценка допустимого интервала расчета  = 0,01 сГрафик 6. Оценка
допустимого интервала расчета = 0,01 сГрафик 6. Оценка
допустимого интервала расчета  = 0,02 с = 0,02 с
|
|
|

|

|
|
График
7. Оценка допустимого интервала расчета  = 0,03 сГрафик 8. Оценка
допустимого интервала расчета = 0,03 сГрафик 8. Оценка
допустимого интервала расчета  = 0,04 с = 0,04 с
|
|
|
 График 9.
Оценка допустимого интервала расчета График 9.
Оценка допустимого интервала расчета  = 0,05 с = 0,05 с
|
6.2 Расчет потенциала клетки
Когда мембрана проницаема для нескольких
различных ионов, суммарный потенциал зависит от трех факторов:
полярности электрического заряда каждого иона;
- проницаемости мембраны (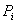 ) для
каждого иона;
) для
каждого иона;
- концентраций (С) соответствующих
ионов внутри (c) и снаружи
мембраны (m).
Во-первых, ионы натрия, калия и
хлора - самые важные ионы, участвующие в генерации мембранных потенциалов
клеток. Градиент концентрации каждого из этих ионов по обе стороны мембраны
помогает определить величину мембранного потенциала.
Во-вторых, степень вклада каждого из
этих ионов в величину мембранного потенциала пропорциональна проницаемости
мембраны для этого иона. Так, если мембрана имеет нулевую проницаемость для
ионов калия и хлора, мембранный потенциал полностью определяется только
градиентом концентрации ионов натрия, и результирующий потенциал равен
потенциалу Нернста для натрия. Это справедливо для любого из двух других ионов,
если мембрана избирательно проницаема только для одного из них.
В-третьих, градиент концентрации
положительного иона, направленный изнутри наружу, ведет к появлению отрицательного
заряда внутри клетки.
Это связано с тем, что при более
высокой концентрации положительных ионов с внутренней стороны мембраны по
сравнению с наружной стороной их избыток диффундирует наружу. При этом
положительные заряды выходят наружу, а не способные к диффузии анионы остаются
внутри клетки, создавая электроотрицательность с внутренней стороны мембраны.
Если существует градиент для
отрицательно заряженного аниона, возникает противоположный эффект. Например,
избыток анионов хлора снаружи ведет к появлению отрицательного заряда внутри
клетки, поскольку отрицательно заряженные ионы хлора диффундируют внутрь
клетки, оставляя снаружи не способные к диффузии положительные ионы.
Расчет потенциала начального
состояния клетки в модели осуществляется согласно уравнению Нернста:
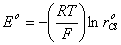 , где
, где 
Дальнейший пересчет мембранного
потенциала клетки согласно условиям электронейтральности:
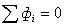 , где
, где 

На каждой итерации рассчитываются
величины всех потоков, учитываемых моделью, строятся графики зависимости
мембранного потенциала от величины потока для каждого из ионов 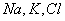 , после чего
все величины суммируются, строится график зависимости потенциала от суммы
потоков ионов
, после чего
все величины суммируются, строится график зависимости потенциала от суммы
потоков ионов 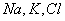 (график
10), а также параллельно решается уравнение для нахождения новой величины
мембранного потенциала, проверкой правильности решения которого служит график.
(график
10), а также параллельно решается уравнение для нахождения новой величины
мембранного потенциала, проверкой правильности решения которого служит график.
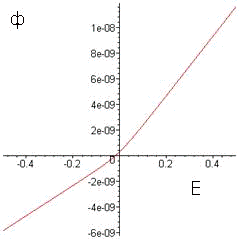
График 10. Зависимость потенциала от
суммы потоков ионов 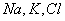
6.3 Определение
области допустимых значений величин проницаемостей 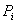 при которых
потенциал будет существовать и не выходить из ОДЗ (графики 11, 12).
при которых
потенциал будет существовать и не выходить из ОДЗ (графики 11, 12).
Графики иллюстрируют влияние
изменения порядка величин проницаемостей для ионов  на величину
мембранного потенциала для ионов
на величину
мембранного потенциала для ионов  (графики 11, 12). При увеличении
величин проницаемостей непосредственно для электродиффузионного потока на два
порядка происходит выход рассчитываемого значения потенциала из ОДЗ (-500…500
(графики 11, 12). При увеличении
величин проницаемостей непосредственно для электродиффузионного потока на два
порядка происходит выход рассчитываемого значения потенциала из ОДЗ (-500…500  ).
).
График 11. Влияние изменения порядка
величин проницаемостей для ионов 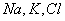 на величину мембранного потенциала
для ионов
на величину мембранного потенциала
для ионов 
А.
График 12. Влияние изменения порядка
величин проницаемостей для ионов 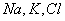 на величину мембранного потенциала
для ионов
на величину мембранного потенциала
для ионов 
Также увеличение величин
проницаемостей для диффузионного потока по сравнению с величинами
проницаемостей для электродиффузионного потока приводит к невозможности
определить значение мембранного потенциала в области допустимых значений
(таблица 3).
Таблица 3. Влияние значений
проницаемостей 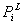 на величину
потенциала
на величину
потенциала 
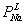 ,
, 
 ,
, 



 ,
, 
 ,
, 
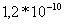

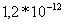
Вычисленные значения для потенциалов
по каждому из ионов  имеют
близкие к литературным [9] значения.
имеют
близкие к литературным [9] значения.
6.4 Влияние
различных величин проницаемости  для воды на скорость изменения
объема клетки
для воды на скорость изменения
объема клетки
«Ахиллесовой пятой» клетки (не только
эритроцита) является проницаемость мембраны для малых молекул, в первую очередь
катионов. Изменение пассивной проницаемости мембраны так же сильно влияет на
величину объема, как и изменение осмотичности. Но в отличие от осмотичности
стабилизировать проницаемость мембраны, по-видимому, невозможно. Главной
причиной значительных изменений проницаемости мембраны являются окислительные
процессы. Значительная концентрация кислорода в крови, свободно-радикальный
характер окислительно-восстановительных процессов, наличие в организме
множества веществ, сильных провокаторов окисления - все это приводит к тому,
что скорость окисления белков и липидов клеточной мембраны может варьировать в
сотни раз. А окисленные липиды сильно увеличивают проницаемость мембраны для
заряженных молекул, поэтому в нормальном организме проницаемость мембраны
клетки для ионов тоже может меняться в 5-10 раз в зависимости от питания,
разнообразных стрессов, мелких очагов воспаления и прочих факторов.
Были искусственно исследованы влияния подобных
изменений проницаемостей для воды на скорость изменения объема клетки (график
13).
График
13. Влияние различных величин проницаемости  для
воды на скорость изменения объема клетки
для
воды на скорость изменения объема клетки
При увеличении константы
проницаемости для воды на один порядок также на один порядок происходит
уменьшение времени сжатия (разбухания) эритроцита, а следовательно и увеличение
скорости сжатия (разбухания) на один порядок (таблица 4).
Таблица 4. Влияние величин
проницаемостей  для воды на
скорость изменения объема клетки
для воды на
скорость изменения объема клетки
Данное уменьшение времени, а следовательно
увеличение скорости сжатия (разбухания) клетки является следствием прямой
зависимости величины потока воды через мембрану от величины проницаемости, так
как водный поток является главным регулятором объема.
Выводы
1. - Объем клетки уменьшается
прямо пропорционально кратности гипертонии (гипотонии) раствора, в котором
данная клетка находится. Скорость изменения объема клетки зависит от величины
потока воды через мембрану  , которая в свою очередь
определяется величиной константы проницаемости для воды
, которая в свою очередь
определяется величиной константы проницаемости для воды  ;
;
. - Градиент концентрации
каждого из ионов 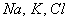 по обе
стороны мембраны определяет величину мембранного потенциала. Степень вклада
каждого из этих ионов в величину мембранного потенциала пропорциональна
проницаемости мембраны для этого иона;
по обе
стороны мембраны определяет величину мембранного потенциала. Степень вклада
каждого из этих ионов в величину мембранного потенциала пропорциональна
проницаемости мембраны для этого иона;
. - Кратные изменения
величины проницаемости  для потока
воды через мембрану клетки приводят к таким же изменениям времени и скорости
изменения объема клетки.
для потока
воды через мембрану клетки приводят к таким же изменениям времени и скорости
изменения объема клетки.
Приложения

Рис. 1 Переменные и компоненты потоков клетки
ЛИТЕРАТУРА
1. Lew V.L., Bookchin R.M.
Volume, pH and ioncontent regulation in human red cells: Analysis of transient
behavior with an integrated model // J. Membrane Biol. - 1986. -
. Tosteson D.C., Hoffman J.F.,
Regulation of cell volume by active cation transport in high and low potassium
sheep red cells// J. Gen. Physiol. 1960. V.
44. P. 169-194
3. Jakobsson E. Interactions of
cell volume, membrane potential, and membrane transport parameters// Amer. J.
Physiol. 1980. V.
238. №5. P. 196-206
. Маркин В.С., Чизмаджев Ю.А.
Индуцированный ионный транспорт. М.:Наука, 1974. С. 38-45
5. Ершов С.С., Орлова Н.В., Шпакова
Н.М. Чувствительность эритроцитов млекопитающих к изменению температурных и
осмотических условий среды // Проблемы криобиологии. - 2004. - №3. - С. 51-57.
. Витвицкий В.М., Фролова Е.В.,
Комарова С.В. Анионная проницаемость и увеличение эритроцита. 2000
. Атауллаханов Ф.И., Корунова Н.О.,
Спиридонов И.С. Как регулируется объем эритроцита, или что могут и чего не
могут математические модели в биологии. 2009, том 26, №3, с. 163-179
. В.Д. Лахно Математическая клетка.
Концепции построения математических моделей переноса заряда в живой клетке //
Вестник РУДН, Серия Прикладная и компьютерная математика, 2003, т.2, No.2, с.
77-84.
. Мороз И.А., Атауллаханов Ф.И.,
Кияткин А.Б., Пичугин А.В., Витвицкий В.М. //Биол.мембр. 1989. Е. 6 № 4. С.
409.
. Tomita M, Hashimoto K, Takahashi
K, Shimizu TS, Matsuzaki Y, Miyoshi F, Saito K, Tanida S, Yugi K, Venter JC,
Hutchison CA 3rd. E-CELL: software environment for whole-cell simulation. Bioinformatics.
1999. 15(1). 72-84.