|
Запасы постав., b i
|
Запросы потребителей, аj
|
ui
|
|
500
|
120
|
180
|
200
|
|
|
490
|
9 490
|
13
|
20
|
11
|
0
|
|
310
|
23 10
|
5 120
|
9 180
|
18 0
|
-14
|
|
200
|
18
|
9
|
12
|
13 200
|
-9
|
|
Vj
|
9
|
-9
|
-5
|
4
|
|
Строим систему потенциалов, соответствующих опорному решению. Для этого
решим системы уравнений:
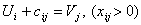 (2.14)
(2.14)
Для
того чтобы найти частное решение системы, одному из потенциалов задаем
произвольно некоторое значение, равное нулю.
Пусть
u1 = 0
u1 + 9
= v1 v1 = 9
u2 +
23 = v1 u2 = 9-23=-14
u2 + 5 = v2 => v2 = -14+5=-9+ 9 =
v3 v3 = -14+9=-5+ 18 = v4 v4
= -14+18=4+ 13 = v4 u3 = 4-13=-9
Составим матрицу оценок, где
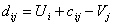 (2.15)
(2.15)
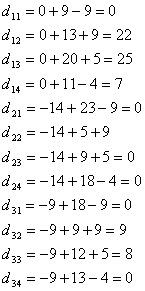
D
= 
Так как матрица положительная, то мы получили план перевозок, полностью
удовлетворяющий партнеров и обеспечивающий минимум затрат на перевозку
продукции.
Вывод: стоимость перевозок для компании ОАО «АвиаМоторс», найденная по
методу потенциалов составляет F3=9460,
и F1= F2= F3.
Минимальные затраты на перевозки машин марки BMW от компании ОАО «АвиаМоторс» в филиалы, находящиеся в
Екатеринбурге «Bayerhof» ул.
Блохера 45, Перми «Верра- Моторс» ул. Героев Хасана 81, Самаре «Aldis» ул. Демократическая 65 и Нижнем
Новгороде «ТрансТехСервис» ул. Бринского 12, равны 9460, что подтверждается
тремя методами.
3. Задача динамического программирования
Динамическое программирование (ДП) - это вычислительный метод для
эффективного решения задач с пересекающимися подзадачами. Возникло и
сформировалось в 1950 - 1953 гг. благодаря работам Р. Беллмана.
Динамическим программированием (в наиболее общей форме) называют процесс
пошагового решения задач, когда на каждом шаге выбирается одно решение из
множества допустимых (на этом шаге) решений, причем такое, которое
оптимизирует заданную целевую функцию или функцию критерия. В основе теории
динамического программирования лежит принцип оптимальности Беллмана: «каково бы
ни было начальное состояние на любом шаге и решение, выбранное на этом шаге,
последующие решения должны выбираться оптимальными относительно состояния, к
которому придет система в конце данного шага». Использование этого принципа
гарантирует, что решение, выбранное на любом шаге, является не локально лучшим,
а лучшим с точки зрения задачи в целом.
Динамическое программирование решает задачу, разбивая её на подзадачи и
объединяя их решения. Рекурсивные алгоритмы также делят задачу на независимые
подзадачи, эти подзадачи - на более мелкие подзадачи и так далее, а затеи
собирают решение основной задачи «снизу вверх». Динамическое программирование
применимо тогда, когда подзадачи не являются независимыми, иными словами, когда
у подзадач есть общие «подподзадачи». В этом случае при использовании рекурсии
будут решаться одни и те же подзадачи несколько раз. Формы алгоритма
динамического программирования могут быть разными - общим для них является заполняемая
таблица и порядок формирования ее элементов.
Алгоритм, основанный на динамическом программировании, решает каждую из
подзадач только один раз и запоминает ответы в специальной таблице. Это
позволяет не вычислять заново ответ к уже встречавшейся подзадаче. Типичными
для динамического программирования являются задачи оптимизации. У подобных
задач может быть много возможных решений а, их «качество» определяется
значением какого-то параметра, и требуется выбрать оптимальное решение, при
котором значение параметра будет минимальным или максимальным (в зависимости от
постановки задачи). В общем случае, оптимум может достигаться для нескольких
разных решений.
В задачах динамического программирования (ДП):
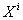 -
состояние системы на
-
состояние системы на 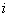 -ом шаге;
-ом шаге;
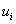 -
управление системой на
-
управление системой на 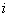 -ом шаге;
-ом шаге;
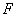 (
(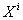 ;
; 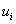 ) -
функция прибыли (или затрат перехода системы из начального состояния в
конечное) (некая количественная характеристика).
) -
функция прибыли (или затрат перехода системы из начального состояния в
конечное) (некая количественная характеристика).
Исходные
данные:
Таблица
3.1 - Таблица стоимостей прокладки участков пути
|
|
28
|
|
35
|
|
15
|
|
32
|
|
39
|
|
|
28
|
|
24
|
|
31
|
|
36
|
|
23
|
|
30
|
|
|
25
|
|
26
|
|
36
|
|
39
|
|
21
|
|
|
38
|
|
30
|
|
29
|
|
35
|
|
27
|
|
35
|
|
|
46
|
|
32
|
|
42
|
|
19
|
|
30
|
|
|
14
|
|
38
|
|
18
|
|
40
|
|
23
|
|
37
|
|
|
38
|
|
40
|
|
37
|
|
41
|
|
24
|
|
|
33
|
|
21
|
|
27
|
|
27
|
|
26
|
|
32
|
|
|
15
|
|
25
|
|
28
|
|
29
|
|
40
|
|
|
32
|
|
28
|
|
35
|
|
34
|
|
34
|
|
30
|
|
|
33
|
|
34
|
|
37
|
|
23
|
|
38
|
|
Задание:
. Задача о выборе оптимального маршрута
Компании ОАО «АвиаМоторс» поступил заказ от филиала «Aldis», находящегося в Самаре ул.
Демократическая 65, на покупку автомобилей марки BMW. Перед компанией встала задача о выборе оптимального
маршрута из г. Санкт-Петербурга (пункт А) в г. Самару (пункт В), который
обеспечивал бы минимальные транспортные расходы.
Известна стоимость дороги по участкам в западном и северном направлениях
(таблица 3.1).Требуется, используя алгоритм Беллмана, определить оптимальный
маршрут прокладки пути от пункта А (северо-западный угол) в пункт В
(юго-восточный угол).
. Задача о распределении ресурсов
Компанию ОАО «АвиаМоторс» распределяет 600 млн. д.е. между 5 филиалами,
находящихся в Екатеринбурге «Bayerhof» ул. Блохера 45, Перми «Верра- Моторс» ул. Героев Хасана 81, Самаре «Aldis» ул. Демократическая 65, Нижнем
Новгороде «ТрансТехСервис» ул. Бринского 12, Краснодаре «Бакра» ул.
Железнодорожная 23, в долях, кратных 100 млн.
Доходы компании зависят от того, как она распределит вложения различных
количеств средств между пятью филиалами. Эффективность от капитальных вложений
в каждый филиал приведена в таблице2. Требуется составить оптимальный план
распределения вкладов компании в развитие филиалов.
Решение:
1. Задача о выборе оптимального маршрута

Рисунок 3.1 - Схема маршрутов и стоимости участков
Следуя алгоритму решения задачи ДП, основанном на принципе Беллмана,
разобьем весь процесс на шаги (m+n = 5+5 = 10). Управлениями будем
считать стоимость прокладки дороги по участкам, выходящим из узла (6;6) в направлении
bji (горизонтально) и cji (вертикально).
Условная оптимизация:
Шаг 0: (6;6), i=10, x10
Шаг 1: (6;5) (5;6), i=9, x9
Шаг 2:
(6;4) (5;5) (4;6), i=8, x8
Шаг 3:
(6;3) (5;4) (4;5) (3;6), i=7, x7
Шаг 4:
(6;2) (5;3) (4;4) (3;5) (2;6), i=6, x6
Шаг 5:
(6;1) (5;2) (4;3) (3;4) (2;5) (1;6), i=5, x5
Шаг 6:
(5;1) (4;2) (3;3) (2;4) (1;5), i=4, x4
Шаг 7:
(4;1) (3;2) (2;3) (1;4), i=3, x3
Шаг 8:
(3;1) (2;2) (1;3), i=2, x2
Шаг 9:
(2;1) (1;2), i=1, x1
Шаг 10: (1;1), i=0, x0
Рассмотрим каждый шаг в отдельности. Воспользуемся основным
функциональным уравнением Беллмана:
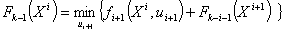
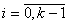 (3.1)
(3.1)
где
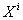 - состояние системы на i-том шаге;
- состояние системы на i-том шаге;
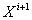 -
состояние системы на (i+1) шаге;
-
состояние системы на (i+1) шаге;
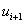 -
управление системой на (i+1) шаге;
-
управление системой на (i+1) шаге;
 -
минимальное значение функции цели, полученное при переходе из некоторого i-ого
состояния в конечное (k-тое состояние);
-
минимальное значение функции цели, полученное при переходе из некоторого i-ого
состояния в конечное (k-тое состояние);
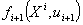 -
приращение функции при переходе из некоторого i-ого состояния в (i+1);
-
приращение функции при переходе из некоторого i-ого состояния в (i+1);
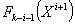 -
минимальное значение функции цели, полученное при переходе из некоторого (i+1)
состояния в конечное (k-тое состояние).
-
минимальное значение функции цели, полученное при переходе из некоторого (i+1)
состояния в конечное (k-тое состояние).
Шаг
0
Точка
В (г. Самара) соответствует состоянию системы x10 = (6;6), i=10
Fk-i-1=F10-9-1=F0=0
Шаг
1 В конечный пункт (г. Самара), определяемый узлом (6,6), ведут 2 узла: (5,6) и
(6,5).
Узел
(5,6) - г. Сызрань, (6,5) - г. Кузнецк
Координатами
вектора состояния системы являются узловые точки. В сечение шага 1 попадают
узлы (5,6) и (6,5):
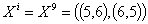
Роль
координат функции управления 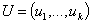 играют
величины bji и сji:
играют
величины bji и сji:
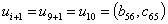
Приращение
функции:  и
и 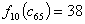
Итак,
найдем минимальное значение функции цели при i=9, используя основное
функциональное уравнение Беллмана (3.1):
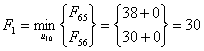

Рисунок 3.2 - Сетевая модель шага 1
Шаг 2
В вектор состояния входят 3 узла:
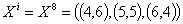
Узел
(4,6) соответствует г. Ульяновску, (5,5) - г. Саранск, (6,4) - г. Нижний Ломов.
Из
узлов (4,6) и (6,4) путь в смежные с ними узлы однозначен. Обходной путь
существует, но он не оптимален.
Стоимость прокладки дороги из г. Ульяновска и г. Ниж. Ломов в конечный
пункт
г. Самару равна:
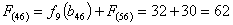
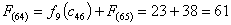
Из
узла (5,5) г. Саранска можно продолжить дорогу к пункту В либо через (5,6)
г.
Сызрань, либо через (6,5) г. Кузнецк.
Путь
из г. Саранска в г. Самару через г. Сызрань складывается из суммы работ:
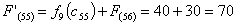
Путь
из г. Саранска в г. Самару через г. Кузнецк складывается из суммы работ:
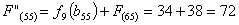
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Сызрань
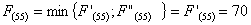
При
выборе оптимального маршрута достаточно знаний прокладывания маршрута в пункт В
из (4,6), (5,5), (6,4).
Найдем минимальное значение функции цели (оптимальный маршрут) при i=8,
используя основное функциональное уравнение Беллмана (3.1):
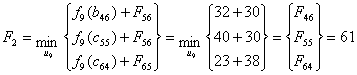

Рисунок 3.3 - Сетевая модель шага 2
Шаг 3
В вектор состояния входят 4 узла:
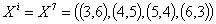
Узел
(3,6) - г. Уфа, (4,5) - г. Пенза, (5,4) - г. Тамбов, (6,3) - Воронеж
Из узлов (3,6) и (6,3) путь в смежные с ними узлы однозначен. Обходной
путь существует, но он не оптимален.
Стоимость прокладки дороги из г. Уфы и г. Воронежа в конечный пункт г.
Самару равна:
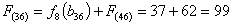
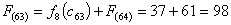
А
для г. Пензы и г. Тамбова следует рассмотреть по 2 варианта маршрута.
Из
узла (4,5) г. Пензы можно продолжить дорогу к пункту В либо через (4,6)
г.
Ульяновск, либо через (5,5) г. Саранск.
Путь
из г. Пензы в г. Самару через г. Ульяновск складывается из суммы работ:
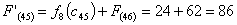
Путь
из г. Пензы в г. Самару через г. Саранск складывается из суммы работ:
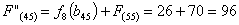
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Ульяновск
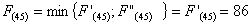
Из
узла (5,4) г. Тамбова можно продолжить дорогу к пункту В либо через (6,4)
Путь
из г. Тамбова в г. Самару через г. Саранск складывается из суммы работ:
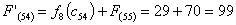
Путь
из г. Тамбова в г. Самару через г. Ниж. Ломов складывается из суммы работ:

Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Ниж. Ломов
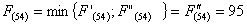
При
выборе оптимального маршрута достаточно знаний прокладывания маршрута в пункт В
из (3,6), (4,5), (5,4), (6,3).
Найдем минимальное значение функции цели (оптимальный маршрут) при i=7,
используя основное функциональное уравнение Беллмана (3.1):
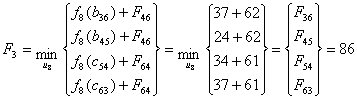

Рисунок 3.4 - Сетевая модель шага 3
Шаг 4
В вектор состояния входят 5 узлов:

Узел
(2,6) - г. Казань, (3,5) - г. Саранск, (4,4) - г. Липецк, (5,3) - г. Курск,
(6,2) - г. Белгород
Из узлов (2,6) и (6,2) путь в смежные с ними узлы однозначен. Обходной
путь существует, но он не оптимален.
Стоимость прокладки дороги из г. Казани и г. Белгорода в конечный пункт
г. Самару равна:
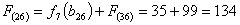
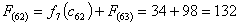
А
для г. Саранска, г. Липецка и г. Курска следует рассмотреть по 2 варианта
маршрута.
Из
узла (3,5) г. Саранска можно продолжить дорогу к пункту В либо через (3,6) г.
Уфу, либо через (4,5) г. Пензу.
Путь
из г. Саранска в г. Самару через г. Уфу складывается из суммы работ:

Путь
из г. Саранска в г. Самару через г. Пензу складывается из суммы работ:
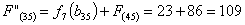
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Пензу
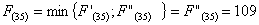
Из
узла (4,4) г. Липецка можно продолжить дорогу к пункту В либо через (4,5) г.
Пензу, либо через (5,4) г. Тамбов.
Путь
из г. Липецка в г. Самару через г. Пензу складывается из суммы работ:
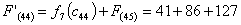
Путь
из г. Липецка в г. Самару через г. Тамбов складывается из суммы работ:
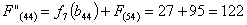
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Пензу
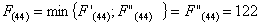
Из
узла (5,3) г. Курска можно продолжить дорогу к пункту В либо через (5,4) г.
Тамбов, либо через (6,3) г. Воронеж.
Путь
из г. Курска в г. Самару через г. Тамбов складывается из суммы работ:
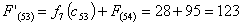
Путь
из г. Курска в г. Самару через г. Воронеж складывается из суммы работ:

Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Тамбов
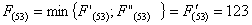
При
выборе оптимального маршрута достаточно знаний прокладывания маршрута в пункт В
из (2,6), (3,5), (4,4), (5,3) и (6,2).
Найдем
минимальное значение функции цели (оптимальный маршрут) при i=6, используя
основное функциональное уравнение Беллмана (3.1):
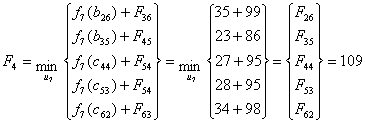

Рисунок 3.5 - Сетевая модель шага 4
Шаг 5
В вектор состояния входят 6 узлов:
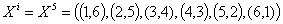
Узел
(1,6) - г. Киров, (2,5) - г. Владимир, (3,4) - г. Калуга, (4,3) - г. Тула,
(5,2) - г. Брянск, (6,1) - г. Гомель.
Из узлов (1,6) и (6,1) путь в смежные с ними узлы однозначен. Обходной
путь существует, но он не оптимален.
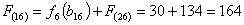
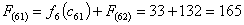
А
для г. Владимира, г. Калуги, г. Тулы, г. Брянска следует рассмотреть по 2
варианта маршрута.
Из
узла (2,5) г. Владимира можно продолжить дорогу к пункту В либо через (2,6) г.
Казань, либо через (3,5) г. Саранск.
Путь
из г. Владимира в г. Самару через г. Казань складывается из суммы работ:
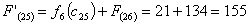
Путь
из г. Владимира в г. Самару через г. Саранск складывается из суммы работ:
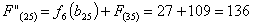
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Саранск

Из
узла (3,4) г. Калуги можно продолжить дорогу к пункту В либо через (3,5) г.
Саранск, либо через (4,4) г. Липецк.
Путь
из г. Калуги в г. Самару через г. Саранск складывается из суммы работ:

Путь
из г. Калуги в г. Самару через г. Липецк складывается из суммы работ:
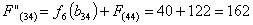
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Саранск
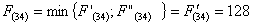
Из
узла (4,3) г. Тулы можно продолжить дорогу к пункту В либо через (4,4) г.
Липецк, либо через (5,3) г. Курск.
Путь
из г. Тулы в г. Самару через г. Липецк складывается из суммы работ:
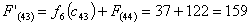
Путь
из г. Тулы в г. Самару через г. Курск складывается из суммы работ:

Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Курск

Из
узла (5,2) г. Брянска можно продолжить дорогу к пункту В либо через (5,3) г.
Курск, либо через (6,2) г. Белгород.
Путь
из г. Брянска в г. Самару через г. Курск складывается из суммы работ:
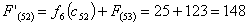
Путь
из г. Тулы в г. Самару через г. Белгород складывается из суммы работ:
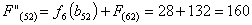
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Курск

При
выборе оптимального маршрута достаточно знаний прокладывания маршрута в пункт В
из (1,6), (2,5), (3,4), (4,3), (5,2) и (6,1)
Найдем
минимальное значение функции цели (оптимальный маршрут) при i=5, используя
основное функциональное уравнение Беллмана (3.1):
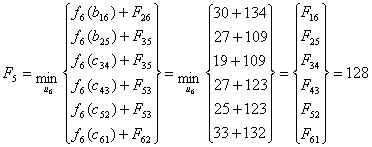

Рисунок 3.6 - Сетевая модель шага 5
Шаг 6
В вектор состояния входят 5 узлов:

Узел
(1,5) - г. Иваново, (2,4) - г. Москва, (3,3) - г. Глазово, (4,2) - г. Рославль,
(5,1) - г. Могилев
Для
г. Иваново, г. Москвы, г. Глазово, г. Рославля, г. Могилев следует рассмотреть
по 2 варианта маршрута.
Из узла (1,5) г. Иваново можно продолжить дорогу к пункту В либо через
(1,6) г. Киров, либо через (2,5) г. Владимир.
Путь из г. Иваново в г. Самару через г. Киров складывается из суммы
работ:
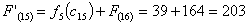
Путь
из г. Иваново в г. Самару через г. Владимир складывается из суммы работ:
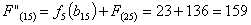
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Владимир
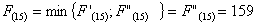
Из
узла (2,4) г. Москвы можно продолжить дорогу к пункту В либо через (2,5) г.
Владимир, либо через (3,4) г. Калугу.
Путь
из г. Москвы в г. Самару через г. Владимир складывается из суммы работ:
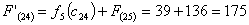
Путь
из г. Москвы в г. Самару через г. Калугу складывается из суммы работ:
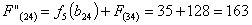
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Калугу

Из
узла (3,3) г. Глазово можно продолжить дорогу к пункту В либо через (3,4) г. Калугу,
либо через (4,3) г. Тулу.
Путь
из г. Глазово в г. Самару через г. Калугу складывается из суммы работ:
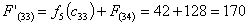
Путь
из г. Глазово в г. Самару через г. Тулу складывается из суммы работ:
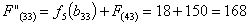
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Тулу
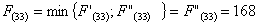
Из
узла (4,2) г. Рославля можно продолжить дорогу к пункту В либо через (4,3) г.
Тулу, либо через (5,2) г. Брянск.
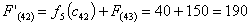
Путь
из г. Рославля в г. Самару через г. Брянск складывается из суммы работ:
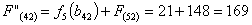
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Брянск
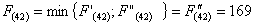
Из
узла (5,1) г. Могилева можно продолжить дорогу к пункту В либо через (5,2) г.
Брянск, либо через (6,1) г. Гомель.
Путь
из г. Могилева в г. Самару через г. Брянск складывается из суммы работ:
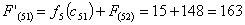
Путь
из г. Могилева в г. Самару через г. Гомель складывается из суммы работ:
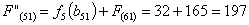
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Брянск
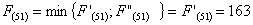
При
выборе оптимального маршрута достаточно знаний прокладывания маршрута в пункт В
из (1,5), (2,4), (3,3), (4,2) и (5,1).
Найдем
минимальное значение функции цели (оптимальный маршрут) при i=4, используя
основное функциональное уравнение Беллмана (3.1):
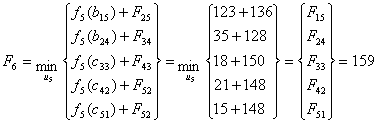

Рисунок 3.7 - Сетевая модель шага 6
Шаг 7
В вектор состояния входят 4 узла:
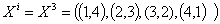
Узел
(1,4) - г. Кострома, (2,3) - г. Вязьма, (3,2) - г. Ярцево, (4,1) - г. Орша Для
г. Костромы, г. Вязьмы, г. Ярцево, г. Орша следует рассмотреть по 2 варианта
маршрута.
Из узла (1,4) г. Костромы можно проложить дорогу к пункту В либо через
(1,5) г. Иваново, либо через (2,4) г. Москву.
Путь из г. Костромы в г. Самару через г. Иваново складывается из суммы
работ:
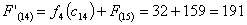
Путь
из г. Костромы в г. Самару через г. Москву складывается из суммы работ:
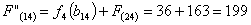
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Иваново
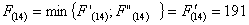
Из
узла (2,3) г. Вязьмы можно продолжить дорогу к пункту В либо через (2,4) г.
Москву, либо через (3,3) г. Глазово.
Путь
из г. Вязьмы в г. Самару через г. Москву складывается из суммы работ:
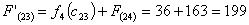
Путь
из г. Вязьмы в г. Самару через г. Глазово складывается из суммы работ:
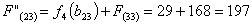
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Глазово
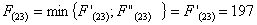
Из
узла (3,2) г. Ярцево можно продолжить дорогу к пункту В либо через (3,3) г.
Глазово, либо через (4,2) г. Рославль.
Путь
из г. Ярцево в г. Самару через г. Глазово складывается из суммы работ:

Путь
из г. Ярцево в г. Самару через г. Рославль складывается из суммы работ:

Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Глазово
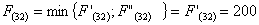
Из
узла (4,1) г. Орши можно продолжить дорогу к пункту В либо через (4,2) г.
Рославль, либо через (5,1) г. Могилев.
Путь
из г. Орши в г. Самару через г. Рославль складывается из суммы работ:

Путь
из г. Орши в г. Самару через г. Могилев складывается из суммы работ:
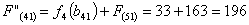
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Могилев
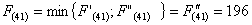
При
выборе оптимального маршрута достаточно знаний прокладывания маршрута в пункт В
из (1,4), (2,3), (3,2), (4,1).
Найдем
минимальное значение функции цели (оптимальный маршрут) при i=3, используя
основное функциональное уравнение Беллмана (3.1):


Рисунок 3.8 - Сетевая модель шага 7
Шаг 8
В вектор состояния входят 3 узла:
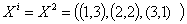
Узел
(1,3) - г. Ярославль, (2,2) - г. Тверь, (3,1) - г. Смоленск
Для
г. Ярославля, г. Твери, г. Смоленска следует рассмотреть по 2 варианта
маршрута.
Из узла (1,3) г. Ярославля можно продолжить дорогу к пункту В либо через
(1,4) г. Кострому, либо через (2,3) г. Вязьмы.
Путь из г. Ярославля в г. Самару через г. Кострому складывается из суммы
работ:
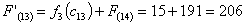
Путь
из г. Ярославля в г. Самару через г. Вязьму складывается из суммы работ:
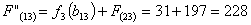
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Кострому
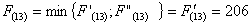
Из
узла (2,2) г. Твери можно продолжить дорогу к пункту В либо через (2,3) г.
Вязьму, либо через (3,2) г. Ярцев.
Путь
из г. Твери в г. Самару через г. Вязьму складывается из суммы работ:

Путь
из г. Твери в г. Самару через г. Ярцев складывается из суммы работ:

Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Вязьму
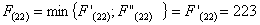
Из
узла (3,1) г. Смоленска можно продолжить дорогу к пункту В либо через (3,2) г.
Ярцев, либо через (4,1) г. Орши.
Путь
из г. Смоленска в г. Самару через г. Ярцев складывается из суммы работ:
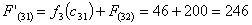
Путь
из г. Смоленска в г. Самару через г. Орши складывается из суммы работ:
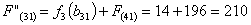
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Орши
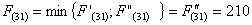
При
выборе оптимального маршрута достаточно знаний прокладывания маршрута в пункт В
из (1,3), (2,2), (3,1).
Найдем
минимальное значение функции цели (оптимальный маршрут) при i=2, используя
основное функциональное уравнение Беллмана (3.1):


Рисунок 3.9 - Сетевая модель шага 8
Шаг 9
В вектор состояния входят 2 узла:
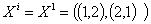
Узел
(1,2) - г. Вологда, (2,1) - г. Великий Новгород
Для
г. Вологды, г. Вел. Новгорода следует рассмотреть по 2 варианта маршрута.
Из узла г. Вологды можно продолжить дорогу к пункту В либо через (1,3) г.
Ярославль, либо через (2,2) г. Тверь.
Путь из г. Вологды в г. Самару через г. Ярославль складывается из суммы
работ:
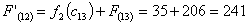
Путь
из г. Вологды в г. Самару через г. Тверь складывается из суммы работ:

Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Ярославль
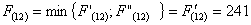
Из
узла (2,1) г. Вел. Новгорода можно продолжить дорогу к пункту В либо через
(2,2) г. Тверь, либо через (3,1) г. Смоленск.
Путь
из г. Вел. Новгорода в г. Самару через г. Тверь складывается из суммы работ:
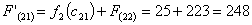
Путь
из г. Вел. Новгорода в г. Самару через г. Смоленск складывается из суммы работ:

Мы
получили два одинаковых значения, можем выбрать любой из этих маршрутов. В
данном случае я выбираю путь, проходящий через г. Тверь
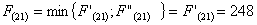
При
выборе оптимального маршрута достаточно знаний прокладывания маршрута в пункт В
из (1,2), (2,1).
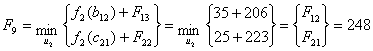

Рисунок 3.10 - Сетевая модель шага 9
Шаг 10
В вектор состояния входит 1 узел:
 - пункт А
(г. Санкт-Петербург)
- пункт А
(г. Санкт-Петербург)
Для г. Санкт-Петербурга следует рассмотреть 2 варианта маршрута.
Из узла (1,1) г. Санкт-Петербурга можно продолжить дорогу к пункту В либо
через (1,2) г. Вологду, либо через (2,1) г. Вел. Новгород.
Путь из г. Санкт-Петербурга в г. Самару через г. Вологду складывается из
суммы работ:
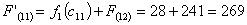
Путь
из г. Санкт-Петербурга в г. Самару через г. Вел. Новгород складывается из суммы
работ:
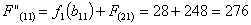
Сравниваем
два значения и выбираем наименьшее значение. В данном случае выбираем маршрут,
проходящий через г. Вологду
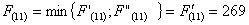
Найдем
минимальное значение функции цели (оптимальный маршрут) при i=1, используя
основное функциональное уравнение Беллмана (3.1):
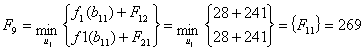

Рисунок 3.11 - Сетевая модель шага 10
Проведенные расчеты позволяют сделать вывод о том, что условная
оптимизация привела к минимальному значению функции цели: Fmin = 269д.е. Данный маршрут по доставки
автомобилей из Санкт-Петербурга (пункт А) в Самару (пункт В) будет оптимальным.
Безусловная
оптимизация:
Необходимый маршрут определяется непрерывным следованием стрелок,
соединяющих А и В (рисунок 3.12).
Минимальные
затраты соответствуют следованию оптимальному пути (вектору управления) - 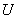
Вектору
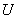
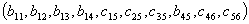 соответствует
затраты (целевая функция):
соответствует
затраты (целевая функция):
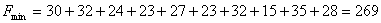
2.
Задача о распределении ресурсов
Таблица 3.2 -Эффективность от вложений в каждое предприятие
|
ui
|
f1
|
f2
|
f3
|
f4
|
f5
|
|
0
|
0
|
0
|
0
|
0
|
0
|
|
100
|
28
|
35
|
15
|
32
|
39
|
|
200
|
53
|
61
|
51
|
71
|
60
|
|
300
|
99
|
93
|
93
|
90
|
90
|
|
400
|
137
|
133
|
130
|
131
|
114
|
|
500
|
152
|
158
|
158
|
160
|
154
|
|
600
|
185
|
192
|
195
|
183
|
192
|
Шаг 1
Полагаем, что все средства переданы 5 предприятию «Bayerhof» в Екатеринбурге.
Если ему не выделяются средства (u0=0), то дохода от этого предприятия компания «АвиаМоторс» не
получит.F5(0) = f5(0) = 0
Для определения прибыли от «Bayerhof» при вложении в него отличных от 0 средств воспользуемся
формулой для данного случая.
F5(ui) = max f5(ui) ui ≤ u=1 F5(u1) = F5(100) = max 0 =
39 => u10 = 100 ui=0..100 39=2 F5(u2) = F5(200) = max 0
= 60 => u10 = 200 ui=0..200 39 =3 F5(u3) = F5(300) = max 0 = 90
=> u10 = 300 ui=0..300 39 =4 F5(u4) = F5(400) = max 0 = 114 =>
u10 = 400 ui=0..400 39 =5 F5(u5) = F5(500) = max 0 = 154 => u10 = 500 ui=0..500
39 =6 F5(u6) = F5(600) = max 0 = 192 => u10 = 600 ui=0..600 39
Шаг 2
Полагаем, что все средства переданы 4 предприятию «Бакра» в Краснодаре и
5 предприятию «Bayerhof» в Екатеринбурге.
F4(ui) = max f4(ui) + F5(U-ui) ui ≤U=0 F4(0) = 0 =>
u20 = 0=1 F4(u1) = F4(100) = max 0 +39 = 39 => u20 = 0 ui=0..100 32 +
0=2 F4(u2) = F4(200) = max 0+60 = 71=> u20 = 200 ui=0..200 32 + 39
=3 F4(u3) = F4(300) = max 0 +90 = 110 => u20 = 200 ui=0..300 32 +
60 =4 F4(u4) = F4(400) = max 0+114 = 131 => u20 = 400 ui=0..400 32 +
90 =5 F4(u5) = F4(500) = max 0 + 154 = 170 => u20 = 400 ui=0..500
32 + 114 =6 F4(u6) = F4(600) = max 0 + 192 = 199 => u20 = 500 ui=0..600 32 +
154
Таблица 3.3 - Доходы фирмы при распределении ресурсов между «Bayerhof» и «Бакра»
|
ui
|
u10
|
u20
|
F4(ui)
|
|
0
|
0
|
0
|
0
|
|
100
|
100
|
0
|
39
|
|
200
|
0
|
200
|
71
|
|
300
|
100
|
200
|
110
|
|
400
|
0
|
400
|
131
|
|
500
|
100
|
400
|
170
|
|
600
|
100
|
500
|
199
|
Шаг 3
Полагаем, что все средства переданы 3 предприятию «Верра - Моторс» в
Перми, 4 предприятию «Бакра» в Краснодаре и 5 предприятию «Bayerhof» в Екатеринбурге.
F3(ui) = max f3(ui) + F2(U-ui) ui ≤U
i=0 F3(0) = 0 => u30 = 0=1 F3(u1) = F3(100) = max 0 +39 =
39 => u30 = 0 ui=0..100 15 + 0=2 F3(u2) = F3(200) = max 0+71 =
71=> u30 = 0 ui=0..200 15 + 39 =3 F3(u3) = F4(300) = max 0 + 110 =
110 => u30 = 0 ui=0..300 15 + 71 =4 F3(u4) = F3(400) = max 0 + 131 = 132
=> u30 = 300 ui=0..400 15 + 110 =5 F3(u5) = F3(500) = max 0 + 170 = 170
=> u30 = 0 ui=0..500 15 + 131 =6 F3(u6) = F3(600) = max 0 + 199 = 203 =>
u30 = 300 ui=0..600 15 + 170
Таблица 3.4 - Доходы фирмы при распределении ресурсов между «Верра
-Моторс», «Bayerhof» и «Бакра»
|
ui
|
u10
|
u20
|
u30
|
F3(ui)
|
|
0
|
0
|
0
|
0
|
0
|
|
100
|
100
|
0
|
0
|
39
|
|
200
|
0
|
200
|
0
|
71
|
|
300
|
100
|
200
|
0
|
110
|
|
400
|
100
|
0
|
300
|
132
|
|
500
|
100
|
400
|
0
|
170
|
|
600
|
100
|
200
|
300
|
203
|
Шаг 4
Полагаем, что все средства переданы 2 предприятию «ТрансТехСервис» в
Нижнем Новгороде, 3 предприятию «Верра - Моторс» в Перми, 4 предприятию «Бакра»
в Краснодаре и 5 предприятию «Bayerhof» в Екатеринбурге.
F2(ui) = max f2(ui) + F3(U-ui) ui ≤U
i=0 F2(0) = 0 => u40 = 0=1 F2(u1) = F2(100) = max 0+39 =
39 => u40 = 0 ui=0..100 35+0=2 F2(u2) = F2(200) = max 0 + 71 = 74 => u40
= 100 ui=0..200 35+39 =3 F2(u3) = F2(300) = max 0 + 110 = 110 => u40 = 0 ui=0..300
35 + 71=4 F2(u4) = F2(400) = max 0 + 132 = 145 => u40 = 100 ui=0..400 35 +
110 =5 F2(u5) = F2(500) = max 0 + 170 = 172 => u40 = 400 ui=0..500
35 +132 =6 F2(u6) = F3(600) = max 0 + 203 = 205 => u40 = 100 ui=0..600 35 +
Шаг 5
Полагаем, что все средства переданы 1 предприятию «Aldis» в Самаре, 2 предприятию
«ТрансТехСервис» в Нижнем Новгороде, 3 предприятию «Верра - Моторс» в Перми, 4
предприятию «Бакра» в Краснодаре и 5 предприятию «Bayerhof» в Екатеринбурге.
F1(ui) = max f1(ui) + F2(U-ui) ui ≤U=0 F1(0) = 0 =>
u50 = 0=1 F1(u1) = F2(100) = max 0 + 39= 39 => u50 = 0 ui=0..100 28 + 0=2
F1(u2) = F2(200) = max 0 + 74 = 74 => u50 = 0 ui=0..200 28 + 39=3 F1(u3) =
F2(300) = max 0 + 110 = 110 => u50 = 0 ui=0..300 28
Таблица 3.6 - Доходы фирмы при распределении ресурсов между «Aldis», «ТрансТехСервис», «Верра -Моторс»,
«Bayerhof» и «Бакра»
|
ui
|
u10
|
u20
|
u30
|
u40
|
u50
|
F1(ui)
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
100
|
100
|
0
|
0
|
0
|
0
|
39
|
|
200
|
100
|
0
|
0
|
100
|
0
|
74
|
|
300
|
100
|
200
|
0
|
0
|
0
|
110
|
|
400
|
100
|
200
|
0
|
100
|
0
|
145
|
|
500
|
100
|
0
|
0
|
0
|
400
|
176
|
|
600
|
100
|
0
|
0
|
100
|
400
|
211
|
Проведенные расчеты позволяют сделать вывод о том, что условная
оптимизация привела к максимальному значению функции цели F0max = 211 млн. д.е.
Такой доход получит компания ОАО «АвиаМоторс», если она вложит:
в «Aldis» г. Самара u50=400, млн. д.е.
в «ТрансТехСервис» г. Нижний Новгород u40=100 млн. д.е.
в «Верра -Моторс» г. Пермь u30=0
млн. д.е.
в «Бакра» г. Краснодар u20=0
млн. д.е.
в «Bayerhof» г. Екатеринбург u10=100 млн. д.е.
Безусловная
оптимизация:
Шаг 1
Максимальный
доход компании ОАО «Авиамоторс» обеспечивается вложением всех 600 млн. д.е. в
предприятия. При этом в первое предприятие в «Aldis» г. Самара
необходимо вложить 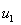 = 400 млн. д.е., что принесет компании доход (см.
таблицу 3.2 исходных данных)
= 400 млн. д.е., что принесет компании доход (см.
таблицу 3.2 исходных данных) 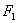 = 137
млн. д.е. Оставшиеся средства (200 млн. д.е.) распределяются между
«ТрансТехСервис» г. Нижний Новгород,
= 137
млн. д.е. Оставшиеся средства (200 млн. д.е.) распределяются между
«ТрансТехСервис» г. Нижний Новгород,
«Верра
-Моторс» г. Пермь, «Бакра» г. Краснодар, «Bayerhof» г.
Екатеринбург.
Шаг
2
Во
второе предприятие «ТрансТехСервис» г. Нижний Новгород компания по расчетам
должна внести 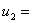 100 млн. д.е. При этом доход компании ОАО «Авиамоторс»
составит
100 млн. д.е. При этом доход компании ОАО «Авиамоторс»
составит  =35 млн. д.е.
=35 млн. д.е.
Шаг
3
В
третье предприятие «Верра -Моторс» г. Пермь компания по расчетам должна внести 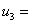 0 млн. д.е. При этом доход компании ОАО «АвиаМоторс»
составит
0 млн. д.е. При этом доход компании ОАО «АвиаМоторс»
составит 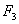 =0 млн. д.е.
=0 млн. д.е.
Шаг
4
В
четвертое предприятие «Бакра» г. Краснодар компания по расчетам должна внести 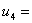 0 млн. д.е. При этом доход компании ОАО «АвиаМоторс»
составит
0 млн. д.е. При этом доход компании ОАО «АвиаМоторс»
составит 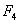 =0 млн. д.е.
=0 млн. д.е.
Шаг
5
В
пятое предприятие «Bayerhof» г. Екатеринбург компания должна внести оставшиеся
средства  = 600 - 400 - 100 - 0 - 0 = 100 млн. д.е. При этом
доход компании ОАО «АвиаМоторс» составит
= 600 - 400 - 100 - 0 - 0 = 100 млн. д.е. При этом
доход компании ОАО «АвиаМоторс» составит 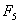 = 39 млн.
д.е.
= 39 млн.
д.е.
Суммарный
доход компании равен:
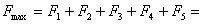 137+35+0+0+39=211
млн. д.е.
137+35+0+0+39=211
млн. д.е.
Значение,
полученное при безусловной оптимизации, совпадает с максимальным значением
функции цели при условной оптимизации. Следовательно, максимальный доход ОАО
«АвиаМоторс» при данных капитальных вложениях в филиалы «Aldis»,
«ТрансТехСервис», «Верра -Моторс», «Bayerhof» и «Бакра» составит 211
млн. д.е.
4.
Теория графов
Обладая
свойствами наглядности, теория графов представляет исследователю простой,
доступный и эффективный инструмент построения моделей экономики (календарное и
сетевое планирования, управление производственными и финансовыми потоками,
оптимизация маршрутов различных процессов).
Задание:
На
графе вершины I (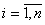 )
представляют состояние процесса производства запчастей для автомобилей марки BMW
компанией ОАО «АвиаМоторс». Вершина 1 - I - вход соответствует началу
производственного процесса. Вершина 8 - S - конец производственного процесса, в
результате которого получаем готовые запчасти. Остальные вершины - события,
совершаемые в процессе производства (плавление металла, обработка заготовки и
т.д.). Дуги - работа, совершаемая для получения определенных событий. Весовые
коэффициенты дуг - продолжительность (время) работы производственного процесса
(амортизация оборудования, стоимость ручного и машинного труда, стоимость
ресурсов, технологий, инноваций и информации - всё это используется в процессе
производства).
)
представляют состояние процесса производства запчастей для автомобилей марки BMW
компанией ОАО «АвиаМоторс». Вершина 1 - I - вход соответствует началу
производственного процесса. Вершина 8 - S - конец производственного процесса, в
результате которого получаем готовые запчасти. Остальные вершины - события,
совершаемые в процессе производства (плавление металла, обработка заготовки и
т.д.). Дуги - работа, совершаемая для получения определенных событий. Весовые
коэффициенты дуг - продолжительность (время) работы производственного процесса
(амортизация оборудования, стоимость ручного и машинного труда, стоимость
ресурсов, технологий, инноваций и информации - всё это используется в процессе
производства).

Рисунок 4.1 - Граф задания
Таблица 4.1 - Весовые коэффициенты дуг
|
n
|
1,2
|
1,3
|
1,4
|
2,3
|
2,5
|
2,6
|
2,7
|
3,4
|
3,5
|
3,6
|
3,7
|
4,5
|
4,6
|
4,7
|
5,6
|
5,8
|
6,7
|
6,8
|
7,8
|
|
12
|
0
|
6
|
5
|
7
|
N
|
3
|
0
|
3
|
5
|
2
|
0
|
7
|
4
|
9
|
2
|
0
|
1
|
4
|
5
|
где n = 12 и N = 3.
Требуется:
. Провести анализ структуры графа. Установить, будет ли неориентированный
граф, соответствующий заданному графу, эйлеровым. Разбить граф произвольным
образом на два несвязных графа. Путем удаления наименее загруженных дуг:
● избавиться от циклов (если они есть в графе);
● построить дерево графа.
. Составить матрицы смежности (для неориентированного графа) и инциденций
(для орграфа).
. Упорядочить нумерацию вершин графа, использую алгоритм Фалкерсона.
. Считая пропускную способность рёбер графа равной заданным
коэффициентам, определить максимальную мощность потока, проходящего через граф.
. Считая граф сетевым, определить его показатели:
критический путь;
ранние и поздние сроки свершения событий;
ранние и поздние сроки начала и окончание работ;
резервы свершения событий и выполнения работ.
Решение:

Рисунок 4.2 - Граф задания
. Анализ структуры графа
Граф, представленный на рисунке 4.2 не является эйлеровым, т.к. в нём не
существует эйлерова цикла, т.е. данный граф нельзя нарисовать, не отрывая руки
от бумаги и не повторяя линий. В этом графе не существует эйлерова цикла, в
который бы входили все ребра графа без повторений.
Граф называется связным, если две любые его вершины связаны хотя бы одной
цепью. Данный в задании граф - связный. Его необходимо разбить на два несвязных
графа произвольным образом. Разобьем граф, изображенный на рис. 4.2, на два
несвязных графа путём удаления наиболее загруженных вершин и инцидентных им
дуг.

Рисунок 4.3 - Несвязные графы, полученные из графа задания.
Мы разбили граф на два несвязных путём удаления вершин 4, 6 и 7 и
инцидентных им дуг.
Далее путём удаления наименее загруженных дуг избавимся от циклов и
построим дерево графа.
Цикл - цепь, вершины начала и конца которой совпадают.
Цепь - маршрут, в котором все дуги попарно различны (нет двух узлов,
соединённых различными дугами).
В заданном графе присутствует очень много циклов. Избавимся от них путём
удаления наименее загруженных дуг.

Рисунок 4.4 - Граф, не имеющий циклов, полученный из графа задания.
Дерево - связный неориентированный граф, не содержащий циклов.
Граф является деревом тогда и только тогда, когда любые две различные его
вершины можно соединить единственным элементарным путём.
Точка сочленения - вершина графа, удаление которой повышает число
компонентов связности. Под удалением вершины понимается удаление самой вершины
и всех инцидентных ей дуг. Компонент связности графа - это его связный подграф.
Построим этот граф, опираясь на граф, изображенный на рис. 4.4.

Рисунок 4.5 - Дерево графа
Удаление вершины 5 из графа, представленного на рис. 4.5, превращает
связный граф в два его компонента связности.
. Матрицы смежности и инциденций
Матрицей смежности вершин неориентированного графа, состоящего из n
вершин, называется матрица А размера nхn, элементы которой определяются следующим образом:
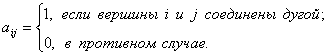
Матрица
смежности для неориентированного графа задания.

Но
матрица смежности не дает полной информации о связях в ориентированном графе,
так как единицы в этой матрице проставляются только в вершинах, из которых дуги
исходят, Поэтому для ориентированных графов используют другой вид матриц.
Матрицей
инцидентности ориентированного графа с 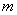 вершинами
и
вершинами
и 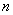 дугами (ребрами) называется прямоугольная матрица
дугами (ребрами) называется прямоугольная матрица 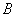 размера
размера 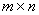 ,
элементы которой определяются следующим образом:
,
элементы которой определяются следующим образом:

Таким
образом, матрица инцидентности для ориентированного графа задания имеет вид:

.
Упорядочение вершин графа. Алгоритм Фалкерсона
Изменение
нумераций узлов и дуг графов, ровно, как и их конфигураций, не изменяет
природной сущности явлений и процессов, которые графы описывают. В данной
работе - процесс производства молочной продукции. Это свойство графов
называется изоморфизмом. Решение задач с привлечением графов упрощается, если
вершины и дуги графов расположить в определенном порядке.
Считается,
что из пары вершин орграфа вершина i является предшествующей, а вершины j -
последующей, если существует путь из i в j, а пути из j в i не существует.
Под
упорядочением вершин орграфа понимают такую нумерацию его вершин, при которой:
вершины
первой группы не имеют предшествующих, а вершины последней группы -
последующих;
вершины
любой другой группы не имеют предшествующих, а вершины последней группы -
последующих;
вершины
одних и тех же групп дугами не соединяются.
После
упорядочения вершин получается граф, изоморфный исходному.
Упорядочение
вершин орграфа можно осуществить, следуя алгоритму Фалкерсона, включающего в
себя следующие шаги:
1. Находят вершины графа, в которые не входят дуги. Это первый
уровень вершин. После нумерации они вместе с инцидентными им дугами мысленно
удаляются из графа.
2. В оставшемся графе, как и в исходном, находят вершины, в которые
не входят дуги. Эти вершины в произвольном порядке нумеруются натуральными
числами, следующими после номеров вершин первого уровня. Это вершины второго
уровня.
. Выделение уровней и нумерация продолжается вплоть до последней
вершины.
Упорядочим нумерацию вершин графа, следуя данному алгоритму:

Рисунок 4.6 - Изоморфный граф
В узел 1 графа задания (рис. 4.2) не входит ни одной дуги, а выходят дуги
(1,3), (1,4). Присваиваем узлу 1 номер 1, изображаем этот узел на рис. 4.6
вместе с выходящими из него дугами и мысленно удаляем эту вершину из исходного
графа.
Среди оставшихся узлов графа в узел 2 теперь не входит ни одной дуги.
Присваиваем узлу номера 2 соответственно и изображаем на рис.4.6. Мысленно
удаляем эту вершину вместе с инцидентными ей дугами из графа.
Теперь в узел 3 не входит ни одной дуги. Присваиваем этой вершине номера
3 и переносим ее на рис. 4.6 и мысленно удаляем из графа.
Далее мы видим, что в узел 4 не входит ни одной дуги. Присваиваем ему
номер 4 и переносим на новый рисунок, мысленно удалив его из исходного графа.
После проделанной операции остался узел 5 без входящих в него дуг.
Присваиваем ему номер 5 и переносим на новый рисунок, мысленно удалив его из
исходного графа.
Среди оставшихся узлов графа в узел 6 теперь не входит ни одной дуги.
Присваиваем узлу номера 6 соответственно и изображаем на рис.4.6. Мысленно
удаляем эту вершину вместе с инцидентными ей дугами из графа.
Теперь в узел 7 не входит ни одной дуги. Присваиваем этой вершине номера
7 , переносим ее на рис. 4.6 и мысленно удаляем из графа.
Остался единственный узел 8 без входящих и выходящих из него дуг.
Присваиваем этому узлу номер 8 и изображаем на рис. 4.6.
Таким образом, у нас получился новый упорядоченный граф (рис. 4.6),
изоморфный исходному графу (рис. 4.2).
. Максимальная мощность потока.
Алгоритм определения максимального потока:
1. Строится
начальный поток 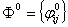
. Выявляются
подмножества А вершин, достижимых из истока I по
ненасыщенным ребрам. Если при этом сток S не попадет в
подмножество А, то построенный поток является максимальным, и задача решена.
Если же сток S попадает в подмножество А, то следует перейти к
следующему пункту алгоритма.
Таблица 4.2 - Матрицы слева - пропускных способностей ребер, справа -
начального потока
|
N
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
N
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
|
|
6
|
5
|
|
|
|
|
|
1
|
|
|
1
|
4
|
|
|
|
|
|
2
|
|
|
7
|
|
3
|
3
|
|
|
|
2
|
|
|
0
|
|
0
|
0
|
|
|
|
3
|
-6
|
-7
|
|
3
|
5
|
2
|
|
|
|
3
|
-1
|
0
|
|
1
|
0
|
0
|
|
|
|
4
|
-5
|
|
-3
|
|
7
|
4
|
9
|
|
|
4
|
-4
|
|
-1
|
|
1
|
4
|
0
|
|
|
5
|
|
-3
|
-5
|
-7
|
|
2
|
|
|
|
5
|
|
0
|
0
|
-1
|
|
1
|
|
|
|
6
|
|
-3
|
-2
|
-4
|
-2
|
|
1
|
4
|
|
6
|
|
0
|
0
|
-4
|
-1
|
|
1
|
4
|
|
7
|
|
|
|
-9
|
|
-1
|
|
5
|
|
7
|
|
|
|
0
|
|
-1
|
|
1
|
|
8
|
|
|
|
|
|
-4
|
-5
|
|
|
8
|
|
|
|
|
|
-4
|
-1
|
|
В
соответствии с пунктом 1 алгоритма на сети необходимо сформировать начальный
поток. Опираясь на таблицу 4.2, составим маршрут, по которому проходит поток 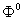 . Для составления маршрута будем двигаться от истока I=1 в
направлении вершины с меньшими номерами до тех пор, пока не достигнем стока S=8
. Для составления маршрута будем двигаться от истока I=1 в
направлении вершины с меньшими номерами до тех пор, пока не достигнем стока S=8
линейный транспортный задача граф
 : 1 -
(6)3- (3)4 - (7)5 - (2)6 - (1)7 - (5)8
: 1 -
(6)3- (3)4 - (7)5 - (2)6 - (1)7 - (5)8
Максимальный
поток, который может пройти по маршруту 
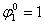 , величину общего потока ограничивает поток ребра
(6,7), которое становится насыщенным.
, величину общего потока ограничивает поток ребра
(6,7), которое становится насыщенным.
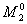 : 1 -
(5)4 - (4)6 - (4)8
: 1 -
(5)4 - (4)6 - (4)8
Максимальный
поток, который может пройти по маршруту 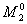
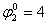 , величину общего потока ограничивают потоки ребер
(4,6) и (6,8), которые становятся насыщенными
, величину общего потока ограничивают потоки ребер
(4,6) и (6,8), которые становятся насыщенными
.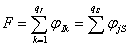
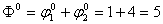
Составляем
матрицу 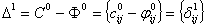 , которая определяет пропускную способность сети при
условии, что через нее проходит поток
, которая определяет пропускную способность сети при
условии, что через нее проходит поток 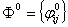 .
Используя данные таблицы 4.3, составим маршруты дополнительных потоков,
проходящие через ненасыщенные ребра.
.
Используя данные таблицы 4.3, составим маршруты дополнительных потоков,
проходящие через ненасыщенные ребра.
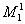 : 1 -
(5)3 - (2)4 - (9)7 - (4)8
: 1 -
(5)3 - (2)4 - (9)7 - (4)8
Максимальный
поток, который может пройти по маршруту 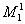
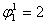 , величину общего потока ограничивает поток ребра
(3,4), которое становится насыщенным.
, величину общего потока ограничивает поток ребра
(3,4), которое становится насыщенным.
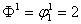
Составляем
матрицу  , которая определяет пропускную способность сети.
, которая определяет пропускную способность сети.
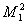 : 1 -
(1)4 - (7)7 - (2)8
: 1 -
(1)4 - (7)7 - (2)8
Максимальный
поток, который может пройти по маршруту 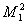
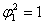 , величину общего потока ограничивает поток ребра
(1,4), которое становится насыщенным.
, величину общего потока ограничивает поток ребра
(1,4), которое становится насыщенным.
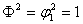
Составляем
матрицу 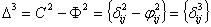 , которая определяет пропускную способность сети. Для
этого из элементов левой таблицы 4.4 вычитаем элементы правой.
, которая определяет пропускную способность сети. Для
этого из элементов левой таблицы 4.4 вычитаем элементы правой.
Так
как больше маршрутов нет, заканчиваем решение и считаем максимальный поток.

Рис. 4.7 - максимальные потоки и резервы дуг
. Сетевой граф
Сетевой граф - граф, вершины которого отображают состояния некоторого
процесса (производство запчастей для автомобиля), а дуги - работы, ведущиеся в
этом процессе. Каждой дуге сопоставляется время, за которое осуществляется
работа и/или число рабочих, которые осуществляют работу.
В сетевом графе между начальным и конечным событиями может быть несколько
путей.
Критический путь - непрерывная последовательность работ и событий от
начального до конечного события, требующая наибольшего времени (затрат) для ее
выполнения. Термин сетевого планирования, означающий самый длинный по временной
протяженности путь в сетевом графе, определяющий продолжительность работ по
выполнению проекта.
Особое значение для сетевого графа имеют следующие понятия:
Ранний срок свершения события - минимальное время, к которому необходимо
завершить все работы, предшествующие этому событию.
Поздний срок свершения события - момент времени, после которого остается
ровно столько времени, сколько необходимо для завершения всех работ, следующих
за этим событием.
При оценке резервов времени удобно использовать еще два вспомогательных
понятия:
Ранний срок окончания работы - срок, раньше которого нельзя закончить
данную работу. Он равен сумме раннего срока свершения работы и
продолжительности данной работы.
Поздний срок начала работы - срок, позже которого нельзя начинать данную
работу, не увеличив общую продолжительность строительства. Он равен разнице
позднего срока окончания работы и продолжительности данной работы.
Полный резерв - это наибольшее время, на которое можно задержать
выполнение данной работы, не увеличивая общую продолжительность работ. Он
определяется разностью между поздним и ранним началом (или поздним и ранним
окончанием).
Свободный резерв - это наибольшее время, на которое можно задержать
выполнение данной работы, не меняя раннего начала последующей. Этот резерв
возможен только тогда, когда в событие входят две или более работы
(зависимости), т.е. на него направлены две или более стрелки (сплошные или
пунктирные). Тогда лишь у одной из этих работ раннее окончание будет совпадать
с ранним началом последующей работы, для остальных же это будут разные
значения. Эта разница у каждой работы и будет ее частным резервом.
Рассчитаем критический путь графа задания:
M1: 1-4-7-8 t1=5+9+5=19
M2: 1-4-5-6-8 t1=5+7+2+4=18
M3: 1-4-6-8 t1=5+4+4=13 M4: 1-4-5-6-7-8 t1=5+7+2+1+5=20
M5: 1-4-6-7-8 t1=5+4+1+5=15
M6: 1-3-4-5-6-7-8 t1=6+3+7+2+1+5=24
M7: 1-3-4-5-6-8 t1=6+3+7+2+4=22
M8: 1-3-4-6-8 t1=6+3+4+4=179: 1-3-4-7-8 t1=6+3+9+5=23
M10: 1-3-5-6-8 t1=6+5+2+4=17
M11: 1-3-6-8 t1=6+5+2+1+5=19
M12: 1-3-6-7-8 t1=6+2+1+5=14
M13: 1-3-5-6-7-8 t1=6+5+2+1+5=19
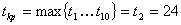
Таким
образом, критическим путём является путь M2
(1-3-4-5-6-7-8), который равен tкр=24.
Вывод:
процесс производства одной детали займёт не более 24 единиц времени.
Рассчитаем
ранние сроки изготовления детали.
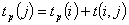
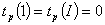
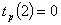
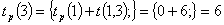
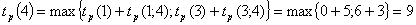
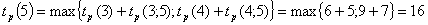
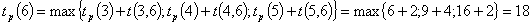
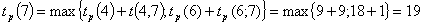
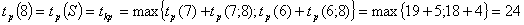
Рассчитаем
поздние сроки изготовления детали.

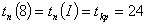
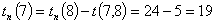
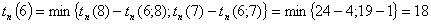
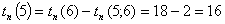
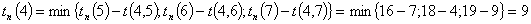
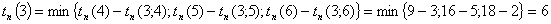
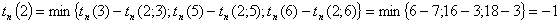
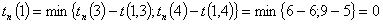
Посчитаем
резервы времени изготовления деталей по формуле:

Полученные
данные вместе с ранними и поздними сроками изготовления деталей занесем в
таблицу 4.6
Таблица 4.6 - Характеристики сроков изготовления деталей
|
j
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
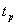 006916181924 006916181924
|
|
|
|
|
|
|
|
|
|
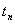 0-16916181924 0-16916181924
|
|
|
|
|
|
|
|
|
|
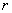 00000000 00000000
|
|
|
|
|
|
|
|
|
Рассчитаем характеристики сроков проведения работ и занесем их в таблицу
4.7
Ранние сроки начала работ:
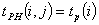
Ранние
сроки окончания работ:
Поздние
сроки начала работ:

Поздние
сроки окончания работ:
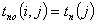
Полные
резервы времени выполнения работ:
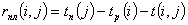
Свободные
резервы времени выполнения работ:
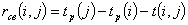
Таблица 4.7- Характеристики сроков выполнения работ
|
(i,j)
|
(1,3)
|
(1,4)
|
(2,3)
|
(2,5)
|
(2,6)
|
(3,4)
|
(3,5)
|
(3,6)
|
(4,5)
|
(4,6)
|
(4,7)
|
(5,6)
|
(6,7)
|
(6,8)
|
(7,8)
|
|
 0000066699916181819 0000066699916181819
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
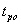 65733911816131818192224 65733911816131818192224
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
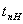 04-11315611169141016182019 04-11315611169141016182019
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
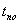 69616189161816181918192424 69616189161816181918192424
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
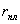 04-1131505100510020 04-1131505100510020
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
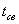 04-1131505100510020 04-1131505100510020
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Рисунок 4.8 - Сетевой граф
Методом сетевого графа мы рассчитали ранние и поздние сроки начала и
окончания изготовления детали (рис. 4.8 ), а так же, что процесс производства
одной детали займёт не более 24 единиц времени, а так же
Заключение
В данной работе я исследовала экономический процесс работы компании ОАО
«АвиаМоторс», занимающейся продажей и транспортировкой автомобилей марки BMW , а так же производством различных
запчастей.
Используя теорию исследования операций, менеджер решает задачи разного
уровня для повышения эффективности деятельности предприятия. В своей работе, на
примере компании ОАО «АвиаМоторс», я определила максимальную прибыль и
минимальные потери предприятия, выгодно распределила инвестиции, рассчитала
оптимальный путь транспортировки продукции потребителям, вычислила ранние и
поздние сроки свершения событий начала и окончания работ, нашла максимальное
время, затрачиваемое на производственный процесс, а так же исследовала сам
процесс производства данного предприятия.
Используя теорию исследования операций, современный менеджер решает
задачи разного уровня для повышения эффективности деятельности предприятия.
Использование этих методов в работе позволяет компании вести успешную
деятельность.
Поэтому изучение и освоение данных методов необходимо для меня как
будущего менеджера.
Список используемой литературы
1. Чернов В.П., Иванов Е.С. Введение в линейное
программирование- М.: ООО «Аквариум-Принт», 2003.
2. Алексеев В.Б. Дискретная математика - М:
Издательство «Мир», 2003г
. Кулаков Ю.В., Шамкин В.Н.- М: Издательство ТГТУ,
2004.
. Палтелеев А.В., Летов Т.А. Методы оптимизации в
примерах и задачах - М: Издательство ТГТУ,2006