Статика твердого тела
Федеральное
агентство по образованию
Государственное
образовательное учреждение высшего профессионального образования
Тульский
государственный университет
Кафедра
«Теоретическая механика»
Расчетно-графическая
работа по дисциплине «Теоретическая механика»
Вариант
22
Выполнил
студент
гр. 120651
Пивоваров
А.В
Проверил
Усманов
М.А
Тула
2006г.
Содержание
СТАТИКА
ТВЕРДОГО ТЕЛА
С1.
Определение реакций опор твердого тела
С2.
Определение реакций опор и сил в стержнях плоской фермы
С3.
Определение реакций опор составной конструкции
С5.
Равновесие сил с учетом сцепления (трения покоя)
С8.
Определение положения центра тяжести тела
КИНЕМАТИКА
К1.
Определение скорости и ускорения точки по заданным уравнениям ее движения
К2.
Определение скоростей и ускорений точек твердого тела при поступательном и
вращательном движениях
К3.
Кинематический анализ плоского механизма
Статика твердого тела
С1. Определение реакций опор твердого тела
Задание:
На схеме показаны три способа закрепления бруса,
ось которого - ломаная линия. Задаваемая нагрузка и размеры во всех случаях
одинаковы. Определить реакции опор для того способа закрепления бруса, при
котором реакция YA имеет
наименьший модуль.
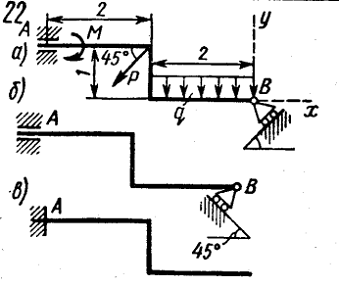
Схема:
Дано:
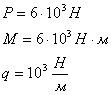
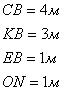
Решение:
Рассмотрим систему
уравновешивающихся сил, приложенных к конструкции. Действие связей на
конструкцию заменяем их реакциями Xa, Ya, Ma. Равномерно
распределенную нагрузку интенсивностью q заменяем равнодействующей Q:
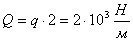
а)

б)

в)
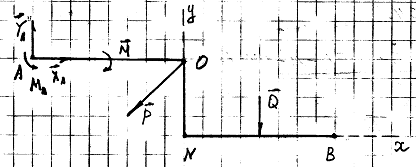
Чтобы выяснить, в каком случае
модуль 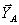 в заделке
является наименьшим, используем сумму моментов сил относительно точки B для всех
трех схем.
в заделке
является наименьшим, используем сумму моментов сил относительно точки B для всех
трех схем.
Для схемы а:
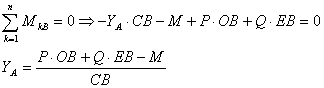
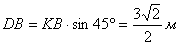
Подставим числовые значения:

Для схемы б:
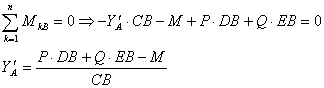
Подставим числовые значения:

Для схемы в:
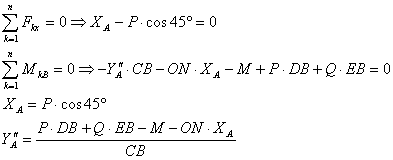
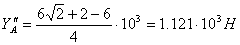
Таким образом, наименьший момент в
заделке получается при закреплении бруса по схеме в. Определим остальные
опорные реакции для этой схемы:
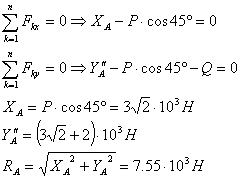
Ответ:
Реакция YA имеет
наименьший модуль в третьем способе закрепления бруса.

С2. Определение реакций опор и сил в
стержнях плоской фермы
Задание:
Определить реакции опор фермы от
заданной нагрузки, а также силы во всех ее стержнях способом вырезания узлов.
Дополнительно определить силы в трех
стержнях фермы от той же нагрузки способом Риттера.

Схема:
Дано:
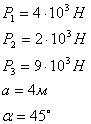
Решение:
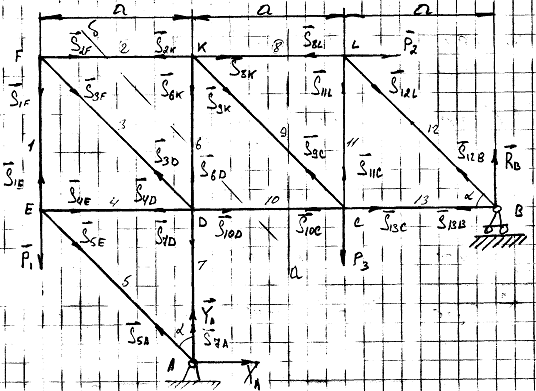
Покажем внешние силы, приложенные к
ферме: активные(задаваемые) силы и реакции опор А и В.
Составим уравнения равновесия сил,
приложенных к ферме:
По закону сохранения импульса:
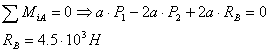
Спроецируем силы на ось OX:

Спроецируем силы на ось OY:
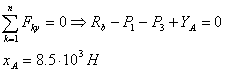
Определение сил в стержнях фермы
способом вырезания узлов.
Стержни, сходящиеся в узле фермы,
являются для узловых соединений - связями. Заменим действие связей на узлы
реакциями.
Направления реакций всех стержней
показаны от узлов внутрь стержней в предположении, что стержни растянуты. Если
в результате решения получится отрицательная реакция, это будет означать, что
соответствующий стержень сжат.
Для каждого узла составляются 2
уравнения равновесия:
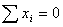 и
и  .
.
1) Рассмотрим узел А:
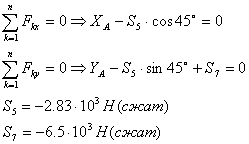
2) Рассмотрим узел B:

3) Рассмотрим узел E:

4) Рассмотрим узел
L:
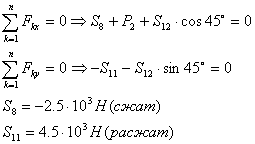
5) Рассмотрим узел С:

6) Рассмотрим узел D:
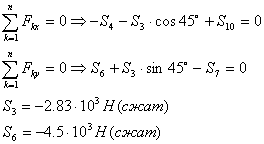
7) Рассмотрим узел F:

Ответ:
Результаты вычислений представлены в
виде таблицы:
|
Номер стержня
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
|
Знак
силы
|
+
|
+
|
-
|
+
|
-
|
-
|
-
|
-
|
+
|
|
+
|
-
|
-
|
|
Сила,
кН
|
2
|
2
|
2.83
|
2
|
2.83
|
4.5
|
6.5
|
2.5
|
6.86
|
0
|
4.5
|
6.36
|
4.5
|
Определение сил в стержнях способом сечений
(способом Риттера). Требуется определить силы в стержнях 4, 5 и 10. По способу
Риттера каждая сила должна выражаться из отдельного уравнения и не должна
выражаться через силы в других стержнях. Для определения сил мысленно разрезаем
ферму I-I.
1) За точкой Риттера примем точку С.
Пересекающиеся в ней силы исключаются из уравнения.

Составим уравнение моментов сил относительно
точки С:
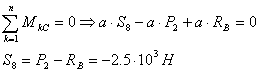
) Точкой Риттера для стержней 2 и 6
является узел, где пересекаются линии действия сил S6 и S10,
исключаемых из уравнения.
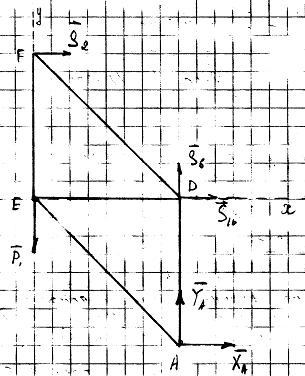
Составим уравнение моментов сил
относительно точки D:
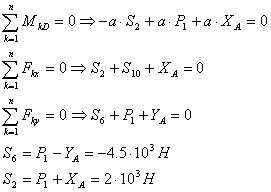
Ответ:
Найденные методом Риттера значения
сил:

С3. Определение реакций опор
составной конструкции
Задание:
Конструкция состоит из двух частей.
Установить, при каком способе соединения частей конструкции модуль реакции
наименьший, и для этого варианта соединения определить реакции опор, а также
соединения С.
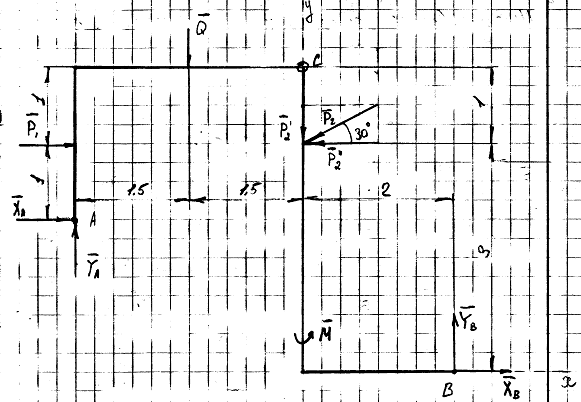
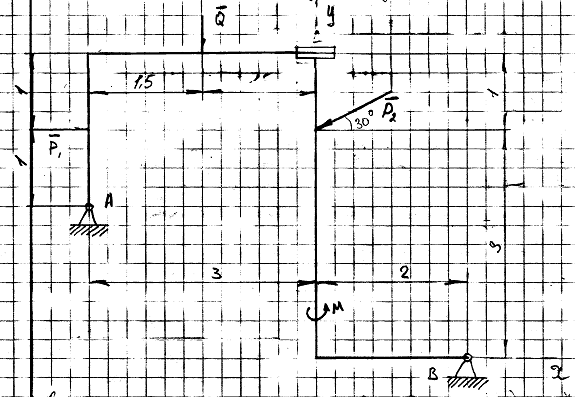
Схема:
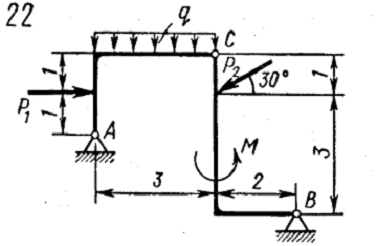
Дано:
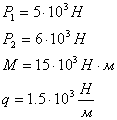
Решение:
Для упрощения вычислений момента
силы  разложим её
на вертикальную и горизонтальную составляющие:
разложим её
на вертикальную и горизонтальную составляющие:
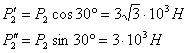
Равномерно распределённую нагрузку q заменяем
равнодействующей:
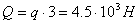
Действие связей на конструкции
заменим их реакциями
Определение реакций опоры А при
шарнирном соединении в точке С.
Рассмотрим систему уравновешенных
сил, приложенных ко всей конструкции.
Составим уравнение моментов сил
относительно точки B.

Рассмотрим систему
уравновешивающихся сил, приложенных к части конструкции расположенной левее С.

Выразим XA из 2
уравнения и подставим в 1.
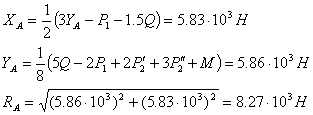
Определение реакций опоры А при
соединении частей конструкции в точке С скользящей заделкой.
Системы сил соответствуют уравнению
1
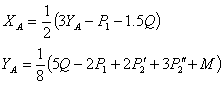
Рассмотрим левую, относительно точки
С, часть схемы.
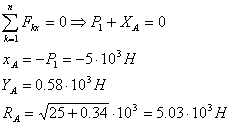
При соединении в точке С скользящей
заделкой модуль реакции опоры А меньше, чем при шарнирном соединении.
Рассчитаем остальные реакции для соединения с помощью скользящей заделки.
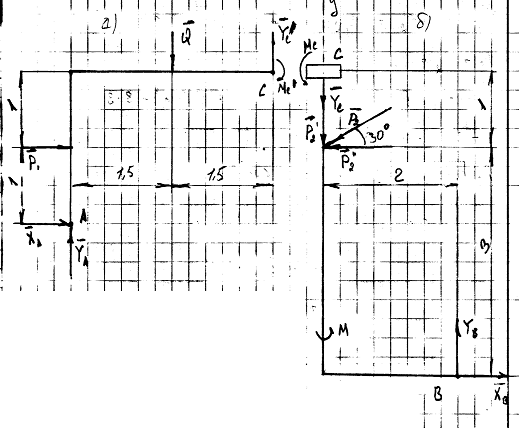
Рассмотрим левую часть схемы,
относительно точки С.
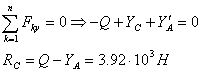
Рассмотрим правую часть схемы,
относительно точки С.:


Ответ:
При соединении в точке С скользящей
заделкой модуль реакции опоры А меньше, чем при шарнирном соединении. Реакции
для этого соединения:
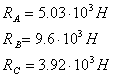
С5. Равновесие сил с учетом
сцепления (трения покоя)
Задание:
Определить максимальное значение
силы P и реакции опор системы в точках A, B, C и D, находящиеся в покое. Учесть
сцепление в двух опорных точках тела весом G.
Схема:
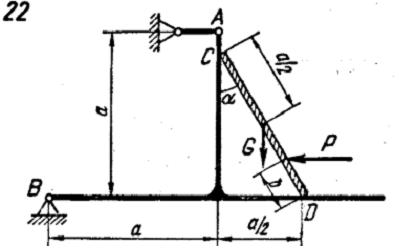
опора твердое тело
движение
Дано:

Решение:
Рассмотрим сначала систему
уравновешенных сил, приложенных к телу весом G. К телу приложена сила 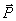 , нормальные
составляющие реакции
, нормальные
составляющие реакции  и
и 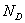 , а также
касательные составляющие силы сцепления
, а также
касательные составляющие силы сцепления  и
и 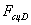 (силы трения покоя).
(силы трения покоя).
Составим три уравнения равновесия
указанных сил:
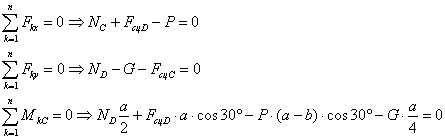
В случае предельного равновесия  . В этом
случае силы сцепления (силы трения покоя) принимают экстремальные значения, а
система уравнений дополняется неравенствами.
. В этом
случае силы сцепления (силы трения покоя) принимают экстремальные значения, а
система уравнений дополняется неравенствами.
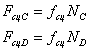
Решая систему всех этих уравнений,
получаем:
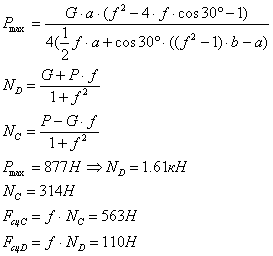
Совокупность сил 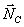 и
и 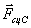 ,
,  и
и 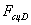 образуют
соответственно опорные реакции в точках D и Е.
образуют
соответственно опорные реакции в точках D и Е.
Рассмотрим теперь равновесие сил 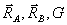 и
и 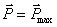 приложенных
ко всей системе.
приложенных
ко всей системе.

Решая эти уравнения, получим:


Искомые реакции и силы приведены в
таблице.
|
RA,
Н
|
RB, кН
|
NC, Н
|
FсцС, Н
|
ND, кН
|
FсцD, Н
|
Pmax, Н
|
|
427
|
1.57
|
314
|
563
|
1.61
|
110
|
877
|
С8. Определение положения центра тяжести тела
Задание:
Найти координаты центра тяжести объёма.

Схема:
Решение:
Координаты центра тяжести плоской фигуры
определяем по формулам:
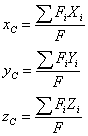
Здесь F - объём фигуры.
Чтобы воспользоваться формулами,
делим объём на части, для которых известны или легко определяются объёмы Fi и
координаты центров тяжести xi,yi и zi.
Все расчетные данные заносим в
таблицу:
|
Номер
элемента:
|
Fi, см2
|
xi, см
|
yi, см
|
zi, см
|
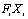 ,см3 ,см3 ,см3 ,см3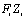 ,см3 ,см3
|
|
|
|
1
|
30000
|
40
|
12.5
|
7.5
|
1200000
|
375000
|
225000
|
|
2
|
-294.524
|
55
|
13
|
7.5
|
-16198.82
|
-3828,81
|
-2208,93
|
|
3
|
2000
|
13.33
|
5
|
3.33
|
26666.67
|
10000
|
6660
|
|
Σ
|
31705.476
|
|
|
|
1210467,85
|
381171,19
|
229451,07
|
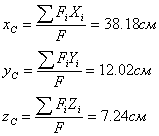
Ответ:
Искомые координаты центра всего
объёма:

Кинематика
К1. Определение скорости и ускорения
точки по заданным уравнениям ее движения
Задание:
По заданным уравнениям движения
точки М установить вид ее траектории и для момента времени t=t1 найти положение
точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а
также радиус кривизны траектории.
Дано:
Дополнительное задание:

Решение:
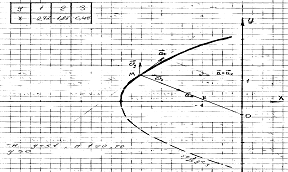
Уравнения движения можно
рассматривать как параметрические уравнения траектории точки. Чтобы получить
уравнения траектории в координатной форме, исключим время t из уравнений:

Вектор скорости точки:
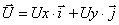
Вектор ускорения точки:
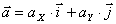
Здесь 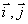 - орты осей x и y. Ux, Uy, ax, ay - проекции
скорости и ускорения точки на оси координат. Найдем их дифференцируя по времени
уравнения движения:
- орты осей x и y. Ux, Uy, ax, ay - проекции
скорости и ускорения точки на оси координат. Найдем их дифференцируя по времени
уравнения движения:

Найдем значения координат в точке М,
подставив в заданные уравнения t1:
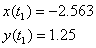
Проекцию скорости на OY найдем,
подставив t в уравнение:
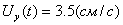
По найденным проекциям определяется
модуль скорости точки:
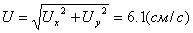
Теперь определим по проекциям модуль
ускорения:

Модуль касательного ускорения точки:
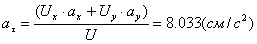
Модуль нормального ускорения точки:
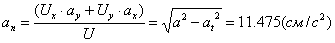
После того как найдено нормальное
ускорение, радиус кривизны окружности определяется из выражения:
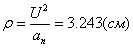
Дополнительное задание. Движение по
пространственной траектории.
Для расчета к двум уравнения
движения добавляется еще и третье.
Найдем третью координату точки М:

Определим из третьего уравнения
скорость и ускорение.
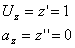
Найдем модуль скорости из проекций:
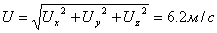
Т.к. проекция ускорения равна нулю,
следовательно, третья координата не повлияет на значения ускорений точки.
Ответ:
|
Координаты,
см
|
Скорость,
см/с
|
Ускорение,
см/с2
|
Радиус
кривизны, см
|
|
x
|
y
|
Ux
|
Uy
|
U
|
ax
|
ay
|
a
|
aτ
|
an
|
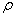
|
|
-2.563
|
1.25
|
3.5
|
5
|
6.1
|
14
|
0
|
14
|
8.033
|
11.475
|
3.243
|
При добавлении третьей координаты: z=0.25,
Uz=1, U=6.2.
Все остальные значения остаются неизменными.
К2. Определение скоростей и ускорений точек твердого
тела при поступательном и вращательном движениях
Задание:
Движение груза описывается уравнением:
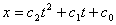 ,
,
где t - время, с1, с2, с0 -
некоторые постоянные.
В начальный момент времени(t=0) положение
груза определяется координатой x0, и имеет скорость U0. Учесть,
что в момент времени t=t2 координата груза равна x2.
Определить коэффициенты c0, c1, c2, при
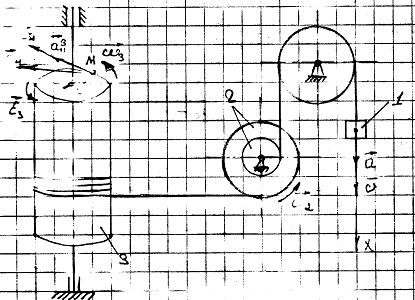
которых осуществляется требуемое движение груза 1. Определить также в момент
времени t=t1 скорость и ускорение груза и точки М одного из колес механизма.
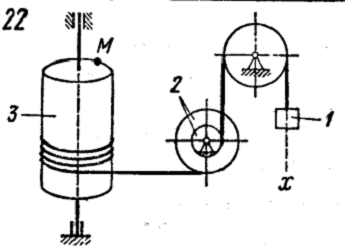
Дано:
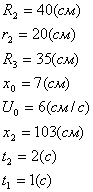
Решение:
Уравнение движения груза 1 имеет
вид:
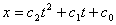
Коэффициенты c0, c1, c2 могут быть
определены из следующих условий:
1) При t0=0:

2) При t2=2
c и x2=103 см:

Таким образом, уравнение движения
груза 1 имеет следующий вид:
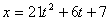
Тогда уравнение скорости:

Ускорение найдем, взяв производную
по уравнению скорости:
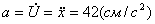
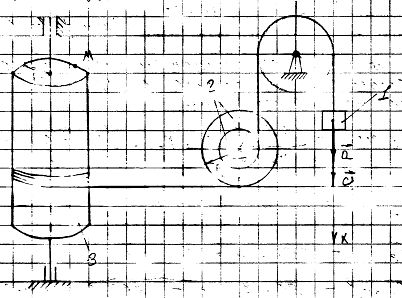
Для определения скорости и ускорения
точки М запишем уравнения, связывающие скорость груза U и угловые скорости w2 и
w3.
В соответствии со схемой механизма:
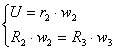
Выразим из двух уравнений угловую
скорость 2. Затем приравняем правые части и из получившегося уравнения можно
будет найти угловую скорость 3:
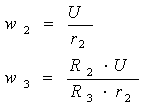
Подставив сюда уравнение скорости,
получим уравнение угловой скорости 3:
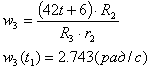
Угловое ускорение - первая
производная по угловой скорости:

Скорость точки М, ее вращательное,
центростремительное и полное ускорения определяются по формулам:
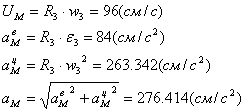
Ответ: результаты вычислений для
заданного момента времени приведены в таблице:
|
U,
см/с
|
a, см/с2
|
w3, рад/с
|
ε3, рад/с2
|
Uм,
см/с
|
амц, см/с2
|
амц,
см/с2
|
ам,
см/с2
|
|
48
|
42
|
2.743
|
2.4
|
96
|
263.342
|
84
|
276.414
|
К3. Кинематический анализ плоского механизма
Задание:
Найти для заданного положения механизма скорости
и ускорения точек В и С, а также угловую скорость и угловое ускорение звена,
которому эти точки принадлежат.

Схема:
Дано:
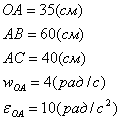
Решение:
Определение скоростей точек и
угловой скорости звена.

Вычисляем модуль скорости пальца А
кривошипа ОА при заданном положении механизма:

Теперь начертим схему, где PAB - мгновенный
центр скоростей АВ шатуна:
Угловая скорость звена АВ:
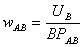
Модули скоростей точек В и С:

Из полученного чертежа получим:
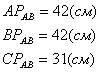
Вычислим угловую скорость звена АВ:

Теперь вычислим скорости точек В и
С:
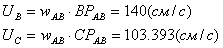
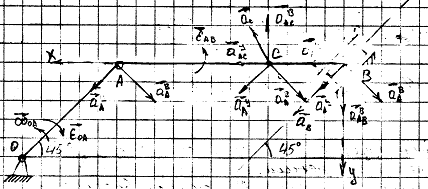
Ускорение точки А складывается из
вращательного и центростремительного ускорений.

Согласно теореме об ускорениях точек
плоской фигуры.
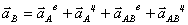
По формулам найдем ускорения звена
АВ и точки А:
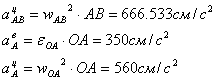
Вектор  направлен
от А к О. Вектор
направлен
от А к О. Вектор 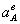 направлен
перпендикулярно к нему и направлен в сторону UA(Вращение
кривошипа - ускоренное).
направлен
перпендикулярно к нему и направлен в сторону UA(Вращение
кривошипа - ускоренное).
Вектор 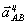 направлен
от В к А. Известны только линии действия этих векторов:
направлен
от В к А. Известны только линии действия этих векторов:  - по
вертикали, вдоль направляющих ползуна;
- по
вертикали, вдоль направляющих ползуна; 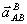 - перпендикулярно АВ. Зададимся
произвольно их направлениями по указанным линиям. Эти ускорения определим из
уравнений проекций векторного равенства на оси координат. Знак в ответе
показывает, истинное ли направление вектора было выбрано.
- перпендикулярно АВ. Зададимся
произвольно их направлениями по указанным линиям. Эти ускорения определим из
уравнений проекций векторного равенства на оси координат. Знак в ответе
показывает, истинное ли направление вектора было выбрано.
Выбрав направление осей x и y
получаем:
1) Проекция на ось OX:

2) Проекция на ось OY:

Теперь найдем угловое ускорение АВ:
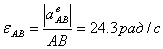
Направление ускорения 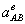 относительно
полюса А определяет направление углового ускорения εАВ. Здесь
под направлением углового ускорения подразумевается направление дуговой
стрелки, которое при ускоренном вращении звена совпадает с направлением его
вращения.
относительно
полюса А определяет направление углового ускорения εАВ. Здесь
под направлением углового ускорения подразумевается направление дуговой
стрелки, которое при ускоренном вращении звена совпадает с направлением его
вращения.
Определяем ускорение точки С:

Найдем проекции ускорения С:
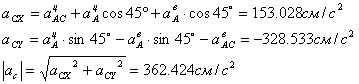
Ответ:
Результаты вычислений для заданного
положения механизма приведены в таблице:
|
υB,см/с
|
υC,см/с
|
ас,
см/с2
|
ав,
см/с2
|
εАВ, рад/с2
|
wAB, рад/с
|
|
140
|
103.393
|
362.424
|
1152.62
|
24.3
|
3.333
|