Параметрический резонанс
Содержание
Введение
. Параметрические колебания
.1 Общие понятия
.2 Параметрическое возбуждение по
периодическому кусочно-постоянному закону
1.3 Параметрическое
возбуждение по закону синуса
. Параметрический резонанс в
механических системах с распределенными параметрами
. Параметрический осциллятор
. Параметрическая
идентифицируемость механических колебательных систем, основанная на модели
равномерного движения материальной точки
5. Новые результаты теории
параметрического резонанса
Заключение
Список используемой литературы
Введение
Параметрические колебания отличаются от
вынужденных характером внешнего воздействия. Они вызываются периодическим
изменением извне какого-либо физического параметра системы (например, массы),
однако при вынужденных колебаниях задана сила или какая-либо другая величина,
совершающая колебания, а параметры системы остаются постоянными.
Параметрические колебания определяются
изменением во времени параметров системы; пример - колебание груза,
закрепленного на горизонтальной консольной балке при периодическом изменении
длины консоли.
Параметрические колебания помимо засорения
спектра обусловливают участки с отрицательным сопротивлением на динамической
характеристике I0 (U0), что может вызвать автоколебательные процессы в цепи,
смещения. При принудительном изменении напряжения с/0 или частоты внешнего
воздействия с0 в этом случае может обнаружиться несколько областей
автомодуляции с гистерезисными явлениями. Например, в процессе
экспериментального исследования при изменении частоты выявлено две
взаимопересекающиеся зоны автомодуляции, первая из которых, соответствующая
основному резонансу, располагалась в области более низких частот по сравнению
со второй, обязанной, по-видимому, параметрическому возбуждению субгармоники.
Параметрические колебания- колебания, вызванные
параметрическим возбуждением. Параметрические колебания возбуждаются в системе
только при определенном соотношении между частотой изменения параметра системы
и частотой собственных колебаний системы, и в этом отношении они сходны с
явлением резонанса. В примере с маятником частота изменения его длины вдвое
превышала частоту собственных колебаний, так как полупериоду колебания маятника
соответствовал полный период изменения его длины. Параметрические колебания
возникают при наличии какого-либо переменного параметра, создающего эффект,
аналогичный действию переменной силы. Обычно таким параметром является
переменная жесткость детали или узла.
Маятник с параметрическим возбуждением.
Параметрическими колебаниями называют колебания системы при периодических
изменениях во времени одного из нескольких параметров системы. Пример
параметрического резонанса. Перемещение центра тяжести человека,
раскачивающегося на качелях и совершающего при этом приседания и выпрямления во
весь рост. Вследствие такого изменения параметра длины маятника амплитуды
увеличиваются - возникает параметрический резонанс.
Устойчивость параметрических колебаний
оказывается зависящей от свойств источника энергии, от величины параметра у,
характеризующего нелинейность, от амплитуды колебаний, от момента инерции У и
от других параметров системы.
При параметрических колебаниях, как и при
обычных, возможно резкое возрастание амплитуды, которое при отсутствии
затухания становится неограниченным. Возможен так называемый параметрический
резонанс. Из простых физических соображений нетрудно установить, когда он
наиболее всего вероятен.
Таким образом, параметрические колебания
отличаются от вынужденных видом внешнего воздействия. При вынужденных
колебаниях извне задана сила или какая-либо другая величина, вызывающая
колебания, а параметры системы при этом остаются постоянными. Параметрические
колебания вызываются периодическим изменением извне какого-либо физического
параметра системы. Так, например, вращающийся вал некруглого сечения, имеющий
относительно различных осей сечения различные моменты инерции, которые входят в
характеристику жесткости при изгибе, испытывает поперечные колебания. Изменение
физического параметра вызывается внешними силами. В приведенном примере внешним
фактором является двигатель, осуществляющий вращение вала. Параметрические
колебания не затухают при наличии сил сопротивления. Поддержание
параметрических колебаний происходит за счет подвода энергии внешними силовыми
воздействиями, изменяющими физические параметры системы.
Частота первой гармоники параметрических
колебаний оказывается в два раза меньше частоты изменения параметра. Физические
основы теории параметрических колебаний представлены в классических работах Л.
И. Мандельштама и Н. Д. Папалекси, а математический аспект проблемы изложен,
например, в монографии, содержащей теорию нелинейного параметрического
резонанса для обыкновенных дифференциальных уравнений. Однако теория линейного
параметрического резонанса продвинута столь далеко, что позволяет придать
результатам строгий смысл.
Поэтому для изучения параметрических колебаний
используются также методы нелинейной теории. Физически процесс возбуждения
параметрических колебаний можно представить следующим образом.
1. Параметрические
колебания
1.1 Общие понятия
Основное дифференциальное уравнение. В
рассмотренных выше задачах о колебаниях действующие силы можно было отнести к
одной из трех категорий:
· позиционные (в частности,
восстанавливающие) силы, зависящие только от обобщенных координат q;
· диссипативные силы, определяемые
обобщенными скоростями q1;
· вынуждающие силы, являющиеся
заданными функциями времени t.
Однако существуют силы более сложной природы, в
частности нестационарные позиционные силы, которые зависят от координат q1,
а также от времени t (в явном виде):
1
= Q1(q1, q2,
..., qs,
t) (j = 1, 2, …, s),
и притом так, что их невозможно представить в
виде суммы двух слагаемых, одно из которых зависит только от координат, а
другое - только от времени.
Ограничимся рассмотрением линейных систем с
одной степенью свободы, когда при малых отклонениях от положения равновесия
обобщенная сила определяется выражением
= -cq,
причем, в отличие от случаев действия
стационарных восстанавливающих сил, параметр c = c(t) является функцией
времени.
Дифференциальное уравнение движения
Aq + c(t)q = 0
содержит переменный коэффициент и описывает
параметрические колебания. Как мы увидим ниже, свойства движения, описываемого
уравнением, существенно отличаются от свойств свободных колебаний, определяемых
дифференциальными уравнениями с постоянными коэффициентами. Важное значение
имеют нередко встречающиеся в приложениях случаи периодического изменения
параметра, когда
c(t + T) = c(t).
Соответствующие этим случаям колебания
называются параметрическими возбуждаемыми или, короче, параметрическими.
Решением дифференциального уравнения при таком
условии мы займемся ниже, но уже здесь отметим, что амплитуды параметрических
колебаний- в зависимости от значений постоянных системы- либо остаются
ограниченными, либо возрастают во времени. Очевидную опасность представляют
колебания с возрастающими амплитудами; это явление называют параметрическим
резонансом. По некоторым признакам, о которых будет сказано ниже,
параметрический резонанс существенно отличается от "обычного"
резонанса и в определенном смысле опаснее последнего.
1.2 Параметрические колебания около положения
равновесия
Прежде чем обратиться к решению
дифференциального уравнения и исследованию возможности параметрического
резонанса, рассмотрим некоторые простые механические системы, колебания которых
являются параметрическими; в этих случаях часто параметрическими называют и
сами системы.
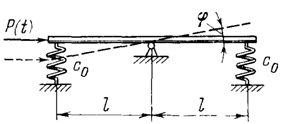
В качестве первого примера рассмотрим
симметричную абсолютно жесткую балку длиной 2l
со средней шарнирно неподвижной опорой и двумя упругими опорами на концах.
Коэффициенты жесткости упругих опор одинаковы и равны с0. К балке
приложена переменная горизонтальная сила P(t), заданная в виде периодической
функции времени. В положении равновесия ось балки горизонтальна. При малых
отклонениях балки от положения равновесия (см. штриховую линию на рисунке) на
нее действует момент сил упругости -с0φl2
и момент продольной силы P(t)φl;
полный момент, представляющий собой обобщенную силу в данной задаче,
M=-[c0l-P(t)]φl,
оказывается функцией координаты φ
и
времени t. Соответствующее дифференциальное уравнение движения имеет вид
-[c0l-P(t)]lφ =
Iφ
(где I-
момент инерции балки относительно оси вращения), или
φ+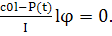
Другим примером может служить маятник с
колеблющейся по вертикали точкой подвеса. Пусть l-
длина маятника, m- масса
груза, y=y(t)- заданный периодический закон движения точки подвеса.
Дифференциальное уравнение малых относительных
колебаний маятника имеет вид (-mg - my)lφ
= ml2φ
(-my- переносная сила
инерции), или
φ+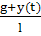 φ=0;
φ=0;
как видно, эта система также относится к типу
параметрических.
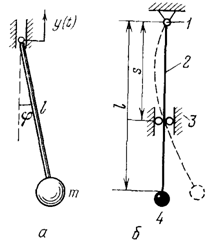
В качестве третьего примера рассмотрим
вертикальный безмассовый упругий стержень 2 длиной l,
показанный на рис б. С концом стержня связан сосредоточенный груз 4. Верхней
опорой служит неподвижный шарнир 1, а нижней опорой служит втулка 5 с коротким
подшипником. Если считать подшипник шарнирной опорой и пренебречь влиянием силы
тяжести груза, то коэффициент изгибной жесткости балки определяется формулой
теории сопротивления материалов
с=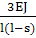 ,
,
где s-
расстояние между опорами.
Втулке задано периодическое движение около
некоторого среднего положения, определяемого расстоянием s0.
Состоянию равновесия соответствует положение груза на вертикали и прямолинейная
форма оси стержня.
При возмущении этого состояния груз отклоняется
в сторону, ось балки изгибается, и последующее движение груза описывается
дифференциальным уравнением
+ =0,
=0,
которое также относится к рассматриваемому здесь
типу.
Исследование решений подобных дифференциальных
уравнений позволит судить об устойчивости состояния равновесия, около которого
происходят колебания. Если параметрически возбуждаемые колебания постепенно
затухают (или по крайней мере не имеют тенденции к возрастанию), то состояние
равновесия следует признать устойчивым; если же колебания происходят с
возрастающими амплитудами (параметрический резонанс), то состояние равновесия неустойчиво.
Поэтому в подобных случаях самым важным является выяснение основной тенденции
параметрических колебаний.
1.3 Параметрические колебания около
стационарного режима движения
К необходимости исследовать свойства решений
дифференциальных уравнений с переменными коэффициентами приводят также задачи
об устойчивости стационарных режимов движения. Обычно дело сводится к
следующему.
Допустим, что после решения некоторой задачи о
движении механической системы найден режим движения, описываемый функцией q=q(t).
Для исследования устойчивости этого режима необходимо предположить, что он
каким-либо образом нарушен и возмущенное движение описывается функцией q+δq,
близкой к функции q(t); здесь δq(t)-
вариация функции q(t), т. е. отклонение системы от исследуемого режима
движения. Если функция δq
с течением времени возрастает, то исследуемый режим q = q(t) неустойчив; в
случае постепенного затухания функции δq режим
q = q(t) устойчив.
Как оказывается, для функции δq(t)
в ряде случаев можно получить дифференциальное уравнение. Характер решения
этого уравнения позволяет сделать заключение об устойчивости режима движения q
= q(t).
Поясним сказанное примером из области
вынужденных колебаний систем с нелинейной восстанавливающей силой.
Дифференциальное уравнение колебаний такой системы имеет вид
aq+F(q)=Q(t),
причем F(q) и Q(t)- заданные функции координаты
и времени. Как мы знаем, решение этого уравнения может быть неоднозначным и
возможно существование нескольких стационарных режимов с различными амплитудами
Так как среди этих режимов физически осуществимы
только устойчивые режимы, то полное решение задачи о вынужденных колебаниях
должно содержать не только выяснение (точное или приближенное) возможных
режимов, но и анализ их устойчивости.
Для исследования устойчивости какого-либо из
найденных режимов, например режима q1= q1(t),
предположим, что он каким-либо образом возмущен и, следовательно, движение
системы будет описываться суммой q1+δq1;
здесь второе слагаемое, δq1,
представляет собой возмущение функции q1.
Об устойчивости стационарного режима q1=q1(t)
можно судить по характеру изменения во времени возмущения δq1.
Если выяснится, что при t ∞ возмущение δq1
0 или остается ограниченным, то возмущенное движение будет стремиться к стационарному
режиму или оставаться вблизи него; следовательно, последний устойчив. Если же
при t ∞ вариация δq1
неограниченно возрастает, то исследуемый стационарный режим неустойчив.
Решение q1(t) должно удовлетворять
дифференциальному уравнению:
аq1+F(q1)=Q(t);
параметрический синус механический
колебательный
но тому же дифференциальному уравнению должна
удовлетворять также функция q1+δq1:
1+aδq1+F(q1+δq1)=Q(t).
Рассматривая малые величины δq1,
мы можем принять
(q1+δq1)≈F(q1)+F'(q1)δq1,
где штрих обозначает дифференцирование по
координате q1,
т.е.
1+aδq1+F(q1)+F'(q1)δq1=
Q(t).
Вычитая первое уравнение из второго уравнения,
получим
aδq1+F'(q1)δq1=0.
Но так как q1 представляет некоторую
известную функцию времени (стационарный режим), то и F'(q1) также является
функцией времени.
Пусть, например,
(q)=βq3,
Q(t)=Hsin ώt,
и необходимо исследовать устойчивость
стационарного режима
q1=А1 sin
ώt.
В данном случае
'(q)=3βq2=3βA21
sin2ώt
и для вариации стационарного режима получим
дифференциальное уравнение
δq+(3βA21
sin2 ώt)δq=0.
В следующих двух параграфах будут рассмотрены
решения дифференциальных уравнений, которое запишем в виде
q+k2(t)q=0.
Однако сразу отметим, что интегрирование этого
уравнения при произвольной периодической функции k2(t) весьма
сложно. Поэтому ниже мы остановимся только на двух относительно простых
случаях, когда изменение параметра следует периодическому кусочно-постоянному
закону либо закону синуса (в обоих случаях с дополнительным постоянным слагаемым).
Параметрическое возбуждение по периодическому
кусочно-постоянному закону
. Колебания при отсутствии трения. Рассмотрим
случай, соответствующий случаю, при котором дифференциальное уравнение
принимает вид:
+k20(1±µ)q=0,
где µ=∆k2/k20.
Ввиду того что в течение каждого полупериода
Т/2=π/k0
дифференциальное уравнение имеет постоянные коэффициенты, можно воспользоваться
способом припасовывания.
Рассмотрим какой-либо период Т изменения
коэффициента к2 и совместим с началом этого периода начало отсчета
времени. В первом полупериоде, когда 0 < t
< Т/2, дифференциальное уравнение имеет вид
1+k20(1±µ)q1=0,
а во втором полупериоде Т/2 < t < Т
соответственно будет
2+k20(1±µ)q2=0.
Дифференциальные уравнения с постоянными
коэффициентами имеют решения
q1=С1
sin k1t+D1 cos k1t,2=C2
sin k2t+D2 cos k2t,
причем k1=k0
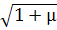 ,
k2=
k0
,
k2=
k0 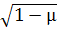 .
В этих решениях содержатся четыре постоянные, C1, D1, С2,
D2, для определения которых необходимы четыре условия. Два условия
относятся к моменту времени t = Т/2, общему для обоих полупериодов; в указанный
момент должно быть
.
В этих решениях содержатся четыре постоянные, C1, D1, С2,
D2, для определения которых необходимы четыре условия. Два условия
относятся к моменту времени t = Т/2, общему для обоих полупериодов; в указанный
момент должно быть
1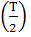 =
=
 2
2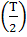 ,
,
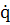 1
1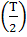 =
= 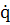 2
2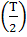 .
.
Это дает следующие соотношения:
C1 sin 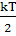 +
D1 cos
+
D1 cos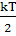 = С2
sin
= С2
sin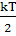 + D2 cos
+ D2 cos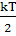 ,1
(C1 cos
,1
(C1 cos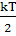 - D1
sin
- D1
sin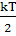 )
= k2 (C2 cos
)
= k2 (C2 cos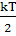 - D2 sin
- D2 sin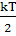 ).
).
Запишем еще два соотношения:
λq1(0)=q2(T),
λ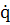 1(0)=
1(0)=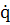 2(T)
2(T)
в которых λ-
некоторое, пока неизвестное число.
Соотношениями утверждается, что по истечении
рассматриваемого периода обобщённая координата и обобщенная скорость изменяются
в λ
раз. Соответственно этому движение в следующем периоде начнется при измененных
в λ
раз начальных условиях, т. е. будет повторять движение в рассматриваемом
периоде, но в измененном в λ
раз масштабе.
Если 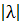 >
1, то колебания в каждом следующем периоде будут усиливаться, а если
>
1, то колебания в каждом следующем периоде будут усиливаться, а если 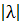 <
1, то они будут постепенно затухать. Таким образом, устойчивость или
неустойчивость системы определяется значением модуля λ.
<
1, то они будут постепенно затухать. Таким образом, устойчивость или
неустойчивость системы определяется значением модуля λ.
Подставив решения в соотношения, получим
1=С2
sin k2T + D2
cos k2T,
λC1k1=С2k2
cos k2T - D2k2 sin k2T.
Система уравнений однородна относительно
постоянных С1, D1, C2,
D2
и имеет отличные от нуля решения только в том случае, если равен нулю
определитель, составленный из ее коэффициентов.
Развернув определитель, получим следующее
квадратное уравнение:
λ2-2Aλ+1=0,
в котором для краткости обозначено
A=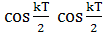 -
-  =
cos πα
=
cos πα 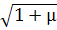 cos πα
cos πα 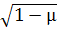 -
-
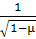 sin
πα
sin
πα 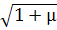 sin πα
sin πα 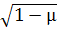
причем α=k0T/(2π)
есть отношение среднего значения k0
собственной частоты к частоте пульсации параметра. Корни уравнения следующие:
λ1=A-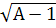 ,
λ2=A+
,
λ2=A+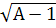 .
.
Для того чтобы числа λ1
и λ2
были вещественными, как это предполагается по смыслу решаемой задачи, должно
быть 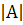 >
1, т. е. либо А > 1, либо А < 1. Но в обоих этих случаях модуль одного из
корней больше единицы:
>
1, т. е. либо А > 1, либо А < 1. Но в обоих этих случаях модуль одного из
корней больше единицы:
если A
> 1, то λ2
> 1;
если А < 1, то λ2
> 1.
Отсюда следует, что если выполнено неравенство,
то колебания будут с каждым новым периодом увеличиваться. Неравенство
представляет собой не только условие вещественности множителя λ,
но одновременно и условие возникновения параметрического резонанса.
Так как значение А зависит от двух постоянных
системы α
и µ, то их значения полностью определяют устойчивость системы.
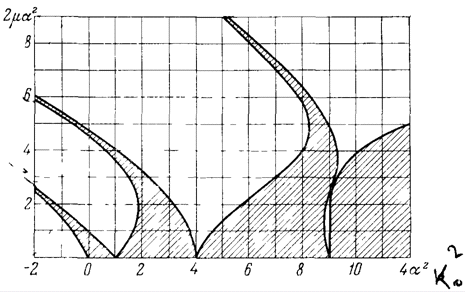
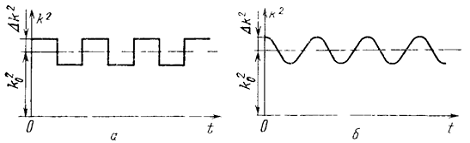
На рисунке представлена построенная с помощью
условия диаграмма устойчивости, по осям которой отложены значения 4α2
и 2µα2.
В незаштрихованных областях значения параметров α
и µ таковы, что условие выполняется, т. е. система неустойчива. Заштрихованные
области диаграммы соответствуют устойчивым состояниям системы. С помощью такой
диаграммы можно сразу судить об устойчивости по данным значениям α
и µ без всяких дополнительных вычислений.
Прежде всего обратим внимание па те зоны
областей неустойчивости, которые расположены вблизи горизонтальной оси, т. е.
соответствуют малым значениям параметра µ. Как видно, в этих зонах 4α2
≈ n2,
т. е.
α ≈  (n=1,2,…)
(n=1,2,…)
То же можно найти, положив µ = 0. В самом деле,
А = cos2 πα
- sin2 πα
= cos 2πα,
т. е. при произвольных значениях а имеем 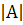 ≤
1. Равенство
≤
1. Равенство 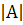 = 1,
соответствующее возникновению параметрического резонанса, возможно при условии,
что аргумент 2πα удовлетворяет
равенству
= 1,
соответствующее возникновению параметрического резонанса, возможно при условии,
что аргумент 2πα удовлетворяет
равенству
2πα = πn
(п = 1, 2, ...),
Таким образом, если выполняется условие, то
параметрический резонанс возникает при сколь угодно малой глубине пульсации.
При этом основное значение имеет случай n
= 1 когда α = 1/2, т. е. когда
среднее значение собственной частоты вдвое меньше частоты параметрического
возбуждения.
При значительной глубине пульсации и заметном
отличии µ от нуля параметрический резонанс возникает в целых областях значений α,
расположенных вблизи значений; чем больше заданное значение µ, тем шире эти
области. По этой причине отстройка от параметрического резонанса труднее, чем
от обычного резонанса; параметрический резонанс более опасен, чем обычный, еще
и по той причине, что линейное демпфирование (которое выше вообще не
учитывалось) лишь несколько суживает области неустойчивости, но неспособно
ограничить возрастание амплитуд колебаний в этих областях).
Пример. Груз 1 массы m
упруго подвешен на цилиндрической витой пружине 2 длиной l;
коэффициент жесткости пружины равен с. Разрезная втулка 3 периодически обжимает
верхнюю часть пружины так, что длительность каждого обжима t*
равна длительности интервала между двумя последовательными обжимами. Длина
деформируемой части пружины при обжиме мало отличается от длины l
(рис.). Найти наименьшее значение t*,
при котором возникает параметрический резонанс.
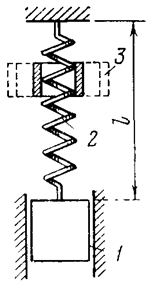
Замечая, что период изменения жесткости Т = 2t*,
и учитывая малость глубины пульсации, запишем условие параметрического
резонанса:
α = k0Т/(2π)
= n/2 (n
= 1, 2, .. .).
Подставляя сюда k0
=  ,
Т = 2t*, находим
,
Т = 2t*, находим
t* =  ;
;
наименьшее значение t*
соответствует n = 1:
t* =  ,
,
т. е. вчетверо меньше периода свободных
колебаний груза.
. Влияние линейного трения. При наличии вязкого
трения вместо дифференциального уравнения имеем
 + 2
+ 2 q
+ k20 (1±µ)q = 0,
q
+ k20 (1±µ)q = 0,
в котором по-прежнему h
= 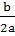 ,
где b- коэффициент
вязкости, а- инерционный коэффициент. Рассуждая, запишем решение для обоих
полупериодов:
,
где b- коэффициент
вязкости, а- инерционный коэффициент. Рассуждая, запишем решение для обоих
полупериодов:
1
= C1e-ht sin k*1t + D1e-ht
cos k*1t,2 = C2e-ht sin
k*2t + D2e-ht cos k*2t,
где
*1
= 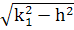 =
=
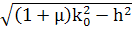
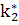 =
=  =
=
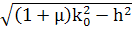
Условия в момент t = Т/2 имеют вид
q1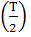 =
=
 2
2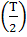 ,
,
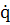 1
1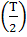 =
= 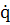 2
2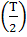 .
.
или

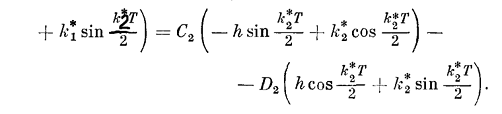
Далее составляем два условия типа:

т. е.
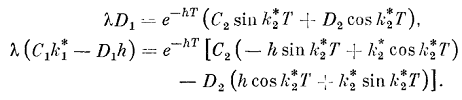
Четыре уравнения образуют систему, однородную
относительно постоянных C1, D1, С2, D2;
отличные от нуля решения соответствуют случаю, когда равен нулю определитель,
составленный из коэффициентов системы, развернув который, придем к квадратному
уравнению
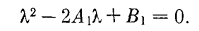
В каждом конкретном случае по заданным значениям
k0,
µ, h, Т можно вычислить значения А1 и B1, а затем
определить корни λ1
и λ2
квадратного уравнения. Признаком неустойчивости служит вещественность корней и
нeравенство 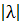 >
1 для наибольшего по модулю корня.
>
1 для наибольшего по модулю корня.
Не останавливаясь на подобном исследовании
корней, заметим, что для их вещественности (т. е. для неустойчивости системы)
необходимо выполнение условия
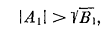
более жесткого, чем условие 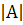 >
1, полученное выше для случая отсутствия трения. В частности, при h
> 0 условие выполняется, т. е. параметрический резонанс невозможен. Это
означает, что для возникновения параметрического резонанса необходима некоторая,
достаточно большая, глубина пульсации µ. В целом трение оказывает
стабилизирующее действие и приводит к некоторому сужению областей
неустойчивости.
>
1, полученное выше для случая отсутствия трения. В частности, при h
> 0 условие выполняется, т. е. параметрический резонанс невозможен. Это
означает, что для возникновения параметрического резонанса необходима некоторая,
достаточно большая, глубина пульсации µ. В целом трение оказывает
стабилизирующее действие и приводит к некоторому сужению областей
неустойчивости.
Параметрическое возбуждение по закону синуса
. Общие сведения. Этот случай изменения
параметра иллюстрирован на рис. б. Соответствующее дифференциальное уравнение
движения запишем в виде

Как в предыдущем параграфе, здесь k0-
среднее значение собственной частоты, µ- относительная глубина пульсации
переменного коэффициента. Дифференциальное уравнение с переменными
коэффициентами называется уравнением Матье. Обычно это уравнение записывают в
форме
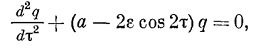
к которой можно прийти, положив в уравнении
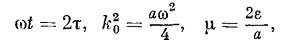
Решениями уравнения служат специальные функции,
называемые функциями Матье, свойства которых подробно изучены. Как и в случае
рассмотренного в предыдущем параграфе параметрического возбуждения, эти решения
могут быть или ограниченными, или неограниченно возрастающими. Выделение
соответствующих этим случаям областей параметров а и ε
приводит к диаграмме устойчивости, которая дана в готовом виде на рис.
(диаграмма Айнса- Стретта); она сходна с диаграммой устойчивости, изображенной
на рисунке. Границам между областями устойчивости и неустойчивости
соответствуют периодические дви5кения. Диаграмма устойчивости симметрична
относительно оси а, так как знак ε в
уравнении не имеет значения.
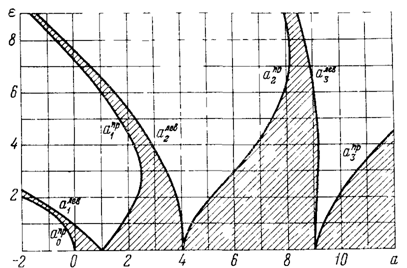
Если дифференциальное уравнение задачи приведено
к той форме, то но данным значениям а и ε
с помощью диаграммы устойчивости можно сразу сделать заключение об устойчивости
или неустойчивости системы. Как и выше, речь может идти либо об устойчивости
состояния равновесия (q- отклонение от этого состояния), либо об устойчивости
некоторого основного движения (в этом случае под q следует понимать вариацию
координаты).
Для приближенного определения границ между
областями устойчивости и неустойчивости в плоскости параметров а, ε
может быть применен способ гармонического баланса. На границах первой области
неустойчивости движение должно быть периодическим, причем период, как мы видели
в предыдущем параграфе, вдвое больше периода изменения параметра. Но период
изменения параметра в уравнении равен π,
так что указанное движение имеет период 2π
и его можно представить в виде ряда
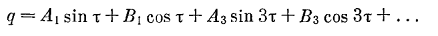
Ограничиваясь первыми двумя членами, подставим
их сумму в уравнение; приравнивая нулю коэффициенты при sin τ
и cos τ,
получаем два однородных уравнения
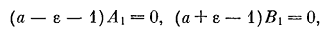
из которых следуют уравнения обеих границ:

Эти уравнения можно уточнить, принимая во
внимание большее число членов ряда. Приведем без вывода более точные уравнения
для первых четырех областей неустойчивости, обозначая значения а на границах n-й
области неустойчивости через  и
и 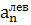 :
:
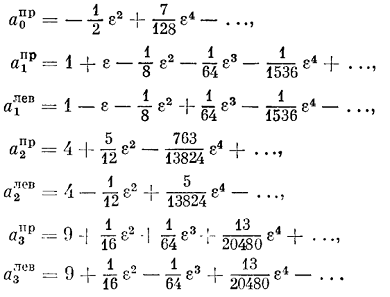
В заключение заметим, что трение несколько
суживает границы областей неустойчивости, подобно тому как ото было пояснено в
предыдущем параграфе.
. Примеры.
Пример 1. Найти условия устойчивости
вертикального состояния равновесия обращенного маятника (рис.), если точка его
подвеса гармонически колеблется около среднего положения по закону y=A
cos ώt
с частотой ώ и амплитудой А.
Длина маятника равна l.
Понятно, что при неподвижной опоре обращенный
маятник неустойчив; однако, как мы сейчас увидим, колебания опорной точки могут
придать устойчивость такому маятнику. Составляя дифференциальное уравнение
относительного движения, необходимо учесть переносную силу инерции-
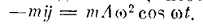
Ее момент составляет 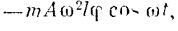 ,
и уравнение моментов запишется в форме
,
и уравнение моментов запишется в форме
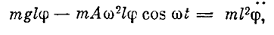
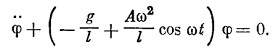
Для приведения уравнения к такому виду положим
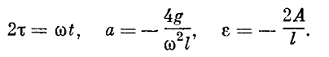
Как видно, в пашем примере оба параметра а и ε
отрицательные. Знак ε вообще роли
не играет (об этом уже говорилось выше), и главной особенностью рассматриваемой
системы является


отрицательность величины а. Как видно из
диаграммы устойчивости, устойчивость возможна и при отрицательных значениях а;
действительно, каждому значению е отвечает некоторая, довольно узкая область
значений а < 0, в пределах которой состояние равновесия устойчиво. Эти значения
лежат в интервале 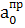 < а <
< а <  ,
т. е.
,
т. е.

При малых амплитудах колебаний А, т. е. малых
значениях параметра ε, правое
неравенство удовлетворяется при любых отрицательных значениях а и практически
остается лишь одно неравенство а > -  ε2,
т. е.
ε2,
т. е.

Подставляя сюда выражения а и е, получим условие
устойчивости в виде

Пример 2. Исследовать устойчивость режимов
стационарно движения
q = A1 sin ώt
(i = 1, 2, 3)
в системе с нелинейной восстанавливающей силой
F(q) = βq3.
Дифференциальное уравнение относительно вариации
δq
было составлено выше. Запишем его в виде
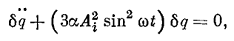
где коэффициент α
равен коэффициенту β,
разделенному на инерционный коэффициент системы. Для того чтобы привести
уравнение к той форме, нужно положить
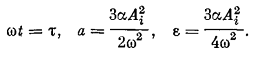
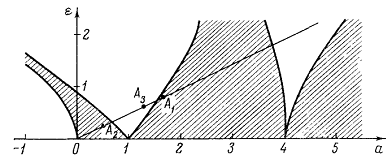
Таким образом, в данном случае а = 2ε
и на диаграмме устойчивости всевозможные пары значений а, е лежат на луче,
который выходит из начала координат под углом arctg 1/2 к оси (см. схему на
рис.). Поочередная подстановка значений A1, А2 и А3
в выражении а и ε приводит к
расположению точек, показанному на рис., т. е. точки A1 и A2
соответствуют устойчивым, а точка Аз- неустойчивым решениям. Этим
подтверждается сказанное относительно устойчивости найденных там решений на
различных ветвях резонансной кривой.
2. Параметрический резонанс в механических
системах с распределенными параметрами

Возникновение колебаний в механической системе с
распределенными параметрами при периодическом изменении ее физических
характеристик
Описание:
Параметрический резонанс - возбуждение
колебаний, наступающее в колебательной системе в результате периодических
изменения величины какого-либо из энергоёмких параметров системы (т. е.
параметров, от величины которых существенно зависят значения потенциальной и
кинетической энергий и периоды собственных колебаний системы). Параметрический
резонанс может происходить в любой колебательной системе, как в механической,
так и в электрической, например при периодическом изменении длины
математического маятника.
Параметрический резонанс наступает в случаях,
когда отношение угловой частоты w0 одного из собственных колебаний
системы к угловой частоте w изменений параметра (w0 / w) оказывается
близким к n/2, где n = 1,2,3,...; тогда в системе могут возбудиться колебания с
частотой, близкой к w0 и точно равной w/2, либо w, либо 3w/2 и т.д.
Параметрический резонанс наступает легче всего, а возникшие колебания
оказываются наиболее интенсивными, когда w0 / w = 1/2.
Классический пример параметрического резонанса в
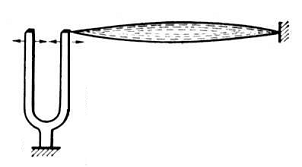
механической системе с распределенными параметрами - возбуждение интенсивных
поперечных колебаний в струне, прикрепленной одним концом к ножке камертона
(рисунок 1) путём периодического изменения её натяжения. Легче всего
параметрический резонанс возникает, когда один из периодов собственных
колебаний струны (её основного тона или какого-либо из гармоник) приблизительно
вдвое больше периода колебаний камертона. При обычном же возбуждении
вынужденных колебаний струны с периодом, равным периоду колебаний камертона,
резонанс наступил бы всякий раз, когда период колебаний камертона совпадал бы с
периодом одного из собственных колебаний струны. Таким образом, явление
параметрического резонанса в этом отношении сходно с силовым резонансом при
возбуждении вынужденных колебаний.
Параметрический резонанс от силового резонанса
отличается формой резонансной кривой - в случае параметрического возбуждения
колебаний резонанс наблюдается в строго ограниченной полосе частот (которая
определяется значением n и амплитудой изменения параметра), в то время как при
силовом воздействии на систему можно добиться существования колебаний на любой
частоте.
Параметрическое возбуждение колебаний струны:
3. Параметрический осциллятор
Параметрический осциллятор - осциллятор,
параметры которого могут изменяться в определённой области.
Параметрический осциллятор принадлежит к классу
незамкнутых колебательных систем, в которых внешнее воздействие сводится к
изменению во времени её параметров. Изменения параметров, например собственной
частоты колебаний ω или
коэффициента затухания β приводит к
изменению динамики всей системы.
Всем известный пример параметрического
осциллятора, это ребенок на качелях, где периодически изменяющаяся высота
центра массы означает периодическое изменение момента инерции, что приводит к
увеличению амплитуды колебаний качелей. (Это, разумеется, не означает, что
ребёнок действует всегда именно так. Гораздо чаще он раскачивается, отклоняясь
синхронно с качелями, и тогда ПР не у дел).
Другим примером, механического параметрического
осциллятора служит физический маятник, точка подвеса которого совершает
заданное периодическое движение в вертикальном направлении или математический
маятник, длина нити которого может периодически изменяться.
Широко используемым на практике,
примером параметрического осциллятора, может служить, используемый во многих
областях, параметрический генератор. Периодическое изменение ёмкости диода, с
помощью специальной схемы называемой "насосом", приводит к
классическим колебаниям варакторного <#"513631.files/image067.gif">(1)
Сделаем замену переменной времени t
→τ, где dτ = m(t)dt,
что приводит уравнение (1) к виду
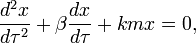 (2)
(2)
Сделаем еще одну замену x(τ)
→ q(τ):
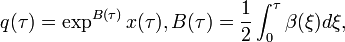 (3)
(3)
Это позволит избавиться от члена, связанного с
затуханием:
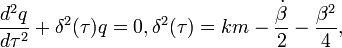 (4)
(4)
Поэтому фактически, без всякого ограничения
общности, вместо уравнения (1), достаточно рассмотреть уравнение движения вида
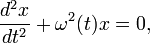 (5)
(5)
которое получилось бы из уравнения (1) при m =
const.
Интересно, что в отличие от случая постоянной
частоты 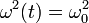 ,
аналитическое решение уравнения (5) в общем виде неизвестно. В случае
периодической зависимости ω(t)
уравнение (5) является частным случаем уравнения Хилла, а в случае
гармонической зависимости ω(t)
- частным случаем уравнения Матье. Наиболее хорошо уравнение (5) изучено в
случае, когда частота колебаний гармонически изменяется относительно некоторого
постоянного значения.
,
аналитическое решение уравнения (5) в общем виде неизвестно. В случае
периодической зависимости ω(t)
уравнение (5) является частным случаем уравнения Хилла, а в случае
гармонической зависимости ω(t)
- частным случаем уравнения Матье. Наиболее хорошо уравнение (5) изучено в
случае, когда частота колебаний гармонически изменяется относительно некоторого
постоянного значения.
. Рассмотрим случай, когда 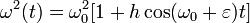 ,
то есть уравнение (5) имеет вид
,
то есть уравнение (5) имеет вид
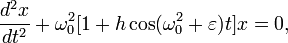 (6)
(6)
Где ω0
- частота собственных гармонических колебаний, амплитуда гармонических вариаций
частоты h < < 1, постоянная 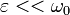 -
небольшая вариация частоты. Надлежащим изменением начала отсчета времени
постоянную h можно выбрать положительной, поэтому, не ограничивая общности,
будем считать, что h > 0. Вместо решения уравнения (6) поставим более
скромный вопрос: при каких значения параметра
-
небольшая вариация частоты. Надлежащим изменением начала отсчета времени
постоянную h можно выбрать положительной, поэтому, не ограничивая общности,
будем считать, что h > 0. Вместо решения уравнения (6) поставим более
скромный вопрос: при каких значения параметра  , происходит
резкое возрастание амплитуды колебаний, то есть решение x(t) неограниченно
возрастает? Можно показать [1], что это происходит в том случае, когда
, происходит
резкое возрастание амплитуды колебаний, то есть решение x(t) неограниченно
возрастает? Можно показать [1], что это происходит в том случае, когда
 (7)
(7)
2. Рассмотрим случай, когда 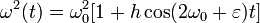 ,
то есть уравнение (5) имеет вид
,
то есть уравнение (5) имеет вид
 (8)
(8)
Иными словами, гармоническое изменение свободных
колебаний происходит с частотой 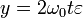 . В этом случае
параметрический резонанс, с точностью до членов h2, происходит в
случае, когда
. В этом случае
параметрический резонанс, с точностью до членов h2, происходит в
случае, когда
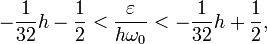 (9)
(9)
В частности, укажем условия параметрического
резонанса для малых колебаний математического маятника с колеблющейся в
вертикальном положении точкой подвеса, для уравнения колебаний имеют вид
 (10)
(10)
где 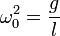 ,
и
,
и  .
В случае, когда a < < l и ограничиваясь первым порядком разложения по h,
получим, что
.
В случае, когда a < < l и ограничиваясь первым порядком разложения по h,
получим, что
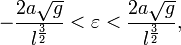 (11)
(11)
Тот факт, что параметрический резонанс
происходит в окрестности частоты свободных колебаний ω
= ω0 и её удвоенного
значения ω = 2ω0,
- не случаен. Можно показать (см. напр. [2]), что в случае уравнения
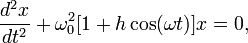 (12)
(12)
Параметрический резонанс имеет место, когда
 (13)
(13)
Главный резонанс происходит при удвоенной
частоте собственных колебаний гармонического маятника ω0,
а ширина резонанса равна hω0.
Важно также, что при наличии трения (см. ур-е (2)), в уравнении
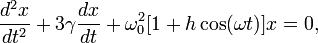 (14)
(14)
Имеет место явление параметрического резонанса
не при любых h < < 1, а лишь при тех 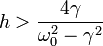 .
Т.о., при наличии трения
.
Т.о., при наличии трения
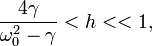 ,(15)
,(15)
что позволяет надлежащим выводом параметров γ,ω0,
и h, в зависимости от практической необходимости, усилить или ослабить явление
параметрического резонанса.
4. Параметрическая идентифицируемость
механических колебательных систем, основанная на модели равномерного движения
материальной точки
При исследовании и анализе механических систем
применяют дискретные и непрерывные методы, основанные на использовании
гармонических возбуждающих воздействий. В частности, находят применение методы
анализа, базирующиеся на экспериментальном снятии амплитудно-частотных
характеристик (АЧХ) исследуемых объектов.
При снятии АЧХ применяют методы: сканирования
частоты возбуждающего испытуемый объект воздействия, одновременное возбуждение
испытуемого объекта конечным числом гармонических сигналов с разными частотами,
возбуждение случайным сигналом, имеющим характер белого или розового шума,
детерминированной или случайной последовательностью импульсных сигналов разной
формы, модулированных по амплитудным значениям , временному положению,
полярности, площади и др.
Более достоверную информацию получают при
использовании режимов сканирования частоты по сравнению с методами, основанными
на использовании импульсной переходной функции исследуемого линейного объекта
за счет обеспечения более высокого значения сигнал/помеха.
Снятие АЧХ методом сканирования частоты является
распространенным. Усложнение такого метода основано на необходимости решения
задачи оптимизации скорости сканирования частоты в смысле минимизации
погрешности снятия АЧХ, т.е. минимального отличия динамического резонансного
пика АЧХ относительно статического.
Предложенный в работе метод идентифицируемости
частот максимумов резонансных пиков основан не на принципе выбора оптимальной
скорости сканирования частоты возбуждающего испытуемый объект воздействия в
смысле минимизации погрешности отклонения частоты максимума динамического
резонансного пика относительно частоты максимума статического, а на принципе
возможности фиксации частот максимумов огибающих полуразмахов колебаний по
крайней мере двух динамических резонансных пиков, соответствующих постоянным и
разным скоростям сканирования частоты по линейному закону без учета строгого
ограничения на максимальную скорость сканирования.
С одной стороны, приближенное вычисление
интеграла Дюамеля за счет учета ограниченного числа слагаемых при разложении
экспоненциального множителя подынтегрального выражения в ряд позволяет получить
замкнутое выражение для определения резонансной частоты статического
резонансного пика.
С другой стороны, рассматривая в качестве модели
режима сканирования частоты при наличии резонансных пиков АЧХ модель
равномерного движения материальной точки, приходим к следующим соотношениям.
В предположении использования модели, основанной
на законе равномерного движения материальной точки для k-го резонансного пика,
имеет место формула
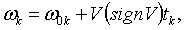 (1)
(1)
Где  - резонансная частота динамического
резонансного пика при скорости V сканирования;
- резонансная частота динамического
резонансного пика при скорости V сканирования;
 - резонансная частота статического
резонансного пика;
- резонансная частота статического
резонансного пика;
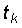 - текущее время.
- текущее время.
При реализации режимов сканирования
частоты w со
скоростями 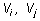
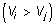 и условии
и условии 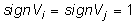 при учете
(1) имеем
при учете
(1) имеем
где 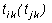 - промежуток времени сканирования
частоты w по
диапазону
- промежуток времени сканирования
частоты w по
диапазону  частот со
скоростью
частот со
скоростью 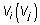 ;
;
 - резонансная частота динамического
резонансного пика, соответствующая резонансной частоте
- резонансная частота динамического
резонансного пика, соответствующая резонансной частоте 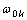 k-го
статического резонансного пика при скорости
k-го
статического резонансного пика при скорости 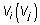 сканирования частоты по диапазону
частот.
сканирования частоты по диапазону
частот.
В некотором ограниченном диапазоне
изменения скорости сканирования
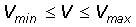 (3)
(3)
можно применять гипотезу линейного
смещения резонансной частоты 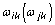 k-го динамического резонансного
пика относительно резонансной частоты
k-го динамического резонансного
пика относительно резонансной частоты 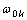 k-го статического.
k-го статического.
В предположении
 (4)
(4)
из (2) получим
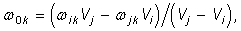 (5)
(5)
что соответствует соотношению, основанному на
применении интеграла Дюамеля.
Представим (5) в виде
 (6)
(6)
Из физических соображений имеет
место неравенство 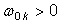 , тогда из
(5) следует система неравенств
, тогда из
(5) следует система неравенств
 (7)
(7)
что соответствует системе неравенств:
 (8)
(8)
Из (8) следует система неравенств:
а) при  имеет место
неравенство
имеет место
неравенство
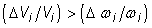 (9)
(9)
Или
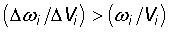 ,(10)
,(10)

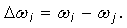
В случае малых изменений скорости из (10)
следует неравенство
 ;(11)
;(11)
б) при 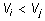 имеют место
неравенства, аналогичные (9), (10).
имеют место
неравенства, аналогичные (9), (10).
Из неравенств (9), (10), (11)
следует утверждение.
Утверждение 1
а) при реализации режимов
сканирования частоты возбуждающего механическую колебательную систему
воздействия, по крайней мере, с двумя постоянными и разными скоростями
сканирования в первом приближении относительное изменение скорости сканирования
возбуждающего воздействия превышает относительное изменение резонансной частоты
динамического резонансного пика;
б) при реализации режимов
сканирования частоты возбуждающего механическую колебательную систему
воздействия, по крайней мере, с двумя постоянными и разными скоростями
сканирования в первом приближении производная резонансной частоты динамического
резонансного пика по скорости сканирования не превышает среднее изменение
резонансной частоты динамического резонансного пика в зависимости от скорости
сканирования.
Из (1) при условии  имеют место
соотношения:
имеют место
соотношения:
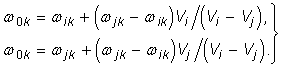 (12)
(12)
Из (1) при условиях
 или
или  (13)
(13)
или в более общем виде
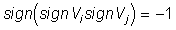 (14)
(14)
имеют место соотношения:
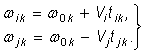 (15)
(15)
В предположении
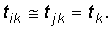 (16)
(16)
Из (15) имеем
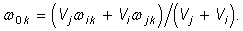 (17)
(17)
Представим (17) в двух формах:
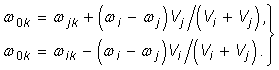 (18)
(18)
Полученные соотношения (5), (18)
позволяют определить резонансную частоту 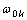 k-го статического резонансного пика
в зависимости от двух скоростей
k-го статического резонансного пика
в зависимости от двух скоростей 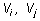 сканирования частоты возбуждающего
испытуемый объект воздействия в явном виде. Такой алгоритм при его технической
реализации создает дополнительные схемотехнические усложнения в эксплуатации,
так как приводит к необходимости изменять режим работы усилительных блоков при
изменении скоростей
сканирования частоты возбуждающего
испытуемый объект воздействия в явном виде. Такой алгоритм при его технической
реализации создает дополнительные схемотехнические усложнения в эксплуатации,
так как приводит к необходимости изменять режим работы усилительных блоков при
изменении скоростей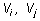 . Приведем
алгоритм, обеспечивающий определение частоты
. Приведем
алгоритм, обеспечивающий определение частоты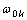 , которая в явном виде не зависит от
скоростей
, которая в явном виде не зависит от
скоростей 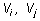 сканирования
частоты w по
диапазону частот. При реализации двух режимов сканирования частоты w со скоростями
сканирования
частоты w по
диапазону частот. При реализации двух режимов сканирования частоты w со скоростями 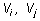 и условии
и условии 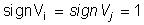 при учете
(1) имеем систему уравнений
при учете
(1) имеем систему уравнений
 (19)
(19)
При реализации двух режимов
сканирования частоты w со
скоростями 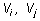 и условии
и условии 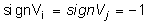 при учете
(1) имеем систему уравнений
при учете
(1) имеем систему уравнений
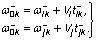 (20)
(20)
В предположении
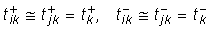 .(21)
.(21)
Из (2), (20) при учете (21) имеем
 (22)
(22)
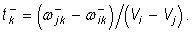 (23)
(23)
Подставляя (22), например, в первое
уравнение (2), а (23) - в первое уравнение (20) и исключая из этих уравнений 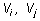 , получим
формулу для определения резонансной частоты
, получим
формулу для определения резонансной частоты 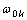 k-го статического резонансного
пика, исключающую зависимость
k-го статического резонансного
пика, исключающую зависимость 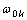 от скоростей сканирования частоты w при условии
от скоростей сканирования частоты w при условии 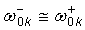 :
:
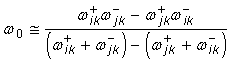 .(24)
.(24)
Приведенные соотношения (5), (17),
(24) для определения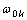 , основанные
на законе равномерного движения материальной точки, и соотношения, полученные
при приближенном вычислении интеграла Дюамеля, позволяют сформулировать
следующие утверждения.
, основанные
на законе равномерного движения материальной точки, и соотношения, полученные
при приближенном вычислении интеграла Дюамеля, позволяют сформулировать
следующие утверждения.
Утверждение 2. Резонансная частота
явно выраженного k-го статического резонансного пика в первом приближении
моделируется и определяется законом равномерного движения материальной точки.
Утверждение 3. Для определения
резонансной частоты при моделировании законом равномерного прямолинейного
движения материальной точки необходимо и достаточно реализации, по крайней
мере, с двумя конечными и разными скоростями 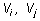 сканирования частоты при фиксации и
запоминания двух частот максимумов огибающих полуразмахов колебаний
динамических резонансных пиков, соответствующих скоростям
сканирования частоты при фиксации и
запоминания двух частот максимумов огибающих полуразмахов колебаний
динамических резонансных пиков, соответствующих скоростям 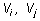 сканирования
частоты.
сканирования
частоты.
Утверждение 4. Для определения
резонансной частоты статического резонансного пика методом сканирования частоты
возбуждения необходимо и достаточно реализации, по крайней мере, двух режимов
сканирования со скоростями 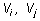 при выполнении одного из условий:
при выполнении одного из условий:
1) 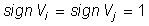 или
или 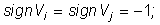
) 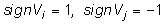 или
или 
Утверждение 5. Для определения
резонансной частоты 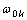 явно
выраженного k-го статического резонансного пика при реализации режимов
сканирования частоты при неявной зависимости
явно
выраженного k-го статического резонансного пика при реализации режимов
сканирования частоты при неявной зависимости 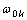 от значений скоростей сканирования
необходимо и достаточно введение, по крайней мере, двух скоростей сканирования
при выполнении двух условий:
от значений скоростей сканирования
необходимо и достаточно введение, по крайней мере, двух скоростей сканирования
при выполнении двух условий:

 .
.
Таким образом, здесь показана
эквивалентность подходов параметрической идентифицируемости резонансных частот
механических колебательных систем, основанных на приближенном вычислении
интеграла Дюамеля, при использовании режимов сканирования частоты и применении
модели равномерного движения материальной точки.
5. Новые результаты теории параметрического
резонанса
Институт механики МГУ им. М.В. Ломоносова.
Рассматриваются линейные динамические системы со
многими степенями свободы с периодическими коэффициентами, зависящие от многих
параметров. Устойчивость тривиального решения в этих системах определяется с
помощью теории Флоке. Дан вывод выражений для первых и вторых производных
матрицы монодромии по параметрам в терминах матрицантов прямой и сопряженной
задачи и производных от матрицы системы. Это позволяет получить производные
простых мультипликаторов, а также их абсолютных значений по параметрам, а также
использовать эти соотношения в градиентных методах для стабилизации или
дестабилизации (резонанса) системы. Приведен численный пример стабилизации
системы, описываемой уравнением Карсона-Камби. Затем исследуются сильные и
слабые взаимодействия мультипликаторов на комплексной плоскости, и дается
геометрическая интерпретация этих взаимодействий.
В качестве приложений развитой теории
исследованы области резонанса для уравнения Хилла с демпфированием. Дано
описание этих областей (половинок конусов) в трехмерном пространстве
параметров. В качестве примера рассмотрен параметрический резонанс маятника с
точкой подвеса, колеблющейся по произвольному периодическому закону. Другим
важным приложением уравнения Хилла является исследование устойчивости
периодических решений в динамике нелинейных систем. Показано, как с помощью
полученных областей резонанса для уравнения Хилла находить устойчивые и
неустойчивые периодические решения гармонически возбуждаемого уравнения
Дуффинга.
Далее рассматриваются линейные колебательные
системы со многими степенями свободы с периодическими коэффициентами, зависящие
от трех независимых параметров: частоты и амплитуды периодического воздействия
и параметра диссипативных сил, причем последние две величины предполагаются
малыми. Исследуется неустойчивость тривиального решения (параметрический
резонанс). Для произвольной матрицы периодического воздействия и положительно
определенной матрицы диссипативных сил получены общие выражения для областей
основного и комбинационного резонансов. Изучены два частных случая матрицы
периодического возбуждения, часто встречающихся в приложениях: симметрической
матрицы и стационарной матрицы, умноженной на скалярную периодическую функцию.
Показано, что в обоих случаях области резонанса в первом приближении
представляют собой конусы в трехмерном пространстве параметров. Полученные
соотношения позволяют проанализировать влияние возрастания частот собственных
колебаний и номера резонанса на области неустойчивости. Метод исследования
областей параметрического резонанса, предложенный в данной работе, является
новым и строгим. Он основан на анализе поведения мультипликаторов на
комплексной плоскости и использует формулы для производных матрицы монодромии
по параметрам.
В качестве механических примеров получено
решение задачи В.В. Болотина об областях динамической устойчивости плоской
формы изгиба балки, нагруженной периодическими моментами, и решена задача об
устойчивости упругого стержня переменного сечения, сжатого периодической
продольной силой.
В данной работе мною изучалась теория
параметрических колебаний и теория параметрического резонанса. Были рассмотрены
несколько вариантов параметрического возбуждения, а именно: колебания около
положения равновесия, колебания около стационарного режима движения, по
периодическому кусочно-постоянному закону (при отсутствии трения, при влиянии
линейного трения), по закону синуса; был изучен параметрический осциллятор,
найдены новые результаты теории параметрического резонанса, полученные Институтом
механики МГУ им. М.В. Ломоносова.
Список используемой литературы
1. Павленко Ю. Г., Лекции по
теоретической механике.- М.: ФИЗМАТЛИТ, 2002.- 392 с.
. Пановко Я. Г., Введение в
теорию механических колебаний.- С.-Петербург, 1989
. Н. В. Бутенина, Я. Л. Лунца
и Д. Р. Маркина, Курс теоретической механики.- Наука
. Бабаков И. М. Теория
колебаний.- 2-е изд.- М.: Наука, 1965.
. Бидерман В. Л. Теория
механических колебаний.- М.: Высшая школа, 1980.
. Болотин В. В. Динамическая
устойчивость упругих систем.- М.: Гостехиздат, 1956.
. Шмидт Г. Параметрические
колебания.- М.: Мир, 1978.