1. Порядок расчета
установившегося случайного процесса в системе управления
Для расчета установившегося
случайного процесса в системе при стационарных случайных воздействиях
применяется спектральный метод.
Данный аналитический метод,
называемый также методом передаточных функций, детально развит в рамках теории
автоматического управления [1,2] и основан на использовании
структурно-динамических схем систем и спектральных плотностей случайных
процессов. Непосредственное использование спектральных плотностей возможно
только для стационарных процессов. Поэтому данный метод позволяет строить
модели процессов, соответствующих некоторым установившимся режимам в
стационарных системах при стационарных воздействиях.
Применение данного метода основано
на использовании двух свойств линейных систем:
. Реакция линейной системы на
совокупность входных воздействий может быть определена как сумма ее реакций на
каждое из них в отдельности (принцип суперпозиции).
. Случайный сигнал на выходе
физически реализуемого линейного динамического звена имеет закон распределения,
близкий к нормальному (свойство фильтра).
Второе свойство, строго говоря,
имеет место при следующем соотношении между порядком знаменателя n и
числителя m передаточной функции звена или системы: n - m ≥ 2. Однако его обычно
используют во всех случаях, когда выполняется условие физической реализуемости
n-m ≥ 1.
Благодаря указанным свойствам
оказывается возможным изолированно рассматривать преобразование линейной
системой детерминированных и центрированных случайных составляющих входных сигналов
и ограничиваться для выходного сигнала или ошибки системы нахождением только
математического ожидания и дисперсии, полностью определяющих нормальный закон
распределения. Для оценки корреляционных свойств выходных сигналов используются
корреляционные функции и спектральные плотности.
Каждый случайный входной сигнал
преобразуется в сумму:
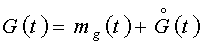 ,
,
где mg(t)
- детерминированная составляющая, или математическое ожидание входного сигнала;
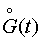 -
центрированная случайная составляющая входного сигнала (случайный процесс с
нулевым математическим ожиданием).
-
центрированная случайная составляющая входного сигнала (случайный процесс с
нулевым математическим ожиданием).
Модель преобразования
детерминированной составляющей строится на основе стандартного аппарата
передаточных функций:
L[my(t)] = Φ(p) L[mg(t)],
где L[mg(t)], L[my(t)]
- изображения по Лапласу детерминированных составляющих соответственно входного
и выходного сигналов; Φ(p)
- передаточная функция звена или системы.
Выходной сигнал в установившемся
процессе может быть определен по теореме о конечном значении:
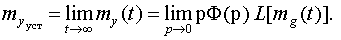
Например, при mg(t)=const для асимптотически устойчивой системы получим: my=Φ(0)
mg=const.
Модель преобразования
центрированной случайной составляющей строится для спектральных плотностей
Sy(ω)=|Φ(jω)|2Sg(ω),
где спектральная
плотность входного сигнала определяется по его корреляционной функции
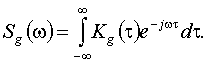
По полученной
спектральной плотности выходного сигнала находят его дисперсию:
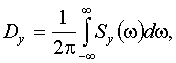
Этот интеграл обычно
удается привести к форме:
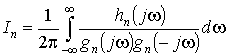 ,
,
где
hn(jω)=b1(jω)2n-2 +b2(jω)2n-4 + … +bn, gn(jω)=a0(jω)n +a1(jω)n-1 + … +an. (1)
Тогда:
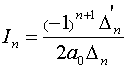 , (2)
, (2)
где ∆n - n-й определитель Гурвица для многочлена gn(p)
[3], а ∆'n получается из ∆nзаменой
1-й строки коэффициентами многочлена hn.
Например, при n=4
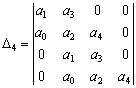 ,
, 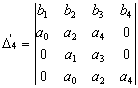 .
(3)
.
(3)
Для системы с
несколькими случайными входными сигналами, если они не коррелированы между
собой, математическое ожидание и дисперсия выходного сигнала определяются на
основе принципа суперпозиции:
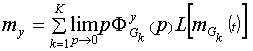 ,
,
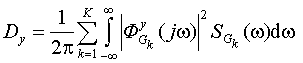 ,
,
где 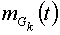 и
и
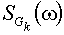 -
математическое ожидание и спектральная плотность k-го входного сигнала
(задающего или возмущающего воздействия);
-
математическое ожидание и спектральная плотность k-го входного сигнала
(задающего или возмущающего воздействия); 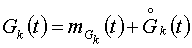 ;
; 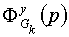 -
передаточная функция системы от k-го входа к выходу.
-
передаточная функция системы от k-го входа к выходу.
Таким образом, выходной
сигнал определяется в форме 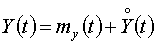 , причем центрированная
случайная составляющая описывается дисперсией Dy.
, причем центрированная
случайная составляющая описывается дисперсией Dy.
Аналогичный подход
используется при нахождении ошибки системы. Она определяется в форме: 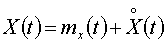 .
Пусть на систему действуют детерминированное задающее воздействие g(t)
и несколько некоррелированных случайных возмущений
.
Пусть на систему действуют детерминированное задающее воздействие g(t)
и несколько некоррелированных случайных возмущений 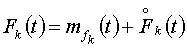 ,
k=1,2,…, K.
,
k=1,2,…, K.
Тогда математическое
ожидание ошибки определяется в виде суммы:
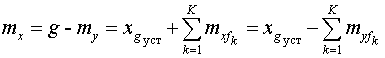 ,
,
где 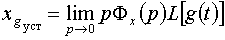 ,
,
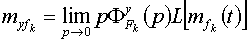 ,
Φx(p) - передаточная функция системы по ошибке от задающего воздействия,
,
Φx(p) - передаточная функция системы по ошибке от задающего воздействия,
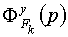 -
передаточная функция системы по k-му возмущающему воздействию, k=1,2,…,
K.
-
передаточная функция системы по k-му возмущающему воздействию, k=1,2,…,
K.
Дисперсия ошибки
совпадает с дисперсией выходного сигнала.
. Статистическая
линеаризация нелинейной части системы
Статистической линеаризацией
называется построение линейной модели нелинейного звена системы управления с
учетом характеристик преобразования случайного сигнала линейной частью системы
(рисунок 2).
Методы статистической
линеаризации основаны на допущении о наличии у линейной части системы свойства
фильтра. Благодаря этому, сигнал на входе нелинейного звена, то есть на выходе
линейной части (рисунок 2), рассматривается в форме 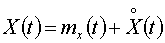 ,
причем для описания центрированной составляющей ограничиваются дисперсией Dx или среднеквадратическим
отклонением σx.
При нескольких входных сигналах для каждого используется аналогичное
представление, а для описания совокупности центрированных составляющих -
матрица моментов.
,
причем для описания центрированной составляющей ограничиваются дисперсией Dx или среднеквадратическим
отклонением σx.
При нескольких входных сигналах для каждого используется аналогичное
представление, а для описания совокупности центрированных составляющих -
матрица моментов.
Для однозначной нечетной
относительно входного сигнала нелинейности j(-x)=-j(x) коэффициент j0
выражают через математическое ожидание входного сигнала: j0
= k0mx.
Коэффициент j0
называется средней статистической характеристикой нелинейности;
коэффициент k0 - статистическим коэффициентом усиления по
математическому ожиданию; коэффициенты k1 -
статистическим коэффициентам усиления по случайным составляющим входных
сигналов.
Значения коэффициентов
статистической линеаризации определяют на основе критериев вероятностной
эквивалентности. Обычно используют два критерия.
Первый критерий состоит
в равенстве математических ожиданий и дисперсий сигналов на выходе
статистически линеаризованного и исходного нелинейного звеньев. Для однозначной
исходной нелинейности имеем:
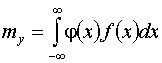 ,
,
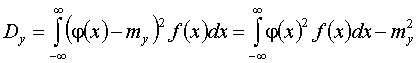 ,
,
где f(x) -
ПРВ сигнала X на входе нелинейного звена.
Математическое ожидание
выходного сигнала линеаризованного звена M[Y] равно j0
(или k0mx
для нечетной нелинейности), а его дисперсия D[Y] связана с дисперсией и среднеквадратическим отклонением входного
сигнала в соответствии с (4.15):
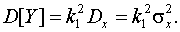
В результате получим:
 или
или 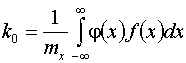 ,
(4)
,
(4)
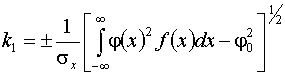 . (5)
. (5)
Знак в формуле
соответствует знаку производной 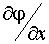 в точке,
соответствующей mx.
в точке,
соответствующей mx.
Второй критерий состоит в
минимизации среднего квадрата ошибки аппроксимации выходного сигнала
нелинейного звена выходным сигналом линеаризованного звена:
 .
.
Раскроем скобки в
выражении для h2 и применим к нему первое необходимое условие экстремума по j0
и k1:
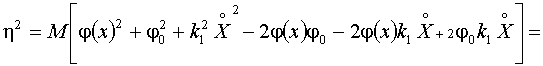
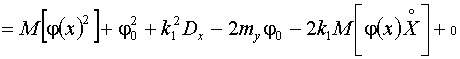 ,
,
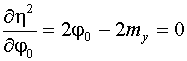 ,
,
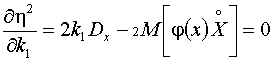 .
.
Решение полученных
уравнений дает выражения для определения j0
и k1,
доставляющих минимум h2:
 ,
,
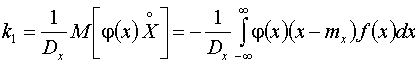 . (6)
. (6)
Обычно рекомендуют вычислять k1 как среднее арифметическое:
 ,
,
где 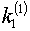 -
значение, получаемое на основе первого критерия по (4.20);
-
значение, получаемое на основе первого критерия по (4.20); 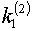 -
значение, получаемое на основе второго критерия по (4.21).
-
значение, получаемое на основе второго критерия по (4.21).
Все полученные расчетные
соотношения для определения коэффициентов статистической линеаризации
предусматривают использование ПРВ сигналов на входе линеаризуемого звена. В
силу допущения о наличии у линейной части системы свойства фильтра, обычно
используется ПРВ нормального закона распределения.
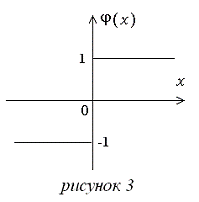
В курсовой работе задано
нелинейное звено с однозначной статической характеристикой типа
двухпозиционного реле (рисунок 3).
Его линеаризация
выполняется в форме 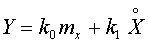 .
Для определения k0 применим формулу (4):
.
Для определения k0 применим формулу (4):


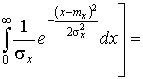
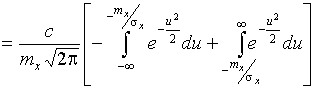 ,
,
где 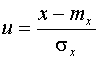 -
стандартизованная нормальная величина. И далее:
-
стандартизованная нормальная величина. И далее:
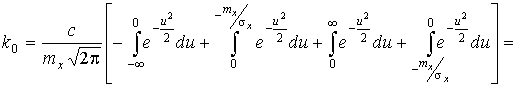
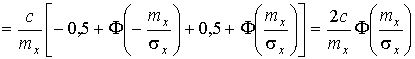 ,
,
где Ф(u) - интеграл вероятностей, рассмотренный в разд. 3.
Аналогично на основе
(5), (6) можно получить:
 ,
,
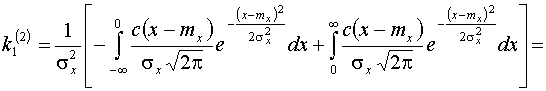
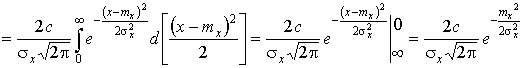 .
.
. Расчет математического
ожидания и среднеквадратического отклонения сигнала ошибки
Замена нелинейного звена
линеаризованной моделью позволяет использовать принцип суперпозиции - провести
раздельный анализ преобразования системой детерминированных и случайных
составляющих входных сигналов. Особенность применения принципа суперпозиции на
основе статистической линеаризации состоит в том, что для случайных
составляющих нелинейное звено заменяется безынерционным звеном с коэффициентом
k1, а для детерминированных - безынерционным звеном с коэффициентом k0 (при нечетной нелинейности) или постоянным сигналом 0.
Определяемые по полученным выше
формулам коэффициенты статистической линеаризации оказываются функциями
моментов распределения сигналов на входе нелинейности, которые, в свою очередь,
вычисляются через передаточные функции системы, включающей в себя
линеаризованное звено, то есть зависят от коэффициентов статистической
линеаризации. Вследствие этого расчет стационарного процесса в статистически
линеаризованной системе сводится к решению системы нелинейных алгебраических
уравнений, требующему применения численных методов.
Для заданной системы (рисунок 1)
передаточная функция линейной части:
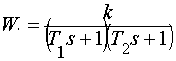 .
.
Задающее воздействие
изменяется по закону g(t)=g1
(t). На входе действует случайная помеха F(t) с нулевым математическим ожиданием и спектральной плотностью 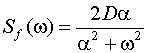 .
Требуется определить математическое ожидание и среднеквадратическое отклонение
сигнала ошибки в установившемся процессе.
.
Требуется определить математическое ожидание и среднеквадратическое отклонение
сигнала ошибки в установившемся процессе.
Выделим
детерминированную и случайную составляющие сигнала ошибки: 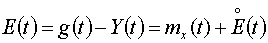 .
С учетом характера входных сигналов и в соответствии с принципом суперпозиции
составляющие сигнала ошибки в линеаризованной системе будут определяться
следующим образом:
.
С учетом характера входных сигналов и в соответствии с принципом суперпозиции
составляющие сигнала ошибки в линеаризованной системе будут определяться
следующим образом:
mx(t)= xgуст,
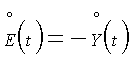 .
.
Для расчета
детерминированной составляющей сигнала ошибки после линеаризации используется
структурная схема (рис. 4, а), а для расчета центрированной случайной
составляющей - структурная схема (рис. 4, б), где
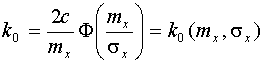 ,
,

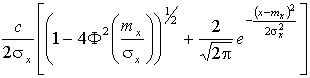 =k1(mx,σx).
=k1(mx,σx).
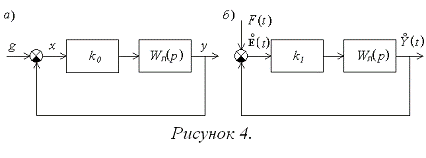
Для полученных структурных схем
искомые характеристики сигнала ошибки определяются следующим образом: mE=mx, DE=DY.
При расчете детерминированной
составляющей передаточная функция замкнутой системы по ошибке имеет вид:
 .
.
В результате: 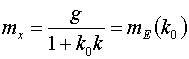 .
.
Среднеквадратическое отклонение
сигнала ошибки в рассматриваемой задаче полностью определяется возмущающим
воздействием и находится через дисперсию выходного сигнала и передаточную
функцию замкнутой системы по возмущению, которая в рассматриваемом примере
примет вид:
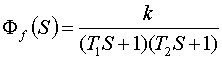 .
.
В результате:  ,
,
Коэффициенты полиномов
(1) примут вид:
a0=T1T2,
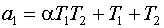 ,
,
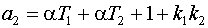 ,
,
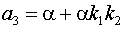 , b0=0, b1=0,
, b0=0, b1=0,
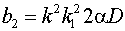 .
.
Определители (3) будут иметь третий
порядок и получаются следующими:
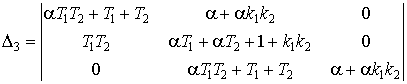 =
=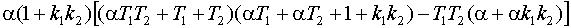
 .
.
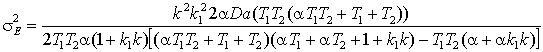
При заданных k, T и c
для расчета характеристик ошибки необходимо решить систему нелинейных
алгебраических уравнений:
mE= ,
,
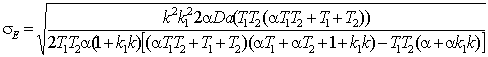 ,
,
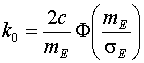 ,
,
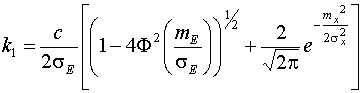 .
.
4. Решение уравнений и
построение зависимостей
С помощью программы,
написанной на языке MATLAB, решив систему методом последовательных
приближений, мы найдем зависимости коэффициентов статистической линеаризации,
математического ожидания и среднеквадратического отклонения ошибки системы E(t) от величины коэффициента передачи k. Для нахождения
зависимости M от k использована функция MATLAB fzero. Текст программы
представлен в приложении А. Графики зависимостей представлены на рисунках 5-9.

Рисунок
5

Рисунок 6
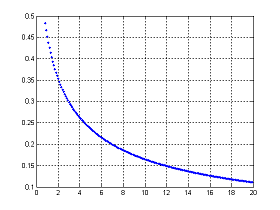
Рисунок 7
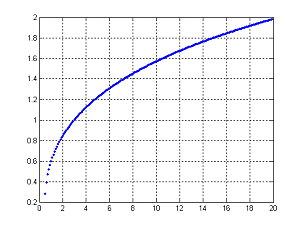
Рисунок 8

Рисунок 9
Заключение
Оптимальным
коэффициентом передачи линейного звена является такое значение, которому
соответствует наименьшее значение параметра M.
С настоящими исходными данными минимума для функции М нет, так как зависимость
монотонно возрастающая.
Список использованных
источников
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического
управления. - СПб: Профессия, 2003.
2. Емельянов В.Ю. Методы моделирования стохастических систем
управления: учеб. пособие для ВУЗов. - СПб: БГТУ, 2004.
3. Андриевский Б.Р., Емельянов В.Ю., Коротков Б.Ф. Теория
управления: Лабораторный практикум в среде MATLAB/SIMULINK. - СПб: БГТУ, 2001.